在大数据时代，随着包括社交网络在内的交互式应用程序的持续发展^[1]，越来越多的数据被构建为图流数据模型. 图流数据模型在网络安全与监控^[2]、用户行为分析^[3]、追踪疫情防控中的密切接触者^[4]等新兴大数据应用领域应用广泛. 为了更好地为大数据应用提供服务，图流测量领域涌现出众多查询任务. 频繁边查询能够检测权重超出阈值的边，为网络拥塞提供服务^[5-6]. 频繁点查询能够识别权重超出阈值的节点，对识别网络中的分布式拒绝服务攻击尤为重要^[7].

学者设计特定的数据结构来存储图流，以实现高效的图流分析. 大数据应用产生的图流规模巨大，导致存储完整图流信息的内存开销增加，因此基于近似存储的图流概要技术备受关注. 典型的图流概要技术如TCM^[8]、gMatrix^[9]和DMatrix^[10]使用多个独立的邻接矩阵来近似地储存图流. 该项技术未有效缓解边间冲突，图流测量的准确性有待提高. 为了进一步提高测量精度，GSS^[11]和Cuckoo Matrix^[12] 通过在邻接矩阵中储存边的指纹对和权重的方式实现了精确的图流查询. GSS和Cuckoo Matrix须记录所有边的指纹，因此内存消耗高. 图流测量除了要准确地完成基于权重的查询任务外，还要完成实时的周期边查询. 周期边查询旨在发现以固定时间间隔到达的边. 在网络流量图中，检测周期性到达的边可以预防和检测破坏性强、危害极大的高持续威胁（advanced persistent threats, APT）攻击^[13-14]，维护网络的安全稳定. 在金融交易图流中存在短时间的大量金钱交易流，通过实时检测超过特定阈值的周期性交易流，能够快速发现可疑客户^[15-16]. 此外，通过检测周期性的交易流还能了解用户购买行为的规律^[17]. 现有的图流概要技术仅在邻接矩阵储存图流的权重信息，未储存图流的时间信息，检测周期边须借助边上一次到达的时间信息来确定图流的边是否具有周期性. 现有的图流概要技术无法测量图流中的周期边. PeriodicSketch^[15]虽然能发现数据流的周期项，但是受到结构限制，图的底层结构未保留，无法执行其他图流查询.

由以上分析可知，现有的图流概要技术既不能在有限的内存中实现高精度和高速度图流测量，也不能储存时间信息来完成周期边测量. 本研究提出面向周期边测量的图流概要技术——周期交互矩阵（periodic interaction matrix, PIM）. PIM由二维邻接矩阵和三维邻接矩阵组成. 二维邻接矩阵存储重边的标识、时间戳和权重，三维邻接矩阵存储轻边的权重，使PIM能够在有限内存下实时完成包括周期边查询在内的多种查询任务. 本研究提出基于权重和基于时间的替换策略，使用共享哈希技术来提高图流查询精度和插入查询速度.

现有的图流概要技术可分为2类：基于三维邻接矩阵的图流概要技术和基于二维邻接矩阵的图流概要技术. 基于三维邻接矩阵的图流概要技术的本质是使用由k个邻接矩阵组成的三维结构来存储图流. 每个矩阵大小相同，使用独立的哈希函数来压缩图流. TCM将图流中的边通过哈希函数平等的映射到每个矩阵对应的储存单元（桶）中以统计边的权重. gMatrix使用可逆哈希函数近似存储图流，通过使结构具备可逆性来实现图流的实时测量. 为了提高频繁边查询的准确性，Hou等^[10]将多数投票算法与TCM结合，提出DMatrix，利用多数投票算法选出重边，再将边的键存入桶中以准确记录重边的权重. 由于桶内其他的边会被聚合，导致DMatrix的整体精度低. 基于三维邻接矩阵的图流概要技术算法简单，具有较高的插入和查询速度，但是该项技术测量的准确性有待提升.

为了进一步提升测量的准确性，学者开始研究基于二维邻接矩阵的图流概要技术. GSS在矩阵的每个桶中记录边的指纹对和权重，使用方形散列技术和额外的缓冲区提高测量精度. Chen等^[18]基于GSS提出Scube，使用图流节点度估计模型和动态地址分配方法进行倾斜图流的高效测量. 为了进一步提高GSS的插入和查询速度，Li等^[12]提出Cuckoo Matrix. 该方法为每条边分配原始桶和候选桶，并在桶内设计多个单元来记录边的指纹对和权重，以快速准确地完成图流概要. 基于二维邻接矩阵的图流概要技术通过在邻接矩阵中储存边的指纹对和权重来实现精确的图流概要，但是该项技术不仅算法复杂，而且会储存所有边的指纹，导致时空开销很大，无法在小内存场景中取得准确的测量结果.

此外，上述图流概要技术均无法完成周期边测量. 因此，当前的图流概要技术无法在小内存下快速准确地完成图流查询，且不支持周期边测量.

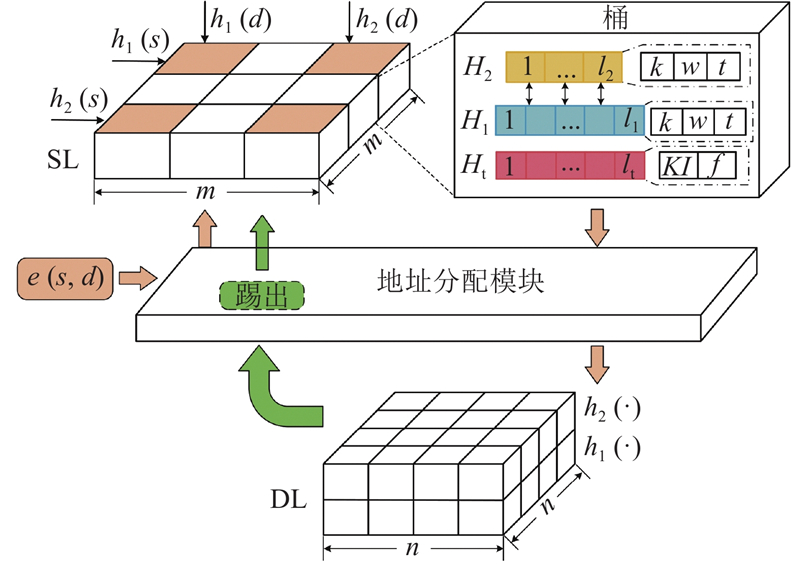
高效完成多种查询任务的关键在于快速分离并使用不同的策略来储存轻重边. 如图1所示为PIM的数据结构，它由二维邻接矩阵SL、三维邻接矩阵DL和地址分配模块3个部分组成. SL用来储存重边，DL用来储存轻边，地址分配模块用来为边和节点生成SL和DL中的索引. SL为包含$ m \times m $个桶的邻接矩阵，每个桶由H_t、H₁和H₂共3个数组构成. H_t记录周期边；H₁记录重边；H₂是H₁的补充，记录H₁中溢出的超重边. H_t包含l_t个单元，每个单元包含2个字段：1) KI字段. 在该字段中，K记录周期边的标识，I记录周期边的时间间隔，以提高周期边的准确性. 2) f字段. 该字段用于记录周期边出现的频率. 为了缓解边聚合引起的冲突，H₁和H₂设计为分别包含l₁和l₂个单元的数组. 每个单元包含3个字段： 1) k字段. 该字段记录边的标识，以提高重边的准确性. 2) w字段. 该字段记录边的权重. H₁和H₂中w字段的内存大小分别为v₁和v₂ ，v₁ < v₂. 3) t字段. 该字段记录边最后一次到达的时间，使结构保留图流的时间信息. DL由2个完全相同的邻接矩阵组成，每个邻接矩阵包含$ n \times n $个计数器，用于记录轻边权重.

为了提高边和节点的索引速度，PIM在地址分配模块使用共享哈希函数技术，SL和DL共用2个哈希函数h₁和h₂. 在SL中，到达的边(s,d)通过地址分配模块被h₁和h₂映射到4个桶中，以寻找位置储存，缓解了多条边聚合产生的冲突. 在DL中，地址分配模块使用h₁和h₂来分别得到(s,d)在2个邻接矩阵的索引位置. 共享哈希函数技术能快速得到边和点在PIM中的储存位置以提高插入和查询速度. 本研究提出能快速分离轻重边的投票替换策略以提高测量精度.

为了完成周期边测量，本研究提出时间投票替换算法. 周期边常由时间间隔$ < {e_i},I > $和频率$ f $判断，符号为$ ( < {e_i},I > ;f) $.e_i和I分别为边的标识和时间间隔，f为边e_i以I为间隔出现的次数. 时间投票替换算法的具体操作如算法1所示，其中输入为边$ e = (s,d;w;t) $、时间间隔$ \Delta t $和访问桶B. 该算法遍历桶中H_t的每个单元，若$ {{{H}}_{\text{t}}}[k].KI $为空或与(s,d;$ \Delta t $)匹配，则在$ {{{H}}_{\text{t}}}[k] $中插入边e. 若遍历结束，没有找到空或匹配的单元，则执行投票替换算法如10~15行所示.

算法1　　时间投票替换算法

输入: 边$ e $、时间间隔$ \Delta t $和访问桶B

1: Procedure Insert_Time (e, $ \Delta t $, B)

2: 　for k = 0 to $ {l_{\mathrm{t}}} - 1 $ //遍历H_t的单元

3:　　 if $ B.{{{H}}_{\text{t}}}[k].KI $== (s,d;$ \Delta t $) then

4:　　　 $ B.{{{H}}_{\text{t}}}[k].f \leftarrow B.{{{H}}_{\text{t}}}[k].f+1 $, Break

6: 　　else if $ B.{{{H}}_{\text{t}}}[k].KI $== 0

7: 　　　$ B.{{{H}}_{\text{t}}}[k].KI \leftarrow (s,d;\Delta t) $

8:　　　 $ B.{{{H}}_{\text{t}}}[k].f \leftarrow 1 $, Break

10:　　 else if k == $ {l_{\mathrm{t}}} - 1 $ then

11:　　　 if $ {{{H}}_{\text{t}}}[{k_{\min }}].f < {{{H}}_{\text{t}}}[k].f $then

12:　　　　 $ B.{{{H}}_{\text{t}}}[{k_{\min }}] \leftrightarrow B.{{\text{H}}_{\text{t}}}[k] $

13:　　　 $ B.{{{H}}_{\text{t}}}[k].f \leftarrow B.{{{H}}_{\text{t}}}[k].f - 1 $

14:　　　 if $ B.{{{H}}_{\text{t}}}[k].f $== 0 then

15: 　　　　在$ B.{{{H}}_{\text{t}}}[k] $中记录$ (s,d;\Delta t) $和1

PIM的插入过程如算法2所示. 对于到达的边e，通过地址分配模块得到SL中需要访问的4个桶$ M_{{\text{SL}}}^{{B_1}}、M_{{\text{SL}}}^{{B_2}}、M_{{\text{SL}}}^{{B_3}}、M_{{\text{SL}}}^{{B_4}} $. e先访问$ M_{{\text{SL}}}^{{B_1}} $，并遍历其中H₂的每个单元. 此时，插入过程被划分为以下4种情况. 1)若$ {{{H}}_2}[j] $为空，则在此单元中记录(s,d)、w和t. 若$ {{{H}}_2}[j] $与(s,d)匹配，则$ {{{H}}_2}[j].w $加w. 将t和$ {{{H}}_2}[j].t $作差，计算e的时间间隔$ \Delta t $，并将t记录在$ {{{H}}_2}[j].t $中. 采用时间投票替换算法，完成周期边的存储. 2)若在H₂中没有插入成功，则遍历H₁的每个单元. 与情况1）的操作相同，寻找空或匹配的单元，并在该单元中记录边的信息. 若找到匹配的单元，则完成情况1）的操作. 若此时$ {{{H}}_1}[j].w $加w后溢出，则触发溢出交换策略如17~18行所示. 3)若在$ M_{{\text{SL}}}^{{B_1}} $插入失败，则依次访问剩余3个桶中H₂和H₁的每个单元，插入过程与情况1）、2）相同. 若在SL中插入失败，则通过地址分配模块得到e在DL中需要访问的计数器$ {M_{{\text{L1}}}}、 {M_{{\text{L}}2}} $，将它们分别增加w. 若$ {M_{{\text{L1}}}}、{M_{{\text{L}}2}} $都发生溢出，则触发溢出替换策略如第9行所示. 4)若$ {M_{{\text{L1}}}}、{M_{{\text{L}}2}} $的最小值大于$ {{{H}}_1}[{I_{\min 1}}].w $，则触发投票替换策略如第11行所示.

算法2　　插入算法

输入: 边$ e = (s,d;w;t) $

1: Procedure Insert(e)

2:　 $ M_{{\text{SL}}}^{{B_1}},M_{{\text{SL}}}^{{B_2}},M_{{\text{SL}}}^{{B_3}},M_{{\text{SL}}}^{{B_4}} \leftarrow {h_1}(e),{h_2}(e) $

3:　 for i =1 to 4

4:　　 InsertBucket($ M_{{\text{SL}}}^{{B_i}} $) //依次在四个桶中插入

5:　 if 在SL中插入失败then //开始在DL中插入

6:　　 $ {M_{{\text{L1}}}} \leftarrow {h_1}(e),{M_{{\text{L2}}}} \leftarrow {h_2}(e) $

7:　　 $ {M_{{\text{L1}}}} \leftarrow {M_{{\text{L1}}}}+w,{M_{{\text{L2}}}} \leftarrow {M_{{\text{L2}}}}+w $

8:　　 if $ {M_{{\text{L1}}}},{M_{{\text{L}}2}} $都溢出then //执行溢出替换策略

9: 　　　Kick_out(e,$ \min ({M_{{\text{L1}}}},{M_{{\text{L}}2}}) $,$ M_{{\text{SL}}}^{{B_{\min }}}.{{{H}}_1}[{I_{\min 1}}] $)

10: 　 else if $ \min ({M_{{\text{L1}}}},{M_{{\text{L}}2}}) > {{{H}}_1}[{I_{\min 1}}].w $ then

11:　　　 Kick_out(e,$ \min ({M_{{\text{L1}}}},{M_{{\text{L}}2}}) $,$ M_{{\text{SL}}}^{{B_{\min }}}.{{{H}}_1}[{I_{\min 1}}] $)

12: function InsertBucket(B) //用于在DL桶中插入

13:　 for j=0 to $ {l_2} - 1 $ //遍历H₂的每个单元进行插入

14:　　 InsertCell(e,$ B.{{{H}}_2}[j] $)

15:　 for j=0 to $ {l_1} - 1 $ //遍历H₁的每个单元进行插入

16: 　　InsertCell(e,$ B.{{{H}}_1}[j] $)

17: 　　if $ B.{{{H}}_1}[j] $发生溢出then

18:　　　 $ {{{H}}_1}[j] \leftrightarrow {{{H}}_2}[{I_{\min 2}}] $, 结束插入

20: 　if $ {{{H}}_1}[{I_{\min 1}}].w > {{{H}}_2}[{I_{\min 2}}].w $then //B中插入失败

21:　　 $ {{{H}}_1}[{I_{\min 1}}] \leftrightarrow {{{H}}_2}[{I_{\min 2}}] $

22: function InsertCell (e, B.cell)

23:　　 if $ {\text{cell}}.k $==(s,d) then

24: 　　　计算$ \Delta t $, 并在cell中更新w和t

25: 　　　InsertTime(e, $ \Delta t $, B), 结束插入

26:　　 else if cell.k==0 then

27: 　　　在cell中插入，结束

28: function KickOut (e,$ {M_{{\text{DL}}{m} }} $,cell) //替换策略

29:　 $ {M_{{\text{L}}k1}} \leftarrow {h_1}({\text{cell}}.k),{M_{{\text{L}}k2}} \leftarrow {h_2}({\text{cell}}.k) $

30: 　$ {M_{{\text{L}}k1}} \leftarrow {M_{{\text{L}}k1}}+{\text{cell}}.w,{M_{{\text{L}}k2}} \leftarrow {M_{{\text{L}}k2}}+{\text{cell}}.w $

31: 　在cell中记录$ (s,d)、t $和权重$ {M_{{\text{DL}}{m} }}+w $

节点权重查询分为节点流出权重查询$ {w_n}(s, \to ) $和节点流入权重查询$ {w_n}( \to ,d) $. 节点权重查询返回节点s的流出（流入）聚合权重. 以节点流出权重为例介绍节点权重查询算法，节点流入权重查询与此类似. 给定节点s，查询节点权重的过程如算法3所示. 访问SL中第$ {x_{{\mathrm{m}}1}} $行和第$ {x_{{\mathrm{m}}2}} $行的所有单元，查询k是否和s匹配. 若匹配，则将该单元的w与$ {\tilde w_n}(s) $相加. 访问DL中L₁第$ {x_{{\mathrm{n}}1}} $行和L₂第$ {x_{{\mathrm{n}}2}} $行的所有计数器，将计数器的值相加得到$ {w_{{\text{L}}1}} $和$ {w_{{\text{L2}}}} $. 将$ {w_{{\text{L}}1}} $和$ {w_{{\text{L2}}}} $的最小值与$ {\tilde w_n}(s) $相加，得到s的节点权重.

算法3　　节点权重查询算法

输入: 节点s

输出: 节点s的估计权重$ {\tilde w_n}(s) $

1: Procedure NodeQuery (s)

2:　 $ {x_{{\mathrm{m}}1}} \leftarrow {h_1}(s)\% m,{x_{{\mathrm{m}}2}} \leftarrow {h_2}(s)\% m $

3: 　访问$ {M_{{\text{SL}}}}[{x_{{\mathrm{m}}1}}] $和$ {M_{{\text{SL}}}}[{x_{{\mathrm{m}}2}}] $中H₁和H₂的单元

4: 　if 单元中k与$ (s, \cdot ) $匹配 then

5:　　 $ {\tilde w_n}(s) \leftarrow w+{\tilde w_n}(s) $ //w为该单元的w

6:　 $ {x_{{\mathrm{n}}1}} \leftarrow {h_1}(s)\% n,{x_{{\mathrm{n}}2}} \leftarrow {h_2}(s)\% n $

7:　 for i=0 to n−1

8:　　 $ {w_{{\text{L1}}}} \leftarrow {M_{{\text{L1}}}}[{x_{{\mathrm{n}}1}}][i]+{w_{{\text{L1}}}} $

9: 　　$ {w_{{\text{L2}}}} \leftarrow {M_{{\text{L2}}}}[{x_{{\mathrm{n}}2}}][i]+{w_{{\text{L2}}}} $

10:　 $ {\tilde w_n}(s) \leftarrow \min ({w_{{\text{L1}}}},{w_{{\text{L2}}}})+{\tilde w_n}(s) $

11:　 return $ {\tilde w_n}(s) $

频繁边查询的任务是找出所有权重大于$ {\alpha _{\text{e}}} $的边，频繁点查询的任务是找出所有流出（流入）总权重大于$ {\alpha _{\text{n}}} $的节点，周期边查询的任务是找出所有频率大于$ {\alpha _{\text{P}}} $的周期边，其中$ {\alpha _{\text{e}}} $、$ {\alpha _{\text{n}}} $和$ {\alpha _{\text{P}}} $为给定的阈值. 以频繁边查询为例，PIM遍历SL中H₁和H₂的每个单元. 若单元中w大于频繁边阈值，则将该单元记录的边加入频繁边集合. 遍历SL的所有单元，返回频繁边集合. 与频繁边查询类似，在进行频繁点和周期边查询时，PIM只需在SL中查询，返回超过相应阈值的频繁点和周期边，即为以上任务的查询结果.

假设DL的参数n =$ \sqrt {{{\mathrm{e}}}/{\varepsilon }} $，其中$ \varepsilon \in (0,1) $为近似参数，e为自然常数.

引理　设向量V = [v₁, v₂, ···, v_n]为图流的节点向量，$ w({v_i}) $和$ \tilde w({v_i}) $分别为第i个节点的真实权重和估计权重. 对于$ \tilde w({v_i}) $，至少有$ 1 - \delta $的概率保证误差边界为

式中：$ \varUpsilon $为DL中的节点权重总和，$ \delta $=$ {{\mathrm{e}}^{ - 2}} $.

证明　由于哈希冲突，容易得到$ \tilde w({v_i}) \geqslant w({v_i}) $. 接下来证明$ \tilde w({v_i}) $的误差上界. 对于节点v_i ($ {v_i} \ne u $)，与节点u冲突的期望为1/n. 因此，节点v_i估计误差的期望为

由马尔科夫不等式得到

实验平台为具有24核 3.50 GHz i9-10920X处理器和64GB DDR4 DRAM 的服务器，操作系统为Ubuntu18.04.6，所有方案均使用C++实现.

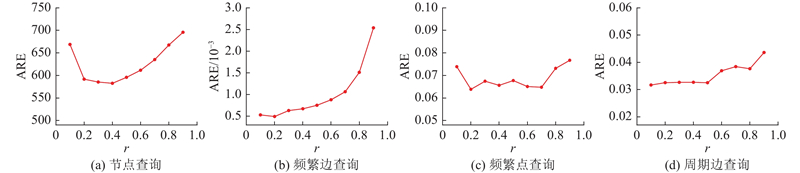
在相同内存下，使用2个真实应用中的数据集对PIM、PTCM、PDMatrix、PCuckoo Matrix （简称PCuckoo）以及PeriodicSketch （简称Periodic）的准确性和速度进行评估. PTCM、PDMatrix和PCuckoo是将布隆过滤器^[19]和图流概要技术结合后的改进方案，可以同时完成包括周期边查询在内的多种查询任务，Periodic仅用于周期边查询实验. 在实验中，DL与总内存之比为r，r的设置由节点查询、频繁边查询、频繁点查询以及周期边查询的平均相对误差来综合考量. 如图2所示，随着r由0.1增大到0.9，节点查询的平均相对误差先下降后上升，且在0.2到0.4的误差较低. 频繁边查询和频繁点查询在0.2时平均相对误差最低，周期边查询在0.1到0.5的平均相对误差较低. 为了准确完成上述4个查询，设置r=0.2. 为了方便实现PIM，计数器的大小设置为2的整数次幂. 根据实验测试，在SL的H₁和H₂中，每个单元k和t的内存大小设置为8字节，可存储边的标识和时间戳，w的v₁和v₂设置为2字节和4字节，可最佳区分重边和超重边. H_t中KI和f的内存大小分别设置为12字节和4字节. 在SL中每个桶的l₁、l₂和l_t分别被设置为25、5和100，可取得最佳的准确性. 在DL中，每个计数器的内存大小设置为1字节，可最佳区分轻重边. 根据数据集中前100条频繁边、频繁点以及周期边得到查询的阈值. 对比方案的其他参数设置与原文献中的保持一致.

采用3个真实的数据集进行测试：Network-Flow^[20]、Wiki^[21]和Lkml^[22]. Network-Flow是2015年真实网络环境中骨干路由器对传输报文的匿名流量跟踪，共包含2 601 005个节点和445 440 480条边，时间戳单位为μs. Wiki是英语维基百科的交互网络，共包含2 987 535个节点和24 981 163条边，时间戳单位是s. Lkml为Linux内核开发者的邮件通信网络，共包含63 399个节点和1 096 440条边，时间戳单位是s.

1) 平均相对误差ARE：测量任务中所有查询误差的平均值为平均相对误差. 查询误差为真实值与测量值之差的绝对值与真实值的比值. 2) 调和平均数F1=2×精确率×召回率/（精准度+召回率）. 以频繁边为例，精确率为方案找到的频繁边中真实频繁边的占比，召回率为所有频繁边中被找到的频繁边的占比. 3) 平均查询时间：测量任务中所有查询消耗时间的平均值.

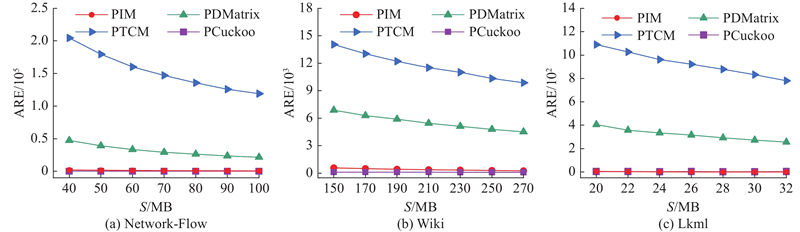
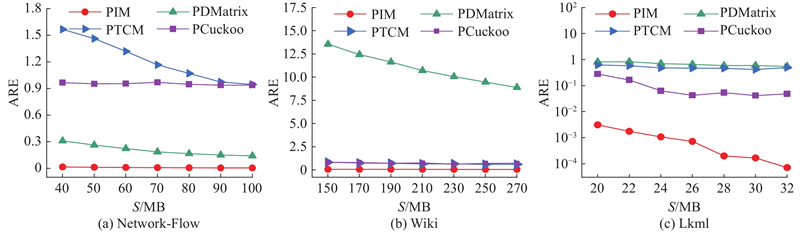
如图3所示为不同规模数据集的节点权重查询平均相对误差. 在Network-Flow中，当内存S=40 MB时，PIM的平均相对误差与PDMatrix和PTCM相比分别降低了1个数量级和2个数量级. 在Wiki中，当S=150 MB时，PIM的平均相对误差与PDMatrix和PTCM相比分别降低了91.41%和95.79%. 在Lkml中，当S=32 MB时，PIM的平均相对误差与PDMatrix、PTCM和PCuckoo相比分别降低了99.95%、99.98%和95.87%. 原因是PIM在DL中使用2个邻接矩阵存储节点权重，提高了测量的准确性. 此外，PIM使用不同大小的计数器存储不同权重的节点，提高了内存利用率. 因此，PIM的整体测量精度更高. 由于PCuckoo储存所有节点的指纹，其节点权重查询的误差很小. 在有限内存下，PCuckoo会丢失一部分节点信息，导致无法准确地完成频繁边查询等其他测量任务.

如图4所示为不同规模数据的频繁边查询平均相对误差. 在Network-Flow和Lkml中，PIM的平均相对误差达到零，极大地减少了PDMatrix、PTCM和PCuckoo的平均相对误差. 此外，PCuckoo在Network-Flow中无法找到频繁边. 在Wiki中，当S=150 MB时，PIM的平均相对误差与PCuckoo、PDMatrix以及PTCM相比分别降低了2个数量级、3个数量级和4个数量级. 原因是PIM通过投票替换策略快速分离轻重边，减少了轻边对重边的影响. 此外，PIM在SL中记录了重边的标识，并在每个桶中设置了多个包含16比特和32比特计数器的单元，以存储重边和超重边. 因此，PIM能实时准确地完成频繁边查询.

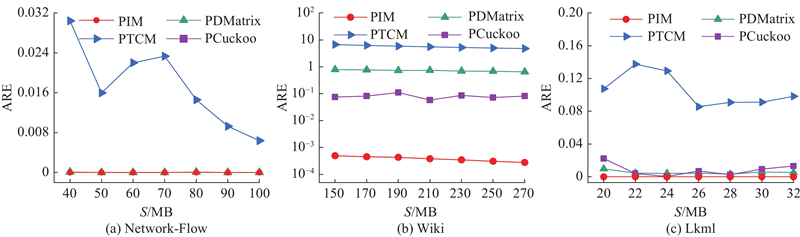
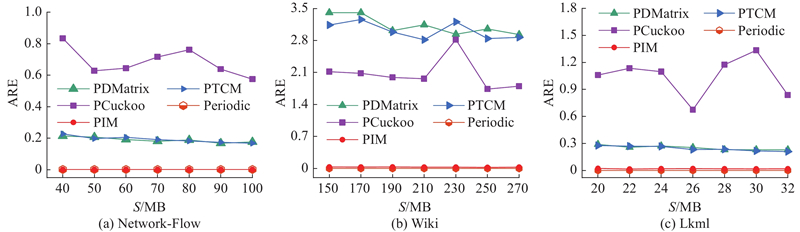
如图5所示为不同规模数据的频繁点查询平均相对误差. 实验结果显示，PIM在所有实验内存，尤其是小内存下，明显优于对比方案. 在Network-Flow中，当S=40 MB时，PIM的平均相对误差与PDMatrix相比降低了1个数量级，与PTCM和PCuckoo相比降低了2个数量级. 在Wiki中，当S=150 MB时，PIM的平均相对误差与PDMatrix、PTCM和PCuckoo相比分别降低了99.54%、92.40%和92.39%. 在Lkml中，当S=20 MB时，PIM的平均相对误差与PDMatrix、PTCM和PCuckoo相比分别降低了99.99%、99.99%和99.97%. 原因是PIM在DL中为每个节点分配了2个哈希函数，并使用2个邻接矩阵来存储节点信息，以适应不同节点度的图流. 此外，PIM在SL中为每个节点分配2个索引，并在每个桶中设置多个单元来储存同一源节点的不同边，使PIM能实时准确地完成频繁点查询.

如图6所示为不同规模数据的周期边查询平均相对误差. 在Network-Flow中，PIM和Periodic的平均相对误差均小于0.5%，能实现准确的周期边测量. PIM与PDMatrix、PTCM以及PCuckoo相比，平均相对误差减少了2个数量级. 在Wiki中，当S=150 MB时，PIM的平均相对误差与PDMatrix、PTCM以及PCuckoo Matrix相比降低了2个数量级. 在Lkml中，当S=20 MB时，PIM的平均相对误差与PDMatrix、PTCM以及PCuckoo相比降低了93.51%、93.23%和98.23%. 原因是PIM在SL中记录边的时间戳和标识，同时采用时间投票替换算法选出多次出现的周期边，以实现准确的周期边查询.

如图7所示为不同规模数据集的频繁边、频繁点和周期边调和平均数. 在Network-Flow中，对于频繁边查询，PIM的调和平均数为1，与PDMatrix性能相同，优于PTCM. 此外，PCuckoo的调和平均数为0，无法完成频繁边查询. 对于频繁点和周期边查询，PIM的调和平均数非常接近1，优于PDMatrix、PTCM和PCuckoo Matrix，且与先进的周期测量方案Periodic性能相近. 在Wiki中，PIM3个任务的调和平均数接近1，明显优于PDMatrix、PTCM和PCuckoo. 在Lkml中，对于频繁边和频繁点查询，PIM的调和平均数为1，高于PDMatrix、PTCM和PCuckoo. 对于周期边查询，PIM的调和平均数与Periodic相近，优于其他对比方案. 这说明PIM可以准确地找到图流中的频繁边、频繁点和周期边，基本没有出现假阳性错误. 原因是PIM将轻重边分开储存，并在SL中记录了边的时间戳和标识. 此外，PIM使用基于权重和基于时间的投票替换策略快速分离轻重边，能够实时准确地完成图流查询.

如表1所示为在Network-Flow中不同图流概要技术的平均插入时间和平均查询时间. PIM的平均插入时间与PDMatrix相比降低了35.47%，与PTCM相比降低了24.88%，与PCuckoo相比降低了97.33%. 原因是PIM的SL和DL共享2个哈希函数，减少了哈希次数. PIM的平均插入时间明显高于Periodic，原因是PIM须完成多项测量任务，操作复杂，而Periodic只进行周期边测量，操作相对简单. 对于节点权重查询，PIM的平均查询时间成本与PDMatrix相比降低了49.9%. 由于PIM须访问SL和DL中的多个单元，平均节点权重查询时间高于PTCM和PCuckoo. 对于频繁点查询，PIM的平均查询时间与PTCM和PCuckoo相比分别降低了72.23%和53.98%，略高于PDMatrix. 对于频繁边和周期边查询，PIM的平均查询时间与PDMatrix、PTCM和PCuckoo相比降低了68.91%~99.91%，且与Periodic的周期边查询时间相近. 原因是PIM只需查询SL即可得到频繁边和周期边的查询结果.

本研究提出面向周期边测量的图流概要技术——PIM. PIM使用2种结构的邻接矩阵分别存储轻、重边，提高了查询精度和内存利用率，在存储重边的邻接矩阵中记录边标识、权重以及时间戳，能够实时完成频繁边、频繁点、周期边查询等多种查询任务. 本研究设计适配PIM结构的插入和查询算法，采用替换策略和共享哈希技术，提高了整体准确性和插入查询性能. 实验结果表明，与其他方案相比，PIM能在小内存下实时高效地完成图流测量，提高了多个查询任务的准确性. 在未来研究中，计划将PIM应用于更大规模且更复杂的图流场景，以进行更深入的图流概要研究.