[36]
LI Changjun, TIAN Miaoyuan, LI Qiwei, et al Action mechanism of acupuncture intervention on hippocampus of Alzheimer’s disease
[J]. Journal of Clinical Acupuncture and Moxibustion , 2023 , 39 (7 ): 102 - 106
[本文引用: 1]
[37]
SELVARAJU R R, COGSWELL M, DAS A, et al. Grad-CAM: visual explanations from deep networks via gradient-based localization [C]// Proceedings of the IEEE International Conference on Computer Vision . Venice: IEEE, 2017: 618–626.
[本文引用: 1]
[1]
YAO Z, WANG H, YAN W, et al Artificial intelligence-based diagnosis of Alzheimer’s disease with brain MRI images
[J]. European Journal of Radiology , 2023 , 165 : 110934
DOI:10.1016/j.ejrad.2023.110934
[本文引用: 1]
[2]
MENG Q, LIN M S, TZENG I S Relationship between exercise and Alzheimer’s disease: a narrative literature review
[J]. Frontiers in Neuroscience , 2020 , 14 : 131
DOI:10.3389/fnins.2020.00131
[3]
GAUTHIER S, ISMAIL Z, GOODARZI Z, et al Clinicians’ perspectives on how disease modifying drugs for Alzheimer’s disease impact specialty care
[J]. The Journal of Prevention of Alzheimer’s Disease , 2023 , 10 : 339 - 341
[5]
LIU S, SONG Y, CAI W, et al. Multifold Bayesian kernelization in Alzheimer’s diagnosis [J] Medical Image Computing and Computer-Assisted Intervention , 2013, 16(3): 303–310.
[本文引用: 1]
[7]
LIN W, GAO Q, DU M, et al Multiclass diagnosis of stages of Alzheimer’s disease using linear discriminant analysis scoring for multimodal data
[J]. Computers in Biology and Medicine , 2021 , 134 : 104478
DOI:10.1016/j.compbiomed.2021.104478
[本文引用: 1]
[8]
FENG W, HALM-LUTTERODT N V, TANG H, et al Automated MRI-based deep learning model for detection of Alzheimer’s disease process
[J]. International Journal of Neural Systems , 2020 , 30 (6 ): 2050032
DOI:10.1142/S012906572050032X
[本文引用: 2]
[9]
LIU M, CHENG D, YAN W Classification of Alzheimer’s disease by combination of convolutional and recurrent neural networks using FDG-PET images
[J]. Frontiers in Neuroinformatics , 2018 , 12 : 35
DOI:10.3389/fninf.2018.00035
[本文引用: 1]
[10]
KONG Z, ZHANG M, ZHU W, et al Multi-modal data Alzheimer’s disease detection based on 3D convolution
[J]. Biomedical Signal Processing and Control , 2022 , 75 : 103565
DOI:10.1016/j.bspc.2022.103565
[本文引用: 1]
[11]
韩坤, 潘海为, 张伟, 等 基于多模态医学图像的Alzheimer病分类方法
[J]. 清华大学学报: 自然科学版 , 2020 , 60 (8 ): 664 - 671
[本文引用: 1]
HAN Kun, PAN Haiwei, ZHANG Wei, et al Alzheimer’s disease classification method based on multimodal medical imaging
[J]. Journal of Tsinghua University: Science and Technology , 2020 , 60 (8 ): 664 - 671
[本文引用: 1]
[12]
LIANG C, LAO H, WEI T, et al Alzheimer’s disease classification from hippocampal atrophy based on PCANet-BLS
[J]. Multimedia Tools and Applications , 2022 , 81 : 11187 - 11203
DOI:10.1007/s11042-022-12228-0
[本文引用: 1]
[13]
DEEPA N, CHOKKALINGAM S P Optimization of VGG16 utilizing the arithmetic optimization algorithm for early detection of Alzheimer’s disease
[J]. Biomedical Signal Processing and Control , 2022 , 74 : 103455
DOI:10.1016/j.bspc.2021.103455
[本文引用: 1]
[14]
张默文. 基于结构磁共振成像和神经网络的阿尔兹海默症诊断方法研究[D]. 济南: 山东师范大学, 2023:1–60.
[本文引用: 1]
ZHANG Mowen. Diagnosis of Alzheimer’s disease based on structural magnetic resonance imaging and neural network [D]. Jinan: Shandong Normal University, 2023: 1–60.
[本文引用: 1]
[15]
MEHTA S C, RASTEGARI M. MobileViT: light-weight, general-purpose, and mobile-friendly vision transformer [EB/OL]. (2022−03−04)[2024−04−16], https://arxiv.org/pdf/2110.02178.
[本文引用: 3]
[16]
JACK C R JR, BERNSTEIN M A, FOX N C, et al The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods
[J]. Journal of Magnetic Resonance Imaging , 2008 , 27 (4 ): 685 - 691
DOI:10.1002/jmri.21049
[本文引用: 1]
[19]
ODUSAMI M, MASKELIŪNAS R, DAMAŠEVIČIUS R Pixel-level fusion approach with vision transformer for early detection of Alzheimer’s disease
[J]. Electronics , 2023 , 12 (5 ): 1218
DOI:10.3390/electronics12051218
[本文引用: 1]
[20]
陈蕊森, 夏军, 陈建良, 等 基于VBM的AD患者整体认知水平与脑灰质容积关系的横断面研究
[J]. CT理论与应用研究 , 2018 , 27 (6 ): 709 - 717
[本文引用: 1]
CHEN Ruisen, XIA Jun, CHEN Jianliang, et al Cross-sectional study on the relationship between integral cognitive level and gray matter volume in patients with Alzheimer’s disease based on VBM
[J]. CT Theory and Applications , 2018 , 27 (6 ): 709 - 717
[本文引用: 1]
[21]
SANDLER M, HOWARD A, ZHU M, et al. MobileNetV2: inverted residuals and linear bottlenecks [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 4510–4520.
[本文引用: 1]
[22]
RUSSAKOVSKY O, DENG J, SU H, et al ImageNet large scale visual recognition challenge
[J]. International Journal of Computer Vision , 2015 , 115 (3 ): 211 - 252
DOI:10.1007/s11263-015-0816-y
[本文引用: 1]
[23]
LI J, WEN Y, HE L. SCConv: spatial and channel reconstruction convolution for feature redundancy [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Vancouver: IEEE, 2023: 6153–6162.
[本文引用: 1]
[24]
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need [C]// Proceedings of the 31st International Conference on Neural Information Processing Systems . Long Beach: [s.n.], 2017: 6000–6010.
[本文引用: 1]
[25]
HUANG Z, ZHANG Z, LAN C, et al. Adaptive frequency filters as efficient global token mixers [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Paris: IEEE, 2023: 6049–6059.
[本文引用: 1]
[26]
DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An image is worth 16x16 words: transformers for image recognition at scale [EB/OL]. (2021−06−03)[2024−04−16]. https://arxiv.org/pdf/2010.11929.
[本文引用: 1]
[27]
CHOLLET F. Xception: deep learning with depth wise separable convolutions [C]// IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 1800−1807.
[本文引用: 1]
[28]
LENG Z Q, TAN M, LIU C, et al. PloyLoss: a polynomial expansion perspective of classification loss functions [EB/OL]. (2022−05−10)[2024−04−16]. https://arxiv.org/pdf/2204.12511.
[本文引用: 2]
[29]
HERINGTON J, MCCRADDEN M D, CREEL K, et al Ethical considerations for artificial intelligence in medical imaging: data collection, development, and evaluation
[J]. Journal of Nuclear Medicine , 2023 , 64 (12 ): 1848 - 1854
DOI:10.2967/jnumed.123.266080
[本文引用: 1]
[30]
ZHU X, SUK H, SHEN D A novel matrix-similarity based loss function for joint regression and classification in AD diagnosis
[J]. Neuroimage , 2014 , 100 : 91 - 105
DOI:10.1016/j.neuroimage.2014.05.078
[本文引用: 1]
[31]
HAO X, BAO Y, GUO Y, et al Multi-modal neuroimaging feature selection with consistent metric constraint for diagnosis of Alzheimer’s disease
[J]. Medical Image Analysis , 2020 , 60 : 101625
DOI:10.1016/j.media.2019.101625
[本文引用: 1]
[32]
ZHU Q, YUAN N, HUANG J, et al Multi-modal AD classification via self-paced latent correlation analysis
[J]. Neurocomputing , 2019 , 355 : 143 - 154
DOI:10.1016/j.neucom.2019.04.066
[本文引用: 1]
[33]
TONG T, GRAY K, GAO Q, et al Multi-modal classification of Alzheimer’s disease using nonlinear graph fusion
[J]. Pattern Recognition , 2017 , 63 : 171 - 181
DOI:10.1016/j.patcog.2016.10.009
[本文引用: 1]
[34]
ZHANG F, LI Z, ZHANG B, et al Multi-modal deep learning model for auxiliary diagnosis of Alzheimer’s disease
[J]. Neurocomputing , 2019 , 361 : 185 - 195
DOI:10.1016/j.neucom.2019.04.093
[本文引用: 1]
[35]
李伟汉, 侯北平, 胡飞阳, 等 阿尔茨海默症的多模态分类方法
[J]. 应用科学学报 , 2023 , 41 (6 ): 1004 - 1018
[本文引用: 1]
LI Weihan, HOU Beiping, HU Feiyang, et al Multi-modal diagnosis method for Alzheimer’s disease
[J]. Journal of Applied Sciences , 2023 , 41 (6 ): 1004 - 1018
[本文引用: 1]
[36]
李长君, 田淼元, 李奇玮, 等 针刺干预对阿尔茨海默症海马体的作用机制探讨
[J]. 针灸临床杂志 , 2023 , 39 (7 ): 102 - 106
[本文引用: 1]
针刺干预对阿尔茨海默症海马体的作用机制探讨
1
2023
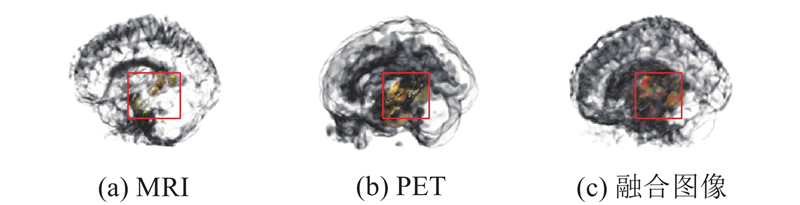
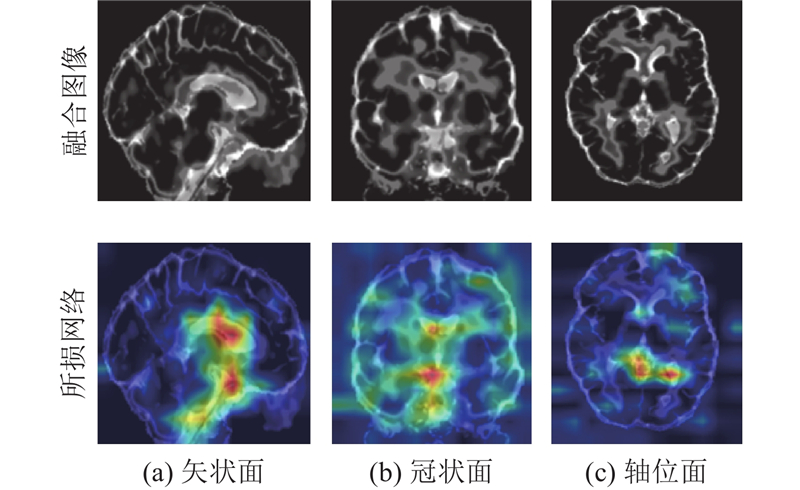
... 海马体损伤是AD的重要发病机制[36 ] . 如图8 所示,海马体位于大脑颞叶内侧,呈弯曲状,主要包括海马回、海马体和亚海马区. 为了检验所提网络训练海马体部位的准确性,对网络中的每个阶段进行可视化处理,使用梯度加权类激活映射Grad-CAM[37 ] 将网络的输出可视化如图9 所示. 图中,第1行为融合图像,第2行为所提网络的训练可视化结果. 由图可知,所提网络能够准确关注脑部影像中的海马体区域,对影像中AD的病灶进行准确定位. ...
1
... 海马体损伤是AD的重要发病机制[36 ] . 如图8 所示,海马体位于大脑颞叶内侧,呈弯曲状,主要包括海马回、海马体和亚海马区. 为了检验所提网络训练海马体部位的准确性,对网络中的每个阶段进行可视化处理,使用梯度加权类激活映射Grad-CAM[37 ] 将网络的输出可视化如图9 所示. 图中,第1行为融合图像,第2行为所提网络的训练可视化结果. 由图可知,所提网络能够准确关注脑部影像中的海马体区域,对影像中AD的病灶进行准确定位. ...
Artificial intelligence-based diagnosis of Alzheimer’s disease with brain MRI images
1
2023
... 阿尔茨海默病(Alzheimer’s disease,AD)是影响65岁以上个体的进行性神经退行性疾病,全球被诊断为AD的人口约有4 400万,中国60岁以上患者已达1 507万[1 -4 ] . AD临床诊断主要依赖神经心理测试、神经影像学和脑脊液检查,包括简易精神状态检查量表(mini-mental state examinationmse, MMSE)、全局退化量表(global deterioration scale total score,GDS) 、全局临床痴呆评定量表(clinical dementia rating,CDR)、功能活动问卷量表(functional activities questionnaire,FAQ)、简易版神经精神症问卷量表(neuropsychiatric inventory–questionnaire,NPI)、磁共振成像(MRI)和正电子发射断层扫描(PET)等检查. 综合多种检查结果有助于医生准确判断患者情况,但AD的确诊过程复杂. ...
Relationship between exercise and Alzheimer’s disease: a narrative literature review
0
2020
Clinicians’ perspectives on how disease modifying drugs for Alzheimer’s disease impact specialty care
0
2023
The China Alzheimer report 2022
1
2022
... 阿尔茨海默病(Alzheimer’s disease,AD)是影响65岁以上个体的进行性神经退行性疾病,全球被诊断为AD的人口约有4 400万,中国60岁以上患者已达1 507万[1 -4 ] . AD临床诊断主要依赖神经心理测试、神经影像学和脑脊液检查,包括简易精神状态检查量表(mini-mental state examinationmse, MMSE)、全局退化量表(global deterioration scale total score,GDS) 、全局临床痴呆评定量表(clinical dementia rating,CDR)、功能活动问卷量表(functional activities questionnaire,FAQ)、简易版神经精神症问卷量表(neuropsychiatric inventory–questionnaire,NPI)、磁共振成像(MRI)和正电子发射断层扫描(PET)等检查. 综合多种检查结果有助于医生准确判断患者情况,但AD的确诊过程复杂. ...
1
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
Multimodal classification of Alzheimer’s disease and mild cognitive impairment
1
2011
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
Multiclass diagnosis of stages of Alzheimer’s disease using linear discriminant analysis scoring for multimodal data
1
2021
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
Automated MRI-based deep learning model for detection of Alzheimer’s disease process
2
2020
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
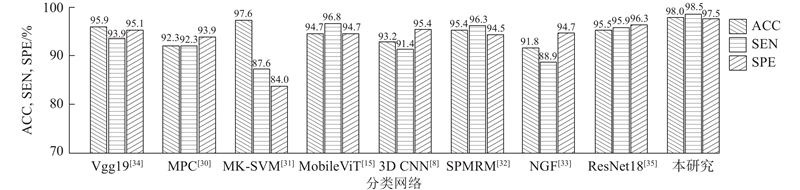
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
Classification of Alzheimer’s disease by combination of convolutional and recurrent neural networks using FDG-PET images
1
2018
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
Multi-modal data Alzheimer’s disease detection based on 3D convolution
1
2022
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
基于多模态医学图像的Alzheimer病分类方法
1
2020
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
基于多模态医学图像的Alzheimer病分类方法
1
2020
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
Alzheimer’s disease classification from hippocampal atrophy based on PCANet-BLS
1
2022
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
Optimization of VGG16 utilizing the arithmetic optimization algorithm for early detection of Alzheimer’s disease
1
2022
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
1
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
1
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
3
... 随着人工智能技术的迅速进步,学者们提出许多有效的早期AD脑部检测方法. 这些方法主要分为2个类别:基于图像的传统方法和基于深度学习的方法. 在传统方法方面,Liu等[5 ] 从MRI和PET图像中提取ROI(region of interest),采用基于贝叶斯框架的多重贝叶斯核化(multifold Bayesian kernelization,MBK)方法检测AD患者;Zhang等[6 ] 将MRI和PET的神经影像结合生物标志物数据,利用支持向量机(SVM)融合多峰特征进行特征提取,依此诊断AD. Lin等[7 ] 融合MRI图像、PET图像、脑脊液数据、基因数据以及年龄数据,采用线性判别分析 (linear discriminant analysis, LDA)的评分方法检测AD患者. 传统方法能够综合多种数据进行特征提取和分类诊断,存在特征提取可能忽略病症重要细节信息的问题. 在深度学习方法方面,3D图像建立深度模型虽然可以极大程度上保留脑部的空间特征,但是计算量和参数量巨大. Feng等[8 ] 将3D卷积网络用于特征提取,SVM分类器用于分类. Liu等[9 ] 将FDG-PET三维图像在矢状面、冠状面和横切面3个方向切片,使用卷积神经网络从切片中提取特征,再将特征输入递归神经网络进行分类,最后融合3个方向的分类结果进行分类预测. Kong等[10 ] 将MRI与PET图像融合,利用3D卷积神经网络提取特征信息,再利用全连接神经网络对提取的多模态特征进行预测. 韩坤等[11 ] 对MRI和PET图像进行3D卷积操作以提取各自模态的特征信息,应用模型融合方法融合模态特征信息以获得多模态特征信息,利用全连接神经网络对AD进行分类,取得了不错的分类结果. 基于3D卷积神经网络对设备要求高,不适合移动医疗器械发展. 有研究倾向于将数据转为二维,采用轻量级网络进行分类. Liang等[12 ] 利用PCA-Net提取二维特征,使用宽度学习系统(broad learning system, BLS)进行更低耗时的分类. Deepa等[13 ] 通过预处理图像的方式处理多数据集,将切片得到的二维图像输入VGG-16网络进行特征提取,再利用全连接层进行分类. 使用二维数据进行分类减少了网络参数,在特征提取中可能丢失空间和上下文信息,影响检测的准确性. 为此,张默文[14 ] 提出2种AD早期诊断方法:1)基于多尺度特征提取和全基因组关联分析的神经网络,2)基于感兴趣区域和基因数据特征融合的算法;采用随机森林集成器实现了比SVM更准确的AD诊断. 一些轻量级分类诊断网络,如Mehta[15 ] 提出的将卷积神经网络和Transformer的优势结合的方法,能够很好地处理局部信息和全局信息,而且在不同任务和数据集上也明显优于传统的卷积神经网络和Vision Transformer网络. ...
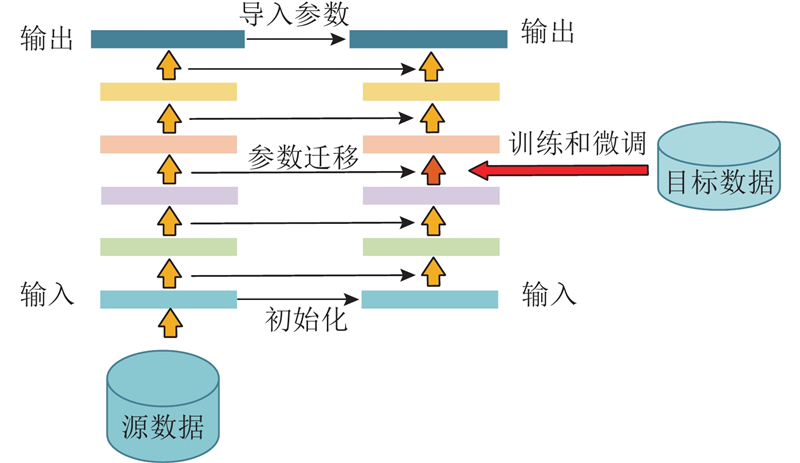
... 医学数据收集的复杂性导致获得较大的医学数据集困难[29 ] . 在深度学习领域,数据集小可能导致过拟合、模型不稳定、特征表示能力受限、泛化能力下降和无法处理复杂任务等问题. 迁移学习利用已经学到的知识来改善新任务的学习过程,核心思想就是通过共享源领域和目标领域之间的相似性,将源领域上学习到的模型参数、特征表示或知识应用到目标任务中.本研究利用有限的数据集获得了比较理想的诊断效果. 如图6 所示,采用迁移学习中基于参数的方法,使用源数据构建模型,再将学习到的模型参数与目标域共享作为预先获得的模型,用于训练参数微调. 本研究源数据来自Imagenet 1k数据集,包含大约1 000万张图像,涵盖1 000个类别,包括动物、植物、物体和场景等各种领域. 模型参数由该数据集在与本研究所提网络结构相同的MobileViT[15 ] 网络上训练得到. 迁移学习能够大幅度降低学习其他数据集的训练时间,提高网络的泛化能力. ...
... Performance parameters of different classification networks
Tab.3 网络 ACC SEN SPE FLOPS8 N P 5 MAC8 MobileViT[15 ] 0.947 0.968 0.947 3.3 9.9 9.2 Mobileswin 0.923 0.945 0.952 2.1 4.9 7.4 图像特征 0.943 0.958 0.934 1.3 3.3 7.6 文本特征 0.948 0.954 0.944 3.2 2.7 1.6 本研究 0.980 0.985 0.975 1.3 3.3 7.6
轻量级网络在训练时常出现过拟合现象,这是网络复杂度过高同时数据的分布不均衡导致的. 虽然本研究在数据搜集阶段注意数据的均衡分布,但数据差异性使得数据在预处理后仍可能面临不均衡的问题. 为了探究不同损失函数对网络训练的效果,选择不同损失函数进行训练,训练效果如表4 所示. 由表可知,多项式损失函数在二分类任务上的准确率比交叉熵损失函数和焦点损失函数的分别提高了0.019,0.008,在三分类任务上分别提高了0.056,0.021. 该结果验证了在数据不均衡的训练任务中,多项式损失函数的表现效果更好. ...
The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods
1
2008
... 使用数据来自AD神经影像学倡议(Alzheimer’s disease neuroimaging initiative,ADNI)数据库[16 ] . 该数据库是全球性的研究项目,项目设置旨在通过使用神经影像学、生物标志物和临床评估等方法增加对AD及相关疾病的理解. 诊断AD使用单一的神经影像难以获得信息丰富的特征,将患者在临床检查中获得的认知功能评分用于诊断能够得到丰富的多模态特征. 本研究选用T1加权的MRI和FDG-PET神经影像数据以及精神认知评分数据诊断AD. 影像数据来自443名受试者,评分数据来自同一批受试者中不同阶段的随访信息. 在AD患者中,女性少于男性,年纪小的少于年纪大的,数据尽量均衡选择. 数据集中受试者的人口学和临床信息如表1 所示. 表中,CN表示健康人,MCI表示轻度认知障碍患者,N M 为男性人数,N F 为女性人数,S MMSE 为简易精神状态检查分数,S GDS 为全局退化量表分数,S CDR 为全局临床痴呆评定量表分数,S FAQ 为功能活动问卷分数,S NPI 为简化版神经精神症状量表问卷分数. ...
FSL
1
2012
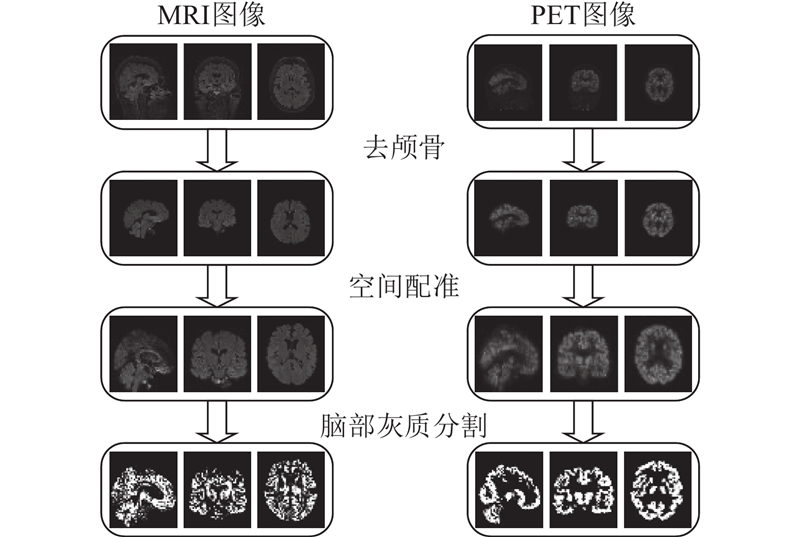
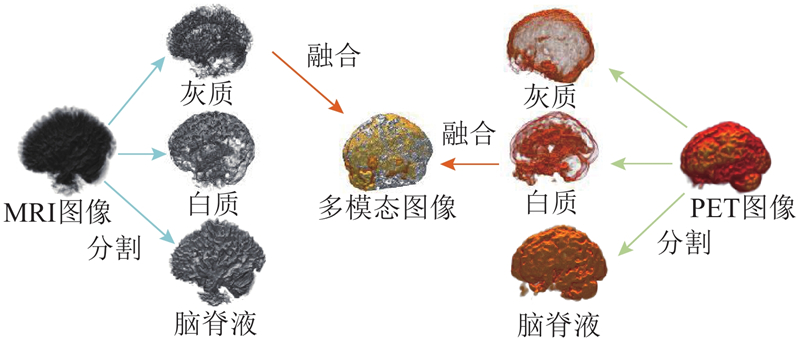
... 如图1 所示,图像预处理主要包含去颅骨、配准、分割以及融合4个部分. 1)利用医学影像处理软件FSL(FMRIB software library)[17 ] 中的BET工具分别将患者脑部MRI和PET图像进行去颅骨操作. 该技术仅保留颅内组织结构,去除了不必要的解剖器官区域. BET工具使用完全自动化的算法在神经影像中将脑部区域与周围的非脑组织(如头盖骨、头皮和脑膜)分离[18 ] ,通过阈值分割、曲面拟合和优化技术等方法准确地估计脑部边界. 2)利用FLIRT工具将MRI和PET图像配准到MNI152空间中. FLIRT通过计算刚体变换和仿射变换将图像与参考图像对齐. 这种线性变换可以在保持图像形态结构的前提下进行平移、旋转和缩放操作,确保2个图像的脑部组织对应. 3)使用FSL中的FAST工具对图像进行脑部灰质区域分割. FAST是基于概率模型和贝叶斯分类器的工具,能够根据MRI图像估计脑部组织类型的空间分布,包括灰质、白质和脑脊液等分割,分别获得仅包含灰质、白质的脑部. 4)融合MRI和PET图像的信息可以获得更全面、准确的大脑结构和功能表示. 为此,将MRI和PET图像在MNI152标准空间中配准,确保这2类图像在空间上对齐,分别对2类图像进行分割后可以获得灰质、白质和脑脊液图像. 海马体主要由灰质构成,本研究采用FLIRT组件将MRI图像分割得到的灰质图像与相应PET图像分割得到的白质图像进行配准,生成配准的融合图像. MRI图像分割得到的灰质图像保留了海马体的结构特征,PET图像分割得到的白质保留了脑组织中的代谢信息. 这种融合方法简单、实用,在有效地保留大脑基本信息的同时最大限度地减少了计算负担. 该方法通过集成丰富的语义信息和图像细节,提高了模型的性能和准确性. 多模态图像融合过程如图2 所示. ...
Diagnosis of Alzheimer’s disease based on the modified Tresnet
1
2021
... 如图1 所示,图像预处理主要包含去颅骨、配准、分割以及融合4个部分. 1)利用医学影像处理软件FSL(FMRIB software library)[17 ] 中的BET工具分别将患者脑部MRI和PET图像进行去颅骨操作. 该技术仅保留颅内组织结构,去除了不必要的解剖器官区域. BET工具使用完全自动化的算法在神经影像中将脑部区域与周围的非脑组织(如头盖骨、头皮和脑膜)分离[18 ] ,通过阈值分割、曲面拟合和优化技术等方法准确地估计脑部边界. 2)利用FLIRT工具将MRI和PET图像配准到MNI152空间中. FLIRT通过计算刚体变换和仿射变换将图像与参考图像对齐. 这种线性变换可以在保持图像形态结构的前提下进行平移、旋转和缩放操作,确保2个图像的脑部组织对应. 3)使用FSL中的FAST工具对图像进行脑部灰质区域分割. FAST是基于概率模型和贝叶斯分类器的工具,能够根据MRI图像估计脑部组织类型的空间分布,包括灰质、白质和脑脊液等分割,分别获得仅包含灰质、白质的脑部. 4)融合MRI和PET图像的信息可以获得更全面、准确的大脑结构和功能表示. 为此,将MRI和PET图像在MNI152标准空间中配准,确保这2类图像在空间上对齐,分别对2类图像进行分割后可以获得灰质、白质和脑脊液图像. 海马体主要由灰质构成,本研究采用FLIRT组件将MRI图像分割得到的灰质图像与相应PET图像分割得到的白质图像进行配准,生成配准的融合图像. MRI图像分割得到的灰质图像保留了海马体的结构特征,PET图像分割得到的白质保留了脑组织中的代谢信息. 这种融合方法简单、实用,在有效地保留大脑基本信息的同时最大限度地减少了计算负担. 该方法通过集成丰富的语义信息和图像细节,提高了模型的性能和准确性. 多模态图像融合过程如图2 所示. ...
Pixel-level fusion approach with vision transformer for early detection of Alzheimer’s disease
1
2023
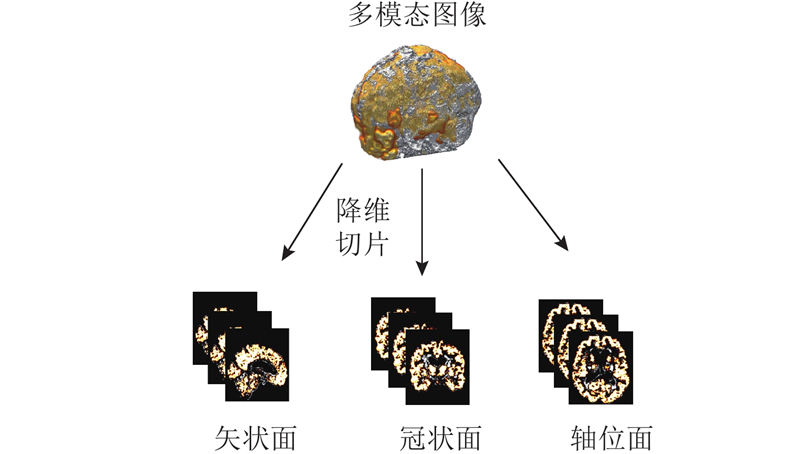
... MRI和PET图像通常以NIFTI格式保存,该格式存储MRI和PET的三维数据[19 ] . 处理三维数据对计算能力的要求高,为了最大限度地减少训练参数的数量和计算复杂性,采用二维数据进行训练. 在矢状面、冠状面和轴面3个方向进行切片处理可以准确地检测和研究AD的相关变化[20 ] ,但不是每个切片都能完全捕捉大脑中的特征信息. 为了保留那些包含关键大脑信息的部分,研究中须过滤获得的图像. 如图3 所示,通过降维切片过程得到多模态图像数据,包含来自2种类型图像的关键信息. ...
基于VBM的AD患者整体认知水平与脑灰质容积关系的横断面研究
1
2018
... MRI和PET图像通常以NIFTI格式保存,该格式存储MRI和PET的三维数据[19 ] . 处理三维数据对计算能力的要求高,为了最大限度地减少训练参数的数量和计算复杂性,采用二维数据进行训练. 在矢状面、冠状面和轴面3个方向进行切片处理可以准确地检测和研究AD的相关变化[20 ] ,但不是每个切片都能完全捕捉大脑中的特征信息. 为了保留那些包含关键大脑信息的部分,研究中须过滤获得的图像. 如图3 所示,通过降维切片过程得到多模态图像数据,包含来自2种类型图像的关键信息. ...
基于VBM的AD患者整体认知水平与脑灰质容积关系的横断面研究
1
2018
... MRI和PET图像通常以NIFTI格式保存,该格式存储MRI和PET的三维数据[19 ] . 处理三维数据对计算能力的要求高,为了最大限度地减少训练参数的数量和计算复杂性,采用二维数据进行训练. 在矢状面、冠状面和轴面3个方向进行切片处理可以准确地检测和研究AD的相关变化[20 ] ,但不是每个切片都能完全捕捉大脑中的特征信息. 为了保留那些包含关键大脑信息的部分,研究中须过滤获得的图像. 如图3 所示,通过降维切片过程得到多模态图像数据,包含来自2种类型图像的关键信息. ...
1
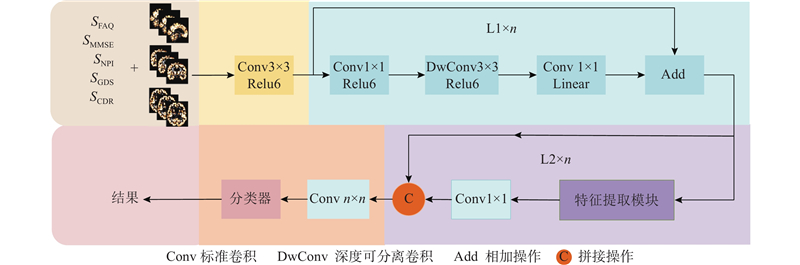
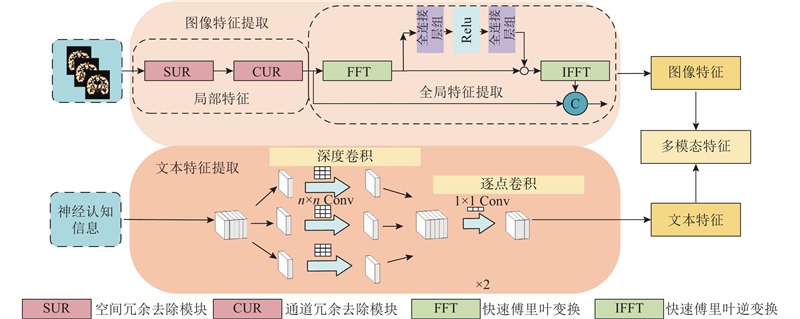
... 如图4 所示为所提网络的结构图. 该网络的目标是在确保准确率的同时降低参数量,为将来在移动设备上的拓展应用奠定基础,因此网络中的特征提取模块的设置主要考虑降低参数量. 利用倒残差结构增加网络深度并降低网络复杂度[21 ] ,再利用图像局部特征提取模块和全局特征提取模块对图像进行特征提取;使用可分离卷积网络对评分信息进行特征提取,将提取的文本特征与图像特征进行融合,以获得多模态特征;最后利用线性分类器进行分类诊断. ...
ImageNet large scale visual recognition challenge
1
2015
... (1)局部特征提取. 在传统卷积过程中,网络参数量往往与卷积核大小以及卷积数量相关[22 ] . 为了获得更好的局部图像特征,研究者通常会选择使用多个卷积或者使用不同尺度的卷积进行特征提取. 无论是加深网络深度还是使用不同尺度卷积都会增加网络参数量. 传统卷积过程存在空间和通道冗余,因此压缩空间和通道冗余成为降低参数量的关键因素. 通过分离重构的方式压缩空间冗余,通过分离变换融合的方式抑制信道冗余[23 ] . 通过这2种方式在减少大量计算负荷的同时实现了可观的性能提升. 空间重构首先使用批量标准化的方法将原特征图$ {\boldsymbol{X}} $
1
... (1)局部特征提取. 在传统卷积过程中,网络参数量往往与卷积核大小以及卷积数量相关[22 ] . 为了获得更好的局部图像特征,研究者通常会选择使用多个卷积或者使用不同尺度的卷积进行特征提取. 无论是加深网络深度还是使用不同尺度卷积都会增加网络参数量. 传统卷积过程存在空间和通道冗余,因此压缩空间和通道冗余成为降低参数量的关键因素. 通过分离重构的方式压缩空间冗余,通过分离变换融合的方式抑制信道冗余[23 ] . 通过这2种方式在减少大量计算负荷的同时实现了可观的性能提升. 空间重构首先使用批量标准化的方法将原特征图$ {\boldsymbol{X}} $
1
... (2)全局特征提取. 在深度学习领域中捕获数据的全局特征通常考虑Transformer架构. Transformer的自注意力机制和多层网络结构会增加整个网络的参数[24 ] ,通过将图像数据的特征转换到频域进行提取的方式来降低参数量[25 ] . 利用快速傅里叶变换将图像数据的特征$ {\boldsymbol{X}} \in {{\bf{R}}^{H\times W\times C}} $ $ {{\boldsymbol{Y}}_{}} $
1
... (2)全局特征提取. 在深度学习领域中捕获数据的全局特征通常考虑Transformer架构. Transformer的自注意力机制和多层网络结构会增加整个网络的参数[24 ] ,通过将图像数据的特征转换到频域进行提取的方式来降低参数量[25 ] . 利用快速傅里叶变换将图像数据的特征$ {\boldsymbol{X}} \in {{\bf{R}}^{H\times W\times C}} $ $ {{\boldsymbol{Y}}_{}} $
1
... 快速傅里叶变换式使该特征提取方式无论是在参数量还是在计算速度上都远好于Vision Transformer. 在特征提取过程中,因为掩膜张量是通过1×1卷积得到的,可以看作全局卷积,所以经过滤波得到的特征都包含图像上下文信息,实现了与Vision Transformer相同的全局特征提取功能[26 ] . ...
1
... 利用可分离卷积提取认知评分信息特征的模块. AD评分信息数量巨大,若使用传统卷积进行特征提取往往会产生大量的参数. 对评分信息进行特征提取不涉及从3个通道进行的特征提取,为此利用可分离卷积[27 ] 对文本信息进行特征提取以降低网络参数量. 深度可分离卷积由2个部分组成:1)深度卷积 ...
2
... 多项式损失函数[28 ] 为理解和改进常用的交叉熵损失和焦点损失函数提供了多项式扩展框架. Leng等[28 ] 通过对泰勒公式展开和求导,分析常见的交叉熵损失函数和焦点损失函数的本质,提出垂直调节损失和水平调节损失的概念. 分析了数据不均衡在损失函数上的机理,提出以简单有效的损失函数解决数据不均衡问题的方法,效果超越交叉熵损失函数和焦点损失函数. 多项式损失函数的表达式为 ...
... [28 ]通过对泰勒公式展开和求导,分析常见的交叉熵损失函数和焦点损失函数的本质,提出垂直调节损失和水平调节损失的概念. 分析了数据不均衡在损失函数上的机理,提出以简单有效的损失函数解决数据不均衡问题的方法,效果超越交叉熵损失函数和焦点损失函数. 多项式损失函数的表达式为 ...
Ethical considerations for artificial intelligence in medical imaging: data collection, development, and evaluation
1
2023
... 医学数据收集的复杂性导致获得较大的医学数据集困难[29 ] . 在深度学习领域,数据集小可能导致过拟合、模型不稳定、特征表示能力受限、泛化能力下降和无法处理复杂任务等问题. 迁移学习利用已经学到的知识来改善新任务的学习过程,核心思想就是通过共享源领域和目标领域之间的相似性,将源领域上学习到的模型参数、特征表示或知识应用到目标任务中.本研究利用有限的数据集获得了比较理想的诊断效果. 如图6 所示,采用迁移学习中基于参数的方法,使用源数据构建模型,再将学习到的模型参数与目标域共享作为预先获得的模型,用于训练参数微调. 本研究源数据来自Imagenet 1k数据集,包含大约1 000万张图像,涵盖1 000个类别,包括动物、植物、物体和场景等各种领域. 模型参数由该数据集在与本研究所提网络结构相同的MobileViT[15 ] 网络上训练得到. 迁移学习能够大幅度降低学习其他数据集的训练时间,提高网络的泛化能力. ...
A novel matrix-similarity based loss function for joint regression and classification in AD diagnosis
1
2014
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
Multi-modal neuroimaging feature selection with consistent metric constraint for diagnosis of Alzheimer’s disease
1
2020
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
Multi-modal AD classification via self-paced latent correlation analysis
1
2019
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
Multi-modal classification of Alzheimer’s disease using nonlinear graph fusion
1
2017
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
Multi-modal deep learning model for auxiliary diagnosis of Alzheimer’s disease
1
2019
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
阿尔茨海默症的多模态分类方法
1
2023
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
阿尔茨海默症的多模态分类方法
1
2023
... 对比不同分类网络的分类效果,结果如图7 所示. 由图可知,本研究所提网络均优于其他网络. MPC[30 ] 、MK-SVM[31 ] 、SPMRM[32 ] 、NGF[33 ] 利用传统图像处理的方法进行多模态数据处理和诊断. 其中MK-SVM基于一致度量约束的多模态神经影像学特征选择方法,准确率为0.976. Vgg19[34 ] 、MobileViT、3D-CNN[8 ] 、ResNet18[35 ] 采用深度学习的方法进行诊断. 研究者或采用增加网络深度的方法,或选择3D卷积神经网络来提高诊断准确率. 在传统2D的深度学习方法中,最高的准确率为0.959. 所提网络比现有的传统学习方法(MK-SVM)的最高准确率提高了0.004,比现有的深度学习方法(Vgg19)最高准确率提高了0.021. 所提网络利用迁移学习方法,在保证准确率的同时减少了参数量,使用多模态数据不仅保证了分类准确率,也提高了多模态辅助诊断的可信性. ...
针刺干预对阿尔茨海默症海马体的作用机制探讨
1
2023
... 海马体损伤是AD的重要发病机制[36 ] . 如图8 所示,海马体位于大脑颞叶内侧,呈弯曲状,主要包括海马回、海马体和亚海马区. 为了检验所提网络训练海马体部位的准确性,对网络中的每个阶段进行可视化处理,使用梯度加权类激活映射Grad-CAM[37 ] 将网络的输出可视化如图9 所示. 图中,第1行为融合图像,第2行为所提网络的训练可视化结果. 由图可知,所提网络能够准确关注脑部影像中的海马体区域,对影像中AD的病灶进行准确定位. ...