永磁同步电机(permanent magnet synchronous motor,PMSM)具有高转矩密度、高功率因数和高过载能力等优点,被广泛应用于工业制造、航空航天以及轨道交通等领域[1-3],应用领域的不断扩展对电机系统高品质的运行性能提出更高的需求[4]. 在低转速高负载领域,传统的永磁同步电机要与变速装置匹配才能实现低速高负载的动力输出,传统永磁电机的单一输出增加了对多电机系统总成的依赖,不利于电机动力的高效利用. 直驱系统省去中间的齿轮传动系统,消除了齿轮带来的振动噪声、机械磨损和动力损耗,因此现代工业动力系统更倾向于直接驱动[5-7]. 为了适应新技术的发展,满足工业多样化的生产需求,国内外许多学者在不断探索新型拓扑下的驱动方式. Jungmayr等[8-9]提出新型的轴向串联磁齿轮复合电机,在结构上实现了磁齿轮与外转子永磁电机的一体化,减少了电机系统的体积和重量; Zhu等[10]基于行星磁齿传动提出混动汽车用磁性行星齿轮永磁无刷电机,该电机采用非接触的行星磁齿轮传动结构,具有功率密度高,调速范围广,体积紧凑等特点. 磁性齿轮与永磁电机的结合拓宽了传统永磁电机的驱动模式,但未解决传统永磁电机输出口单一、直驱能力弱以及功率和能量分配效率低的问题. Liu等[11]提出结合盘式电机与行星转子的多端口空间电机,能够实现多自由度动力输出;由于特殊的半包角式定子结构,该电机存在明显的端部效应. 分布式的驱动模式增加了电枢励磁绕组,导致散热性较差,并使控制难度增加.
本研究提出新型盘式行星永磁电机(disc planetary permanent magnet motor),该电机在驱动方式和拓扑结构上有别于以往的磁齿轮复合电机,且相比于传统的盘式行星永磁电机,具有轴向尺寸短、散热性好、结构简单和易于控制等优势. 永磁行星驱动具有直驱、低噪音及过载保护等优点,能够在有限的空间里实现多自由度的动力输出,为多源动力领域带来更多的驱动模式和功能. 本研究所提电机具有电磁驱动与磁齿轮传动2种动力传输模式,实现了机电磁的有机结合. 作为新型盘式行星永磁电机的重要指标表征的电磁性能是本文研究的重点. 该电机空间结构比较特殊,磁场呈现三维特性,传统的二维电机的分析方法不再适用,计算精确的三维有限元会消耗大量的计算资源和时间,给新型电机的初期设计带来不便[12]. 等效磁网络法通过构建区域磁通网络对磁场进行整体的等效计算,该方法结合磁路法计算速度快和有限元法求解精度高的优点,在电机的初期设计阶段具有很大的优势[13-14]. 曹东辉等[15]提出基于网格剖分的等效磁网络建模法,在考虑漏磁与局部饱和的情况下,精确地评估了转子磁障结构对降低永磁体涡流损耗的作用,提高了计算精度. 宫晓等[16]考虑漏磁形式,对轴向盘式永磁电机进行设计及优化,建立了这种电机的等效磁路网络模型,模型的计算结果与有限元以及实验结果吻合较好. 张淦等[17]建立针对磁通切换型永磁电机的非线性磁网络模型,通过引入深度饱和系数计算电机的磁链和反电势,该方法在电机的初期设计中可节省大量的计算时间. Ding等[18]提出新的基于等效磁网络建模方法,通过建立模块化的磁网格,对永磁电机的性能进行优化设计,该方法无需重复编程和建模,在电磁性能分析上具有很大优势.
本文针对新型盘式行星永磁电机复杂的空间磁场,研究定转子间磁场的时变性等效动态磁网络模型. 1)利用径向分环法,将该新型电机的三维磁路模型等效分环为二维模型,分析二维等效模型的磁路变化. 2)针对该电机气隙不均的特点,构建不均匀气隙位置分布函数,对各段气隙磁阻和漏磁磁阻进行等效计算,进一步建立该电机在单个电周期下的等效磁网络模型. 3)通过求解该等效磁网络模型得到该电机的磁链和空载反电势. 4)通过有限元仿真和样机实验验证该电机等效动态磁网络模型的有效性.
1. 所提电机的结构及工作原理
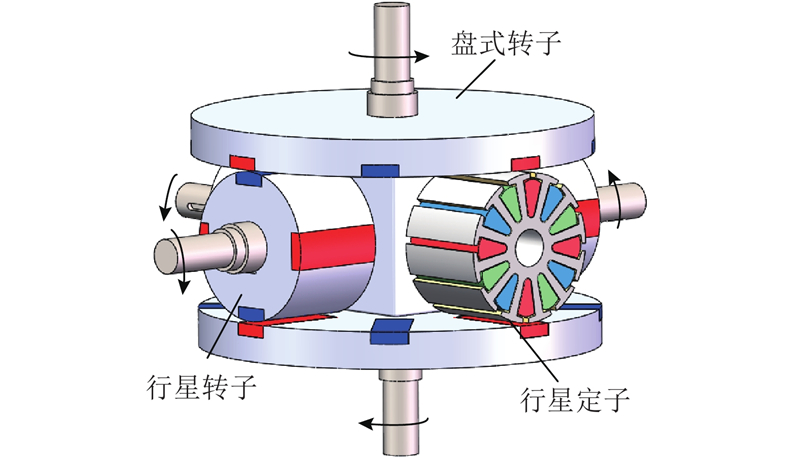
如图1所示,新型盘式行星永磁电机主要由3个基本驱动部件构成:盘式转子、行星转子和行星定子. 行星定子由硅钢片叠压而成,绕组槽内放置通电线圈. 盘式转子和行星转子表面嵌有N-S极相间的永磁体,永磁体的布置由定转子间的磁力啮合关系决定,盘式转子上的永磁体径向布置,行星转子的永磁体内嵌于转子表面,并与转轴平行,保证在动力传递过程中磁力能够有效传递. 行星定子绕组通入三相交流电后,表面产生旋转的磁场,驱动上下2个盘式转子旋转;同时盘式转子上的永磁体与行星转子上的永磁体发生磁力耦合,带动行星转子转动. 新型拓扑结构下的盘式行星永磁电机有2种驱动方式: 1)通电的行星定子与盘式转子间的电磁驱动, 2)盘式转子与行星转子间的磁力驱动. 行星转子受到上下2个盘式转子的同步驱动,与盘式转子之间存在传动关系,两者满足一定传动比,在电机结构层面实现盘式电机与行星驱动系统的一体化设计. 在实际应用中,可根据不同的工况选择输出端口,提高电机的工作效率.
图 1
2. 动态磁路模型分析
2.1. 分环等效模型
图 2
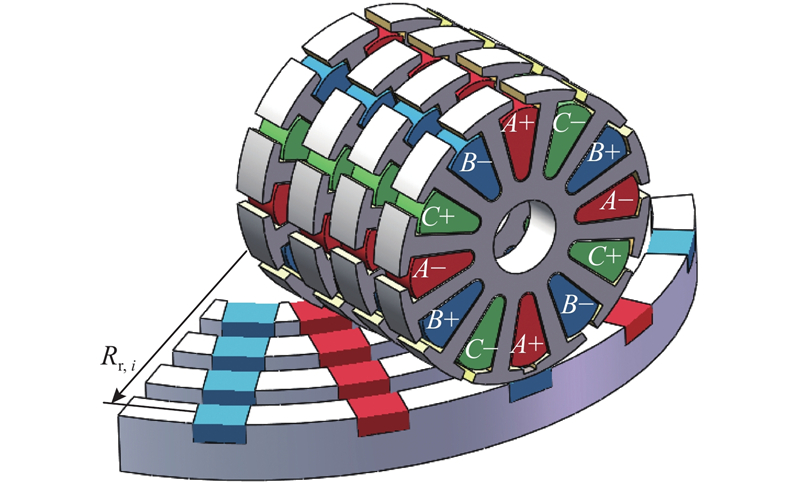
图 2 单个盘式转子与行星定子的分环模型
Fig.2 Sectors-of-rings model of single disc rotor and planetary stator
2.2. 分环模型动态磁路分析
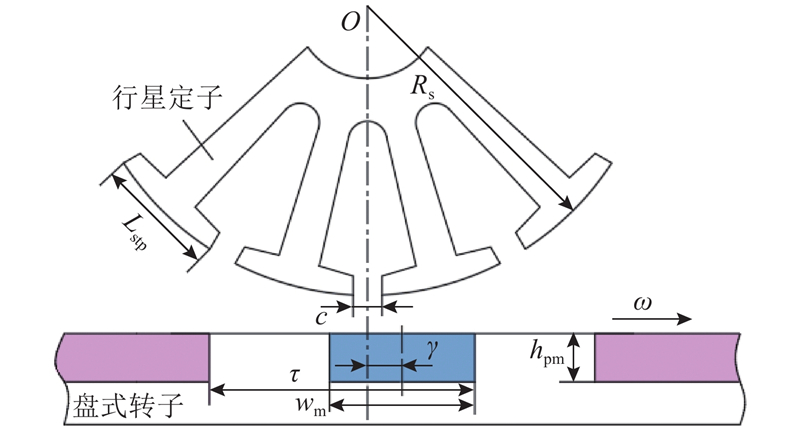
在盘式行星永磁电机运行过程中,盘式转子和行星定子之间的磁通路径随着盘式转子的转动不断变化,磁路模型也随之改变. 根据磁路的周期性,将盘式转子与行星定子间的磁路划分为4个区域,分别分析每个区域里的磁路. 在盘式转子与行星定子的磁路分环模型中,假设盘式转子永磁体等间隔. 定、转子分环模型参数如图3所示. 图中,τ为盘式转子齿间距,wm为盘式转子齿宽,c为行星定子槽口宽度,Lstp为行星定子极靴宽度,hpm为永磁体厚度,Rs为行星定子半径,
图 3
式中:Rr,i为盘式转子第i个分环的平均转动半径(i=1,2,3,···),p为盘式转子磁齿的极对数.
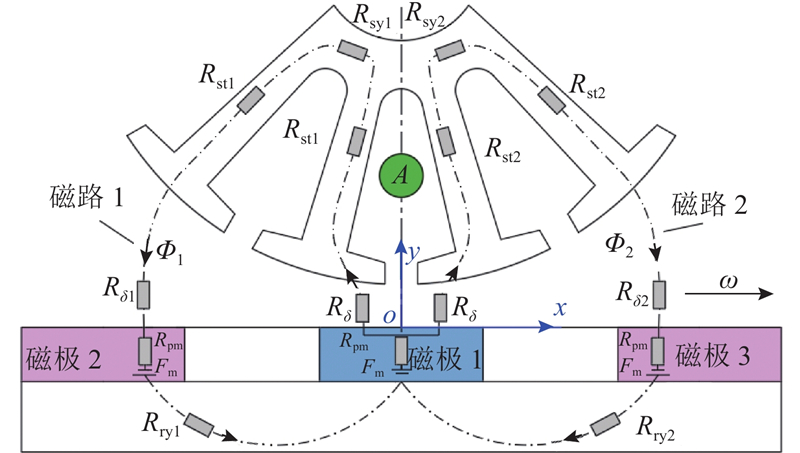
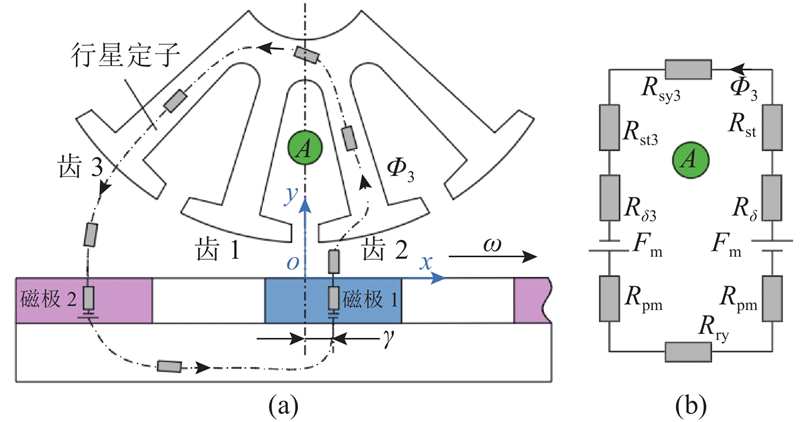
为了分析与行星定子A相绕组匝链的磁通,以A相绕组磁链为零的位置为起始位置,建立分环模型下定转子的等效磁路模型,起始位置处的等效磁路关于行星定子中心线对称,磁路模型如图4所示. 图中,Φ1、Φ2分别为流向两侧的主磁通,Rδ、Rδi均为主磁通等效气隙磁阻,Rsti、Rsyi分别为行星定子齿和轭部等效磁阻,Rryi为盘式转子轭部等效磁阻(i=1,2···),Rpm为永磁体内部磁阻,Fm为永磁体磁动势. 当盘式转子转动时,盘式转子上永磁体与行星定子极靴的相对位置发生变化,磁路的气隙长度改变,盘式转子上的磁通不断与绕组匝链. 在时刻t,分环模型中盘式转子的转动路径为
图 4
式中:
图 5
图 5 区域1中的磁通路径及等效磁路模型
Fig.5 Flux path and equivalent magnetic circuit model in region 1
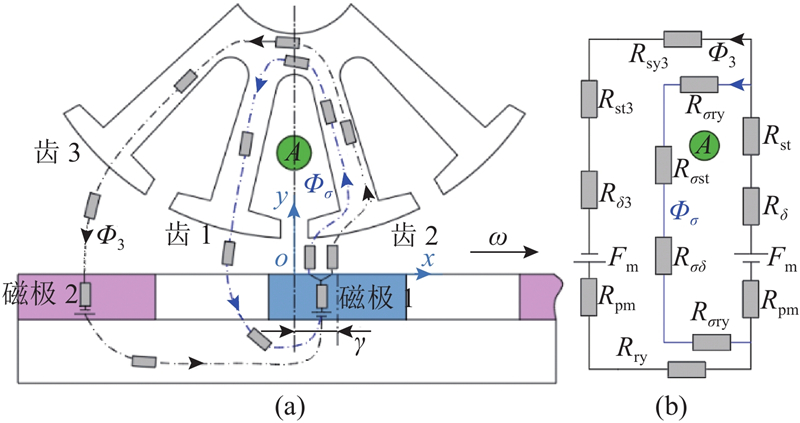
2)区域2:
图 6
图 6 区域2中的磁通路径及等效路模型
Fig.6 Flux path and equivalent magnetic circuit model in region 2
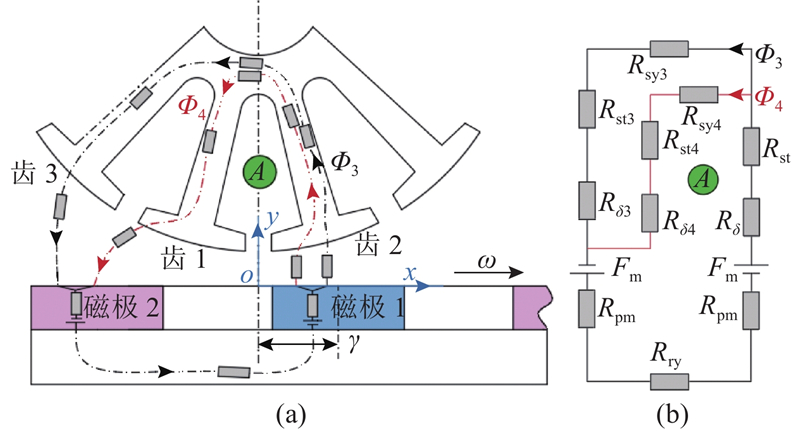
3)区域3:
图 7
图 7 区域3中的磁通路径及等效磁路模型
Fig.7 Flux path and equivalent magnetic circuit model in region 3
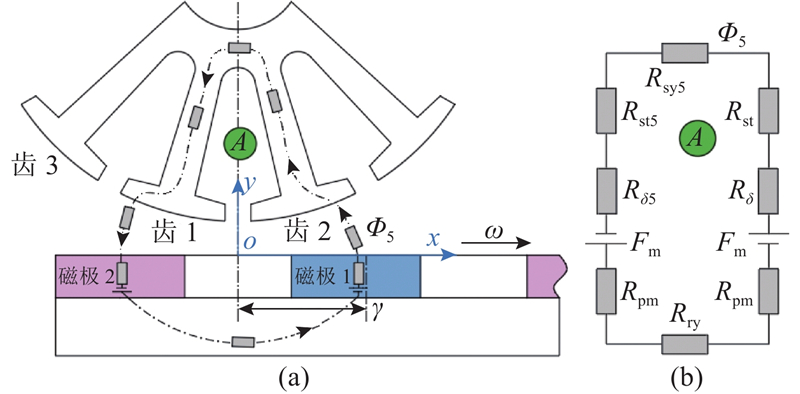
图 8
图 8 区域4中的磁通路径及等效磁路模型
Fig.8 Flux path and equivalent magnetic circuit model in region 4
图 9
3. 等效动态磁网络模型建立
在盘式转子转动过程中,定转子间的气隙在不断变化,气隙长度不是常数,而是关于盘式转子转动位置的函数. 气隙长度分布函数是建立等效气隙磁阻模型和构建等效动态磁网络的关键.
3.1. 不均匀气隙位置分布函数
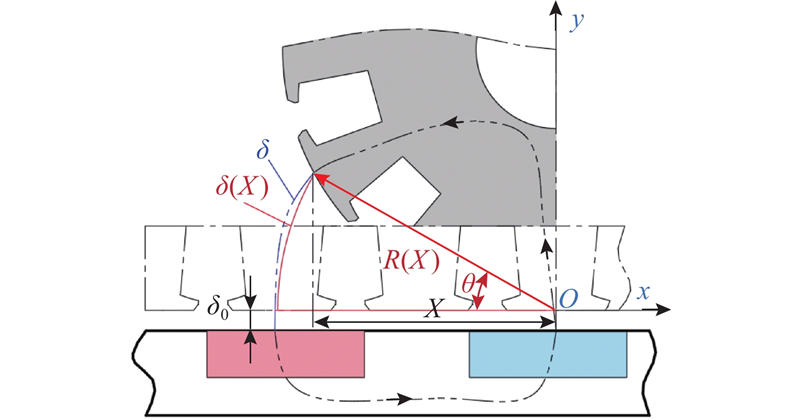
为了得到随盘式转子位置变化的气隙长度,建立不均匀气隙位置分布函数δ(X). 如图10所示,以盘式转子和行星定子一侧的气隙分布为分析对象,行星定子沿x轴展开为等效的直线定子模型,在定转子磁通回路中,实际的气隙长度δ(虚线部分)可以等效为磁力线流出时与行星定子上的交点在展开直线定子过程中以O点为圆心半径为R(X)的圆扫过的圆弧δ(X)(实线部分). 由不均匀气隙长度等效模型得到盘式行星永磁电机的等效气隙长度为
图 10
式中:
图 11
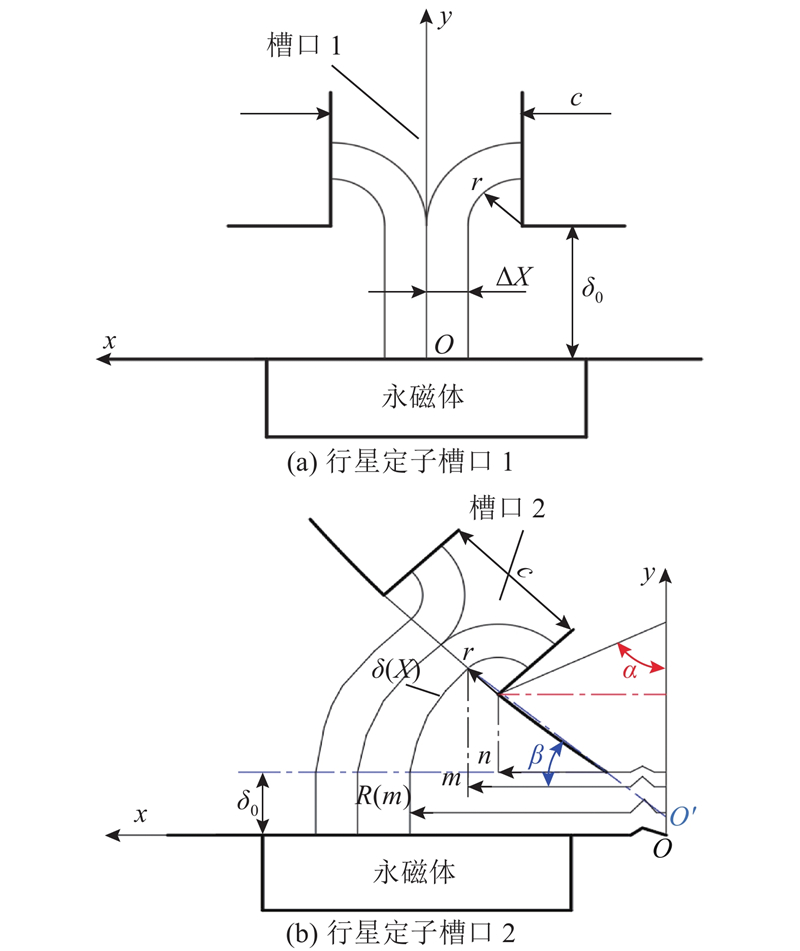
图 11 行星定子齿槽气隙磁路模型
Fig.11 Air gap magnetic circuit model of planetary stator slot
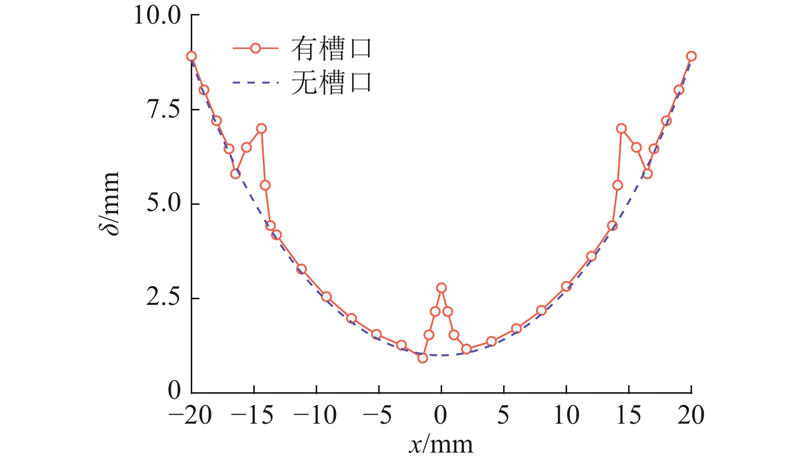
由式(5)得到定转子在半径Rr,1处的气隙长度,对比等效无槽行星定子的气隙长度,结果如图12所示. 可以看出,行星定子在槽口处气隙长度有明显的突变,此突变会影响流经槽口的气隙磁阻大小. 须用槽口气隙长度分布函数求解槽口处的气隙磁阻.
图 12
3.2. 等效气隙磁阻模型
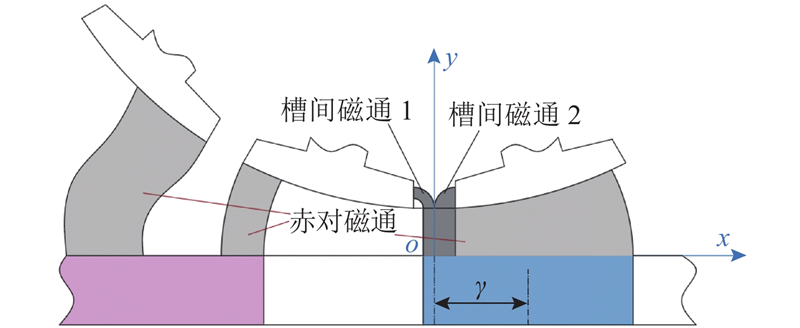
由动态磁路的分析可知,气隙磁通模型随着盘式行星永磁电机的转动而不断变化. 为了求得所提电机变化的气隙磁阻,建立盘式转子与行星定子之间的气隙磁通模型,示意图如图13所示. 根据气隙磁通的流向,气隙磁通模型可分为齿对磁通和槽间磁通,槽间磁通由于行星定子槽口的影响,磁路产生畸变,使得槽间磁通形状与齿对磁通有所不同.
图 13
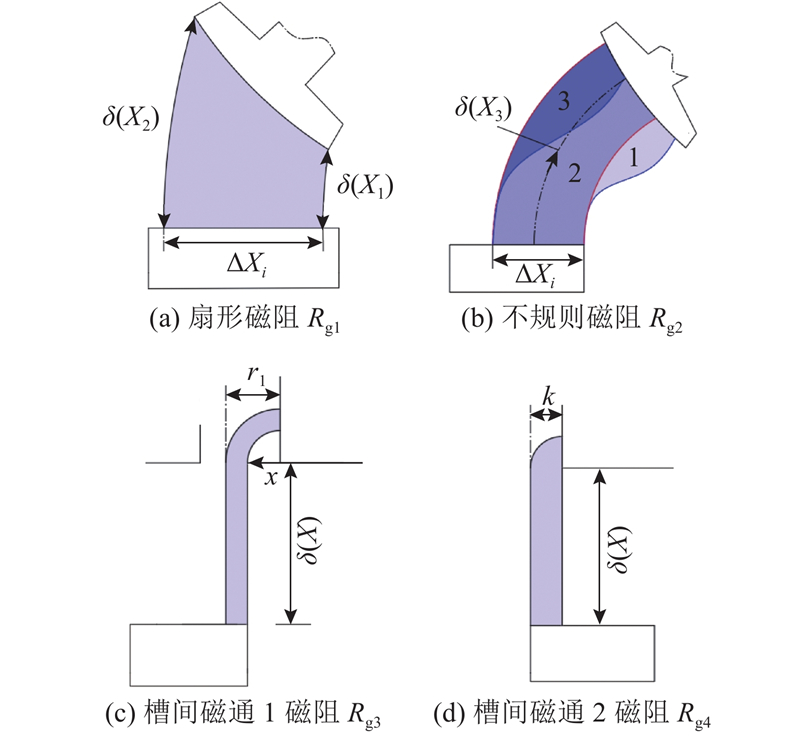
如图14所示,通过分析磁通模型可以得到4种典型的气隙磁阻模型,其中齿对磁通形状等效为扇形磁通和不规则磁通. 在进行齿对磁通求解时,扇形磁通两侧的气隙长度根据盘式转子与行星定子的相对位置并由不均匀气隙位置分布函数求得;将不规则气隙模型(阴影1、2)等效成扇形磁通模型(阴影2、3),便可按照扇形磁通求解气隙磁阻Rg2. 槽间磁通1为矩形加1/4圆环,槽间磁通2为矩形加1/4半圆,槽间磁通的气隙长度由有槽口气隙长度分布函数得到. 由上述气隙磁通模型可以得到4种典型气隙磁通的磁导表达式,分别为
图 14
式中:
3.3. 漏磁模型建立
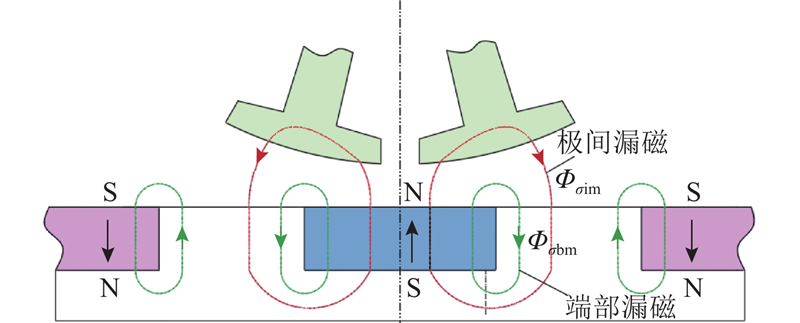
为了简化磁网络模型,建立动态磁路模型时只分析与绕组匝链的主磁通Φi和有效漏磁通Φσ,没有考虑未与电枢绕组匝链的漏磁通Φσm. 对盘式行星永磁电机在运行过程中定转子间产生的漏磁进行分析计算[22],具体漏磁形式如图15所示. 图中,Φσbm、Φσim分别为永磁体端部漏磁通和定转子齿之间的极间漏磁通. 可以看出,盘式行星永磁电机的漏磁[23]主要2个部分组成: 永磁体的端部漏磁, 盘式转子与行星定子齿之间的极间漏磁. 在盘式转子与行星定子间的磁通中,由于不均匀气隙的存在,盘式转子上永磁体齿与行星定子极靴有相对错位,导致永磁体一部分磁通在流经行星定子极靴后未经过行星定子轭部又流回盘式转子永磁体齿,这一部分漏磁通被称为极间漏磁. 通过分析发现,极间漏磁仅存在于磁齿与行星定子齿1、2之间,并随着永磁体与定子极靴的重合面积增加而不断减少;端部漏磁是由永磁体的端部而产生的漏磁,是永磁电机不可避免的漏磁情况.
图 15
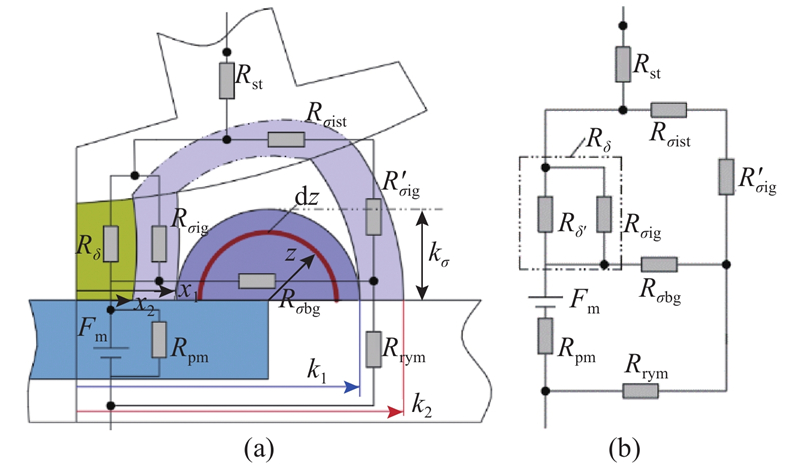
为了得到漏磁通的气隙磁阻,建立盘式行星永磁电机定转子间漏磁模型如图16所示,其中Rσig、Rσbg分别为极间漏磁和端部漏磁对应的气隙漏磁磁阻,Rσist为极间漏磁经过的定子齿部磁阻,Rrym为漏磁通经过的转子轭部磁阻. 漏磁区域中各部等效气隙磁阻及磁导的表达式分别为
图 16
3.4. 动态等效磁网络建立
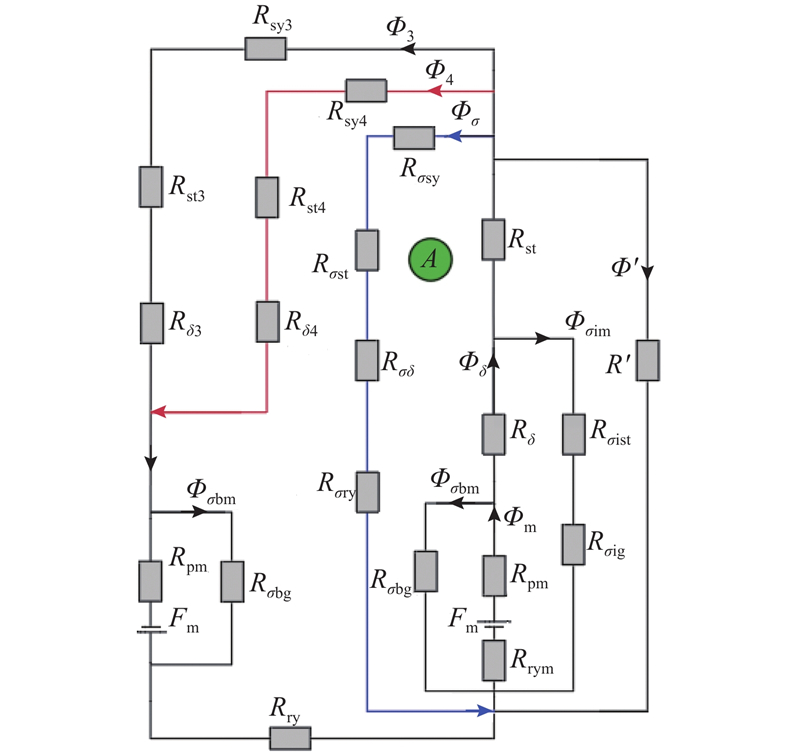
由动态磁路模型分析可知,每支与A相绕组匝链的磁路都要经过行星定子齿2. 将划分的动态磁路进行整合并简化成具有时变性的二维等效磁网络模型,得到一对极下的等效动态磁网络模型,如图17所示. 根据基尔霍夫定律列出等效动态磁网络的磁动势方程矩阵. 各磁通在半个电周期内的磁网络磁动势表达式为
图 17
图 17 一对极下的等效磁网络模型
Fig.17 Equivalent magnetic network model for one pair of poles
式中:Φ为各支路中的磁通向量,F为支路中的磁动势列向量,R为等效磁阻系数矩阵.
4. 有限元分析及实验验证
4.1. 电机三维有限元分析
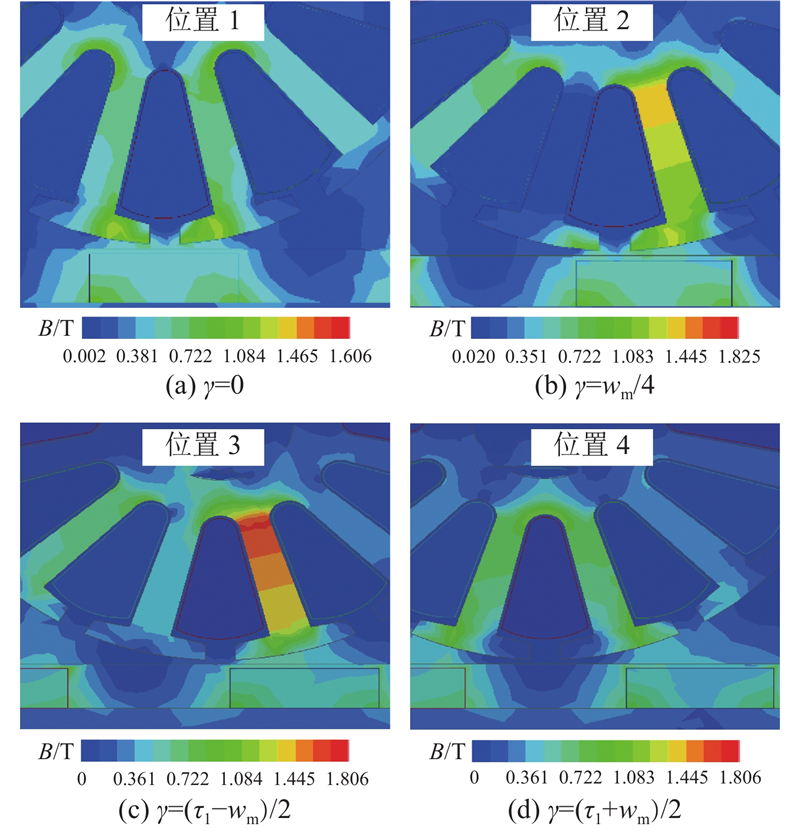
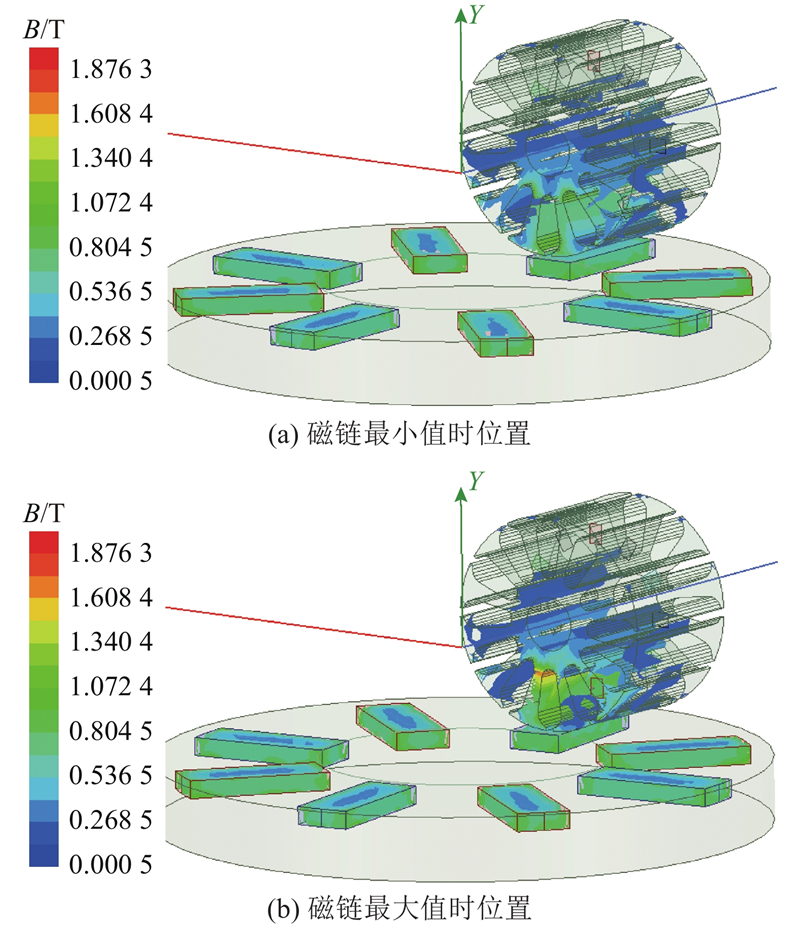
图 18
图 18 磁链极值的行星定子磁场分布
Fig.18 Planetary stator magnetic field distribution for flux linkage extreme values
4.2. 磁网络解析计算及实验验证
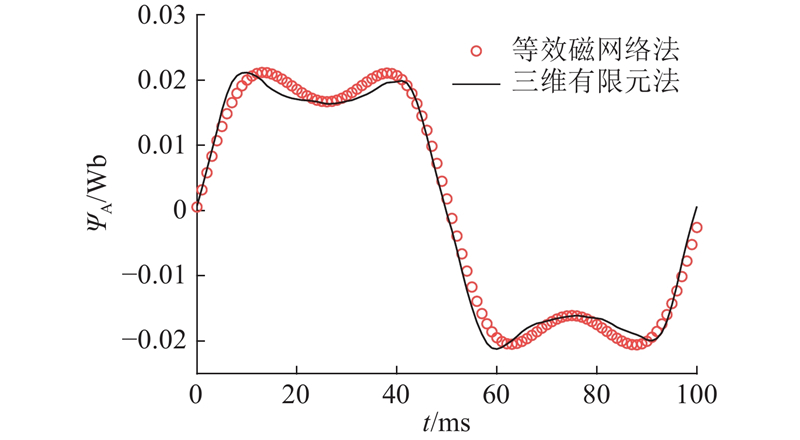
为了提高电机初期设计效率,通过有限元分析,在误差允许范围内,将盘式转子和行星定子模型的分环数最终确定为6个,利用等效磁网络法分别求解磁链和空载反电势,进行结果叠加,再与有限元和样机实验进行对比. 三维有限元和等效磁网络模型计算得到该电机A相的磁链波形如图19所示. 由于空气磁导率远小于铁心,使得气隙磁阻两端的磁压降远大于铁心磁阻,在忽略铁心磁阻,不考虑磁饱和的情况下,动态磁网络求解结果与有限元仿真得到的磁链波形基本吻合. 由图可知,动态磁网络计算结果的峰值与三维有限元仿真的平均相对误差为6.97%. 误差的主要原因是未考虑电机空间漏磁,使得磁网络计算结果偏大. 2种方法计算的磁链波形在波峰处有一定位置偏离,原因是在对盘式转子与行星定子分环时,将分环后的盘式转子等效成直线运动下的转子,行星定子与等效直线转子之间的各磁路区域与分环前实际定转子各磁路区域存在位置上的偏离.
图 19
图 19 一对极在单个电周期下的磁链波形对比
Fig.19 Comparison of flux linkage waveform for one pair of poles in one electrical cycle
等效磁网络和三维有限元所用的时间Ts以及对应的剖分网格数Ng如表1所示,由表可知,采用等效磁网络法求解磁场的精度相对较高,耗时少,效率高,适用于新型电机设计的初期阶段.
表 1 不同有限元分析方法的计算资源比较
Tab.1
| 方法名称 | Ng | Ts/s |
| 等效磁网络法 | 32 | 318 |
| 三维有限元法 | 16 157 |
图 20
表 2 电机设计的主要参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| 行星定子外径Dsout/mm | 60 | 行星轮轴向长度la/mm | 40 | |
| 盘式转子外径Drout/mm | 180 | 盘式转子磁齿数z1 | 8 | |
| 行星转子外径Dpout/mm | 60 | 行星轮磁齿数z2 | 4 | |
| 永磁体厚度hpm/mm | 5 | 行星定子极数 | 4 | |
| 永磁体长度lm/mm | 40 | 绕组匝数 | 100 | |
| 行星轮 | 4 | 最小气隙长度δ0/mm | 1 |
式中:EA为A相绕组空载反电势,ΨA为A相绕组磁链. 等效磁网络法与样机实验及三维有限元仿真得到的A相绕组一对极在一个电周期内的空载反电势波形如图21所示. 可以看出,利用磁网络法解析计算的空载反电势波形与样机实验及三维有限元的变化基本一致,能够反映该电机的空载反电势变化趋势和幅值大小. 磁网络求解得到的空载反电势波形相对于样机实验和有限元有一定的误差,这是求导对磁链偏差有放大作用导致的. 此外,A相绕组磁链波峰的偏离使得对磁链求导后空载反电势的波形受到有一定影响.
图 21
图 21 一对极在单个电周期下的反电势波形对比
Fig.21 Comparison of back electromotive force waveform for one pair of poles in one electric cycle
5. 结 论
(1)利用分环的思想,将盘式转子与行星定子间的三维磁路模型简化为二维磁路模型. 该方法能够节省大量的分析时间,提高所提新型电机初期设计效率.
(2)针对所提新型电机气隙结构不均匀的特点,在考虑行星定子槽口影响下构建不均匀气隙位置分布函数. 计算气隙磁阻时引入该函数,得到随位置变化的动态气隙磁阻模型,进一步提高气隙磁阻计算的精度.
(3)考虑不均匀气隙长度和漏磁的影响,建立所提新型电机的等效气隙磁阻和漏磁磁阻. 通过划分动态磁路区域,构建电机动态等效磁网络模型. 等效磁网络能够简化磁场的计算模型,有利于提高磁场计算效率.
(4)通过对比三维有限元仿真与等效磁网络模型的磁链计算结果以及实验样机的空载反电势结果,验证了所建等效磁网络模型的有效性和正确性. 等效动态磁网络模型可以节省计算时间,提高所提电机的初期设计效率,为后续该电机的电磁参数优化奠定基础.
新型盘式行星永磁电机仍处于初期研究阶段,通过进一步优化该电机结构参数来提高其气隙磁密,改善反电势的正弦性是未来研究的方向和重要课题.
参考文献
Multimode optimization research on a multiport magnetic planetary gear permanent magnet machine for hybrid electric vehicles
[J].DOI:10.1109/TIE.2018.2813966 [本文引用: 1]
高性能电机系统的共性基础科学问题与技术发展前沿
[J].
Common basic scientific problems and development of leading-edge technology of high performance motor system
[J].
新型外转子磁齿轮复合电机的设计与研究
[J].DOI:10.3321/j.issn:0258-8013.2008.30.011 [本文引用: 1]
Design and research of a novel magnetic-geared outer-rotor compact machine
[J].DOI:10.3321/j.issn:0258-8013.2008.30.011 [本文引用: 1]
Design, analysis and realization of a high-performance magnetic gear
[J].
低速大转矩永磁直驱电机研究综述与展望
[J].
Review and prospect of low-speed high-torque permanent magnet machines
[J].
Conveyor system with a highly integrated permanent magnet gear and motor
[J].DOI:10.1109/TIA.2020.2977877 [本文引用: 1]
Multimode optimization research on a multiport magnetic planetary gear permanent magnet machine for hybrid electric vehicles
[J].
Modeling of uneven air gap magnetic field for disc planetary permanent magnet machine with segmented gap Halbach array
[J].DOI:10.1109/TEC.2022.3206403 [本文引用: 1]
Analysis of end-effect torque and multi-objective optimization for multi-port spatial permanent magnet synchronous motor
[J].
A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnet synchronous motors in wide speed range
[J].
聚磁式横向磁通永磁直线电机的变磁导等效磁网络
[J].
Variable permeability equivalent magnetic circuit network of flux-concentrated transverse flux permanent magnet linear machine
[J].
无刷双馈电机运行特性的等效磁网络分析法
[J].
Operating performances analysis of brushless doubly-fed machine using magnetic equivalent circuit
[J].
新型横向磁通永磁电机三维磁路分析
[J].
3D magnetic circuit analysis of a novel transverse flux permanent magnet machine
[J].
基于网格剖分法的磁通切换永磁电机等效磁网络建模与分析
[J].DOI:10.1360/SST-2020-0388 [本文引用: 1]
Modeling and analysis of a mesh-based equivalent magnetic circuit for a flux switching PM machine
[J].DOI:10.1360/SST-2020-0388 [本文引用: 1]
轴向磁场盘式永磁电机等效磁路网络及气隙漏磁的分析计算
[J].
Lumped parameter magnetic circuit analysis of axial flux permanent magnet motor and its analytical calculation of air gap leakage
[J].
磁通切换型永磁电机非线性磁网络分析
[J].DOI:10.3969/j.issn.1000-6753.2015.02.005 [本文引用: 1]
Analysis of nonlinear magnetic network models for flux-switching permanent magnet machines
[J].DOI:10.3969/j.issn.1000-6753.2015.02.005 [本文引用: 1]
A novel mesh-based equivalent magnetic network for performance analysis and optimal design of permanent magnet machines
[J].DOI:10.1109/TEC.2019.2900263 [本文引用: 1]
单边盘式感应电机的数学模型与转矩分析
[J].
Modeling and torque analysis of a disc induction motor
[J].
横向磁通永磁同步电机非线性动态等效磁网络模型分析
[J].
Nonlinear dynamic equivalent magnetic network model analysis of transverse flux permanent magnet synchronous motor
[J].
轴向磁通永磁电机空载气隙磁场建模分析
[J].
Analysis and modeling for open circuit air gap magnetic field prediction in axial flux permanent magnet machines
[J].
Analysis and modeling of air-gap and zigzag leakage fluxes in a surface-mounted permanent-magnet machine
[J].DOI:10.1109/TIA.2003.821790 [本文引用: 1]
Performance analysis of a coreless axial-flux PMSM by an improved magnetic equivalent circuit model
[J].DOI:10.1109/TEC.2020.3040009 [本文引用: 1]