浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(10): 2171-2181 doi: 10.3785/j.issn.1008-973X.2024.10.021

电子与电气工程

基于滑模自抗扰的储能变流器控制策略

皇金锋,, 周杰, 黄红杰

陕西理工大学 电气工程学院，陕西 汉中 723001

Control strategy of power conversion system based on sliding mode active disturbance rejection control

HUANG Jinfeng,, ZHOU Jie, HUANG Hongjie

School of Electrical Engineering, Shaanxi University of Technology, Hanzhong 723001, China

收稿日期: 2023-09-19  

基金资助: 陕西省自然科学研究资助项目（2023-JC-YB-442）.

Received: 2023-09-19  

Fund supported: 陕西省自然科学研究资助项目（2023-JC-YB-442）.

作者简介 About authors

皇金锋（1978—），男，教授，硕导，从事电力电子变换器的非线性控制研究.orcid.org/0000-0003-4846-3699.E-mail：jfhuang2000@163.com , E-mail：jfhuang2000@163.com

摘要

为了提高储能变流器(PCS)的动态性能，设计基于降阶级联扩张状态观测器(ESO)和互补滑模控制(CSMC)的改进自抗扰控制(ADRC)策略，将改进ADRC策略应用于PCS的双向DC/AC变流器电压外环. 改进ESO为降阶级联ESO以提高状态变量和系统总扰动的估计速度，增加扰动估计能力；更改PD控制为CSMC以设计状态误差反馈律，提升PCS的系统鲁棒性；设计改进指数趋近律以抑制抖振现象. 为了证明改进ADRC策略相较于PI控制和传统ADRC的优越性，建立仿真模型并搭建相关实验平台. 仿真与实验结果表明，改进ADRC策略减小了PCS暂态时直流母线电压波动，提高了PCS交流侧功率响应速度，改善了交流侧的输出电能质量.

关键词： 储能变流器（PCS） ; 自抗扰控制（ADRC） ; 降阶级联扩张状态观测器 ; 互补滑模控制（CSMC） ; 改进指数趋近律

Abstract

In order to improve the dynamic performance of the power conversion system (PCS), an improved active disturbance rejection control (ADRC) strategy based on reduced-order cascaded extended state observer (ESO) and complementary sliding mode control (CSMC) was designed and applied to the voltage outer loop of the bidirectional DC/AC converter in the PCS. The ESO was modified to a reduced-order cascaded ESO to improve the estimation speed of the state variables and the overall disturbance, enhancing the disturbance estimation capability. The PD control was replaced with CSMC to design a state error feedback law to enhance the robustness of the system, and an improved exponential reaching law was designed to suppress the chattering phenomenon. A simulation model was established and a related experimental platform was built to demonstrate the superiority of the improved ADRC strategy compared to PI control and traditional ADRC. The simulation and experimental results show that the improved ADRC strategy reduces the fluctuation of the DC bus voltage during the transient operation of the PCS, improves the power response speed on the AC side of the PCS, and enhances the output power quality on the AC side.

Keywords： power conversion system (PCS) ; active disturbance rejection control (ADRC) ; reduced-order cascaded extended state observer ; complementary sliding mode control (CSMC) ; improved exponential reaching law

PDF (1993KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

皇金锋, 周杰, 黄红杰. 基于滑模自抗扰的储能变流器控制策略. 浙江大学学报(工学版)[J], 2024, 58(10): 2171-2181 doi:10.3785/j.issn.1008-973X.2024.10.021

HUANG Jinfeng, ZHOU Jie, HUANG Hongjie. Control strategy of power conversion system based on sliding mode active disturbance rejection control. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(10): 2171-2181 doi:10.3785/j.issn.1008-973X.2024.10.021

全球能源消耗迅速增长，传统能源面临巨大危机，各国都在积极发展清洁能源[1-3]. 分布式电源应运而生，它具有一定的间歇性，输出的功率不稳定，直接接入电网会影响配电网的稳定运行，严重时还会降低配电网的安全性. 建立储能系统是解决这一问题的有效方法. 以光储联合发电系统[4]为例，光照、温度和负荷投切等因素导致功率流动方向随机变化，直流母线电压发生波动，从而影响系统的稳定性[5-6].

控制储能变流器(power conversion system, PCS)达到最大化匹配负载，减少暂态直流母线电压的波动具有重要意义. 根据微电网的实际需求，不同情况下须采用不同的控制框架，常用的控制策略有电压电流双闭环控制、VSG控制、恒功率控制、恒压恒频控制和下垂控制等[7]. 并网变流器大多采用电压电流双闭环控制以保证直流母线电压的稳定性，降低冲击电流对储能电池的影响[8]. 在PCS的控制算法中，传统的PI控制是线性算法，易于实现但难以达到理想的控制效果，因此学者们提出了许多非线性的控制策略. 韩刚等[9]提出LCL型变流器的滑模控制策略，该策略虽然提高了风电变流器电网电压不平衡故障下的运行稳定性，但是滑模控制会引发抖振问题，使得系统能耗增加. Kim等[10]在变流器上提出基于干扰观测器的无偏置模型预测控制算法，该控制算法虽然克服了传统电压定向控制策略的缺点，但是模型预测控制的计算量较大且参数众多，实际应用受限. 林晓冬等[11]在T型三电平变流器上提出能量成型控制策略，该策略能够抑制谐波畸变并实现了较好的功率跟踪性能，但是基于数学模型设计的能量成型控制器对数学模型精度要求较高，在现实中难以获得. 王宁[12]提出自适应算法和模糊控制相结合的控制策略，提高了储能变流器的动态和稳态性能，但模糊控制规则中的模糊子集和隶属度函数选择均凭经验设计，缺少相应的理论根据和数学推导. 在众多非线性控制中，自抗扰控制(active disturbance rejection control, ADRC)无需系统有精确的模型，是以扩张状态观测器(extended state observer, ESO)为核心的非线性控制策略，它通过估计系统的内外部总扰动并加以补偿来提升系统的控制精度，在电力电子领域被广泛使用[13-16]. 系统实际运行过程中会受到各种环境因素的影响，电容和电感的实际值不是标称值，将ADRC策略应用于PCS，可以在系统参数估计不准确的情况下获得良好的控制效果以满足实际需求. 传统ADRC策略采用ESO，观测器的观测能力有限，容易造成观测残留而限制ADRC的性能[17]，采用PD控制作为误差反馈律存在鲁棒性不高、响应速度慢的问题[18].

本研究以PCS为对象，为双向DC/AC变流器部分电压外环设计基于降阶级联ESO和改进互补滑模控制(complementary sliding mode control, CSMC)的ADRC策略. 与传统ADRC相比，降阶级联ESO能够提升对状态变量和总扰动的观测能力和估计速度；CSMC能够优化状态误差反馈律，提升系统鲁棒性；改进指数趋近律能够抑制滑模固有的抖振现象. 开展仿真和实验，验证所提控制策略的正确性.

1. 储能变流器的数学模型

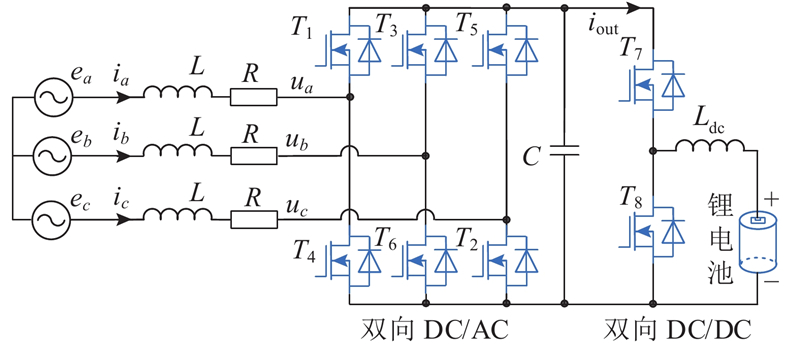
如图1所示，PCS的电路拓扑结构由双向DC/AC变流器和双向DC/DC变换器组成. 图中，L为滤波电感，R为电网侧线路等效电阻，ia、ib、ic均为电网侧相电流，ea、eb、ec均为电网侧相电压，ua、ub、uc均为PCS交流侧各相的电压，开关管T1~T8构成PCS的主体结构，C为直流侧稳压电容，iout为前级双向DC/AC变流器输入后级双向DC/DC变换器的电流.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   储能变流器的电路拓扑结构

Fig.1   Circuit topology of power conversion system


当电网电压三相波形对称时，根据基尔霍夫定律得到双向DC/AC变流器在a、b、c三相静止坐标系下的电压和电流方程为

$ \left. \begin{gathered} L\frac{{{\mathrm{d}}{i_a}}}{{{\mathrm{d}}t}} = {e_a} - {u_a} - R{i_a}, \\ L\frac{{{\mathrm{d}}{i_b}}}{{{\mathrm{d}}t}} = {e_b} - {u_b} - R{i_b}, \\ L\frac{{{\mathrm{d}}{i_c}}}{{{\mathrm{d}}t}} = {e_c} - {u_c} - R{i_c}, \\ C\frac{{{\text{d}}{u_{{\text{dc}}}}}}{{{\text{d}}t}} = {S _a}{i_a}+{S _b}{i_b}+{S _c}{i_c} - {i_{{\text{out}}}}. \\ \end{gathered} \right\} $
(1)

式中：udc为电容C两端的电压，即直流母线电压；Sk为晶闸管工作状态的开关函数，定义式为

$ {S} _{k}=\left\{ \begin{array}{l}1\text{，}上桥臂导通；\\ 0\text{，}下桥臂导通.\end{array}\right.\; $
(2)

$k=a,b,c. $通过派克变换得到在d、q两相旋转坐标系下的电压和电流方程为

$ \left. \begin{gathered} L\frac{{{\text{d}}{i_d}}}{{{\text{d}}t}} = {e_d} - R{i_d}+\omega L{i_q} - {v_d}, \\ L\frac{{{\text{d}}{i_q}}}{{{\text{d}}t}} = {e_q} - R{i_q} - \omega L{i_d} - {v_q}, \\ C\frac{{{\text{d}}{u_{{\text{dc}}}}}}{{{\text{d}}t}} = \frac{3}{2}({S _d}{i_d}+{S _q}{i_q}) - {i_{{\text{out}}}}. \\ \end{gathered} \right\} $
(3)

式中：ω为电网电压的角频率，ed、id、Sd分别为电网侧在d轴上的电压、电流、开关函数，eq、iq、Sq分别为电网侧在q轴上的电压、电流、开关函数，vd、vq分别为双向DC/AC变流器逆变侧输出电压在d、q轴上的分量.

2. 控制器设计

2.1. 观测器设计

ESO是ADRC的核心部分，根据观测器的设计思想，将影响被控对象的总扰动扩张成新的状态变量加以补偿，对udc求二阶导，由式(3)得到

$ {\ddot u_{{\text{dc}}}} = b{i_d}+F .$
(4)

式中：F为系统的总扰动，b为系统的输入增益，

$ \begin{split} & F = \frac{{3{S _d}}}{{2CL}}({e_d}+\omega L{i_q} - {v_d})+\frac{{3{S _q}}}{{2CL}}({e_q} - R{i_q} - {v_q}) - \frac{{{\text{d}}{i_{{\text{out}}}}}}{{{\text{d}}t}} \text{，}\\& b = - \left( {\frac{{3R{S _d}}}{{2CL}}+\frac{{3\omega {S _q}}}{{2C}}} \right) .\end{split} $

定义直流母线电压跟踪误差为

$ \theta = {u_{{\text{ref}}}} - {u_{{\text{dc}}}}. $
(5)

式中：uref为直流母线的参考电压. 联立式(4)和式(5)得到

$ \ddot \theta = {F_{\text{d}}} - {b_0}{i_d}. $
(6)

式中：$ {b_0} $为系统输入增益的估计值；Fd为系统新的总扰动，满足$ {F_{\text{d}}} = {\ddot u_{{\text{ref}}}} - F+({b_0} - b){i_d} $. 将$ {F_{\text{d}}} $扩张为新的状态变量，令$ {x_1} = \theta $、$ {x_2} = {\dot x_1} $、$ {x_3} = {F_{\text{d}}} $，系统的状态方程为

$ \left[ \begin{gathered} {{\dot x}_1} \\ {{\dot x}_2} \\ {{\dot x}_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \\ 0&0&0 \end{array}} \right]\left[ \begin{gathered} {x_1} \\ {x_2} \\ {x_3} \\ \end{gathered} \right]+\left[ \begin{gathered} 0 \\ - {b_0}{i_d} \\ {{\dot F}_{\text{d}}} \\ \end{gathered} \right]. $
(7)

针对式(7)设计ESO为

$ \left[ \begin{gathered} {{\dot \varphi }_1} \\ {{\dot \varphi }_2} \\ {{\dot \varphi }_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} { - 3{\omega _0}}&1&0 \\ { - 3{\omega _0}^2}&0&1 \\ { - {\omega _0}^3}&0&0 \end{array}} \right]\left[ \begin{gathered} {\varphi _1} \\ {\varphi _2} \\ {\varphi _3} \\ \end{gathered} \right]+\left[ \begin{gathered} 3{\omega _0}{x_1} \\ 3{\omega _0}^2{x_1} - {b_0}{i_d} \\ {\omega _0}^3{x_1} \\ \end{gathered} \right]. $
(8)

式中：ω0为观测器带宽，φ1、φ2、φ3分别为x1、x2、x3的估计值.

传统ESO对总扰动存在不完全估计，使用这种观测器的控制精度有限，限制了ADRC的性能[17]，为此Lakomy等[19]提出采用2个ESO级联的方式来提高扰动估计精度，改善系统动态性能. 为了提高扰动估计速度，减小相位滞后，本研究提出降阶级联ESO，设计过程如下. 状态变量x1由电压传感器测得，将式(8)改写为

$ \left[ \begin{gathered} {\varphi _2} \\ {\varphi _3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right]\left[ \begin{gathered} {z_2} \\ {z_3} \\ \end{gathered} \right]+\left[ \begin{gathered} 2{\omega _0} \\ {\omega _0}^2 \\ \end{gathered} \right]{x_1}. $
(9)

中间变量z2、z3满足

$ \left[ \begin{gathered} {{\dot z}_2} \\ {{\dot z}_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} { - 2{\omega _0}}&1 \\ { - {\omega _0}^2}&0 \end{array}} \right]\left[ \begin{gathered} {z_2} \\ {z_3} \\ \end{gathered} \right]+\left[ \begin{gathered} - 3{\omega _0}^2{x_1} - {b_0}{i_d} \\ - 2{\omega _0}^3{x_1} \\ \end{gathered} \right]. $
(10)

通过式(9)对ESO进行降阶处理，构建第二级降阶ESO估计剩余扰动，观测器设计为

$ \left[ \begin{gathered} {{\dot \varphi }_4} \\ {{\dot \varphi }_5} \\ \end{gathered} \right] = \left[ \begin{gathered} 2{\omega _0} \\ {\omega _0}^2 \\ \end{gathered} \right]\left( {{\varphi _2} - {\varphi _4}} \right)+\left[ \begin{gathered} {\varphi _3}+{\varphi _5} - {b_0}{i_d} \\ 0 \\ \end{gathered} \right]. $
(11)

式中：φ4、φ2均用以估计状态变量x2，φ5用以观测状态变量x3的残留观测值. 最终x2的观测值v2、x3的观测值v3分别表示为

$ {v_2} = {\varphi _4},\;{v_3} = {\varphi _3}+{\varphi _5}. $
(12)

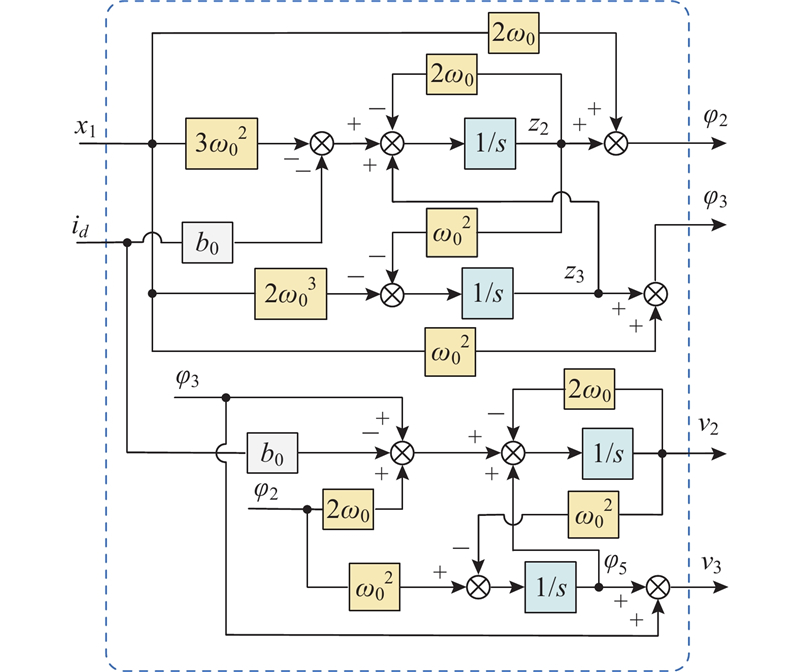
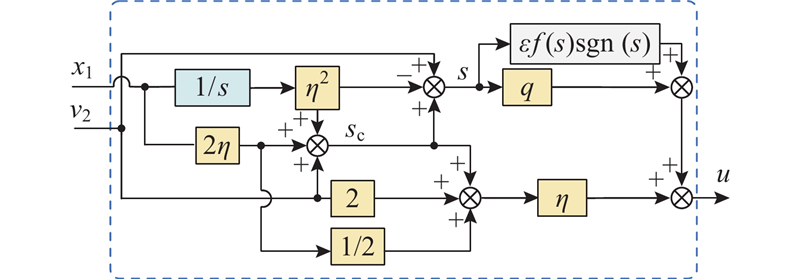
降阶级联ESO的控制策略框图如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   降阶级联扩张状态观测器控制策略框图

Fig.2   Block diagram of reduced-order cascaded extended state observer control strategy


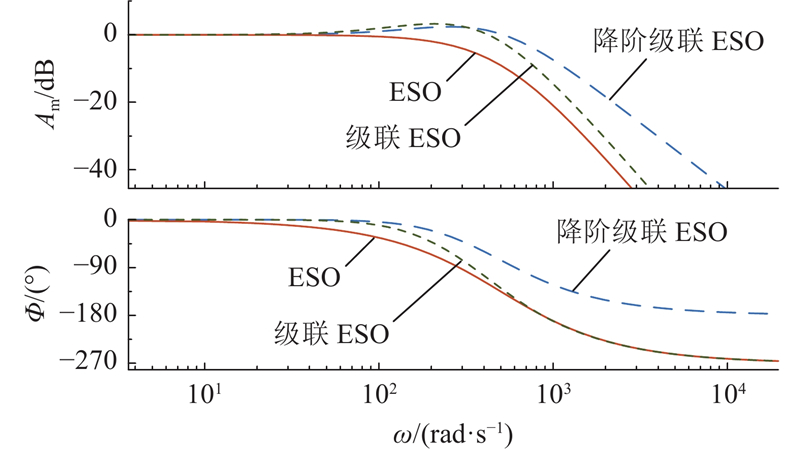
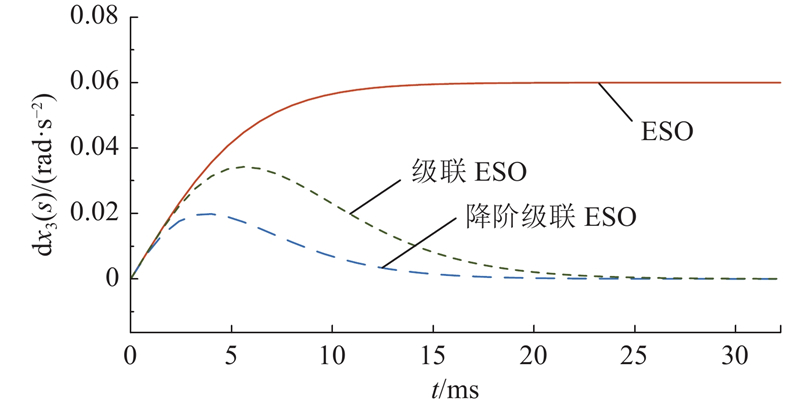
2.2. 观测器扰动估计能力评估

对式(8)和式(12)应用拉普拉斯变换，得到ESO和降阶级联ESO在复频域（s域）的扰动估计传递函数：

$ \frac{{{\varphi _3}(s)}}{{{x_3}(s)}} = \frac{{{\omega _0}^3}}{{{{\left( {s+{\omega _0}} \right)}^3}}},\quad\quad\quad\quad\quad\quad $
(13)

$ \frac{{{v_3}(s)}}{{{x_3}(s)}} = \frac{{{\omega _0}^2\left( {2{s^2}+4{\omega _0}s+{\omega _0}^2} \right)}}{{{{\left( {s+{\omega _0}} \right)}^4}}}. $
(14)

基于Lakomy等[19]所提方法求解得到三阶级联ESO的扰动估计传递函数为

$ G(s) = \frac{{{\omega _0}^3\left( {2{s^3}+6{\omega _0}{s^2}+6{\omega _0}^2s+{\omega _0}^3} \right)}}{{{{\left( {s+{\omega _0}} \right)}^6}}}. $
(15)

固定ω0=300 rad/s，式(13)~式(15)的波特图如图3所示. 图中，Am为幅值，Φ为相位. 由图可知，级联提高了中低频段的幅值增益，增强了扰动估计能力，降阶的引入有效改善了相位滞后的问题，在增强扰动估计能力的同时提高了扰动估计速度. 当集总扰动以斜率为10的斜坡变化时，不同观测器下的扰动估计误差对比结果如图4所示. 可以看出，传统ESO在斜坡扰动下存在稳态误差，ESO在级联后可以精确估计斜坡扰动. 此外，级联ESO在降阶处理后暂态估计误差更小，速度更快，有利于提高ADRC的性能.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   不同观测器的扰动估计能力

Fig.3   Disturbance estimation ability of different observers


图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   斜坡扰动的估计误差

Fig.4   Estimation errors of slope disturbance


2.3. 状态误差反馈律设计

传统的二阶ADRC系统状态误差反馈律由PD控制实现，当偏差过大时会降低系统的鲁棒性[20-21]，本研究引入CSMC来提高ADRC的控制性能和抗干扰能力. 定义广义滑模面为

$ {s_{\text{g}}} = \dot \theta +2\eta \theta +{\eta ^2} \int _0^t \theta (\tau ){\text{d}}\tau . $
(16)

式中：η为滑模面常数，满足η>0. 设计与广义滑模面正交的互补滑模面为

$ {s_{\text{c}}} = \dot \theta - {\eta ^2}\int_0^t \theta (\tau ){\text{d}}\tau . $
(17)

由式(16)和式(17)得到最终滑模面为

$ s = {s_{\text{c}}}+{s_{\text{g}}} = 2(\dot \theta +\eta \theta ). $
(18)

基于等效控制方法，设计等效控制律为

$ {u_{{\text{eq}}}} = \frac{{{v_3}+\eta (2{v_2}+\eta \theta +{s_{\text{g}}})}}{{{b_0}}}. $
(19)

进行切换控制器设计. 为了使闭环系统状态变量在有限时间内到达滑模面，选用指数趋近律. 传统的指数趋近律的表达式[22]为

$ \dot s = - \varepsilon {{\mathrm{sgn}}}\; (s) - qs. $
(20)

式中：ε、q为常数，满足ε>0，q>0. ε的取值无法调和滑模抖振问题和收敛速度问题，ε越大，滑模收敛速度越快，同时到达滑模面的速度也会越快，系统的抖振现象越明显[23]. 为此，研究设计新型趋近律，表达式为

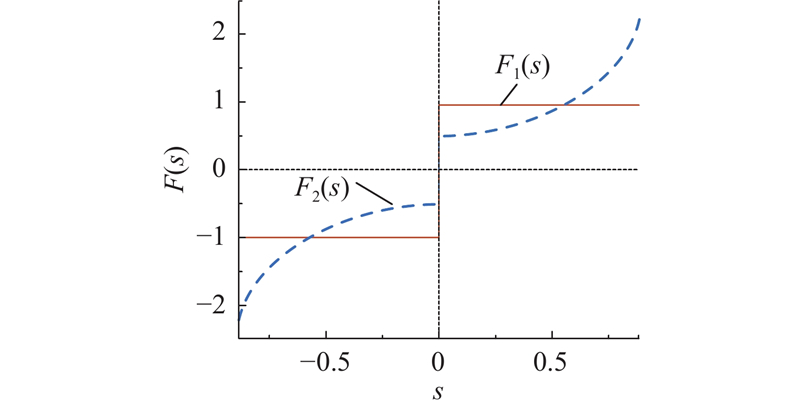
$ \left. \begin{gathered} \dot s = - \varepsilon f(s){\text{sgn}}\;(s) - qs, \\ f(s) = \frac{{{{\mathrm{e}}^{|s|}}}}{{1+{{\mathrm{e}}^{ - |s|}}}}. \\ \end{gathered} \right\} $
(21)

为了方便比较，定义函数$ {F_1}(s) = {{\mathrm{sgn}}}\; (s) $，$ {F_2}(s) = f(s){{\mathrm{sgn}}}\; (s) $，绘制函数$ {F_1}(s) $和$ {F_2}(s) $的图像如图5所示. 可以看出，当$ \left| s \right| \to \infty $时，$ \left| {{F_2}(s)} \right| \to \infty $，有$ \left| {{F_1}(s)} \right| < \left| {{F_2}(s)} \right| $，即在远离滑模面时，改进趋近律可以加快系统状态的趋近速度；当$ \left| s \right| \to 0 $时，$ \left| {{F_2}(s)} \right| \to 0.5 $,有$ \left| {{F_1}(s)} \right| > \left| {{F_2}(s)} \right| $，即在靠近滑模面时，改进趋近律可以降低系统状态的趋近速度，削弱抖振现象. 根据式(21)将切换鲁棒控制律设计为

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   改进指数趋近律函数的图像对比

Fig.5   Image comparison of functions for improved exponential reaching law


$ {u_{{\text{sw}}}} = \frac{{\varepsilon f(s){{\mathrm{sgn}}}\; (s)+qs}}{{{b_0}}}. $
(22)

联立式(19)和式(22)得到

$ {i_d} = {u_{{\text{eq}}}}+{u_{{\text{sw}}}} = \frac{{{v_3}+u}}{{{b_0}}}. $
(23)

其中，$ u = \eta [2{v_2}+\eta \theta +{s_{\text{g}}}]+\varepsilon f(s){{\mathrm{sgn}}} \;(s)+qs $. CSMC的控制策略框图如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   互补滑模控制策略框图

Fig.6   Block diagram of complementary sliding mode control strategy


2.4. 改进指数趋近律性能分析

以二阶典型系统为例，验证本研究设计的改进指数趋近律.

$ {{\dot a}_1} = {a_2}, \;{{\dot a}_2} = - 10{a_2} - 80d. $
(24)

式中：a1、a2为状态变量，d为输入变量. 根据CSMC的设计方法，取式(20)为趋近律，得到控制律为

$ {d_1} = \frac{{\eta (2{a_2}+\eta {a_1}+{s_{\text{g}}})+\varepsilon {{\mathrm{sgn}}}\; (s)+qs - 10{a_2}}}{{80}}. $
(25)

取式(21)为趋近律，得到控制律为

$ {d_2} = \frac{{\eta (2{a_2}+\eta {a_1}+{s_{\text{g}}})+\varepsilon f(s){{\mathrm{sgn}}}\; (s)+qs - 10{a_2}}}{{80}}. $
(26)

其中$ {s_{\text{g}}} = {a_2}+2\eta {a_1}+{\eta ^2}\displaystyle\int_0^t {a_1}(\tau ){\mathrm{d}}\tau $. 设定q=10、ε=50、η=5，系统初始状态为a1=a2=0.2. 根据式(25)、式(26)，对式(24)所示的系统进行仿真，结果如图7所示. 由图可知，相比于传统指数趋近律，改进指数趋近律趋近速度更快，不仅削弱了抖振现象，降低了控制器负担，还提高了系统性能.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

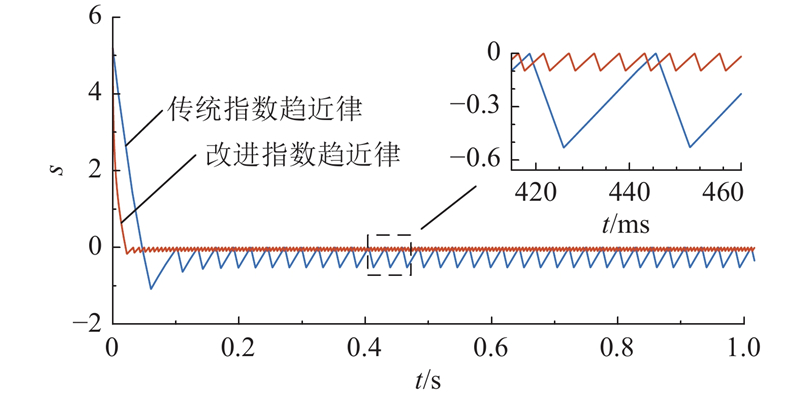
图 7   不同指数趋近律下滑模面随时间的变化

Fig.7   Variation of sliding mode surface with time under different exponential reaching laws


2.5. 储能变流器整体控制设计

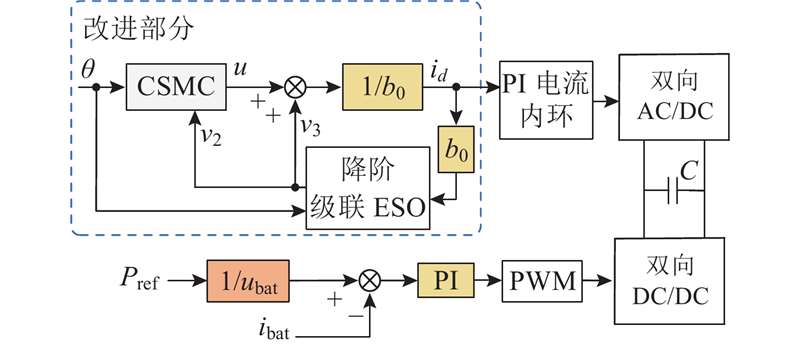
如图8所示为PCS的整体控制框架. 图中，ibat为储能电池侧输出电流，ubat为储能电池侧输出电压，Pref为储能电池发出或吸收功率的参考值. 双向DC/AC变流器采用改进的电压外环和PI电流内环控制策略，通过双向DC/AC变换器控制直流母线电压的稳定以及直流侧和交流侧之间能量的转换；双向DC/DC变换器采用PI电流单环控制策略，通过双向DC/DC变换器控制储能电池的输出功率匹配负荷所需功率.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   储能变流器的框图

Fig.8   Block diagram of power conversion system


3. 稳定性证明

3.1. 降阶级联扩张状态观测器稳定性证明

将降阶级联ESO的状态变量观测误差定义为$ {\xi _2} = {v_2} - {x_2} $、$ {\xi _3} = {v_3} - {x_3} $. 联立式(9)~式(12)，得到

$ \left[ \begin{gathered} {{\dot \xi }_2} \\ {{\dot \xi }_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} { - 2{\omega _0}}&1 \\ { - {\omega _0}^2}&0 \end{array}} \right]\left[ \begin{gathered} {\xi _2} \\ {\xi _3} \\ \end{gathered} \right] - \left[ \begin{gathered} 0 \\ {{\dot F}_{\text{d}}} \\ \end{gathered} \right]. $
(27)

令$ {E_2} = {\xi _2} $、$ {E_3} = - 2\omega {\xi _2}+{\xi _3} $，则式(27)化为

$ \left[ \begin{gathered} {{\dot E}_2} \\ {{\dot E}_3} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 0&1 \\ { - {\omega _0}^2}&{ - 2{\omega _0}} \end{array}} \right]\left[ \begin{gathered} {E_2} \\ {E_3} \\ \end{gathered} \right] - \left[ \begin{gathered} 0 \\ {{\dot F}_{\text{d}}} \\ \end{gathered} \right]. $
(28)

本研究考虑的扰动为变化不甚激烈的扰动，该扰动的微分$ {\dot F_{\text{d}}} $有界. 构造二次型$ W = - 2{\omega _{\text{0}}}^2{E_3}^2 $，求解满足条件dV/dt=2W的李亚普洛夫函数[24]为

$ V = 2{\omega _0}^3{E_2}^2+2{\omega _0}{E_3}^2 \geqslant 0. $
(29)

对式(29)求导得到

$ \dot V = - 8{\omega _0}^2{E_3}^2 - 4{\omega _0}{E_3}{\dot F_{\text{d}}}. $
(30)

当扰动微分项$ {\dot F_{\text{d}}} = 0 $时，有$ \dot V < 0 $，系统以零点为平衡点大范围渐进稳定[25]；当扰动微分项$ {\dot F_{\text{d}}} \ne 0 $时，规定$ \left| {{{\dot F}_{\text{d}}}} \right| \leqslant R $，R为常数，当系统达到稳态后有

$ {\dot E_2} = {\dot E_3} = 0. $
(31)

将式(31)代入式(28)，得到稳态误差范围:

$ \left| {{\xi _2}} \right| \leqslant R/{\omega _0}^2, \;\left| {{\xi _3}} \right| \leqslant 2R/{\omega _0}. $
(32)

3.2. 互补滑模控制稳定性证明

定义如下李亚普洛夫函数：

$ V = \frac{1}{2}{s_{\mathrm{c}}}^2+\frac{1}{2}{s_{\mathrm{g}}}^2 \geqslant 0. $
(33)

对式(33)求导得到

$ \dot V = s({\dot s_{\mathrm{g}}} - \eta s+\eta {s_{\mathrm{g}}}). $
(34)

将式(6)和式(23)代入式(34)得到

$ \dot V = s({e_3}+2\eta {e_2} - (q+\eta )s - \varepsilon f(s){{\mathrm{sgn}}} \;(s)). $
(35)

式中：e2=$\ddot \theta $−v2，e3=Fd−v3. 降阶级联ESO的稳定性已被证明，式(35)变为

$ \dot V = - (q+\eta ){s^2} - \varepsilon sf(s){{\mathrm{sgn}}}\; (s) \leqslant 0. $
(36)

因此，所设计滑模控制律在李亚普洛夫意义上稳定，系统状态变量将在有限时间内到达滑模面. 在到达滑模面$ s = 2(\dot \theta +\eta \theta ) $之后，系统状态变量将沿着滑模面渐进收敛到零. 当状态误差反馈律采用普通滑模控制时，有

$ s = \dot \theta +\eta \theta . $
(37)

由式(37)得到

$ \theta = \int_0^t {{\theta ^{ - \eta (t - \tau )}}} s(\tau ){\mathrm{d}}\tau . $
(38)

当系统状态点在边界层内时，存在领域Φ满足$ \left| s \right| \leqslant \varPhi $，即

$ \theta \leqslant \varPhi \int_0^t {{\theta ^{ - \eta (t - \tau )}}} {\mathrm{d}}\tau = \frac{\varPhi }{\eta }\int_0^t {{\theta ^{ - \eta (t - \tau )}}} {\mathrm{d}}\tau \leqslant \frac{\varPhi }{\eta }. $
(39)

同理，当采用CSMC控制时，由式(18)得到

$ \theta \leqslant \frac{\varPhi }{{2\eta }}. $
(40)

对比式(39)和式(40)可知，相比于普通滑模控制，CSMC的系统稳态误差减小了一半，控制精度提高.

4. 仿真与实验验证

4.1. 仿真分析

为了验证所设计控制策略的有效性，在Matlab/Simulink仿真软件中搭建仿真电路，进行所设计控制策略和传统ADRC策略的对比分析. 电路拓扑参数如表1所示. 观测器带宽的选择须综合考虑噪声影响和状态估计速度. ω0选取过大会引入较多噪声，选取过小又会降低状态估计速度，权衡后，取ω0=600 rad/s；取ε=150、q=300、η=650以实现降低互补滑模抖振的同时保证较快的收敛速度[26].

表 1   电路拓扑参数

Tab.1  Circuit topology parameter

参 数数 值参 数数 值
电网电压幅值/V311直流稳压电容C/mF2.2
直流母线电压udc/V700电池额定容量/（A·h）100
滤波电感L/mH1.0电池标称电压vbat/V400
电路等效电阻R/Ω0.01电池初始荷电状态SOC/%50

新窗口打开| 下载CSV


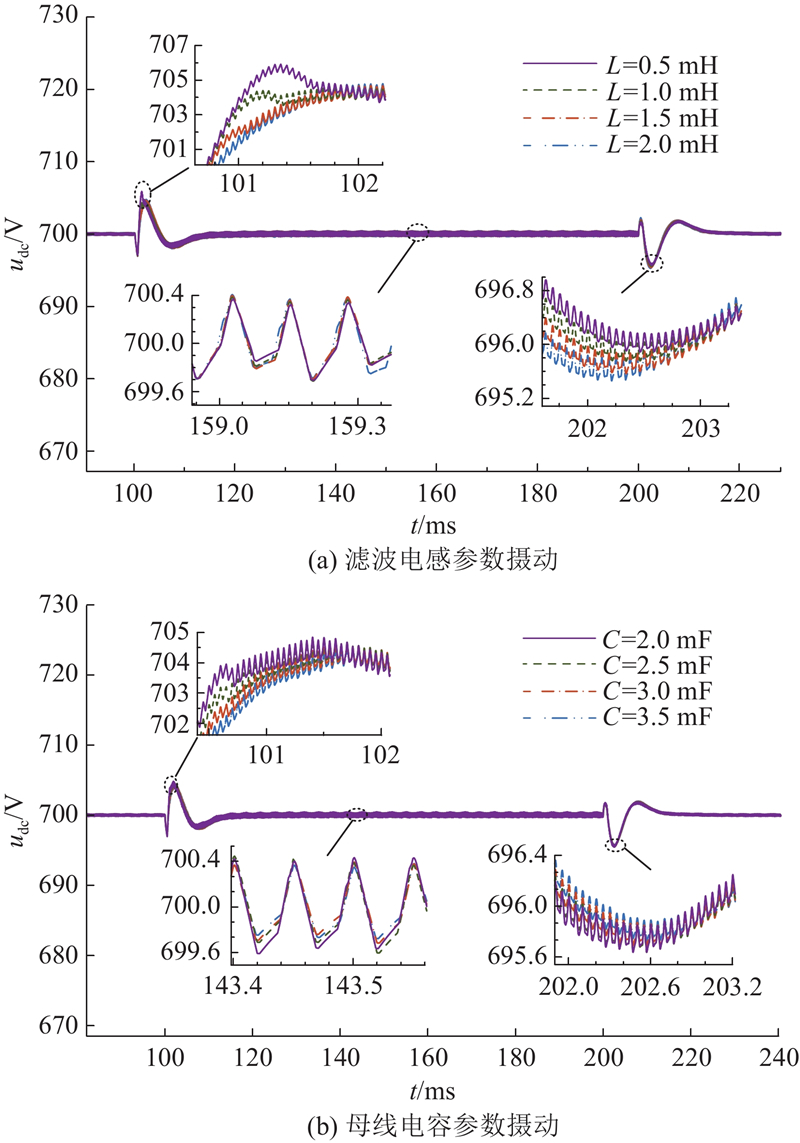
4.1.1. 电路参数摄动影响

受温度和大功率运行元器件老化影响，电路在实际运行时电容和电感的实际值往往不是标称值. 为了验证所设计控制策略对数学模型要求不高的特点，对滤波电感L和母线电容C进行参数摄动. 在0.1 s时储能电池由发出10 kW突变为吸收15 kW功率，在0.2 s时突变为发出25 kW功率，滤波电感L在0.5~2.0 mH变化时的直流母线电压波形如图9(a)所示，母线电容C在2.0~3.5 mF变化的时直流母线电压波形如图9(b)所示. 由图可知，在不同的电感量和电容容值情况下，直流母线电压动态性能基本一致，调节时间相似，表明所设计控制策略能够很好地解决实际工况下系统参数的不确定性问题.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   参数摄动时直流母线电压波形对比

Fig.9   Comparison of DC bus voltage waveform under parameter perturbation


4.1.2. 电能质量对比分析

为了验证所设计控制策略在改善交流侧三相电流电能质量上的有效性，选取储能电池在输出功率为20 kW情况下的PCS交流侧a相输出电流波形进行快速傅里叶分析. 总谐波失真(total harmonic distortion，THD)公式[27]为

$ {\text{THD}} = \frac{1}{{{H_1}}}{\sqrt {\displaystyle\sum\limits_{i = 2}^n {{H_i}^2} } } \times 100{\text{%}} . $
(41)

式中：H1为基波分量的幅值，Hi为第i次谐波分量的幅值. 取a相输出电流的前40次谐波进行分析，不同控制策略下的THD对比如图10所示. 由图可知，在传统PI控制策略下的THD=1.80%，谐波含量最大；采用传统ADRC策略的THD下降，为0.92%；改进ADRC策略降低了输出电流谐波含量，THD=0.69%. 分析结果表明，相比其他2种策略，所设计控制策略的抑制谐波能力更强，电能质量更好.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   稳态时交流侧电流总谐波失真对比

Fig.10   Total harmonic distortion comparison of AC current at steady state


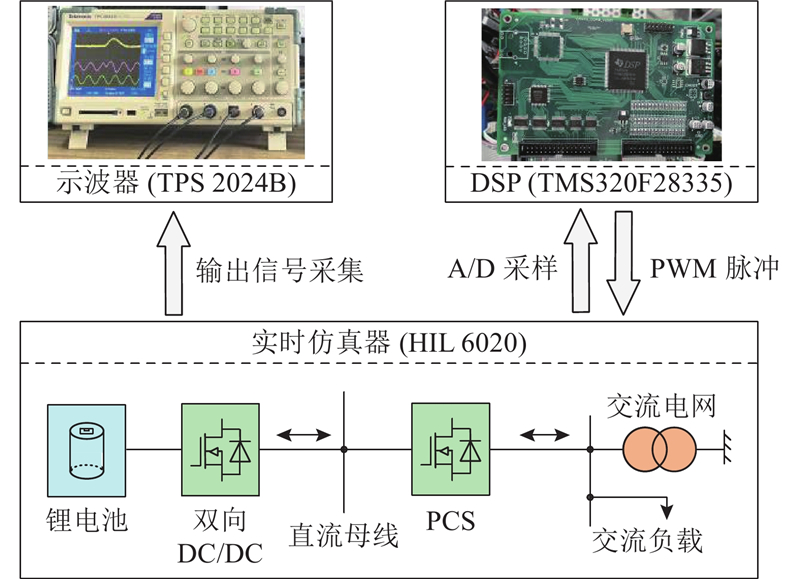
4.2. 实验对比分析

搭建实验平台验证理论分析，通过硬件在环对整体供电系统与控制策略进行验证. 实验平台如图11所示，其中电力系统模型运行在HIL 6020实时仿真器中，电路元器件采用基于开关LC建模的后向欧拉法进行离散，电路运行步长为1 μs；控制电路采用DSPTMS32F28335为主控器件，PWM频率选用10 kHz，控制器A/D转换频率设置为1 MHz. 控制器与主电路部分通过真实物理IO相连，在Tektronix TPS 2024B示波器中采集实时仿真器的输出值. 不同控制策略下的电路控制参数如表2所示. 表中，ωc为传统ADRC控制器带宽，kpd、kpq分别为双向DC/AC变流器电流内环d轴和q轴的比例系数，kid、kiq分别为双向DC/AC变换器电流内环d轴和q轴的积分系数，kpb、kib分别为双向DC/DC变换器的比例系数和积分系数.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   硬件在环测试系统

Fig.11   Hardware in loop test system


表 2   控制电路参数

Tab.2  Control circuit parameter

策略控制对象参数
PIDC/AC电压外环kp=20、ki=5
DC/AC电流内环kpd=kpq=40、kid=kiq=0.5
DC/DCkpb=0.1、kib=10
传统ADRCDC/AC电压外环ω0=600、ωc=1200
改进ADRCDC/AC电压外环ω0=600、η=300、q=25、ε=20

新窗口打开| 下载CSV


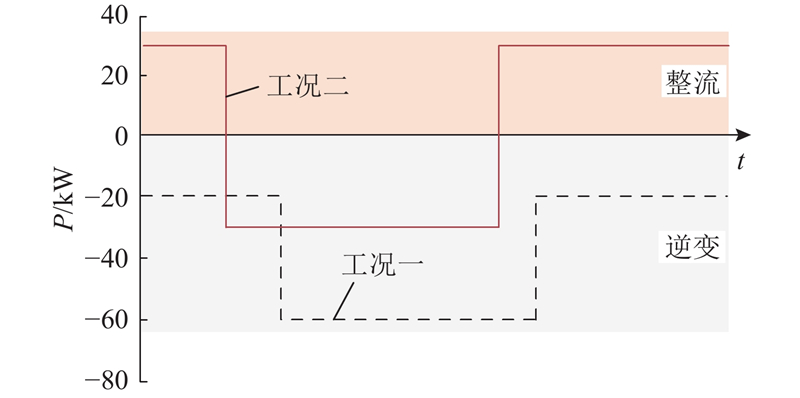
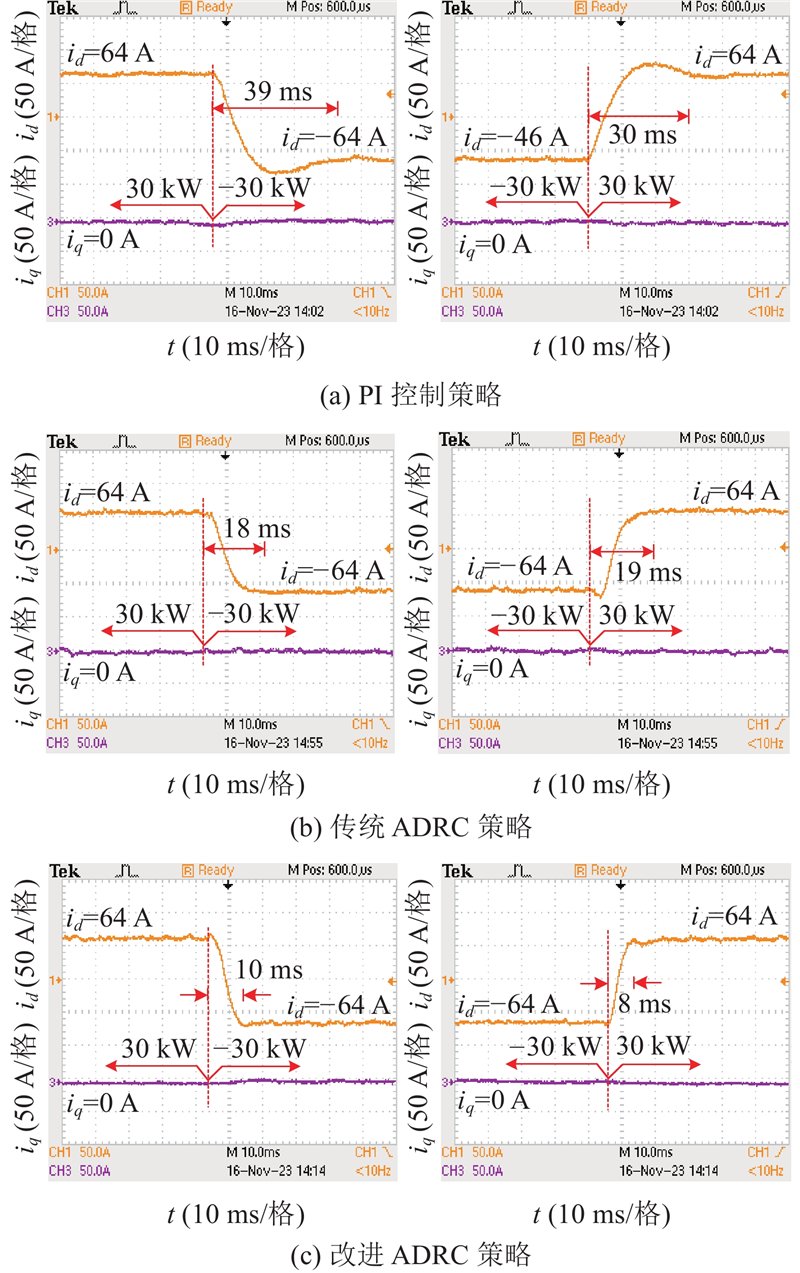
为了更好对比在PI控制、传统ADRC和改进ADRC控制策略下的PCS暂态性能，以如图12所示的2种工况为例进行分析. 工况一：PCS在逆变状态下，输出功率在20 kW和60 kW之间切换. 工况二：PCS在逆变输出30 kW状态和整流储能30 kW状态的切换.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   实验对比典型工况

Fig.12   Experimental comparison of typical working conditions


4.2.1. 直流母线电压波动对比分析

如图13所示为PCS在逆变状态下负载功率突变时，不同控制策略下的直流母线电压暂态波形以及PCS交流侧输出电压和输出电流响应波形. 图中，udc为直流母线电压，ia为交流侧a相电流波形，ua为交流侧的a相电压波形. 由图可知，当PCS工作在工况一时，相比于PI控制策略，传统ADRC策略减小了直流母线电压暂态时间，但超调量仍然很大，相比于前两者控制策略，改进ADRC策略具有更小的直流母线电压超调量，且暂态时间更短. 如图14所示为储能电池在发出功率和吸收功率切换过程中，2种控制策略下的直流母线电压响应波形以及PCS交流侧输出电压和输出电流响应波形. 当PCS工作在工况二时，在2暂态过程中，相比于传统ADRC策略和PI控制策略，改进ADRC策略直流母线电压的超调量更小，且暂态时间更短. 分析结果表明，所提控制策略提高了直流母线电压的动态性能，减小了直流母线电压的波动.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   不同控制策略在工况一下的实验波形

Fig.13   Experimental waveforms of different control strategies under working condition one


图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   不同控制策略在工况二下的实验波形

Fig.14   Experimental waveforms of different control strategies under working condition two


4.2.2. 功率响应速度对比分析

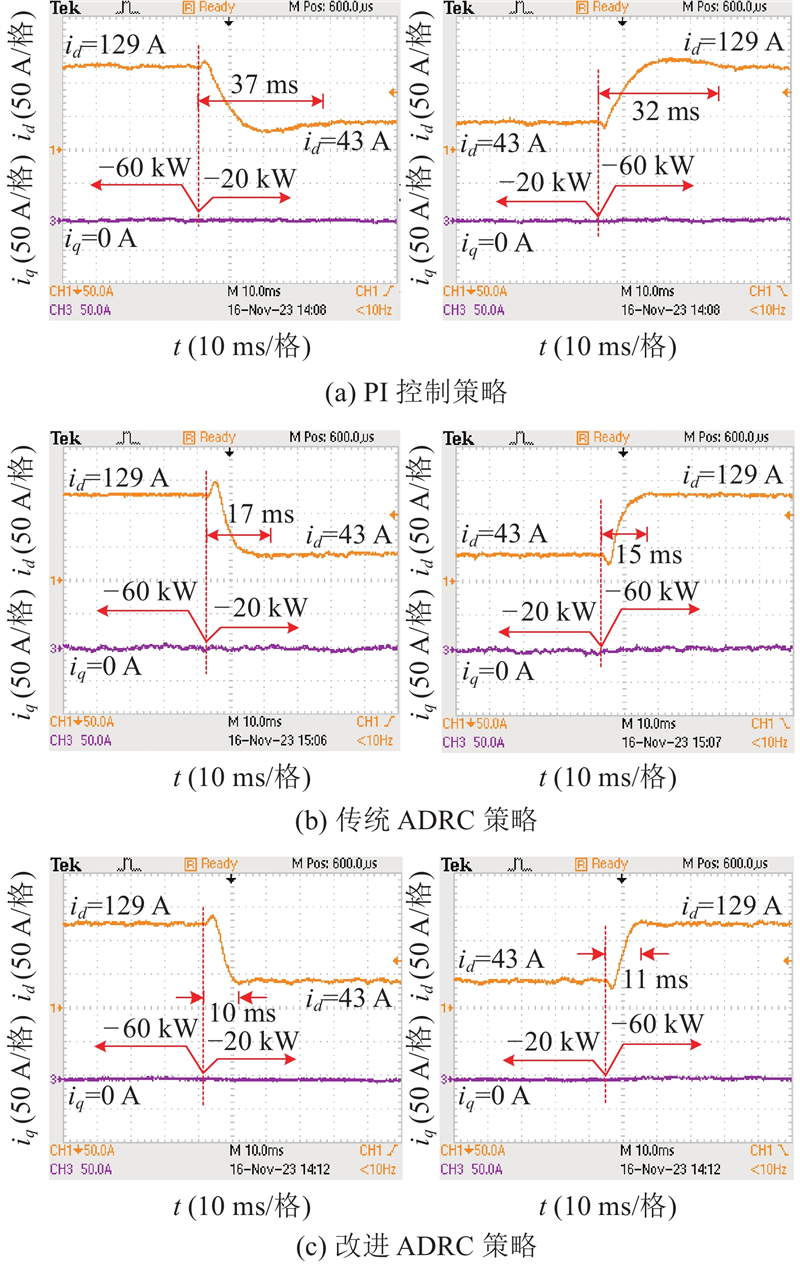
为了验证3种控制策略下的功率响应速度，通过d轴电流的变化表征功率的响应速度，当负载功率突变时d轴电流id和q轴电流iq的暂态波形如图15所示. 由图可知，当PCS工作在工况一时改进ADRC策略性能优于PI控制和传统ADRC策略，d轴的电流暂态时间更短，且超调量更小，即功率响应速度更快. 如图16所示为储能电池在发出功率和吸收功率切换过程中，2种控制策略下的d轴电流和q轴电流的暂态波形. 当PCS工作在工况二时，与图15情况相同，无论是由逆变状态向整流状态的切换，还是由整流状态向逆变状态的切换，在改进ADRC策略下的d轴电流暂态时间更短，超调量更小. 分析结果表明，相比于PI控制和传统ADRC策略，在改进ADRC策略下的d轴电流暂态时间更短，超调量更小，即在所提控制策略下PCS交流侧功率响应速度更快，该控制策略的优越性得到验证.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   不同控制策略在工况一下的电流响应

Fig.15   Current response of different control strategies under condition one


图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   不同控制策略在工况二下的电流响应

Fig.16   Current response of different control strategies under condition two


5. 结　语

为了提高PCS的动态性能和输出电能质量，本研究提出改进的ADRC策略；通过理论分析、仿真和实验验证对比，相较于PI控制策略和传统ADRC策略，得出以下结论. 1）当负荷发生功率突变以及储能电池充放电状态切换时，所提改进ADRC策略能够更好抑制直流母线电压波动并减小暂态时间，有效降低冲击电流对储能电池的影响，延长储能电池的使用寿命；2）所提控制策略减小了负荷功率突变和储能电池充放电状态切换时PCS交流侧输出功率的响应时间，有效提高了变流器输出侧的能量利用率，缓解了功率滞留问题；3）所提改进ADRC策略降低了系统输出谐波含量，使输出电流的THD减小、暂态时间变短，有效改善了PCS交流侧的输出电能质量，降低了用电设备发热，增加了用电设备的使用寿命. 所提改进ADRC策略经济性高，具有一定的工程意义. 下一步研究工作：在现有控制策略基础上，研究当电网电压不平衡时的控制策略，以解决PCS交流侧电流波形畸变严重和峰值过大的问题.

参考文献

ANSARI S, ZHANG J, SINGH R E

A review of stabilization methods for DCMG with CPL, the role of bandwidth limits and droop control

[J]. Protection and Control of Modern Power Systems, 2022, 7 (1): 1- 12

DOI:10.1186/s41601-021-00223-w      [本文引用: 1]

李远征, 任潇, 葛磊蛟, 等

基于可逆固体氧化物电池的电氢耦合微电网全生命周期规划-运营研究

[J]. 中国电机工程学报, 2024, 44 (13): 5169- 5184

LI Yuanzheng, REN Xiao, GE Leijiao, et al

Research for entire lifecycle planning-operation of electric-hydrogen coupled microgrid based on reversible solid oxide cell

[J]. Proceedings of the CSEE, 2024, 44 (13): 5169- 5184

DRAGICEVIC T, LU X, VASQUEZ J C, et al

DC microgrids-part ii: a review of power architectures, applications, and standardization issues

[J]. IEEE Transactions on Power Electronics, 2016, 31 (5): 3528- 3549

DOI:10.1109/TPEL.2015.2464277      [本文引用: 1]

王逸超, 李湘旗, 陈仲伟, 等

一种光储独立并网式虚拟同步发电机控制方法

[J]. 太阳能学报, 2022, 43 (1): 249- 255

[本文引用: 1]

WANG Yichao, LI Xiangqi, CHEN Zhongwei, et al

A virtual synchronous generator control method based on independent grid-connected structure of photovoltaic system and energy storage system

[J]. Acta Energiae Solaris Sinica, 2022, 43 (1): 249- 255

[本文引用: 1]

张宇涵, 杜贵平, 雷雁雄, 等

直流微网混合储能系统控制策略现状及展望

[J]. 电力系统保护与控制, 2021, 49 (3): 177- 187

[本文引用: 1]

ZHANG Yuhan, DU Guiping, LEI Yanxiong, et al

Current status and prospects of control strategy for a DC micro grid hybrid energy storage system

[J]. Power System Protection and Control, 2021, 49 (3): 177- 187

[本文引用: 1]

陈晓龙, 周宁, 韩小文, 等

一种具备自适应重合闸能力的混合式直流断路器

[J]. 电网技术, 2022, 46 (12): 4718- 4728

[本文引用: 1]

CHEN Xiaolong, ZHOU Ning, HAN Xiaowen, et al

A hybrid DC circuit breaker with adaptive reclosing ability

[J]. Power System Technology, 2022, 46 (12): 4718- 4728

[本文引用: 1]

韩子钰. 光储并网变流器系统的负载匹配控制策略研究[D]. 西安: 西安理工大学, 2022.

[本文引用: 1]

HAN Ziyu. Research on load-matching control strategy of photovoltaic-storage grid-connected converter system [D]. Xi’an: Xi’an University of Technology, 2022.

[本文引用: 1]

刘芳, 李研, 何国庆, 等

极弱电网下直驱风电并网变流器小信号建模及稳定性运行策略分析

[J]. 电力自动化设备, 2022, 42 (8): 167- 173

[本文引用: 1]

LIU Fang, LI Yan, HE Guoqing, et al

Small signal modeling and stable operation strategy analysis of direct drive wind power grid-connected converter in extremely weak power grid

[J]. Electric Power Automation Equipment, 2022, 42 (8): 167- 173

[本文引用: 1]

韩刚, 蔡旭

不平衡电网下风电并网交流器的滑模电流控制

[J]. 上海交通大学学报, 2018, 52 (9): 1065- 1071

[本文引用: 1]

HAN Gang, CAI Xu

Sliding-mode control of current for wind power grid-connected converter under unbalanced grid voltage

[J]. Journal of Shanghai Jiao Tong University, 2018, 52 (9): 1065- 1071

[本文引用: 1]

KIM S, LEE Y. Model predictive control for the power control of three-phase AC/DC converters using a disturbance observer [C]// 2015 15th International Conference on Control, Automation and Systems . Busan: IEEE, 2015: 2070−2075.

[本文引用: 1]

林晓冬, 雷勇

基于T型三电平变流器的超导磁储能系统及其能量成型控制策略

[J]. 电网技术, 2018, 42 (2): 607- 613

[本文引用: 1]

LIN Xiaodong, LEI Yong

Three-level T-type converter for superconducting magnetic energy storage system and its energy-shaping control strategy

[J]. Power System Technology, 2018, 42 (2): 607- 613

[本文引用: 1]

王宁. 光储微网在不同运行模式下的储能换流器控制策略研究[D]. 沈阳: 沈阳工业大学, 2021.

[本文引用: 1]

WANG ning. Research on control strategy of energy storage converter under different operating modes of optical storage microgrid [D]. Shenyang: Shenyang University of Technology, 2021.

[本文引用: 1]

杨天翔, 程志江, 杨涵棣, 等

基于自抗扰控制的风电并网变流器锁相环设计

[J]. 太阳能学报, 2023, 44 (4): 147- 155

[本文引用: 1]

YANG Tianxiang, CHENG Zhijiang, YANG Handi, et al

Design of phase-locked loop of grid connected converter based on active disturbance rejection control

[J]. Acta Energiae Solaris Sinica, 2023, 44 (4): 147- 155

[本文引用: 1]

GUO B, BACHA S, ALAMIR M, et al. An enhanced phase-locked loop with extended state observer [C]// 2019 20th International Symposium on Power Electronics . Novi Sad: IEEE, 2019: 1−6.

周雪松, 刘乾, 马幼捷, 等

基于改进自抗扰的光伏并网逆变器直流母线电压控制

[J]. 太阳能学报, 2022, 43 (10): 65- 72

ZHOU Xuesong, LIU Qian, MA Youjie, et al

DC-link voltage control of photovoltaic grid-connected inverter based on improved active disturbance rejection

[J]. Acta Energiae Solaris Sinica, 2022, 43 (10): 65- 72

ZHENG H, DU G, LEI Y, et al

Hybrid energy storage bidirectional DC–DC converter based on Hermite interpolation and linear active disturbance rejection control

[J]. Journal of Power Electronics, 2023, 23: 959- 971

DOI:10.1007/s43236-023-00602-6      [本文引用: 1]

杨文奇, 卢建华, 姜旭, 等

基于改进ESO的四旋翼姿态自抗扰控制器设计

[J]. 系统工程与电子技术, 2022, 44 (12): 3792- 3799

[本文引用: 2]

YANG Wenqi, LU Jianhua, JIANG Xu, et al

Design of quadrotor attitude active disturbance rejection controller based on improved ESO

[J]. Systems Engineering and Electronics, 2022, 44 (12): 3792- 3799

[本文引用: 2]

程启明, 张昕, 赖宇生, 等

电网不平衡工况下三电平直接矩阵变换器反步滑模控制策略

[J]. 电力系统保护与控制, 2023, 51 (8): 73- 85

[本文引用: 1]

CHENG Qiming, ZHANG Xin, LAI Yusheng, et al

Back-stepping sliding-mode control strategy for a three-level direct matrix converter in unbalanced grid conditions

[J]. Power System Protection and Control, 2023, 51 (8): 73- 85

[本文引用: 1]

LAKOMY K, MADONSKI R, DAI B, et al

Active disturbance rejection control design with suppression of sensor noise effects in application to DC-DC buck power converter

[J]. IEEE Transactions on Industrial Electronics, 2022, 69 (1): 816- 824

DOI:10.1109/TIE.2021.3055187      [本文引用: 2]

李中奇, 黄琳静, 周靓, 等

高速列车滑模自抗扰黏着控制方法

[J]. 交通运输工程学报, 2023, 23 (2): 251- 263

[本文引用: 1]

LI Zhongqi, HUANG Linjing, ZHOU Liang, et al

Sliding mode active disturbance rejection adhesion control method of high-speed train

[J]. Journal of Traffic and Transportation Engineering, 2023, 23 (2): 251- 263

[本文引用: 1]

李冰林, 曾励, 张鹏铭, 等

主动磁悬浮轴承的滑模自抗扰解耦控制

[J]. 电机与控制学报, 2021, 25 (7): 129- 138

[本文引用: 1]

LI Binglin, ZENG Li, ZHANG Pengming, et al

Sliding mode active disturbance rejection decoupling control for active magnetic bearings

[J]. Electric Machines and Control, 2021, 25 (7): 129- 138

[本文引用: 1]

陈闯, 王勃, 于泳, 等

基于改进指数趋近律的感应电机滑模转速观测器研究

[J]. 电工技术学报, 2020, 35 (Suppl.1): 155- 163

[本文引用: 1]

CHEN Chuang, WANG Bo, YU Yong, et al

An improved exponential reaching law based-sliding mode observer for speed-sensorless induction motor drives

[J]. Transactions of China Electrotechnical Society, 2020, 35 (Suppl.1): 155- 163

[本文引用: 1]

CHEN X, LI Y, MA H, et al

A novel variable exponential discrete time sliding mode reaching law

[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68 (7): 2518- 2522

[本文引用: 1]

范云生, 陈欣宇, 赵永生, 等

基于扩张状态观测器的四旋翼吊挂飞行系统非线性控制

[J]. 自动化学报, 2023, 49 (8): 1758- 1770

[本文引用: 1]

FAN Yunsheng, CHEN Xinyu, ZHAO Yongsheng, et al

Nonlinear control of quadrotor suspension system based on extended state observer

[J]. Acta Automatica Sinica, 2023, 49 (8): 1758- 1770

[本文引用: 1]

王玉鑫, 梅晓榕, 郭育生

一类四阶非线性系统的滑模模糊控制

[J]. 电机与控制学报, 2006, 10 (2): 208- 211

[本文引用: 1]

WANG Yuxin, MEI Xiaorong, GUO Yusheng

Sliding-mode fuzzy control for a class of forth-order nonlinear systems

[J]. Electric Machines and Control, 2006, 10 (2): 208- 211

[本文引用: 1]

刘金琨. 滑模变结构控制MATLAB仿真: 基本理论与设计方法[M]. 北京: 清华大学出版社, 2019: 38–42.

[本文引用: 1]

王兆安, 黄俊. 电力电子技术[M]. 北京: 机械工业出版社, 2004: 69–74.

[本文引用: 1]

/

〈 〉