学者们对于不同类型的管桥地震动力特性开展了大量的试验研究,提出采用流固耦合效应来模拟水体和管道在地震下的工作特性. Singh等[7-8]对管桥的输送管道进行简化计算,根据Timoshenko理论研究了管道内液体对管桥的冲击作用并推广至其他管道系统. 徐建国等[9-10]建立槽内水体流固耦合大跨度管桥结构模型,表明考虑管道内水体流固耦合系统建立的耦合模型能够准确反映大跨度管桥结构工作特性. Yau等[11]将管道中的液体流动载荷简化为匀速运动的连续质量载荷,模拟分析了管桥的振动响应. 周敉等[12]采用势流体单元模拟水流,建立考虑流固耦合效应的有限元模型并进行动力响应分析,定量得出地震激励下水-结构相互作用对桥墩或桥梁结构的影响程度. 伍平等[13-14]等基于流固耦合理论对比分析管桥结构数值模拟与试验结果,判定过桥水管与桥梁结构不会发生共振,并开展水流流速对输水管道的影响研究. 应磊等[15]在考虑土与结构间相互作用的情况下,开展某渡槽的动力特性及响应研究,结果表明土与结构间相互作用对流体频率影响较小,但对结构频率的影响不可忽视. 官杨等[16]以漾濞江油气集输悬索管桥为对象,研究悬索管桥的地震响应、抗震性能数值模拟,揭示了管桥体系的危险区域和可能存在的破坏形式. 岑文祥[17]结合具体工程,针对大中口径给水管道的桁架形式,从结构受力角度对断面形式进行了设计优化与分析. 张社荣等[18]应用时域分析法对排架式U型大跨度管桥结构在强震作用下的动力响应规律及损伤破坏发展过程进行分析. 王俊等[19]研究摩擦摆式减震支座在大跨度管桥中的应用,结果表明采用隔震支座可以延长大跨度管桥结构的基本周期,减、隔震作用明显. 彭辉等[20]在漕河渡槽振动台试验中,主要对漕河渡槽的动力特性,横纵向地震作用下漕河渡槽的动力反应以及槽内有水、无水对渡槽结构的振动影响进行分析研究;结果表明,横向地震作用下漕河渡槽的动应力反应比纵向及竖向地震作用下的动应力大;槽身内有水比无水的地震反应大,动水压力反应的规律与用Westergaard刚性结构面假设下的动水压力附加质量模型计算得到的结果一致. 王海波等[21]通过振动台试验研究渡槽和水体的相互作用,通过深入分析不同激励作用下渡槽结构的动态响应,确定大型薄壁渡槽中水体对结构自振频率及渡槽两端支座力产生的重要影响,给出试验对象渡槽结构槽内水体与渡槽动态相互作用的等价质量定量关系.
大流量斜拉压力输水管桥结构体系复杂,强震时结构的损伤破坏部位尚不明确,为了定量研究大流量斜拉压力输水管桥的抗震性能,为大流量斜拉压力输水管桥抗震设计开展缩尺比为1∶20的等代模型振动台试验,分析试验现象、动力特性变化、地震位移和纵筋应变等响应,对比分析振动台试验结果与数值模拟结果.
1. 振动台模型试验
1.1. 等代模型与原型相似性验证
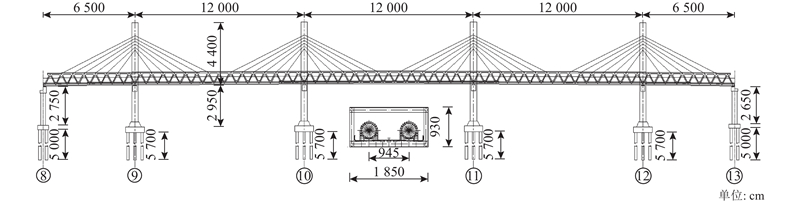
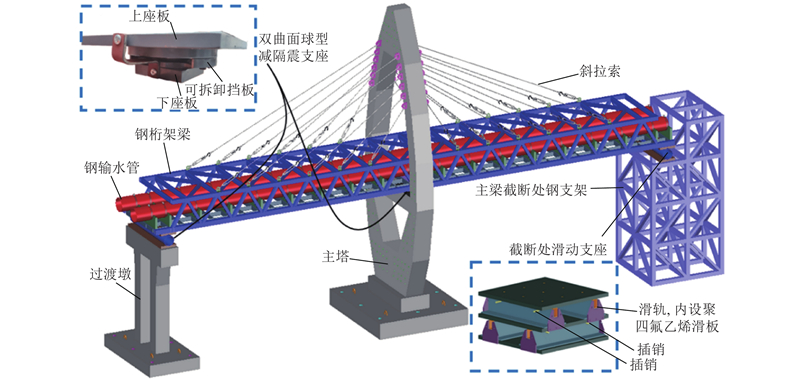
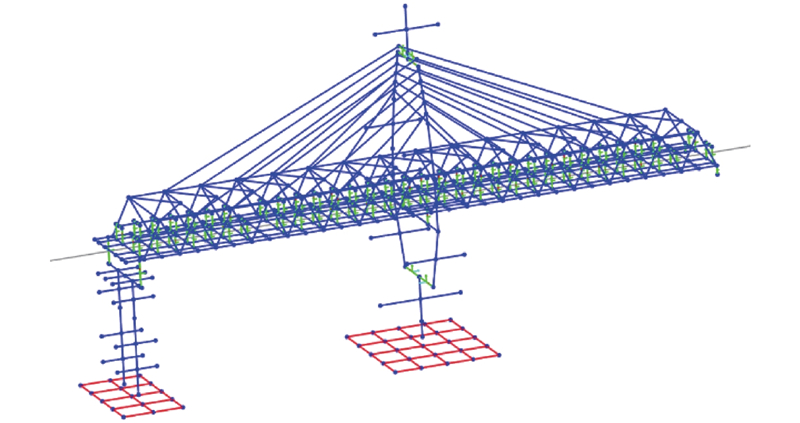
本研究依托引汉济渭项目的某大流量斜拉管桥. 如图1所示,主桥长490 m,为四塔多跨斜拉桥,采用塔梁分离的半漂浮体系;跨径布置为(65+3×120+65)m,桥梁总宽18.5 m;主塔采用水滴型混凝土结构,桥塔总高约72 m,其中桥面以上44.2 m,桥面以下27.8 m,截面为3.5m×4.0 m;主梁采用钢桁梁,桁内净宽16.5 m;斜拉索按双索面布置,斜拉索间距8.0 m,单塔布置12对,全桥共布置48对.
图 1
图 1 大流量斜拉管桥桥型布置及主梁断面
Fig.1 Layout and main beam cross section of large flow cable-stayed pipeline bridge
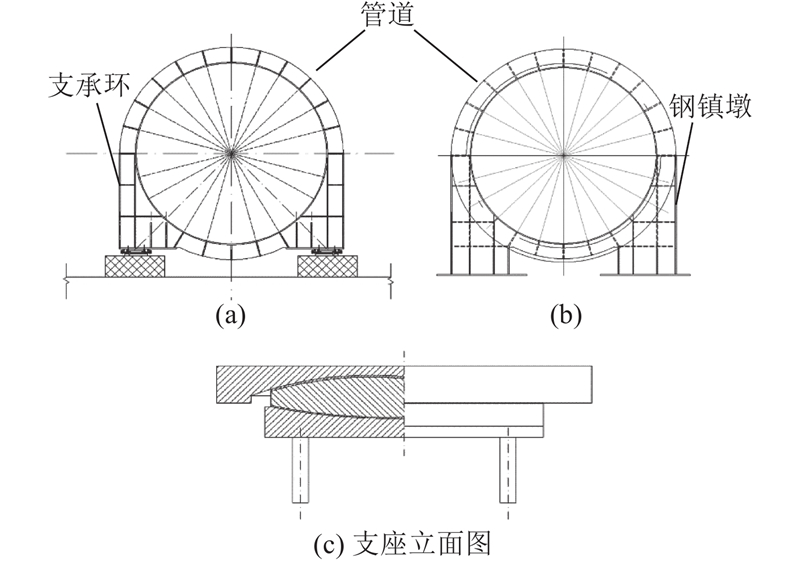
原桥输水管道采用内径为3.4 m、厚度为22 mm的钢输水管道,管道外侧设保温措施,管道间隔设置支承环,在主塔处支承环加厚,也称为镇墩. 主桥段,每个桥塔设置1个钢镇墩. 在桥梁上布置伸缩节,对于桥梁位移大的节段,以桥梁为主,伸缩节起协调管道与桥梁变形的作用,对于桥梁位移小的节段,按常规伸缩节布置. 主桥采用隔震橡胶支座,中支点型号为KZQZ-12500,边支点型号为KZQZ-3500. 相关结构断面如图2所示.
图 2
图 2 输水管及镇墩、支承环、支座断面图
Fig.2 Cross-sectional diagram of water pipeline, abutment piers, bearing ring, and support pad
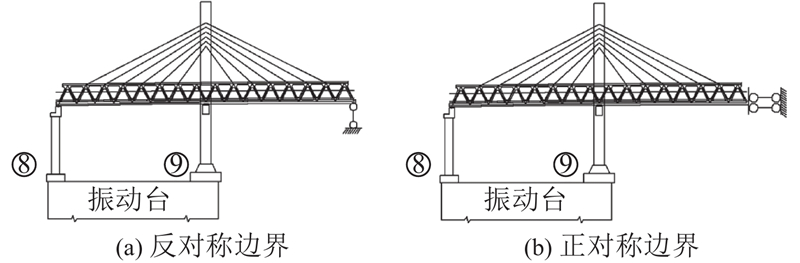
全桥模型的缩尺振动台试验对试验设备要求较高,须进行多个振动台设备的台阵试验. 如图3所示,根据半桥理论进行全桥简化,取包含8号过渡墩和9号主塔在内的边跨结构添加合适的边界条件形成全桥模型的等代模型,将等代模型置于单个台面上进行单台振动台试验,大大降低试验对设备的要求. 本次试验采用MTS公司生产的三维六自由度大型地震模拟振动台试验系统,其台面尺寸为4.1 m×4.1 m,最大承载能力为30 t,试验频率为0.1~50.0 Hz,满载30 t时最大水平X向和水平Y向加速度为±1.0g,最大竖向加速度为±0.9g.
图 3
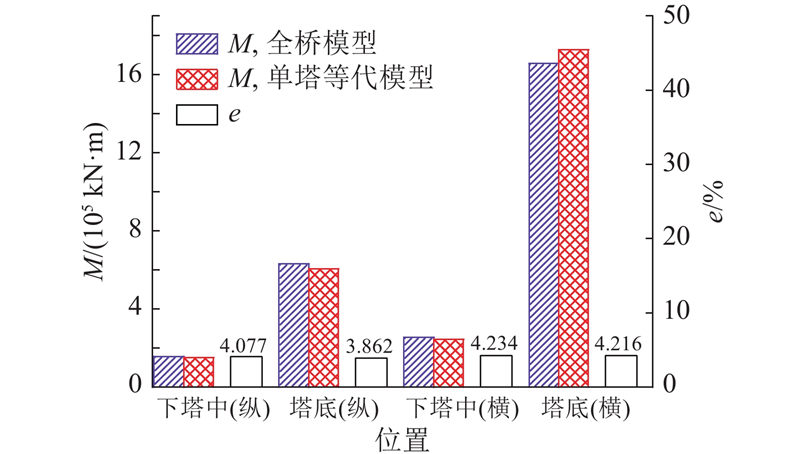
袁万城[22]以南昌朝阳大桥为研究对象,提出对半桥赋予正反对称的边界条件推演全桥结构在一致激励、非一致激励下结构响应的试验方法. 该研究结果表明,顺桥向一致激励下的结构反应呈现反对称形态,横桥向一致激励下的结构反应呈现正对称形态;利用结构自身的对称性,分别在边界条件为正对称和反对称的情况下输入正对称激励和反对称激励,以此来推算全桥地震特性及响应. 为了保证在截断处添加边界条件后的模型与原型基本等效,采用有限元软件建模进行模拟对比,通过在截断处的纵桥向或横桥向施加单向弹簧约束来改变等代模型的各阶振型,保证2个模型在纵飘及其他主要振型的周期大致相同. 根据振型及周期确定截断处的边界条件后,选取E2地震作用下的某条时程曲线输入模型进行计算,2个模型的地震响应对比如图4所示,其中M为关键截面地震弯矩响应,e为模型地震响应误差. 由原型和等代模型的地震响应计算结果可知,无论在E2纵竖向地震输入还是横竖向地震输入下,原型与等代模型的地震响应误差都在3.862%~4.234%,可以认为等代模型和原型具有一定的相似性,表明简化的边跨单塔模型研究对全桥的地震响应分析具有参考价值.
图 4
图 4 原型与等代模型在E2地震输入下的弯矩响应
Fig.4 Bending moment response of prototype and equivalent models under E2 seismic excitation
1.2. 相似比及试验设计
考虑振动台面尺寸及承载能力条件,平面几何尺寸在振动台台面范围内,立面高度满足试验室制作场地高度要求以及模型吊装行车的高度要求,选取模型与原型的相似系数
表 1 试验模型参数的相似系数
Tab.1
| 参数 | 数值 |
| 长度相似系数 | 0.05 |
| 加速度相似系数 | 1.5 |
| 弹性模量相似系数 | 0.5 |
| 质量相似系数 | |
| 时间相似系数 | |
| 应力相似系数 | 0.5 |
| 应变相似系数 | 1 |
| 密度相似系数 | |
| 面积相似系数 | |
| 体积相似系数 | |
| 抗弯刚度相似系数 | |
| 频率相似系数 | |
| 位移相似系数 | 0.05 |
| 速度相似系数 | |
| 力相似系数 | |
| 弯矩相似系数 |
试验模型中桥塔和过渡墩采用微粒混凝土浇筑而成,模型中采用HPB300钢筋及镀锌铁丝来模拟原型结构中的主筋及箍筋,桥塔主筋公称直径为6 mm,过渡墩主筋公称直径为4 mm,根据抗力相似原则,由原型结构关键截面配筋面积计算得到模型结构的配筋面积,进而确定钢筋数和直径. 钢桁架和钢输水管道分别采用Q420和Q345钢材制作,主塔及过渡墩处支座均采用双曲面球型减隔震支座,在过渡墩及主塔处横桥向均设置纵单向活动支座和双向活动支座,纵单向活动支座的上座板限位挡条设计为可拆卸结构. 试算求得的等代模型单向弹簧刚度为0.635 kN/mm,设计滑动支座中槽道的滑动摩擦系数即可等效单向弹簧约束的作用,结合如图3所示边界条件,在跨中主梁截断处布置双向滑动支座,通过插拔销钉控制双向滑动支座仅纵桥向滑动或者仅横桥向滑动,分别对应跨中截断处的反对称边界条件和正对称边界条件. 模型试验的现场照片和振动台试验模型布置图分别如图5、图6所示.
图 5
图 6
管道中水体的模拟是振动台模型设计的难点. 按照相似比,计算得到模型水体的质量为1 937 kg,仅在管道中填充水体显然无法满足质量要求,考虑流固耦合对结构响应的影响,参考文献[23],试验采用高堆积密度铁砂来模拟水体;通过是否在管道中填充铁砂的方式模拟空、满管工况. 在纵向地震输入时,管内铁砂因自身惯性力的作用与管道的运动方向相反,使得管内铁砂对管壁产生摩阻力,说明使用铁砂能够有效模拟水体的流动性. 在横向地震输入时,管道由于自身的横向抗弯刚度较小,会产生振动和变形,管道横向的振动与铁砂的振动耦合,能够实现流固耦合作用.
1.3. 试件测点布置及加载工况
表 2 应变片布置及编号
Tab.2
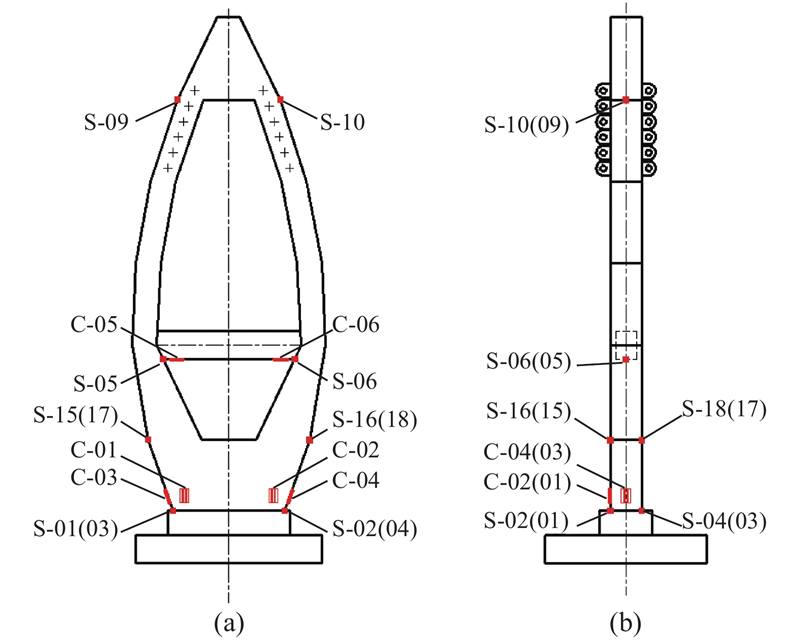
| 名称 | 位置 | 编号 | 位置 | 编号 | |
| 钢应变片 | 主塔塔底-西北 | S-01 | 下塔中-西南 | S-16 | |
| 主塔塔底-西南 | S-02 | 下塔中-东北 | S-17 | ||
| 主塔塔底-东北 | S-03 | 下塔中-东南 | S-18 | ||
| 主塔塔底-东南 | S-04 | 过渡墩顶-北 | S-19 | ||
| 主塔横梁底-北 | S-05 | 过渡墩顶-南 | S-20 | ||
| 主塔横梁底-南 | S-06 | 西梁底跨中-北 | S-21 | ||
| 塔顶分叉处-北 | S-09 | 西梁底跨中-南 | S-22 | ||
| 塔顶分叉处-南 | S-10 | 梁顶跨中-北 | S-23 | ||
| 过渡墩墩底-北 | S-11 | 梁顶跨中-南 | S-24 | ||
| 过渡墩墩底-南 | S-12 | 东梁底跨中-北 | S-25 | ||
| — | — | 东梁底跨中-南 | S-26 | ||
| 砼应变片 | 塔底正面-北 | C-01 | 塔横梁底-南 | C-06 | |
| 塔底正面-南 | C-02 | 过渡墩底正-南 | C-07 | ||
| 塔底侧面-北 | C-03 | 过渡墩底正-北 | C-08 | ||
| 塔底侧面-南 | C-04 | 过渡墩底侧-南 | C-09 | ||
| 塔横梁底-北 | C-05 | 过渡墩底侧-北 | C-10 |
表 3 传感器布置及编号
Tab.3
| 名称 | 位置 | 编号 | 位置 | 编号 | |
| 加速度传感器 | 西侧梁跨中X向 | J-11 | 过渡墩盖梁顶X | J-9 | |
| 西侧梁跨中Y向 | J-12 | 过渡墩盖梁侧Y | J-10 | ||
| 西侧梁跨中Z向 | J-13 | 过渡墩承台顶X | J-8 | ||
| 东侧梁跨中X向 | J-14 | 主塔承台X | J-1 | ||
| 东侧梁跨中Y向 | J-15 | 主塔承台Y | J-2 | ||
| 东侧梁跨中Z向 | J-16 | 主塔横梁X | J-4 | ||
| 塔顶X | J-7 | 主塔横梁侧面Y | J-5 | ||
| 主梁跨中X | J-6 | 振动台面X | J-17 | ||
| 主塔基座X | J-3 | 振动台面Y | J-18 | ||
| — | — | 振动台面Z | J-19 | ||
| 位移传感器 | 西侧梁跨中Y向 | W-11 | 过渡墩盖梁顶X | W-8 | |
| 西侧梁跨中Z向 | W-12 | 过渡墩盖梁侧Y | W-10 | ||
| 东侧梁跨中Y向 | W-13 | 主塔承台X | W-1 | ||
| 东侧梁跨中Z向 | W-14 | 主塔承台Y | W-2 | ||
| 塔顶Y | W-6 | 主塔横梁X | W-3 | ||
| 塔顶X | W-5 | 主塔横梁侧面Y | W-7 | ||
| 主梁跨中X | W-4 | 振动台面X | W-15 | ||
| 过渡墩顶主梁X | W-9 | 振动台面Y | W-16 | ||
| — | — | 振动台面Z | W-17 |
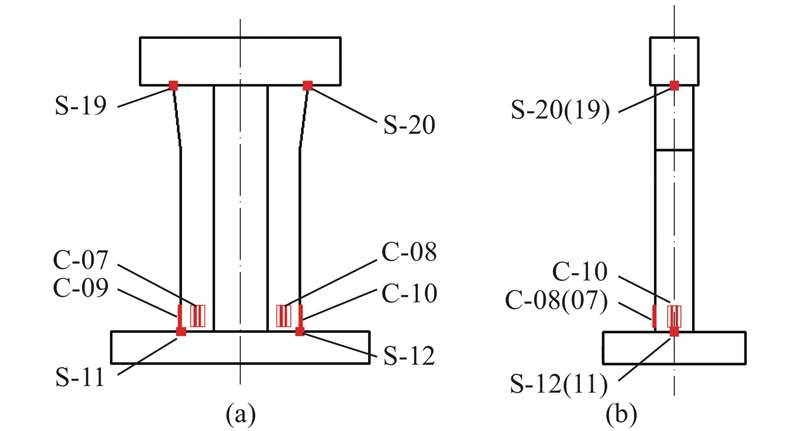
图 7
图 7 过渡墩应变片布置及编号
Fig.7 Arrangement and numbering of strain gauges on transition pier
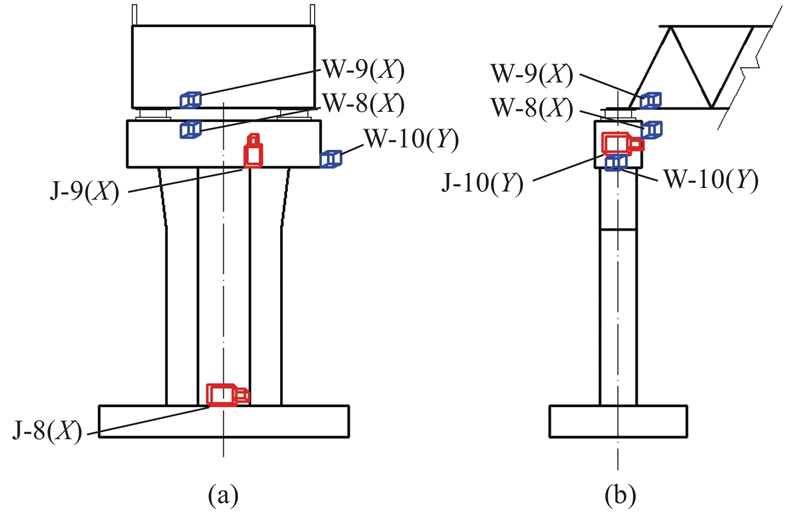
图 8
图 9
图 9 主塔加速度和位移传感器布置及编号
Fig.9 Arrangement and numbering of acceleration and displacement sensors for main tower
图 10
图 10 过渡墩加速度和位移传感器布置及编号
Fig.10 Arrangement and numbering of acceleration and displacement sensors for transition piers
将1条天然波和3条场地人工波作为试验的加载波,以这4条地震波作为基准波,经过加速度调幅生成试验输入的地震波,根据时间的相似常数对相应地震波进行时间上的压缩以满足试验的相似性要求. 地震波加速度时程曲线如图11所示. 振动台单个试件的地震波加载是损伤累积的过程,加载过程中应尽量避免地震能量大的地震波先于地震能量小的波加载到结构构件上. 在E1地震作用下斜拉输水管桥处于弹性状态,因此认为在E1对应地面峰值加速度(peak ground acceleration, PGA)之前的工况下模型没有损伤累计,在空管模型工况逐级加载至E1地震对应的峰值加速度后,暂停加载,添加铁砂配重后进行满管模型工况的逐级加载,直至E2地震对应的峰值加速度.
图 11
图 11 输入地震波加速度时程曲线
Fig.11 Acceleration time history curve of input seismic wave
根据模型试验的研究目标和研究内容,将本次振动台试验的工况按测试目标分为动力性能测试工况和地震性能反应测试工况. 动力性能测试采用白噪声随机激振法(振幅为0.05g),所选白噪声频段能够覆盖模型的主要自振频率,结构地震反应工况采用双向输入基准地震波调幅到一定峰值加速度,并按照模型时间相似常数进行时间步压缩后得到的加速度时程. 激励方向分为纵向+竖向和横向+竖向激励. 鉴于场址位于7.5级潜在震源区,竖向地震动参数取水平向地震动参数值. 试验加载时台面输入峰值加速度由小到大逐级增加,试验加载工况如表4所示.
表 4 试验加载工况表
Tab.4
| 工况 | 激振方向 | 管道情况 | 原型峰值加速度 |
| 1~11 | 纵+竖/横+竖 | 空管 | 0.1g |
| 12~21 | 纵+竖/横+竖 | 空管 | 0.15g |
| 22~31 | 纵+竖/横+竖 | 空管 | 0.23g(E1) |
| 32~41 | 纵+竖/横+竖 | 满管 | 0.1g |
| 42~51 | 纵+竖/横+竖 | 满管 | 0.15g |
| 52~61 | 纵+竖/横+竖 | 满管 | 0.23g(E1) |
| 62~71 | 纵+竖/横+竖 | 满管 | 0.4g(E2) |
| 72~81 | 纵+竖/横+竖 | 满管 | 0.5g |
| 82~88 | 纵+竖/横+竖 | 满管 | 0.567g |
2. 试验结果分析
2.1. 试验现象
在纵桥向+竖向组合地震输入时,当原型输入峰值加速度小于0.15g时,主塔及主梁纵桥向振动幅度比较小,边界墩处滑动支座未见明显滑动,主塔及过渡墩表面均未出现裂缝;当原型输入峰值加速度为0.23g时,过渡墩南侧墩底上方26~27 cm处出现1条微裂缝,裂缝宽度小于0.1 mm;当满管工况原型输入峰值加速度达0.23g时,过渡墩北侧墩底上方28~30 cm处出现新的微裂缝,原有微裂缝略有延展;当原型输入峰值加速度达到0.4g时,过渡墩南、北侧距墩底15~20 cm处均出现水平裂缝,墩身中部有新的水平裂缝出现;当原型输入峰值加速度在0.500g~0.567g时,主塔和过渡墩表面均出现贯通的水平裂缝,主塔在分肢处形成贯穿的环状裂缝.
在横桥向+竖向组合地震输入时,当原型输入峰值加速度为0.23g时,过渡墩墩柱顶部下方7~8 cm和10 cm处出现微小裂缝,裂缝宽度均小于0.1 mm;在满管、横向地震输入工况下,当原型输入峰值加速度达到0.4g时,过渡墩墩底原有裂缝沿水平方向开展直至贯通,过渡墩墩柱顶部下方10 cm处出现水平方向贯通裂缝,过渡墩盖梁底部出现竖向裂纹;当原型输入峰值加速度在0.500g~0.567g时,主塔塔柱内侧出现多条水平向贯通裂缝,下塔柱部分裂缝发展成为贯穿的环状裂缝,主塔横梁部分配重孔附近出现混凝土剥落;过渡墩墩身与盖梁连接处附近出现多条水平的贯通裂缝,墩顶与盖梁连接处出现的数条水平裂缝削弱了双柱墩的框架效应,因此墩底没有发生更加严重的破坏. 为了试验安全考虑,停止试验加载,试验停止后主塔及过渡墩的损伤情况如图12所示.
图 12
2.2. 动力特性
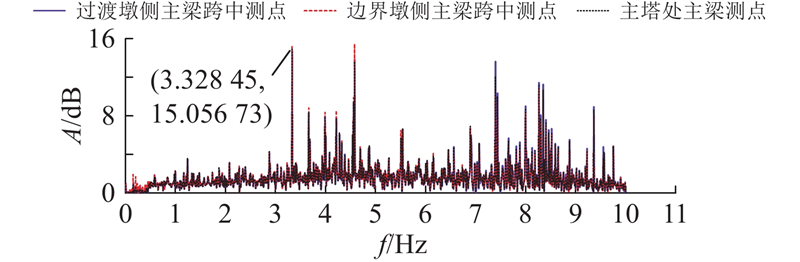
试验时在不同的地震动输入前后采用白噪声随机激振法(峰值加速度为0.05g)分别对纵桥向和横桥向体系进行扫频试验. 所选的白噪声频段能够覆盖模型的主要自振频率. 分别对主梁测点的加速度响应和台面测点的加速度信号进行傅里叶变换,在此基础上构造观测点相对于台面输入信号的传递函数,得到如图13所示的传递函数幅频图,其中A为振幅比. 由图可知,3个测点的加速度幅频曲线基本吻合,能够明显辨别试验模型一阶自振频率f=3.328 45 Hz,有限元模型计算所得一阶自振频率目标值为3.164 60 Hz,试验值与目标值误差约为4.92%,可以认为试验模型的动力特征参数与设计预期基本相符.
图 13
图 13 白噪声激励下主梁加速度测点传递函数幅频图
Fig.13 Amplitude frequency diagram of transfer function of main beam acceleration measurement point under white noise excitation
为了研究主塔和过渡墩在加载全过程中的损伤情况,在各白噪声扫频工况中选取工况1、6和11-1等共17个扫频工况,分别对相应台面测点信号作传递函数,得到各个白噪声扫频工况下主塔和过渡墩的加速度幅频曲线,从而得到试验加载过程中主塔和过渡墩的一阶自振频率变化曲线,如图14所示. 由图可知,在工况1~26中,主塔及过渡墩一阶自振频率略有浮动,但基本不变,曲线十分平缓,因此工况1~26主塔和过渡墩几乎没有损伤;在工况31-1~56中,主塔和过渡墩表面逐渐出现微小裂缝,一阶自振频率逐渐减小;在工况56~66中,过渡墩自振频率下降曲线的斜率明显大于主塔频率的下降曲线,因此过渡墩先于主塔出现较为明显的损伤;在工况76之后,主塔和过渡墩的一阶自振频率均明显下降,因此在0.75g~0.85g的峰值加速度台面输入水平下,结构出现明显损伤,刚度明显退化. 由自振频率变化规律所得试验模型的损伤情况和试验时记录的试验现象基本一致,增加了试验结果的可信度.
图 14
图 14 主塔和过渡墩自振频率变化图
Fig.14 Changes in natural vibration frequencies of main tower and transition piers
2.3. 位移响应
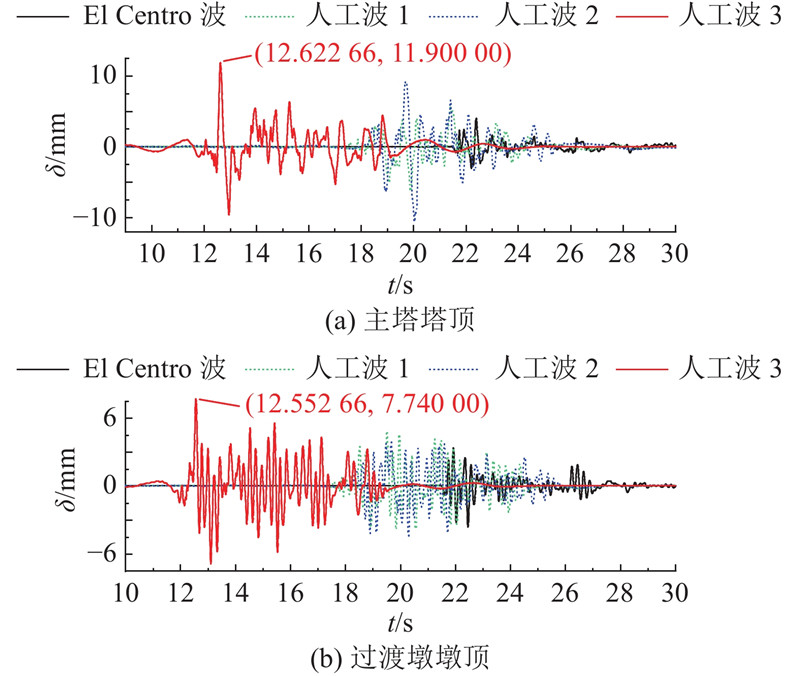
以台面输入峰值加速度0.345g为例,根据加速度相似比可知对应原型加速度峰值为0.23g(E1地震作用),在天然波El Centro波和3条场地人工波纵向+竖向输入时,主塔塔顶及过渡墩顶测点的纵桥向位移时程曲线如图15所示,其中
图 15
图 15 不同组件顶部测点的纵向位移时程曲线(PGA=0.345g)
Fig.15 Time history curve of longitudinal displacement at top measurement point of different modules (PGA=0.345g)
在场地人工波3纵向+竖向输入和横向+竖向输入时,选取台面输入PGA为0.15g、0.225g、0.345g、0.6g、0.75g和0.85g的6个工况分别提取主塔塔顶测点和过渡墩顶测点的位移时程曲线,得到测点最大位移响应随台面输入PGA的变化关系如图16所示,其中
图 16
图 16 不同测点最大位移随台面输入地面峰值加速度的变化
Fig.16 Variation of maximum displacement at different measurement points with peak ground acceleration inputs on platform
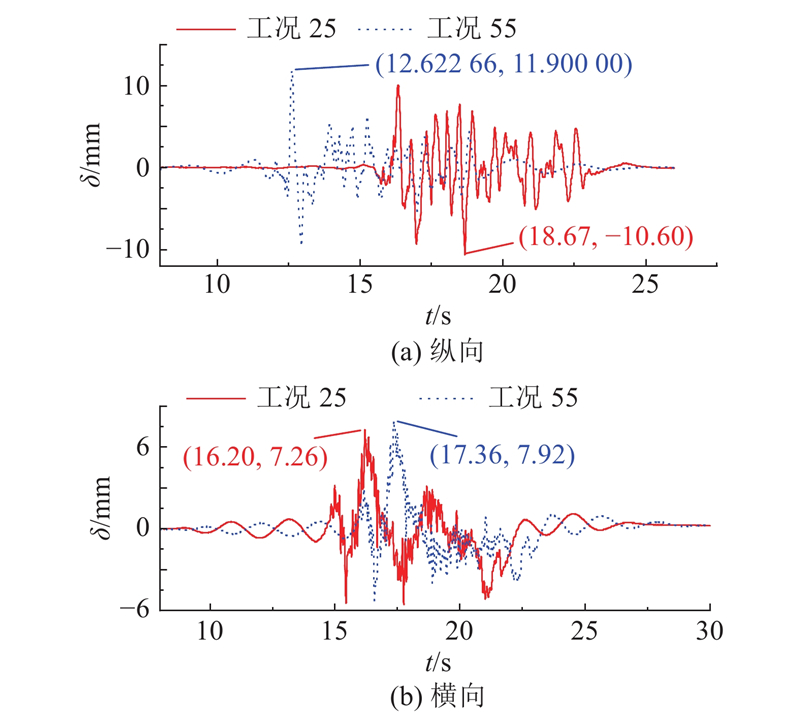
在实际工程中正常运营状态下管道为满载状态,不会出现半管的运营情况,因此选取空管和满管2种典型工况对比地震响应. 试验的前30个工况为空管模型试验工况,从工况32开始为满管工况. 选取峰值加速度均为0.345g的工况25和工况55,如图17所示为相同台面输入PGA下空、满管工况纵向位移响应对比. 由图可知,塔顶空、满管纵向最大位移分别为10.6、11.9 mm,增加了12.26%;塔顶空、满管横向最大位移分别是7.26、7.92 mm,满管时主塔顶横向最大位移响应较之空管增大了9.09%.
图 17
图 17 主塔塔顶的位移时程曲线
Fig.17 Time history curve of displacement at top of main tower
2.4. 应变响应
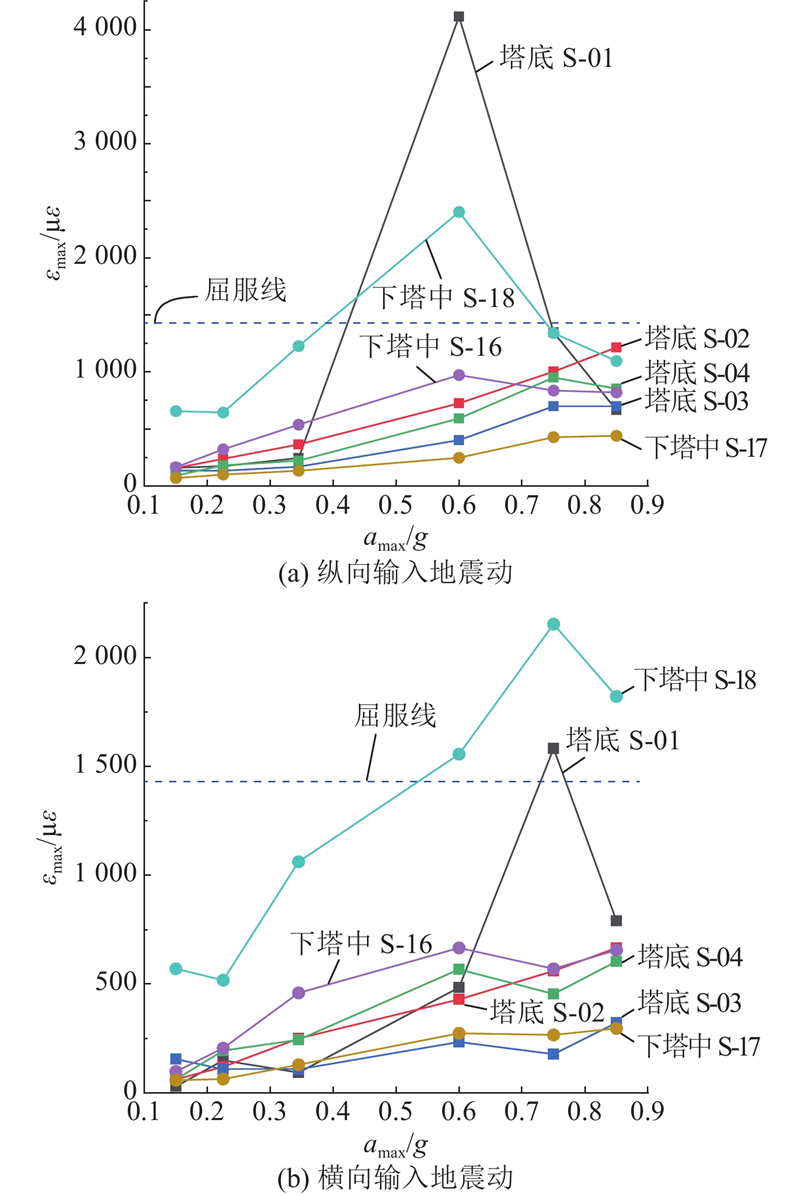
以场地人工波3为例,在纵向+竖向输入和横向+竖向输入时,选取台面输入PGA为0.15g、0.225g、0.345g、0.6g、0.75g和0.85g的6个工况分别提取主塔底部和下塔中测点的应变时程曲线,得到各测点最大应变响应随台面输入PGA的变化关系如图18所示,其中
图 18
图 18 主塔不同测点最大应变响应随台面输入地面峰值加速度的变化
Fig.18 Variation of maximum strain response at different measurement points of main tower with peak ground acceleration inputs on platform
3. 斜拉管桥的数值分析
3.1. 振动台试验模型的有限元建模
图 19
图 20
图 20 约束混凝土及非约束混凝土的应力-应变曲线
Fig.20 Stress-strain curves of constrained and unconstrained concrete
式中:
3.2. 典型工况下地震响应模拟值与试验值对比
以台面输入PGA=0.6g为例,对应原型PGA=0.4g(E2地震作用),在场地人工波3纵向+竖向和横向+竖向输入满管模型时,提取关键测点的最大位移响应模拟值,同测点最大位移响应试验值进行对比,对比结果整理如图21所示. 图中,
图 21
图 21 关键测点最大位移响应模拟值与试验值对比
Fig.21 Comparison between simulated and experimental values of maximum displacement response at key measurement points
当台面输入PGA=0.6g时,对应原型PGA=0.4g时(E2地震作用),有限元模型计算可得主塔底部绕纵桥向最大弯矩为146.3 kN·m,对应时刻截面最大压应力为5 389 kN/m2,经理论推导可得塔底两侧混凝土应变值分别537.52
图 22
图 22 塔底侧面混凝土应变时程曲线(PGA=0.6g)
Fig.22 Strain time history curve of concrete on side of tower bottom (PGA=0.6g)
3.3. 空、满管工况地震响应对比
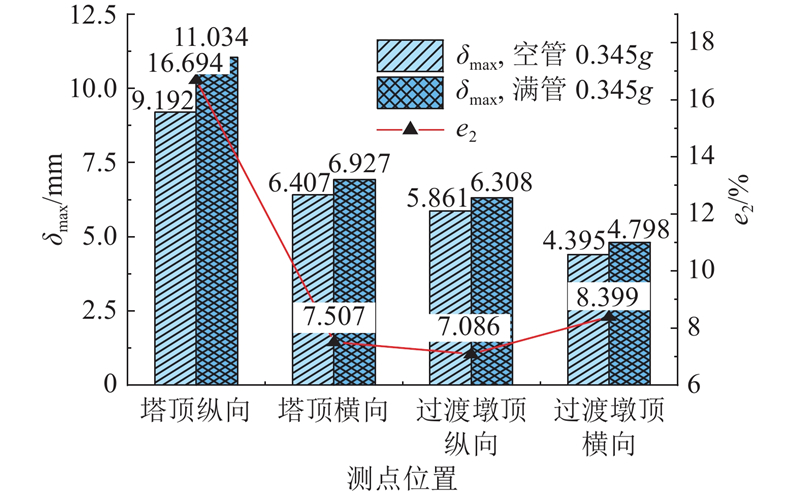
以台面输入PGA=0.345g为例,分别在空管模型和满管附加质量模型中提取关键测点的纵向和横向最大位移响应,对比结果整理如图23所示. e2为差值百分比. 纵向输入地震波时,塔顶满管相较空管的最大位移响应增大了16.694%,过渡墩顶满管相较空管的最大位移响应增大了7.086%. 横向输入地震波时,塔顶满管相较空管的最大位移响应增大了7.507%,过渡墩顶满管相较空管的最大位移响应增大了8.399%.
图 23
图 23 空、满管工况关键测点位移响应对比
Fig.23 Comparison of displacement response at key measurement points under empty and full pipe conditions
由振动台试验空、满管工况对比结果可知,纵向输入地震波时满管塔顶纵向位移比空管增大了12.26%,横向输入地震波时满管塔顶横向位移比空管增大了9.09%. 对比数值模拟结果与试验结果可知,在纵向地震波输入时,有限元软件计算所得满管较空管最大位移响应增幅16.694%,大于试验所得最大位移响应增幅12.260%;在横向输入地震波时,有限元软件计算所得最大位移响应增幅7.507%,略小于试验所得最大位移响应增幅9.090%. 振动台试验与有限元模拟在管内配重处理的差异导致地震波输入时位移响应增幅的不同. 等代模型的有限元杆系模型没有考虑流固耦合效应,模型中管内配重采用附加质量模拟,在试验中管道内采用高堆积密度的铁砂配重. 在纵向地震输入时,管内铁砂因自身惯性力的作用和管道的运动方向相反,使得管内铁砂对管壁产生摩阻力,因此试验时位移增幅小于数值模拟的位移增幅;在横向地震输入时,管道由于自身的横向抗弯刚度较小会产生振动和变形,管道在横向的振动与铁砂的振动耦合之后,横向地震输入时试验的最大位移增幅比采用附加质量模型计算的增幅略大.
杨元浩[24]建立全桥有限元流固耦合模型:管道采用壳单元模拟,水体采用20节点三维势流体单元模拟,水体两端采用固壁边界条件,水与输水管道接触面采用流固耦合边界. 考虑流固耦合的有限元模型与集中质量有限元模型的结果对比表明,纵向输入时,流固耦合模型地震响应小于集中质量模型;横向输入时,流固耦合模型地震响应大于集中质量模型. 该结果与振动台试验观测到的现象一致.
3.4. 试验模型与原全桥有限元模型地震响应对比
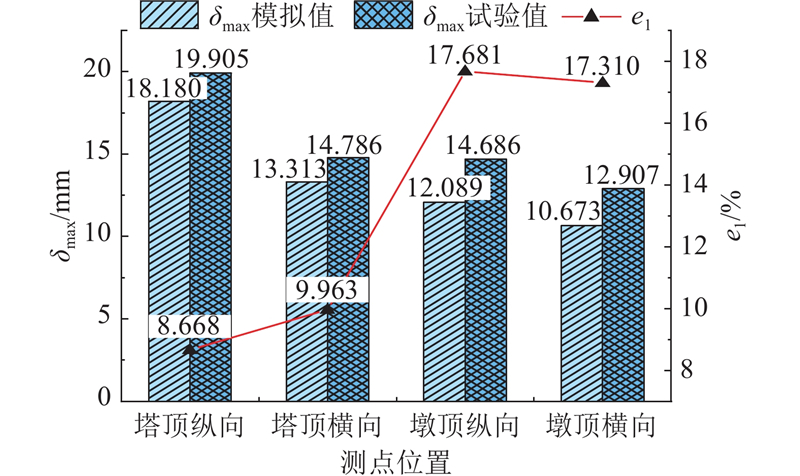
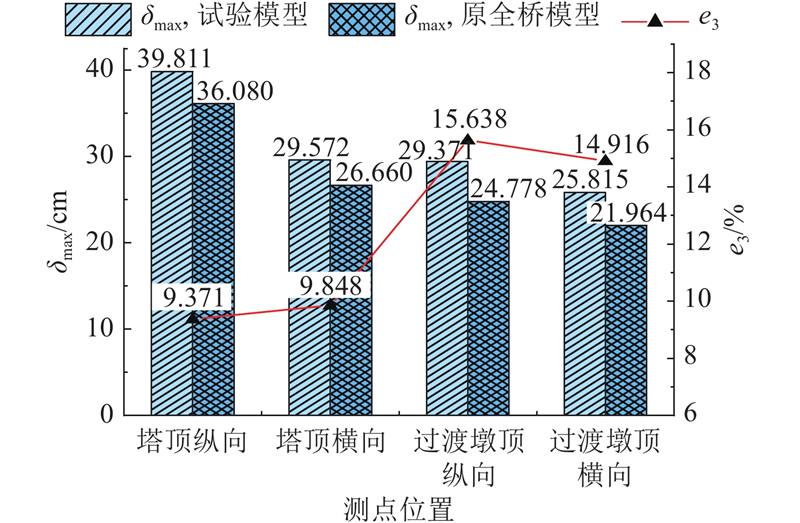
根据相似理论,满足相似关系设计的试验模型与原型在地震响应值上满足一定的相似比,为了验证该试验相似关系设计的可靠性,以原型输入PGA=0.4g为例(E2地震水平),选择场地人工波3输入结构,提取振动台试验关键测点的位移响应并根据位移相似比换算至原全桥模型位移响应,试验模型与原型对比结果如图24所示. e3为原全桥有限元模型与试验模型位移响应差值百分比. 振动台试验得到塔顶纵、横向位移换算至原全桥模型分别为39.811、29.572 cm,全桥有限元模型计算的塔顶纵、横向位移分别为36.08、26.66 cm,差值百分比分别为9.371%和9.848%;全桥有限元模型计算的关键测点位移峰值均略小于试验所得位移换算值,该规律与3.2节中试验模型与等代模型的对比结果一致;过渡墩顶测点的差值百分比比主塔测点处略大,该结果与试验模型和等代模型的对比结果一致. 试验模型同等代模型和原全桥模型的响应对比结果说明,等代模型与原全桥模型差值较小,试验模型与等代模型、原全桥模型均存在一定差值,但差值百分比不超过16%.
图 24
图 24 试验与原全桥模型关键测点位移响应对比
Fig.24 Comparison of displacement response at key measurement points between test and original full bridge model
4. 结 论
(1)在E1地震输入下,管内满载时各关键截面保持在弹性阶段,结构基本无损伤;在E2地震输入下,部分钢筋进入屈服,混凝土出现局部裂缝,但混凝土保护层完好,保持基本弹性,结构安全、满足规范要求. 对比试验结果与数值模拟结果表明,试验模型与原型在动力特性和地震响应方面均满足相似关系,振动台试验结果可信.
(2)对于相同水平下的台面输入PGA,由于场地人工波的特征周期较长,包含的长周期成分更加丰富,场地人工波导致的结构地震响应比El Centro波造成的结构地震响应大.
(3)在相同台面输入PGA下,满管模型地震响应较之空管总体呈增大趋势;随着地震输入PGA的增大,结构一阶自振频率总体呈减小趋势,结构关键测点的位移和钢筋应变响应峰值总体呈增大趋势.
(4)高密度铁砂模拟管道中的水体能够反映流固耦合效应. 试验中,在纵向输入地震动的情况下,满管相较于空管的位移响应增幅小于仅采用附加质量模拟水体时数值模拟的位移响应增幅;在横向输入地震动的情况下,试验中满管的位移响应增幅大于仅采用附加质量模拟水体时数值模拟的位移响应增幅.
(5)本文根据相似理论设计了大跨斜拉压力输水管桥的等代模型,开展了振动台试验,利用高密度铁砂模拟管道中水体,研究了多个工况下输水管桥的地震响应,获得了以上结论性的认识. 未来计划开展考虑桥梁桩土相互作用以及地震动空间变化性的计算研究.
参考文献
综合管线过桥方案探讨
[J].DOI:10.3969/j.issn.0451-0712.2013.06.026 [本文引用: 1]
Discussion on the scheme of integrated pipeline over the bridge
[J].DOI:10.3969/j.issn.0451-0712.2013.06.026 [本文引用: 1]
大跨度输水管道钢管桁架管桥设计选型与优化
[J].DOI:10.3969/j.issn.1001-3598.2019.03.015 [本文引用: 1]
Form design and optimization on large span steel pipe truss for water pipe
[J].DOI:10.3969/j.issn.1001-3598.2019.03.015 [本文引用: 1]
悬索管桥在输水工程中的应用
[J].DOI:10.3969/j.issn.1006-7175.2020.03.007 [本文引用: 1]
Application of suspension pipeline bridge in water conveyance project
[J].DOI:10.3969/j.issn.1006-7175.2020.03.007 [本文引用: 1]
水电站管桥结构分析与布置优化研究
[J].
Structure analysis and optimum design of pipeline bridge in hydropower station
[J].
过桥管道的斜拉桥全桥受力性能数值模拟分析
[J].
Numerical simulation analysis of the mechanical performance of cable-stayed bridges with crossing pipes
[J].
Methods used for calculating seismic response of multiply supported piping systems
[J].
Active control of multi-modal propagation of tonal noise in duets
[J].DOI:10.1006/jsvi.1996.0402 [本文引用: 1]
不同地基模拟及流固耦合方式对渡槽地震响应分析
[J].
Seismic response analysis of aqueduct under different ground simulation and fluid solid coupling modes
[J].
Vibration of a suspension bridge installed with a water pipeline and subjected to moving trains
[J].DOI:10.1016/j.engstruct.2007.05.006 [本文引用: 1]
地震作用下不同形式深水桥墩流固耦合效应研究
[J].
Fluid-solid coupling effect of different forms of deep-water piers under earthquake
[J].
基于流固耦合的过桥水管动力特性研究
[J].
Study on dynamic characteristics of water pipes across bridge based on fluid-solid coupling
[J].
基于双向流固耦合的多跨过桥水管模态分析
[J].
Study on multi-span fluid conveying pipe with bidirectional FSI method
[J].
考虑SSI效应的带隔板渡槽动力特性及其地震响应
[J].
Dynamic characteristics and seismic response of rectangular aqueduct with baffle considering SSI effect
[J].
油气集输悬索管桥动特性及地震非线性时程反应分析
[J].
Dynamic characteristics and seismic nonlinear time history response analysis of suspension pipe bridge for oil and gas gathering and transportation
[J].
适用于大中口径给水管道的梯形断面桁架管桥设计与分析
[J].
Analysis and design of the truss pipe bridge with trapezoid section suitable for medium-large sized pipe
[J].
强震作用下大型排架式U型渡槽的损伤破坏分析
[J].
Seismic damage analysis of U-shaped aqueduct with the bent-type structure subjected to strong earthquake
[J].
减隔震装置在特大型渡槽中的应用
[J].
Application of seismic reduction and isolation device to especially large-scale aqueduct
[J].
南水北调中线漕河渡槽结构地震动力特性研究
[J].
Study on seismic dynamic characteristics of aqueduct of caohe in the middle of south-to-north water diversion project
[J].
大型薄壁输水渡槽流固耦合振动台试验研究
[J].
Experimental study of dynamic interaction between large thin wall aqueduct and water
[J].