关于凹坑壁面附近空泡破裂过程的研究很少,空泡动力学理论研究多为对Rayleigh-Plesset方程的修正,空泡溃灭多发生在近壁区,具有非球形、非线性和瞬时性等特点,往往无法求得解析解. Zhang等[5]基于双渐进分析方法(double progressive analysis method),引入三维波动方程,将双渐进法扩展为非球形空泡的边界积分法,研究了弱可压缩流场下的空泡运动. Zhang等[6]建立新的振荡气泡动力学理论,考虑了边界条件、气泡相互作用、流场可压缩性等影响,统一了经典气泡方程. 固壁[7]和自由表面[8]是研究较多的两类边界,由于空泡与壁面的相互作用,空泡在近壁面的溃灭过程相比在自由场中的溃灭过程更为复杂. Cui等[9]使用电火花生成气泡和高速摄像技术(high speed video technology)研究具有圆形开口舱底附近的水下爆炸气泡的振荡特性,发现气泡的演化过程高度依赖于开口距离和开口半径;从180个实验中总结出7种独特的振荡场景,即边缘约束振荡、向内射流、向外射流、凸起和凹陷、准球形振荡、有射流的球形振荡和无射流的球形振荡. Kim等[10]对有脊状和凹槽图案结构附近的水下空泡溃灭过程开展实验研究,发现脊上的气泡在收缩过程中损失了一些能量,削弱了向表面射流的强度,有效减少了对结构表面的侵蚀. Ma等[11]以半球为主要研究边界,通过使用400 V的高压电产生电火花空泡研究3种半球形边界与空泡运动特性之间的关系,发现在同一曲率下,空泡与壁面距离越大,壁面受到的冲击载荷越大;在同一壁面距离下,曲率越大,空泡的射流速度越小. Aziz等[12]使用边界积分法(boundary integral method)对弯曲刚性板间的三维气泡振荡进行数值模拟,发现随着空泡溃灭程度的增加,空泡沿径向拉伸长度逐渐增大并最终分裂为2个空泡,空泡射流速度随偏心距的增大而增大. Manmi等[13]采用边界积分法研究处于声场中的两弯曲刚性板间的微气泡,发现空泡最大半径及射流速度不受声场影响,空泡破裂产生的高压区与射流方向受声场影响较大.
上述研究多以半球形壁面形式分析空泡在不同曲率壁面下的运动特性,揭示了空泡在不同曲率壁面下射流速度、压力载荷和空泡形态等变化规律. 本研究以单空泡为对象,基于欧拉方法的可压缩两相流求解器CavitatingFoam,给定多种凹坑曲率,探究空泡在不同曲率凹坑壁面附近的空泡溃灭特性和载荷特性.
1. 数值方法
1.1. 控制方程
式中:ρm为混合物密度;p为压力;t为时间;ψm为混合物的压缩系数,
βs为等熵压缩率,
c为混合物的声速. 将式(3)代入式(2)得到
蒸汽和液体的状态方程分别为
式中:ρv、ρl分别为蒸汽密度和液体密度,ψv、ψl分别为蒸汽和液体的压缩系数,
式中:ρls、ρvs分别为液体和蒸汽的饱和密度. 液体饱和密度降低到蒸汽饱和密度,出现空化现象. 当
式中:psa为饱和压力,
定义μv、μl分别为蒸汽和液体的黏度,则混合物的黏度计算式为
定义U为流体速度矢量,连续方程[17]为
动量方程为
1.2. 空泡作用力
式中:FB、FD分别为次Bjerknes力和黏性阻力,根据双空泡理论推导凹坑壁面下单空泡溃灭时的次Bjerknes力及阻力,得到
式中:Ri为主空泡半径,ρ为流场密度,Rj为镜像空泡半径,
式中:Rm为空泡初始半径,Rs为凹坑半径,L为空泡中心与凹坑壁面的距离.
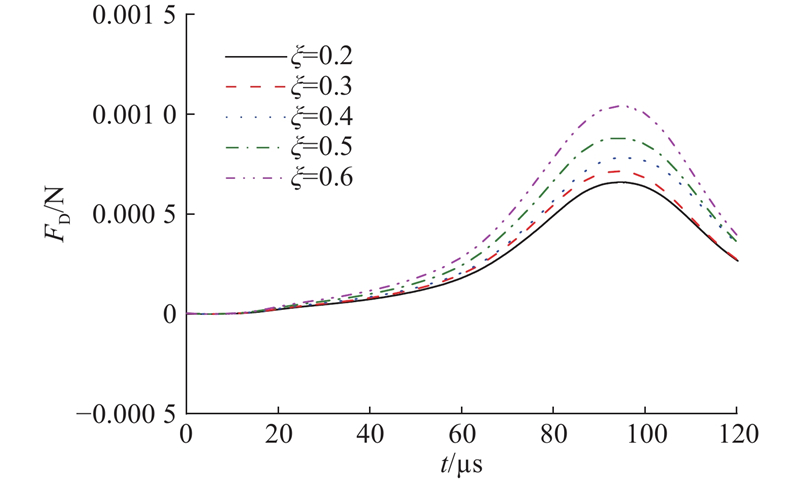
由于空泡溃灭时会向周围的流场辐射声波,形成次级声场,当次级声场反作用于空泡时,会产生相互作用力(次Bjerknes力),当脉动中的空泡同向振荡时相互吸引,反向振荡时相互排斥,这种现象被称为次Bjerknes效应. 如图1所示,分析不同凹坑相对曲率下空泡溃灭时受到的次Bjerknes力,当凹坑相对曲率增大时,作用在空泡上的次Bjerknes力逐渐增大. 随着空泡溃灭时间增加,次Bjerknes力先表现为引力并逐渐减小,接着表现为斥力,在空泡溃灭末期次Bjerknes力表现为引力,凹坑相对曲率越大,引力越大. 如图2所示为不同凹坑相对曲率下次Bjerknes力随空泡溃灭过程的变化. 对比图1与图2发现,在空泡溃灭的过程中,次Bjerknes力对空泡溃灭产生的作用力比阻力大一个数量级,说明次Bjerknes效应对空泡溃灭时动力学特性影响较大.
图 1
图 1 不同凹坑相对曲率下次Bjerknes力随空泡溃灭过程的变化
Fig.1 Change of Bjerknes force with vacuole collapse process under different relative pit curvature
图 2
图 2 不同凹坑相对曲率下阻力随空泡溃灭过程的变化
Fig.2 Changes of resistance with vacuole collapse process under different relative pit curvature
1.3. 几何模型
如图3所示为研究空泡在凹坑壁面附近的溃灭过程. 所研究流场的环境压力为1.0×105 Pa,流场介质选用清水,密度为998 kg/m3,空泡初始半径为1 mm,空泡内部初始压力为298 K时的饱和蒸汽压为3 160 Pa,蒸汽饱和密度为0.59 kg/m3,考虑重力和表面张力系数的影响,表面张力系数为0.072 N/m. 设计时,将空泡放置于凹坑中心正上方L处,Ld为凹坑的深度.
图 3
表 1 单空泡性能特性参数
Tab.1
| Rs/mm | ξ | γ | Rs/mm | ξ | γ | |
| ∞ | 0 | 0.4 | 2.50 | 0.4 | 1.2 | |
| 5.00 | 0.2 | 0.7 | 2.00 | 0.5 | 1.5 | |
| 3.33 | 0.3 | 1.0 | 1.67 | 0.6 | 2.0 |
图 4
1.4. 网格划分及计算设置
设定Rm=1 mm,设置二维平面计算域面积为50 mm×50 mm. 将空泡放置于计算域底部凹坑壁面附近,避免计算域其他边界对空泡溃灭过程的影响. 如图5所示,对空泡溃灭区域网格进行加密. 图5(b)中圆形部分体积分数为1,表示为蒸汽,其他部分体积分数为0,表示为水. 使用有限体积法离散控制方程,方程中数值离散格式如下:时间导数项使用欧拉隐式格式,梯度项为高斯积分,插值格式采用中心差分格式,面法向梯度项采用未修正的离散格式,网格体心到网格面心的插值使用线性化插值格式. 压力速度的耦合采用压力-速度耦合算法进行循环求解,为了保证数值稳定性,将最大库朗数q和最大声学库朗数设置为0.5;流场的4个壁面速度边界设置为无滑移壁面,压力边界设置为零梯度边界.
图 5
图 5 计算域和网格划分示意图
Fig.5 Schematic diagram of calculation domain and grid division
1.5. 网格无关性验证
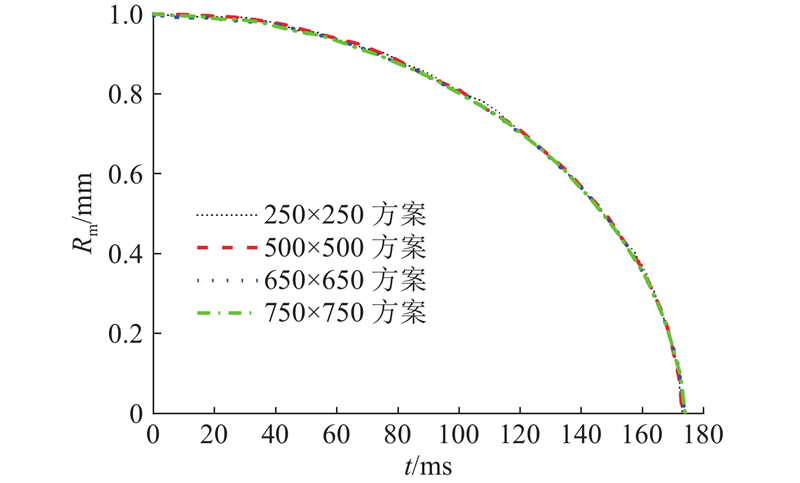
为了检查数值模拟结果对网格的依赖性,设计4套网格划分方案,以自由场空泡溃灭过程作为验证实例. 不同网格方案下空泡半径随时间的变化如图6所示,可以看出,不同网格方案下空泡体积的变化过程差异极小,基本上保持一致,说明4套网格方案均具有足够的精度来计算空泡的溃灭过程. 为了保证足够的分辨率来捕捉空泡溃灭过程中释放的压力波,也为了节约计算资源,采用650×650的网格方案进行后续的数值模拟,最小网格尺寸
图 6
图 6 不同网格方案下空泡半径随时间的演化
Fig.6 Evolution of vacuole radius with time under different mesh scheme
2. 结果分析
2.1. 数值模拟与实验结果的对比
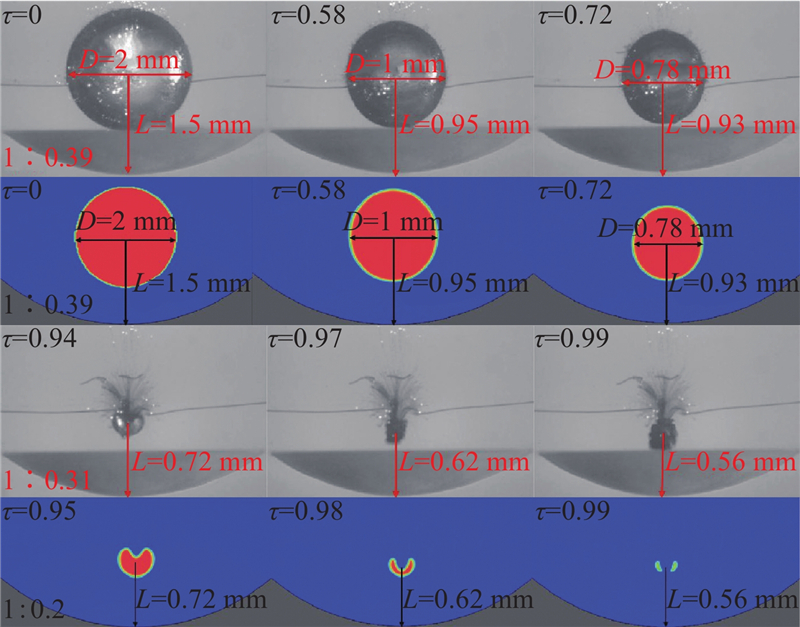
Cui等[20]采用相似理论,在静止水箱中进行电火花实验产生空泡并模拟空泡的溃灭过程. 当凹坑相对曲率ξ=0.5,空泡近壁系数γ=1.5时进行实验,球形空泡由于内部压力远小于外界压力,随着空泡溃灭时间增加,空泡体积不断缩小,但横向收缩速度大于纵向收缩速度,空泡最终表现为纵向尺寸大于横向尺寸的椭球形. 空泡上表面收缩速度大于下表面收缩速度,因此在空泡溃灭末期,空泡上表面曲率大于下表面曲率,导致空泡向内凹陷,最终分裂为2个环形空泡. 如图7所示,由于空泡溃灭时间较短,数值模拟与实验条件完全一致,且实验结果与数值模拟结果基本一致,证明本研究采用的数值模拟方法可靠. 本研究通过数值模拟得到不同凹坑曲率下空泡坍塌到最小半径所需要的时间t*,进而计算空泡溃灭时间无量纲系数τ:
图 7
图 7 空泡形态演变的实验及数值模拟图(ξ=0.3, γ=1.5)
Fig.7 Experimental and numerical simulation of vacuole morphology evolution (ξ=0.3, γ=1.5)
式中:t为空泡溃灭过程时间.
2.2. 凹坑相对曲率和空泡近壁系数对溃灭时间的影响
图 8
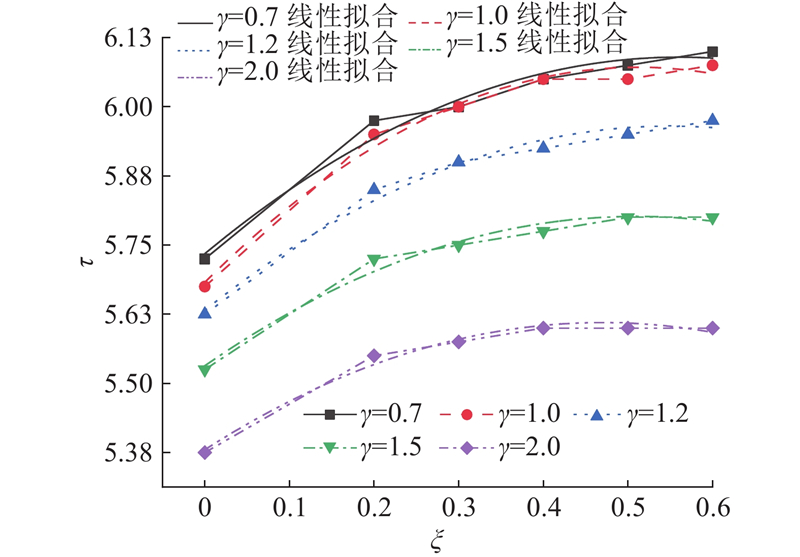
图 8 不同凹坑相对曲率下的空泡溃灭时间
Fig.8 Vacuole collapse time under different relative pit curvature
由式(18)可知,空泡溃灭时间系数与凹坑相对曲率近似呈指数函数关系并单调递增,与空泡近壁系数近似呈一次函数关系.
2.3. 凹坑相对曲率和空泡近壁系数对射流的影响
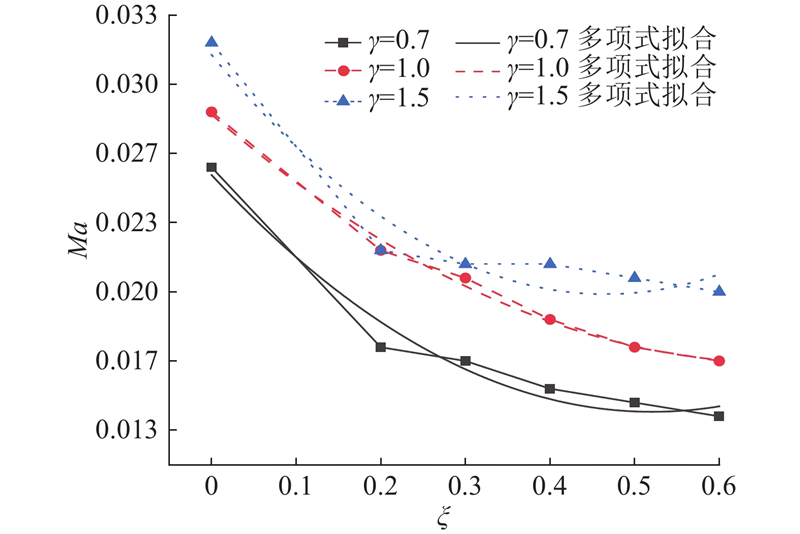
如图9所示,在同一个空泡近壁系数下,随着凹坑相对曲率逐渐增大,空泡轮毂逐渐向两侧延伸,空泡溃灭形态为环形空泡在二维平面的2个环形轮廓,空泡尾部相互接近且内表面呈一定角度. 如图10所示,进一步研究空泡射流速度与凹坑相对曲率以及空泡近壁系数之间的变化关系,随着凹坑相对曲率增大,空泡溃灭时射流速度逐渐减小,当ξ=0时,空泡溃灭时射流速度最大;随着空泡近壁系数逐渐增大,空泡溃灭时射流速度逐渐增大. 空泡溃灭射流速度变化说明随着凹坑相对曲率和壁面与空泡间的次Bjerknes效应逐渐增大,空泡溃灭对壁面的作用增强,空泡溃灭过程加快. 通过非线性拟合,使用20 ℃清水中声速V*=1 500 m/s将所得射流速度处理为马赫数:
图 9
图 9 不同凹坑相对曲率下射流对空泡形态的影响(τ=5.95)
Fig.9 Effect of jet on vacuole morphology with different relative pit curvature (τ=5.95)
图 10
图 10 不同凹坑相对曲率的射流速度(τ=5.95)
Fig.10 Jet velocity with different relative pit curvature (τ=5.95)
式中:V为空泡射流速度. 建立空泡射流马赫数随凹坑相对曲率和空泡近壁系数变化的关联关系:
由式(20)可知,空泡射流马赫数与凹坑相对曲率呈指数关系并单调递减,与空泡近壁系数近似呈一次函数关系.
2.4. 凹坑相对曲率和空泡近壁系数对壁面中心压力冲击载荷的影响
通过非线性拟合,使用环境压强p=1.0×105 Pa,计算得到压力冲击载荷峰值系数:
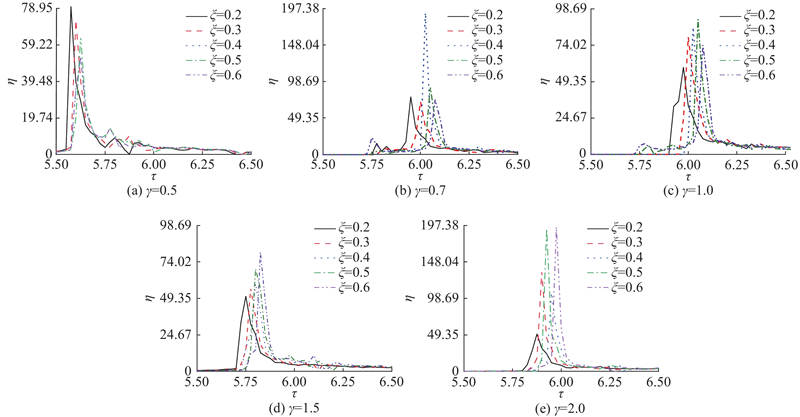
式中:pmax为壁面压力冲击载荷峰值点. 如图11所示,随着空泡溃灭时间的增加,壁面中心的压力冲击载荷均呈先增大到最高点后快速下降直至平缓的趋势. 随着空泡近壁系数的增加,壁面中心的压力冲击载荷逐渐减小,并且在同一空泡近壁系数下,壁面中心的载荷压力峰值最大的工况表现出壁面曲率由0.2向0.6增大的趋势. 随着凹坑相对曲率的增加,壁面中心压力冲击载荷到达峰值的时间逐渐延缓,说明空泡初始位置距离壁面越近,次Bjerknes效应越强烈,对壁面的作用越大;不同的壁面曲率使得空泡受到的作用力不同,改变了空泡溃灭过程中的几何形状,进而影响空泡溃灭对壁面的压力冲击载荷. 在空泡近壁系数由0.5向1.0增加的过程中,空泡与壁面间的距离逐渐增大,而空泡溃灭末期凹坑壁面中心的压力冲击载荷峰值逐渐减小,说明在空泡与壁面距离增大的过程中,空泡溃灭产生的压力波传播时间延长,导致凹坑壁面中心受到的压力减小,空泡对凹坑壁面中心的作用随之减小,使得凹坑壁面中心压力冲击载荷峰值随着空泡近壁系数的增加而逐渐向凹坑相对曲率更大的方向移动.
图 11
2.5. 凹坑附近空泡溃灭时的压力波传播特性
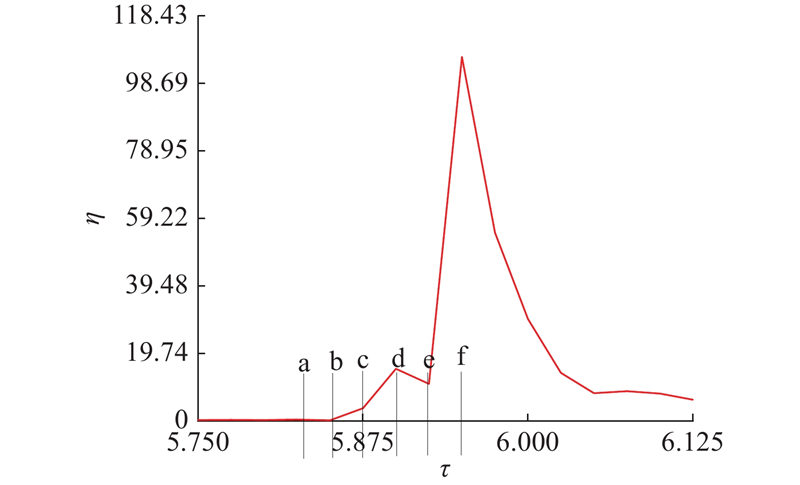
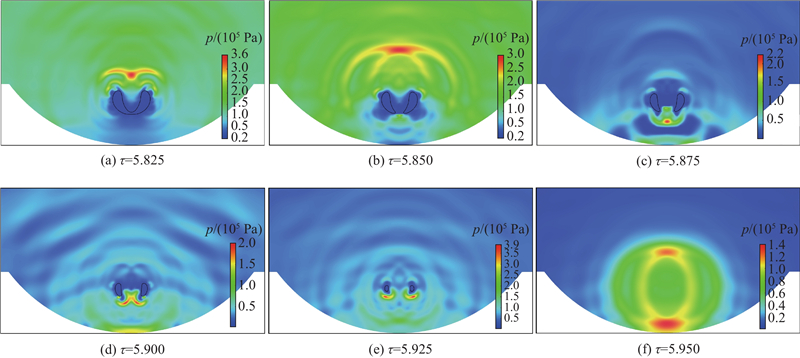
如图12所示为凹坑壁面中心冲击载荷的时间历程. 由图12得到凹坑壁面附近压力波的传播过程图,如图13所示. 以ξ=0.5、γ=1.2的工况为例,选取a、b、c、d、e、f时刻研究空泡溃灭末期压力波传播特性. 结合对二维平面空泡溃灭过程的研究发现,当空泡由a向b发展时,空泡上表面压力逐渐增大,空泡表面不断向内凹陷,在b时刻射流贯穿空泡,在二维平面中为中空的环形空泡的2个环形轮廓并向斜上方传播2束压力波. 壁面中心所受到的压力急剧上升,在d时出现第一个峰值. 当d向e发展时,在环形空泡尾部出现高压区,壁面中心受到的压力出现短暂下降,说明2个环形空泡间存在相互作用力并对流场产生扰动. 当空泡溃灭发展到f时刻时,空泡完全溃灭,同时产生2束环形压力波向周围传播,压力峰值的同向叠加在底部靠近壁面的位置产生高压区,壁面中心受到的压力载荷出现远大于其他时刻的第二个压力峰值,说明2束压力波相互叠加,对凹坑壁面中心载荷压力的影响剧烈,对凹坑壁面的作用力增强.
图 12
图 12 壁面中心冲击载荷的时间历程(ξ=0.5, γ=1.2)
Fig.12 Time course of impact loads at wall center (ξ=0.5, γ=1.2)
图 13
图 13 壁面附近压力波的传播过程(ξ=0.5, γ=1.2)
Fig.13 Propagation process of pressure wave near wall (ξ=0.5, γ=1.2)
3. 结 语
在环境压力为1个大气压,20 ℃ 清水的不同凹坑相对曲率和空泡近壁系数下,用CavitatingFoam对初始直径为1 mm的单空泡进行数值模拟,得到以下结论. 1)在同一空泡近壁系数下,凹坑相对曲率与空泡溃灭时间呈指数关系,在同一凹坑相对曲率下,空泡近壁系数与空泡溃灭时间呈一次函数关系. 2)在凹坑相对曲率逐渐增大的过程中,空泡溃灭产生的射流速度逐渐增大,空泡射流马赫数与凹坑相对曲率呈指数关系,与空泡近壁系数呈一次函数关系. 在相同的空泡近壁系数下,空泡壁面压力中心载荷峰值呈现凹坑相对曲率由0.2向0.6变化的趋势. 3)对空泡溃灭时向周围流场辐射的两束压力波进行监测,发现随着空泡溃灭时间的增加,压力波首先在空泡溃灭的上表面产生高压区,接着在空泡溃灭的下表面产生高压区,当空泡完全溃灭后,2束压力波峰值同向叠加,出现压力峰值,此时高压区的压力载荷最大. 本研究揭示了空泡溃灭时压力波的传播特性,得到单空泡在凹坑附近溃灭时的动力学特性,总结出的普适性规律能够为抑制空化破坏及利用空化的工程应用提供理论依据和技术参考. 由于多空泡和不规则壁面的动力学特性研究还存在不足,未来计划探索多空泡与不同形状壁面的动力学特性.
参考文献
The effect of surface geometry of solid wall on the collapse of a cavitation bubble
[J].DOI:10.1115/1.4053350 [本文引用: 1]
固壁面附近空化泡溃灭过程的数值模拟
[J].DOI:10.3969/j.issn.1006-4303.2015.05.008
Collapse simulation of a cavitation bubble near a rigid boundary
[J].DOI:10.3969/j.issn.1006-4303.2015.05.008
刚性壁面附近气泡和自由面的耦合效应研究
[J].DOI:10.7638/kqdlxxb-2020.0060 [本文引用: 1]
Study on the interaction between the bobble and free surface close to a rigid wall
[J].DOI:10.7638/kqdlxxb-2020.0060 [本文引用: 1]
Simulation of bubble motion in a compressible liquid based on the three dimensional wave equation
[J].
A unified theory for bubble dynamics
[J].
Dynamics of a cavitation bubble near a solid wall
[J].DOI:10.1134/S0869864316020074 [本文引用: 1]
Dynamic features of a laser-induced cavitation bubble near a solid boundary
[J].DOI:10.1016/j.ultsonch.2013.01.010 [本文引用: 1]
Experimental investigation of bubble dynamics near the bilge with a circular opening
[J].DOI:10.1016/j.apor.2013.03.002 [本文引用: 1]
Underwater bubble collapse on a ridge-patterned structure
[J].DOI:10.1063/5.0006372 [本文引用: 1]
Experimental research on the influence of different curved rigid boundaries on electric spark bubbles
[J].DOI:10.3390/ma13183941 [本文引用: 1]
Modeling three dimensional gas bubble dynamics between two curved rigid plates using boundary integral method
[J].DOI:10.1016/j.enganabound.2019.09.008 [本文引用: 1]
Three-dimensional oscillation of an acoustic microbubble between two rigid curved plates
[J].DOI:10.1007/s42241-021-0090-0 [本文引用: 1]
单个蒸汽气泡溃灭过程的边壁效应数值研究
[J].
Numerical study of boundary effect during the collapse of single vapor bubble
[J].
Modeling of the bubble collapse with water jets and pressure loads using a geometrical volume of fluid based simulation method
[J].DOI:10.1016/j.ijmultiphaseflow.2022.104103 [本文引用: 1]
Bjerknes forces between small cavitation bubbles in a strong acoustic field
[J].DOI:10.1103/PhysRevE.56.2924 [本文引用: 1]
Bjerknes forces in motion: long-range translational motion and chiral directionality switching in bubble-propelled micromotors via an ultrasonic pathway
[J].DOI:10.1002/adfm.201702618 [本文引用: 1]
Pulsating bubbles dynamics near a concave surface
[J].DOI:10.1016/j.oceaneng.2022.110989 [本文引用: 1]