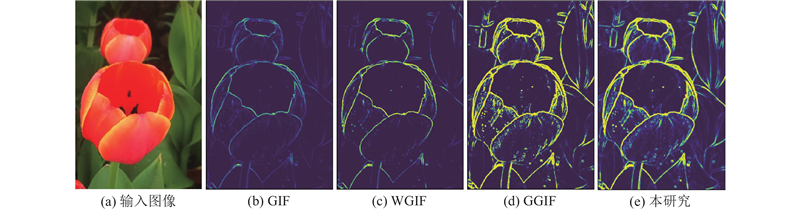
图像平滑方法可以分为具有边缘保持特性滤波和没有边缘保持特性滤波2个类别. 高斯滤波器是典型的各向同性的平滑算子, 不具有保边特性, 会导致图像边缘模糊从而出现光晕和伪影. 针对这一缺陷, 出现了许多具有边缘保持特性的图像平滑方法, 比如基于全变分 (total variation, TV) 的模型^[1-2]、双边滤波器^[3-4]、加权最小二乘滤波器^[5-6]、基于直方图均衡化的模型^[7-8]、侧窗滤波器^[9-10]等. 具有边缘保持特性滤波的方法在计算领域的摄影和图像处理方面应用广泛, 典型的应用包括图像去噪^[11-12], 细节增强^[13-14], 高动态范围的图像色调映射^[15-16], 图像融合^[17-18], 纹理去除^[19-20]等.

引导滤波算法是具有边缘保持性能的图像平滑算法. 引导图像滤波器 (guided image filter, GIF)^[21]依据从引导图像提取的信息来计算滤波输出. GIF具有保边性能且计算效率高, 但是无法保留比较锐利的边缘, 会出现边缘模糊的平滑结果. 研究人员提出GIF的改进模型^[21-26]. Li等^[22]提出加权引导滤波器 (weighted guided image filter, WGIF), 通过在GIF中引入边缘感知权重来提高模型提取图像结构信息的能力, 这一定程度上改善了GIF无法保留锐边的缺点. 梯度域引导图像滤波器 (gradient domain guided image filter, GGIF)^[23]也是基于局部优化, 不同的是多尺度约束被引入损失函数的正则化项, 使图像的边缘与细节更好地分离, 能够进一步提升滤波器的保边性能, 但是GGIF对于结构区域附近的纹理平滑效果欠佳. 单边窗引导滤波器 (side window guided filter, SWGIF)^[24]以单边窗口为局部窗口, 视每个像素为潜在边缘, 侧窗策略计算引导滤波的输出, 能够一定程度上提高滤波器的保边性能, 但是SWGIF会保留图像结构区域附近的纹理和异常噪声点. 基于Steering核的引导滤波器 (weighted guided image filtering with steering kernel, SKWGIF)^[25]基于加权平均策略, 以Steering核获取引导图像的局部结构信息, 增强了滤波器的边缘保持性能. 由于Steering核算法的复杂性, SKWGIF比GIF、WGIF、GGIF等方法计算耗时多. Deng等^[26]将广义伽马分布作为先验分布, 将平滑和锐化统一到单个模型中, 提出基于广义伽马分布的边缘感知平滑-锐化滤波器, 该模型的边缘保持的性能有很大的提升空间. Liu等^[27]提出峰值感知引导滤波，用于噪声频谱信号的保峰平滑. 峰值感知作为引导滤波器的权重, 能够较好地保留输入频谱信号的峰值高度、峰值宽度和峰值位置, 但是峰值感知自适应对于图像中的细小结构和微弱边缘的保持能力有待提高. Li等^[28]提出用于图像增强的自适应加权引导图像滤波算法, 为了更好地保持边缘和结构, 以初始深度图构建引导图像, 通过设置自适应的系数来抑制噪声和增强细节. 虽然该算法一定程度上提高了模型的边缘保持能力, 但是引导图像的构建和平滑系数的定义依赖于估计得到的深度图像, 聚焦算法本身的局限性会影响滤波结果.

针对以上问题，本研究提出基于峰值感知和多尺度约束的加权引导滤波器. 该滤波器使用峰值感知作为边缘感知加权定义方法, 引入多尺度约束以提高滤波模型的结构保留能力; 通过引导图像的方差信息实现正则化项系数的自适应, 进一步提高加权引导滤波算法的边缘保持能力.

假设$G$为引导图像, $X$为待处理图像.窗口${\varOmega _k}$代表第$k$个半径为$r$以像素点$q$为中心的局部窗口, 像素数为$N = {(2r+1)^2}$. ${G_k}(p)$为像素点$p \in {\varOmega _k}$的像素值, 对$G$的每个局部窗口的像素进行线性变换：

(1)$ {I_k}(p) = {a_k}{G_k}(p)+{b_k} . $

式中：$ {I_k}(p) $为滤波的输出结果, ${a_k}$、${b_k}$均为局部窗口${\varOmega _k}$的模型系数, 损失函数为

(2)$ L = \frac{1}{N}\sum\limits_{p \in {\varOmega _k}} {{{[{I_k}(p) - {X_k}(p)]}^2}+\lambda a_k^2} . $

将式 (1) 代入式 (2) 得到

(3)$ L = \frac{1}{N}\sum\limits_{p \in {\varOmega _k}} {{{[{a_k}{G_k}(p)+{b_k} - {X_k}(p)]}^2}+\lambda a_k^2} . $

式中：$\lambda $为正则化项系数. 令$ \partial L/\partial {b_k} = 0 $, 得到

(4)$ {b_k} = {\overline X _k} - {a_k}{\mu _k}. $

式中：${\overline X _k}$、${\mu _k}$分别为$X$和$G$的局部窗口的像素均值, 将式 (4) 代入式 (2) 得到新的损失函数, 令$ \partial L/\partial {a_k} = 0 $, 得到

(5)$ {a_k} = \frac{{\phi _k^{}}}{{\sigma _k^2+\lambda }}. $

式中：$\sigma _k^2$为$G$半径为$r$的局部窗口的方差, 定义为

(6)$ \sigma _k^2 = \frac{1}{N}\sum\limits_{p \in {\varOmega _k}} {{{[{G_k}(p) - {\mu _k}]}^2}} . $

$ {\phi _k} $为局部协方差, 定义为

(7)$ {\phi _k} = \frac{1}{N}\sum\limits_{p \in {\varOmega _k}} {\left( {{G_k}(p) - {\mu _k}} \right)\left( {{X_k} - {{\overline X }_k}} \right)} . $

若输入图像作为引导图像, 则$\sigma _k^2 = \phi _k^{}$. 求解得到${a_k}$、${b_k}$, 在局部窗口${\varOmega _k}$的滤波输出结果为

(8)$ {I_k}(p) = {a_k}{G_k}(p)+\left( {{{\overline X }_k} - {a_k}{\mu _k}} \right). $

输入图像的像素$p$，最终的滤波输出结果由$M$个不同局部窗口上的滤波结果加权平均得到, 为

(9)$ I(p) = \sum\limits_{k = 1}^M {{\omega _k}{I_k}(p)} ,\quad \displaystyle\sum\limits_{k = 1}^M {{\omega _k}} = 1. $

在WGIF^[22] 中, 权重${\omega _k}$=$1/M$.

在峰值感知引导滤波方法^[27]中, 峰值感知权重的2种定义分别是基于二阶导数和输入信号的值. 在图像处理中, 结构和边缘区域的二阶导数明显大于非结构区域, 基于二阶导数可以定义权重w₁来获得图像$J(p)$的结构信息：

(10)$ {w_1} = \exp \left[ { - {{\left( {{{| {{J^{''}}(p)} |}}/{k}} \right)}^2}} \right]. $

式中：$k > 0$为常数参数.频谱信号的局部最大值通常表示峰值的位置. 对于图像来说, 结构区域通常像素值较大. 通过像素值定义权重w₂来获得图像的结构信息：

(11)$ {w_2} = \exp \left[ { - {{\left( {{{\left| {J(p)} \right|}}/{k}} \right)}^2}} \right]. $

GIF、WGIF、GGIF等和所提滤波器基于共同的假设：滤波输出满足式 (1) . 若${a_k} = 1$, 则结构和边缘可以保留; 在平坦区域, ${a_k}$接近0, 纹理平滑效果越好. 为了防止${a_k}$过大, 可以通过调整式 (2) 的$\lambda $实现对${a_k}$的惩罚, 从而获得更好的自适应边缘感知加权. 基于以上思考, 将式 (11) 的峰值感知权重引入引导滤波器模型, 通过峰值感知权重获得图像的结构信息. 引入多尺度约束, 对正则化项系数进一步自适应, 得到新的损失函数为

(12)$ L = \frac{1}{N}\sum\limits_{p \in {\varOmega _k}} {{{[{I_k}(p) - {X_k}(p)]}^2}} +\lambda {w_1}\left( {a_k^2 - \gamma _k^2} \right), $

(13)$ \gamma _k^2 = 1 - 1/\left( {1 + \exp \left( {\left( {\mathop \sigma \nolimits_k^2 - \overline {\mathop \sigma \nolimits_k^2 } } \right)/{\eta }} \right)} \right) . $

式中：$ \overline {\sigma _k^2} $为$ \sigma _k^2 $的均值, $ \eta = \overline {\sigma _k^2} - \min \left( {\sigma _k^2} \right) $. 式 (13) 使用引导图像半径为$r$的局部窗口的像素方差定义$\gamma _k^2$, GGIF^[23]的损失函数根据引导图像半径分别为$r$和3的局部窗口的像素方差的乘积定义. $\lambda $须指定, 以控制模型平滑的尺度. 图像不同区域的信息和结构不同，为此将平滑尺度参数基于图像信息进行重新定义, 让滤波器模型在图像结构区域的平滑尺度尽可能小，而在纹理区的平滑尺度尽可能大.

(14)$ \lambda = \frac{{{\lambda _0}}}{{1+{{\left( {{{\sigma _k^2}}/{{\overline {\sigma _k^2} }}} \right)}^2}}} . $

式中：${\lambda _0}$为正常数. 通过图像方差信息对正则化项系数自适应, 进一步提高模型的边缘保持能力. 求解式 (12) 得到局部线性模型的系数为

(15)$ {a_k} = \frac{{\phi _k^{}{\text+}\lambda {w_1}\gamma _k^2}}{{\sigma _k^2+\lambda {w_1}}},\quad{b_k} = {\overline X _k} - {a_k}{\mu _k}. $

所提滤波器的最终输出由式(9)加权平均得到，

将$ {I_k}(p) $代入式(9) 得到

(16)$ I(p) = G(p)\sum\limits_{k = 1}^M {{\omega _k}{\alpha _k}} +\sum\limits_{k = 1}^M {{\omega _k}\left( {{{\overline X }_k} - {a_k}{\mu _k}} \right)} . $

当引导图像和输入图像相同时, 模型系数表示为

(17)$ {a_k} = \frac{{\sigma _k^2{\text+}\lambda {w_1}\gamma _k^2}}{{\sigma _k^2+\lambda {w_1}}}. $

若像素点位于平坦区域, 则$\gamma _k^2$接近0, 此时${a_k}$通常小于1. 若像素点位于结构区域, $\gamma _k^2$接近1, 此时${a_k}$接近1, 且此时的${a_k}$比GIF和WGIF中的${a_k}$更加接近1, 这也对应了对结构区域更小的平滑处理, 提升了保边能力. 如图1所示, 在窗口半径均为3的情况下对比不同${a_k}$包含的边缘信息. 由图可知, 所提模型系数比对比模型系数包含的结构信息更多, 因此在图像平滑中的边缘保持能力更好.

为了说明峰值感知加权和多尺度约束在模型中作用，通过图像结构相似度SSIM (structural similarity)来评估多组参数设置下WGIF(模型1)、使用峰值感知加权(模型2)以及使用峰值感知加权和多尺度约束(模型3)的图像平滑处理结果, 如表1所示. 可以看出,在9种参数设置下模型1和模型2的SSIM平均值相差0.02, 即同等平滑强度下2种加权方式的结构保持能力近似. 模型3的SSIM最大, 比模型1平均高0.1989，比模型2平均高0.2206，有较大幅度的提升.

对比正则化项系数自适应前后的模型性能, 其中未自适应的工况对应式 (12). 自适应工况$\lambda $对应式 (14) . 在不同的参数设置下对图2（a）进行滤波处理, 滤波结果的峰值信噪比PSNR (peak signal to noise ratio) 和SSIM如表2所示. 可以看出, $\lambda $自适应后PSNR平均提高0.98 dB, SSIM平均提高0.005, 自适应后的正则化项系数提高了模型的边缘保持能力.

在边缘感知平滑、图像细节增强、图像纹理去除平滑、图像去噪等领域进行图像滤波应用实验. 实验硬件为NVIDIA GeForce RTX 2060显卡, AMD Ryzen7-4800H CPU, 16G显存. 软件环境为Windows 10操作系统，python 环境为 python3.6.15.

设计2个边缘感知平滑实验，对比不同模型的保边性能. 选用PSNR, SSIM作为评价指标. 模型的引导图像均为输入图像本身, 分别取$r$=2、4、8, $\lambda $= ${0.1^2}$、${0.2^2}$、${0.4^2}$, 6个模型在不同参数设置下的平滑输出图像如图3所示, 对应的PSNR和SSIM如表3所示. 可以看出, 滤波输出结果模糊越少, 对应的PSNR和SSIM越大. 当$r$固定时, 随着$\lambda $从${0.1^2}$增加到${0.4^2}$, 滤波器的输出结果越来越模糊, PSNR和SSIM都逐渐减小, 其中GIF、WGIF和SKWGIF更为明显. 当$\lambda $固定时, 随着$r$逐渐增大, GIF、WGIF、SWGIF和SKWGIF的滤波输出结果越来越模糊, 结构保留效果越来越差，同时PSNR和SSIM随着$r$增大逐渐减小. 随着$r$和$\lambda $逐渐增大, 所提滤波器模型和GGIF的滤波输出结果没有出现明显的结构模糊, 所提滤波器模型在所有的参数组合下的PSNR均最大, 且比GGIF平均高2.62 dB. 当$r$=4、8时, 所提滤波器的SSIM均最高, 且所有参数组合下所提滤波器的SSIM平均比GGIF高0.0286. 实验结果表明所提滤波器的边缘保持性能良好.

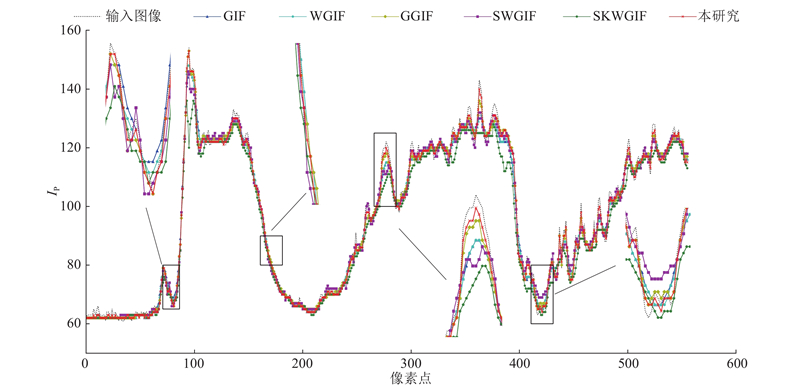
将图2(b)的灰度图作为6个滤波器的引导图像和输入图像, 共有参数设置为$r = 8$和$\lambda = 0.01$, 得到6个滤波模型的输出结果. 输入图像和6个滤波模型输出的第180个水平剖面的像素强度I_P如图4所示, 对比原始图像和滤波输出图像不同区域像素的大小，评估各个滤波器的边缘保持性能. 可以看出, GIF与原始图像相差最多, 其他滤波器的输出结果与原始图像相似的程度由远到近依次是WGIF、SWGIF、SKWGIF. GGIF和所提滤波器模型的输出结果在结构和边缘区域与原始图像接近. 由局部放大图可以看出, 所提滤波器在像素变化较大的区域比GGIF更接近原始图像, 表明所提滤波器对结构破坏最少.

图像细节增强是图像处理的任务之一, 图像增强的目标是通过处理图像, 提高图像重要细节信息或者目标的辨识度, 使增强后的图像比原始图像更适应于特定应用. 图像细节增强的基本思路是由滤波器得到输入图像$I$的平滑结果${I^{'}}$, 再得到图像的细节层$d = I - {I^{'}}$, 将$d$的整数倍加到${I^{'}}$，得到细节增强图像：

(18)$ \begin{split} \\[-10pt]E = {I^{'}}+{M^{'}}\left( {I - {I^{'}}} \right).\end{split} $

式中：${M^{'}}$为正整数, 控制图像细节增强的程度, 通常较大的${M^{'}}$会产生较多的光晕和伪影. 如图5所示, 引导图像为输入图像本身, 当$r = 4$、$\lambda = {0.05^2}$、${M^{'}} = 5$ 的情况下, 对比不同滤波器的增强效果. 可以看出, GIF、WGIF、SKWGIF都有明显结构模糊和图像变化的区域, 原因是这3种滤波器在进行图像平滑时对图像的结构信息破坏较多. SWGIF虽然没有明显的图像变化，但是在部分结构区域的增强效果不理想. GGIF和所提滤波器在视觉效果上最接近, 所提滤波器在2张图片上都得到最好的细节增强效果.

图像纹理去除通过抑制输入图像中的纹理细节得到图像的结构, 是计算机视觉中具有挑战性的任务之一. 常见的纹理去除平滑通常包含基于滤波的方法^[29]和基于优化的方法^[1]. Zhang等^[30]提出滚动引导滤波器, 在纹理去除领域有成功的应用. 参考滚动引导滤波器的思想, 在图像纹理去除时，首次平滑以输入图像本身为引导图像, 之后的每次平滑都以上次的平滑结果作为引导图像, 而输入图像保持不变. 设置6个滤波器模型的共有参数$r = 9$, $\lambda = 4$,2张纹理图片分别经过4次迭代得到滤波输出, 结果如图6所示. 可以看出，GIF、WGIF和SKWGIF过度模糊了输入图像的结构和边缘, 造成光晕和伪影; GGIF有轻微的边缘模糊但保留了一些纹理； SWGIF边缘模糊较少，但是去除离结构区域较近纹理的效果欠佳；所提滤波器可以很好地去除纹理且不会使得边缘模糊.

自然图像通常含有噪声, 噪声会影响对图像的分析和理解. 选择如图7所示的12张彩色图像作为无噪声的测试图像, 在每张图像上添加均值为0, 方差是0.1的高斯噪声, 得到12张待处理的噪声图像. 输入图像是噪声图像, 引导图像是无噪声图像, 设置$r = 4$、$\lambda = 0.04$, 迭代1次得到去噪结果. 12张带噪声图像经过6种滤波器模型的图像去噪效果对比如表4所示. 图中，T_S为去噪处理所用时间的平均值. 可以看出, SKWGIF耗时最多; GGIF和所提滤波器耗时和相关指标最接近, 所提滤波器的PSNR和SSIM均最大, 耗时仅比GIF和WGIF多0.004 s.

直观对比6种滤波器的去噪性能, 设置相同的参数, 可视化不同滤波器模型迭代不同次数的去噪结果. 如图8 (b) 所示为添加均值为0, 方差为0.1的高斯噪声得到的噪声图像. 迭代去噪每次迭代的引导图像均为无噪声图像, 第一次迭代的输入图像为待处理的噪声图像，之后每一次迭代的输入图像均为上次迭代的输出图像. 设置6个滤波器模型的共有参数$r = 4$、$\lambda = 0.04$, 分别迭代1、5、10次得到去噪的结果, 如图9所示. 可以看出, 经过1次迭代, GGIF、SWGIF和所提滤波器都有不错的去噪结果, GIF、WGIF和SKWGIF保留模糊和噪声的程度较严重. 经过5次迭代, GIF、WGIF和SKWGIF的图片更加模糊; 所提滤波器在这些情况下都很好地去除了噪声, 结构信息保留在参与对比的滤波器模型中最好.

本研究提出基于峰值感知和多尺度约束的加权引导图像滤波器, 同时将滤波模型损失函数的正则化项系数改进为基于方差的自适应参数, 提高了引导滤波模型的边缘保持能力, 解决了经典的引导滤波算法无法提取锐利的图像结构信息的问题. 实验分析显示，所提滤波器的局部线性模型的系数比GIF、GGIF、WGIF等包含的图像的边缘和结构信息更多, 表明所提滤波器保边性能更好. 将所提滤波器应用到边缘感知平滑、图像去噪、图像细节增强以及纹理去除平滑领域, 证明了所提滤波器优越性. 对比视觉效果发现, 在相同参数设置下, 所提滤波器优于对比的5种滤波器模型; 在边缘感知平滑实验中, 在相同参数设置下，所提滤波器的PSNR比GGIF的PSNR平均高2.62 dB, SSIM平均高0.0286. 在图像去噪实验中, 在相同参数设置下, 所提滤波器不增加时间复杂度且获得最大的PSNR和最高的SSIM. 提出滤波器中的权重均相等, 如何基于输入图像实现权重的自适应, 以进一步增强引导滤波器模型的边缘保持性能是未来的研究方向.