级联失效是复杂网络中节点失效导致负载平衡被打破,进而引起其他节点过载失效的现象[3]. 为了解析城市轨道交通网络级联失效,大多数研究基于复杂网络理论,利用Space-L或Space-P方法建模,并结合轨道网络站点换乘特性[4]、线路结构特性[5-6]以及网络拓扑特性[7]研究轨道交通网络级联失效[6, 8-9]. 然而,轨道交通网络承载大量乘客,客流的演化对级联失效的传播有着显著的影响. 因此,学者们通过建立静态客流加权网络[10]、双向客流加权网络[11]、时变客流加权网络[12]等方法探究地铁网络级联失效的传播机理. 为了研究失效下客流的动态演化行为对级联失效的影响,学者们通过度[13]、介数中心性[14]、网络连接性[15]、费用最少[16]、时间最短[17]、邻接站点剩余容量[18] 等指标将客流分配到邻接站点,探究级联失效动态传播机理.
综上,现有研究剖析了城市轨道交通网络级联失效在邻接站点及次相邻站点间的传播特征. 然而,大型城市轨道交通网络的线路密集,站点分布集中. 一个站点失效后,乘客仍可通过周围其他站点完成出行,导致非拓扑连接的站点间产生功能耦合,进而传播级联失效. 此外,忽视邻接站点与耦合站点间级联失效的交互作用,也会低估失效传播规模.本研究综合考虑邻接站点及耦合站点在拓扑及客流上对级联失效的影响,提出改进的耦合映射格子模型,量化分析站点耦合关系对级联失效传播的影响机理,以为保障大型城市轨道交通网络高效运营提供理论支撑.
1. 解耦大型城市轨道交通网络级联失效
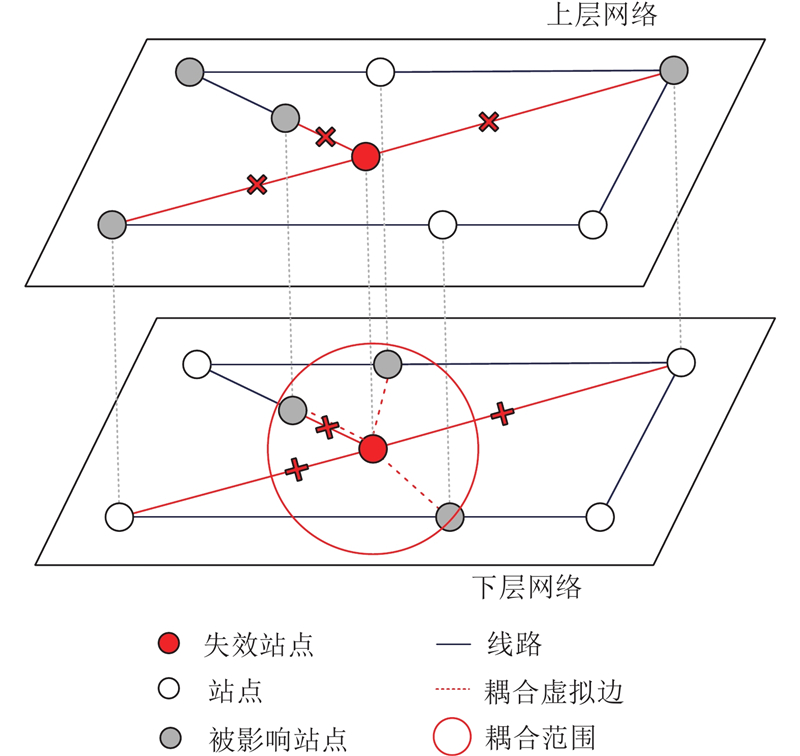
为了剖析大型城市轨道交通网络级联失效传播机理,将其传播过程解耦为邻接站点间与耦合站点间的失效传播2个过程. 通过客流加权的双层耦合网络表征级联失效传播过程. 如图1所示,上层网络为邻接站点间的级联失效过程,下层网络表征耦合站点间的级联失效.
图 1
图 1 大型城市轨道交通网络级联失效
Fig.1 Cascading failures on large-scale urban rail transit network
具体来说,定义城市轨道交通网络为
1.1. 邻接站点间的客流演化
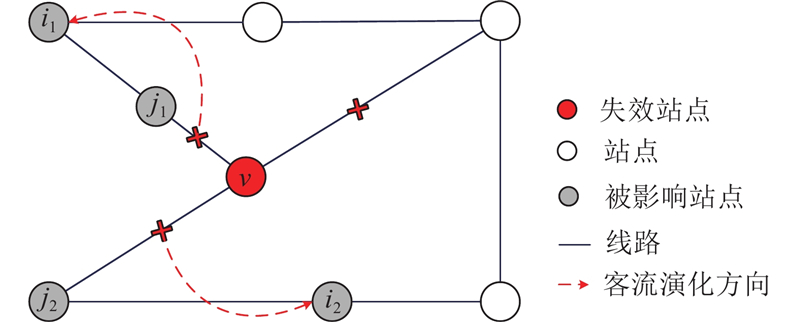
如图2所示,当站点
图 2
图 2 级联失效下邻接站点间客流演化示意图
Fig.2 Graphical representation of evolution of passenger flow between adjacent stations under cascading failures
式中:
1.2. 耦合站点间的客流演化
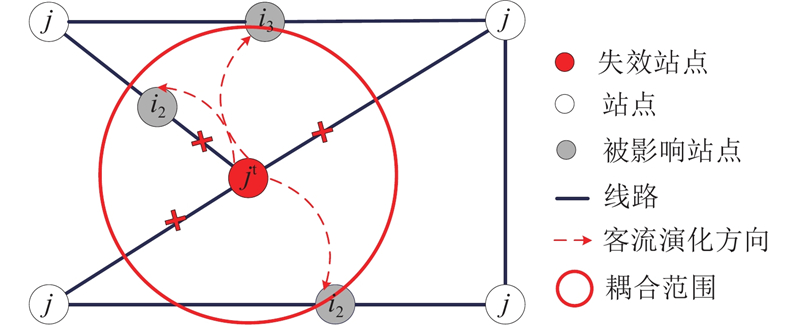
如图3所示,当站点
图 3
图 3 级联失效下耦合站点间客流演化示意图
Fig.3 Graphical representation of evolution of passenger flow between coupled stations under cascading failures
式中:
2. 考虑耦合站点失效传播的大型城市轨道交通网络级联失效建模
2.1. 耦合映射格子模型
式中:
传统的CML模型可以将城市轨道交通网络中影响级联失效传播的拓扑因素和客流因素进行解耦分析. 然而,大型城市轨道交通网络的级联失效传播过程更为复杂,失效不仅在邻接站点之间传播还会在耦合站点间传播,且这2种过程的交互作用也会进一步影响级联失效的传播. 因此,本研究结合大型城市轨道交通网络特征,对CML模型进行改进.
2.2. 大型城市轨道交通网络级联失效模型
为了表征级联失效在邻接站点间及耦合站点间的传播以及其相互作用,从耦合站点的拓扑影响以及客流影响2方面改进CML模型,提出的C-CML模型表达式如下:
式中:
式中:o、d分别为网络OD(origin-destination)对的起点和终点;
式中:
所提出的C-CML模型从拓扑结构和客流2方面,解析大型城市轨道交通网络级联失效在邻接站点和耦合站点间的传播. 在拓扑上,
2.3. 大型城市轨道交通网络级联失效评价
为了验证提出的C-CML模型,衡量大型城市轨道交通网络级联失效传播过程与结果,从级联失效对网络拓扑结构和功能的影响方面分别提出失效站点数量比和网络效率比指标.
2.3.1. 失效站点数量比
在网络拓扑结构方面,将失效站点比作为级联失效评价指标.
式中:
2.3.2. 网络效率比
结合客流加权网络的出行时间,计算OD间的时间阻抗. 对于整个城市轨道交通网络而言,所有OD对之间的效率平均值为网络效率,表达式如下:
式中:
网络效率比为级联失效过程中网络效率与初始网络效率的比值,表达式如下:
式中:
3. 案例分析
3.1. 数据获取与仿真实验
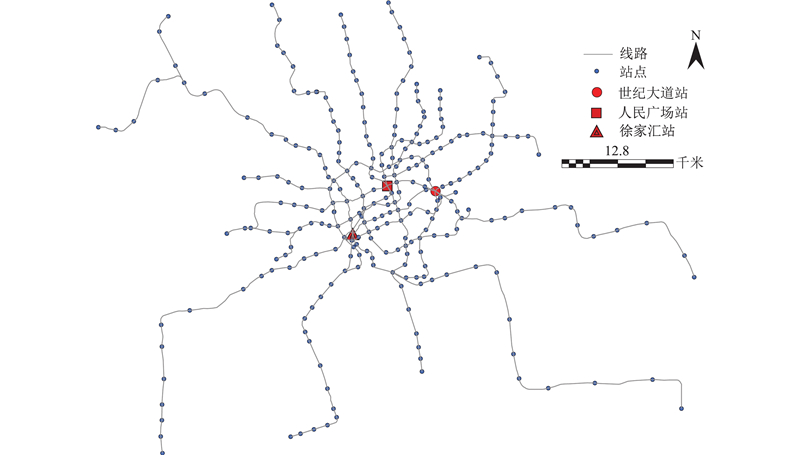
选取上海城市轨道交通网络的281座车站和14条线路进行级联失效分析. 采用Space-L法构建研究区域的网络结构,如图4所示. 从上海市公共交通卡中提取工作日早高峰时段7:00—9:30的OD数据,用于分析交通压力最大情况下的网络级联失效.
图 4
表 1 蓄意攻击场景下的站点属性
Tab.1
| 场景 | 场景名称 | 失效站点 | 站点属性 (Ki) | 早高峰期间) | |
| 场景1 | 度最大站失效 | 世纪大道站 | 换乘站(8) | 0.14 | 5 460 |
| 场景2 | 介数中心性 最大站失效 | 人民广场站 | 换乘站(6) | 0.25 | 5 433 |
| 场景3 | 进站客流量 最大站失效 | 徐家汇站 | 换乘站(6) | 0.24 | 9 320 |
3.2. 结果分析
3.2.1. 模型有效性验证分析
为了解析大型轨道交通网络级联失效传播特征,验证C-CML模型的有效性,对比考虑CML模型[10]与C-CML模型在不同场景下的仿真结果,如图5所示. 可以看出,在场景1~3中,C-CML模型仿真的失效站点明显多于CML模型的. 这主要是因为C-CML模型考虑了耦合站点间的级联失效及其与邻接站点间失效的交互作用. 上海城市轨道交通网络规模大、站点和线路密集、乘客步行范围内的可换乘站点多,导致可在耦合站点间换乘的客流量大,会产生严重的级联失效. 因此,在大型城市轨道交通网络中考虑耦合站点间的级联失效很有必要. 此外,在突发事故下,为因站点关闭而无法上车的乘客提供便捷的替代交通模式,也是缓解大型城市轨道交通网络级联失效的关键.
图 5
图 5 CML与C-CML模型在不同场景下的级联失效仿真结果对比
Fig.5 Comparison of cascading failure simulation results of CML and C-CML model under different scenarios
在3种场景下,C-CML的曲线增长趋势较为均匀;CML的曲线在3种场景下有较大的不同. 在场景1下,相比于C-CML,CML的曲线在级联失效初期增长较快,而在t>25后,曲线增长速度变慢. 这是因为场景1模拟的是度最大的站点失效,此站点周围的站点多数与失效站点相连接,均可能受到失效站关闭的影响. 然而,失效站点周围的多个站点与多条线路会缓解失效影响,使得失效在邻接站点之间的传播速度变慢. 与CML不同,C-CML模型考虑了失效在耦合站间的传播. 随着失效的不断扩散,耦合站点间的失效与邻接站间的失效相互作用,加快了失效的传播速度. 在场景2下,CML模型模拟的级联失效一开始超过了C-CML模型,然而在t>20后,C-CML模型的失效站点数量却反超了CML模型. 场景2模拟了介数中心性最大的站点失效下的级联失效. 这意味着场景2下通过失效站点的客流最多. 在级联失效初期,此站点的失效使得大量乘客不得不在地铁内部换乘,导致地铁沿线站点客流量突增,引起邻接站点间级联失效的快速传播. 因此,只考虑邻接站点间级联失效的CML模型的失效传播速度较大. 然而,C-CML模型中考虑的耦合站间的级联失效最终加剧了失效的传播,使得C-CML模型的失效站点数量最终大于CML模型的. 与前2种场景不同,场景3下2个模型的仿真结果在一开始就表现出显著差异. 可以看到,在级联失效初期,相较于C-CML模型,CML模型模拟的失效传播速度明显较慢. 直至t>35,CML模型模拟的级联失效传播速度才骤然加快. 场景3的失效站点是进站客流量最大站,此站点失效后,耦合站点间的级联失效更为严重. 由图4可知,场景3下失效站点徐家汇站周围线路密集. 因此,因徐家汇站失效而行程受到影响的乘客可以换乘到其多个邻接站点,徐家汇站的失效被分散到多个邻接站点,邻接站点间的失效强度减小,导致级联失效得到缓解. 在后期,随着失效站点的增加,失效线路逐渐增加,失效难以被分散和缓解,进而使得级联失效快速传播开来.
对比C-CML模型和CML模型模拟的级联失效,在场景1、3下,C-CML模型模拟得到的级联失效站点数量是CML模型的约2倍,传播速度比CML模型快约50%. 这说明场景1、3下耦合站点间的失效强度明显大于邻接站点间的. 场景2下的C-CML模型模拟的失效站点数量与CML模型的并无显著差异. 这主要源于场景1、3下的失效站点是度最大站点和进站客流量最多站点,失效站点的邻接站点之间的失效以及大量不能通过失效站点进入地铁的客流在耦合站间的转移所产生的级联失效没有被考虑在CML模型内. 然而,场景2的失效站点是介数中心性最大的站点,说明其周围站点之间也存在良好的连通性,可以缓解级联失效. 另外,通过此站点的客流量大,导致邻接站点间的失效更为严重. 因此,CML和C-CML模型的失效传播结果差异不明显.
综上所述,本研究所提出的C-CML模型能识别级联失效在大型城市轨道交通网络的耦合站点间以及邻接站点间的传播特征以及两者的交互影响. 在大型城市轨道交通网络中,耦合站间的级联失效传播强度在一些场景下甚至大于邻接站点间的. 因此,在研究大型城市轨道交通网络级联失效时,考虑耦合站间的级联失效非常必要.
3.2.2. 大型城市轨道交通网络级联失效分析
为了进一步解析大型城市轨道交通网络级联失效的传播特征,通过调整拓扑耦合系数
图 6
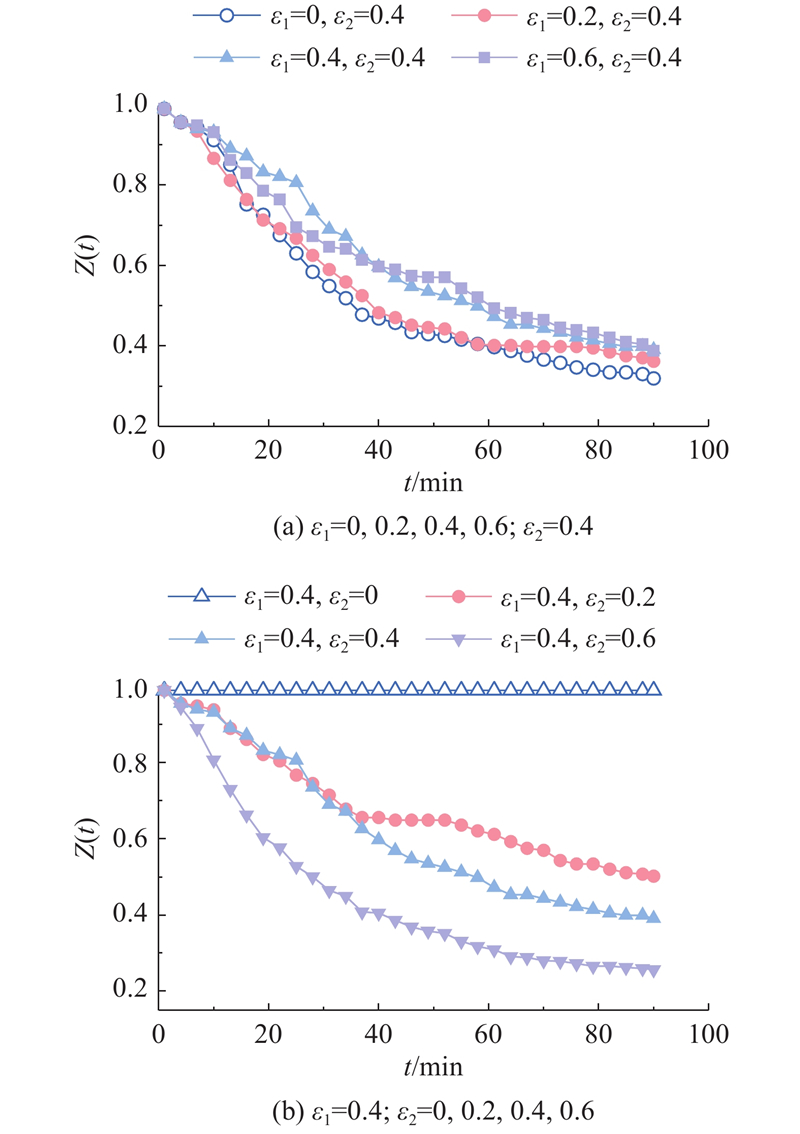
图 6 不同耦合系数下的网络效率比
Fig.6 Network efficiency ratio under different coupling coefficients
在图6(a)中,随着拓扑耦合系数ε1的增加,级联失效造成的网络效率比的下降得以缓解. 这是因为拓扑耦合系数的增加意味着相邻站点间及耦合站点间在拓扑上的交互关系变强. 拓扑耦合系数越高,失效更容易受到拓扑结构变化的影响. 对拓扑结构有影响的往往是有着多个邻接结点和耦合节点的站点,因此,失效偏向于向这些站点传播. 然而,这些站点却拥有强的分散失效的能力,进而使得失效得以缓解. 另外,C-CML模型识别了失效站点的耦合站点,耦合站点间的传播分担了邻接站点间的失效传播压力. 因此,随着站点间拓扑耦合系数的增大,网络中的站点在拓扑上的交互关系变强,导致站点的失效能够由相近的耦合站点以及邻接站点共同分担,从而抑制了级联失效,延缓了网络效率比的下降. 同时,可以看出,当ε1≥ε2时,拓扑耦合作用对级联失效的缓解作用更加明显. 这是因为密集的网络拓扑结构与站点分布能够有效疏散被延误的乘客,从而缓解级联失效.
在图6(b)中,随着ε2的增加,级联失效造成的网络效率比下降加剧. 这是因为随着ε2的增加,失效站点的客流转移趋势得以甄别. 在失效下,客流并不会均匀地换乘到失效站点周围的耦合站点和邻接站点,而是更倾向于换乘到性能更强的站点. 大量的换乘需求加大了站点运输压力,加速了站点的失效,进而产生大规模的级联失效,使得网络效率比急剧下降. 另外,当ε2=0时,网络效率比变化不大. 这是因为当客流耦合系数为0时,网络状态变化不受客流因素的影响. 因此,初始失效站点的状态不会影响到其他站点,不能引发级联失效,网络效率比也不会随着时间变化.
当客流耦合系数ε2大于拓扑耦合系数ε1时,网络的级联失效被加剧,促使网络效率加速下降. 因此,大型城市轨道交通网络的设计应该将级联失效考虑在内,保证重要站点周围站点性能均匀,以缓解级联失效的传播.
3.2.3. 大型城市轨道交通网络级联失效评价
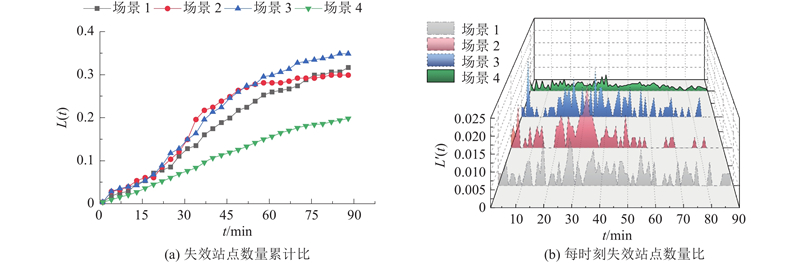
图 7
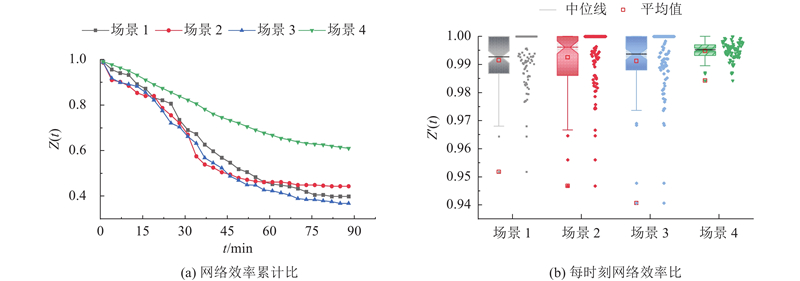
图 8
由图7(a)可以看出,城市轨道交通网络抵抗场景3下的级联失效能力最差. 这是因为场景3失效的是进站客流量最大的站点. 当该站点失效后,大量乘客须在耦合站点间换乘,加强了耦合站点间的连接强度,而具有偏好性的乘客选择与失效站点周围站点参差不齐的抵抗能力加速了失效的传播,使得网络难以抵抗客流量大的站点关闭导致的级联失效. 场景1与场景3下曲线的形状相似. 场景1失效的是度最大的站点,与场景3相似的是,其失效站点世纪大道站的周围站点之间相互并无连接,导致局部网络换乘路径少,乘客不得不通过耦合站点进行换乘,从而加强了耦合站点之间失效传播的强度. 失效同时在邻接站点与耦合站点之间传播,其交互作用增强了失效的传播,使得网络难以抵抗级联失效. 场景2下网络抵抗失效的能力在一开始较强. 然而,在级联失效中期,网络抵抗失效的能力明显降低,导致网络失效站点数量比大于场景1和场景3的. 这是因为场景2的失效站点人民广场站有着最大的介数中心性,且相邻近站点之间的连接紧密,网络可以抵抗初期的级联失效. 然而随着失效的进一步传播,此失效站点周围的站点大量失效,导致失效在多条路径传播,叠加耦合站点间的失效传播,网络失效传播被强化. 同时,随着失效逐渐分散到多条线路,该场景下的网络的失效传播最早开始消散. 可以看到,场景1、3的失效站点数量比均大于场景2的,说明网络中耦合站点之间的级联失效传播越严重,网络的失效越难以抵抗.
由图7(b)可见,3个蓄意攻击场景下的失效站点数量比的第1个高峰出现的时间与高峰出现前后失效站点数量比的变化趋势均不同. 场景1的高峰出现时间最迟,且高峰前的失效站点数量比值均较大. 这说明网络对场景1下的初期级联失效具有良好的抵抗性. 场景2、3的失效站点数量比的第1次高峰出现时间相近,但场景3的第1次高峰明显高于场景2的. 这说明在级联失效初期,场景3下的级联失效更难抵抗. 同时可以观察到,3种场景下的失效站点数量比在第1次高峰出现后均有明显下降,说明大型城市轨道交通网络失效站点周围的拓扑结构能够有效抵抗级联失效. 由图7(b)可见,场景1、2的低峰持续时间约为5个时间歩,而场景3下的低峰持续时间为20个时间歩,说明在级联失效初期,有足够的时间缓解失效的进一步传播.
与级联失效的初期不同,在失效的高峰期,3种蓄意攻击在失效站点数量比上均呈现出明显的增加,再次证明,在级联失效的初期控制失效的传播尤为重要. 同时,可以看到,在3种蓄意攻击下,网络的失效站点数量比呈现出不同的特点. 场景1的每时刻失效站点数量比分布较均匀,说明在度大的站点失效的中期,多条线路的正常运营受到影响,再叠加耦合站点间的失效传播,使得多数站点的状态值均增大,失效概率也增大. 但同时耦合站点之间的换乘与紧密的拓扑结构,增加了网络的抵抗能力. 此现象在场景3下更为明显,虽然场景3是进站客流量最大的站点失效,但是耦合站点间的换乘同样使得失效沿着多条线路快速传播,最终其高峰期的失效与度最大的站点呈现出相似的特点. 然而,与场景1、3不同,场景2的每时刻失效站点数量比最为集中,且高峰值更高. 这是因为场景2的初始失效站点的介数中心性最大,失效后对于线路的扰动最大,叠加耦合站点的影响,导致失效更为快速.
在3种蓄意攻击下,网络效率比的降低有显著不同. 由图8(a)可见,场景1、3的网络效率比都下降至原本的60%和66%,场景2的网络效率比下降至原来的55%. 这表明度和进站客流量大的站点失效引起的级联失效在最终的网络功能降级上比介数中心性的分别低5%和10%. 然而,场景2的网络效率比下降速度最快,说明虽然度与进站客流量大的站点失效引发的级联失效的最终影响规模大,但是介数中心性大的站点失效传播速度快,更难以阻断.
如图8(b)所示,场景1的每时刻网络效率比中值和平均值均较其他场景的低. 结合图7(b)可知,相较于其他蓄意攻击场景,场景1下每时刻失效站点数量比较为均匀. 可以看出,场景1失效下引发的级联失效破坏了多个关键站点,导致每时刻的网络效率比平均值和中值较其他场景的低. 在场景2下,每时刻网络效率比值较分散,说明场景2下的级联失效破坏了一些抵抗特性和传播特性较强的站点,这些站点的失效会引发大量的站点失效,进而快速降低网络效率. 然而,场景2下的网络效率比的中值和平均值相较其他场景下的更高. 结合图7(b)可知,场景2下失效站点数量较多,说明场景2下的级联失效只是破坏了少数关键站点,使得网络效率得到了大幅度降低. 这也说明,网络中存在一些对级联失效过程具有促进的关键传播站点. 相比于场景1、2,场景3的网络效率比最低值最低,且每时刻网络效率比值分布较为集中. 这说明场景3下的级联失效不仅传播速度快,失效传播对网络效率比的影响更显著. 因此,场景3下的级联失效对网络效率的影响最严重,不仅在最终结果上最大程度地降低了网络效率,每时刻的网络效率比都有大幅度的降低.
4. 结 论
(1)在剖析大型城市轨道交通网络级联失效传播机理时,耦合站点间的级联失效效应当被考虑在内. 考虑耦合站点间的失效传播后,级联失效的整体规模明显增大且传播速度明显加快. 尤其在度和进站客流量大的站点失效时,耦合站点间的级联失效规模是邻接站点间的约2倍,传播速度快约50%.
(2)在大型城市轨道交通网络中,客流对级联失效的影响要明显大于拓扑的. 客流对大型城市轨道交通网络级联失效的作用力是拓扑结构的约9倍. 另外,连通性好的拓扑结构能够缓解级联失效的传播,而站间大量的换乘客流会严重加剧级联失效的传播.
(3)大型城市轨道交通网络对不同特征站点失效下的级联失效抵抗能力不同. 随机攻击下的失效传播速度约为蓄意攻击下的75%. 度和进站客流量大的站点失效引起的级联失效在最终的网络功能降级上比介数中心性的分别低5%和10%. 但是,介数中心性大的站点引发的级联失效传播最快.
本研究提出的C-CML模型能识别耦合站点间和邻接站点间的级联失效传播模式,捕捉不同失效场景下的级联失效特征. 本研究能为大型城市轨道交通网络的规划设计与事故管控提供科学合理的建议. 在规划设计大型城市轨道交通网络时,站点分布密集的区域应保障站点运输性能均衡,以降低乘客选择偏好差异性,使得周围的站点能够较为均衡地疏散换乘客流,提高局部网络抵抗级联失效的能力,阻碍级联失效进一步传播. 另外,进站客流量大或邻接站点连接程度低的站点周围应设计充足的运输能力,以便在站点发生事故时,将客流疏散到其他交通模式,进而降低地铁负荷. 在事故影响范围控制方面,对介数中心性大的站点应尽早采取客流控制,以避免快速传播的大范围失效发生.
本研究假设地铁站失效后乘客依然选择地铁出行,然而乘客可能利用其他交通模式如公交、网约车、共享单车等完成出行. 因此,进一步的研究应该考虑多模式交通网络中级联失效传播机理. 另外,也应将交通事故下乘客选择行为纳入考虑.
参考文献
2022年世界城市轨道交通运营统计与分析综述
[J].
Statistical analysis of urban rail transit operation in the world in 2022: a review
[J].
Scenario inference model of urban metro system cascading failure under extreme rainfall conditions
[J].DOI:10.1016/j.ress.2022.108888 [本文引用: 1]
Error and attack tolerance of complex networks
[J].DOI:10.1038/35019019 [本文引用: 1]
城市轨道交通网络鲁棒性分析
[J].DOI:10.3969/j.issn.1671-1815.2020.28.043 [本文引用: 1]
Robustness analysis of urban rail transit network
[J].DOI:10.3969/j.issn.1671-1815.2020.28.043 [本文引用: 1]
Structural characteristics analysis and cascading failure impact analysis of urban rail transit network: from the perspective of multi-layer network
[J].DOI:10.1016/j.ress.2021.108161 [本文引用: 1]
环线对地铁网络弹性的影响研究
[J].
Influence of circle lines on the resilience of subway networks
[J].
城轨网络站点重要度评估与级联失效抗毁性分析
[J].
Evaluation of station importance and cascading failure resistance analysis of urban rail transit network
[J].
基于加权网络的城市轨道交通网络特性与级联失效分析
[J].
Analysis of the structural characteristics and cascading failure of urban rail transit network based on weighted network model
[J].
Vulnerability assessment of urban rail transit based on multi-static weighted method in Beijing, China
[J].DOI:10.1016/j.tra.2017.12.008 [本文引用: 3]
Cascading failure analysis and robustness optimization of metro networks based on coupled map lattices: a case study of Nanjing, China
[J].DOI:10.1007/s11116-019-10066-y [本文引用: 1]
Modeling cascading failures of urban rail transit network based on passenger spatiotemporal heterogeneity
[J].DOI:10.1016/j.ress.2023.109726 [本文引用: 1]
A method of examining the structure and topological properties of public-transport networks
[J].DOI:10.1016/j.physa.2016.01.060 [本文引用: 1]
Vulnerability of nodes under controlled network topology and flow autocorrelation conditions
[J].DOI:10.1016/j.jtrangeo.2017.02.002 [本文引用: 1]
Performance indicators for public transit connectivity in multi-modal transportation networks
[J].DOI:10.1016/j.tra.2012.04.006 [本文引用: 1]
城市轨道交通网络级联失效机理研究
[J].
Cascading failure mechanism of urban rail transit network
[J].
城市群客运网络动态分配策略应急疏散仿真
[J].
Simulation of emergency evacuation under dynamic distribution strategy of passenger transport network un urban agglomeration
[J].
考虑时间特性的城市群客运网络抗毁性研究
[J].
Study on invulnerability of urban agglomeration passenger traffic network considering time characteristics
[J].
The “weak” interdependence of infrastructure systems produces mixed percolation transitions in multilayer networks
[J].DOI:10.1038/s41598-018-20019-7 [本文引用: 1]
Modeling the resilience of interdependent networks: the role of function dependency in metro and bus systems
[J].DOI:10.1016/j.tra.2023.103907 [本文引用: 1]
具有弱依赖组的复杂网络上的级联失效
[J].DOI:10.7498/aps.70.20210850 [本文引用: 1]
Cascading failures on complex networks with weak interdependency groups
[J].DOI:10.7498/aps.70.20210850 [本文引用: 1]
Dynamic robustness analysis of a two-layer rail transit network model
[J].DOI:10.1109/TITS.2021.3058185 [本文引用: 1]
Cascading failure with preferential redistribution on bus-subway coupled network
[J].DOI:10.1142/S0129183121501035 [本文引用: 1]
Revealing the determinants of the intermodal transfer ratio between metro and bus systems considering spatial variations
[J].DOI:10.1016/j.jtrangeo.2022.103415 [本文引用: 1]
Modeling network vulnerability of urban rail transit under cascading failures: a coupled map lattices approach
[J].DOI:10.1016/j.ress.2022.108320 [本文引用: 2]
Vulnerability assessments of weighted urban rail transit networks with integrated coupled map lattices
[J].DOI:10.1016/j.ress.2021.107707
Urban rail transit system network reliability analysis based on a coupled map lattice model
[J].
A coupled map lattice model for dendritic patterns
[J].DOI:10.1016/S0378-4371(99)00273-3 [本文引用: 1]
Cascading failure in urban rail transit network considering demand variation and time delay
[J].DOI:10.1016/j.physa.2023.129290 [本文引用: 1]