随着城市化进程的加快,地下空间的开发逐渐成为城市规划的重点. 隧道工程是地下工程的一个重要方向,盾构法和顶管法作为2种常用的非开挖隧道施工技术,在城市地铁建设、地下通道、管道铺设中发挥了重要作用.
在顶管、盾构法隧道掘进引起的土体位移研究中,主要有经验公式法、理论解析法、模型试验法、数值模拟法等方法. 在理论方法的研究中,常采用如下方法. 1)Mindlin法,该方法利用弹性力学Mindlin解将隧道施工各个力学效应产生的位移进行叠加得到总的地层位移解. 魏纲等[1]利用该解进行了一系列研究. 2)随机介质理论,该方法将隧道开挖分解为无数个无限小开挖单元,将所有无限小单元对地层的影响叠加后即可得到整个开挖过程对地层的影响. 朱忠隆等[2]将该方法用于预测软土中盾构隧道开挖产生的地表沉降;刘大刚等[3-4]将该方法用于双线隧道地表沉降的预测. 3)影像源法. 该方法最早由Sagaseta[5]提出,其结合流体力学与弹性力学的思想,推导半无限空间内土体损失引起的位移解析解. Verruijt等[6]从隧道椭圆化的角度拓展了影像源法. Loganathan等[7]进一步考虑土体非均匀收敛,修正了Verruijt解,得到了沉降槽更符合实际情况的解. Park等[8-9]考虑不同土体收敛模式下的位移解,丰富了影像源法的理论体系. 影像源法除了广泛地用于计算隧道开挖土体损失引起的变形外,还常用于基坑这类地下工程中[10-11].
此外,曹小林[12]采用复变函数法给出了半无限空间中复杂隧道横断面下的应力和位移理论解答.
随着隧道施工环境日趋复杂,在实际工程中不可避免地会出现隧道开挖邻近边坡、河道驳坎的边界条件较为复杂的情况,然而目前隧道开挖引起的土体位移理论研究,大多是基于平面半无限空间条件或利用对称性构造出的平面半无限空间条件而提出的. 对于半无限空间表面存在“河道”的有“缺口”情况下隧道开挖的理论解析研究则较少,因此研究复杂边界条件下隧道开挖引起的土体位移解具有重要意义. 本研究基于影像源法,提出临近既有河道条件下的隧道施工引起的地表沉降解析解,为复杂边界条件下隧道施工引起的土体位移预测提供了新的途径.
1. 影像源法基本原理
影像源法[5]常用于计算半无限空间中由土体损失引起的位移场,假定土体为各向同性、均质、不可压缩弹性体,圆孔外部土体的收敛模式为均匀径向收敛. 其原理和主要步骤如下:1) 忽略土体表面的影响,将平面半无限空间问题转化为平面无限空间问题. 空间内某一点空隙产生位移U1. 2) 步骤1)在引起位移的同时产生应力,不符合半无限空间自由表面无应力的条件,采用虚拟镜像(正镜像或负镜像)消除部分应力以简化计算,镜像产生的位移为U2. 3) 经前2步叠加,土体表面仅剩剪应力τ或正应力σ,施加与之大小相等方向相反的力使其自由表面应力为零,这部分力产生的位移为U3.
将3个位移叠加后即可得到隧道开挖产生的总位移:
若采用负镜像,则U3中因消除剪应力产生的位移可利用二维Cerruti解答[13]:
式中:uCx、uCz分别为按Cerruti解答得到的计算点P(x, z)的水平和竖直方向位移,r为P点到空隙圆心的距离,G为土体剪切模量,ν为土体泊松比.
若采用正镜像,U3中因消除正应力产生的位移可利用二维Boussinesq解答[13]:
式中:uBx、uBz分别为按Boussinesq解答得到的计算点P(x, z)的水平和竖直方向位移.
2. 分析模型及解析方法
2.1. 计算模型
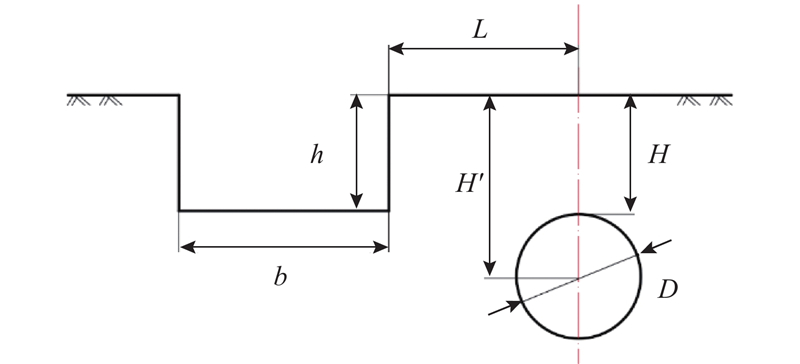
杭州某大直径顶管法隧道工程临近既有河道环境条件施工,基于该实际案例,建立隧道施工环境影响问题的简化分析模型,如图1所示. 图中,H为隧道埋深,H'=H+D/2为顶管隧道轴线埋深,D为顶管机外径(R为半径),h为河道深度,b为河道宽度,L为河道右边界与隧道轴线间的水平距离. 为了简化问题,假定河道侧壁为竖直面,忽略实际工程中可能采用的驳坎或其他护岸结构以及河道内水体的影响,即假定河道处于干涸状态.
图 1
图 1 临近河道掘进的隧道简化分析模型
Fig.1 Simplified analytical model for tunnels excavated near river channels
传统的影像源法是基于半平面空间提出的,在不考虑多层土的情况下,有且仅有土体表面可以作为镜面. 在面对如图1所示隧道附近有河道存在的问题时,可以将镜面的思想进一步延伸,把各边界看作不同的镜面,分别对各镜面应用影像源法,将所有计算结果叠加即可得到当前边界条件下土体位移场.
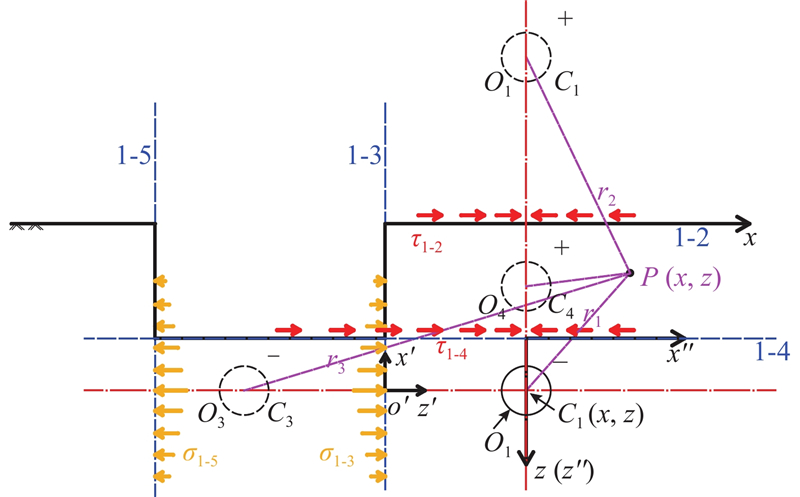
基于影像源法计算的土体位移由2大部分组成,第1部分是以流体力学为基础的实际空隙和镜像产生的位移,第2部分是以弹性力学为基础的分布力产生的位移,因此可将土体位移分为源汇部分和力的部分计算. 临近河道顶管施工的地表沉降解析计算模型如图2所示.
图 2
2.2. 求解过程
具体计算过程如下. 如图2所示,O1表示实际的汇,圆心为C1(x1, z1),空隙面积由隧道施工引起的土体损失率η决定(即顶管掘进引起的空隙面积为ηπR2),O1产生的位移记为UO1,在任意一点
式中:x1=0,z1=H+R;r1为C1到P的距离,r12=(x−x1)2+(z−z1)2.
O2为镜面1-2产生的虚拟负镜像,圆心为C2(x2, z2),其产生的位移记为UO2,任意一点P(x, z)处的位移分量分别如下:
式中:x2=x1,z2=−z1;r2为C2到P的距离,
此处采用负镜像,因此镜面1-2上须施加剪应力,该剪应力记为τ1-2,假定剪应力仅分布于河道边界上,而不延伸至缺口以及土体内部,对于后文中的正应力也采用相同的处理方式. τ1-2产生的位移记为U1-2,位移分量分别如下:
考虑到河道的边界并非无限边界,为了使源汇部分的位移满足河道尺寸变化的要求,在以河道边界为镜像的源汇部分和以河道底部为镜像的源汇部分位移分别添加指数函数,使其满足当h=0或b=0即无河道存在时,问题退化为半无限空间问题;当h或b无限大时,任意河道边界都能够成为半无限空间的界面.
O3为镜面1-3产生的虚拟正镜像,圆心为C3(x3,z3),考虑河道深度的影响,在式(6)、(7)的基础上作适当修正,其产生的位移记为UO3,位移分量分别如下:
式中:x3=−2L,z3=z1;r3为C3到P的距离,r32=(x−x3)2+(z−z3)2.
此处采用正镜像,因此镜面1-3上须施加正应力,该正应力记为σ1-3,其产生的位移记为U1-3,位移分量分别如下:
由于σ1-3是施加在河道侧壁上的,须将全局坐标系xoz中的点P(x,z)转换为局部坐标系x'o'z'中的点P(x', z'),各坐标系位置如图2所示. 由于两坐标系角度相差90°,U1-3水平位移分量对应积分中Boussinesq解的竖直分量,竖直位移分量对应积分中Boussinesq解的水平分量.
O4为镜面1-4(河底所在平面)产生的虚拟负镜像,圆心为C4(x4, z4),同时考虑河道宽度变化的影响,其产生的位移记为UO4,位移分量分别如下:
式中:x4=x1,z3=2h−H+R;r4为C4到P的距离,r42=(x−x4)2+(z−z4)2.
同时镜面1-4上须施加剪应力,该剪应力记为τ1-4,其产生的位移记为U1-4,位移分量形式同U1-2,计算时同样须考虑全局坐标系xoz与局部坐标系x''o''z''之间的坐标转换.
O5为镜面1-5产生的虚拟正镜像(因图2宽度所限,未在图中画出),圆心为C5,其产生的位移记为UO5,形式与计算方法同UO3. 镜面1-5上须施加正应力σ1-5,其产生的位移记为U1-5,形式与计算方法同U1-3.
综上所述,应用叠加原理,得到基于影像源法的临近河道顶管掘进引起的土体位移解:
式中:USS为由源汇引起的位移,UF为由剪应力引起的位移,Ut为影像源法得到的总位移.
2.3. 土体非均匀收敛的修正
3. 工程验证
杭州某电力顶管隧道工程采用泥水平衡式顶管掘进机,场地的第4纪覆盖层厚度约为70 m,其上部为河口相粉砂性土地层,中部为软、硬土层交替沉积地层,下部为洪积沉积的砂砾石层,基岩为砂岩岩组. 该工程采用双线顶管先后施工,其中西线顶管隧道临近且平行于河道先行施工,全长为285 m,在后行顶管施工前,可以作为单线隧道考虑. 根据图1中的简化模型,施工现场参数如下:H=4.1 m,D=2R= 4.18 m,L=9.5 m,h=4.0 m,b=20.0 m. 以地表沉降槽体积作为土体损失率的判断依据,根据实测数据,顶管隧道掘进引起的土体损失率取1.6%[14]. 考虑到顶管隧道施工影响地层均在上部深厚的砂质粉土层中,取G=4.15 MPa,ν=0.3.
图 3
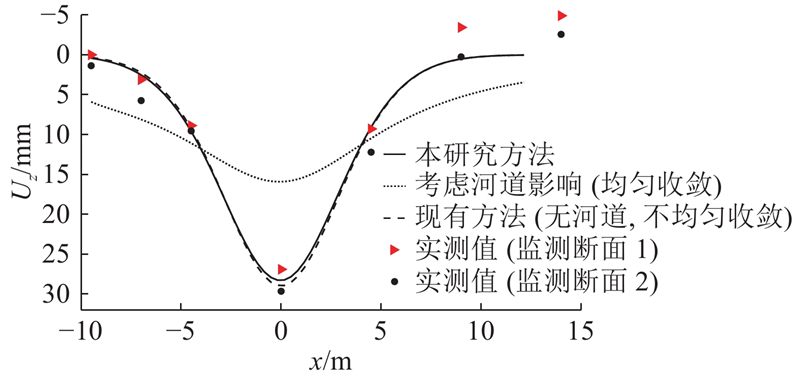
图 3 各方法计算结果与实测地表沉降的比较
Fig.3 Comparison between calculation results of various methods and measured surface settlement
4. 影响因素分析
4.1. 河道与隧道水平距离
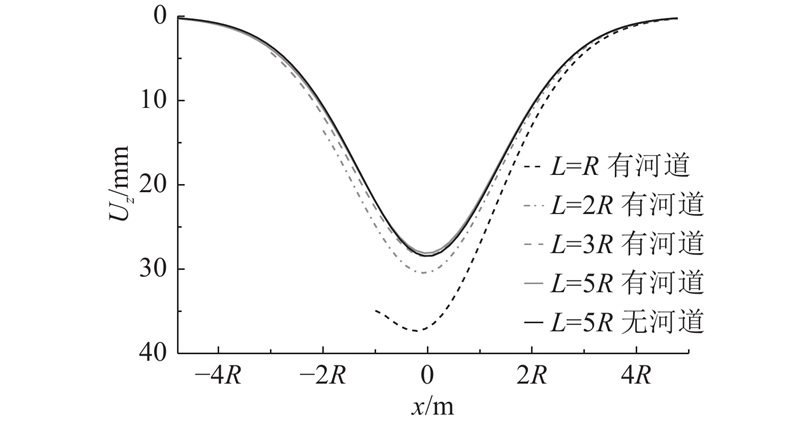
如图4所示为河道与隧道轴线水平距离L变化情况下的地面沉降曲线. 可以看出,隧道距离河道越近,相对于无河道情况,地表沉降槽的不对称性越明显,具体表现为地表沉降槽峰值对应水平位置更偏离隧道轴线,且与峰值距离相同处左侧沉降量大于右侧的. 当土体损失率一定时,隧道距离河道越近,由于隧道掘进引起的地表沉降越大,与无河道情况相比,沉降槽峰值的增幅最大可超过30%. 可见在隧道施工时距离河道不宜过近. 随着距离L逐渐变大,既有河道的存在对隧道开挖的影响逐渐减小,沉降槽趋于对称并逐渐接近无河道情况. 当L>3R时,沉降槽形状变化不再显著. 前文实际案例的L=9.5 m,在3R和5R之间,因此沉降曲线对称性较强,与无河道情况更为接近.
图 4
4.2. 河道深度
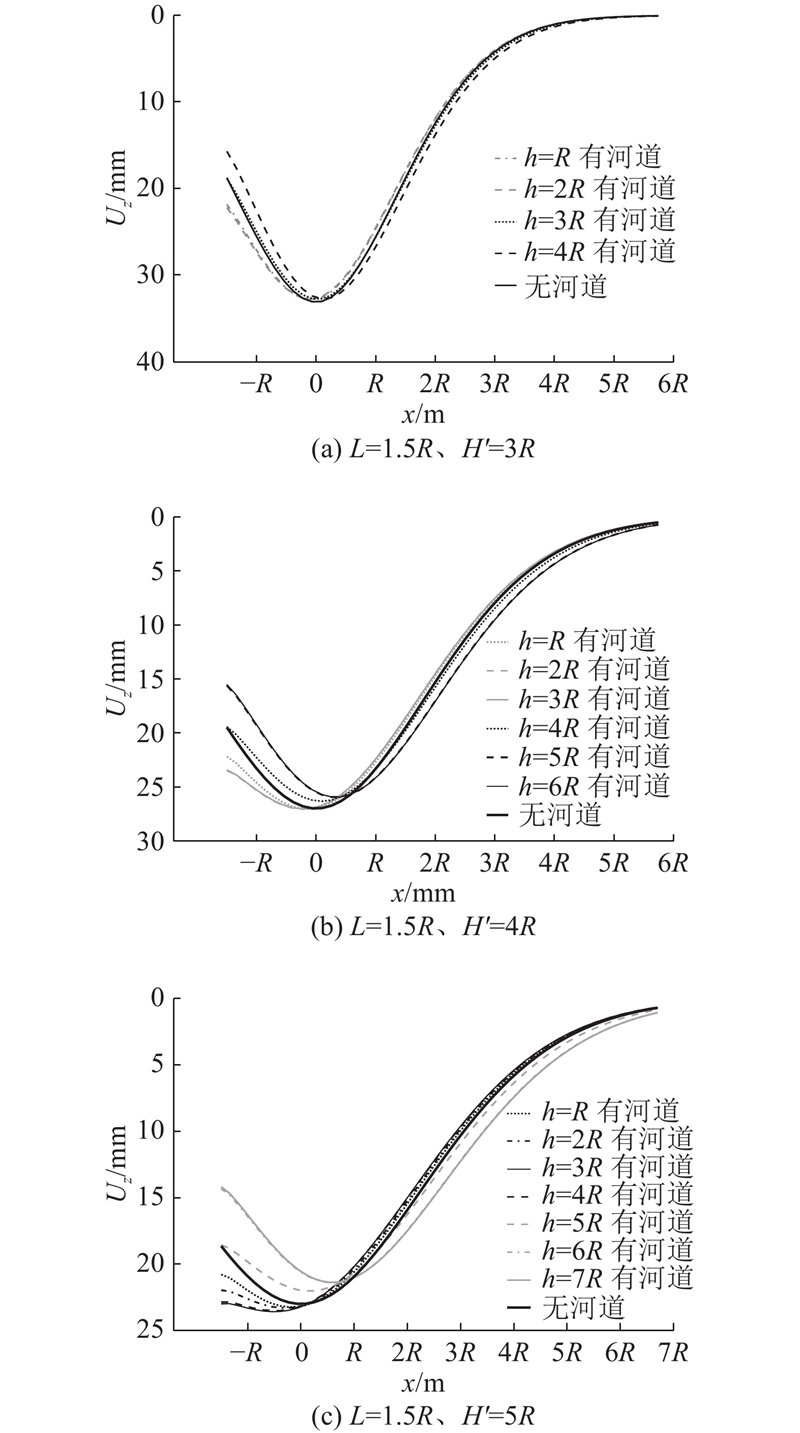
如图5(a)~(c)所示分别为不同隧道埋深下,改变河道深度的地表沉降曲线. 以隧道拱腰深度H'与河道深度h相等时为分界,可以看出,当h ≥ H',即隧道位于河道旁侧时,随着河道深度的增加,地表沉降槽峰值比无河道情况时减小,峰值点对应位置朝远离河道方向移动,继续增大则该趋势变缓;当h<H',即隧道位于河道侧下方时,沉降槽峰值相比于无河道的情况略有增大,峰值点对应横坐标更靠近河道;随着隧道深度的增大,有无河道对隧道掘进引发地表沉降的影响也愈加明显.
图 5
图 5 不同河道深度情况下的地表沉降曲线
Fig.5 Surface settlement curve under different river depths
4.3. 隧道埋深
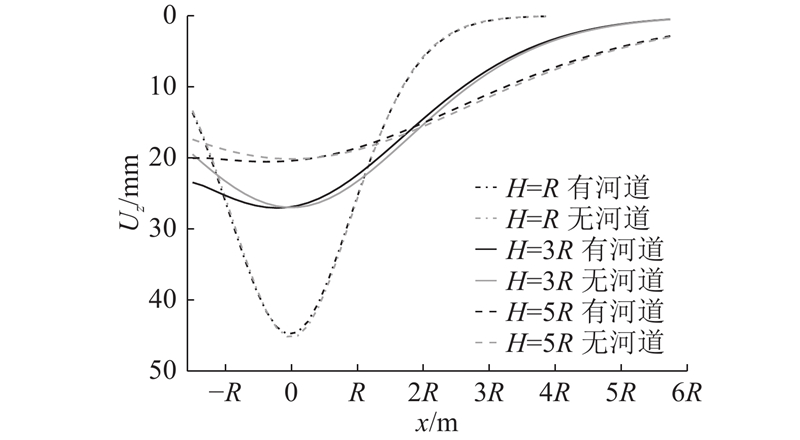
如图6所示为L=1.5R、h=2R时不同隧道拱顶埋深H下的地表沉降曲线. 可以看出,在隧道与河道水平距离较小的情况下,随着隧道埋深的增大,地表沉降槽发生较为明显的变化,沉降峰值逐渐减小. 当H=R时,顶管位于既有隧道旁侧,沉降槽与无河道情况下的沉降槽较为接近;当H=3R、H=5R即顶管位于河道侧下方时,靠近河道附近由隧道掘进引起的地表沉降明显大于无河道情况下的.
图 6
图 6 不同隧道埋深情况下的地表沉降曲线
Fig.6 Surface settlement curve under different tunnel depths
4.4. 土体泊松比
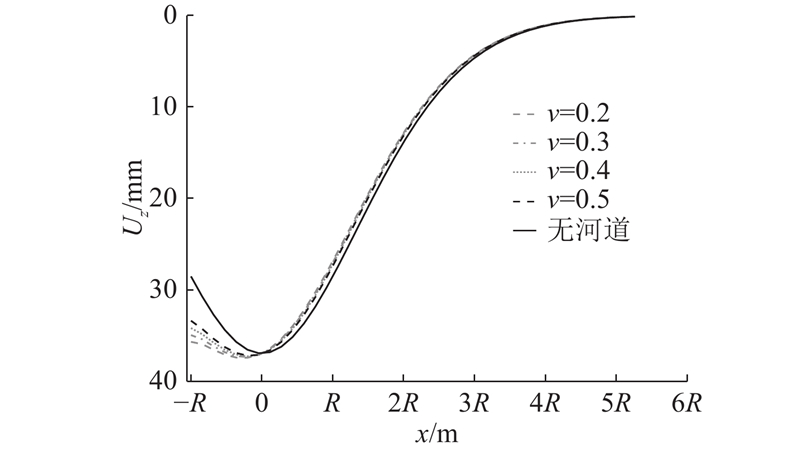
如图7所示为H=2R,h=2R,L=R时不同地基土泊松比情况下的地表沉降曲线. 可以看出,即使在L较小的情况下,泊松比对地表沉降曲线的影响也较小,仅在靠近河道一侧的沉降曲线稍有差异. 究其原因,主要由于本研究解析方法是基于影像源法,泊松比仅在弹性力学部分力产生的位移上有所体现,对于借鉴流体力学的源汇部分位移则没有影响. 从前文推导过程可以看出,为了保证自由表面无应力条件而施加的应力都是水平方向的,对竖直方向的地面沉降影响较小.
图 7
图 7 不同泊松比情况下的地表沉降曲线
Fig.7 Surface settlement curve under different Poisson's ratios
5. 结 论
(1)基于影像源法与土体位移的非均匀收敛模式,采用叠加法提出邻近既有河道情况下隧道掘进引发地面沉降的解析解,将计算结果与顶管隧道实例的现场地表监测数据进行对比,验证了本研究方法的合理性.
(2)隧道与河道水平距离在临近河道隧道掘进引起地表沉降的影响中起主要作用,水平距离越小,沉降槽的非对称性越显著,临河道侧的沉降更大,与无河道情况相比,沉降槽峰值的增幅最大可超过30%,实际工程中隧道施工应尽量远离河道.
(3)随着隧道埋深的增大,由隧道掘进引起的地表沉降越小,而当隧道拱腰深度大于邻近既有河道深度时,靠近河道附近的地表沉降明显大于无河道情况,此时更应考虑既有河道的影响.
参考文献
软土隧道盾构法施工引起的纵向地面变形预测
[J].DOI:10.3321/j.issn:1000-4548.2005.09.020 [本文引用: 1]
Prediction of longitudinal ground deformation due to tunnel construction with shield in soft soil
[J].DOI:10.3321/j.issn:1000-4548.2005.09.020 [本文引用: 1]
地铁双隧道施工引起地表沉降及变形的随机预测方法
[J].DOI:10.3969/j.issn.1000-7598.2008.12.045 [本文引用: 1]
Stochastic method for predicting ground surface settlement and deformation induced by metro double tube tunneling
[J].DOI:10.3969/j.issn.1000-7598.2008.12.045 [本文引用: 1]
随机介质理论预测近距离平行盾构引起的地表沉降
[J].
A simplified method for predicting ground settlement caused by adjacent parallel twin shield tunnel construction based on stochastic medium theory
[J].
Analysis of undrained soil deformation due to ground loss
[J].
Discussion: surface settlements due to deformation of a tunnel in an elastic half plane
[J].
Analytical prediction for tunneling-induced ground movements in clays
[J].DOI:10.1061/(ASCE)1090-0241(1998)124:9(846) [本文引用: 2]
Elastic solution for tunneling-induced ground movements in clays
[J].DOI:10.1061/(ASCE)1532-3641(2004)4:4(310) [本文引用: 1]
盾构掘进地面沉降虚拟镜像算法
[J].DOI:10.11779/CJGE201408009 [本文引用: 1]
Estimation of shield tunneling-induced ground surface settlements by virtual image technique
[J].DOI:10.11779/CJGE201408009 [本文引用: 1]
基于影像源法的基坑开挖对邻近单桩影响简化分析
[J].
Simplified analysis of adjacent single-pile response subjected to foundation pit excavation based on virtual image technique
[J].
基于影像源法的基坑开挖引起的土体水平位移预测
[J].
Prediction of horizontal displacement of soils caused by excavation of foundation pits based on virtual mirror technology
[J].
双线平行顶管上跨地铁盾构隧道施工环境影响实测分析
[J].
Observed environment response caused by construction of double-line parallel pipe jacking crossing over metro shield tunnels
[J].