传统钢框架结构在地震作用下多呈“剪切型”变形,如若设计不当,地震作用下的结构损伤易集中于局部楼层并形成薄弱层,于抗震不利. 若为钢框架结构附设摇摆钢桁架,或者去除支撑钢框架结构的首层支撑立柱构件,可形成摇摆钢框架结构[1]. 在地震作用下,主体钢框架结构各楼层的不均匀变形将被摇摆钢桁架抑制,整体结构的变形能力和承载力获得提高. 进一步,若在摇摆钢桁架的转动底脚设置阻尼器,即形成消能摇摆钢框架结构(steel frame coupled with rocking structure and dampers,SRF),可提高结构抗震性能.
消能摇摆结构的研究可以追溯至1960年智利大地震,Housner[2]对摇摆高位水箱的减震效应进行了讨论. Meek[3]分析框架-摇摆剪力墙结构的动力响应,对比了影响摇摆结构减震效果的各种因素. Mander等[4-5]提出释放梁柱节点刚性约束、通过预应力钢筋实现构件连接和震后自行复位的装配式结构体系. MacRae等[6]提出反映摇摆构件刚度约束效应的评价指标,即层间位移集中系数(drift concentration factor,DCF). Roh等[7]从构件层面研究钢筋混凝土摇摆柱的破坏全过程. Eatherton等[8-10]提出支座可抬起的消能摇摆钢桁架体系,通过钢桁架中轴线位置布设自复位钢索和耗能钢筋,实现消能减震与震后自行复位的功能,并通过E-defense试验展开验证. 曲哲等[11-12]总结摇摆墙-框架结构的抗震设计方法,并应用于东京工业大学G3教学楼改建项目. 杨树标等[13-14]推导摇摆-框架体系的基本方程,评估摇摆构件刚度对于整体结构变形模式的约束效应. 张文津[1]针对消能摇摆钢框架结构的抗震性能及影响因素展开系统研究,基于现行规范体系的设计原则提出设计方法. 为了进一步提高消能摇摆结构对高层建筑结构的适用性,Wiebe等[15-16]提出柱脚可抬起的分段摇摆结构,并通过理论分析和振动台试验,论证该结构能够显著降低高阶振型对摇摆结构抗震设计内力的影响.
目前,面向消能摇摆结构的力学推导和实验研究较成熟,实用设计流程基本形成,也已经应用于部分工程. 但是,既有研究工作仍存在以下局限性:1)在不同分布形式侧向荷载作用下,消能摇摆钢框架结构变形和内力的弹性计算方法有待推导. 2)面向消能摇摆钢框架结构地震反应计算方法的研究较少,为了高效、准确地评估SRF地震反应,基于等效线性化原理的等效单自由度分析模型有待深入研究. 3)SRF的弹塑性刚度可等效为“双折线”形式,等效屈服后刚度比取值范围较大. 既有研究所获得的延性需求谱不适用于SRF.
本研究采用结构力学经典理论[17],推导消能摇摆钢框架结构的力学方程,给出结构内力和变形的弹性计算方法. 提出消能摇摆钢框架结构的等效单自由度分析模型,推导结构非线性地震反应的计算方法,得到不同场地条件下适用于消能摇摆钢框架结构的延性需求谱.
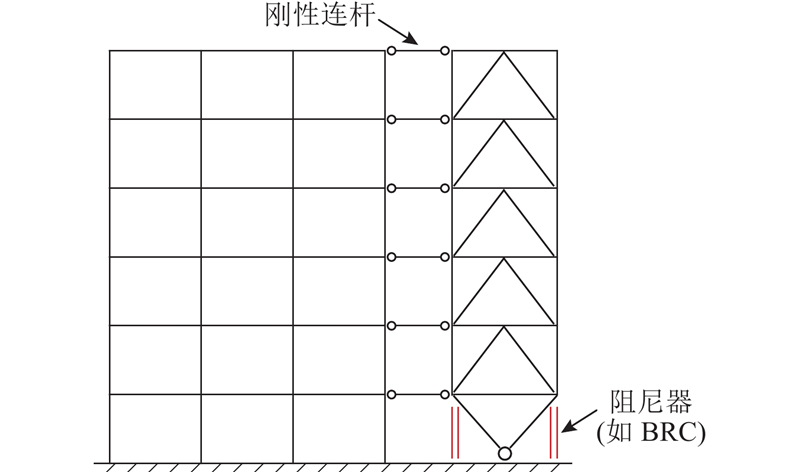
1. 消能摇摆钢框架结构的概念
图 1
消能摇摆钢框架结构的组成如下.
1)主体钢框架结构. 发挥竖向承载和部分侧向承载的功能,与普通钢框架结构基本相同.
2)摇摆结构,即摇摆钢桁架. 可抑制薄弱层,提高整体结构的延性与抗震性能.
3)刚性楼板,以刚性连杆简化表示. 连接主体钢框架结构与摇摆钢桁架,保证两者在地震作用下侧向变形协调.
4)阻尼器. 布设于摇摆钢桁架转动底脚,可以根据设计要求选用位移型阻尼器(如屈曲约束柱BRC)或速度型阻尼器(如黏滞阻尼器VFD). 阻尼器在地震作用下可发挥消能减震的作用,震后便于更换和修复.
摇摆钢桁架既可通过去除支撑钢框架结构的支撑柱构件实现,也可作为附设结构,与普通钢框架结构相连[1]. 因此,消能摇摆钢框架结构既可以用于新建建筑的结构选型,也可以作为既有建筑的加固、改造方案.
2. 结构弹性计算方法
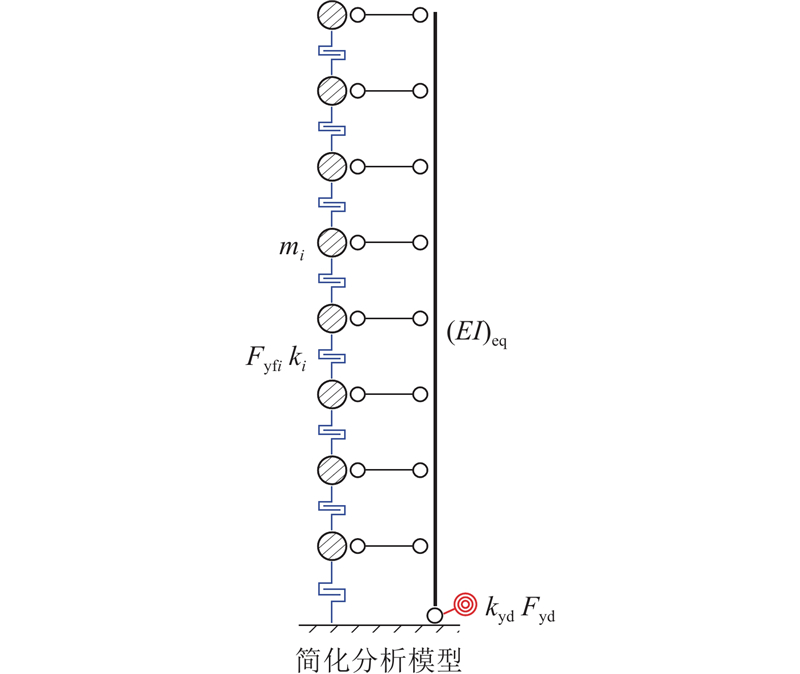
2.1. 简化分析模型
图 2
为了建立SRF连续化力学方程,进行如下假定:
1)以刚性连杆代替楼板,服从刚性楼面假定,主体钢框架结构各楼层侧移与摇摆钢桁架相应位置的侧移保持协调.
2)主体钢框架结构各层剪切刚度服从连续化假定,整体结构连续化刚度的平均值记为CF,表示主体钢框架结构发生单位转角所产生的剪力. 第i层钢框架连续化剪切刚度记为CFi[17]:
式中:Di表示按“D值法”[17]计算得到的主体钢框架结构第i层的层间刚度,hi为第i层层高.
3)假定主体钢框架结构层间刚度变化不大,根据文献[17],(EI)eq、CF可等效为常量,如下式所示.
式中: (EI)eq为摇摆钢桁架等效抗弯刚度的均值[17],(EI)ti为摇摆钢桁架在第i层的等效抗弯刚度.
2.2. 消能摇摆钢框架结构的弹性计算方法
支撑钢框架结构的计算理论不能考虑位移型阻尼器刚度贡献,边界条件不能完全适用SRF的弹性计算. 基于消能摇摆钢框架结构的多自由度简化分析模型,可以得到SRF的连续化微分方程[17]:
式中:H为结构总高度,ξ为结构相对高度,y为结构的水平侧移,x为结构绝对高度,p(ξ)为侧向荷载的分布函数. 式(3)的边界条件如下:
在均布荷载作用下,荷载p(ξ)为常数q0,此时式(3)的通解如下:
式中:VF表示主体钢框架结构沿高度方向的剪力分布,Vtruss表示摇摆钢桁架沿高度方向的剪力分布. 由边界条件确定系数A、B、C、D的取值:
在倒三角分布荷载作用下,荷载表达式为
式中:p0为倒三角荷载的线密度幅值. 此时微分方程式(3)的通解如下:
系数A、B、C、D的取值由边界条件确定:
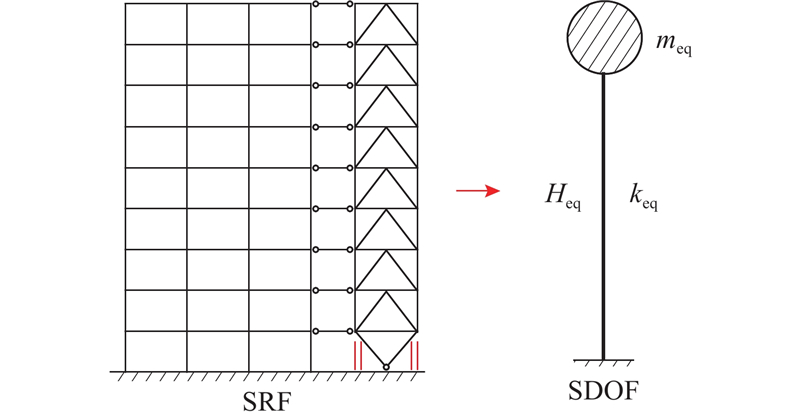
3. 等效单自由度分析模型
3.1. 等效单自由度分析模型
为了快速、准确评估SRF非线性地震反应,基于2条原则提出SRF等效单自由度模型(single degree of freedom model, SDOF):1)在倒三角侧向分布加速度作用下,SRF分布质量惯性力所产生的基底弯矩,与SDOF集中质量惯性力所产生的基底弯矩相等. 2)SRF顶点侧移刚度与SDOF集中质量的侧移刚度相等. SRF等效质量meq的计算方法如下:
式中:Heq为SDOF的等效高度,n表示SRF结构层数,H表示SRF结构总高度,Hi表示SRF第i层高度.
图 3
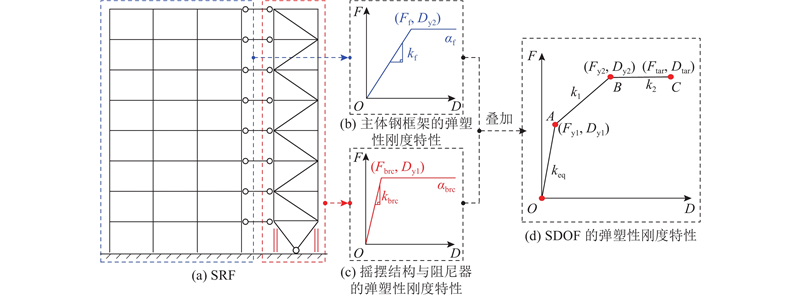
SDOF的弹塑性刚度特性由主体钢框架结构及摇摆钢桁架(含BRC)共同决定,呈现“三阶段”特征,如图4所示. 图中,阶段OA表示BRC未屈服,整体结构处于弹性;阶段AB表示BRC屈服而主体钢框架结构基本保持弹性;阶段BC表示主体钢框架结构发生屈服. 须说明的是,应当通过设计保证摇摆钢桁架在地震作用下始终保持弹性.
图 4
图 4 SRF等效SDOF的弹塑性刚度特性
Fig.4 Elastoplasticity characteristics of equivalent SDOF for SRF
将主体钢框架结构与摇摆结构(含BRC)弹塑性刚度特性简化为“双折线”模型,相关参数可按如下公式计算:
式中:Ff和Fbrc分别表示主体钢框架结构与摇摆结构(含BRC)的屈服力;αf和αbrc分别表示主体钢框架结构与摇摆结构(含BRC)的屈服后刚度比;Dy2和Dy1分别表示主体钢框架结构与摇摆结构(含BRC)的屈服位移,BRC应早于钢框架结构发生屈服,即Dy1<Dy2;Fy1表示SDOF一阶屈服承载力,即BRC屈服时对应的SDOF承载力;Fy2表示SDOF二阶屈服承载力,即主体钢框架结构屈服时对应的SDOF承载力;Dtar表示目标位移;Ftar为Dtar对应的目标承载力;k1和k2分别表示SDOF一阶、二阶屈服后刚度;kf表示主体钢框架结构顶点侧移刚度,按“D值法”[17]计算;kbrc表示摇摆结构(含BRC)刚度;Δmax表示SRF屈服层间位移角.
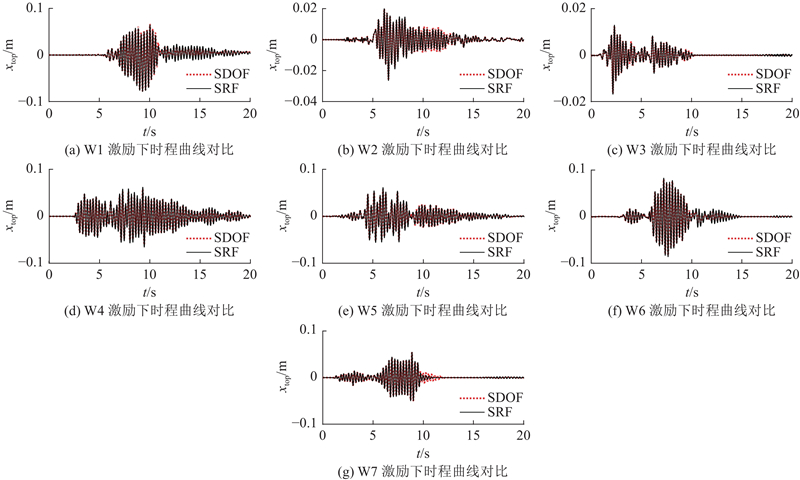
3.2. 等效单自由度分析模型的有效性验证
表 1 SDOF基础计算参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| kf /(kN·m−1) | kbrc /(kN·m−1) | |||
| Dy2 /m | Dy1 /m | |||
| Ff /kN | 229.5 | Fbrc /kN | 280.4 | |
| αbrc | 0.008 | αf | 0.055 | |
| meq /t | 271.7 | — | — |
图 5
图 5 SRF与SDOF弹塑性地震反应的比较
Fig.5 Elastic-plastic seismic response comparison of SRF and SDOF
4. 基于等效线性化原理的消能摇摆钢框架结构地震反应计算方法
地震作用下SDOF的等效阻尼比ξeq主要包含:1)结构固有阻尼比ξ0;2)主体钢框架塑性耗能的等效阻尼比ξf;3)阻尼器塑性耗能的等效阻尼比ξd.
因此,ξeq可按照如下公式进行计算:
式中:Wf表示在目标地震位移下,主体钢框架结构往复一周产生的塑性耗能;Wd表示在目标地震位移下,BRC往复一周产生的塑性耗能;We表示在目标地震位移下整体结构的应变能.
根据等效线性化原理,在达到预期的结构最大目标响应时,以SDOF的割线刚度kSDOF作为等效线性化刚度,以ξeq作为结构阻尼比,可以得到SDOF的动力方程:
式中:xg(t)表示输入激励的位移时程,x(t)表示SDOF的位移响应时程. 对式(14)进行求解,即可得到基于等效线性化原理的结构地震反应.
5. 消能摇摆钢框架结构延性需求谱
5.1. 等效双折线弹塑性刚度模型
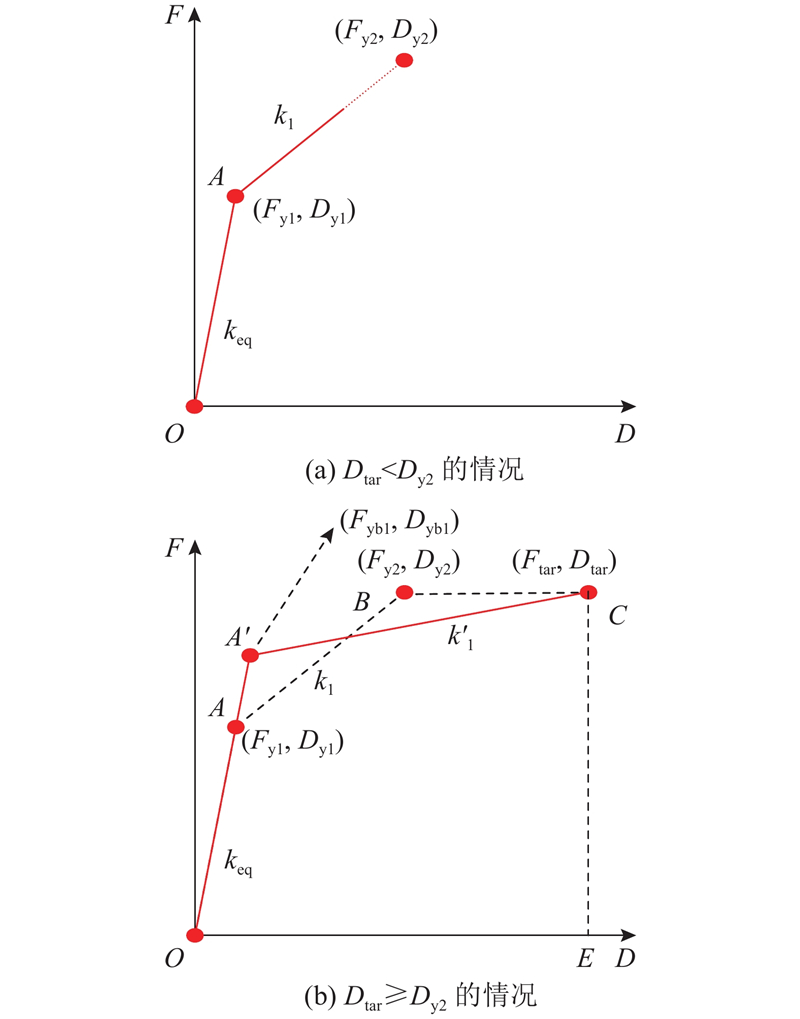
式(11)~(14)给出SDOF的计算方法,其弹塑性刚度特性呈现“三折线”的特征. 为了得到能够应用于实际设计的消能摇摆钢框架结构的延性需求谱,有必要将SDOF“三折线”弹塑性刚度特征进一步等效为“双折线”弹塑性刚度特征. 文献[18]根据F-D曲线下围面积相等的原则,提出将SDOF“三折线”弹塑性刚度模型等效为“两折线”弹塑性刚度模型的方法,并通过结构弹塑性地震反应分析,验证了该等效方法的有效性. 将SDOF“三折线”弹塑性刚度模型等效为“双折线”弹塑性刚度模型,须分2种情况讨论:
1)Dtar<Dy2. 此时BRC屈服而主体钢框架结构未屈服,SDOF的弹塑性刚度模型仅包含“双折线”部分,无需等效.
2)Dtar
图 6
图 6 SDOF等效“双折线”弹塑性刚度模型
Fig.6 Equivalent bilinear elastic-plastic stiffness model of SDOF
如图6所示为SDOF等效“双折线”弹塑性刚度模型. 图中,红色实线表示等效后SDOF“双折线”弹塑性刚度模型,黑色虚线表示等效前SDOF “三折线”弹塑性刚度模型. 在式(15)的基础上,定义延性系数μ与屈服强度系数ξy,表达式如下:
式中:Fe表示SDOF在地震作用下的弹性内力.
5.2. 延性需求谱
图 7
屈服强度系数ξy表示结构屈服承载力与地震作用下弹性内力的比值,如图7所示共分为ξy=0.167、0.200、0.250、0.333、0.500这5种情况;同时列举了屈服后刚度比的7种取值情况,α=0.02、0.10、0.20、0.30、0.40、0.50、0.60. 各工况取50条波计算结果的均值.
由图7的延性需求谱可以得到如下结论:
1)在同等条件下,屈服强度系数ξy越高,结构在地震作用下的塑性发展程度越浅,结构延性系数越低.
2)在同等条件下,结构屈服后刚度比α越高,结构延性系数越低,地震作用下结构的损伤塑性发展越缓慢.
3)在同等条件下,结构基本周期越短,地震反应越大,延性系数越高,结构的塑性发展程度越严重. 随着结构周期的增长,地震反应越小,延性系数逐渐下降并趋于稳定.
4)当屈服后刚度比α
5)长周期结构(基本周期大于1.0 s)的延性系数受地震动类型和屈服后刚度比α的影响较小.
6. 结 论
(1)推导了消能摇摆钢框架结构的弹性计算方法,可用于计算其在水平荷载作用下的内力、变形及动力特性参数.
(2)提出消能摇摆钢框架结构的等效单自由度分析模型,并通过弹塑性地震反应分析,验证其准确、有效,能够反映完整结构的弹塑性刚度特征.
(3)基于等效单自由度分析模型和等效线性化方法,推导了消能摇摆钢框架结构地震反应的计算方法,可用于预估整体结构的地震反应.
(4)基于等效单自由度分析模型,给出了适用于消能摇摆钢框架结构的延性需求谱,可用于设计参考.
上述关于消能摇摆钢框架结构非线性地震反应的研究是在SDOF基础上开展的,未考虑高阶振型的影响. 下一步,将推导结构等效多自由度分析模型,进而讨论高阶振型对结构地震反应的影响.
参考文献
The behavior of inverted pendulum structures during earthquakes
[J].DOI:10.1785/BSSA0530020403 [本文引用: 1]
Dynamic response of tipping core buildings
[J].
Seismic response of precast prestressed concrete frames with partially debonded tendons
[J].DOI:10.15554/pcij.01011993.58.69 [本文引用: 1]
Effect of column stiffness on braced frame seismic behavior
[J].DOI:10.1061/(ASCE)0733-9445(2004)130:3(381) [本文引用: 1]
Modeling and seismic response of structures with concrete rocking columns and viscous dampers
[J].DOI:10.1016/j.engstruct.2010.03.013 [本文引用: 1]
Design concepts for controlled rocking of self-centering steel-braced frames
[J].DOI:10.1061/(ASCE)ST.1943-541X.0001047 [本文引用: 1]
Earthquake resilient steel braced frames with controlled rocking and energy dissipating fuses
[J].
Computational study of self-centering buckling restrained braced frame seismic performance
[J].
框架-摇摆墙结构简化计算方法研究
[J].DOI:10.3969/j.issn.1002-8412.2014.02.015 [本文引用: 1]
Simplified calculation method of frame rocking-wall structure system
[J].DOI:10.3969/j.issn.1002-8412.2014.02.015 [本文引用: 1]
A distributed parameter model of a frame pin-supported wall structure
[J].DOI:10.1002/eqe.2550 [本文引用: 1]
Mitigation of higher mode effects in base-rocking systems by using multiple rocking sections
[J].
Mechanisms to limit higher mode effects in a controlled rocking steel frame. 1: concept, modelling, and low-amplitude shake table testing
[J].DOI:10.1002/eqe.2259 [本文引用: 1]
延性需求谱在基于性能的抗震设计中的应用
[J].DOI:10.3969/j.issn.1000-1301.2004.01.005 [本文引用: 2]
Application of ductility demand spectra in performance-based seismic design
[J].DOI:10.3969/j.issn.1000-1301.2004.01.005 [本文引用: 2]