随着车辆通信网络飞速发展,智能交通系统[1](intelligent transportation systems, ITS)通过车联网(Internet of vehicles, IoV)中的车辆与基础设施(vehicle to infrastructure, V2I)和车与车(vehicle to vehicle, V2V)的通信机制[2],实现了车辆和路边接入点(access point, AP)之间的自主数据交换[3]. 在此网络上,用户车辆对体验质量(quality of experience, QoE)[4]的要求的提高,如何均衡车辆和基础设施间的利益,以满足更高的计算和存储需求,成为研究的关键.
针对上述问题,Deng等[15-17]提出基于博弈的合作激励方案,为每个参与者达到最佳定价策略,不过,上述方案均未考虑数据包的大小以及自身存储空间受限因素,导致结果存有一定偏差. Hui等[18] 提出的合作博弈中继选择定价方案提升了吞吐量和传输性能,但未考虑中继车辆存储空间有限的实际问题. Xiong等[19-20]提出的方案使得节点的收益根据其剩余存储空间进行调整,缓解存储压力,但对用户QoE提升有限. Ramamooryhy等[21]提出QoE驱动的车间通信定价方案,该方案采用三方Stackelberg博弈模型,引入中继车辆帮助基础设施转发多媒体内容给远程用户车辆,中继车辆较基础设施更接近用户车辆,能解决通信盲区问题,但因收益有限,中继车辆的数据转发积极性并不高,进而一定程度上影响了用户的QoE.
针对未考虑中继车辆存储空间有限与数据转发积极性低下而导致用户车辆QoE降低的问题,本研究提出基于三方Stackelberg博弈的动态多媒体定价方案(dynamic multimedia pricing scheme, DMPS). 构建基于路侧单元(roadside unit, RSU)、中继车辆和用户车辆三方之间的多媒体内容定价框架,激励中继车辆参与转发内容. 设计基于Stackelberg博弈的动态定价模型,建立三方实体的效用函数并将其转化为四阶段Stackelberg博弈定价模型,采用反向归纳法达到纳什均衡得到各自最优策略.
1. 系统模型
1.1. 通信模型
假设车辆进入RSU的通信范围的数量遵循泊松分布. 如图1所示,车辆以速度
图 1
在进行V2I和V2V通信时,无线信号在传输过程中可能会存在阴影衰落、多径衰落、路径损失等问题,因此上、下行链路的传输速率会受到影响,故无线数据传输速率表达式如下:
式中:
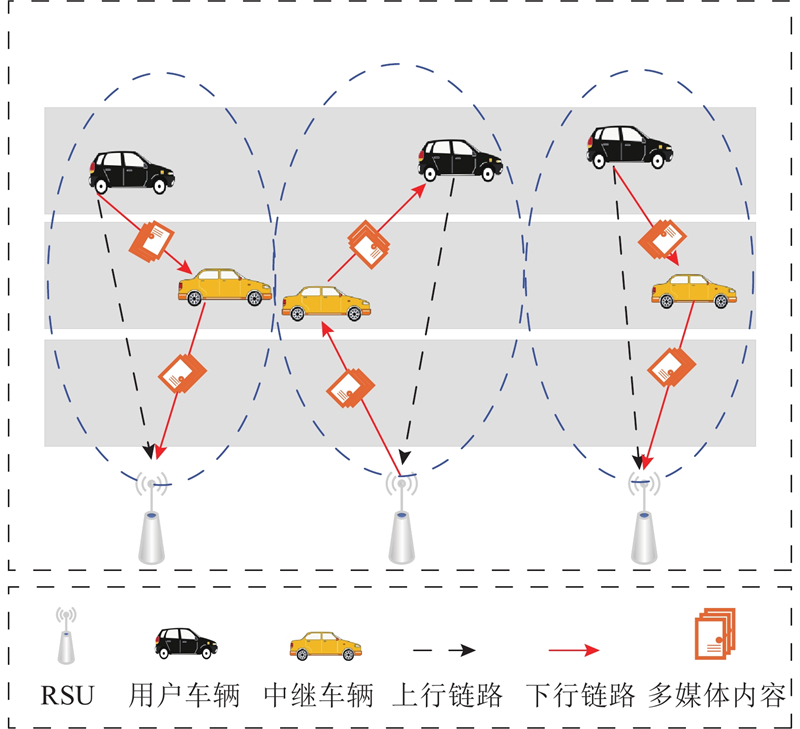
1.2. 网络模型
如图2所示,在一个RSU通信覆盖范围内,RSU、中继车辆与用户车辆之间通过定价关系进行三方交互. 若用户车辆想要购买多媒体内容
图 2
2. 基于三方的DMPS设计
本研究所提出的系统模型中有3个实体,分别为RSU、中继车辆和用户车辆. 通过引入DMPS,系统中的参与者动态调整自己策略的过程被描述为三方博弈. 对于用户车辆,为了最大化满足用户车辆需要的内容,须建立一个用户效用函数,通过数学模型表现用户车辆体验的满意度;对于中继车辆,为了得到更多的奖励,其目标是最大化自身收益函数,须制定合适的佣金比例
2.1. 用户车辆的效用
用户车辆在行驶过程中有着不同的多媒体内容需求以增强娱乐性,并且用户希望获得高质量的多媒体内容体验. 将用户车辆对于购买内容的满意度问题转化为基于RSU的内容定价、中继车辆发送内容消耗的成本以及选择合适数量
式中:
假设各个用户车辆之间是相互独立的,用户车辆向中继车辆支付的全额佣金的表达式如下:
式中:
因此,用户车辆的效用函数
2.2. 中继车辆的效用
中继车辆的选择采用Sennan等[22]所提出的方法,选择的最佳中继车辆相比于用户车辆距离RSU更近,可以通过V2V通信为用户车辆提供高质量的多媒体内容. 为了激励更多的中继车辆利用自己储存空间参与到内容转发的行为中,中继车辆只须向RSU支付少量的服务费,而自身获取来自用户车辆的全额佣金. 中继车辆在RSU通信覆盖范围内移动,将接收的内容转发给距离RSU较远的用户车辆,在获得来自用户车辆的全额佣金后,向RSU支付一定比例
式中:
中继车辆支付的佣金表达式如下:
式中:
假设车辆的存储容量相同,接收的最大内容数据
无线信道传输内容所需的能量成本
式中:
中继车辆的效用方程表达式如下:
2.3. RSU的效用
RSU通过中继车辆帮助转发内容,减轻了RSU的通信负担,降低了运营成本. RSU的效用方程表达式如下:
式中:
RSU传输多媒体内容产生的费用可以建模为分配频谱[23]的函数,并给出
式中:
因此,RSU的效用方程表达式如下:
3. 三方四阶段Stackelberg博弈分析
为了系统内各方都能实现利润最大化,将RSU、中继车辆与用户车辆之间的交流互动建模为非合作Stackelberg博弈模型. RSU充当中继车辆和用户车辆的领导者,而中继车辆又是用户车辆的领导者. 领导者通过预测跟随者的策略调整自己的策略,跟随者根据领导者的策略来最大优化自己的利益. 通过反向归纳法先预测跟随者的最优策略,最后推导出领导者的最优策略. 三方的最优策略用
3.1. 用户车辆的优化(第1阶段)
给定中继车辆的佣金比例
对用户车辆的效用进行二阶求导:
通过一阶导数
定理1 存在性. 用户车辆在博弈中存在纳什均衡点.
证明:由式(13)可知,数据传输速率不为负且
定理2 唯一性. 用户车辆博弈的纳什均衡解是唯一的.
证明:从定理1可以得出用户博弈存在纳什均衡. 设定
要证明最佳响应函数是一个标准函数,其必须满足以下性质.
1) 正性. 传输内容大小
2) 单调性. 若给定
3) 可测量性.
综上,用户的响应函数是标准函数,证毕.
3.2. 中继车辆的优化(第2、3阶段)
中继车辆会根据用户车辆的策略相应调整自己的策略,将第1阶段得出的
式中:
定理3 当给定RSU的成本时,连续凸函数在闭区间上有唯一的最大值,并由一阶导数等于零确定.
证明:观察其一阶导数、二阶导数的结果. 二阶导数的分母是平方关系,所以分母总是正的. 分子
3.3. RSU的优化(第4阶段)
RSU作为三方的领导者,基于跟随者的最优策略来决定自己的最优策略. 将上述两方的最优策略分别为
式(22)是多元非线性函数方程,计算二阶导数证明其是凸函数较困难. 因此,先引用定理4和定理5证明RSU存在唯一纳什均衡,再运用全局搜索算法来求解纳什均衡
定理4 可微的函数一定连续.
定理5 在闭区间上的连续函数一定存在最大值和最小值.
证明:验证式(22)是否可微以便确定效用方程是连续函数,分别对
由式(23)、(24)可以确定式(21)、(22)均是连续可微函数,则函数存在唯一的纳什均衡
3.4. 方案设计算法流程
对于上述三方四阶段Stackelberg博弈过程,本研究提出全局搜索迭代算法决策出三方各自的最优策略. 该算法为RSU、用户车辆和中继车辆找到相互响应的最佳成本、最优空间率以及最优内容数据大小. 具体算法如下.
算法1. 三方-四阶段Stackelberg博弈迭代算法
输入: 参数初始化
输出: 区间
1. for
2. for
3. 设置
4. 计算
5. if
6. 更新
7. 设置
8. end if
9. end for
10. end for
11. 根据式(21)计算中继车辆最优空间利用率
12. 根据式(15)计算用户车辆最优内容数据量
13. 分别将
4. 仿真分析
4.1. 仿真参数分析
为了验证本研究所提方案的有效性,基于MATLAB 2022a软件平台对其部分仿真数值进行分析,相关参数设定如表1所示. 表中,Pmax为车辆最大发射功率.
表 1 三方-四阶段Stackelberg博弈迭代算法的仿真参数表
Tab.1
如图3所示,展示了不同佣金比例
图 3
图 3 佣金比例变化对中继车辆效用与RSU效用的影响
Fig.3 Impact of commission ratio changes on relay vehicle utility and RSU utility
如图4所示为不同传输内容大小下车辆的传输速率对用户效用的影响. 可见传输内容更大,用户可获得的效用也更高,但随着传输速率的增加,用户效用略微减少,这是因为本研究设定的效用受传输内容大小、车载存储空间利用率以及成本等因素共同影响,设定决策方式的特殊性使得速率增大后效用会略微降低. 传输速率非决定性因素,其发生变化对效用的影响较少,因此只须采用固定的传输速率,通过本研究所设定的博弈策略,即可以获得三方各自的最优效用.
图 4
图 4 不同传输速率对用户效用的影响
Fig.4 Effect of different transmission rates on user utility
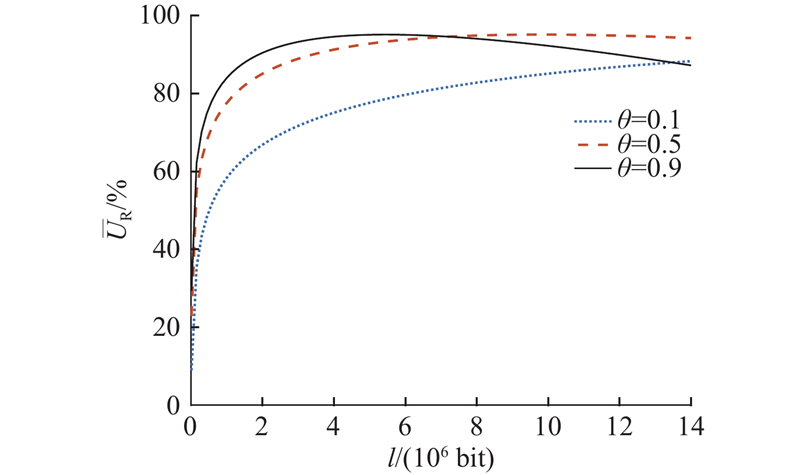
如图5所示,中继车辆的不同空间利用率
图 5
图 5 不同空间利用率下中继车辆效用
Fig.5 Utility of relay vehicle under different space utilization values
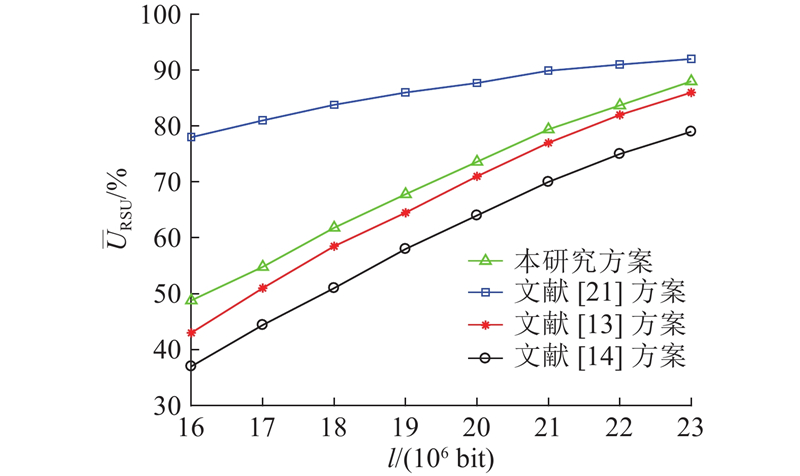
4.2. RSU的效用对比
图 6
4.3. 中继车辆的效用对比
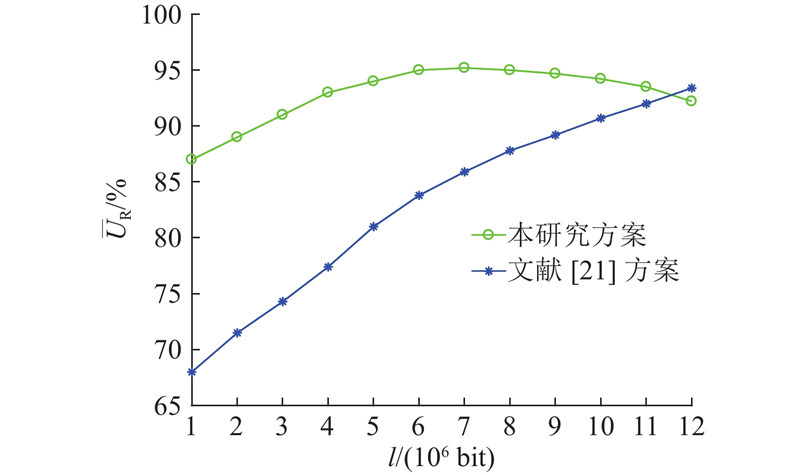
如图7所示,将本研究所提方案与文献[21]的进行对比,得出不同方案下中继车辆的效用(文献[13]和[14]方案没有考虑中继车辆,因此不参与本节的效用对比). 可以看出,本研究方案在中继车辆传输内容数量为1×106~11×106 bit时拥有更高的效用,这是因为中继车辆传输给用户的内容增加,获得佣金也随之增多,激励了中继车辆更积极地参与转发内容. 文献[21]方案中RSU支付中继车辆的佣金是采用传统支付方法,中继车辆得到的佣金不及本研究方案的,即表现出了较低的效用. 虽然文献[21]方案的效用整体呈上升趋势,但其在传输内容数量较少时与本研究方案有较大差距,即当用户想要获取的内容数量偏低时,中继车辆的效用不高,进而影响了中继车辆参与转发的积极性. 当传输内容数量持续增大时,本研究方案的效用会逐渐低于文献[21]方案的,这是因为本研究引入了存储空间利用率来限制中继车辆的整体效用,即本研究考虑到了传输内容过多会使中继车辆整体效用降低(内容过多时会造成中继车辆存储过载),而文献[21]方案没有考虑到中继车辆的存储空间问题,效用才会持续呈上升趋势.
图 7
图 7 不同方案的中继车辆效用对比
Fig.7 Comparison of utility of relay vehicle under different schemes
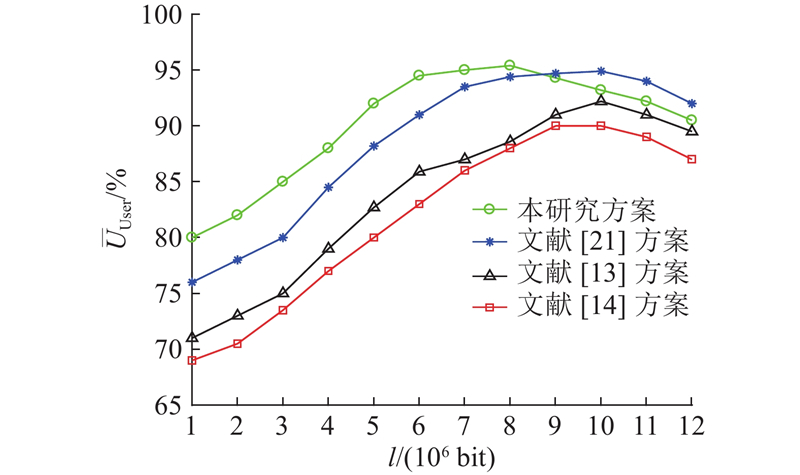
4.4. 用户车辆的效用对比
如图8所示,将本研究所提方案与文献[13]、[14]和[21]方案进行比对,得出不同方案下用户车辆的效用. 随着内容数据的增加,各方案用户车辆的效用不断增加,而采用本研究方案能够获得整体最佳效用. 文献[13]、[14]方案不借由中继转发,使得远程服务造成了更大的成本开销,从而导致用户效用最低. 当传输内容数量在一定范围时(1×106~8×106 bit),由于本研究方案的中继车辆拥有用户的全额佣金,其数据转发积极性较高,用户效用更高,而文献[21]方案的中继车辆积极性不如本研究的,用户支付同等价格时能够获得的收益较低,因而其效用低于本研究方案的. 当数量继续增大时,由于文献[13]、[14]与[21]方案均理想化了车辆存储空间,效用会持续增长. 然而传输内容数量不断增长,会提高成本定价,导致用户车辆的开销超过QoE,所有方案的效用最终均会呈现下降趋势.
图 8
图 8 不同方案的用户车辆效用对比
Fig.8 Comparison of utility of user vehicle under different schemes
5. 结 语
提出IoV中基于三方Stackelberg博弈的DMPS. 该方案同时考虑中继车辆、用户车辆和RSU三方之间的相互作用,根据存储空间利用率、内容数据大小和成本建立效用函数,利用反向归纳法得到最佳内容数据大小、最优空间利用率和最佳成本. 仿真结果表明,本研究所提方案不仅提高了QoE与中继车辆积极性,还解决了中继车辆的有限存储空间问题,较传统方案有一定优势. 未来计划研究在5G-IoV的实际广播或转发的应用场景,将多个车辆的密度、车间距离,以及卸载和存储转发的文件大小等因素作为策略集,建立数学模型制定更符合实际应用环境的定价机制.
参考文献
Green Internet of vehicles (IoV) in the 6G era: toward sustainable vehicular communications and networking
[J].DOI:10.1109/TGCN.2021.3127923 [本文引用: 1]
Augmenting drive-thru internet via reinforcement learning-based rate adaptation
[J].DOI:10.1109/JIOT.2020.2965148 [本文引用: 1]
Resource-aware video delivery in fog radio access networks: a joint QoE and QoS perspective
[J].DOI:10.1109/TVT.2023.3234141 [本文引用: 1]
以用户QoE预测值为奖励的视频自适应比特率算法
[J].DOI:10.12178/1001-0548.2020325 [本文引用: 1]
A video adaptive bitrate algorithm with user QoE prediction as reward
[J].DOI:10.12178/1001-0548.2020325 [本文引用: 1]
QoE-based reduction of handover delay for multimedia application in IEEE 802.11 networks
[J].DOI:10.1109/LCOMM.2015.2459048 [本文引用: 1]
QoE-driven mobile edge caching placement for adaptive video streaming
[J].DOI:10.1109/TMM.2017.2757761 [本文引用: 1]
Three dynamic pricing schemes for resource allocation of edge computing for IoT environment
[J].DOI:10.1109/JIOT.2020.2966627 [本文引用: 1]
Reservation service: trusted relay selection for edge computing services in vehicular networks
[J].DOI:10.1109/JSAC.2020.3005468 [本文引用: 1]
An equivalent exchange based data forwarding incentive scheme for socially aware networks
[J].DOI:10.1007/s11265-020-01610-6 [本文引用: 1]
Two-dimensional behavior-marker-based data forwarding incentive scheme for fog-computing-based SIoVs
[J].DOI:10.1109/TCSS.2021.3129898 [本文引用: 1]
A QoE-driven pricing scheme for inter-vehicular communications with four-stage Stackelberg game
[J].DOI:10.1109/TVT.2021.3138328 [本文引用: 14]
MADCR: mobility aware dynamic clustering-based routing protocol in Internet of Vehicles
[J].DOI:10.23919/JCC.2021.07.007 [本文引用: 1]
Competitive spectrum sharing in cognitive radio networks: a dynamic game approach
[J].DOI:10.1109/TWC.2008.070073 [本文引用: 2]