根据现有的隧道工程研究可知,开挖后的岩体变形并非瞬时完成,而要持续一定的时间才趋于稳定,即岩体的流变性质和时效性特征. 岩体流变力学中的蠕变效应是国内外众多学者研究范围最广、内容最深入的一个方面[3]. Xu等[4]考虑结构效应,分析层状岩体的蠕变特性,结果表明层状岩体蠕变参数受结构效应的影响显著. 范庆忠等[5]对红砂岩进行单轴分级加载蠕变试验,研究发现岩体的瞬时弹性模量受应力水平的影响较大. 李永盛[6]对4种不同力学性质的岩体进行单轴压缩蠕变试验,发现岩体的蠕变速率呈现3个阶段,各阶段持续时长与岩体性质和应力水平有关. 徐卫亚等[7]建立非线性黏弹塑性模型,实现了对岩体加速蠕变的描述. 胡涛涛等[8]对含软弱夹层炭质板岩的单轴压缩力学行为进行数值模拟研究,总结了端部约束对抗压强度及塑性区发展的影响规律. 周晓飞等[9]借助幂函数,对泥质夹层剪切蠕变曲线进行拟合,提出基于幂级次求解泥质夹层长期强度的方法. Li等[10]建立岩体损伤蠕变模型,该模型能够反映裂隙岩石在衰减、稳态和加速阶段蠕变曲线的非线性特征. 宋洋等[11]在传统Nishihara模型中引入GTN模型,建立可描述节理岩体剪切蠕变全过程的蠕变模型. 赵晨阳等[12]建立非线性元件并将其串联到Burgers模型中,实现了对含软弱结构面岩体三阶段的模拟. Trzeciak等[13]采用Burgers模型,对波兰北部波罗的海盆地试样进行黏弹性分析,得到Burgers模型参数的各向异性特征. Lv等[14]将Kachanov损伤理论引入到经典蠕变本构模型中,提出新的岩体蠕变损伤本构模型建立的方法. Tian等[15]推导了层状岩石的横观各向同性蠕变模型,总结了层理面刚度比对蠕变行为的影响规律. 张向东等[16]对冻黏土进行三轴蠕变试验,建立符合冻黏土蠕变特性的对数形蠕变方程. 周传涛等[17]对含不同层理倾角的黄砂岩开展常规三轴压缩试验,得到其峰值强度随倾角呈现先降低后升高的趋势. 刘开云等[18]将三轴压缩过程中岩石弹性模量的衰减方程引入本构方程,推导得到反映岩石蠕变全过程的三维非线性黏弹塑蠕变本构模型. He等[19]针对有结构面的大理岩,提出描述损伤时变特征的时变统计损伤本构模型,验证了模型的合理性. 目前,虽然学者们通过开展蠕变试验和建立蠕变本构模型,研究节理、软弱夹层及层理倾角等单一因素对岩体流变特性的影响,但对于炭质板岩这一特定岩体,考虑内部裂损和层理倾角这2个因素对蠕变特性的影响的研究较少,现有的蠕变损伤模型往往不能全面、准确地描述岩石蠕变的全过程.
为了研究考虑层理倾角的炭质板岩非线性蠕变损伤本构模型,本文采用炭质板岩开展分级加载蠕变试验. 基于试验结果,考虑层理结构对炭质板岩蠕变过程的影响以及Nishihara模型无法描述岩石加速蠕变的问题,建立考虑层理倾角和裂隙损伤的改进Nishihara非线性蠕变损伤本构模型,为解决隧道工程建设和运营过程中的变形稳定问题提供理论依据.
1. 分级加载蠕变试验
1.1. 蠕变试验方案
不同层理倾角炭质板岩的蠕变试验在长安大学RTX-1000伺服控制岩石三轴流变系统上开展. 试样均采集自渭武高速木寨岭隧道,通过岩石取芯机在采集的岩样中取得不同角度的圆柱体试样. 试样高 为100 mm,直径为50 mm,通过打磨机将试样两端面打磨平整,控制端面平整度小于0.02 mm ,断面垂直度小于0.25°. 分别对层理倾角θ = 0°、45°和90° 3组炭质板岩试样在给定围压等级5、10和15 MPa下进行三轴分级加载蠕变试验,试样破坏图片如图1所示. 试验时先将围压加载至指定值,再施加轴压. 轴压按分级加载的形式施加,根据常规三轴压缩强度σc 确定每一级加载的应力,并以100 N/s的加载速率加载至三轴压缩强度的 20%、40%、60%、80%及 100%后保持24 h,具体的应力分级如表1所示. 表中,p为围压,σt为轴向应力. 常规三轴试验的结果表明, 0°层理倾角试样的峰值应变随着围压的增大而减小,炭质板岩表现出贯穿层理面的剪切破坏. 45°层理倾角试样的峰值应变随着围压的增大而增大,表现出沿层理面产生破坏面的弱面剪切破坏. 90°层理倾角试样的峰值应变随着围压先减小后增大,破坏模式呈现张拉-剪切形态.
图 1
图 1 不同层理倾角的试样破坏图片
Fig.1 Failure images of specimen with different bedding angle
表 1 不同层理倾角炭质板岩的分级加载蠕变试验方案
Tab.1
| θ/(°) | p/MPa | σt/MPa | ||||
| 第1级 | 第2级 | 第3级 | 第4级 | 第5级 | ||
| 0 | 5 | 12 | 24 | 36 | 48 | 60 |
| 0 | 10 | 13 | 26 | 39 | 52 | 65 |
| 0 | 15 | 14 | 28 | 42 | 56 | 70 |
| 45 | 10 | 5 | 10 | 15 | 19 | 24 |
| 45 | 15 | 6 | 13 | 19 | 25 | 31 |
| 90 | 10 | 12 | 23 | 35 | 47 | 59 |
| 90 | 15 | 14 | 27 | 41 | 54 | 68 |
开展分级加载蠕变试验,全程记录试样的轴向应变. 加载阶段的应变记录时间间隔为15 s,蠕变阶段的应变记录时间间隔为60 s,在试验结束后绘制全程时间-应变曲线.
在蠕变试验中,0°层理倾角试样内部的损伤会沿着某一倾斜角度发展,导致0°层理倾角炭质板岩发生剪切破坏. 随着切应力的堆积,45°倾角层理面逐渐开始破坏,最终形成贯通破坏面. 在损伤沿着某一倾斜角度发展最终形成贯通破坏面的同时,90°层理上产生的拉应力未能达到可以形成张拉破坏面的程度,只产生剪切破坏面,呈现出剪切破坏形态.
1.2. 蠕变曲线
图 2
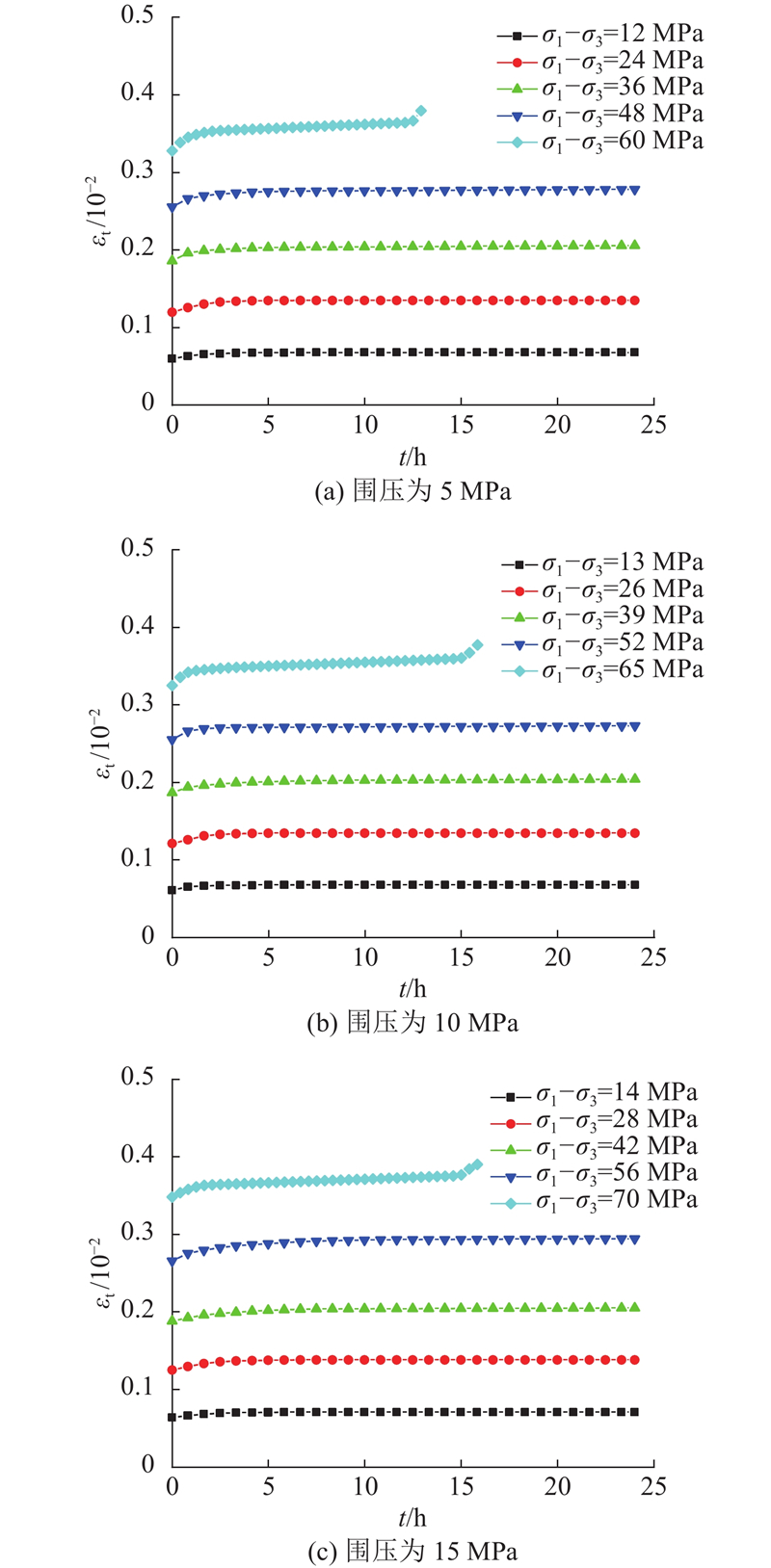
图 2 0°层理倾角炭质板岩的分级加载蠕变曲线
Fig.2 Graded loading creep curve of 0° stratigraphic dip carbonaceous slate
图 3
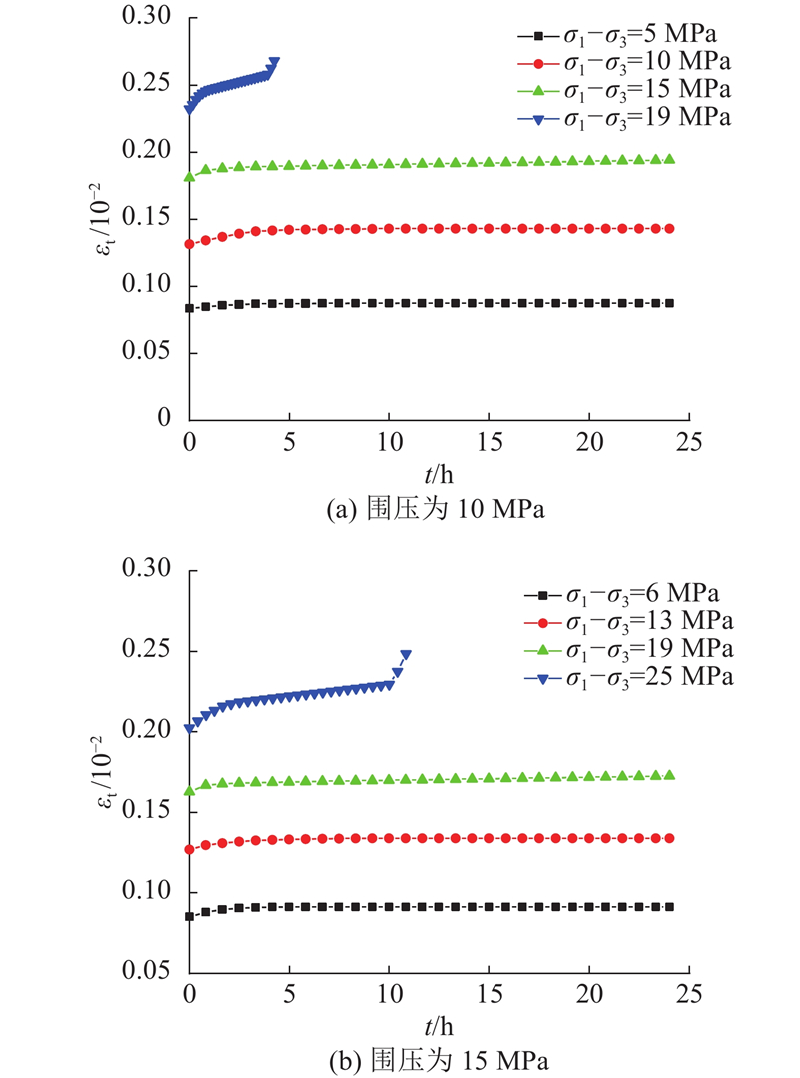
图 3 45°层理倾角炭质板岩的分级加载蠕变曲线
Fig.3 Graded loading creep curve of 45° stratigraphic dip carbonaceous slate
图 4
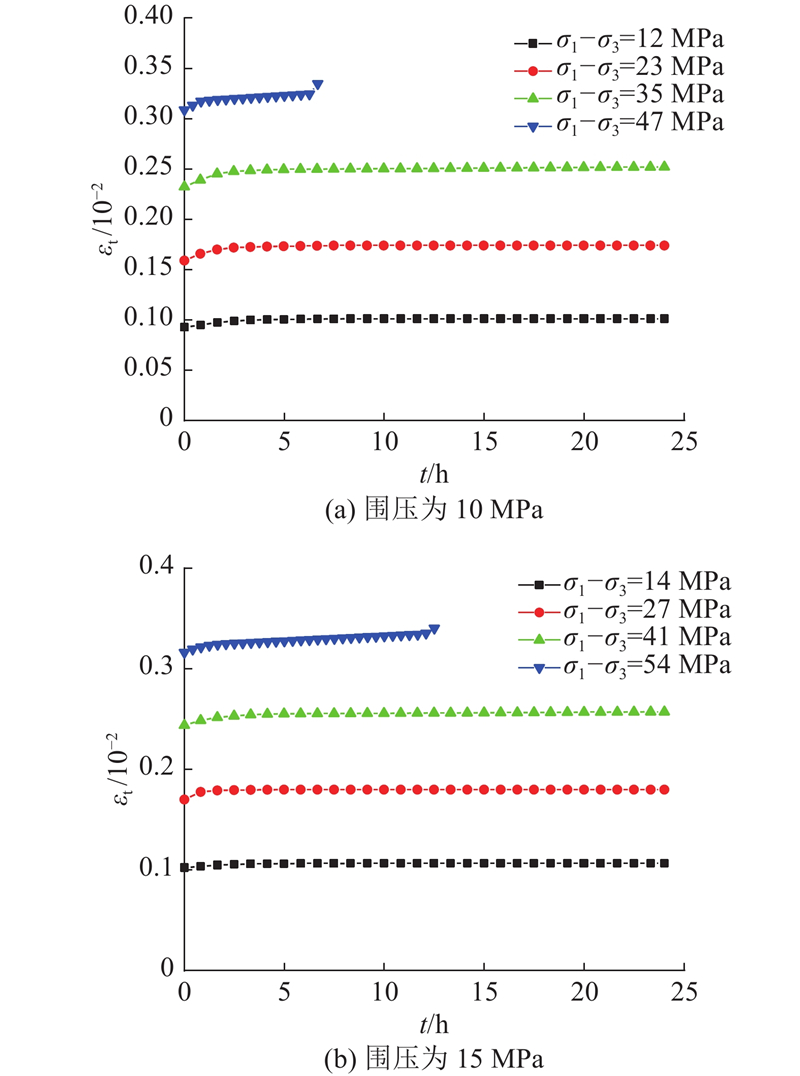
图 4 90°层理倾角炭质板岩的分级加载蠕变曲线
Fig.4 Graded loading creep curve of 90° stratigraphic dip carbonaceous slate
炭质板岩的蠕变量随着应力的提高而逐渐增大,并在破坏应力级陡然增大,这与试样发生加速蠕变有关. 炭质板岩在蠕变过程中发生的总蠕变量随着围压的增大而减小,可见围压越大,炭质板岩越不容易发生蠕变,围压对炭质板岩的蠕变有抑制作用.
2. 本构模型的建立
2.1. 层理损伤的引入
图 5
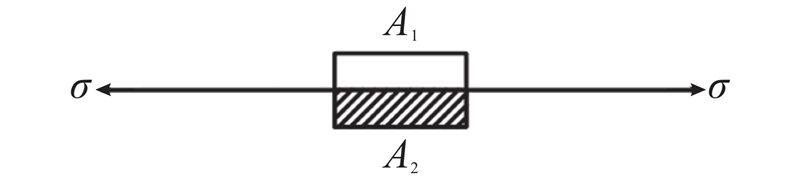
层状损伤元件的理论基础是连续损伤力学,其物理意义在于描述层状复合材料的损伤行为. 将上述弹塑性层理损伤元件看成由未损伤区域A1及损伤区域A2并联组成. 在某一应力下,该元件所产生的应变ε与A1、A2产生的应变ε1、ε2相等,其平衡关系为
式中:σ为整个元件所受的应力,σ1为未损伤区域所受的应力.
损伤前,损伤区域A2未发生作用,该元件退化为弹性元件,其应力-应变关系满足胡克定律.
式中:E为弹性模量.
由此可知,层状损伤元件中损伤部位的损伤变量为Dc=A2/A,则元件中应力之间的关系为
根据未损伤元件的应力应变关系及元件各部分应变相等的原则,可得
根据Kachanov蠕变损伤演化理论可知,定义的损伤有效应力如下:
假定在加速蠕变阶段,炭质板岩应变微元破坏服从Weibull分布,分布函数为
假设蠕变开始(t = t0 = 0)时的损伤因子Dc = 0,蠕变破坏(t = tc)时的损伤因子Dc = 1,则岩石经历加速蠕变后,定义层状损伤元件中的损伤演化方程为
式中:c为与层理倾角相关的损伤参数.
在岩石蠕变过程中,超过某个时间阈值后,弹塑性损伤元件中的损伤区域A2将开启,定义该阈值为ts(即岩体裂缝开始产生),则损伤演化方程可以改进为
综上,可得层状损伤元件的蠕变本构方程为
2.2. 非线性损伤元件的引入
黏性损伤是指岩体介质在外力作用下产生裂隙并随时间不断演化的现象,不可恢复是其主要特点. 为了解决Nishihara模型无法描述加速蠕变的问题,引入非线性黏性损伤元件. 该元件的理论基础包括非线性力学和损伤力学,物理意义是描述材料在黏性流动过程中的损伤行为. 该元件在黏性元件中引入可描述岩体内部损伤演化规律的损伤变量,损伤变量的演化受到非线性应力和黏性流动的影响,导致岩石内部产生微裂纹、空穴的损伤形态,最终导致岩石材料的失效. 元件示意图如图6所示.
图 6
Kachanov蠕变损伤演化理论可以用于加速蠕变阶段,能够有效地模拟岩石蠕变的全过程,描述材料的逐渐衰变. 根据该理论定义岩体内部损伤变量为Dn(为净截面积与无损截面积之比,即连续度),损伤演化方程为
式中: tn为岩石开始产生加速蠕变的时间.
当t
2.3. 改进Nishihara蠕变本构模型
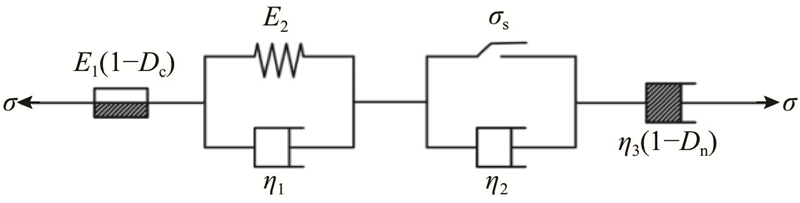
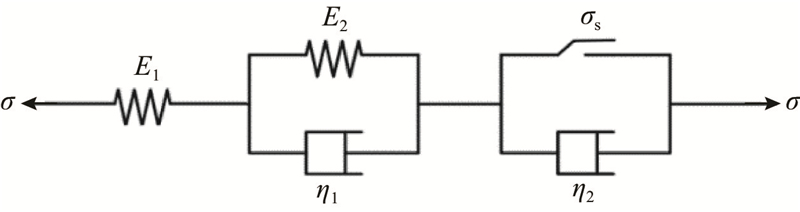
将上述两元件引入Nishihara中,建立考虑层理损伤的改进Nishihara非线性蠕变损伤本构模型,示意图如图7所示. 图中,η1、η2、η3分别为衰减、稳态和加速阶段的蠕变速率,E1为蠕变阶段开始前的瞬时弹性模量,E2为衰减蠕变阶段的弹性模量.
图 7
图 7 改进Nishihara非线性黏弹塑性蠕变模型
Fig.7 Improved Nishihara nonlinear viscoelastic plastic creep model
当t
图 8
式中:
当t > ts且t > tn时,模型中的损伤变量开始发挥作用,此时模型中各元件的状态方程如下所示:
综上,根据 Boltzmann叠加原理,建立改进Nishihara非线性损伤蠕变模型的本构方程:
2.4. 改进Nishihara蠕变本构模型的三维形式
天然状态下的岩体基本处于三维应力状态下. 只单纯地建立岩体的一维蠕变本构方程无法满足实际需要,故将一维本构方程扩展到三维具有重要意义[22-25]. 将一维蠕变本构方程扩展到三维应满足如下假定. 1)材料的体应变为弹性变形,且与时间因素无关,即在加载瞬间完成. 2)球应力张量不会引起岩石蠕变,只有偏应力张量才能产生蠕变变形. 3)在蠕变过程中,泊松比ν 不随时间推移而变化. 在黏塑性变形中,仅通过屈服强度σs判断岩石的屈服是不正确的,岩石的屈服由屈服函数确定,变形特性与流动法则有关,因此岩石蠕变本构方程中黏塑性变形阶段应包括屈服函数f与塑性势函数g. 此外,简单地将一维应力σ换成三维应力状态的偏应力Sij不太合理.
根据弹塑性理论,将改进Nishihara模型一维蠕变本构方程扩展到三维,建立改进Nishihara模型的三维蠕变本构方程.
将应力σij分解为球应力
式中:δij为Kronecker函数,
根据弹性力学理论可知,三维状态下弹性体的应力-应变关系可以表示为
式中:K和G分别为弹性体的体积模量和切变模量,
式中:
综上所述,弹性体的三维本构关系可以表示为
由于球应力张量不会引起蠕变变形,黏弹性体的三维本构关系可以表示为
对于黏塑性体,应变的开启与应力阈值有关. 应力阈值函数fs与屈服函数f的确定方法由蠕变试验确定. 黏塑性体应变可以表示为
式中:
式中:m为试验常数,通常取1. [·]为越阶函数,则式(23)可以展开为
非线性黏性体的三维本构关系可以表示为
与改进Nishihara模型的一维本构方程进行类比,采用Boltzmann叠加原理,将上述元件的三维本构关系进行叠加,得到改进Nishihara模型本构方程的三维形式.
常规三轴压缩试验中有第二主应力σ2 = σ3,则式(26)中的一些参数可以转换为如下形式:
对于屈服函数,有
式中:J2为应力偏量的第二不变量.
将式(25)、(26)代入式(24),取岩石屈服函数的初始参考值f0 = 1,则得到改进Nishihara模型的轴向蠕变方程:
3. 模型参数辨识
3.1. 模型适用性的研究
最小二乘法具有参数辨识度精度高、方法简便的优点,因而成为蠕变本构模型参数辨识最常用的方法. Levenberg-Marquardt算法是基于最小二乘法提出的非线性优化算法,Origin分析软件将该算法集成于非线性拟合功能中. 利用Origin分析软件中的Levenberg-Marquardt算法,对改进Nishihara模型进行拟合及参数辨识. 当t<ts且t
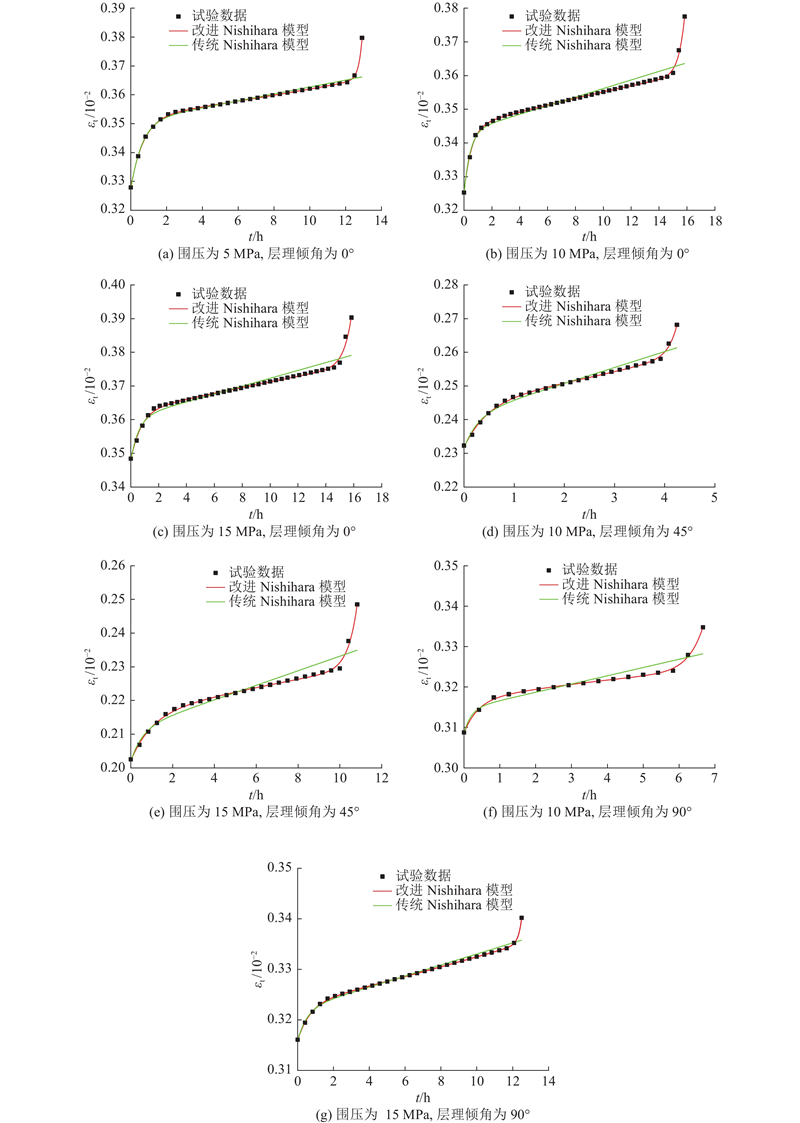
通过图9的拟合对比发现,改进Nishihara模型对蠕变曲线的拟合度较高,可以描述炭质板岩蠕变的三阶段,解决了传统Nishihara模型无法描述加速蠕变阶段的缺点,验证了改进Nishihara模型描述炭质板岩的蠕变规律的适用性.
图 9
图 9 传统和改进Nishihara蠕变模型的拟合曲线
Fig.9 Traditional and improved Nishihara creep model fitting curves
3.2. 参数辨识结果
表 2 0°层理倾角炭质板岩改进Nishihara蠕变模型参数
Tab.2
| p/MPa | Sij/MPa | E1/GPa | E2/GPa | η1/(GPa·h) | η2/(GPa·h) | η3/(GPa·h) | c | d | R2 |
| 5 | 12 | 20.03 | 149.57 | 206.07 | — | — | — | — | 0.9996 |
| 24 | 20.08 | 154.47 | 211.19 | — | — | — | — | 0.9966 | |
| 36 | 19.32 | 222.34 | 227.36 | 3580.58 | — | — | — | 0.9953 | |
| 48 | 18.75 | 253.63 | 311.70 | 11902.83 | — | — | — | 0.9971 | |
| 60 | 18.31 | 246.96 | 174.45 | 109.77 | 3.603 2×105 | 0.0023 | 5.03 | 0.9997 | |
| 10 | 13 | 21.25 | 188.53 | 186.02 | — | — | — | — | 0.9854 |
| 26 | 21.49 | 187.59 | 247.63 | — | — | — | — | 0.9909 | |
| 39 | 20.81 | 273.81 | 464.56 | 4284.29 | — | — | — | 0.9945 | |
| 52 | 20.36 | 340.45 | 226.54 | 16819.23 | — | — | — | 0.9997 | |
| 65 | 19.99 | 329.98 | 174.83 | 144.38 | 33541.08 | 0.0086 | 2.22 | 0.9985 | |
| 15 | 14 | 21.89 | 205.91 | 312.29 | — | — | — | — | 0.9955 |
| 28 | 22.41 | 209.95 | 329.29 | — | — | — | — | 0.9969 | |
| 42 | 22.31 | 264.51 | 661.23 | 12515.25 | — | — | — | 0.9987 | |
| 56 | 20.98 | 225.25 | 564.58 | 15635.21 | — | — | — | 0.9946 | |
| 70 | 20.12 | 482.04 | 356.82 | 144.70 | 31182.07 | 0.0037 | 1.74 | 0.9946 |
表 3 45°层理倾角炭质板岩改进Nishihara蠕变模型参数
Tab.3
| p/MPa | Sij/MPa | E1/GPa | E2/GPa | η1/(GPa·h) | η2/(GPa·h) | η3/(GPa·h) | c | d | R2 |
| 10 | 5 | 5.99 | 123.77 | 224.56 | — | — | — | — | 0.9987 |
| 10 | 7.63 | 83.12 | 176.43 | — | — | — | — | 0.9932 | |
| 15 | 8.29 | 201.24 | 135.85 | 1241.02 | — | — | — | 0.9996 | |
| 19 | 8.19 | 143.29 | 66.01 | 12.08 | 3182.85 | 0.011 | 5.67 | 0.9981 | |
| 15 | 6 | 7.05 | 96.64 | 117.56 | — | — | — | — | 0.9991 |
| 13 | 10.22 | 190.94 | 393.47 | — | — | — | — | 0.9973 | |
| 19 | 11.67 | 373.81 | 222.53 | 2517.73 | — | — | — | 0.9992 | |
| 25 | 12.37 | 183.29 | 186.14 | 55.31 | 3464.38 | 0.0095 | 2.22 | 0.9967 |
表 4 90°层理倾角炭质板岩改进Nishihara蠕变模型参数
Tab.4
| p/MPa | Sij/MPa | E1/GPa | E2/GPa | η1/(GPa·h) | η2/(GPa·h) | η3/(GPa·h) | c | d | R2 |
| 10 | 12 | 12.98 | 136.51 | 259.46 | — | — | — | — | 0.9968 |
| 23 | 14.46 | 155.12 | 201.05 | — | — | — | — | 0.9982 | |
| 35 | 15.08 | 202.90 | 254.32 | 4438.78 | — | — | — | 0.9959 | |
| 47 | 15.23 | 580.14 | 225.93 | 35.99 | 6679.86 | 0.0108 | 2.24 | 0.9981 | |
| 15 | 14 | 13.70 | 323.48 | 550.76 | — | — | — | — | 0.9947 |
| 27 | 15.87 | 276.99 | 159.38 | — | — | — | — | 0.9978 | |
| 41 | 16.82 | 367.70 | 507.97 | 5322.29 | — | — | — | 0.9993 | |
| 54 | 17.09 | 769.91 | 525.69 | 68.57 | 22744.76 | 0.00103 | 5.31 | 0.9997 |
3.3. 模型参数分析
图 10
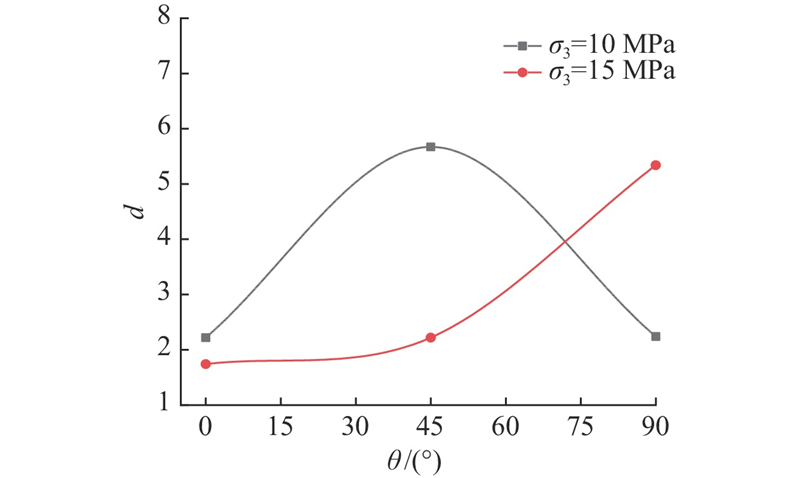
图 10 损伤参数d随层理倾角的变化规律
Fig.10 Change rule of damage parameter d with laminar inclination
图 11
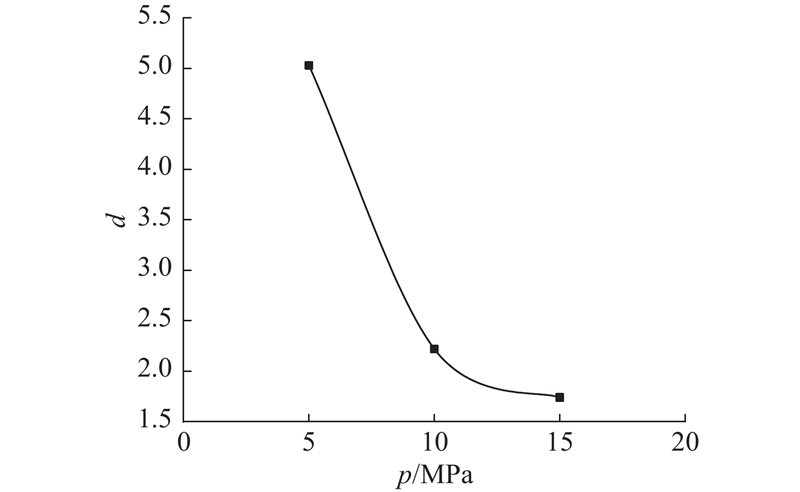
图 11 损伤参数d随围压的变化规律
Fig.11 Change rule of damage parameter d with peripheral pressure
图 12
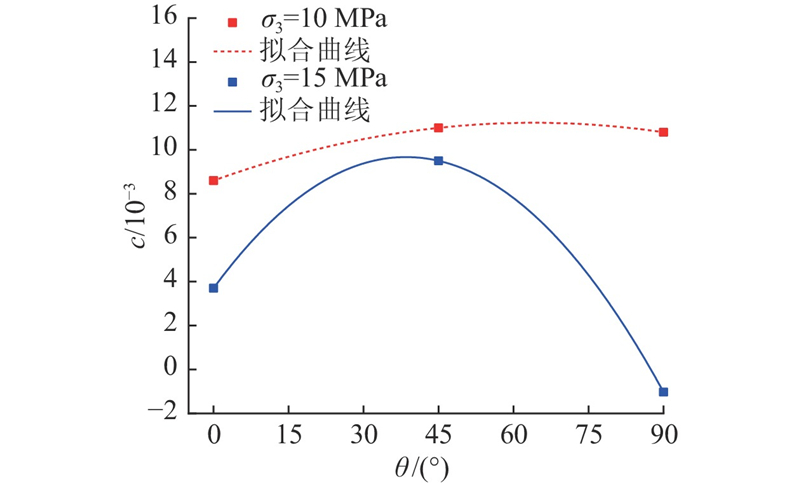
图 12 损伤参数c随层理倾角的变化规律
Fig.12 Change rule of damage parameter c with laminar inclination angle
图 13
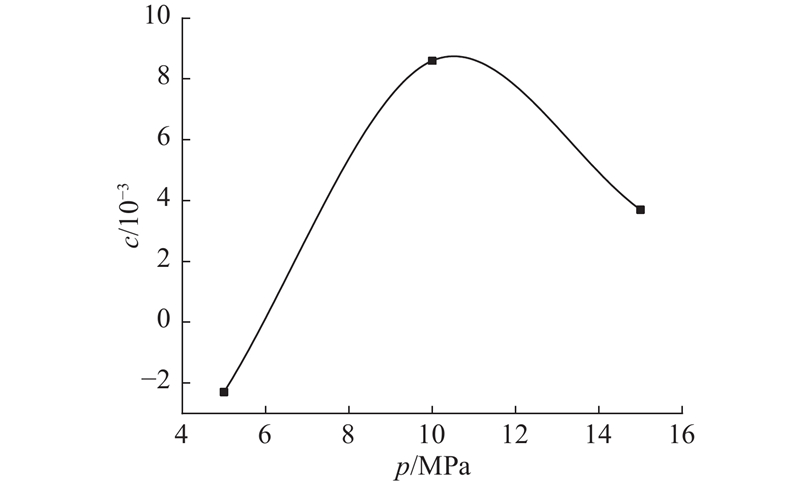
图 13 损伤参数c随围压的变化规律
Fig.13 Change rule of damage parameter c with perimeter pressurization
当围压为15 MPa时,c与θ的关系为
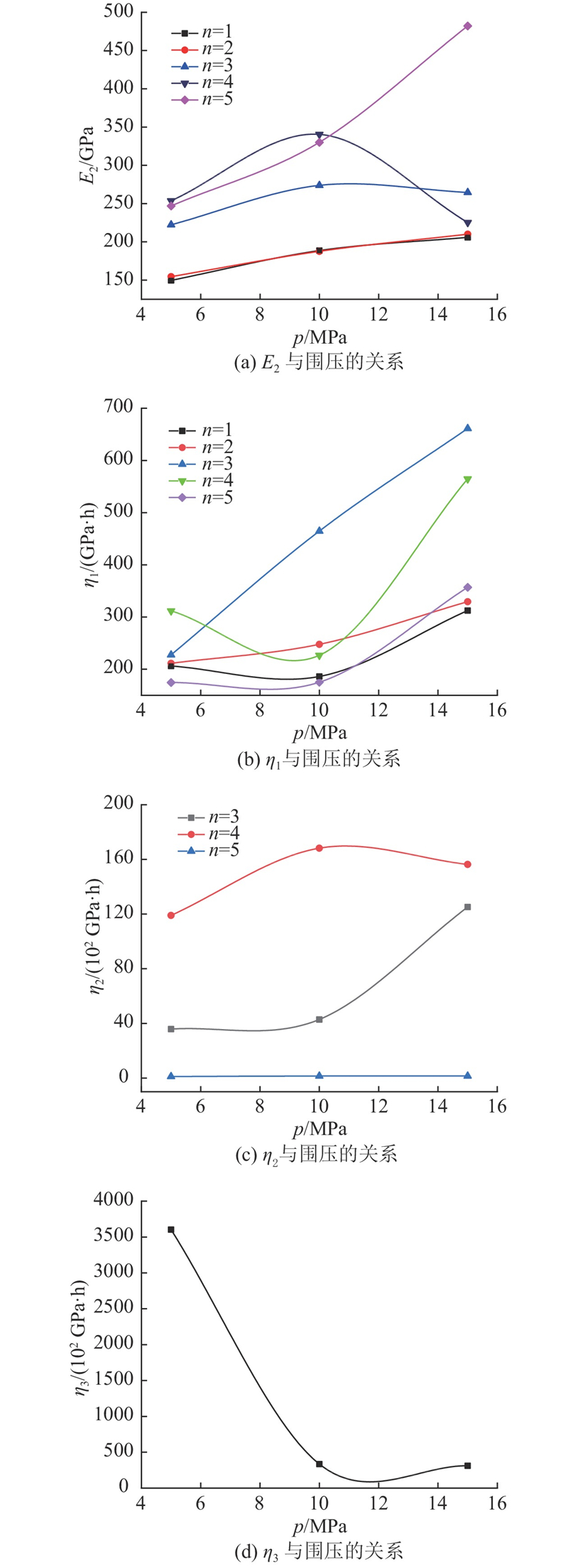
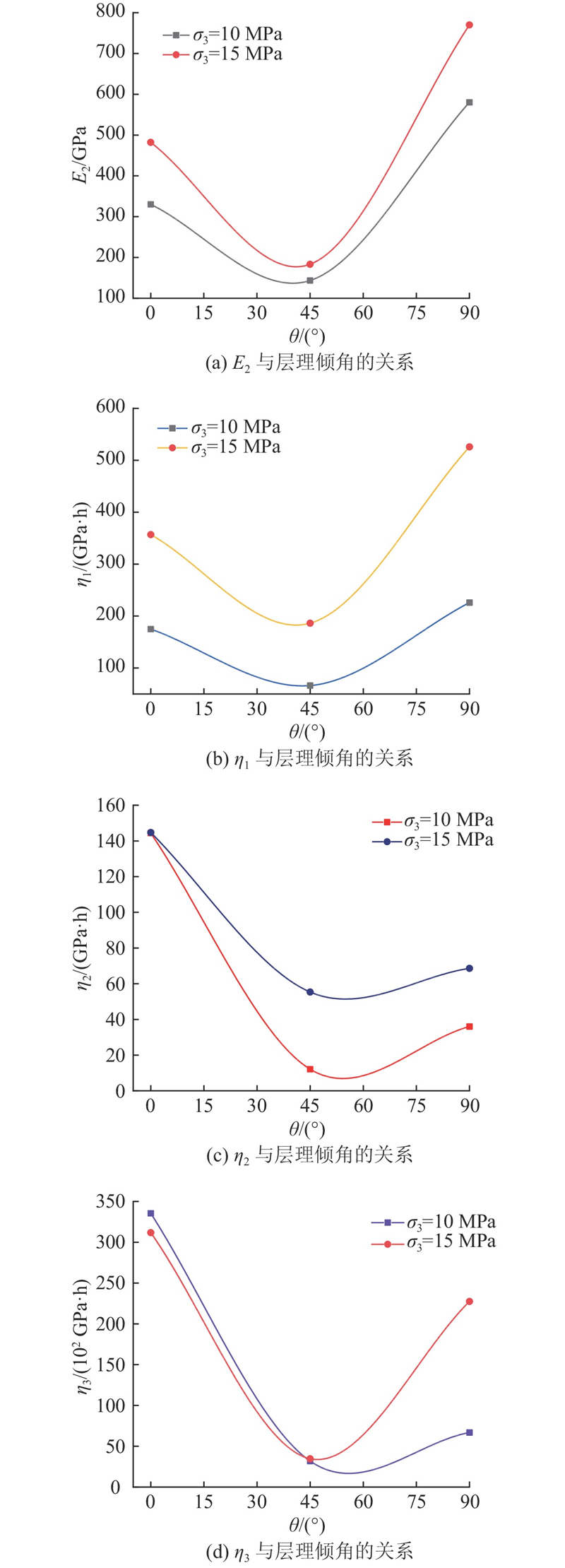
图14给出改进Nishihara模型的蠕变参数随围压的关系曲线. 图中,n为不同应力加载级次. 从图14(a)可以看出,不同应力水平下蠕变参数E2呈现随围压增大而增大的趋势,在第4级应力水平下,E2随围压增大呈现先增大后减小的趋势. E2越大,则衰减蠕变阶段产生的应变越小. 从图14(b)可以看出,不同应力水平下η1随围压呈逐渐增大的趋势,在第4级应力水平下η1随围压先减小后增大,η1越大,衰减蠕变阶段的蠕变速率越小. 从图14(c)可以看出,不同应力水平下η2随围压总体上呈逐渐增大的趋势,η2越大,稳态蠕变速率越小,由此可得不同应力水平下稳态蠕变速率随围压的增大而减小. 从图14(d)可知,η3随围压逐渐减小,而η3越大,加速蠕变阶段的蠕变速率越小,因此加速蠕变阶段的蠕变速率随围压逐渐增大.
图 14
图 14 改进Nishihara蠕变模型参数与围压的关系
Fig.14 Relationship between parameter of improved Nishihara creep model and confining pressure
为了方便研究,选取最后一级应力水平下的蠕变参数,探讨蠕变参数与层理倾角的关系. 从图15可以看出,不同围压下改进Nishihara模型的蠕变参数均随着层理倾角先减小后增大. E2在层理倾角为45°时取到最小值,在层理倾角为90°时取到最大值,各向异性比分别达到4.04与4.20,可以评价为高级各向异性. E2随层理倾角先减小后增大表征衰减蠕变阶段的弹性模量先减小后增大,则衰减蠕变阶段产生的应变先增大后减小. η1在层理倾角为45°时取到最小值,在层理倾角为90°时取到最大值,最大值与最小值的比值分别达到3.42与2.82,各向异性明显. η1随层理倾角先减小后增大,证明衰减蠕变阶段的蠕变速率减小速率随层理倾角先减小后增大. η2在层理倾角为45°时取到最小值,在层理倾角为0°时取到最大值,最大值与最小值的比值分别达到11.95与2.62,各向异性明显. η2随层理倾角先减小后增大,表示在应力达到或超过屈服应力后,稳态蠕变阶段的蠕变速率随层理倾角先增大后减小. η3在层理倾角为45°时取到最小值,在层理倾角为0°时取到最大值,最大值与最小值的比值分别达到10.54与9.0,各向异性明显. η3随层理倾角先减小后增大,表明加速蠕变阶段的蠕变速率随层理倾角先增大后减小.
图 15
图 15 改进Nishihara蠕变模型参数与层理倾角的关系
Fig.15 Relationship between parameter of improved Nishihara creep model and bedding dip angle
3.4. 加速蠕变阶段模型参数的敏感度分析
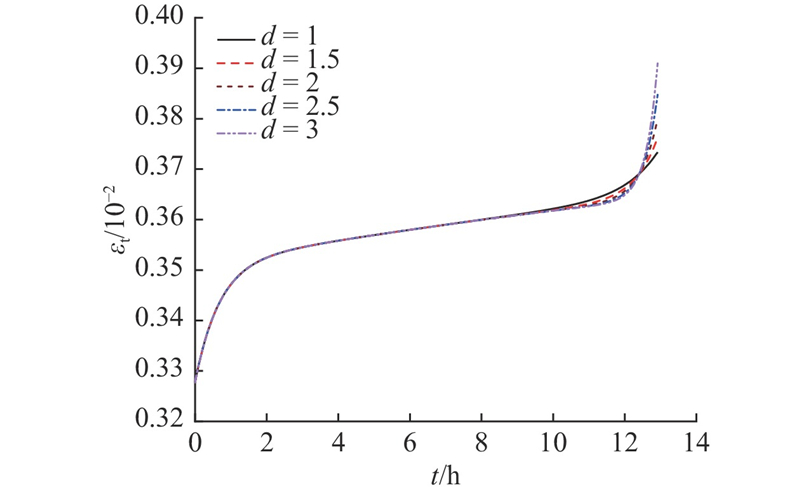
图16给出不同损伤参数d对模型加速蠕变阶段的影响规律. 可以看出,不同的d对加速蠕变阶段产生的蠕变量及加速蠕变时间有着明显的控制作用,d越大,加速蠕变阶段产生的蠕变量越多,加速蠕变持续时间越短. 不同的d对加速蠕变阶段的蠕变速率和蠕变速率增量有着明显的影响,d越大,则加速蠕变速率和加速蠕变速率增量越大. 从试验中试样的破坏方式角度分析可知,随着d的增大,试样从延性破坏发展为脆性破坏. 本文中d随围压先增大后减小,但总体上呈现减小的趋势,即随着围压的增大,炭质板岩更趋向于延性破坏.
图 16
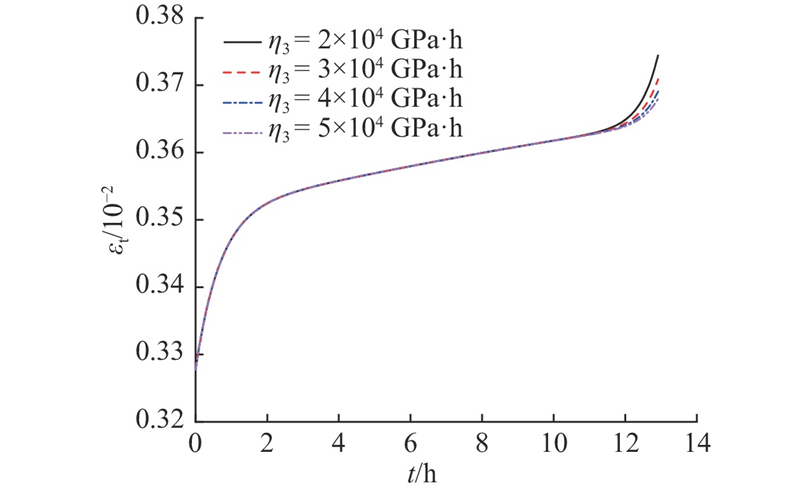
图17给出不同蠕变速率η3对模型加速蠕变阶段的影响规律. 可以看出,η3越大,加速蠕变阶段产生的蠕变量越少,η3对加速蠕变开启时间无明显影响. 不同的η3对加速蠕变阶段的蠕变速率和蠕变速率增量有着明显的影响,η3越大,则加速蠕变速率和加速蠕变速率增量越小.
图 17
4. 结 论
(1)炭质板岩的蠕变过程存在明显的阈值σs. 通过总结规律发现,σs均出现在第2、3级应力水平之间. 当应力小于σs时炭质板岩只发生衰减蠕变;当应力达到或大于σs时,开始发生稳态蠕变;当应力达到或超过破坏应力时,炭质板岩发生加速蠕变并发生蠕变破坏. 在蠕变过程中,层理倾角为0°的炭质板岩发生剪切破坏,45°层理倾角面上形成贯通破坏面,而90°层理倾角面上产生了剪切破坏面,呈现出剪切破坏形态.
(2)模型参数反演辨识结果表明,改进Nishihara模型能够较好地拟合各阶段的蠕变曲线,解决了传统Nishihara模型无法描述加速蠕变阶段的缺点,验证了改进Nishihara本构模型的正确性.
(3)基于参数辨识结果,探讨模型参数与围压和层理倾角的关系,得到损伤参数c与层理倾角的关系式. 归纳了损伤参数d与黏滞系数η3对加速蠕变阶段的敏感程度. d越大,则加速蠕变阶段产生的蠕变量越多,加速蠕变速率和增量越大;η3越大,则加速蠕变阶段产生的蠕变量越少,加速蠕变速率和增量越小,但η3对加速蠕变开启时间无明显影响.
参考文献
考虑互层状岩体接触状态的地下洞室围岩稳定分析
[J].
Stability analysis of underground cavern surrounding rock considering the contact state of interlayered rock body
[J].
Creep structure effect of layered rock mass based on acoustic emission characteristics
[J].
分级加载条件下岩石流变特性的试验研究
[J].
Experimental study of rock rheological properties under graded loading conditions
[J].
单轴压缩条件下四种岩石的蠕变和松弛试验研究
[J].
Experimental study on creep and relaxation of four rocks under uniaxial compression conditions
[J].
含软弱夹层的层状岩体流变力学特性试验
[J].
Test of rheological mechanical properties of layered rock mass with soft interbed
[J].
含软弱夹层炭质板岩单轴压缩力学行为模拟研究
[J].
Simulation study on uniaxial compressive mechanical behavior of carbonaceous slate with weak interbed
[J].
基于幂函数的边坡岩体泥质夹层长期强度直剪蠕变试验研究
[J].
Experimental study on long-term strength direct shear creep of argillaceous interlayer of slope rock mass based on power function
[J].
Study on creep characteristics and constitutive relation of fractured rock mass
[J].
加锚节理岩体剪切蠕变特性及其本构模型分析
[J].
Shear creep characteristics of anchored joint rock mass and its constitutive model analysis
[J].
含软弱结构面岩体蠕变力学模型
[J].
Creep mechanical model of rock mass with soft structural surface
[J].
Long-term creep tests and viscoelastic constitutive modeling of lower paleozoic shales from the baltic basin, N poland
[J].DOI:10.1016/j.ijrmms.2018.10.013 [本文引用: 1]
A creep damage constitutive model for a rock mass with nonpersistent joints under uniaxial compression
[J].
Analytical model of layered rock considering its time-dependent behaviour
[J].DOI:10.1007/s00603-021-02421-2 [本文引用: 1]
冻土三轴蠕变特性试验研究及平面冻土墙厚度的确定
[J].
Experimental study on triaxial creep characteristics of frozen soil and determination of thickness of flat frozen soil wall
[J].
含不同层理倾角黄砂岩损伤破裂机理研究
[J].
Study on the damage and rupture mechanism of yellow sandstone with different laminar dip angles
[J].
基于改进Bingham模型的软岩参数非定常三维非线性黏弹塑性蠕变本构研究
[J].
Research on unsteady three-dimensional nonlinear viscoelastic plastic creep constitutive behavior of soft rock parameters based on improved Bingham model
[J].
Shear creep tests and creep constitutive model of marble with structural plane
[J].
考虑硬化和损伤效应的盐岩蠕变本构模型研究
[J].
Research on creep constitutive model of salt rock considering hardening and damage effects
[J].
橄榄岩蠕变特性及本构模型研究
[J].
Study on creep characteristics and constitutive models of peridotite
[J].
岩石黏弹塑性损伤蠕变模型研究
[J].
Research on creep model of rock viscoelastic plastic damage
[J].
A nonlinear creep damage model for brittle rocks based on time-dependent damage
[J].