离心泵在运行过程中,由于叶轮前、后盖板受力不平衡,会产生与轴线方向平行的力,称为轴向力,轴向力与泵运行的稳定性和轴承寿命有着直接的联系. 在实际运用中,常见的平衡叶轮轴向力方法包括平衡孔、背叶片、平衡鼓及平衡盘等结构[1-9]. 近年来,国内外研究者提出新的平衡方法,即不带轴向定位的浮动叶轮与平衡孔、密封环相结合,实现轴向力的自动平衡. 魏清顺等[10]设计带有平衡孔和后密封环的浮动叶轮结构,研究轴向力的变化规律,达到最大限度平衡轴向力的目的. 刘在伦等[11]研究浮动叶轮不同轴向位置对泵水力性能和平衡腔液体压力的影响,发现浮动叶轮轴向位移可以调节平衡腔液体压力,改变轴向力特性. Jin等[12]采用数学建模的方法,建立浮动叶轮轴向自平衡运动微分方程,采用动网格技术计算叶轮达到稳定状态所需的时间,证实了浮动叶轮设计的合理性. 从现有的研究来看,相对缺少对浮动叶轮自动平衡轴向力的理论解释与实际运用,因此有必要进一步研究浮动叶轮轴向力平衡作用的机理和影响因素,提高浮动叶轮轴向力平衡的可靠性.
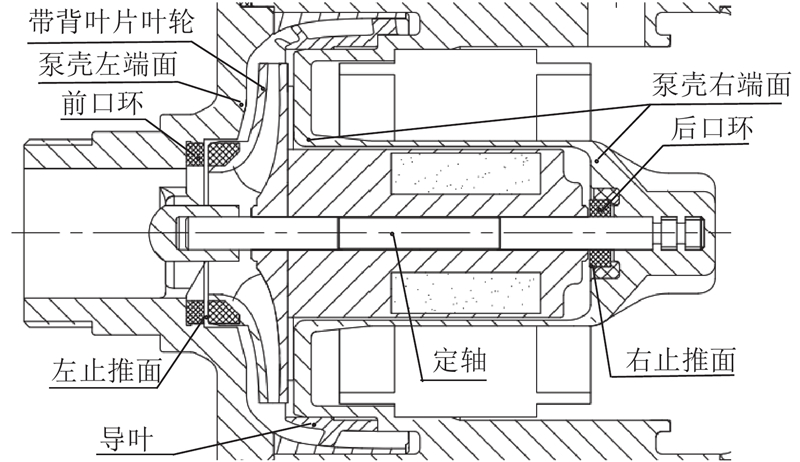
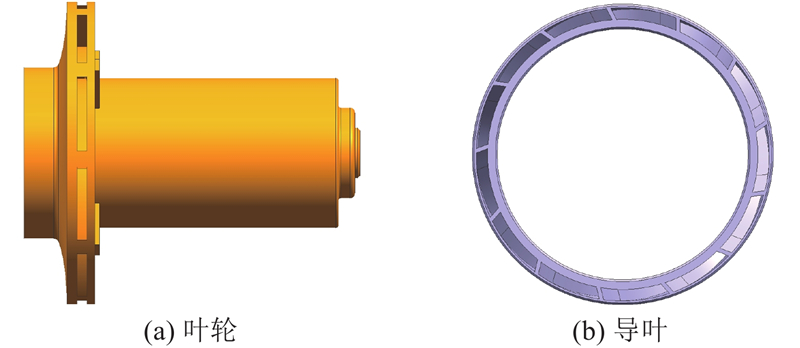
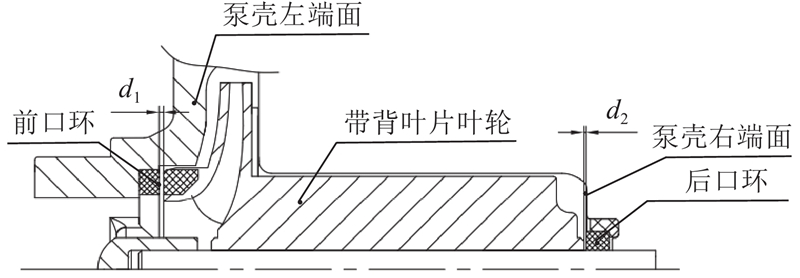
1. 浮动叶轮的基本结构与原理
图 1
图 2
上述装置的轴向力平衡原理可以描述如下:当屏蔽泵开始工作时,背叶片的存在可以平衡掉大部分叶轮轴向力,将其控制在较低水平. 若残余轴向力方向向左,在轴向力作用下,叶轮开始左移,随着叶轮前口环轴向间隙减小,泄漏量开始减小,平衡左腔逐渐形成局部高压,叶轮前盖板受到的向右的轴向力
2. 计算模型与研究内容
2.1. 泵的主要参数
图 3
表 1 泵的主要参数
Tab.1
| 参数 | 数值 |
| 比转速 | 61 |
| 叶轮入口直径 | 22 |
| 叶轮出口直径 | 60 |
| 叶轮出口宽度 | 2 |
| 叶片数 叶片包角 叶片厚度 | 5+5 120 1 |
| 导叶数 | 13 |
| 背叶片数 | 4 |
| 背叶片高度 | 13 |
| 背叶片宽度 | 3 |
| 背叶片厚度 | 1.65 |
| 叶轮轴向浮动范围 | 0.8 |
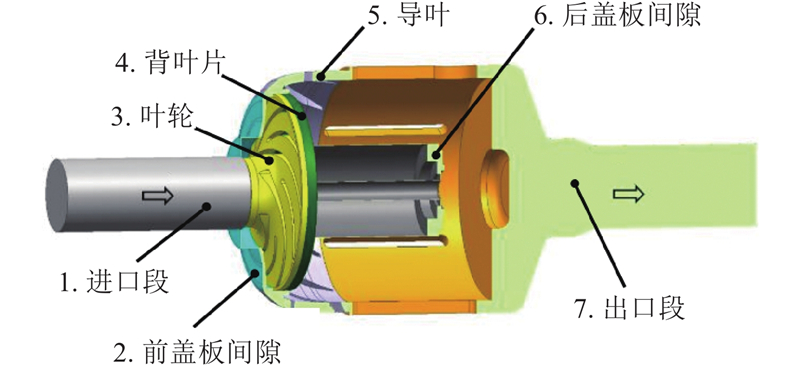
2.2. 计算域网格的划分
图 4
表 2 网格划分情况
Tab.2
| 计算域 | N/ | 网格类型 |
| 进口段 | 0.33 | 非结构化 |
| 前盖板间隙 | 1.40 | 结构化 |
| 叶轮 | 1.10 | 结构化 |
| 背叶片 导叶 | 1.74 1.91 | 非结构化 结构化 |
| 后盖板间隙 | 1.37 | 结构化 |
| 出口段 | 0.96 | 非结构化 |
计算域的网格单元总数为
图 5
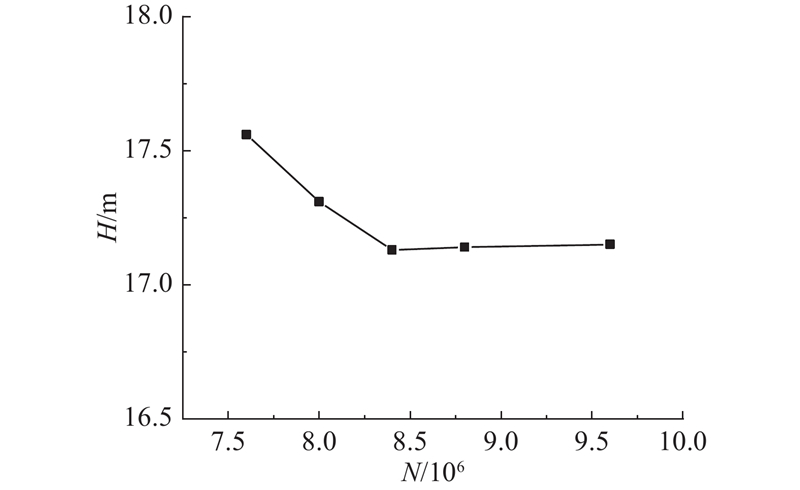
2.3. 网格无关性分析
为了验证网格无关性,确定基准网格,网格单元总数约为
图 6
2.4. 数值模拟方法的验证
图 7
表 3 测量仪表的量程及精度
Tab.3
| 项目 | 精度 | 量程 |
| 进口压力表 | ||
| 出口压力表 | ||
| 流量计 | ||
| 转速 | ||
| 电压 | ||
| 电流 |
在商用计算流体动力学软件Fluent中进行数值模拟,湍流模型选择
由于试验中确定转子轴向位置的难度较大,以额定流量下转子轴向位置的仿真结果作为试验参考,即取前口环轴向间距
图 8
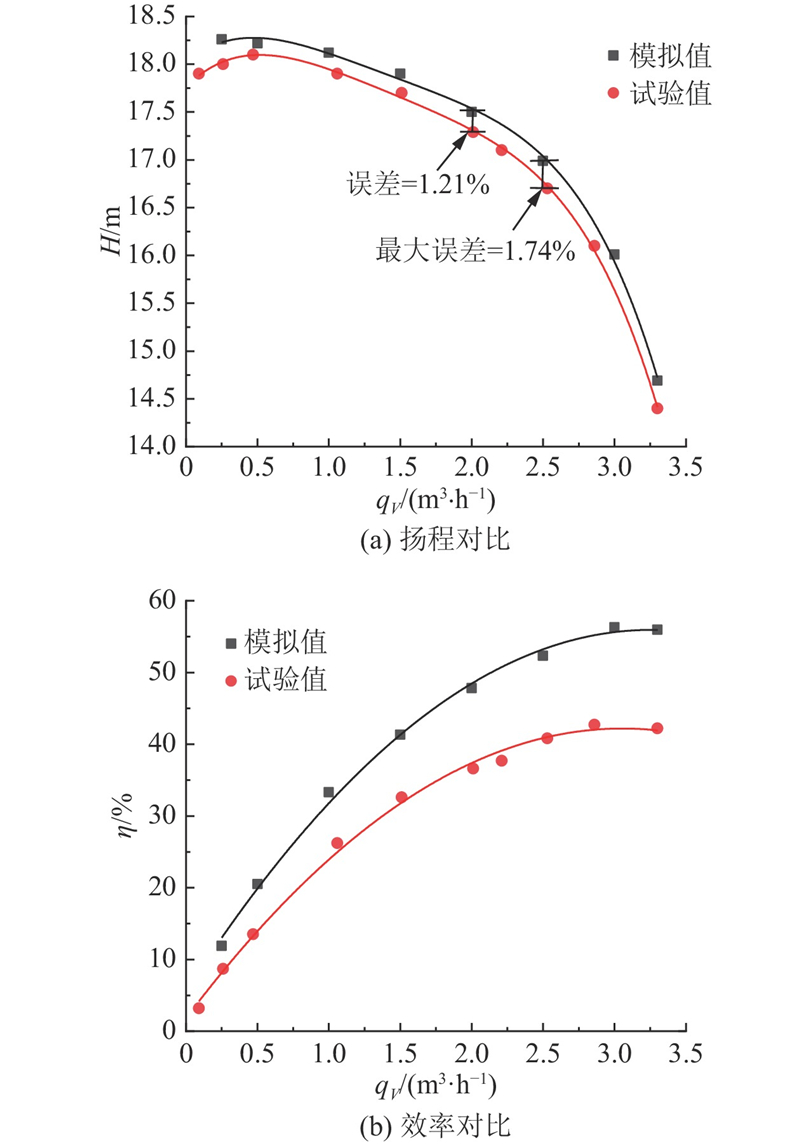
图 8 水力性能模拟与试验对比曲线
Fig.8 Hydraulic performance simulation and test comparison curve
从数值模拟与试验结果来看,全流量下模型泵的外特性曲线趋势基本一致,其中扬程曲线模拟值和试验值的相对误差较小,设计工况下的相对误差为1.21%,最大相对误差为1.74%. 因为电机效率和电机控制器效率损耗未计入,效率曲线的试验值低于模拟值. 考虑到本文主要关注浮动叶轮工作时所受的轴向力情况,主要通过流场数值模拟的压力场积分得到,数值模拟的扬程精度较高,可以满足对轴向力模拟的精度要求.
2.5. 研究内容
如图9所示为叶轮轴向相对位置的示意图. 图中,
图 9
图 9 叶轮轴向相对位置的示意图
Fig.9 Schematic diagram of axial relative position of impeller
3. 数值计算结果及分析
3.1. 叶轮轴向位置对泵性能及轴向力的影响
如图10所示为前口环泄漏质量流量qm与叶轮轴向位置的关系曲线. 当
图 10
图 10 前口环泄露质量流量与叶轮轴向位置的关系曲线
Fig.10 Curve of relationship between leakage of front ring and axial position of impeller
如图11所示为泵水力性能参数与叶轮轴向位置的关系曲线. 当
图 11
图 11 泵水力性能参数与叶轮轴向位置的关系曲线
Fig.11 Relationship curve of pump hydraulic performance parameter and impeller axial position
分析上述结果可知,在叶轮逐渐左移的过程中,随着
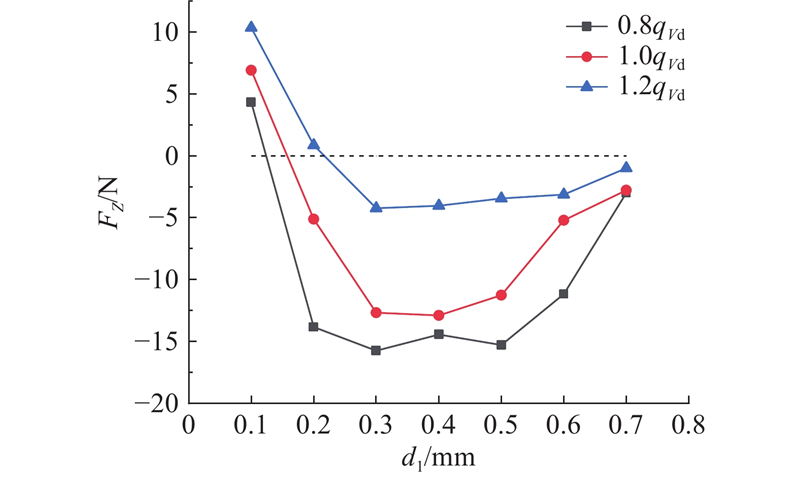
如图12所示为叶轮所受轴向力与轴向位置的关系曲线,其中轴向力为负表示方向指向泵入口,轴向力为正表示方向指向泵出口. 可知,背叶片的存在将叶轮轴向力控制在较低水平(不超过15 N),避免因轴向力过大损坏泵结构,为叶轮实现动态平衡奠定基础. 当流量从
图 12
图 12 叶轮轴向合力与轴向位置关系的曲线
Fig.12 Curve of relationship between axial force and axial position of impeller
3.2. 叶轮各部分轴向力的分布
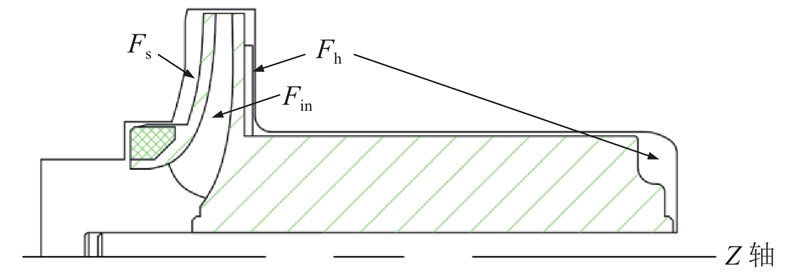
如图13所示,可以将离心泵叶轮所受的轴向力分为3部分,分别来自叶轮内部流道
图 13
图 13 叶轮各部分轴向力分布表面
Fig.13 Axial force distribution surface of each part of impeller
如图14所示为不同工况下的轴向力分量,负值表示方向指向泵入口. 在不同流量下,在叶轮轴向浮动范围内,来自叶轮内部流道的轴向力分量
图 14
图 14 不同工况下的叶轮轴向力分量
Fig.14 Axial force component of impeller under different working condition
整体来看,来自叶轮内部流道的轴向力分量占比较小,且相对稳定,所以前后盖板平衡腔内的压力变化对整体轴向力平衡起着决定性作用. 当
3.3. 叶轮前后盖板间隙的压力分布
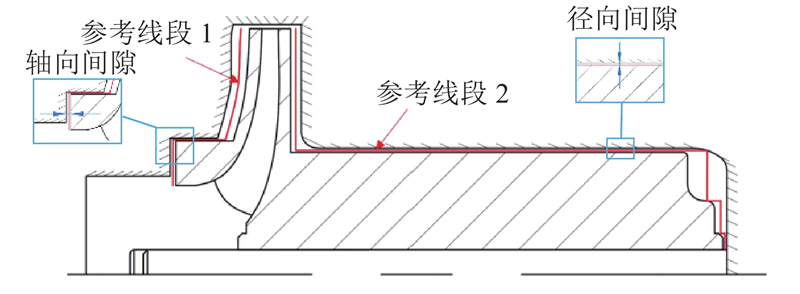
为了探究叶轮轴向位置改变后间隙内压力分布的变化规律,如图15所示,设置了参考线段1和参考线段2. 参考线段1位于前盖板间隙内,它位于前腔体轴向中心截面处,从叶轮出口到叶轮入口. 参考线段2位于后盖板间隙内,它位于后腔体轴向中心截面处,从叶轮出口到轮縠. 其中,前后盖板径向间隙均取0.2 mm.
图 15
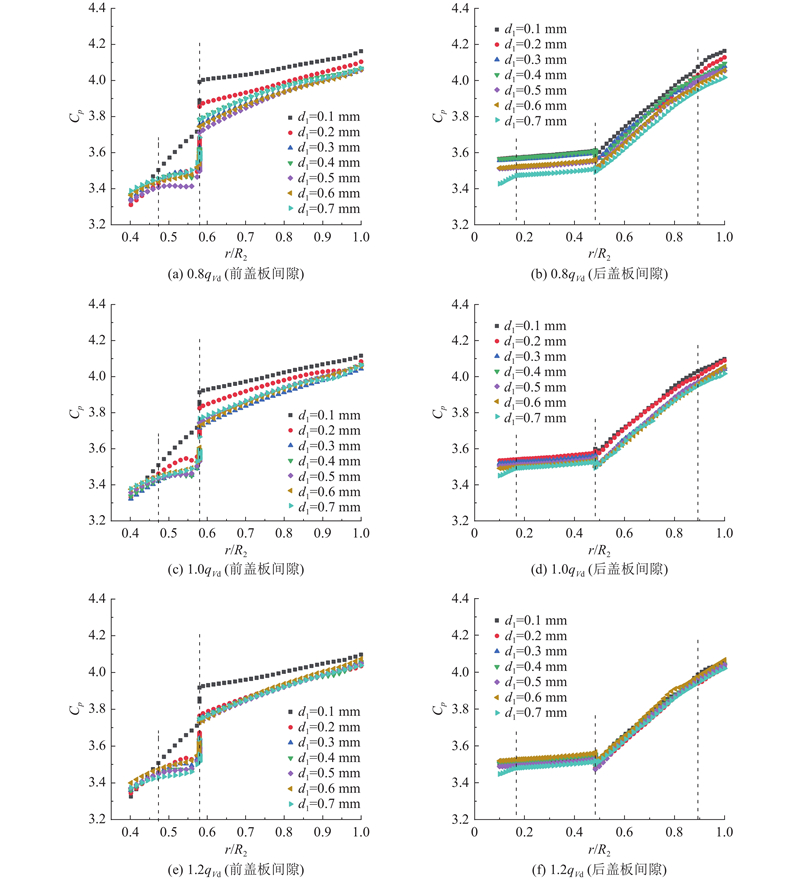
如图16所示为不同工况下前后盖板间隙的静压分布图. 图中,
图 16
图 16 不同工况下的前、后盖板间隙静压分布
Fig.16 Static pressure distribution of gap between front and rear cover plate under different working condition
对于后盖板间隙,随着半径的减小,静压变化可以分为3个阶段,用虚线分隔. 第1阶段为
4. 结 论
(1)当叶轮向入口方向移动时,qm减小,扬程增大,效率也增大. 在设计工况下,
(2)通过添加背叶片可以平衡大部分轴向力,将轴向力控制在较低水平(不超过15 N),同时实现叶轮在轴向浮动范围内靠近泵入口时的轴向力为正,方向指向泵出口,远离泵入口时轴向力为负,方向指向泵入口. 这种轴向力变化趋势可以使叶轮在工作时始终处于轴向浮动状态,并在轴向力合力为零的平衡点附近实现动态平衡.
(3)来自叶轮内部流道的轴向力占比不超过8%且相对稳定,轴向力平衡主要取决于来自前、后盖板间隙内的压力变化. 当
参考文献
多级离心泵轴向力平衡装置的设计与分析
[J].DOI:10.3969/j.issn.1002-6819.2010.08.018 [本文引用: 1]
Design and analysis of axial force balance device for multi-stage centrifugal pumps
[J].DOI:10.3969/j.issn.1002-6819.2010.08.018 [本文引用: 1]
平衡孔位置对离心泵轴向力影响的数值模拟研究
[J].DOI:10.3969/j.issn.1008-0813.2021.10.003
Numerical simulation study on the effect of balance hole position on axial force of centrifugal pumps
[J].DOI:10.3969/j.issn.1008-0813.2021.10.003
后密封环直径对离心泵轴向力特性的影响
[J].
The effect of rear sealing ring diameter on the axial force characteristics of centrifugal pumps
[J].
多级泵平衡盘动态平衡的理论研究
[J].DOI:10.3969/j.issn.1005-0329.2012.09.008
Theoretical study on dynamic equilibrium of multistage pump balance disc
[J].DOI:10.3969/j.issn.1005-0329.2012.09.008
Numerical investigation of back vane design and its impact on pump performance
[J].
叶轮背叶片对离心泵轴向力影响的试验及分析
[J].
Experimental and analytical study on the influence of impeller back blades on axial force of centrifugal pumps
[J].
An experimental study on influence of wearing seal groove shape to performance of the pump
[J].
Effect of impeller reflux balance holes on pressure and axial force of centrifugal pump
[J].
叶轮背叶片与盖板的间隙对平衡轴向力的影响
[J].DOI:10.3969/j.issn.1001-3997.2013.12.068 [本文引用: 1]
The effect of the clearance between the impeller back blade and the cover plate on the balanced axial force
[J].DOI:10.3969/j.issn.1001-3997.2013.12.068 [本文引用: 1]
基于CFD的离心泵浮动叶轮平衡腔压力数值分析与验证
[J].
Numerical analysis and verification of balance chamber pressure of floating impeller in centrifugal pump based on CFD
[J].
浮动叶轮轴向位移量对泵水力性能的影响
[J].DOI:10.3969/j.issn.1673-5196.2015.02.011 [本文引用: 1]
The effect of axial displacement of floating impeller on pump hydraulic performance
[J].DOI:10.3969/j.issn.1673-5196.2015.02.011 [本文引用: 1]
Stability of the axial-auto-balanced impeller of centrifugal pump
[J].
Reduction of the axial force of water pump using CFD
[J].DOI:10.7467/KSAE.2012.20.3.083
Coupling CFD-DEM with dynamic meshing: a new approach for fluid-structure interaction in particle-fluid flows
[J].