曲面屋盖由于其独特的轮廓线深受建筑学家的青睐,例如中国古代建筑多采用凹曲面屋盖,欧洲国家多采用凸曲面屋盖[1]. 凹曲面屋盖逐渐应用于大跨空间结构,例如京张高铁清河站主站房、山西潇河国际会展中心北展厅、贵州威宁体育馆、玉环博物馆等. 风荷载是曲面屋盖大跨空间结构的主要设计荷载. 国内外学者对典型凸曲面屋盖(球形、柱面、拱形等)的抗风设计开展了系列研究,明确了典型凸曲面屋盖的风荷载特性[2-5]. 相比凸曲面屋盖,凹曲面屋盖风荷载特性的研究较少. 高亮等[6]基于风洞试验,开展西安曲江国际会议中心波浪形凹曲面屋盖结构的风压分布特性研究,发现波浪线形凹面屋盖除屋顶顶部区域外,其余均为负压. 基于风洞试验或数值模拟,在研究了屋盖由两片高斯叶状凹曲面和中间隆起的球壳组成的贵州威宁奥体中心体育馆、具有单凹曲面屋盖的青海果洛机场航站楼、凹形连续坡屋面的石家庄国际会展中心D展厅的风荷载特性后,桑冲等[7-9]发现,在不同风向角下,凹曲面屋盖的风压均以负压为主,风向角对屋盖风压系数分布规律有较大的影响. 马文勇等[10]基于风洞试验,研究了某二次凹面结构在不同风速、不同风场类型下的风荷载特性,结果表明来流风速对结构表面风荷载特性的影响不大,紊流度的影响不可忽略. 依据现有研究,不同外形凹曲面屋盖的风压均以负压为主,风荷载分布规律较为复杂,桑冲等[7-10]探讨了风向角、风速、风场等因素对凹曲面屋盖风荷载特性的影响,但对多跨联排凹曲面屋盖的研究鲜见. 现有研究多以实际工程为背景,研究对象的外形独特,研究结果不具有普适性.
本研究以典型垂跨比为1/8的凹曲面屋盖为对象[14],基于单跨、双跨、三跨屋盖的风洞测压试验,探讨联排数及风向角对屋盖升力系数、平均风压系数及极值风压系数分布规律的影响,明确联排凹曲面屋盖的风荷载分布特性,给出各屋盖平均风压系数与极值风压系数的分区值.
1. 风洞试验
1.1. 试验模型
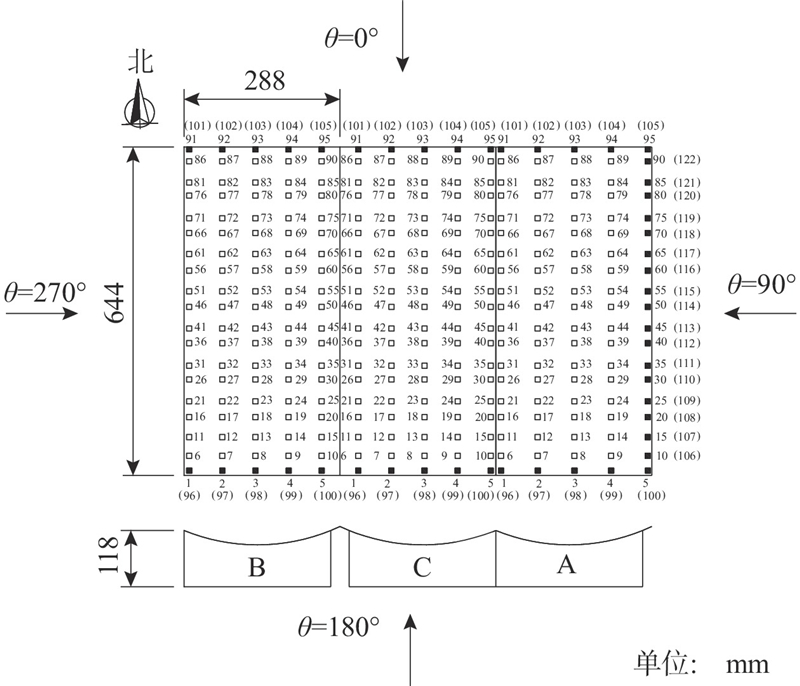
单屋盖的足尺尺寸如下:长161 m、宽72 m、最高点处高29.5 m,最低点处高20.5 m. 本试验模型属于有尖角的钝体,忽略雷诺数效应[15-17]. 考虑到阻塞率,取试验模型的几何缩尺比为1/250,对应单屋盖长0.644 m、宽0.288 m、最高点处高0.118 m,最低点处高0.082 m. 试验模型主体采用ABS板材制成,满足刚性模型的要求. 试验工况如表1所示. R2工况:左侧的边缘屋盖为B屋盖,右侧的边缘屋盖为C屋盖. R3工况:左侧的边缘屋盖为B屋盖,中间屋盖为C屋盖,右侧的边缘屋盖为A屋盖. 根据试验要求对各屋盖进行测点布置,每个测点通过PVC管与电子压力扫描阀相连,获得风压时程. A屋盖总测点为122个,其中上表面95个,编号为A1~A95;下表面27个,编号为 A96~A122. B屋盖总测点为105个,其中上表面95个,编号为B1~B95;下表面10个,编号为 B96~B105. C屋盖总测点为105个,其中上表面95个,编号为 C1~C95;下表面10个,编号为 C96~C105. 各屋盖测点布置、编号及风向角如图1所示,模型的局部挑檐部分采用上下表面测点布置方式(图中标记为实心方块),括号内的编号对应下表面测点,试验风向角θ沿顺时针方向增加.
表 1 风洞试验工况及测点
Tab.1
| 工况 | 屋盖形式 | 联排数 | 测点数 |
| R1 | A | 单跨 | 122 |
| R2 | B-C | 双跨 | 210 |
| R3 | B-C-A | 三跨 | 332 |
图 1
图 1 三跨屋盖测点布置及风向角
Fig.1 Testing points arrangement of three-span roofs and wind direction angle
1.2. 试验装置
测压风洞试验在交通运输部天津水运工程科学研究院的TKS-1大气边界层风洞进行. 该风洞为水平直流吹出式单试验段风洞,风洞试验段长15 m、宽4.4 m、高2.5 m,试验段设计空风洞最大风速为30 m/s. 试验模型安装固定于风洞试验段的木质转盘上,屋盖于风洞的安装如图2所示. 木质转盘实现不同风向角的调整,风向角见图1. 测试时,在模型上游屋盖高度0.12 m处设置风速参考点,以眼镜蛇三维脉动风速测量仪测量的风速作为风压系数的参考风速. 试验时,参考点平均风速设置为10 m/s,风向角为0°~360°,每组工况计36个风向角,风向角间隔为10°. 计算得到最不利工况对应阻塞率为0.9 %,满足不超过5 %的要求.
图 2
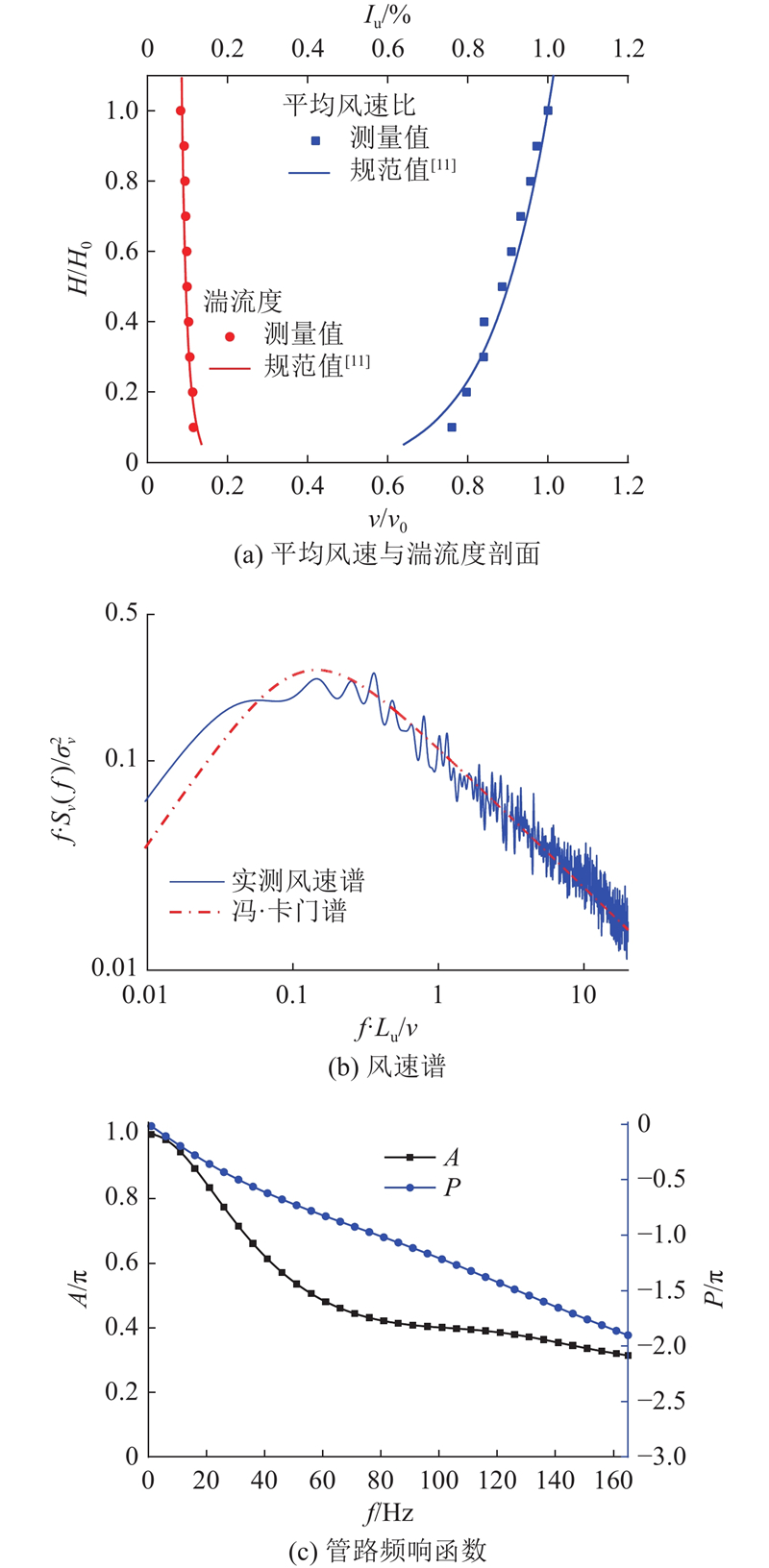
通过在风洞入口处设置尖劈和粗糙元,模拟文献[11]的B类地貌(地面粗糙度指数α=0.15). 未放置模型时,模拟测试得到的风剖面、湍流度剖面如图3(a)所示,其中H、H0、v、v0、Iu分别为试验高度、参考高度、试验高度处风速、参考点风速及湍流度. 观察发现,风洞试验测得的平均风速比、湍流度与规范值整体吻合,即风洞模拟地貌与规范地貌整体吻合. 本研究的缩尺模型高约0.1 m,在0.1 m高度处,平均风速比测量值略大于规范计算值. 针对凹面外形的大跨屋盖结构的不同风速风洞测压试验结果表明,来流风速不影响平均风压系数及其分布规律[10],因此本实验风洞风场所得缩尺模型的无量纲风压系数满足精度要求. 如图3(b)所示为屋顶高度处风速谱曲线,遵循冯·卡门谱,其中f、Sv(f)、σv、Lu分别为频率、风速功率谱、风速标准差、积分尺度. 测压管长为1.2 m,通过管道校准试验[18]修正测压管路,得到管路的频响函数如图3(c)所示,其中A、P、f分别为幅值、相位、频率. 采用PSI压力扫描阀对测点进行同步采集,各风向单个测点的样本总长度为19 800,采样频率为330 Hz. 如表2所示为屋盖模型与屋盖原型的风洞试验参数,其中屋盖模型的采样时长为60 s,根据斯托罗哈相似准则换算得到的屋盖原型实际采样时长为83.9 min.
图 3
表 2 风洞试验缩尺比
Tab.2
| 项目 | 尺度/m | 风速/(m·s−1) | 时间/min |
| 模型尺度 | 1 | 10.0 | 1.0 |
| 原型尺度 | 250 | 29.8 | 83.9 |
2. 升力系数
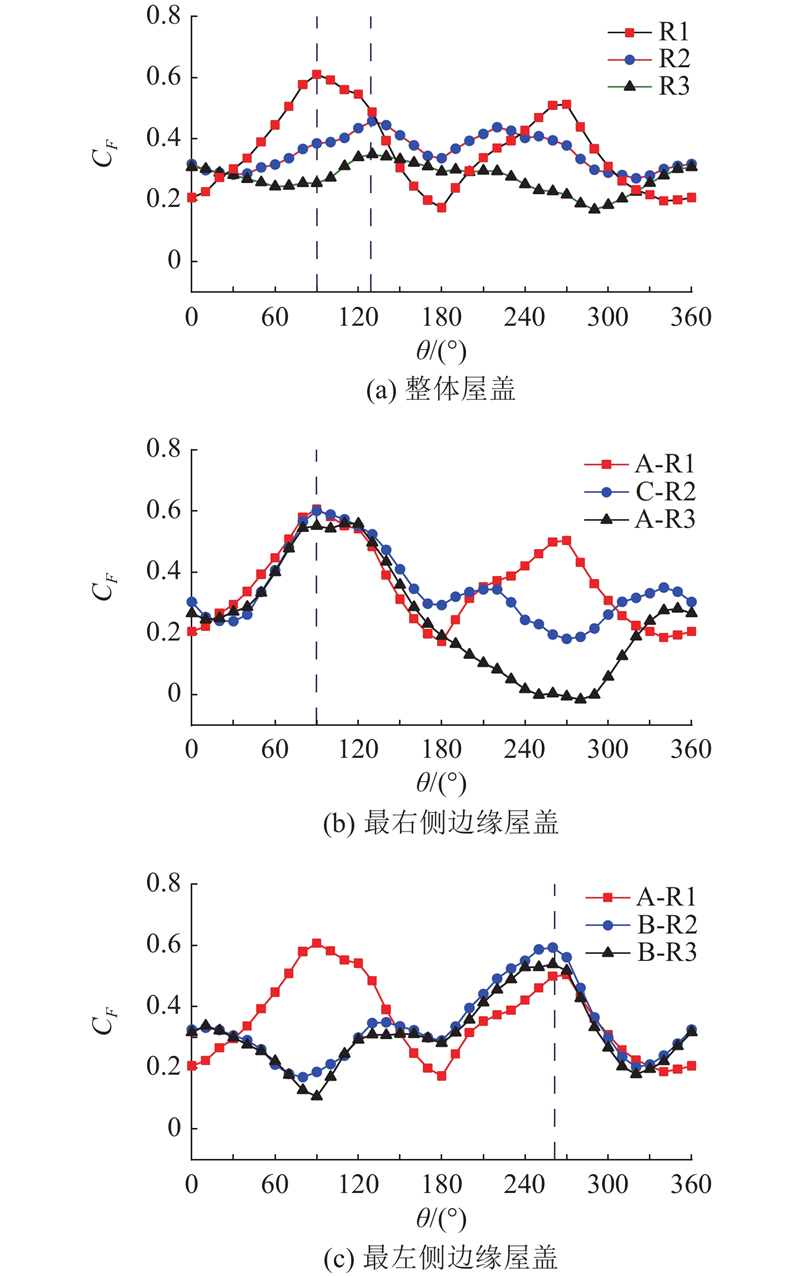
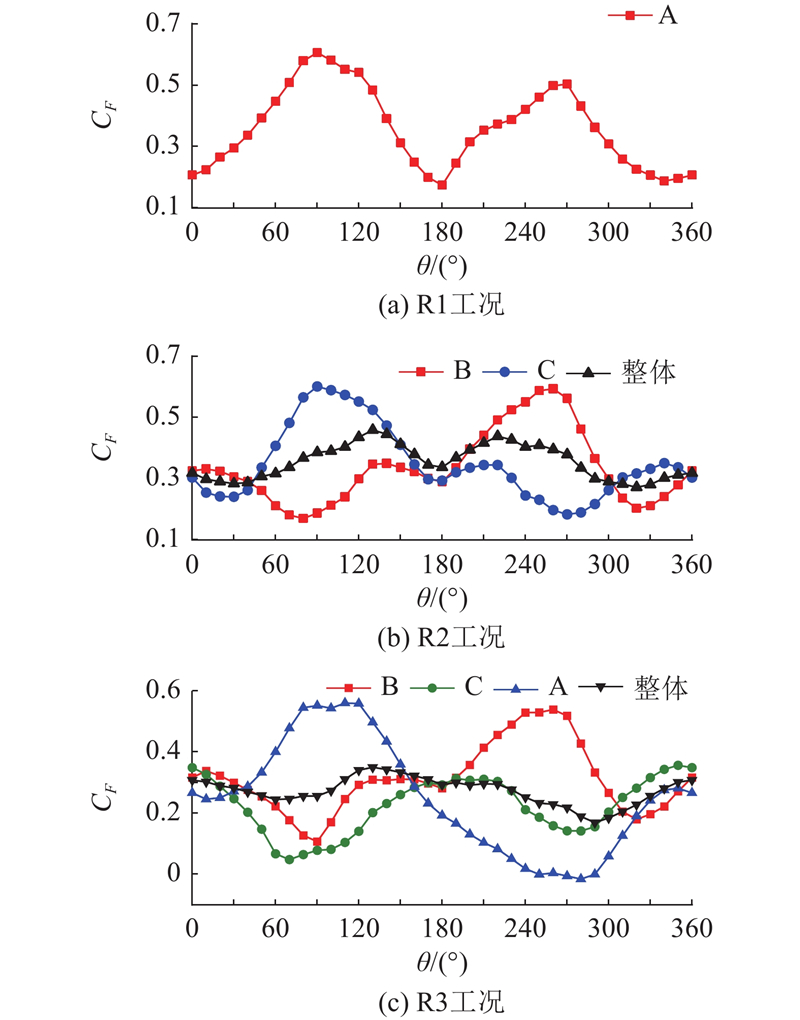
基于测压数据,计算得到屋盖的升力系数CF[4]. 绘制各工况下屋盖整体及边缘屋盖升力系数随风向角的变化如图4所示. 1)图4(a)中,R1的屋盖升力系数波动最大,随着屋盖联排数的增加,屋盖整体升力系数逐渐降低. R1工况的最不利风向角为横风向,对应的风向角为90°或270°;R2工况和R3工况的最不利风向角为斜风向,对应的风向角为130°或220°. 整体而言,不同工况的升力系数关于竖直轴(风向角为180°)对称,这与结构的对称性对应,升力系数不完全对称性的误差归因于边缘局部挑檐的影响. 以风向角为0°~180°进行分析, R1工况的整体升力系数随着风向角的增加表现出先增加后减小的变化趋势,且对称于90°风向角;但R2工况和R3工况的整体升力系数都表现出先减小后增加再减小的变化趋势. 2)由图4(b)观察发现,当来流直接作用右侧屋盖(θ=0°~180°)时,各工况下最右侧边缘屋盖的升力系数基本一致,且最不利风向角均为90°. 在θ=180°~360°作用下,由于迎风屋盖的干扰, R2工况和R3工况下最右侧边缘屋盖的升力系数小于R1工况的升力系数. 3)由图4(c)观察发现,在θ=0°~180°下,最左侧边缘屋盖升力系数类似于最右侧边缘屋盖在θ=180°~360°下的变化规律. 在θ=180°~360°下,各工况下最左侧边缘屋盖的升力系数基本一致,且最不利风向角均为270°. 不同于R1工况,边缘屋盖的升力系数在R2工况和R3工况下呈反对称分布.
图 4
图 5
3. 平均风压系数
3.1. 平均风压系数
基于测压数据,计算得到各测点的平均风压系数[4],绘制相应的平均风压系数分布图如图6所示. 考虑到屋盖整体结构的对称性,考察的风向角为0°、30°、60°和90°. 观察发现,各风向角作用下的屋盖表面整体风压均以负压为主,即屋盖整体承受向上的风吸力. 当风向角为0°或90°时,来流垂直于屋盖边缘,并且在边缘处发生分离,风压系数等压线基本与来流方向垂直. 屋盖的最不利平均风压系数均出现在迎风前檐处,这与平屋盖出现在角部有所不同[19-21]. 迎风边缘处的风吸力较大且波动幅度较大,随着与迎风边缘处距离的增加,平均风压系数绝对值逐渐减小且趋于稳定. 在0°风向角下,不同工况下各屋盖的平均风压系数逐渐稳定于−0.1. 由于挑檐的影响,屋盖A右侧边缘靠近迎风处的局部区域出现正压. 在90°风向角下,单跨屋盖A的平均风压系数绝对值沿着屋盖短跨方向逐渐减小,在背风侧两角端发生气流再附着现象,对应较小正压区域,大跨平屋盖在背风侧没有发生气流再附着现象[19]. 对于R2工况,气流在迎风屋盖C的迎风侧端部形成漩涡分离,对应出现较大负压区域;沿着来流方向,漩涡逐渐减小,对应背风屋盖B的负压值显著降低,同时漩涡沿屋盖长跨方向的两侧逐渐减弱,在长跨方向的两端,气流出现再附现象,形成较小正压区域. 对于R3工况,迎风屋盖A的风压分布规律同R1工况,沿着迎风方向,气流分离作用逐渐减弱,中间屋盖C和背风屋盖B的大部分区域呈现较小负压;各屋盖在长跨方向的两侧均出现气流再附,对应正压区域. 此外,对于多跨屋盖,在各屋盖交界处,由于屋脊的影响,出现较小区域的气流分离,对应负压.
图 6
以风向角60°为例进行斜风向分析,来流在R1工况迎风边缘处形成锥形涡,对应处产生较大负压,凹面屋盖影响了锥形涡的发展,在迎风侧下凹区域出现再附现象,形成正压区域,该现象不同于大跨平屋盖锥形涡的发展规律[16]. 锥形涡沿着长跨方向继续发展,越往下游,作用越弱,等压线分布越稀疏、整体趋势较平缓,对应风压系数绝对值逐渐减小. 对于R2工况,迎风屋盖C的风压规律类似于R1工况;背风屋盖B的迎风区域产生较大负压值,沿着长跨方向气流分离作用减弱,对应负压绝对值减小且稳定于−0.1. 对于R3工况,由于背风屋盖B对中间屋盖C的干扰,屋盖C的风压稳定区域(约−0.1)增大,屋盖B的屋脊处产生气流分离,对应负压值为−0.3. 对比各工况,迎风侧屋盖下凹区域的正压值及其范围随着屋盖数的增加逐渐扩大.
如表3所示为R3工况下不同风向角对应各屋盖整体的平均风压系数Cp [22]. 观察发现,随着风向角的增加,迎风屋盖A的风吸力逐渐增加,背风屋盖B和中间屋盖C的风吸力逐渐减小,中间屋盖C的下降速率大于背风屋盖B. 原因是在0°风向角下,屋盖短边为迎风边,屋盖迎风边缘风吸力较大而中下游区域基本稳定在−0.1,各屋盖间干扰较小;在90°风向角下,屋盖长边为迎风边,迎风屋盖发生分离的面积较大,整体风吸力较大,背风屋盖(中间屋盖和边缘屋盖)受干扰影响,风吸力均相对较小. 随着联排屋盖数的增加,在0°风向角下,各屋盖的变化规律一致,屋盖间的干扰作用较小,归因于联排方向同来流方向一致;在90°风向角下,由于气流的分离作用,迎风屋盖均出现较大负压区,平均风压系数为−0.6,下游屋盖大部分区域的平均风压系数稳定于−0.1;在斜风向角下,各屋盖迎风边缘处均出现一定范围的较大负压,迎风屋盖整体负压较大,其余屋盖整体负压较小,屋盖间的干扰作用明显. 在30°、60°、90°风向角下,下游屋盖的屋脊处均出现局部气流分离,对应局部负压值增加,为−0.3.
表 3 不同风向角下屋盖的整体平均风压系数(R3工况)
Tab.3
| 屋盖形式 | Cp | |||
| θ=0° | θ=30° | θ=60° | θ=90° | |
| A(迎风屋盖) | −0.36 | −0.38 | −0.41 | −0.52 |
| C(中间屋盖) | −0.48 | −0.34 | −0.09 | −0.07 |
| B(背风屋盖) | −0.45 | −0.36 | −0.20 | −0.07 |
3.2. 分区平均风压系数
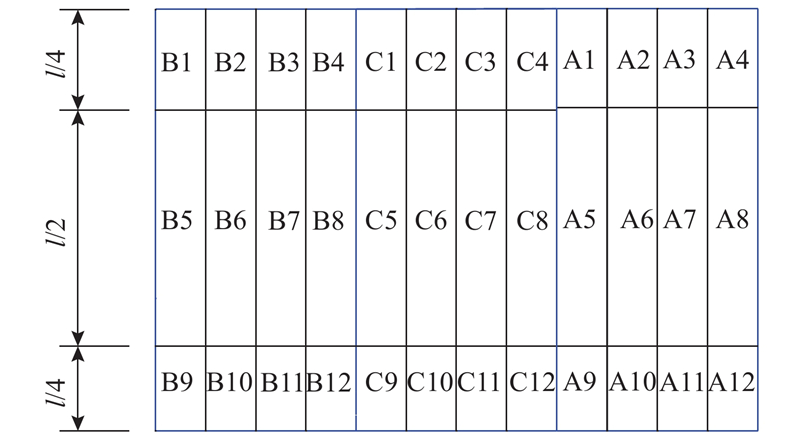
依据屋盖结构形态及平均风压系数分布规律,对屋盖进行合理分区,用于指导屋盖主体结构的抗风设计. 本研究的每个屋盖属于单向凹曲面屋盖,短跨方向是屋盖曲面的曲率变化方向,平均风压系数的变化梯度较大,对应较小的分区尺寸;长跨方向是屋盖保持同一曲面的延展,平均风压系数的变化梯度小于短跨方向,对应较大的分区尺寸. 由图6观察发现,长跨方向中部区域风压系数波动小于边缘区域,故中部区域分区尺寸较大. 参考文献[12]对平屋盖、坡屋盖的分区方法以及文献[22]对大跨平屋盖的分区方法,将每个屋盖短跨方向平均分为4份,长跨方向按照l/4、l/2、l/4进行分区(l为长跨长度),每个屋盖划分为12个分区,如图7所示.
图 7
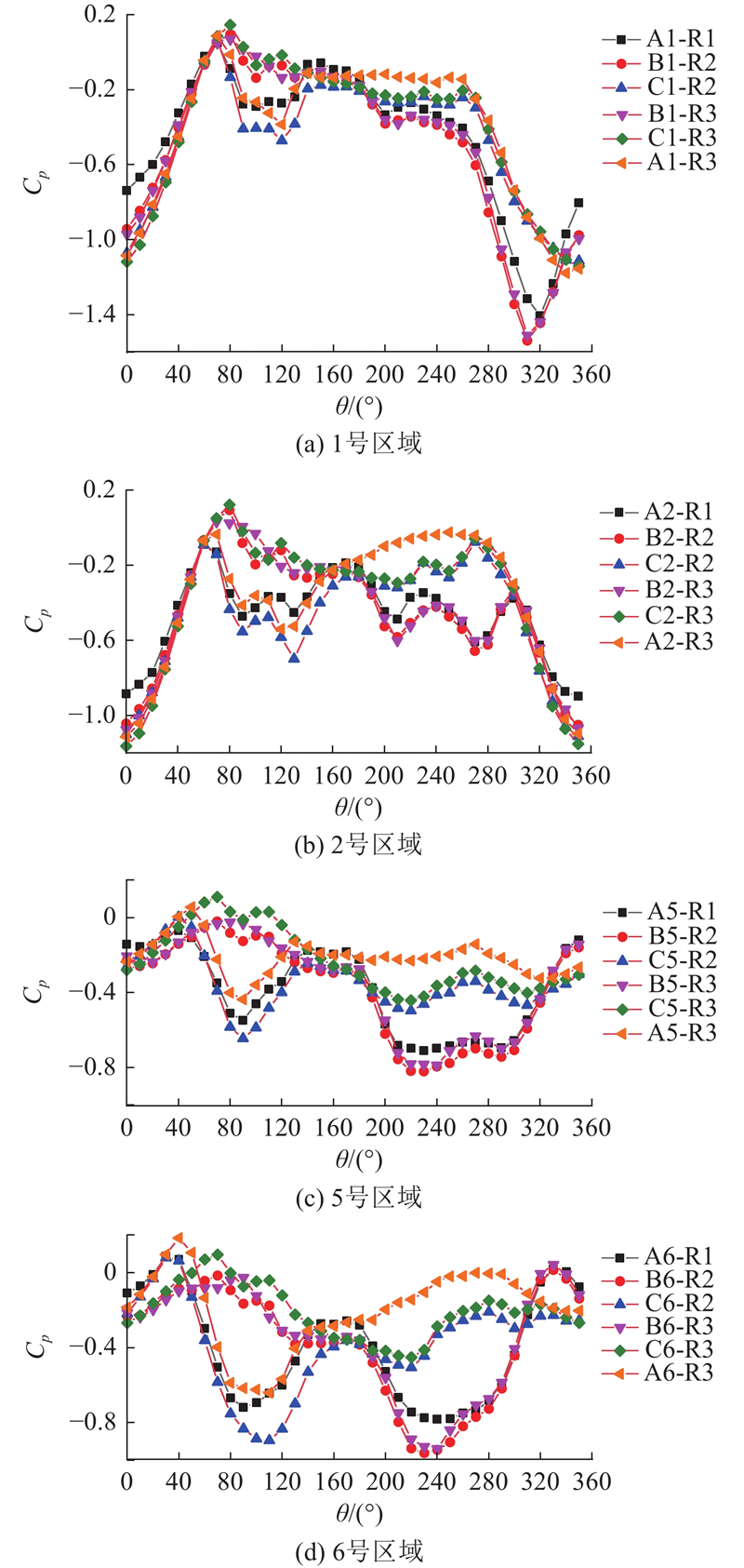
分区平均风压系数通过分区内测点平均风压系数的面积加权平均计算得到[4]. 绘制各分区平均风压系数随风向角的变化规律,选取1、2、5、6分区的平均风压系数进行研究,如图8所示. A1-R1代表R1工况下A屋盖的第一分区A1,A1-R3代表R3工况下A屋盖的第一分区A1,以此类推. 由图8(a)、8(b)发现,当风向角为0°~70°时,由于各屋盖间干扰较小,各屋盖1、2分区风压系数基本一致. 对于1号区域,当θ=70°~360°时,各屋盖分区平均风压系数波动较大,即屋盖干扰作用明显,整体表现为迎风屋盖的负压绝对值较大. 对于2号区域,当θ=70°~300°时,各屋盖分区平均风压系数波动较大,当θ=300°~360°时,各屋盖的分区平均风压系数基本一致. 由图8(c)、8(d)发现,对于5、6号区域,随着风向角的改变,当来流方向垂直于屋盖短跨方向时(0°和180°风向角),由于各屋盖间干扰较小,对应各屋盖5、6号分区的平均风压系数基本一致;当来流方向与短跨方向呈一定角度时,各屋盖的干扰作用逐渐体现;当来流方向平行于短跨方向时(θ=80°~90°和θ=220°~270°),干扰作用最大,对应各屋盖5、6号分区的平均风压系数值差别最大,迎风屋盖的负压绝对值以及数值波动远大于其他屋盖. 整体而言,中间屋盖5、6号分区的平均风压系数在各风向角下的数值波动较小,边缘屋盖的数值波动较大.
图 8
表 4 屋盖分区的平均风压系数参考值
Tab.4
| 分区 | Cp,R1工况 | Cp,R2工况 | Cp,R3工况 | |||||||||||
| θ=0° | θ=30° | θ=60° | θ=90° | θ=0° | θ=30° | θ=60° | θ=90° | θ=0° | θ=30° | θ=60° | θ=90° | |||
| B1 | — | — | — | — | −0.88 | −0.54 | −0.06 | −0.04 | −0.91 | −0.61 | −0.05 | 0.02 | ||
| B2 | — | — | — | — | −1.02 | −0.67 | −0.06 | −0.08 | −1.05 | −0.73 | −0.07 | 0.01 | ||
| B3 | — | — | — | — | −1.05 | −0.74 | −0.27 | −0.16 | −1.08 | −0.77 | −0.25 | −0.09 | ||
| B4 | — | — | — | — | −1.01 | −0.90 | −0.63 | −0.23 | −1.04 | −1.48 | −0.59 | −0.17 | ||
| B5 | — | — | — | — | −0.22 | −0.18 | −0.05 | −0.12 | −0.19 | −0.08 | −0.05 | −0.03 | ||
| B6 | — | — | — | — | −0.23 | −0.11 | −0.04 | −0.16 | −0.21 | −0.09 | −0.08 | −0.03 | ||
| B7 | — | — | — | — | −0.25 | −0.22 | −0.24 | −0.25 | −0.24 | −0.03 | −0.28 | −0.12 | ||
| B8 | — | — | — | — | −0.27 | −0.39 | −0.39 | −0.31 | −0.27 | −0.44 | −0.39 | −0.22 | ||
| B9 | — | — | — | — | −0.09 | −0.05 | −0.01 | 0.07 | −0.07 | −0.02 | −0.06 | 0.07 | ||
| B10 | — | — | — | — | −0.10 | −0.08 | −0.01 | 0.05 | −0.07 | −0.10 | −0.10 | 0.06 | ||
| B11 | — | — | — | — | −0.11 | −0.21 | −0.13 | −0.09 | −0.09 | −0.14 | −0.22 | −0.09 | ||
| B12 | — | — | — | — | −0.14 | −0.28 | −0.25 | −0.26 | −0.11 | −0.35 | −0.27 | −0.23 | ||
| C1 | — | — | — | — | −1.00 | −0.62 | −0.04 | −0.38 | −1.05 | −0.54 | −0.05 | 0.03 | ||
| C2 | — | — | — | — | −1.08 | −0.70 | −0.09 | −0.54 | −1.14 | −0.70 | −0.07 | −0.02 | ||
| C3 | — | — | — | — | −1.07 | −0.73 | −0.44 | −0.55 | −1.14 | −0.77 | −0.27 | −0.10 | ||
| C4 | — | — | — | — | −0.93 | −1.45 | −1.13 | −0.47 | −0.94 | −0.90 | −0.45 | −0.20 | ||
| C5 | — | — | — | — | −0.24 | −0.06 | −0.19 | −0.60 | −0.26 | −0.18 | 0.08 | −0.01 | ||
| C6 | — | — | — | — | −0.20 | 0.07 | −0.34 | −0.78 | −0.25 | −0.14 | 0.07 | −0.07 | ||
| C7 | — | — | — | — | −0.17 | −0.06 | −0.65 | −0.80 | −0.26 | −0.24 | −0.10 | −0.16 | ||
| C8 | — | — | — | — | −0.18 | −0.47 | −0.76 | −0.68 | −0.28 | −0.37 | −0.28 | −0.25 | ||
| C9 | — | — | — | — | −0.12 | 0.03 | −0.34 | −0.23 | −0.11 | −0.05 | 0.10 | 0.11 | ||
| C10 | — | — | — | — | −0.10 | −0.01 | −0.41 | −0.54 | −0.10 | −0.07 | 0.09 | 0.07 | ||
| C11 | — | — | — | — | −0.09 | −0.27 | −0.42 | −0.69 | −0.10 | −0.17 | −0.02 | −0.05 | ||
| C12 | — | — | — | — | −0.11 | −0.35 | −0.38 | −0.61 | −0.11 | −0.22 | −0.17 | −0.20 | ||
| A1 | −0.69 | −0.45 | −0.02 | −0.26 | — | — | — | — | −1.01 | −0.65 | −0.04 | −0.23 | ||
| A2 | −0.87 | −0.59 | −0.09 | −0.46 | — | — | — | — | −1.09 | −0.74 | −0.07 | −0.40 | ||
| A3 | −0.87 | −0.64 | −0.40 | −0.49 | — | — | — | — | −1.07 | −0.80 | −0.33 | −0.45 | ||
| A4 | −0.50 | −1.38 | −1.22 | −0.67 | — | — | — | — | −0.61 | −0.76 | −1.42 | −0.71 | ||
| A5 | −0.13 | −0.10 | −0.19 | −0.51 | — | — | — | — | −0.22 | −0.11 | −0.04 | −0.41 | ||
| A6 | −0.11 | 0.09 | −0.29 | −0.71 | — | — | — | — | −0.18 | −0.10 | −0.13 | −0.60 | ||
| A7 | −0.11 | −0.12 | −0.57 | −0.72 | — | — | — | — | −0.13 | −0.19 | −0.47 | −0.62 | ||
| A8 | −0.06 | −0.57 | −0.89 | −0.86 | — | — | — | — | −0.08 | −0.34 | −0.91 | −0.86 | ||
| A9 | −0.06 | 0.02 | −0.28 | −0.20 | — | — | — | — | −0.08 | −0.04 | −0.26 | −0.17 | ||
| A10 | −0.05 | 0.05 | −0.33 | −0.46 | — | — | — | — | −0.06 | −0.05 | −0.34 | −0.41 | ||
| A11 | −0.06 | −0.18 | −0.35 | −0.58 | — | — | — | — | −0.05 | −0.12 | −0.35 | −0.53 | ||
| A12 | −0.07 | −0.31 | −0.49 | −0.86 | — | — | — | — | −0.06 | −0.22 | −0.51 | −0.88 | ||
4. 极值风压系数
4.1. 极值风压系数
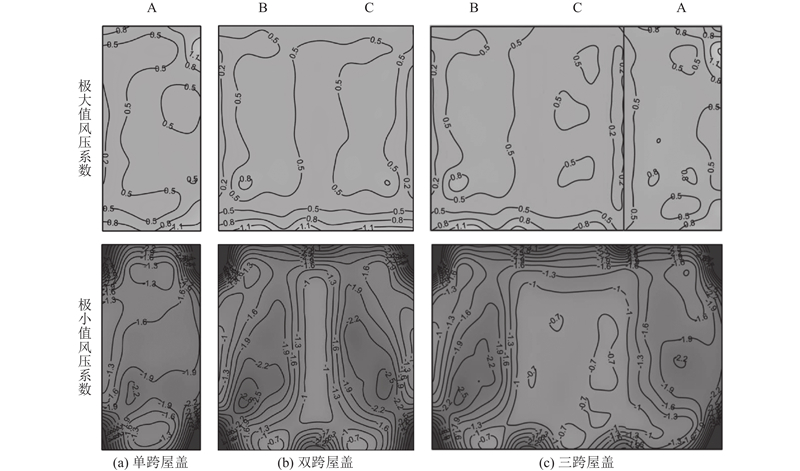
进行屋盖极值风压分析,用于指导围护结构的抗风设计. 参考文献[17]条文3.4.4的规定,采用峰值因子方法计算极值风压. 各测点处考虑非高斯分布特征的正负峰值因子由基于矩的Hermite多项式模型(Hermite polynomial model, HPM)估计[4,23]. 绘制各工况下屋盖的极值风压系数分布图如图9所示. 由图可见,各工况对应各屋盖的极大值风压系数分布规律基本一致,且数值整体波动较小,屋盖南侧短边局部出现较大的极值波动,归因于局部挑檐影响;由于气流分离作用,各工况下各屋盖边角处均出现绝对值较大的极小值风压系数,边缘屋盖的下凹区域出现大范围的较小值负压. 随着联排数的增加,由于两侧屋盖的遮挡,减缓了气流在中间屋盖的分离作用,对应中间屋盖极小值风压系数的绝对值及变化梯度均减小,且中间屋盖中部较大区域的极小值风压系数稳定于−0.7. 综上,随着联排数的增加,各屋盖极大值风压系数的变化较小,屋盖间的干扰作用不大;各屋盖极小值风压系数的变化较大,中间屋盖对应的数值及波动明显小于边缘屋盖.
图 9
4.2. 分区极值风压系数
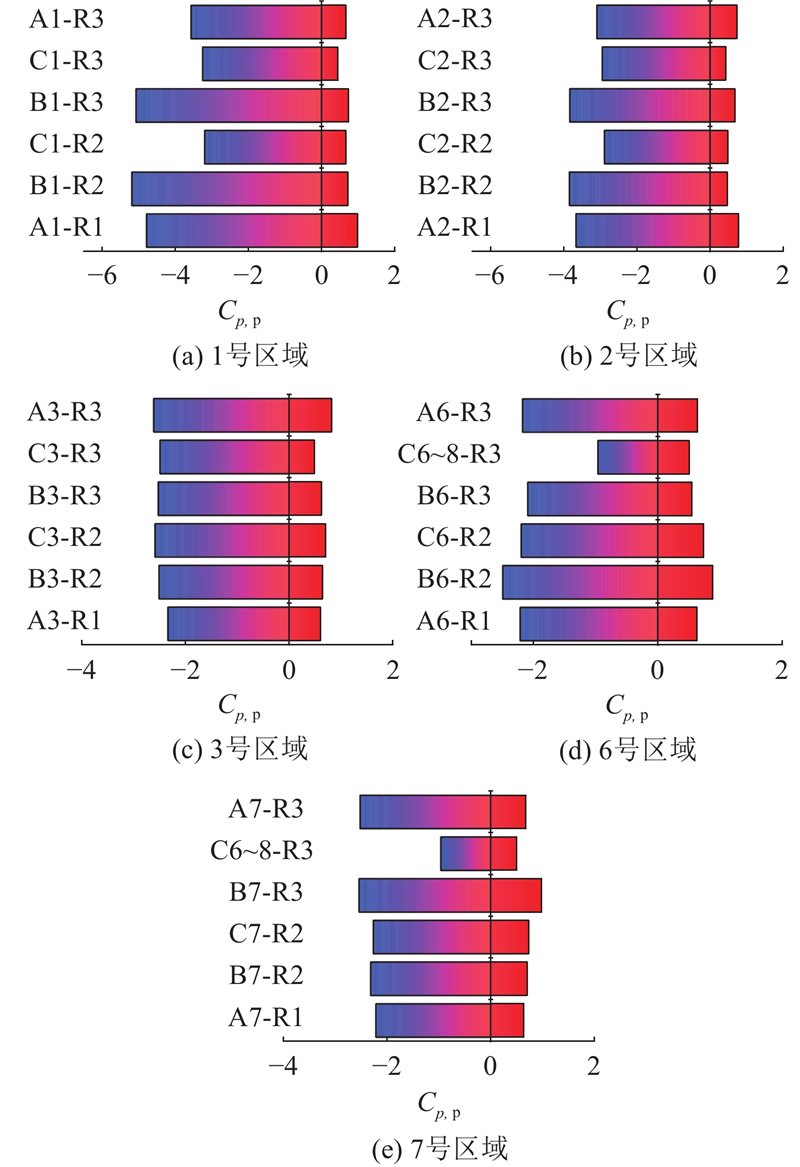
依据屋盖结构形态及极值风压系数分布规律,将每个屋盖分区并给出极值风压系数的分区值. 考虑到工程的安全性和保守性,将极值风压的分区值定为该区域中的极大值Cpmax和极小值Cpmin. 屋盖极值风压在前缘和边角气流分离处对应的波动较大,屋盖中部区域变化幅度较小,整体分布具有明显的区域性. 参考大跨平屋盖[22] 、鞍形屋盖[24]的分区方法,各屋盖的分区及编号如图10所示. 各屋盖分区尺寸如下:短跨方向按b/4、b/2、b/4划分(b为短跨长度),长跨方向按l/8、3l/4、l/8划分,4个拐角处进行细部分区,对应窄边尺寸分别为b/16、l/32. R3工况中间屋盖的中部区域极值风压系数的数值稳定,将6、7和8号分区合并,命名为C6~8. 基于对称性,对各工况下各屋盖1、2、3、6、7区域的极值风压进行对比讨论,如图11所示,其中正负方向分别表示该区域值的极大极小值. 由图可知,屋盖联排数对各屋盖各分区极值正压的影响较小,对极值负压的影响不可忽略. 由图11(a)发现,左侧边缘屋盖西北侧区域(A1-R1、B1-R2、B1-R3)的风吸力较大. 由于联排屋盖的遮挡,其余屋盖该区域负压绝对值显著降低,对应风吸力降低40%. 由图11(b)发现,左侧边缘屋盖西北侧区域(A2-R1、B2-R2、B2-R3)的风吸力仍然较大,但数值相比于图11(a)下降20%. 由图11(c)发现,屋盖联排数的增加对区域3极值风压系数的影响较小. 由图11(d)、11(e)发现,中间屋盖C的6、7区域(C6~8-R3)的风吸力是其余屋盖该区域的40%,该现象归因于中间屋盖的气流分离作用远小于边缘屋盖.
图 10
图 11
各工况1、2、3、6、7分区极值风压系数的参考值如表5所示,其余的区域值可以根据对称性确定. 观察发现,各区域极大值较为接近,各屋盖极小值均出现在角部区域(1、2分区),中间屋盖的C6、C7分区极小值明显小于其余屋盖的各分区值.
表 5 屋盖分区的极值风压系数参考值
Tab.5
| 分区 | R1工况 | R2工况 | R3工况 | |||||
| Cpmax | Cpmin | Cpmax | Cpmin | Cpmax | Cpmin | |||
| B1 | — | — | 0.7 | −5.2 | 0.7 | −5.1 | ||
| B2 | — | — | 0.5 | −3.8 | 0.7 | −3.8 | ||
| B3 | — | — | 0.6 | −2.5 | 0.6 | −2.5 | ||
| B6 | — | — | 0.9 | −2.5 | 0.6 | −2.1 | ||
| B7 | — | — | 0.7 | −2.3 | 1.0 | −2.5 | ||
| C1 | — | — | 0.7 | −3.2 | 0.4 | −3.3 | ||
| C2 | — | — | 0.5 | −2.9 | 0.4 | −2.9 | ||
| C3 | — | — | 0.7 | −2.6 | 0.5 | −2.5 | ||
| C6 | — | — | 0.7 | −2.2 | 0.5 | −1.0 | ||
| C7 | — | — | 0.7 | −2.3 | 0.5 | −1.0 | ||
| A1 | 1.0 | −4.8 | — | — | 0.7 | −3.6 | ||
| A2 | 0.8 | −3.7 | — | — | 0.7 | −3.1 | ||
| A3 | 0.6 | −2.3 | — | — | 0.8 | −2.6 | ||
| A6 | 0.6 | −2.2 | — | — | 0.6 | −2.2 | ||
| A7 | 0.6 | −2.2 | — | — | 0.7 | −2.5 | ||
5. 结 论
(1)随着屋盖联排数的增加,屋盖整体升力系数的波动及数值减小;各屋盖及整体屋盖升力系数变化规律差别较大. 屋盖最不利风向角受联排数影响较大,单屋盖为横风向(风向角为90°或270°),双屋盖或三屋盖为斜风向(风向角为130°或220°).
(2)在不同联排数及风向角下,各屋盖均以负压为主,屋盖的平均风压系数表现出复杂的波动规律. 在0°风向角下,屋盖间干扰作用较小;在斜风向角(30°、60°、90°)下,屋盖间干扰作用较大,下游屋盖的屋脊处均出现局部气流分离,对应局部平均风压系数增加,为−0.3. 当来流从垂直于联排方向逐渐向平行于联排方向改变时,屋盖干扰作用所致各屋盖平均风压系数的差别逐渐增大.
(3)对于多跨联排凹曲面屋盖,迎风屋盖边缘处存在较大的气流分离现象,对应较大风吸力;越远离迎风侧的屋盖,平均风压系数的波动越小,数值稳定于−0.1.
(4)联排数对极大值风压系数的分布规律及数值影响较小,对极小值风压系数的影响显著. 对于三跨屋盖而言,边缘屋盖分区极小值负压系数的最小值为−5.1,中间屋盖分区极小值负压系数的最小值为−3.3.
(5)联排数对各屋盖分区平均风压系数及极值风压系数的影响不可忽略,在结构抗风设计时须考虑各屋盖间的干扰效应及屋盖所处位置. 本研究给出分区形式及分区风压系数,为工程设计实践提供参考.
(6)本文工作基于实际工程开展,研究对象的几何参数为定值. 后续将对凹曲面屋盖开展系统性参数分析,探讨垂跨比、长跨比对风荷载特性的影响规律,进一步完善研究结论.
参考文献
关于传统建筑屋面凹曲的探讨
[J].
Discussion on the roof concave of the traditional architectures
[J].
Modeling the mean wind loads on cylindrical roofs with consideration of the Reynolds number effect in uniform flow with low turbulence
[J].DOI:10.1016/j.jweia.2014.02.011 [本文引用: 1]
Wind loading and its effects on single-layer reticulated cylindrical shells
[J].DOI:10.1016/j.jweia.2006.04.004
Wind tunnel investigation on the wind load of large-span coal sheds with porous gables: influence of gable ventilation
[J].DOI:10.1016/j.jweia.2020.104242 [本文引用: 4]
大跨度屋盖结构极值风压概率分布特征研究
[J].
Probability distribution characteristics of extreme wind pressure for large span roofs
[J].
某大跨度波浪形屋面体型系数取值研究
[J].
Analogical researchon shape coefficient of the abnormal roofing structure with the standard
[J].
体育馆凹曲面屋盖风压特性及干扰效应的风洞试验研究
[J].
Wind tunnel test research on wind load and interference effect on the concave surface roof of gymnasium
[J].
弧形内凹大跨屋盖结构风荷载特性的风洞试验与数值模拟
[J].
Wind tunnel test and numerical simulation on wind load characteristics of large-span roof with concave surface
[J].
弧形内凹连续坡屋面风压特性的数值模拟
[J].
Numerical simulation of wind pressure characteristics on a slope roof with consecutive concave surfaces
[J].
具有凹面外形的大跨屋盖结构风荷载分布及风洞试验研究
[J].DOI:10.3969/j.issn.1000-3835.2012.22.007 [本文引用: 3]
Wind load distribution and wind tunnel test for a curved concave long-span roof
[J].DOI:10.3969/j.issn.1000-3835.2012.22.007 [本文引用: 3]
矢跨比和垂跨比对张弦立体桁架性能的影响分析
[J].DOI:10.3969/j.issn.1006-6578.2005.01.007 [本文引用: 1]
Influences of rise-to-span ratio and sag-to-span ratio on the prestressed spatial truss string structure
[J].DOI:10.3969/j.issn.1006-6578.2005.01.007 [本文引用: 1]
Experiments on 2D rectangular prisms at high Reynolds numbers in a pressurised wind tunnel
[J].
大跨度平屋盖表面的特征湍流研究
[J].DOI:10.3969/j.issn.0258-1825.2007.03.007 [本文引用: 1]
Characteristics of signature turbulence on long span flat roofs
[J].DOI:10.3969/j.issn.0258-1825.2007.03.007 [本文引用: 1]
Robustness of the digital filter to differing calibration flows
[J].DOI:10.1016/j.jweia.2019.104061 [本文引用: 1]
不同排列方式平屋面建筑群极值风荷载干扰效应影响研究
[J].
Investigation on interference effects on peak wind loads on a group of buildings with flat roof under different arrangements
[J].
基于动力学模态分解的大跨度平屋盖风压场研究
[J].DOI:10.6052/j.issn.1000-4750.2021.04.0247
Research on wind pressure field of large-span flat roof based on dynamic mode decomposition
[J].DOI:10.6052/j.issn.1000-4750.2021.04.0247
大跨平屋盖风荷载特性及风压预测研究
[J].
Wind load characteristics and wind pressure prediction of long-span flat roof
[J].
非高斯风压峰值因子估计: 基于矩的转换过程法的对比研究
[J].
A comparative study on moment-based translation process methods for the peak factor estimation of non-gaussian wind pressures
[J].