(7) $ \begin{split} & {{f_{{1i}}}\left( z \right) =} \\ & \left\{ {\begin{array}{*{20}{l}} { - \dfrac{{{\varphi _{{\mathrm{c}}}}{A_{{\mathrm{c}}}}z}}{{{l_1}}}\left( {\gamma _{{\mathrm{c}}}^\prime z+{p_{{\mathrm{s}}}}} \right),}& {0 < z \leqslant {l_1};} \\ { - {\varphi _{{\mathrm{c}}}}{A_{c}}\left( {\gamma _{{\mathrm{c}}}^\prime z+{p_{{\mathrm{s}}}}} \right),}& {{l_1} < z \leqslant {l_{{\mathrm{c}}}};} \\ { - {\varphi _{{\mathrm{s}}}}{A_{{\mathrm{s}}}}\left[ {\gamma _{{\mathrm{c}}}^\prime {l_{{\mathrm{c}}}}+\gamma _{{\mathrm{s}}}^\prime \left( {z - {l_{{\mathrm{c}}}}} \right)+{p_{{\mathrm{s}}}}} \right],}& {{l_{{\mathrm{c}}}} < z \leqslant {l_2};} \\ { - \dfrac{{{\varphi _{{\mathrm{s}}}}{A_{{\mathrm{s}}}}\left( {{l_2}+{l_3} - 2z} \right)}}{{{l_3} - {l_2}}}\left[ {\gamma _{{\mathrm{c}}}^\prime {l_{{\mathrm{c}}}}+\gamma _{{\mathrm{s}}}^\prime \left( {z - {l_{c}}} \right)+{p_{{\mathrm{s}}}}} \right],}& {{l_2} < z \leqslant {l_0};} \\ {\dfrac{{{\varphi _{{\mathrm{s}}}}{A_{{\mathrm{s}}}}\left( {2z - {l_2} - {l_3}} \right)}}{{{l_3} - {l_2}}}\left[ {\gamma _{c}^\prime {l_{{\mathrm{c}}}}+\gamma _{{\mathrm{s}}}^\prime \left( {z - {l_{{\mathrm{c}}}}} \right)+{p_{{\mathrm{s}}}}} \right],}& {{l_0} < z \leqslant {l_3};} \\ {{\varphi _{{\mathrm{s}}}}{A_{{\mathrm{s}}}}\left[ {\gamma _{{\mathrm{c}}}^\prime {l_{{\mathrm{c}}}}+\gamma _{{\mathrm{s}}}^\prime \left( {z - {l_{{\mathrm{c}}}}} \right)+{p_{{\mathrm{s}}}}} \right],}& {{l_3} < z \leqslant {l_{{\mathrm{p}}}}.} \end{array}} \right. \end{split} $
(8) $ {f_{2i}}\left( z \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{\delta _{u}}{z^2}}}{{2{l_1}}},}&{0 < z \leqslant {l_1};} \\ {\dfrac{{{\delta _{u}}}}{2}\left( {2z - {l_1}} \right),}&{{l_1} < z \leqslant {l_{{\mathrm{c}}}};} \\ {\dfrac{{{\delta _{u}}}}{4}\left( {3{l_2}+{l_3} - 4z} \right),}&{{l_{{\mathrm{c}}}} < z \leqslant {l_2};} \\ {\dfrac{{{\delta _{u}}}}{{4\left( {{l_3} - {l_2}} \right)}}{{\left( {{l_2}+{l_3} - 2z} \right)}^2},}&{{l_2} < z \leqslant {l_0};} \\ {\dfrac{{{\delta _{u}}}}{{4\left( {{l_3} - {l_2}} \right)}}{{\left( {2z - {l_2} - {l_3}} \right)}^2},}&{{l_0} < z \leqslant {l_3};} \\ {\dfrac{{{\delta _{u}}}}{4}\left( {4z - {l_2} - 3{l_3}} \right),}&{{l_3} < z \leqslant {l_{{\mathrm{p}}}}.} \end{array}} \right. $
[1]
刘汉龙, 赵明华 地基处理研究进展
[J]. 土木工程学报 , 2016 , 49 (1 ): 96 - 115
[本文引用: 1]
LIU Hanlong, ZHAO Minghua Review of ground improvement technical and its application in China
[J]. China Civil Engineering Journal , 2016 , 49 (1 ): 96 - 115
[本文引用: 1]
[3]
周志军, 陈昌富, 肖水强 可控刚性桩与排水体组合型复合地基受力与变形特性的模型试验研究
[J]. 岩土工程学报 , 2020 , 42 (12 ): 2308 - 2315
DOI:10.11779/CJGE202012018
[本文引用: 1]
ZHOU Zhijun, CHEN Changfu, XIAO Shuiqiang Model tests on stress and deformation properties of composite foundation with controllable rigid piles and drainage bodies
[J]. Chinese Journal of Geotechnical Engineering , 2020 , 42 (12 ): 2308 - 2315
DOI:10.11779/CJGE202012018
[本文引用: 1]
[4]
王正振, 龚维明, 戴国亮, 等 厚垫层–砂桩复合地基现场试验研究
[J]. 岩土力学 , 2018 , 39 (10 ): 3755 - 3762
[本文引用: 2]
WANG Zhengzhen, GONG Weiming, DAI Guoliang, et al Field test on composite foundation with thick cushion and sand pile group
[J]. Rock and Soil Mechanics , 2018 , 39 (10 ): 3755 - 3762
[本文引用: 2]
[5]
商庆坤, 裴利华, 桂跃, 等 泥炭质土水泥土搅拌桩复合地基承载特性研究
[J]. 地基处理 , 2022 , 4 (1 ): 40 - 47
[本文引用: 1]
SHANG Qingkun, PEI Lihua, GUI Yue, et al Experimental investigations on bearing characteristic of peaty soil stabilized by a group of cement deep mixed columns
[J]. Journal of Ground Improvement , 2022 , 4 (1 ): 40 - 47
[本文引用: 1]
[6]
张伟丽, 蔡健, 林奕禧, 等 垫层对水泥土搅拌桩复合地基沉降的影响研究
[J]. 岩土力学 , 2010 , 31 (12 ): 4027 - 4032
DOI:10.3969/j.issn.1000-7598.2010.12.053
[本文引用: 3]
ZHANG Weili, CAI Jian, LIN Yixi, et al Study of influence of cushion on settlement of cement–soil mixing pile composite foundation
[J]. Rock and Soil Mechanics , 2010 , 31 (12 ): 4027 - 4032
DOI:10.3969/j.issn.1000-7598.2010.12.053
[本文引用: 3]
[7]
赵明华, 徐泽宇, 张承富 带锥形桩帽复合地基桩土应力比计算及其数值模拟
[J]. 湖南大学学报: 自然科学版 , 2020 , 47 (3 ): 1 - 10
ZHAO Minghua, XU Zeyu, ZHANG Chengfu Calculation and numerical simulation on pile–soil stress ratio of composite foundation with taper–capped pile
[J]. Journal of Hunan University: Natural Sciences , 2020 , 47 (3 ): 1 - 10
[8]
闫旭政, 应宏伟, 周建, 等 堆筑期土石坝软土碎石桩复合地基固结有限元分析
[J]. 地基处理 , 2023 , 5 (3 ): 205 - 214
[本文引用: 1]
YAN Xuzheng, YING Hongwei, ZHOU Jian, et al FEM analysis on consolidation of stone-column improved soft soil composite foundation during earth-rock dam construction period
[J]. Journal of Ground Improvement , 2023 , 5 (3 ): 205 - 214
[本文引用: 1]
[9]
ALAMGIR M, MJURA N, POOROOSHASB H B, et al Deformation analysis of soft ground reinforced by columnar inclusions
[J]. Computers and Geotechnics , 1996 , 18 (4 ): 267 - 290
DOI:10.1016/0266-352X(95)00034-8
[本文引用: 4]
[11]
吕文志, 俞建霖, 龚晓南 柔性基础下桩体复合地基的解析法
[J]. 岩石力学与工程学报 , 2010 , 29 (2 ): 401 - 408
[本文引用: 6]
LU Wenzhi, YU Jianlin, GONG Xiaonan Analytical method for pile composite ground under flexible foundation
[J]. Chinese Journal of Rock Mechanics and Engineering , 2010 , 29 (2 ): 401 - 408
[本文引用: 6]
[12]
曹文贵, 王江营, 罗忠涛, 等 考虑桩–土滑移的柔性基础下复合地基沉降分析方法
[J]. 中国公路学报 , 2012 , 25 (6 ): 9 - 16
DOI:10.3969/j.issn.1001-7372.2012.06.002
[本文引用: 3]
CAO Wengui, WANG Jiangying, LUO Zhongtao, et al Settlement calculation method for composite ground considering pile–soil slip under flexible foundation
[J]. China Journal of Highway and Transport , 2012 , 25 (6 ): 9 - 16
DOI:10.3969/j.issn.1001-7372.2012.06.002
[本文引用: 3]
[13]
曹文贵, 杨泽华 柔性基础下碎石桩加筋复合地基沉降分析方法
[J]. 岩土工程学报 , 2012 , 34 (11 ): 1997 - 2004
[本文引用: 1]
CAO Wengui, YANG Zehua Method for analyzing settlement of reinforced–gravel–pile composite ground under flexible foundation
[J]. Chinese Journal of Geotechnical Engineering , 2012 , 34 (11 ): 1997 - 2004
[本文引用: 1]
[14]
李海芳. 路堤荷载下复合地基沉降计算方法研究[D]. 杭州: 浙江大学, 2004.
[本文引用: 1]
LI Haifang. Study of settlement computation method of composite foundation under embankment [D]. Hangzhou: Zhejiang University, 2004.
[本文引用: 1]
[16]
俞建霖, 徐山岱, 杨晓萌, 等 刚性基础下砼芯水泥土桩复合地基沉降计算
[J]. 中南大学学报: 自然科学版 , 2020 , 51 (8 ): 2111 - 2120
[本文引用: 4]
YU Jianlin, XU Shandai, YANG Xiaomeng, et al Settlement calculation of composite foundation with concrete–cored DCM pile under rigid foundation
[J]. Journal of Central South University: Science and Technology , 2020 , 51 (8 ): 2111 - 2120
[本文引用: 4]
[17]
俞建霖, 徐嘉诚, 周佳锦, 等 混凝土芯水泥土复合桩混凝土–水泥土界面摩擦特性试验研究
[J]. 土木工程学报 , 2022 , 55 (8 ): 93 - 104
[本文引用: 1]
YU Jianlin, XU Jiacheng, ZHOU Jiajin, et al Experimental study on frictional capacity of concrete–cemented soil interface of concrete–cored cemented soil column
[J]. China Civil Engineering Journal , 2022 , 55 (8 ): 93 - 104
[本文引用: 1]
[18]
闫磊, 韩恒, 贺拴海, 等 深中通道沉管临时锚拉系统承载性能足尺模型试验
[J]. 中国公路学报 , 2022 , 35 (10 ): 47 - 54
DOI:10.3969/j.issn.1001-7372.2022.10.005
[本文引用: 2]
YAN Lei, HAN Heng, HE Shuanhai, et al Full–scale model test of bearing capacity of temporary anchorage system for immersed tube in Shenzhen–Zhongshan Link
[J]. China Journal of Highway and Transport , 2022 , 35 (10 ): 47 - 54
DOI:10.3969/j.issn.1001-7372.2022.10.005
[本文引用: 2]
[19]
付佰勇, 宋神友, 徐国平, 等 碎石垫层与深层水泥搅拌桩复合地基沉降研究
[J]. 公路 , 2021 , 66 (5 ): 65 - 70
[本文引用: 3]
FU Baiyong, SONG Shenyou, XU Guoping, et al Research on settlement of composite foundation with gravel cushion and deep cement mixing pile
[J]. Highway , 2021 , 66 (5 ): 65 - 70
[本文引用: 3]
[20]
OLSEN T, KASPER T, DE WIT J Immersed tunnels in soft soil conditions experience from the last 20 years
[J]. Tunnelling and Underground Space Technology , 2022 , 121 : 104315
DOI:10.1016/j.tust.2021.104315
[本文引用: 1]
[21]
潘树杰, 张伟, 陈小强. 海上深层水泥搅拌技术在香港的应用 [C]// 中国土木工程学会2019年学术年会论文集. 北京:中国建筑工业出版社, 2019: 661–670.
[本文引用: 1]
PAN Shujie, ZHANG Wei, CHEN Xiaoqiang. Marine based deep cement mixing in Hong Kong [C]// Proceeding of 2019 Annual Conference of China Civil Engineering Society . Beijing: China Architecture and Building Press, 2019: 661–670.
[本文引用: 1]
[22]
中华人民共和国交通运输部. 公路土工试验规程: JTG E40—2007 [S]. 北京: 人民交通出版社, 2007.
[本文引用: 1]
[23]
中华人民共和国住房和城乡建设部. 建筑地基处理技术规范: JGJ 79—2012 [S]. 北京: 中国建筑工业出版社, 2012.
[本文引用: 1]
[24]
中华人民共和国住房和城乡建设部. 复合地基技术规范: GB/T 50783—2012 [S]. 北京: 中国计划出版社, 2012.
[本文引用: 2]
[25]
张忠苗. 桩基工程[M]. 北京: 中国建筑工业出版社, 2007: 98–99.
[本文引用: 2]
[26]
RANDOLPH M F, WROTH C P An analysis of the vertical deformation of pile groups
[J]. Géotechnique , 1979 , 29 (4 ): 423 - 439
[本文引用: 1]
[27]
EVGIN E, FAKHARIAN K Effect of stress paths on the behaviour of sand steel interfaces
[J]. Canadian Geotechnical Journal , 1996 , 33 (6 ): 853 - 865
DOI:10.1139/t96-116-336
[本文引用: 1]
[29]
中华人民共和国住房和城乡建设部. 建筑地基基础设计规范: GB 50007—2011 [S]. 北京: 中国建筑工业出版社, 2011.
[本文引用: 1]
[30]
CHEN R P, XU Z Z, CHEN Y M, et al Field tests on pile–supported embankments over soft ground
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2010 , 136 (6 ): 777 - 785
DOI:10.1061/(ASCE)GT.1943-5606.0000295
[本文引用: 1]
地基处理研究进展
1
2016
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
地基处理研究进展
1
2016
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
广义复合地基理论及工程应用
2
2007
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
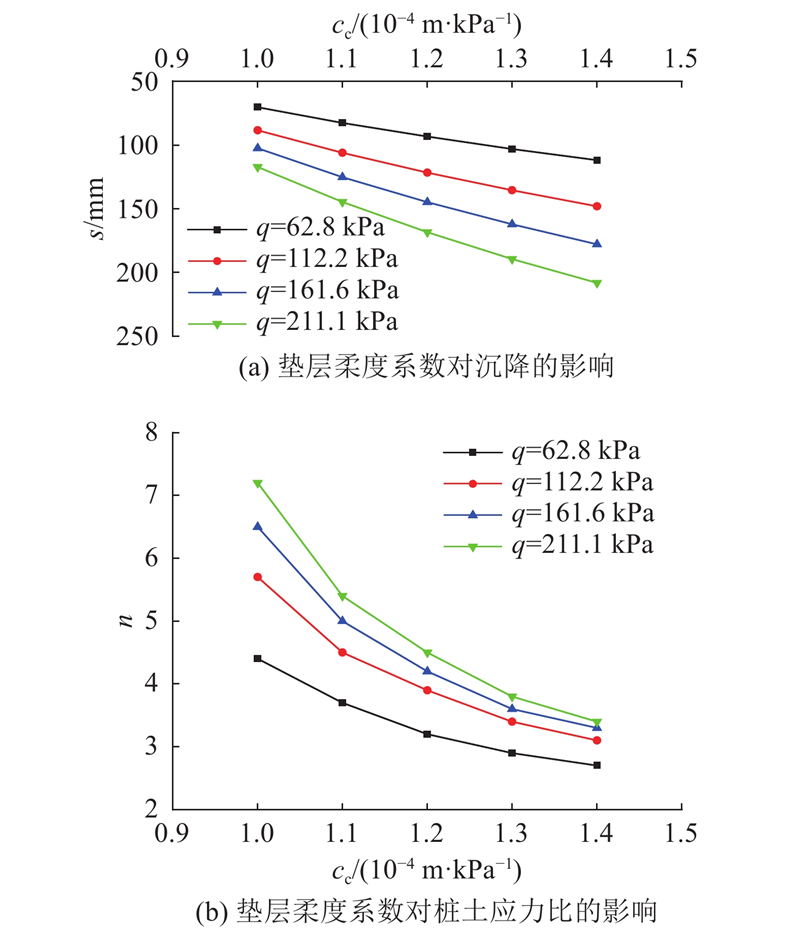
... 当置换率为0.47时,在各级荷载作用下复合地基沉降和桩土应力比随垫层柔度系数变化的曲线如图12 所示. 由图可知,在各级荷载作用下,沉降随着垫层柔度系数的增大而增大,桩土应力比随着垫层柔度系数的增大而减小. 当垫层柔度系数为1.0×10−4 m·kPa−1 时,在各级荷载作用下,沉降依次为70.2、88.2、102.4、117.1 mm,桩土应力比依次为4.4、5.7、6.5、7.2;当垫层柔度系数为1.4×10−4 m·kPa−1 时,在各级荷载作用下,沉降依次为111.8、148.0、177.8、208.1 mm,桩土应力比依次为2.7、3.1、3.3、3.4. 原因是当垫层柔度系数增大时,垫层调节桩土应力比的效果越来越明显,荷载由桩体向土体转移,桩体承担的荷载变小,土体承担的荷载变大,相应地桩土应力比随之减小,复合地基沉降随之增大. 此外,垫层柔度系数变大,有利于发挥土体的承载能力,使复合地基的破坏模式转变为桩土共同破坏,从而提高复合地基承载力[2 ] . 理想情况(垫层的施工质量良好,不考虑垫层模量随荷载的变化,垫层柔度系数仍然为1.0×10−4 m·kPa−1 )下,各级荷载作用时由本研究所提方法计算得到的复合地基沉降依次为30.2、55.2、74.4、90.1 mm,桩土应力比依次为6.1、6.7、7.1、7.3,与垫层施工质量不好的情况相比,在相同荷载作用下沉降更小,桩土应力比更大. 因此,提高垫层的施工质量能够有效减小复合地基沉降,增大桩土应力比,使复合地基的承载性能得到优化. ...
广义复合地基理论及工程应用
2
2007
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 当置换率为0.47时,在各级荷载作用下复合地基沉降和桩土应力比随垫层柔度系数变化的曲线如图12 所示. 由图可知,在各级荷载作用下,沉降随着垫层柔度系数的增大而增大,桩土应力比随着垫层柔度系数的增大而减小. 当垫层柔度系数为1.0×10−4 m·kPa−1 时,在各级荷载作用下,沉降依次为70.2、88.2、102.4、117.1 mm,桩土应力比依次为4.4、5.7、6.5、7.2;当垫层柔度系数为1.4×10−4 m·kPa−1 时,在各级荷载作用下,沉降依次为111.8、148.0、177.8、208.1 mm,桩土应力比依次为2.7、3.1、3.3、3.4. 原因是当垫层柔度系数增大时,垫层调节桩土应力比的效果越来越明显,荷载由桩体向土体转移,桩体承担的荷载变小,土体承担的荷载变大,相应地桩土应力比随之减小,复合地基沉降随之增大. 此外,垫层柔度系数变大,有利于发挥土体的承载能力,使复合地基的破坏模式转变为桩土共同破坏,从而提高复合地基承载力[2 ] . 理想情况(垫层的施工质量良好,不考虑垫层模量随荷载的变化,垫层柔度系数仍然为1.0×10−4 m·kPa−1 )下,各级荷载作用时由本研究所提方法计算得到的复合地基沉降依次为30.2、55.2、74.4、90.1 mm,桩土应力比依次为6.1、6.7、7.1、7.3,与垫层施工质量不好的情况相比,在相同荷载作用下沉降更小,桩土应力比更大. 因此,提高垫层的施工质量能够有效减小复合地基沉降,增大桩土应力比,使复合地基的承载性能得到优化. ...
可控刚性桩与排水体组合型复合地基受力与变形特性的模型试验研究
1
2020
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
可控刚性桩与排水体组合型复合地基受力与变形特性的模型试验研究
1
2020
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
厚垫层–砂桩复合地基现场试验研究
2
2018
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
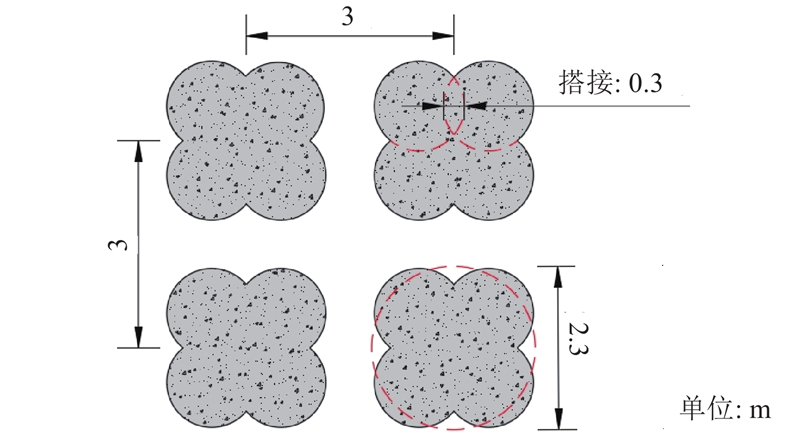
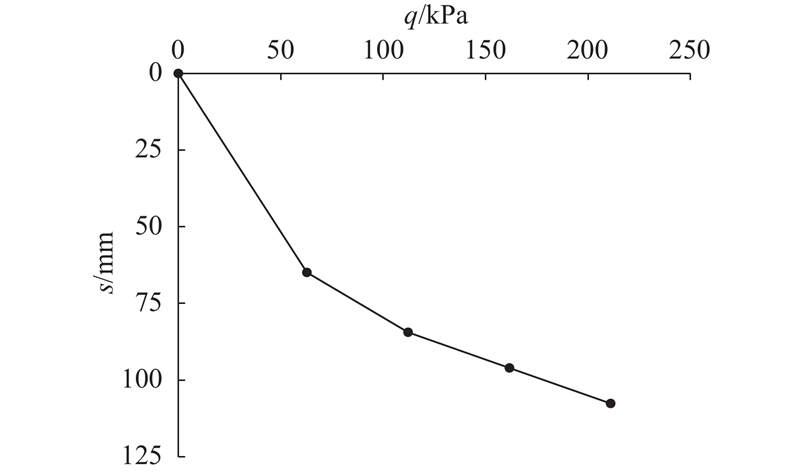
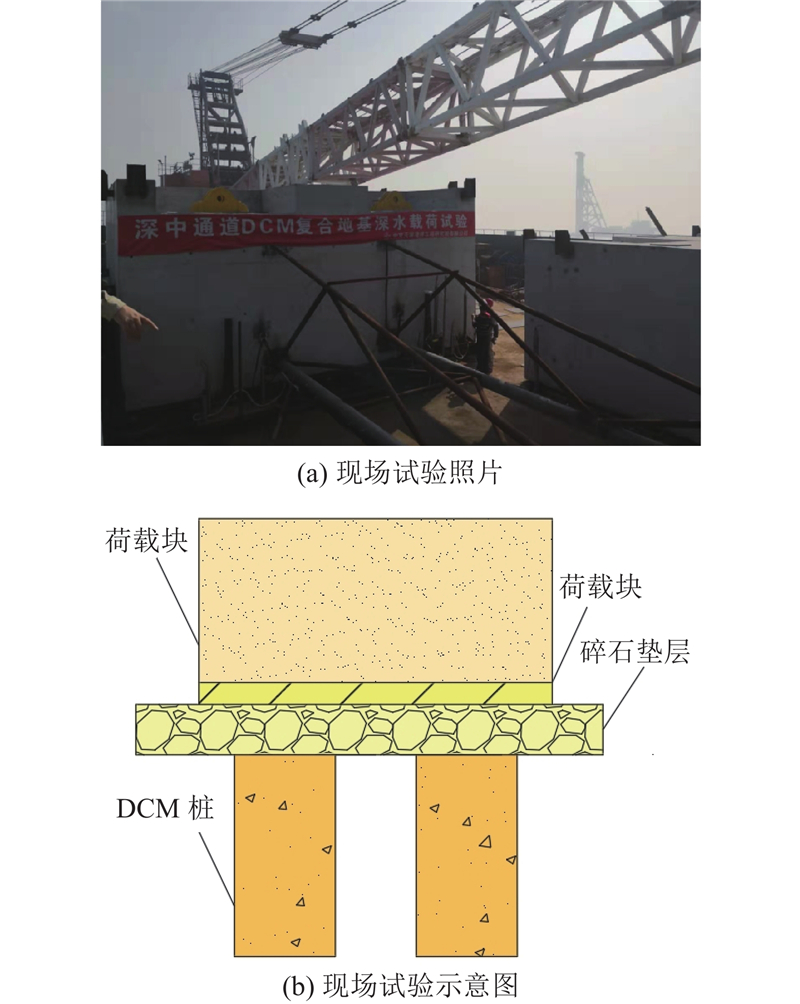
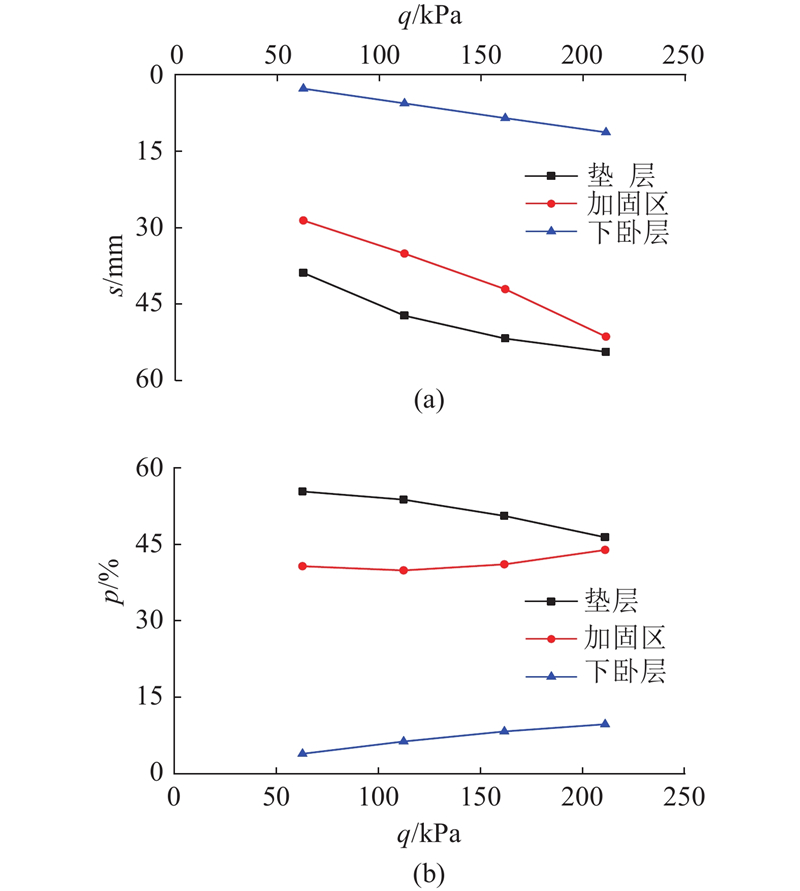
... 为了研究DCM桩复合地基的沉降变形规律,在西岛斜坡段开展现场荷载板试验. 如图1 所示,试验区域桩长18 m,采用3 m×3 m的布置形式.如表1 所示,试验区域土体及结构计算参数由室内土工试验得到,执行标准为《公路土工试验规程:JTG E40—2007)》 [22 ] . 表中,γ sat 为饱和重度,h 为厚度,E s 为压缩模量,c′ 为有效黏聚力,φ ′为有效内摩擦角,v 为泊松比. 为了便于推导计算,不考虑加固区土体的成层性,计算参数采用桩长范围内各土层厚度的加权平均值. 试验参照《建筑地基处理技术规范(JGJ 79—2012)》 [23 ] 执行,采用慢速维持荷载法,每加一级荷载前后各读记荷载板沉降量一次,以后每0.5 h读记一次,当1 h的沉降量小于0.1 mm时,即可加下一级荷载,现场试验照片及示意图如图2 所示. 整理荷载板试验结果,得到DCM桩复合地基沉降s 随荷载q 的变化曲线,如图3 所示. 由图可知,与常规复合地基荷载位移曲线不同,现场试验的第一级荷载为62.8 kPa,约占总荷载的28.4%;在第一级荷载作用下,荷载板沉降达到64.8 mm,占总沉降的60.2%;在后续荷载作用下,荷载板位移随着荷载的增大近似线性增加. 进一步分析试验结果发现,在碎石垫层施工过程中,海底浮力较大,垫层密实度没有达到设计要求,导致垫层压缩模量较小,约为1.8 MPa,因此在第一级荷载作用下总沉降量主要为垫层压缩量;后续荷载作用下的碎石垫层被逐渐压密,压缩模量逐渐增长至8~10 MPa. 陆上复合地基的试验结果与此不同,由于垫层的施工质量一般较好,且厚度较小,压缩模量在加载过程中变化较小,在达到极限承载力之前,荷载位移曲线近似线性增长[4 ] . ...
厚垫层–砂桩复合地基现场试验研究
2
2018
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
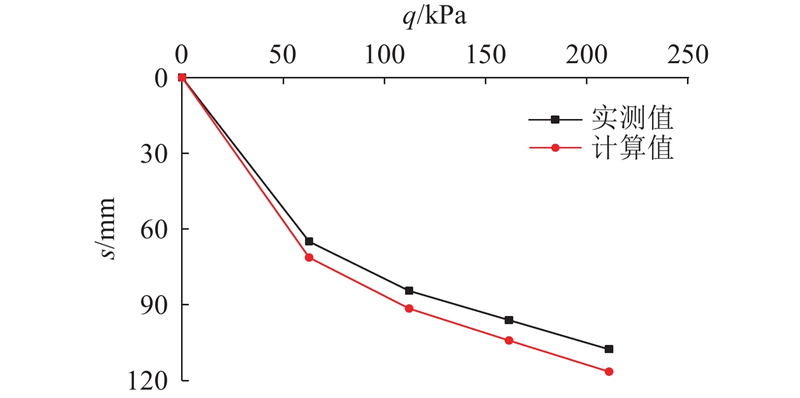
... 为了研究DCM桩复合地基的沉降变形规律,在西岛斜坡段开展现场荷载板试验. 如图1 所示,试验区域桩长18 m,采用3 m×3 m的布置形式.如表1 所示,试验区域土体及结构计算参数由室内土工试验得到,执行标准为《公路土工试验规程:JTG E40—2007)》 [22 ] . 表中,γ sat 为饱和重度,h 为厚度,E s 为压缩模量,c′ 为有效黏聚力,φ ′为有效内摩擦角,v 为泊松比. 为了便于推导计算,不考虑加固区土体的成层性,计算参数采用桩长范围内各土层厚度的加权平均值. 试验参照《建筑地基处理技术规范(JGJ 79—2012)》 [23 ] 执行,采用慢速维持荷载法,每加一级荷载前后各读记荷载板沉降量一次,以后每0.5 h读记一次,当1 h的沉降量小于0.1 mm时,即可加下一级荷载,现场试验照片及示意图如图2 所示. 整理荷载板试验结果,得到DCM桩复合地基沉降s 随荷载q 的变化曲线,如图3 所示. 由图可知,与常规复合地基荷载位移曲线不同,现场试验的第一级荷载为62.8 kPa,约占总荷载的28.4%;在第一级荷载作用下,荷载板沉降达到64.8 mm,占总沉降的60.2%;在后续荷载作用下,荷载板位移随着荷载的增大近似线性增加. 进一步分析试验结果发现,在碎石垫层施工过程中,海底浮力较大,垫层密实度没有达到设计要求,导致垫层压缩模量较小,约为1.8 MPa,因此在第一级荷载作用下总沉降量主要为垫层压缩量;后续荷载作用下的碎石垫层被逐渐压密,压缩模量逐渐增长至8~10 MPa. 陆上复合地基的试验结果与此不同,由于垫层的施工质量一般较好,且厚度较小,压缩模量在加载过程中变化较小,在达到极限承载力之前,荷载位移曲线近似线性增长[4 ] . ...
泥炭质土水泥土搅拌桩复合地基承载特性研究
1
2022
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
泥炭质土水泥土搅拌桩复合地基承载特性研究
1
2022
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
垫层对水泥土搅拌桩复合地基沉降的影响研究
3
2010
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... ,6 ,11 ,15 ],DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
垫层对水泥土搅拌桩复合地基沉降的影响研究
3
2010
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... ,6 ,11 ,15 ],DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
带锥形桩帽复合地基桩土应力比计算及其数值模拟
0
2020
带锥形桩帽复合地基桩土应力比计算及其数值模拟
0
2020
堆筑期土石坝软土碎石桩复合地基固结有限元分析
1
2023
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
堆筑期土石坝软土碎石桩复合地基固结有限元分析
1
2023
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
Deformation analysis of soft ground reinforced by columnar inclusions
4
1996
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... [9 ]的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
路堤荷载下柔性悬桩复合地基的沉降分析
3
2000
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
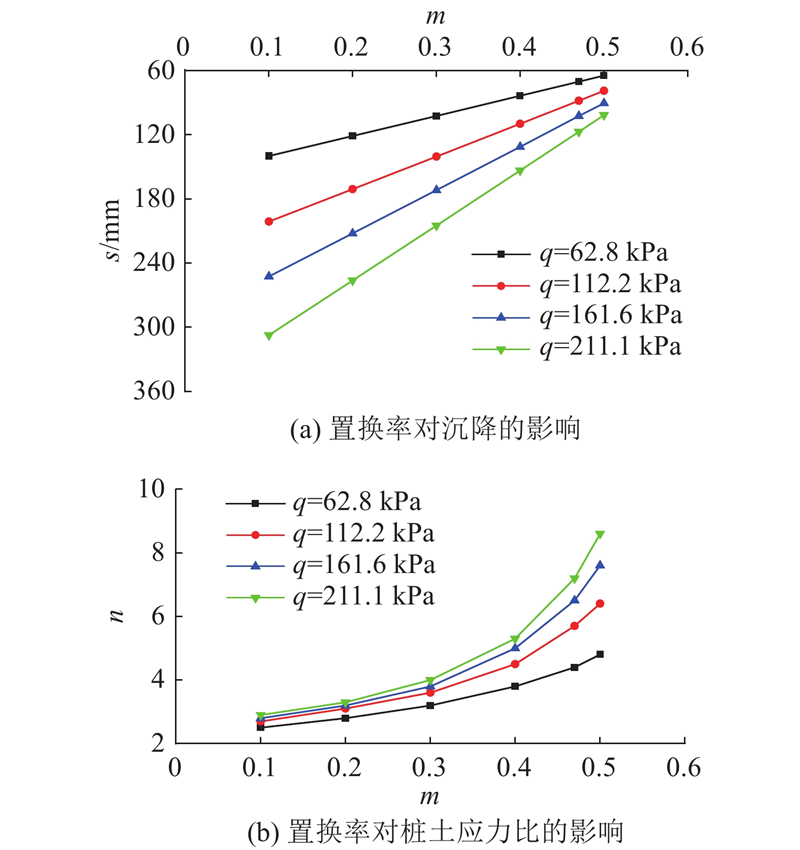
... 深中通道沉管隧道DCM桩复合地基与陆域工程的明显区别是复合地基中的DCM桩置换率大[10 -16 ] ,并且复合地基加固区和沉管隧道基础之间设置超厚垫层,因此改变复合地基置换率m (假设桩间距恒为3 m,仅改变桩径大小)和垫层柔度系数c c (荷载板试验中置换率和垫层柔度系数分别为0.47和1.0×10−4 m·kPa−1 ),探讨2种因素对复合地基沉降和桩土应力比的影响. ...
路堤荷载下柔性悬桩复合地基的沉降分析
3
2000
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 深中通道沉管隧道DCM桩复合地基与陆域工程的明显区别是复合地基中的DCM桩置换率大[10 -16 ] ,并且复合地基加固区和沉管隧道基础之间设置超厚垫层,因此改变复合地基置换率m (假设桩间距恒为3 m,仅改变桩径大小)和垫层柔度系数c c (荷载板试验中置换率和垫层柔度系数分别为0.47和1.0×10−4 m·kPa−1 ),探讨2种因素对复合地基沉降和桩土应力比的影响. ...
柔性基础下桩体复合地基的解析法
6
2010
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... ,11 ,15 ],DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... -11 ],未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 碎石垫层厚度较大且压缩模量较小,为此在分析荷载传递机理时,将沉管隧道基础视为柔性基础,依据文献[11 ]假定桩间土的竖向位移模式为 ...
... 根据文献[11 ],将f 1i (z )理解为桩侧摩阻力分布函数,考虑到桩土在分界面处的应力协调,引入应力协调常数φ i f 1i (z )分段表示为 ...
柔性基础下桩体复合地基的解析法
6
2010
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... ,11 ,15 ],DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... -11 ],未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 碎石垫层厚度较大且压缩模量较小,为此在分析荷载传递机理时,将沉管隧道基础视为柔性基础,依据文献[11 ]假定桩间土的竖向位移模式为 ...
... 根据文献[11 ],将f 1i (z )理解为桩侧摩阻力分布函数,考虑到桩土在分界面处的应力协调,引入应力协调常数φ i f 1i (z )分段表示为 ...
考虑桩–土滑移的柔性基础下复合地基沉降分析方法
3
2012
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... [12 -15 ],使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
考虑桩–土滑移的柔性基础下复合地基沉降分析方法
3
2012
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... [12 -15 ],使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
柔性基础下碎石桩加筋复合地基沉降分析方法
1
2012
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
柔性基础下碎石桩加筋复合地基沉降分析方法
1
2012
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
1
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
1
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
考虑桩土滑移的路堤下刚性桩复合地基沉降计算
8
2018
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... ,15 ],DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... -15 ],使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 式中:τ sai 为位置i 处的桩侧摩阻力. 假设桩土界面处的桩土相互作用服从等单位长度极限剪切位移δ u 理想弹塑性模型[15 ,26 -27 ] ,以表征桩侧摩阻力τ 与δ 的关系. 以δ u 为界限,在弹性阶段,α i α i δ 和α i 图6 所示.分别在深度范围[l c ,l 0 ]和[l 0 ,l p ]对δ 积分,得到桩顶处桩土相对位移Δ a 和桩端处桩土相对位移Δ b ,计算式分别为 ...
... 基于文献[15 ]的假定,桩顶向上刺入变形w a 和桩端向下刺入变形w b 分别为 ...
... 根据文献[30 ]的原位试验结果,取碎石垫层等沉面的高度为桩净距. 桩侧极限摩阻力发挥系数α 采用β 法确定[25 ] ,本研究取碎石垫层α =0.3,加固区土体α =0.2. 单位长度桩土极限相对位移参考罗强等[15 ] 的统计结果,本研究取桩长范围内各土层厚度的加权平均值,即δ u =0.15%. 碎石垫层的压缩模量根据现场试验结论和反演分析[19 ] 取值,在第一级荷载下取1.8 MPa,后续荷载下取10 MPa,其他计算参数见表1 . ...
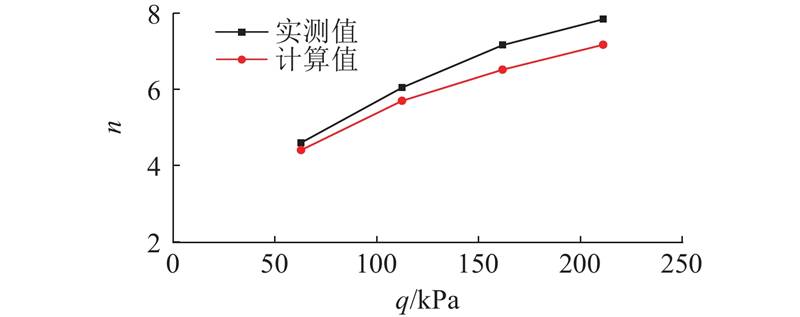
... 实测和理论计算桩土应力比n 随荷载变化的对比结果如图10 所示. 由图可知,根据理论计算得到的桩土应力比和现场试验所得桩土应力比的变化趋势一致,都随着荷载的增加而增大. 在第一级荷载下,理论计算和实测得到的桩土应力比分别为4.4、4.6,理论计算值比实测值小4.3%;在最后一级荷载作用下,理论计算和实测得到的桩土应力比分别增加到7.2、7.8,理论计算值比实测值小7.7%. 理论计算和实测的桩土应力比都随着荷载的增加而增大,但是增长幅度越来越小. 这是因为当荷载增加时,由于垫层的调节作用,桩体分担了更多的荷载,所以桩土应力比增大;当荷载增加到接近复合地基的极限承载力时,垫层的调节作用也会达到极限[15 ] . 总体来说,理论计算和实测得到的桩土应力比相差不大,误差不超过10%,可以认为理论计算的结果可靠. ...
考虑桩土滑移的路堤下刚性桩复合地基沉降计算
8
2018
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... ,15 ],DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... -15 ],使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 式中:τ sai 为位置i 处的桩侧摩阻力. 假设桩土界面处的桩土相互作用服从等单位长度极限剪切位移δ u 理想弹塑性模型[15 ,26 -27 ] ,以表征桩侧摩阻力τ 与δ 的关系. 以δ u 为界限,在弹性阶段,α i α i δ 和α i 图6 所示.分别在深度范围[l c ,l 0 ]和[l 0 ,l p ]对δ 积分,得到桩顶处桩土相对位移Δ a 和桩端处桩土相对位移Δ b ,计算式分别为 ...
... 基于文献[15 ]的假定,桩顶向上刺入变形w a 和桩端向下刺入变形w b 分别为 ...
... 根据文献[30 ]的原位试验结果,取碎石垫层等沉面的高度为桩净距. 桩侧极限摩阻力发挥系数α 采用β 法确定[25 ] ,本研究取碎石垫层α =0.3,加固区土体α =0.2. 单位长度桩土极限相对位移参考罗强等[15 ] 的统计结果,本研究取桩长范围内各土层厚度的加权平均值,即δ u =0.15%. 碎石垫层的压缩模量根据现场试验结论和反演分析[19 ] 取值,在第一级荷载下取1.8 MPa,后续荷载下取10 MPa,其他计算参数见表1 . ...
... 实测和理论计算桩土应力比n 随荷载变化的对比结果如图10 所示. 由图可知,根据理论计算得到的桩土应力比和现场试验所得桩土应力比的变化趋势一致,都随着荷载的增加而增大. 在第一级荷载下,理论计算和实测得到的桩土应力比分别为4.4、4.6,理论计算值比实测值小4.3%;在最后一级荷载作用下,理论计算和实测得到的桩土应力比分别增加到7.2、7.8,理论计算值比实测值小7.7%. 理论计算和实测的桩土应力比都随着荷载的增加而增大,但是增长幅度越来越小. 这是因为当荷载增加时,由于垫层的调节作用,桩体分担了更多的荷载,所以桩土应力比增大;当荷载增加到接近复合地基的极限承载力时,垫层的调节作用也会达到极限[15 ] . 总体来说,理论计算和实测得到的桩土应力比相差不大,误差不超过10%,可以认为理论计算的结果可靠. ...
刚性基础下砼芯水泥土桩复合地基沉降计算
4
2020
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... -16 ]. 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 深中通道沉管隧道DCM桩复合地基与陆域工程的明显区别是复合地基中的DCM桩置换率大[10 -16 ] ,并且复合地基加固区和沉管隧道基础之间设置超厚垫层,因此改变复合地基置换率m (假设桩间距恒为3 m,仅改变桩径大小)和垫层柔度系数c c (荷载板试验中置换率和垫层柔度系数分别为0.47和1.0×10−4 m·kPa−1 ),探讨2种因素对复合地基沉降和桩土应力比的影响. ...
刚性基础下砼芯水泥土桩复合地基沉降计算
4
2020
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... -16 ]. 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 深中通道沉管隧道DCM桩复合地基与陆域工程的明显区别是复合地基中的DCM桩置换率大[10 -16 ] ,并且复合地基加固区和沉管隧道基础之间设置超厚垫层,因此改变复合地基置换率m (假设桩间距恒为3 m,仅改变桩径大小)和垫层柔度系数c c (荷载板试验中置换率和垫层柔度系数分别为0.47和1.0×10−4 m·kPa−1 ),探讨2种因素对复合地基沉降和桩土应力比的影响. ...
混凝土芯水泥土复合桩混凝土–水泥土界面摩擦特性试验研究
1
2022
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
混凝土芯水泥土复合桩混凝土–水泥土界面摩擦特性试验研究
1
2022
... 复合地基能够提高软土地基承载性能并减少沉降量,被广泛应用于各种软基加固工程[1 ] . 龚晓南[2 ] 指出,复合地基的本质是桩和桩间土共同直接承担荷载. 众多学者通过现场、室内试验[3 -5 ] 和数值模拟[6 -8 ] 等方法,系统研究了复合地基的荷载传递机理和沉降特性. 在复合地基沉降解析计算方面,Alamgir等[9 ] 推导了柔性基础复合地基桩身应力、桩侧摩阻力和沉降计算的解析式,但采用的位移模式没有考虑桩土相对滑移. 杨涛[10 ] 在Alamgir等[9 ] 的研究基础上提出“中性点”的概念,重新假定了桩侧摩阻力的分布形式. 吕文志等[11 ] 基于文献[9 ]的位移模式,将基础、垫层、复合地基和下卧层土体视为共同作用的系统,考虑了系统各部分的应力和变形协调. 曹文贵等[12 -13 ] 改进文献[14 ]的位移模式,考虑桩土相对滑移及桩、土、垫层在分界面处的变形协调,得到柔性桩复合地基沉降的计算方法. 罗强等[15 ] 建立非均匀变化的桩侧摩阻力分布模型,推导了刚性桩复合地基沉降和桩土应力比的解析式. 俞建霖等[16 -17 ] 基于荷载传递法,考虑界面相对位移对界面侧摩阻力的影响,研究了砼芯水泥土桩复合地基的工作性状和沉降计算方法. ...
深中通道沉管临时锚拉系统承载性能足尺模型试验
2
2022
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 深中通道隧道总长6 845 m,其中敞开段长695 m,暗埋段长1 115 m,沉管段长5 035 m[18 ] . 深中通道沉管隧道西岛斜坡段DCM桩采用单桩式布置形式,单桩直径为1.3 m,搭接为0.3 m,4桩一簇,等效直径约为2.3 m. 单桩纵向间距为3 m,根据上部荷载的大小,横向间距分为3、4、5 m 3种,综合置换率为41%~47.4%[19 ] . ...
深中通道沉管临时锚拉系统承载性能足尺模型试验
2
2022
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 深中通道隧道总长6 845 m,其中敞开段长695 m,暗埋段长1 115 m,沉管段长5 035 m[18 ] . 深中通道沉管隧道西岛斜坡段DCM桩采用单桩式布置形式,单桩直径为1.3 m,搭接为0.3 m,4桩一簇,等效直径约为2.3 m. 单桩纵向间距为3 m,根据上部荷载的大小,横向间距分为3、4、5 m 3种,综合置换率为41%~47.4%[19 ] . ...
碎石垫层与深层水泥搅拌桩复合地基沉降研究
3
2021
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 深中通道隧道总长6 845 m,其中敞开段长695 m,暗埋段长1 115 m,沉管段长5 035 m[18 ] . 深中通道沉管隧道西岛斜坡段DCM桩采用单桩式布置形式,单桩直径为1.3 m,搭接为0.3 m,4桩一簇,等效直径约为2.3 m. 单桩纵向间距为3 m,根据上部荷载的大小,横向间距分为3、4、5 m 3种,综合置换率为41%~47.4%[19 ] . ...
... 根据文献[30 ]的原位试验结果,取碎石垫层等沉面的高度为桩净距. 桩侧极限摩阻力发挥系数α 采用β 法确定[25 ] ,本研究取碎石垫层α =0.3,加固区土体α =0.2. 单位长度桩土极限相对位移参考罗强等[15 ] 的统计结果,本研究取桩长范围内各土层厚度的加权平均值,即δ u =0.15%. 碎石垫层的压缩模量根据现场试验结论和反演分析[19 ] 取值,在第一级荷载下取1.8 MPa,后续荷载下取10 MPa,其他计算参数见表1 . ...
碎石垫层与深层水泥搅拌桩复合地基沉降研究
3
2021
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
... 深中通道隧道总长6 845 m,其中敞开段长695 m,暗埋段长1 115 m,沉管段长5 035 m[18 ] . 深中通道沉管隧道西岛斜坡段DCM桩采用单桩式布置形式,单桩直径为1.3 m,搭接为0.3 m,4桩一簇,等效直径约为2.3 m. 单桩纵向间距为3 m,根据上部荷载的大小,横向间距分为3、4、5 m 3种,综合置换率为41%~47.4%[19 ] . ...
... 根据文献[30 ]的原位试验结果,取碎石垫层等沉面的高度为桩净距. 桩侧极限摩阻力发挥系数α 采用β 法确定[25 ] ,本研究取碎石垫层α =0.3,加固区土体α =0.2. 单位长度桩土极限相对位移参考罗强等[15 ] 的统计结果,本研究取桩长范围内各土层厚度的加权平均值,即δ u =0.15%. 碎石垫层的压缩模量根据现场试验结论和反演分析[19 ] 取值,在第一级荷载下取1.8 MPa,后续荷载下取10 MPa,其他计算参数见表1 . ...
Immersed tunnels in soft soil conditions experience from the last 20 years
1
2022
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
1
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
1
... 复合地基主要应用于陆上地基处理工程,设计时垫层厚度一般取0.2~0.6 m[6 ,11 -12 ,15 -16 ] ,置换率一般不超过0.2[10 -16 ] . 海底复合地基位于复杂的海洋环境,施工较为困难,为了保证施工质量,往往采用垫层厚度大、置换率高的地基处理方式. 深中通道大规模使用深层水泥搅拌(deep cement mixing,DCM)桩处理海底沉管隧道地基,碎石垫层厚度达到1 m,DCM桩置换率为0.41~0.48,与常规的陆上复合地基不同[18 ] . 垫层厚度和置换率会影响复合地基的荷载传递机理和沉降特性[4 ,6 ,11 ,15 ] ,DCM桩复合地基现场荷载板试验的结果也反映出类似的规律[19 ] . 忽视垫层的自身沉降[9 -11 ] ,未全面考虑垫层、复合地基和下卧层的应力变形协调[12 -15 ] ,使得现有计算方法不适用于海底DCM桩复合地基的沉降计算. 海底DCM桩复合地基在项目中的成功应用已有报道[20 -21 ] ,但是相关理论研究落后于工程实践,有必要对其荷载传递机理和沉降特性开展系统研究. ...
1
... 为了研究DCM桩复合地基的沉降变形规律,在西岛斜坡段开展现场荷载板试验. 如图1 所示,试验区域桩长18 m,采用3 m×3 m的布置形式.如表1 所示,试验区域土体及结构计算参数由室内土工试验得到,执行标准为《公路土工试验规程:JTG E40—2007)》 [22 ] . 表中,γ sat 为饱和重度,h 为厚度,E s 为压缩模量,c′ 为有效黏聚力,φ ′为有效内摩擦角,v 为泊松比. 为了便于推导计算,不考虑加固区土体的成层性,计算参数采用桩长范围内各土层厚度的加权平均值. 试验参照《建筑地基处理技术规范(JGJ 79—2012)》 [23 ] 执行,采用慢速维持荷载法,每加一级荷载前后各读记荷载板沉降量一次,以后每0.5 h读记一次,当1 h的沉降量小于0.1 mm时,即可加下一级荷载,现场试验照片及示意图如图2 所示. 整理荷载板试验结果,得到DCM桩复合地基沉降s 随荷载q 的变化曲线,如图3 所示. 由图可知,与常规复合地基荷载位移曲线不同,现场试验的第一级荷载为62.8 kPa,约占总荷载的28.4%;在第一级荷载作用下,荷载板沉降达到64.8 mm,占总沉降的60.2%;在后续荷载作用下,荷载板位移随着荷载的增大近似线性增加. 进一步分析试验结果发现,在碎石垫层施工过程中,海底浮力较大,垫层密实度没有达到设计要求,导致垫层压缩模量较小,约为1.8 MPa,因此在第一级荷载作用下总沉降量主要为垫层压缩量;后续荷载作用下的碎石垫层被逐渐压密,压缩模量逐渐增长至8~10 MPa. 陆上复合地基的试验结果与此不同,由于垫层的施工质量一般较好,且厚度较小,压缩模量在加载过程中变化较小,在达到极限承载力之前,荷载位移曲线近似线性增长[4 ] . ...
1
... 为了研究DCM桩复合地基的沉降变形规律,在西岛斜坡段开展现场荷载板试验. 如图1 所示,试验区域桩长18 m,采用3 m×3 m的布置形式.如表1 所示,试验区域土体及结构计算参数由室内土工试验得到,执行标准为《公路土工试验规程:JTG E40—2007)》 [22 ] . 表中,γ sat 为饱和重度,h 为厚度,E s 为压缩模量,c′ 为有效黏聚力,φ ′为有效内摩擦角,v 为泊松比. 为了便于推导计算,不考虑加固区土体的成层性,计算参数采用桩长范围内各土层厚度的加权平均值. 试验参照《建筑地基处理技术规范(JGJ 79—2012)》 [23 ] 执行,采用慢速维持荷载法,每加一级荷载前后各读记荷载板沉降量一次,以后每0.5 h读记一次,当1 h的沉降量小于0.1 mm时,即可加下一级荷载,现场试验照片及示意图如图2 所示. 整理荷载板试验结果,得到DCM桩复合地基沉降s 随荷载q 的变化曲线,如图3 所示. 由图可知,与常规复合地基荷载位移曲线不同,现场试验的第一级荷载为62.8 kPa,约占总荷载的28.4%;在第一级荷载作用下,荷载板沉降达到64.8 mm,占总沉降的60.2%;在后续荷载作用下,荷载板位移随着荷载的增大近似线性增加. 进一步分析试验结果发现,在碎石垫层施工过程中,海底浮力较大,垫层密实度没有达到设计要求,导致垫层压缩模量较小,约为1.8 MPa,因此在第一级荷载作用下总沉降量主要为垫层压缩量;后续荷载作用下的碎石垫层被逐渐压密,压缩模量逐渐增长至8~10 MPa. 陆上复合地基的试验结果与此不同,由于垫层的施工质量一般较好,且厚度较小,压缩模量在加载过程中变化较小,在达到极限承载力之前,荷载位移曲线近似线性增长[4 ] . ...
2
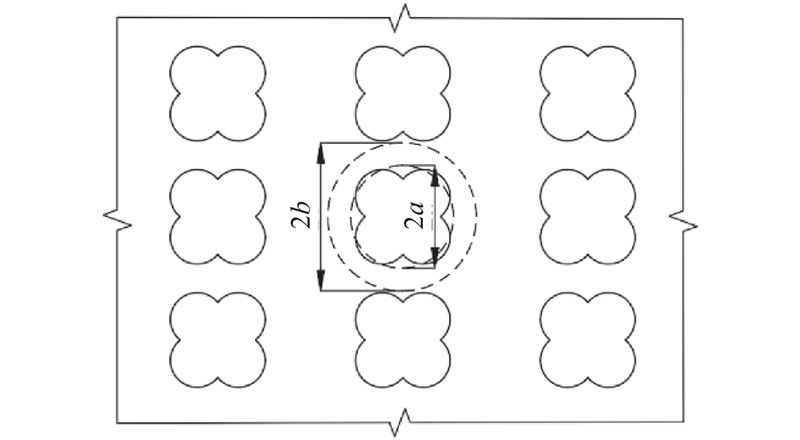
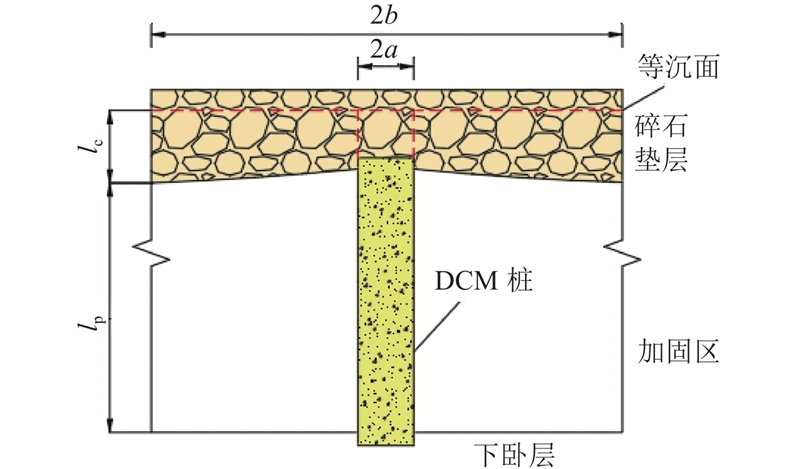
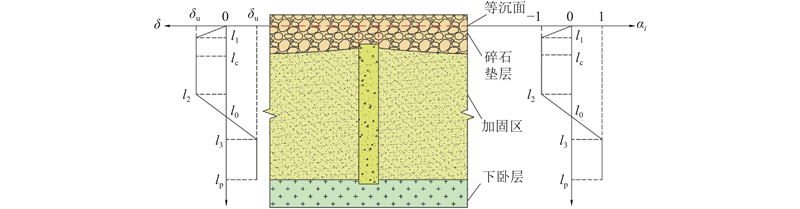
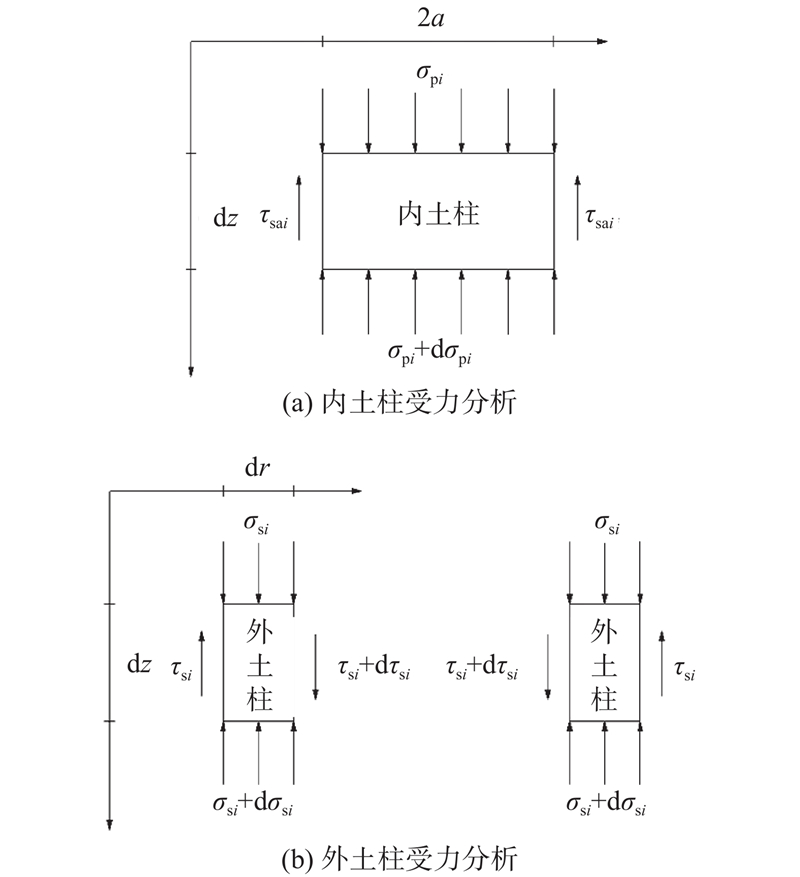
... 沉管隧道基础的最大宽度超过55 m,为了简化模型,取单个桩体及其影响范围内土体形成的同心圆柱体作为典型单元体进行分析,如图4 所示. 图中,a 、b 分别为单个桩体及其影响范围内土体的等效半径. 假设桩体及其上方垫层部分为内土柱(半径为a ),桩间土体及其上方垫层部分为外土柱(半径为b ),外土柱半径b 由布桩方式和桩间距得到[24 ] . 在此基础上,将DCM桩复合地基简化为如图5 所示的模型,其中l c 为碎石垫层等沉面以下的厚度,l p 为加固区的厚度. ...
... 式中:c c 、c r 分别为垫层和下卧层的柔度系数[24 ] . 在z =l c 处,w a 与Δ a 相等,联立式(5)、式(32)有 ...
2
... 式中:τ sui 采用β 法计算[25 ] ;β i i 处的桩侧摩阻力系数;$ \sigma _{v}^\prime $ $ \gamma _j^\prime $ $ {z_j} $ i 处以上土体及结构的有效重度和厚度;p s 为碎石垫层等沉面处外土柱的应力. 位置i 处的桩侧摩阻力发挥系数为 ...
... 根据文献[30 ]的原位试验结果,取碎石垫层等沉面的高度为桩净距. 桩侧极限摩阻力发挥系数α 采用β 法确定[25 ] ,本研究取碎石垫层α =0.3,加固区土体α =0.2. 单位长度桩土极限相对位移参考罗强等[15 ] 的统计结果,本研究取桩长范围内各土层厚度的加权平均值,即δ u =0.15%. 碎石垫层的压缩模量根据现场试验结论和反演分析[19 ] 取值,在第一级荷载下取1.8 MPa,后续荷载下取10 MPa,其他计算参数见表1 . ...
An analysis of the vertical deformation of pile groups
1
1979
... 式中:τ sai 为位置i 处的桩侧摩阻力. 假设桩土界面处的桩土相互作用服从等单位长度极限剪切位移δ u 理想弹塑性模型[15 ,26 -27 ] ,以表征桩侧摩阻力τ 与δ 的关系. 以δ u 为界限,在弹性阶段,α i α i δ 和α i 图6 所示.分别在深度范围[l c ,l 0 ]和[l 0 ,l p ]对δ 积分,得到桩顶处桩土相对位移Δ a 和桩端处桩土相对位移Δ b ,计算式分别为 ...
Effect of stress paths on the behaviour of sand steel interfaces
1
1996
... 式中:τ sai 为位置i 处的桩侧摩阻力. 假设桩土界面处的桩土相互作用服从等单位长度极限剪切位移δ u 理想弹塑性模型[15 ,26 -27 ] ,以表征桩侧摩阻力τ 与δ 的关系. 以δ u 为界限,在弹性阶段,α i α i δ 和α i 图6 所示.分别在深度范围[l c ,l 0 ]和[l 0 ,l p ]对δ 积分,得到桩顶处桩土相对位移Δ a 和桩端处桩土相对位移Δ b ,计算式分别为 ...
基于荷载传递法的CFG桩复合地基沉降计算
1
2010
... 联立式(23)~式(25)得到下卧层顶面处由桩端应力与桩间土平均应力引起的附加应力σ r [28 ] ,表达式为 ...
基于荷载传递法的CFG桩复合地基沉降计算
1
2010
... 联立式(23)~式(25)得到下卧层顶面处由桩端应力与桩间土平均应力引起的附加应力σ r [28 ] ,表达式为 ...
1
... 式中:m 为面积置换率,m = a 2 /b 2 . 将σ r 代入分层总和法,得到下卧层压缩量w r [29 ] ,表达式为 ...
Field tests on pile–supported embankments over soft ground
1
2010
... 根据文献[30 ]的原位试验结果,取碎石垫层等沉面的高度为桩净距. 桩侧极限摩阻力发挥系数α 采用β 法确定[25 ] ,本研究取碎石垫层α =0.3,加固区土体α =0.2. 单位长度桩土极限相对位移参考罗强等[15 ] 的统计结果,本研究取桩长范围内各土层厚度的加权平均值,即δ u =0.15%. 碎石垫层的压缩模量根据现场试验结论和反演分析[19 ] 取值,在第一级荷载下取1.8 MPa,后续荷载下取10 MPa,其他计算参数见表1 . ...