道路网络在城市及经济发展中发挥着不可或缺的作用，灾害事件可能严重影响其功能. 2012年10月29日飓风“桑迪”袭击纽约市，造成近500亿美元的经济损失^[1]，导致一系列交通问题^[2]. 研究者从可达性^[3]、连通性^[4]、脆弱性^[5]、韧性^[6]等角度法分析极端天气下的路网性能. Hansen^[7]提出，可达性是一个地区到多个目的地的互动能力的总体衡量标准,可达性与区域间的互动机会和出行成本相关，即可达性应由吸引系数和阻抗函数决定，体现区域间的互动能力. Hansen可达性体现人们的实际出行情况，常被用于研究人们的出行规律. 在极端天气下的可达性研究方面，Qiang等^[3]使用吸引系数相等的Hansen可达性指标衡量公路网络韧性，发现暴雪灾害下可达性较低的区域相较指正于可达性高的区域恢复能力更差，灾害对长距离旅行的可达性影响明显. 秦艺帆等^[8]将出行时间作为可达性指标，从时空角度分析暴雪天气下早高峰时段南京市各小区的可达性变化，发现交通枢纽附近道路的通勤延误较为明显，灾害下的车速降低是导致可达性变化的主要原因. 李睿等^[9]将出行时间作为可达性指标的分级标准并对暴雨内涝情景进行建模，研究上海市消防设施的可达性并发现暴雨会使城市内的不可达单元增多. 已有研究对可达性的定义类似，但构建的指标大多存在差异，使用不同的指标甚至会得到相反的结果^[10]，有必要对灾害下可达性指标进行比较分析.

选取可达性指标的常用方法有2种：累积机会法和基于重力的方法^[11-12]. 累计机会法认为只有在特定时间阈内区域间才有互动的机会；这种方法简单且易于量化^[13]，但是二元化式的简单加权方式倍受质疑^[14]. 基于重力的方法认为互动机会随着衰减因子（如距离）的变化而改变；这种方法因接近现实情况而备受推崇^[15-16]，也由于复杂和难以理解而饱受诟病^[17]. 为了明确可达性指标使用范围，Palacios等^[18]利用蒙特利尔市的公交时刻表数据对2种方法的可达性指标进行相关性分析，发现它们的相关性较高，并建议使用累积机会型指标来替代复杂的重力型指标. 在对加拿大8个城市的公交系统时刻表进行进一步研究后，Kapatsila等^[19]也发现这2种方法的可达性指标高度相关性，证明了累积机会型可达性指标的优势. Klar等^[20]研究公交系统重新设计前后的可达性变化，发现在交通干预前后这2种可达性指标的变化表现为低相关性，并通过波动性分析证明了重力型可达性指标在交通干预条件下有更好的性能. 关于可达性指标选取问题的研究大多集中于正常的交通环境场景下，没有考虑交通量剧烈变化的特殊情况，因此已有结论可能不适用于极端天气. 此外，已有的可达性研究大多选取人口、工作机会、兴趣点数量等静态因素来衡量吸引系数，忽略了灾害下吸引系数随出行需求变化，缺少对吸引系数比较的分析.

本文基于出租车数据，研究飓风“桑迪”灾害下的纽约市曼哈顿区的可达性，对比由2类吸引系数和3类阻抗函数组成的可达性指标在灾害下的相关性和时空特点，明确不同类型可达性指标的差异和各类可达性指标的适用条件，并根据选取的可达性指标对灾害下的可达性时空变化进行分析，揭示灾害下可达性的变化特点，为极端天气下路网恢复调度提供相关的决策建议.

定义可达性为区域间的吸引系数与阻抗函数的乘积. 基于Hansen可达性模型^[7]，量化吸引系数和阻抗函数计算区域间的可达性，并根据区域的可达性进行加权求和获得网络的可达性. 区域和网络可达性表达式分别为

(1)$ {A_j}(t) = \displaystyle\sum\limits_{i = 1}^N {{W_{ij}}(t)f(t)} , $

(2)$ A(t) = {{\displaystyle\sum\limits_{j = 1}^N {{A_j}(t)} }}/N. $

式中：${A_j}$为区域$j$($j$=1,2,3,···,140)的可达性，$ A(t) $为时间段$t$的路网可达性，${W_{ij}}$为区域$j$对区域$i$的吸引程度，$f(t)$为由区域$i$到区域$j$的阻抗函数.

吸引系数是指终点所在区域$j$对起点所在区域$i$出行者的吸引能力. 吸引系数分为2类：基于人口的吸引系数和基于需求的吸引系数；前者强调不同区域间人口不同对互动能力的影响，后者考虑灾害对人们出行行为存在较大影响，且一天内不同时间段的吸引系数动态变化.

人口吸引系数定义为区域$i$与区域$j$的人口数的乘积与人口总数之比^[11]，表达式为

(3)$ {W_{ij}}(t) = {{{P_i} {P_j}}}/{{\displaystyle\sum\limits_{i = 1}^N {{P_i}} }}. $

式中：${P_i}$、${P_j}$分别为区域$i$与区域$j$的人口数；$N$为区域的总数.

区域间的需求以区域$i$与区域$j$间的出租车流量进行量化. 需求吸引系数定义为区域$i$与区域$j$的需求与总需求之比，表达式为

(4)$ {W_{ij}}(t) = \frac{\;{{D_{ij}}(t)}\;}{\;{\overline {{D_{ij}}(t)} }\;}, $

(5)$ {D_{ij}}(t) = \sum\limits_{m{\text{ = 1}}}^M {P^m_{ij}}(t) . $

式中：${D_{ij}}(t)$为时间段$t$的路网区域间需求，${P^m_{ij}}(t)$为时间段$t$的第$m$条车辆轨迹的乘客数，$M$为时间段$t$区域$i$到区域$j$的总车辆轨迹数.

阻抗函数描述交通参与者在出行过程中的出行阻抗. 阻抗函数有3种类型，分别为基于累积机会型、基于重力型和基于累积机会与重力的混合型^[20].

累积机会型阻抗函数采用一般性的基于累计机会矩阵法，表达式为

(6)$ f(t) = \frac{1}{M}\sum\limits_{m = 1}^M {{\varphi _m}} , $

(7)$ {\varphi _m} = \left\{ {\begin{array}{*{20}{c}} 1,&{{t^m_{ij}} \leqslant T}; \\ 0,&{{t^m_{ij}} > T} .\end{array}} \right. $

式中：$ {t^m_{ij}} $为区域$i$与区域$j$间第$m$条轨迹对应的行程时间；$T$为行程时间阈；$ {\varphi _m} $为二元变量，判断行程是否满足要求.

重力型阻抗函数考虑区域间的互动能力会随行程时间下降，定义为出行成本的倒数，表达式为

(8)$ f(t) = \frac{{\text{1}}}{M}\sum\limits_{m = 1}^M {\frac{1}{{{C^m_{ij}}}}} . $

式中：$ {C^m_{ij}} $为时间段$t$内区域$i$与区域$j$间第$m$条轨迹对应的旅行成本，由实际车费标定.

混合型阻抗函数在设置时间阈的同时强调阻抗函数的衰减性，表达式为

(9)$ f(t) = \frac{1}{M}\sum\limits_{m = 1}^M {{{{\varphi _m}}}/{{{C^m_{ij}}}}} . $

根据美国国家海洋和大气管理局的飓风数据，飓风“桑迪”于2012年10月29日12时登陆美国纽约市，并于10月31日12时消散. 选择飓风登陆前一周到灾害消散后一周(10月22日至11月6日)共计16 d的出租车数据进行分析. 划分灾害为灾前、灾中和灾后3个阶段：灾前阶段被划定为飓风登陆前一周，即10月22日0时至10月29日12时；灾后阶段为飓风消散后的一周，即10月31日12时至11月7日0时；灾中阶段选取飓风登陆与消散之间的2 d.

出租车数据源于纽约市出租车和豪华轿车委员会(NYC taxi and limousine commission，TLC)提供的2012年10月22日至11月7日的黄色出租车开源数据集^[21]. 该数据集包括出租车出行记录的乘客上车和下车时间、上车下车地点、出行距离、乘客数量和收费等情况. 根据已有规则^[22]，计算得到平均出行时间约为726 s，平均出行距离约为2.12 km，说明出租车在曼哈顿区的行程以短距离行程为主. 剔除数据集中行程时间大于60 min、行驶距离大于24 km、速度高于60 km/h、车费大于100 美元的异常数据，在出租车数据集中删除了13%的异常数据. 在保留的约532 万条有效出租车行程数据中，灾前和灾后有日均超过40 万人次的行程，灾害中有约15 万人次的日均行程. 使用Worldpop网站^[23]收集的2012 年美国各州的人口数据，该数据显示纽约州的人口密度为1 km×1 km，将该人口密度数据映射至划分的地理栅格.

为了确保研究的准确性，考虑到黄色出租车集中运行在纽约市曼哈顿区，选取出租车流量最密集的曼哈顿区作为研究区域. 曼哈顿是纽约市的中央商务区，面积约59.5 km²，拥有约169 万居民^[24]. 该区域的出租车流量约为13 500 辆/d，大部分出租车装备GPS定位器^[1]. 曼哈顿由北向南主要可以分为哈莱姆区、上城区、中城区和下城区^[24]. 为了探究灾害对可达性的空间影响，如图1所示，依据已有的地理栅格划分方式^[24-25]将曼哈顿总体划分为140 个1 km×1 km的地理栅格，计算栅格间的可达性.

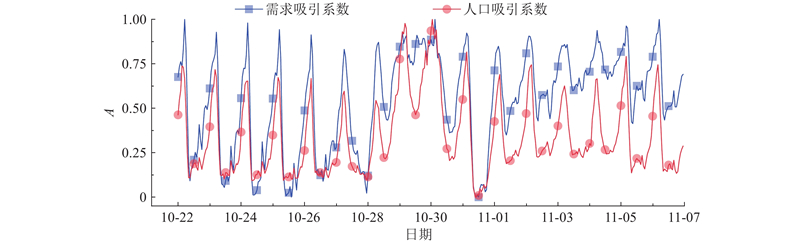
2类吸引系数在灾害不同阶段的标准化可达性A时变特性如图2所示. 采用重力型阻抗函数计算可达性，对2类可达性指标进行MAX-MIN归一化，在不改变自身分布的前提下使可达性指标落入区间[0,1.0].可以看出，可达性在全周期下均呈现相似的变化趋势， 表现出以日为单位的周期性规律. 在灾前和灾后阶段，日间可达性较高、晚间较低.需求吸引系数的可达性比人口吸引系数的可达性高18.24%. 原因可能是日间高峰期人们倾向短距离出行，9：00—21：00的平均出行距离比非高峰期的短11%，相邻区域的出行增多，这些区域的吸引系数上升. 近距离出行的时间较短，可达性比非高峰期高. 人口吸引系数无法体现需求结构的变化，认为一天内人们的出行需求不变，会低估路网的可达性.在灾中的起始阶段，人口可达性大幅上升，需求吸引系数的可达性在该时间段已经达到较高水平，原因可能是当天的出租车流量下降至前一天的31%，道路清空使得道路的服务水平提高，道路的周期性拥堵现象得到缓解. 人口吸引系数的可达性无法捕捉需求变化，对灾害的响应存在滞后性.

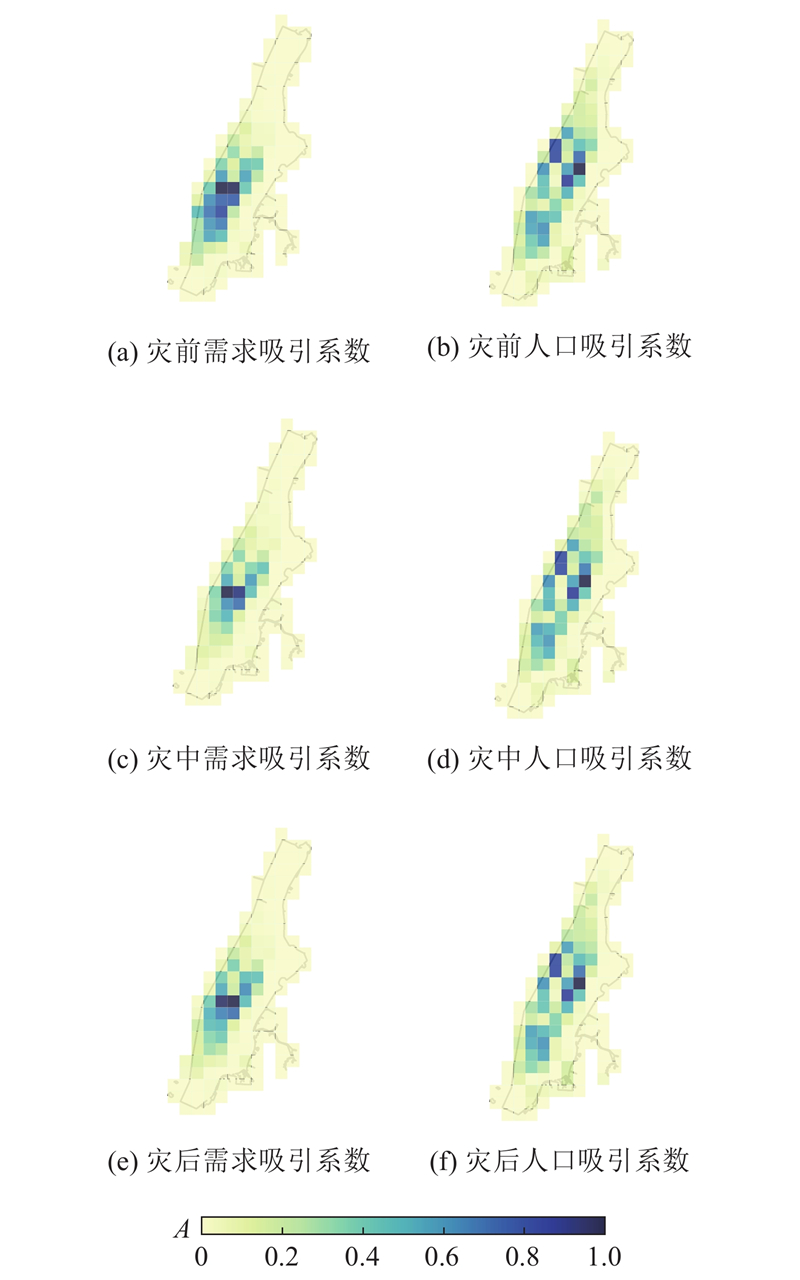
2类吸引系数在灾害不同阶段标准化可达性的空间分布如图3所示，其中每个格子的可达性均为平均值. 可以看出，2类可达性均较高的区域集中于上城区和中城区. 上城区是曼哈顿的市中心商业区，基础设施完善^[24]，以该区域为目标的经济活动较多，可达性处于高水平. 中城区为曼哈顿的高档住宅区，人口稠密，需求较大，在日常情况下该区域的可达性也处于较高水平. 哈莱姆区和下城区以住宅区为主，可达性水平较低，一方面是该区域基础设施较为落后，另一方面是该区域远离市中心，居民倾向于使用其他交通工具出行，导致该区域内的出租车流量较少，可达性较低. 在哈莱姆区，人口吸引系数的可达性处于中等水平而需求吸引系数的可达性处于较低水平，这可能与人们的出行方式有关. 人口吸引系数的可达性空间分布在灾前、灾中、灾后3个时段的变化不显著，可达性在灾中下降8.2%，灾后回升了4.4%，并且在不同区域的变化类似，说明灾害对人口吸引系数的可达性空间分布的影响较小. 需求吸引系数的可达性在灾中的中城区下降了14.4%，灾后回升了18.1%；在下城区下降了42.1%，灾后回升了38.3%，主要原因是商业区附近的基础设施密集，受灾害的影响较大. 灾中和灾后流量分布变化与需求吸引系数的可达性分布变化基本相似，说明需求吸引系数的可达性很好地描述了灾害在空间上对流量影响，符合灾害下出租车出行需求大幅变化的实际情况.

综上所述，相比人口吸引系数，需求吸引系数能够更好地描述灾害下路网的性能变化，它能够更好地在空间上体现灾害对流量的影响，在时间上体现灾害下需求结构的变化.

实际车费与行程时间的关系接近于线性、指数和对数关系^[19]，为此将重力型阻抗函数分为3类，表达式分别为

(10)$ {C_{ij}} = a{t_{ij}}+b, $

(11)$ {C_{ij}} = {t^a_{ij}}+b, $

(12)$ {C_{ij}} = a {\ln \;({b{t_{ij}}+c}}). $

式中：${C_{ij}}$为区域$i$到区域$j$的旅行成本；${t_{ij}}$为起点区域$i$到终点区域$j$的出行时间；a、b、c均为标定系数，结果如表1所示. 出行成本由出租车实际车费衡量，并以旅行时间为自变量，使用非线性最小二乘法拟合得到. 一般情况下，拟合优度R² >0.7，认为拟合程度较好，由表可知，3类模型拟合效果均较好，因此使用这3类模型来估计重力型可达性的出行成本.

考虑到3类阻抗函数在形式上的相似性，使用皮尔逊相关系数r计算灾前、灾中、灾后阶段3种可达性的相关性. 皮尔逊相关系数是2个变量的协方差和标准差的商，值域为(−1.0，1.0)，绝对值越大表示2个变量的相关性越强，正值表示2个变量间正相关，负值表示负相关^[26]. 当|r|>0.7时，认为2个变量存在强相关；当0.5$\leqslant $|r|$\leqslant $0.7时，认为2个变量存在中等相关；当|r|<0.5时，认为2个变量弱相关. 累积机会型可达性的时间阈取为出行时间的不同分位数，以2%为间隔取50个时间阈值. 重力型和混合型的可达性采用线性的阻抗系数. 吸引系数为需求吸引系数.

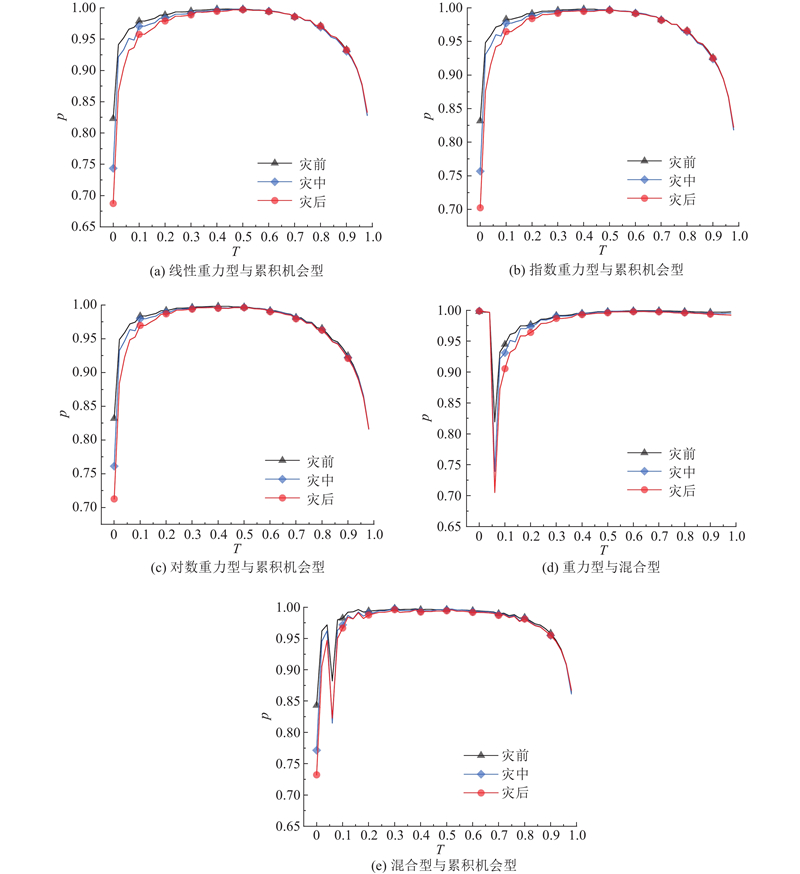
分别计算不同阻抗函数可达性的皮尔逊相关系数，绘制相关性曲线如图4所示. 由图4(a)、(b)、(c)可以看出，在灾害3个阶段的相似性曲线类似，均为先上升后下降，并且相关系数在时间分位数大于0.05后均超过0.8，为强相关性，说明累积机会型与重力型可达性有相似的变化趋势；随着灾害阶段的变化，相关系数曲线均呈现下降趋势，但是下降的程度不明显，说明灾害对2种可达性的相关性影响较小. 重力型与混合型可达性的相关性曲线如图4(d)所示，两者的相关性随时间阈增大而增大，当时间阈取为最大值时，混合型会退化为重力型，相关性为1.0；可以看出，当T > 0.15时，两者便显现出强相关性. 累积机会型与混合型可达性的相关性曲线如图4(e)所示，两者的相关性呈先上升再下降再上升的趋势，前一个峰值出现在T = 0.04的位置，两者的相关性会先下降再上升并超过0.9，并保持；采用极低的时间阈将会舍弃大部分数据，可以认为两者具有强相关性.

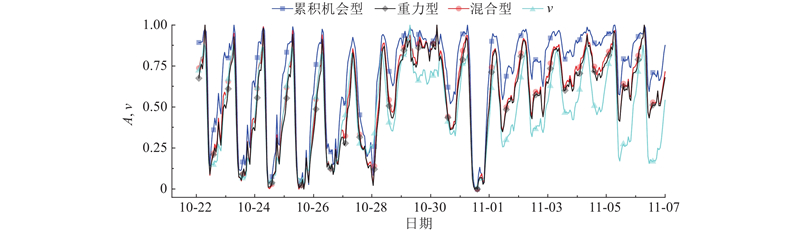
为了进一步分析3类阻抗函数的关系，分别选取行程时间的85%分位数作为累积机会型和混合型的时间阈，吸引系数为需求吸引系数，对3类可达性指标进行MAX-MIN归一化后的时变特征曲线如图5所示. 由图可知，混合型和重力型可达性曲线的变化基本重合，这符合两者在表达式上相似的特点. 累积机会型可达性比重力型可达性平均高25.7%，原因可能是累积机会型可达性是二元化的指标，当行程时间在阈值范围内时，阻抗函数便处于最大值；重力型可达性区分了不同出行时间的差异，只有当出行时间较短时可达性才会处于较高水平，长时间行程的存在使得重力型可达性偏低.

绘制3类阻抗函数标准化可达性差值A₁曲线，如图6所示. 由图可知，累积机会型可达性与重力型可达性的差值在一天内波动较大. 出行需求的时变特征如图7所示. 可以看出在早晚高峰累积机会型可达性与重力型可达性的差值处于一天内的最大水平，在晚间出租车流量较少时累积机会型可达性与重力型可达性都达到最小值，在灾中阶段出租车流量较低时累积机会型可达性与重力型可达性的差值也较低，说明流量的提升会加大2种指标的差异.

综上所述，3类阻抗函数在灾害的全周期均表现出较强的相似性，它们的可达性时变规律也基本相似，因此3类阻抗函数均可用于灾害下的可达性分析. 累积机会型可达性与重力型可达性的差值存在与出租车流量对应的峰值情况，说明3类阻抗函数的可达性变化趋势相似，均可体现灾害下路网性能的变化. 3类阻抗函数的可达性变化幅度存在差异，使用累积机会型可达性指标在出租车流量较高的时段有高估可达性水平的风险，在评估路网的实际性能时，重力型或混合型阻抗函数更符合实际情况.

为了验证可达性计算结果的可靠性，分析可达性的比较结果. 在图5可达性曲线的基础上绘制灾害全周期的标准化后出租车平均行驶速度v时变特征曲线. 经计算，在灾前阶段，3类阻抗函数可达性与v的皮尔逊相关系数均超过0.9，表现为强相关性；且3类阻抗函数可达性和速度的时变特性曲线高度重合，说明可达性在通常状况下与速度的时变特性相似，可以认为可达性指标与传统指标（如速度）在灾前有相似的变化规律，证明可达性的计算结果具有可靠性.

对比分析时空比较方法与皮尔逊相关性系数比较方法的优劣. 分析结果显示，在灾害的整个过程中3类阻抗函数可达性的皮尔逊相关系数都超过0.8，呈现强相关性，这与Kapatsila等^[19]的实验结论相似. 这种强相关性并没有因为灾害的出现而遭到显著的破坏，与交通线路重新设计前后可达性指标间的相关系数较低^[20]的结论相反，原因可能是外部因素（如天气因素）对阻抗函数的相关性影响较小，而内部因素（如路网的大规模改道）会显著影响相关性. 因此，只使用皮尔逊相关性比较的方案不能体现极端天气对可达性的影响. 本研究采用时空特征分析的方法绘制灾害全阶段的可达性时变特性曲线(图5)和空间分布变化图(图3)，能够直观地体现灾害对路网的影响. 本研究认为结合皮尔逊相关系数和时空特征分析的方法可以有效地分析不同路网可达性指标在极端天气下的性能.

为了评估灾害下的路网性能水平，使用需求吸引系数和线性重力型阻抗函数组成的可达性指标研究灾害全周期的时变规律. 灾前的可达性曲线呈现周期性的高峰低谷现象，夜间可达性处于较高的水平，白天（主要时段为7: 00—18: 00）可达性处于较低水平，这与人们在日间的出行高峰现象对应. 在灾中阶段，灾前的周期性遭到很大程度的破坏，具体表现为29日整天的可达性均处于较高的水平，原因可能是美国气象部提前发布了飓风的预报^[1]，人们的出行受到很大限制，在29日的出租车流量锐减70%，使得道路被清空，行程时间大幅减少，可达性也因为行程时间的减少而上升. 在30日，在台风实际登陆后的第二天，可达性显著下降，11: 00以后的流量上升，说明当天人们的需求有一定程度的恢复，流量的增多导致可达性下降. 在31日可达性到达低谷，当日的8: 00—18: 00道路的可达性处于极低水平.

如图8所示为行程时间的时变特征，可以看出，31日的行程时间均处于极高的水平，原因可能是城市道路出现大范围的拥堵，出现拥堵与灾害对道路的破坏有关，人们出行成本的大幅提高导致可达性大幅下降. 在灾后阶段，可达性呈现逐步上升的趋势，这可能与灾后路网的修复工作有关，随着道路服务水平不断提升，行程时间持续下降，与此同时流量需求仍在缓慢恢复，道路仍处于较为空旷的状态，可达性仍处于较高水平. 通过对灾害全周期的分析，所提可达性指标能够同时体现灾害对出行时间和需求变化的影响. 在灾中和灾后的可达性总体上高于灾前的可达性，说明灾害使道路清空的现象间接降低了仍在路网上行驶的车辆的出行成本，提高了区域间的互动能力. 此外，极端天气对路网功能的影响显著，尤其是在灾中和灾后的交替时段，路网的可达性大幅下降.

需求吸引系数能够有效描述灾害对城市路网的影响. 长期以来，城市一般使用人口规模或兴趣点总数量化可达性的吸引系数，这不适用于灾害下需求明显变化的情况. 在曼哈顿区，使用人口规模计算得到的可达性空间分布在灾害的全周期内基本不变(图3(a)、(b)、(c))，但在使用需求吸引系数时，下城区的可达性在灾中下降42.1%，灾后回升38.3%，具有明显的先下降再上升的过程(图3(d)、(e)、(f)). 该变化过程符合实际情况，因此使用动态的需求因素可以更有效地体现出灾害对城市路网的影响.

灾害下3类阻抗函数的功能相似，但可达性变化幅度不同. 在飓风“桑迪”灾前、灾中、灾后3个阶段的阻抗函数对比中，3类阻抗函数可达性的皮尔逊相关系数均超过0.8 (图4)，说明3类可达性指标的变化趋势相同. 累积机会型忽略了长时间行程对可达性的影响，使累积机会型比重力型可达性平均高25.7%，因此重力型或混合型阻抗函数组成的可达性指标对可达性的评估更加准确，建议使用行程时间的50%~85%分位数作为混合型的时间阈值.

飓风灾害会使路网可达性水平显著上升. 灾中和灾后的路网可达性整体高于灾前(图5)，主要原因是需求大幅降低导致道路清空，路网的可达性在灾中和灾后较灾前分别提升了45.5%和40%. 灾中和灾后的交替时段路网可达性降至最低，也与灾害结束时路网需求的恢复有关. 因此，应密切关注灾害下道路流量的变化，并结合城市路网可达性的时空变化制定道路管控和修复计划. 同时，灾后的修复资源调配和其他恢复准备工作应早于灾害结束，从而避开灾害刚结束时路网可达性最低的阶段，加快灾后恢复的速度.

灾害对基础设施相对较少的区域影响更为显著. 在灾中阶段，基础设施密集的中城区可达性下降了14.4%，住宅区的可达性下降了57.9%(图3(b)、(c)). 因此，在灾中和灾后的恢复工作应着重考虑基础设施相对较少区域的道路恢复，建议将修复资源更多地调配至基础设施稀疏的区域（如住宅区），从而更有效地支持灾后重建工作.

本研究基于美国纽约州曼哈顿区的黄色出租车数据，对飓风“桑迪”下曼哈顿区的2类吸引系数和3类阻抗函数组成的可达性指标进行对比分析. 结果表明，使用动态需求作为吸引系数能够更好地体现灾害对城市路网的影响. 3类阻抗函数在灾害全周期内均高度相似，但累积机会型可达性会高估路网性能，证明了灾害下使用重力型或混合型阻抗函数组成的可达性指标的优越性. 选取可达性指标进一步分析曼哈顿区在飓风“桑迪”下灾前、灾中、灾后的可达性变化，揭示了可达性在3个阶段的变化情况，从时间和空间上分别给出飓风天气下城市路网的恢复建议. 本研究以曼哈顿地区为例分析极端天气的可达性时空变化，未来计划对人口密度较小、需求较少的地区（如郊区）开展相关研究，从而更全面地了解城市交通在极端天气下的可达性变化规律.