第19届亚运会于2023年9月23日—10月8日在杭州举行. 大气污染物质量浓度的超标对运动员危害严重，易引起人体感官和生理机能的不适, 刺激运动员的心血管和呼吸系统，影响运动员的比赛发挥甚至身体健康^[1]. 因此，在亚运会场馆及周边数公里范围的重要微尺度保障区域，应对突发性大气污染，确定污染源的位置和强度进行靶向治理，对提升城市环境和保护运动员健康都有重大意义.

国内外大气污染溯源的已有研究主要包括排放源解析和扩散模型法. 排放源解析方法着重通过分析各个区域贡献比例和行业比例的大气污染排放数据进行污染溯源. Qiu等^[2]通过土地覆盖数据集进行排放源估算，得到的结果是中国的6项污染物排放的主要来源是农田燃烧；Huang等^[3]结合监测数据解析了南宁市一次PM_2.5污染的成因，发现生物质燃烧和二次无机源污染占比最高；Tian等^[4]分析了馏分中的化学成分，发现扬尘与柴油车是产生颗粒物污染的前2位因素. 上述排放源解析方法，可以将大气污染物排放的来源解析到行业、区域组分中，为污染的治理提供策略，但是他们的缺陷是须进行化学组分的分析，成本高昂，需要全面的监测数据，数据来源复杂. 此外，这些方法致力于确定省际或地区的大范围污染排放来源，对于确定污染源的地理位置有所欠缺，难以适应微尺度的污染来源分析^[5]. 扩散模型方法为数值模拟方法，考虑风速、风向、地理条件等因素影响和气体扩散方程，建立气体扩散模型，运用数学模型模拟大气污染物的排放、扩散、沉降等过程. Liu等^[6]使用伴随概率方法建立了流体动力学模型，能识别污染物位置和释放时间；Wang等^[7]提出几种基于混合遗传算法的STE复合代价函数，对污染源位置进行估计；贝叶斯方法和马尔可夫链蒙特卡罗抽样方法也在源强反算中得到验证^[8]. 上述扩散模型法可以快速实现气体泄露源的定位和源强反算，求解效率高. 但当前此类方法多针对有毒气体的泄露和核泄漏问题，其验证方法也基本停留在仿真模拟阶段，无法验证该方法在真实气象条件和地理环境下搜索PM_2.5污染源的位置和强度的可行性、准确性和即时性.

高斯烟羽模型常常被用于污染扩散溯源的正向大气扩散模型中^[9-11]. 也可以通过满足修正系数的方法应用在PM_2.5污染物的扩散场景里，比如He等^[12]使用改进修正因数的方法预测PM_2.5的扩散过程. 遗传算法通过模拟生物进化过程搜索最优解，可以应用在源项反算的搜索阶段. Akcelik等^[13]根据扩散方程建立了源强直接优化求解的方法, 但是这种方法对初值依赖性较大；Ma等^[14]提出吉洪诺夫与粒子群耦合算法，并对潜在危险气体源参数进行了反演求解, 但目前尚不能投入使用；Thomson等^[15]发现模拟退火算法和随机搜索算法对源强反算具有良好的鲁棒性. 通过耦合遗传算法和模式搜索算法，结合遗传算法的高效全局搜索能力和模式搜索算法的局部搜索效率，增强污染溯源模型的搜索效率和准确率.

为了解决几十到几百公里的微尺度区域的空气监测和污染溯源问题，填补此类方法的空缺，对可能出现的突发性大气污染进行准确高效的污染源源头追溯，提出结合高斯烟羽模型和遗传-模式搜索算法的大气污染溯源方法. 通过高斯烟羽模型建立污染源反算模型，将污染源反算模型得到的污染物理论质量浓度与传感器网络观测到的实际质量浓度匹配关系作为适应度函数，使用模式搜索算法嵌入遗传算法加快反算模型的搜索过程，达到快速定位污染源的目的.

微尺度管控区域污染溯源问题是源强反算问题. 根据源强分布场中点的理论质量浓度，寻找最佳的源强分布场，使得源强分布场中点的理论质量浓度尽可能接近观测值.

首先构建物理意义上的大气污染源反算模型，使用高斯烟羽模型作为大气污染物扩散模型. 高斯烟羽模型假定在均匀、定常的湍流大气中，大气污染源下风向污染物浓度分布服从正态分布. 实际大气不满足均匀定常条件，由此可以根据地形、气象条件和排放源几何形状的特殊性推导出一系列高斯扩散模式^[16]. 目前，高斯烟羽模型是广泛应用于模拟大气污染物扩散的模型. 以PM_2.5污染源位置为坐标原点，设定流程坐标系，x方向为风向. 高斯烟羽模型的质量浓度（即理论质量浓度$ {\rho }_{\mathrm{c}\mathrm{a}\mathrm{l}} $）表达式如下：

(1)$ \begin{split} {\rho }_{\mathrm{c}\mathrm{a}\mathrm{l}}=&\rho (x,y,z)=\frac{q}{2\text{π} u{\sigma }_{y}{\sigma }_{z}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{y}^{2}}{2{{\sigma }_{y}}^{2}}\right) \times \\&\left\{\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{\left(z-H\right)}^{2}}{2{{\sigma }_{z}}^{2}}\right]+\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{{\left(z+H\right)}^{2}}{2{{\sigma }_{z}}^{2}}\right]\right\}.\end{split} $

式中：$ \rho (x,y,z) $为监测点在点$ (x,y,z) $处的质量浓度，q为大气污染源排放源强，u为平均风速，H为排放源高度$ ，{\sigma }_{y} $为气体污染物的水平扩散系数$ ，{\sigma }_{z} $为气体污染物的垂直扩散系数.

扩散系数的取值随着大气稳定度的改变而改变. 大气稳定度是影响污染物在大气中扩散的重要因素，通过风速、太阳辐射强度确定大气稳定度的等级. 如表1所示为大气稳定度的分类，如表2所示为扩散系数^[17]. 表中，v为风速. 通过表1、2的匹配，确定大气稳定度并获得扩散系数. 从而可在污染源位置和源强已知的情况下计算大气污染物在区域任意位置的质量浓度. 然后，实时采集大气污染物质量浓度数据和气象数据. 在微尺度管控区域布设大气污染感知器网络，监测各个感知器点位PM_2.5的质量浓度和风速风向数据. 由气体扩散模型（式（1））计算得到点（$ {x},{y},{z} $）的理论质量浓度为$ {\rho }_{\mathrm{c}\mathrm{a}\mathrm{l}} $, 由该位置大气污染感知器i上传的测量浓度为$ {\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}}^{{i}} $. n台大气感知器点位理论质量浓度与测量质量浓度的误差平方和表达式如下：

(2)$ f\left({x},{y},{z},{q}\right)= \sum _{{i}=1}^{{n}}{\left({\rho }_{\mathrm{m}\mathrm{e}\mathrm{a}}^{{i}}-{\rho }_{\mathrm{c}\mathrm{a}\mathrm{l}}\right)}^{2}. $

所求f最小（趋近于零），即PM_2.5污染源位置和源强最接近实际污染源.

$ {\rho }_{\mathrm{c}\mathrm{a}\mathrm{l}} $由式（1）得出，代入式（2）可以得到

(3)$\begin{split} f\left( {{{{x}}},{{{y}}},{{{z}}},{{{q}}}} \right) =& \sum\limits_{{{i}} = 1}^{{n}} {\left[ {\rho _{{\rm{mea}}}^{{i}} - \frac{{{q_0}}}{{\text{π} u{\sigma _{y}}{\sigma _{z}}}}} \right.} \exp \;\left( { - \frac{1}{2}} \right. \times \\&{\left. {\left. {\left( {{{\left( {\frac{{{y} - {y_0}}}{{{\sigma _{y}}}}} \right)}^2} + {{\left( {\frac{{{z} - {z_0}}}{{{\sigma _{z}}}}} \right)}^2}} \right)} \right)} \right]^2}.\end{split} $

式中：（x₀，y₀, z₀）为污染源位置，q₀为污染源源强.

至此，将污染源的溯源问题通过气体扩散模型和数学变换转化为式（3）的解的最优化问题.

为了达到微尺度管控区域大气污染管控的精确性和即时性，要求溯源用时较短，污染源追溯结果较精确，提出使用遗传-模式搜索算法对模型进行求解. 遗传算法是广泛应用的进化算法，在最新的研究中遗传算法常与其他算法进行耦合增强其搜索性能^[18-19]. 在遗传算法模型中，通常选用适应度作为目标函数（式（3））的评价的指标参数，适应度越高，解越接近真实值，且适应度要求为非负（零或正数）. 适应度定义如下：

(4)$ {\gamma }=\frac{\exp\;\left({-\left|f\left({x},{y},{z},{q}\right)\right|/T}\right)}{\displaystyle {\sum} _{{i}=1}^{{n}}\exp\;{\left(-\left|f\left({x}_{{i}},{y}_{{i}},{z}_{{i}},{q}_{{i}}\right)\right|/T\right)}}. $

式中：T为可调节常数. 可以看出，目标函数的f越小，则适应度$ {\gamma } $越高. 因此，当污染源源强和位置参数取到真实值附近时，适应度最大.

在求解模型过程中，遗传算法的“选择”步骤中使用roulette算法. roulette算法是常用的选择方法，在该方法中，各个个体的选择概率和其适应度成比例，适应度越大，选中概率也越大. 为了保留适用性强的个体，以父代中适应度大的个体替换适应度小的个体；对适应度最大的个体，直接复制到子代. 通过遗传操作获得新的种群，直到达到设定的迭代次数.

模式搜索法用于解决最优化问题，在求解函数最大值时，通过找出接近梯度方向的向量、沿着该方向进行变化调整来搜索极值。本研究将遗传算法和模式搜索法结合起来，以遗传算法为主体，再对族群中的最差群体引入模式搜索算法增强搜索能力，从而加快模型的收敛速度。

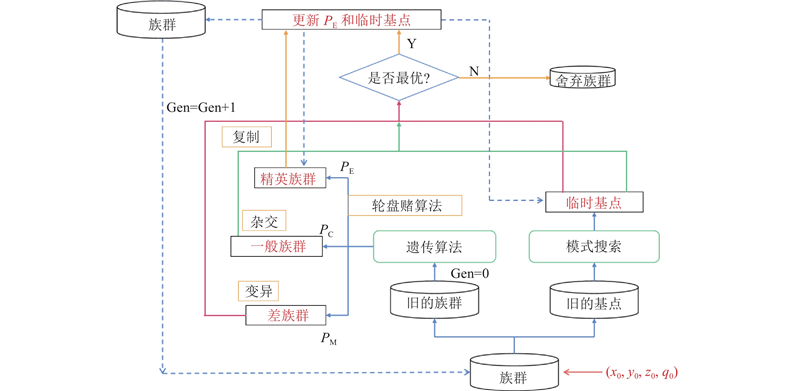
如图1所示为将模式搜索算法嵌入遗传算法的流程图. 图中，P_M、P_C、P_E分别为遗传算法的变异率、交叉率和选择率. P_E是对精英子代直接保留和选择的概率. 同时将遗传算法中复制和杂交筛选出的族群适应度与模式搜索算法产生的临时基点适应度进行比较，选择其中的最优点更新P_E和临时基点，得到下一代的新群体和新基点. 遗传-模式搜索混合优化算法可以弥补遗传算法收敛速度较慢及模式搜索算法初值敏感的不足.

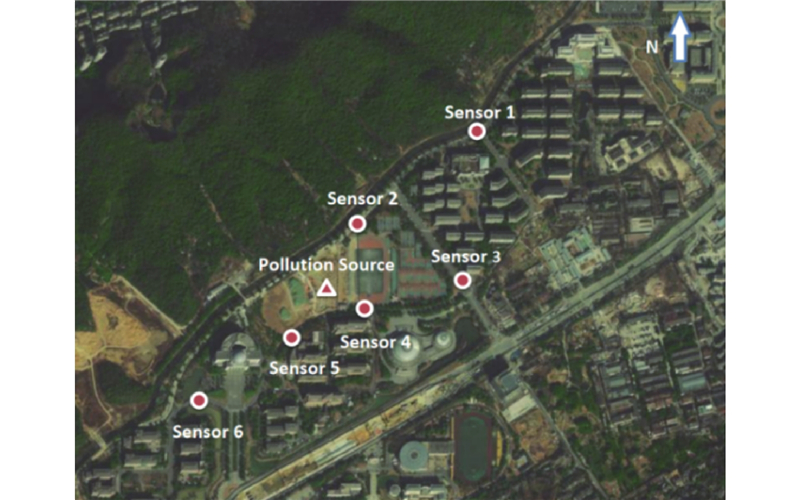
采用的亚运场馆管控区域为杭州市西湖区亚运会板球场馆区域，在管控区域周边布设大气污染感知器. 大气污染感知器为实验室自主研发，可以采集PM_2.5、PM₁₀质量浓度，风速风向，温度等数据并上传服务器端进行数据处理和分析. 将大气污染感知器布置在管控区域地势开阔、建筑物遮挡物较低的道路旁组成杭州市亚运板球场馆大气感知器网络. 所使用的数据区间为大气污染感知网络采集的2021年10月大气污染感知器网络观测到的数据. 大气污染感知网络布置位置如图2所示，实验期为2021年10月1日0时—2021年11月1日0时，与亚运会举办时间气候接近. 大气感知器网络数据包括6台大气污染感知器上传的PM_2.5质量浓度数据、PM₁₀质量浓度数据、风速数据、风向数据，上传频率为15条/min，如表3所示. 表中，N为数据条数.

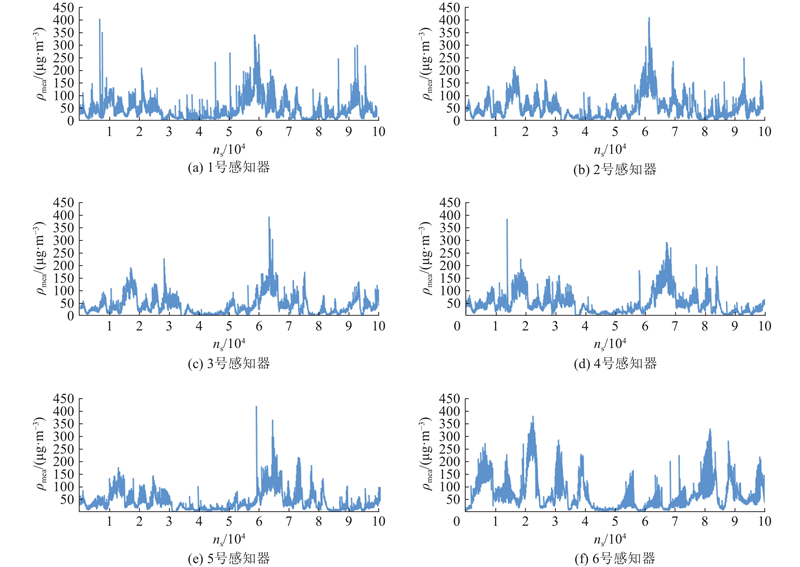
如图3所示为6台感知器的PM_2.5监测数据折线图. 图中，n_s为时序编号. 各台感知器上传的PM_2.5质量浓度数据显示，6个监测点位的PM_2.5质量浓度变化较大，有明显的峰谷现象，高值达到近500 μg/m³，存在PM_2.5污染现象.

表3中各感知器采集的数据量庞大且无法直接应用，因此须对感知器上传的风速风向数据及PM_2.5质量浓度数据进行预处理. 首先，对6台大气污染感知器的数据进行时间序列的匹配；其次，对PM_2.5质量浓度数据异常值进行处理. PM_2.5质量浓度数据出现异常值的主要原因及处理方式如下. 1）由于颗粒物传感器的特性，监测设备偶尔会因外界环境的变化产生突发异常数据，如暴雨天气下，PM_2.5质量浓度数据偶尔会跳跃至负数或超出量程显示示数为9999，此类异常数据直接在预处理过程中予以剔除. 2）设备进行维护时会出现短暂的连续性数据缺失，针对这种异常值，直接剔除过于奢侈，使用多层感知器神经网络(multi-layer perceptron，MLP)的方法对数据进行补全. 为了减少计算负担，并满足数据须覆盖10月全月较长时段的要求，最终选取全月130000条数据进行反演.

使用多层感知器神经网络进行时序缺失数据的补全，MLP是一种前馈人工神经网络模型^[20]，常见于数据预测和数据补全. 输入PM₁₀质量浓度、温度、湿度、风速风向数据作为协变量，应用MLP预测方法对PM_2.5质量浓度数据中2%缺失数据段进行补全，如图4所示为1号感知器数据缺失时段预处理后的PM_2.5质量浓度数据。

在实验期间的亚运会板球场馆大气质量监测范围内，因为存在建筑施工、建筑物料搬运、地面垃圾焚烧等活动，污染物质量浓度远高于其他区域的. 以污染高值区域作为PM_2.5污染源原点，根据《污染源源强核算技术指南》（HJ884-2018）^[21]核算得到PM_2.5污染源源强为1.39 g/s，即污染源为（0，0，0，1.39）.

在实验期间，以某时刻实验数据为例，该时刻大气稳定度为D，风向为东偏南45°，风力为2 m/s，各感知器PM_2.5质量浓度观测值如表4所示.

利用遗传-模式搜索算法对目标函数（式（3））进行寻优，结果如表5所示.

当循环次数为400次时，输出结果已经较好，且即使初值的选取偏离目标值较大，也能搜索到与期望值较接近的结果.

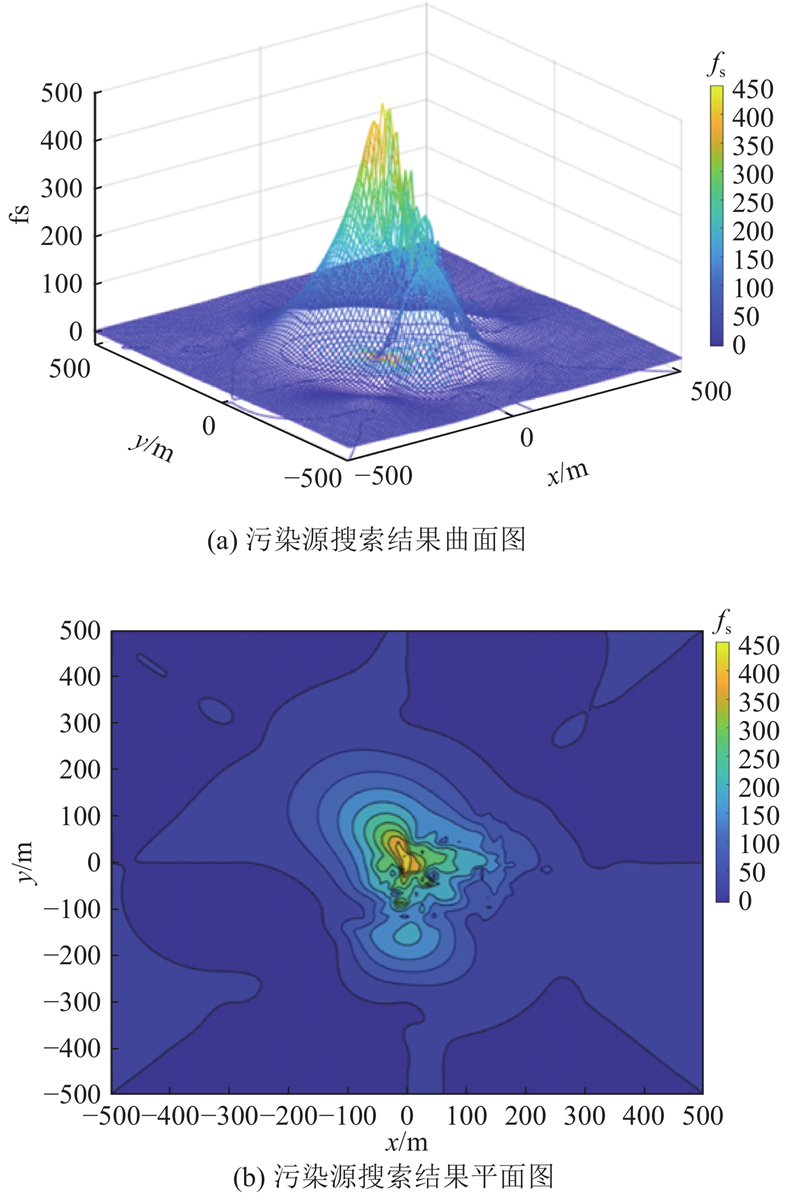
由于所使用的遗传算法可能出现算例抽样误差，使用10月全月780 000条PM_2.5质量浓度数据对污染源位置进行搜索，并将搜索次数结果拟合曲面显示在管控区域坐标系中，得到可视化的污染源定位结果，如图5所示. 图中，f_s为搜索次数. 显然，搜索结果较集中，且接近真实污染源位置（0,0），（0,0）位置附近搜索次数远高于管控区域内其他位置. 在x方向上，搜索结果偏离不超过5 m，y方向上偏离不超过30 m.

为了体现遗传-模式搜索算法在亚运会场馆大气污染物溯源问题上的优越性，与其他大气污染溯源方法进行对比分析. 适用于微尺度区域污染溯源的方法较少，其中基于机器学习方法进行气体污染溯源模型求解是目前较主流的方法. 选取遗传-Nelder Mead单纯形混合（GA-NM）^[22]算法、粒子群与单纯形耦合（PSO-NM）^[23]算法和遗传-模式搜索（GA-PS）算法进行对比. GA-NM算法是常见的气体污染溯源模型求解方法，以GA算法为主体, 采用群体分类的方式构建，其在毒气泄漏领域的应用较广泛，已经在仿真实验中得到了验证^[22]. PSO-NM方法，是在PSO算法执行后, 再执行NM算法寻优, 直到满足收敛条件，其在美国奥尼尔镇经典草场SO₂泄漏实验中得到过验证，效果较好^[23]，且有研究表明该方法在成功率和计算均值方面较有优势^[24]. 因此选用这2种主流方法与GA-PS算法在源强反演中开展对比研究.

仍以上述场景为实验对象，真实污染源$ （{x}_{0},\; {y}_{0},\;{z}_{0},\;{q}_{0}） $=（0, 0, 0, 1.39），选取10月PM_2.5质量浓度数据及风速风向数据共130 000条数据作为输入. 各算法循环次数均为1 000次，搜索结果如表6所示. 其中，源强取搜索结果的平均值，位置搜索结果取全月搜索结果的几何形心. 表中，t为响应时间，q₀为源强，x₀、y₀为位置变量，Δq₀为源强相对误差，Δx₀、Δy₀为位置变量绝对误差.

对其中位置变量（x₀，y₀）的结果进行研究分析，将各优化算法搜索次数拟合曲面的热点等高线图显示在管控区域坐标系中，如图6所示.

分析图6及表6中各算法的比较结果，结论如下.

1)运算时间. 由于使用模式搜索增强了局部搜索的能力，遗传-模式搜索的运算速度相比较单独使用遗传算法提升较大，相对其他典型优化算法在搜索速度上也有一定提升. GA-PS算法平均运算时间为2.44 s，比GA-NM算法（2.57 s）和PSO-NM算法（2.65 s）速度更快，在输入样本庞大的时候，其具有搜索速度较快的优势.

2)污染源源强反算. 对于源强q₀解的搜索，遗传-模式搜索算法的效果较好. 在算例中，q₀相对误差为7.2%，而GA-NM算法（24.5%）和PSO-NM算法（41.1%）的污染源源强误差较大，几乎不能获得较为准确的源强.

3)污染源位置搜索. 污染源位置的搜索精确度是微尺度污染溯源的重点. 对于污染源位置（x₀，y₀）的搜索，由图6可以看出，各算法对污染源反演的位置搜索结果的热点都较集中，GA-PS、GA-NM、PSO-NM算法的搜索结果分别为（−7.1 m, 4.8 m）、（−21.1 m，4.5 m）、（41.1 m，−35.0 m）. GA-PS算法的搜索效果最好，其x方向位置变量的搜索偏差不超过10 m，y方向位置变量搜索偏差不超过5 m，位置搜索精度最高，在3种优化算法中表现最好. 可以满足亚运场馆周边污染源的搜索要求.

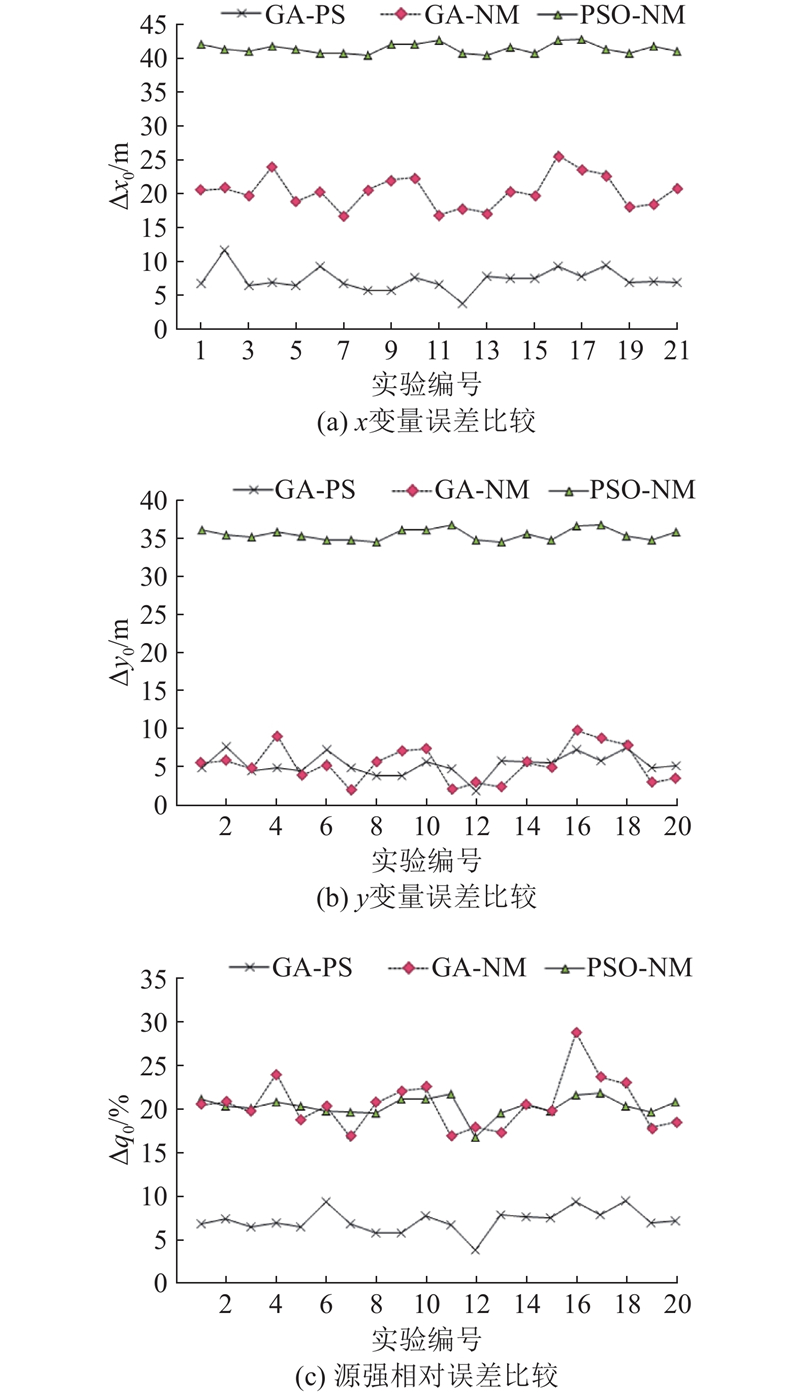
4)算法稳定性. 为了比较算法的稳定性，选取同一组数据，在多次实验中，x、y、源强参数在约500次循环达到收敛. 为了对比算法性能，使用3种算法进行20次运算，每次运算的循环次数均为1 000次. 输出的误差值如图7所示，GA-PS、GA-NM、PSO-NM算法的x方向位置变量绝对误差范围分别为6.5~11.7 、16.8~24.1、40.8~42.8 m，显然，PSO-NM算法对x方向位置参数的搜索稳定性最好. 在y方向位置变量的搜索稳定性上，PSO-NM算法也优于另外2个算法. PSO-NM算法对位置参数的搜索稳定性最好，而对于源强的反算，3种算法的稳定性没有明显优劣.

由上述对比可以得出，在微尺度管控区域大气污染物溯源上，GA-PS算法在搜索速度、污染源位置搜索准确度、污染源源强反算准确度等方面具有明显的优势. 实验结果显示，PSO-NM算法与GA-PS算法相比，没有受到遗传算法操作过程中随机性的影响，显然在求解稳定性方面具有优势，但PSO-NM算法很难准确求解出污染源的源强数值，而且对污染源位置的搜索精准度也远不如GA-PS算法的.

(1)结合气体扩散方程和遗传-模式搜索算法，构造了亚运场馆大气污染物PM_2.5的溯源算法. 有别于传统的仿真验证，在亚运会板球场馆进行应用，证明了该方法在真实气象条件和地理环境下搜索PM_2.5污染源的位置和强度的可行性、准确性和即时性.

(2)所提溯源方法在污染源位置多维变量搜索的应用上较为精准，且不受初值影响，即使初值远离期望值，也能得到较好的结果.

(3)所提算法适用于多维变量的搜索，相较其他优化算法具有搜索时间短、污染源位置搜索精确度高、污染源源强反算准确度高等优势，可以满足亚运会管控区域或其他类似物理场景中对于突发性气体污染防治的应急决策需要.

（4）本研究不足在于无法对同时作用的多个污染源进行溯源，下一步计划使用本研究的思路和方法，通过构造叠加的大气污染源扩散模型，进行多污染源溯源的研究.