小比例试验台是研究轮轨滚动接触行为与损伤机理的重要工具,与线路跟踪试验相比,具有经济、安全、高效、易控等优点[1];与数值仿真[2-4]相比,在某些成因复杂的轮轨损伤研究中能够无差异复刻服役轮轨材料的力学性能[5-7]. 其中,传统的缩尺双盘试验台[8-11]采用直径数十至数百毫米的圆盘状试样,基于圣维南原理能够较好地模拟轮轨接触点局部的材料损伤和磨耗行为,但无法考虑服役线路中的钢轨弯曲应力以及复杂边界条件造成的轮轨瞬态滚动振动因素;缩尺车轮-直轨试验台[12-13]的轮轨接触斑和重力角刚度更贴近于服役轮轨,但由于轨道长度有限,车轮的循环往复滚动必须经历周期性加减速,无法模拟长时间的稳态滚动接触,尤其是高速工况. 区别于以上两者,缩尺车轮-环轨试验台具有轨下离散支承结构,同时能够实现恒定速度及恒定蠕滑率下的循环滚动,更全面地模拟线路服役条件下轮轨相互作用. 例如,基于1∶5缩尺车轮-环轨试验台[14]开展轨枕空吊模拟实验以验证车辆-轨道耦合动力学模型,以及基于“V-Track”试验台[15]进行的2种摩擦调节剂在不同轮轨冲角下的效果对比试验. 然而,环轨的极小曲线半径与参数缩尺势必造成一定的模拟误差,其能否正确重现线路服役条件下的轮轨滚动行为,或试验结果定量推至现场时须作何修正,其核心在于缩尺车轮-环轨的滚动接触特性. 对此,Naeimi等[13,16-17]利用有限元法对比1∶5、1∶7缩尺车轮-环轨和1∶1全尺轮轨的接触应力、接触斑几何和钢轨疲劳寿命,随后对比车轮-环轨垂直布置和平行布置的模拟效果,最终选择1∶5的缩比搭建了垂直式的“V-Track”试验台并成功复现了钢轨接头激励下的动态轮轨力. 与“V-Track”试验台不同,轮轨滚动行为(wheel-rail rolling behavior,WRRB)模拟试验台[18]的环轨安装于回转台上,与车轮同时转动,最高速度可达380 km/h,但目前尚未正式投入试验. 除此之外,此类试验台的应用罕见于文献中,针对其滚动接触和磨耗特性的研究亦较少.
为了明晰缩尺车轮-环轨的滚动接触与磨耗特性,基于WRRB轮轨滚动行为模拟试验台的设计参数建立瞬态滚动接触有限元模型,于时域内重现滚动接触行为,并通过实验验证模型的合理性. 利用该模型求解实物实验中难以获取的轮轨力、弹性蠕滑率、接触应力、相对滑移速度矢量、钢轨磨耗深度,研究车轮驱动扭矩和运行速度对上述因素的影响规律,拟合得到其经验公式,为将来基于此类试验台的设计和试验工作提供理论依据.
1. 缩尺车轮-环轨滚动接触建模
1.1. WRRB轮轨滚动行为模拟试验台简介
图 1
1.2. 缩尺车轮-环轨瞬态滚动接触的有限元模型
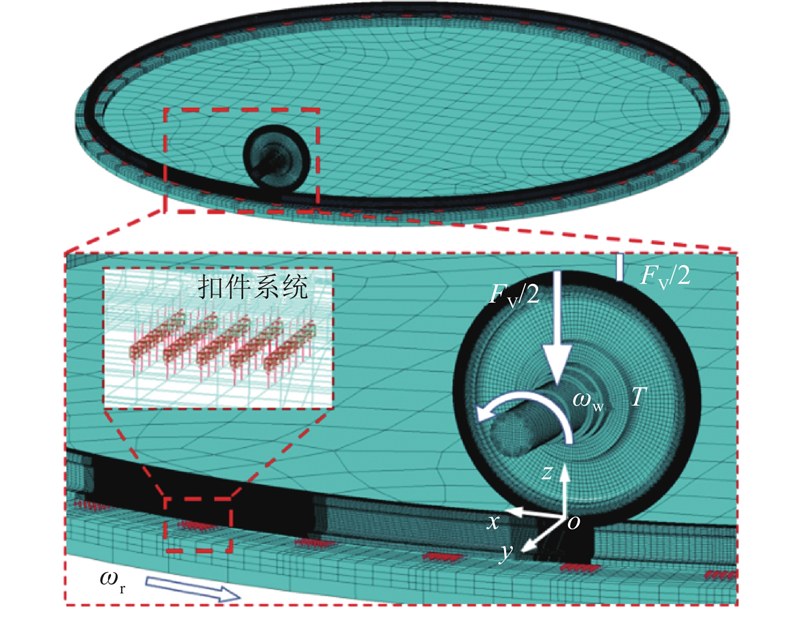
根据赵鑫等[19-20]的建模思路,利用ANSYS/LS-DYNA建立如图2所示的轮轨瞬态滚动接触有限元模型,模型参数如表1所示. 轮轨相对位置由轮背与轨距标定点的距离确定,对应现场中的轮对内侧距和轨距. 为了便于描述,建立如图2所示的笛卡尔坐标系,其原点位于轮轨静态接触点,x轴为钢轨纵向,y轴平行于车轴指向轮缘侧,z轴竖直向上. 钢轨设置1∶40的轨底坡,每组扣件下的橡胶垫离散为5×7的弹簧-阻尼单元阵列. 本研究不涉及扣件弹条性能退化、螺栓松脱失效工况,因此耦合每对节点的x和y向自由度,如此实现回转台与环轨的同步转动. 试验车轮由具有反馈回路的垂向液压加载装置进行加载,在模型中通过向车轴上直接施加恒定的垂向力来模拟. 回转台为几何结构复杂、刚度足够大的大型焊接件,故将其简化为具有绕z轴转动惯量的刚性圆盘. 轮轨接触采用基于罚函数的“面-面接触算法”进行求解,黏着系数取干燥清洁条件下的典型值0.5[21]. 由于轮轨长期服役后表层材料因加工硬化而强度得到提高,且工作状态多位于线弹性或安定区间内[22],车轮、环轨均考虑为线弹性材料本构并采用六面体网格进行离散. 为了提高模型的精度和求解效率,采用非均匀网格划分技术. 服役轮轨模型的细化求解区最小网格尺寸通常取约1 mm[2-3,19-20],而缩尺车轮-环轨的接触斑长短半轴长约为服役轮轨的1/3,为了保证接触斑覆盖足够多的网格,最小网格尺寸取0.33 mm. 最终有限元模型节点数和单元数分别约为260万、240万.
图 2
图 2 缩尺车轮-环轨瞬态滚动接触有限元模型
Fig.2 Transient rolling contact finite element model of scaled wheel-ring rail
表 1 轮轨瞬态滚动接触有限元模型参数
Tab.1
| 参数 | 取值 |
| 车轮名义滚动圆直径/m | 0.35 |
| 钢轨曲线半径/m | 1.6 |
| 轨枕间距/m | 0.21 |
| 轨枕支承长度/m | 0.043 |
| 轨底坡 | 1∶40 |
| 黏着系数 | 0.5 |
| 车轮质量/kg | 40.7 |
| 回转台转动惯量/(kg·m2) | 223.5 |
| 轮轨材料密度/(kg·m−3) | 7 790 |
| 轮轨材料弹性模量/MPa | 205 900 |
| 轮轨材料泊松比 | 0.3 |
| 轮轨材料阻尼常数 | 1.0×10−4 |
| 基座材料密度/(kg·m−3) | 7 850 |
| 基座材料弹性模量/MPa | 210 000 |
| 基座材料泊松比 | 0.3 |
| 基座材料阻尼常数 | 1.0×10−4 |
| 轨下橡胶垫刚度系数/(MN·m−1) | 5.05 |
| 轨下橡胶垫阻尼系数/(kN·s·m−1) | 12.78 |
为了使显式求解的轮轨力快速达到稳定,采用隐式-显式顺序求解方法数值重现轮轨瞬态滚滑行为:首先施加车轮垂向载荷和重力,隐式积分求解静态接触;随后将节点静态位移场作为初始条件,显式积分求解时域的瞬态滚动接触. 该方法的非完美初始条件引起的激扰须通过足够长的动态松弛区进行衰减. 经试算,动态松弛区取0.42 m(弧长,覆盖2跨)能保证车轮在进入细化求解区前达到准稳态滚动. 选用带有沙漏控制的缩减积分单元,以提高求解效率并克服“零能模式”. 受限于最小网格尺寸与材料属性,显式求解的时间积分步长取2.82×10−8 s. 施加沙漏控制后的单元在显式求解过程中不会畸变,因此该时间积分步长保持不变,显式求解得以稳定进行.
在试验台中使用单轮单轨进行模拟加载,不同于服役线路上全轮对的横移和侧滚相互耦合. 由于高速铁路正线上多为直线和大半径曲线,轮对横移量和轮轨冲角较小,本研究模型在求解过程中保持车轮的横移量、侧滚角、冲角为0. 具体边界条件设置如下:在隐式求解时,对回转台底面所有节点以及轴线上的节点平动自由度进行全约束,对车轴两端面和轴线上与轴承对应的节点约束x、y向自由度,随后为整个模型施加重力并对车轴施加垂向载荷. 在显式求解时,释放钢轨回转台底面节点的x、y向自由度以及车轴两端面的x向自由度,分别为车轮和回转台赋予初始转动速度. 车轮的驱动扭矩通过梁单元于车轴端面施加. 须说明,本研究模型未考虑环轨由直轨轧制成形时形成的残余应力,这是因为当轧制方向为横向,即环轨转轴与车轮转轴垂直时,轮轨接触斑靠近钢轨径向弯曲的中性层,此处的残余应力相对较低[13];此外,经轧制的环轨还会通过热处理手段尽可能消除残余应力,因此在建模时可忽略环轨径向弯曲的残余应力对其表面服役性能的影响.
1.3. 车轮-环轨蠕滑率定义
蠕滑率是表征轮轨滚滑行为的关键参数[23]. 虽然缩尺车轮的纵、横向刚体平动速度为0,但环轨的转动和弹性变形会造成两者的相对运动,因此在蠕滑率计算公式中引入环轨速度项:
式中:ξx、ξy和ξn分别为纵向、横向、自旋蠕滑率,ωw、rw分别为车轮的转动角速度和实际滚动圆半径,ωr、rr分别为环轨的转动角速度和轮轨接触点钢轨曲率半径,vyw、vyr分别为车轮、钢轨在接触区域附近的横向平动速度,ωnw、ωnr分别为车轮和环轨的角速度在轮轨接触斑处的法向分量. 为了尽可能地减小轮轨节点振动造成的误差,上述运动学变量均由多个节点的矢量结果平均得到. 须说明,不同于无量纲的纵向和横向蠕滑率,自旋蠕滑率的单位为m−1.
1.4. 模型验证
如图3所示为由有限元模型求解的纵、横、垂向轮轨力Fx、Fy、Fz随仿真时间tsim的变化以及垂向轮轨力随试验时间texp的变化,模型中垂向载荷和轮轨速度分别为10.0 kN和166.7 km/h. 可见,由于环轨的旋转效应以及轮轨转动惯量差异,轮轨力在细化求解区以前已趋于稳定但存在显著的波动. 具体而言,纵向力最终在0附近波动,波动幅值不超过0.10 kN,符合自由滚动的特征. 由于缩尺车轮-环轨的物理本质是极小半径曲线通过,轮轨间具有约1.33 kN的横向力,在细化求解区内的波动幅值不超过0.22 kN. 垂向力波动幅度最大,似乎与轮轨接触界面无不平顺激励的现实相矛盾,因此须验证轮轨瞬态滚动接触建模的正确性.
图 3
图 3 时域轮轨力仿真与试验结果
Fig.3 Simulation and experimental results of wheel-rail force in time domain
利用WRRB轮轨滚动行为模拟试验台开展滚动试验. 设定垂向载荷和轮轨速度分别为10.0 kN和166.7 km/h,通过控制液压加载器和驱动电机将轮轨力由0逐步提升至最大值,所得结果如图3所示. 可见,即使在轮轨接触界面平顺的情况下,轮轨力也呈现出明显的波动特性. 图3中,局部放大图展示了准稳态滚动时的轮轨垂向力的实测和仿真结果,为了方便对比,2条曲线的横坐标进行了一定的缩放处理,这是由于试验台与有限元模型的采样频率差异极大(分别为0.1 kHz和37.0 kHz),其轮轨力曲线无法在时域上对应. 但当数据点足够多且不存在周期性不平顺激励时,可认为数据涵盖原始信号的统计学特征,因此对准稳态滚动区间内的数据进行统计:有限元模型求解得到的轮轨垂向力平均值为10.42 kN,极差为平均值的20%;实测轮轨垂向力平均值为10.00 kN,极差为平均值的18%. 可见,仿真所得垂向力平均值和极差的相对误差分别为4.2%和11.1%,说明有限元模型能较为准确地模拟真实的缩尺车轮-环轨的滚动接触行为. 同时也可推断,轮轨力的波动来自于缩尺车轮-环轨本身的弹性连续体的高频振动,而非外界不平顺激励.
2. 模拟结果
2.1. 时域滚滑行为
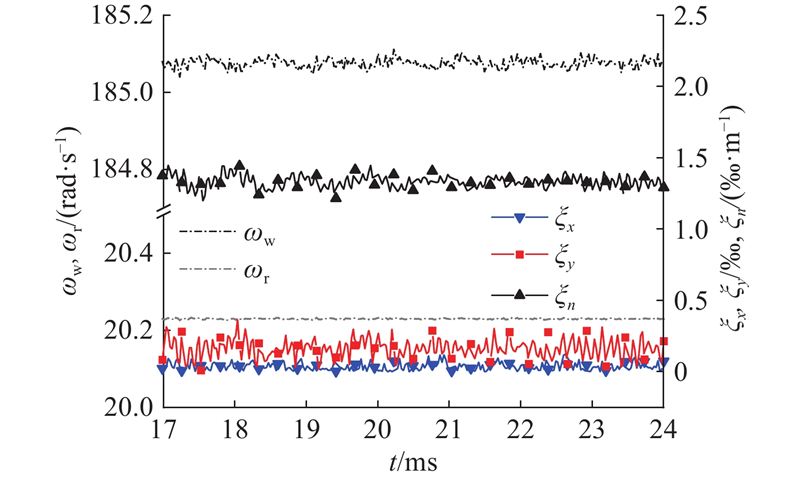
具有完整的轨下离散支承结构是缩尺环轨的主要特征之一,这使得此类试验台能更加完善地考虑钢轨弯曲效应和轨下离散支承刚度阻尼特性对试验对象的影响,因此保持和线路服役条件下相同的过枕频率,即取速度缩比为1∶3. 为了模拟线路服役条件下轴重为17 t、运行速度为350 km/h的高速轮轨的法向接触应力水平,取车轮垂向载荷为10.58 kN,轮轨初始线速度为117 km/h[24-26]. 求解得到的时域轮轨力与图3类似,仅有幅值方面的差异. 如图4所示为车轮与环轨的转速随时间的变化. 可以看出,由于模拟的是未施加驱动扭矩的自由滚动工况,且仿真时长仅为24 ms,两者的转速分别稳定在185.08、20.23 rad/s附近,名义线速度略低于初速度,分别为116.59、116.52 km/h,可认为未出现宏观滑动.
图 4
图 4 车轮/环轨时域转速及蠕滑率
Fig.4 Rotation speeds and creepages of wheel and ring-rail in time domain
如图4所示,还展示了蠕滑率随时间的变化. 可以看出,试验轮轨自由滚动时的纵向蠕滑率趋近于0,存在明显的横向和自旋蠕滑率,这是因为环轨的曲线半径极小,且本研究的蠕滑率计算公式中考虑了环轨与车轮的相对转动. 对细化求解区内的数据进行统计,得到纵向、横向蠕滑率平均值分别为0.04‰、0.16‰,自旋蠕滑率平均值为1.33‰ m−1.
2.2. 接触斑局部特征
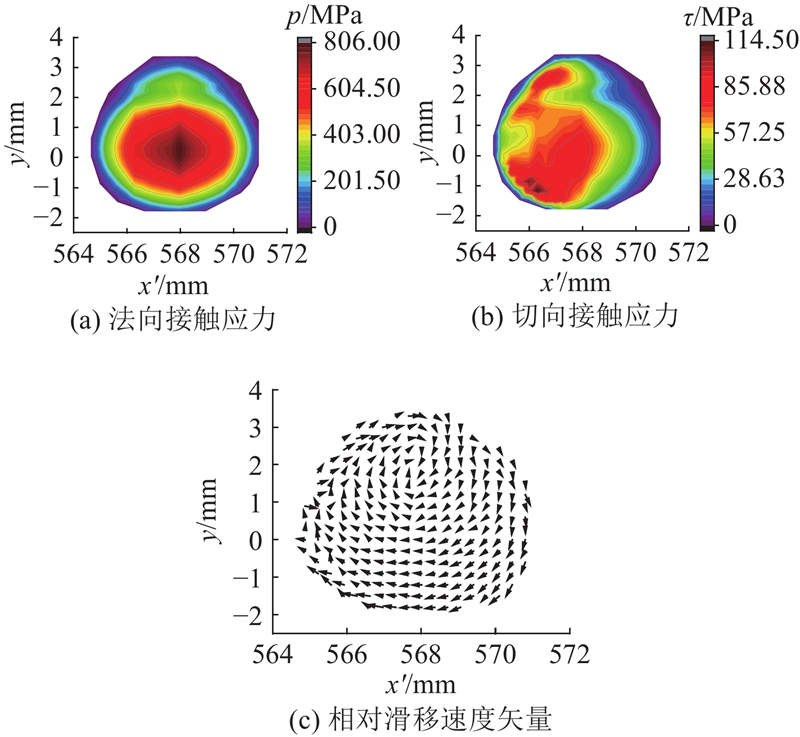
如图5所示为准稳态滚动下的接触斑节点的法、切向接触应力(p、τ)分布和相对滑移速度矢量. 为了方便观察,通过坐标变换将横轴转换为滚动距离x',并将原本弯曲的环轨从静态接触斑处展开成直轨进行展示(下文作相同处理). 可以看出,准稳态滚动时的接触斑符合LMA型踏面与CN60轨相匹配的接触斑形状[27]. 接触斑中心的最大法向接触应力为806.00 MPa,切向接触应力最大值出现在接触斑后沿,车轮尾部一侧的应力水平(114.50 MPa)高于轮缘侧(90.47 MPa),与线路服役轮轨的直线或大半径曲线通过工况下的接触应力分布形式具有显著的差别. 可以推断,由于该工况下未对车轮施加扭矩,此处的切向接触应力主要来源于轮轨横向力,而纵向力的贡献较小. 由图5(c)可以看出,接触斑内的节点存在明显的自旋现象,这反映了试验台模拟极小半径曲线通过的本质,也证明了图4中试验轮轨自旋蠕滑率偏高的结论是合理的.
图 5
2.3. 钢轨磨耗
式中:i为分析时刻,n为总时间步数,Δtw为时间步长;A和vi分别为节点(x, y)代表的面积和车轮滚动速度,细化求解区内接触面网格均匀,因此A为常数;上标T表示Tγ磨耗模型. 根据我国轮轨材料参数和接触应力进行折减和验证后的磨耗数
式中:τi、si分别为轨面节点(x, y)处的切向力和相对滑移速度. 当单元尺寸足够小,可认为该节点表示的区域内的材料磨损质量是恒定的,则磨耗深度wd可以表示为
式中:ρ为钢轨材料的密度.
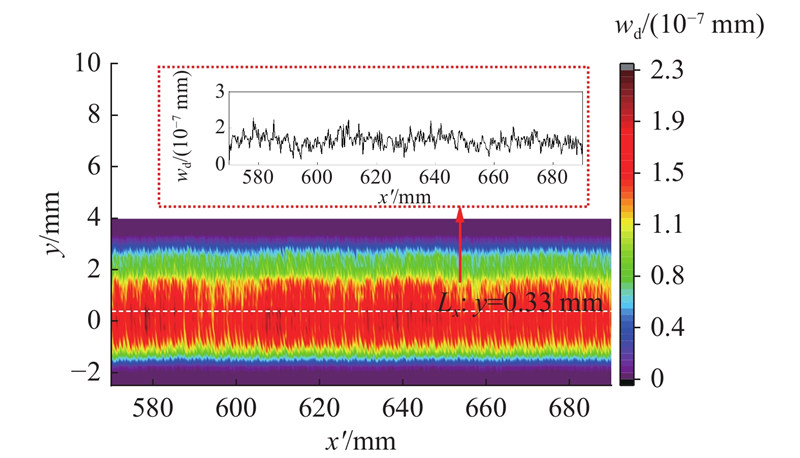
将钢轨细化求解区内所有表面节点的磨耗深度在时间和空间上进行叠加,即可得到车轮滚过后的钢轨磨耗深度分布. 如图6所示为环轨的磨耗深度wd云图,其中黑色曲线为纵向路径Lx(经过磨耗深度最大的节点)上的磨耗深度分布. 可以看出,钢轨最大磨耗深度为2.28×10−7 mm,钢轨磨耗光带与轮轨接触斑的横向位置一致,横向磨耗宽度约为4.2 mm. 钢轨在此条路径上的平均磨耗深度为1.65×10−7 mm,磨耗深度分布较均匀,无明显的周期性磨耗,符合平顺条件下钢轨磨耗特征.
图 6
2.4. 车轮驱动扭矩影响规律
车轮驱动扭矩是影响轮轨纵向动力学行为的重要参数,可用于模拟车辆牵引和制动工况,须研究其对试验轮轨滚动接触与磨耗特性的影响. 保持轮轨运行速度为117 km/h、黏着系数为0.5不变,对车轮施加不同的驱动扭矩(Mt=0~555 N·m),模拟不同牵引系数(μ=0~0.3)下的牵引工况.
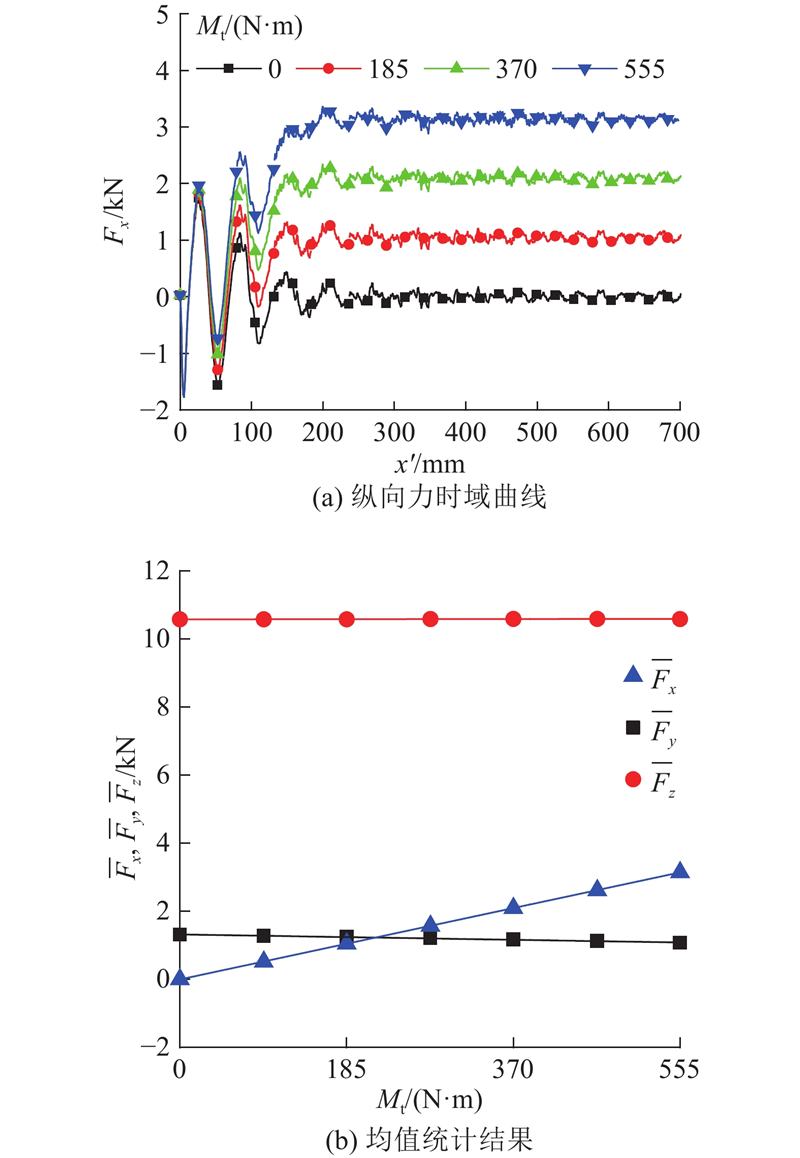
如图7所示为不同驱动扭矩作用下的轮轨力. 经计算,扭矩对横向力、垂向力以及准稳态轮轨力的波动特征几乎无影响,图7(a)给出纵向力的时域曲线, 图7(b)统计了三向轮轨力的平均值
图 7
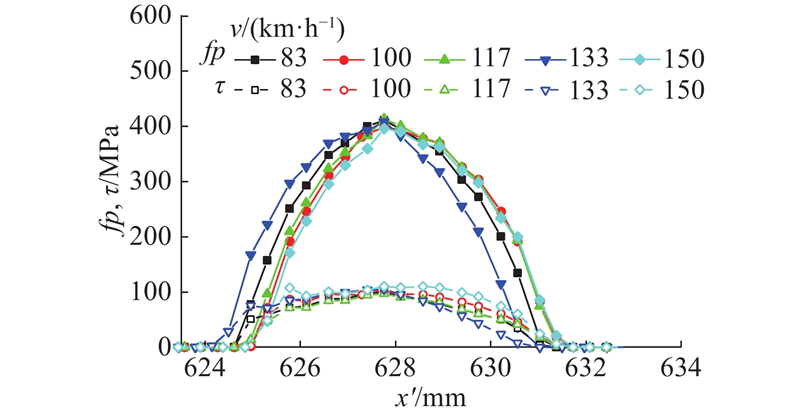
如图8所示为不同扭矩作用下的轮轨黏着系数与法向接触应力之积fp和切向接触应力τ的分布,以最大法向接触应力节点所在的纵向路径进行定量展示. 可见,试验轮轨在较大扭矩作用下的法、切向接触应力变化规律与服役轮轨的相似,接触斑前、后沿可根据Column摩擦定律明显区分出黏着区和滑移区. 不过,在扭矩不高于185 N·m的工况下,接触斑中央的切向应力高于其后沿滑移区. 法向接触应力受扭矩的影响较小,变化范围为795.21~827.28 MPa,而切向接触应力受到的影响更加明显. 具体而言,当扭矩为0、185、370、555 N·m时,接触斑后沿的切向接触应力水平分别为63.44、13.63、178.03、285.11 MPa. 值得注意的是,当试验轮轨自由滚动时,接触斑尚且存在一定的滑移区;当驱动扭矩为185 N·m时,接触斑滑移区和切向接触应力的变化不明显. 这是因为试验轮轨横向力偏高,贡献了一部分切向力,并且,试验轮轨在牵引工况下的滑移区更靠近轮缘一侧.
图 8
图 8 接触应力随车轮驱动扭矩的变化
Fig.8 Wheel-rail contact stress versus wheel driving torque
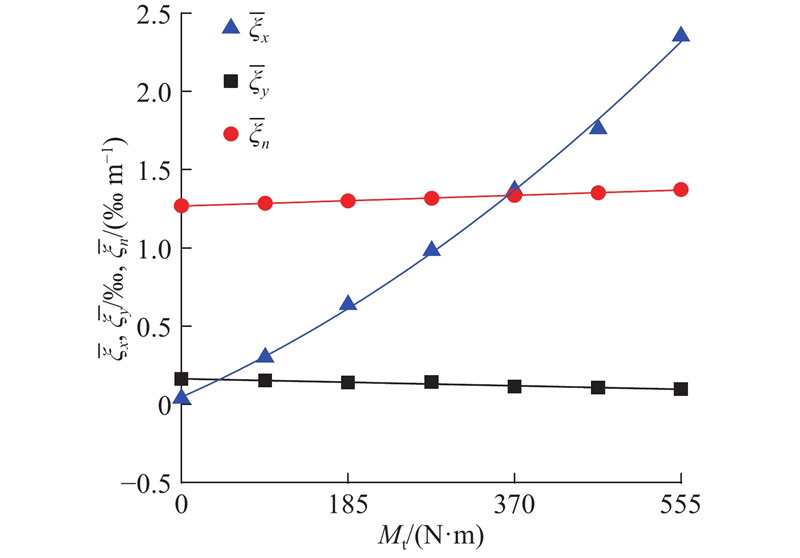
如图9所示,统计了不同驱动扭矩作用下的试验轮轨蠕滑率平均值
图 9
图 9 蠕滑率均值随车轮驱动扭矩的变化
Fig.9 Mean value of wheel-rail creepage versus wheel driving torque
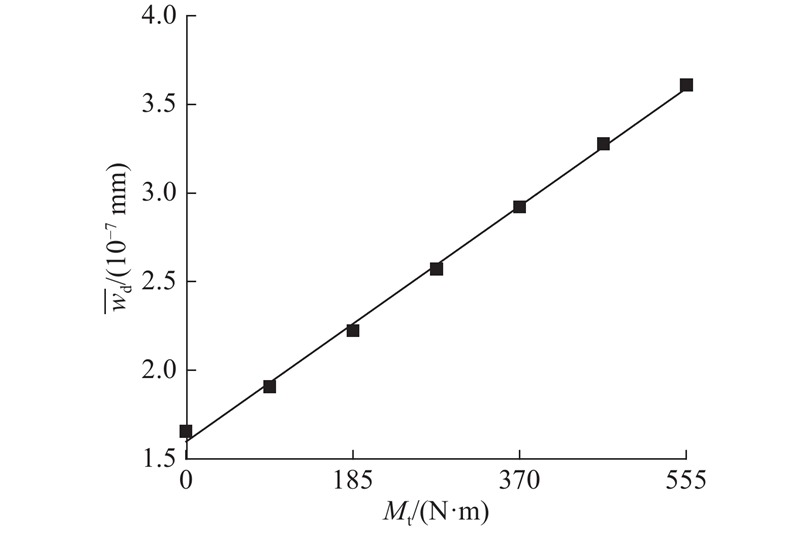
图 10
图 10 钢轨磨耗深度均值随车轮驱动扭矩的变化
Fig.10 Mean value of rail wear depth versus wheel driving torque
式中:
2.5. 轮轨速度影响规律
我国现役高速动车组最高设计速度为400 km/h,运营速度通常为250~350 km/h,设计速度为450 km/h的动车组研发工作也已纳入日程[34],未来有待利用缩尺车轮-环轨试验台开展高速轮轨滚动接触模拟及轮轨损伤机理试验. 为了对比分析试验轮轨在不同速度下的瞬态滚动接触行为,保持驱动扭矩为185 N·m(对应牵引系数为0.1)、黏着系数为0.5不变,针对不同速度(v=83~150 km/h)进行模拟.
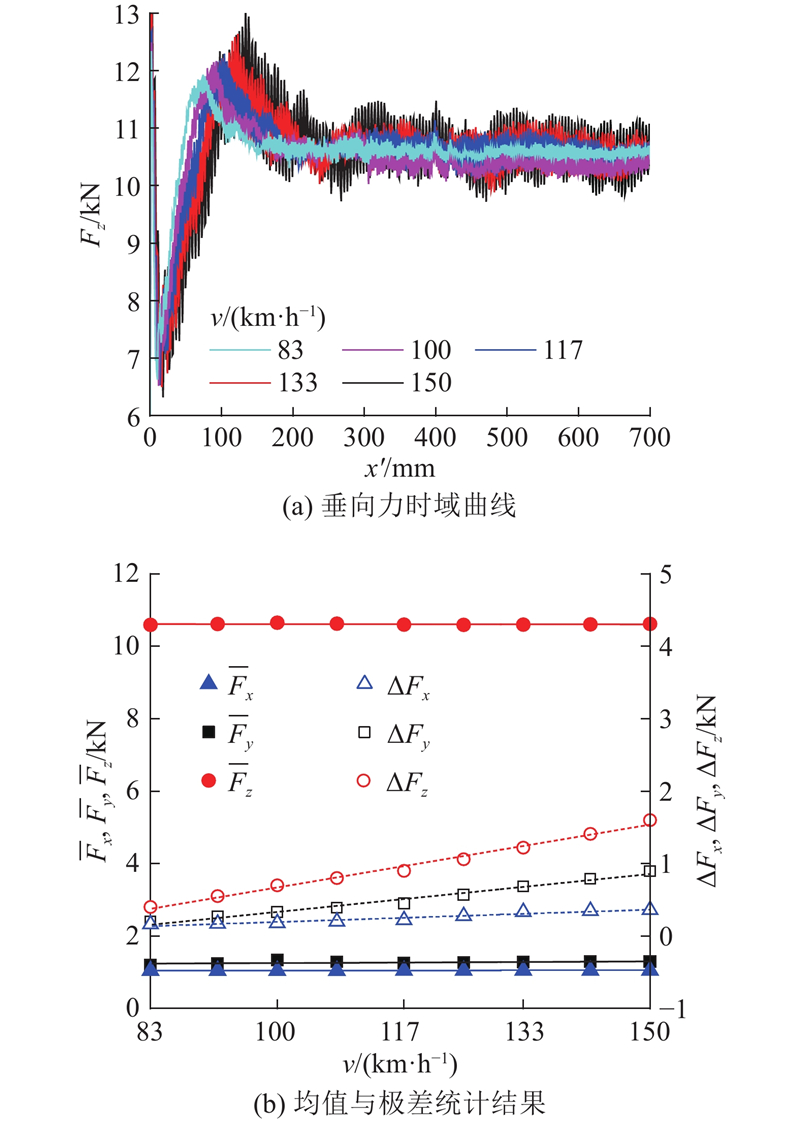
图 11
如图12所示为不同速度下达到准稳态滚动后的法、切向接触应力分布. 可以看出,运行速度对法向接触应力水平的影响不大,不同速度下接触斑黏着区和滑移区的分布也基本相同. 具体而言,法向接触应水平为791.83~827.28 MPa,相邻速度等级之间的变化量不超过25.5 MPa,而接触斑滑移区切向应力为13.62~50.76 MPa,总体水平不高,且滑移区切向接触应力水平低于接触斑中心.
图 12
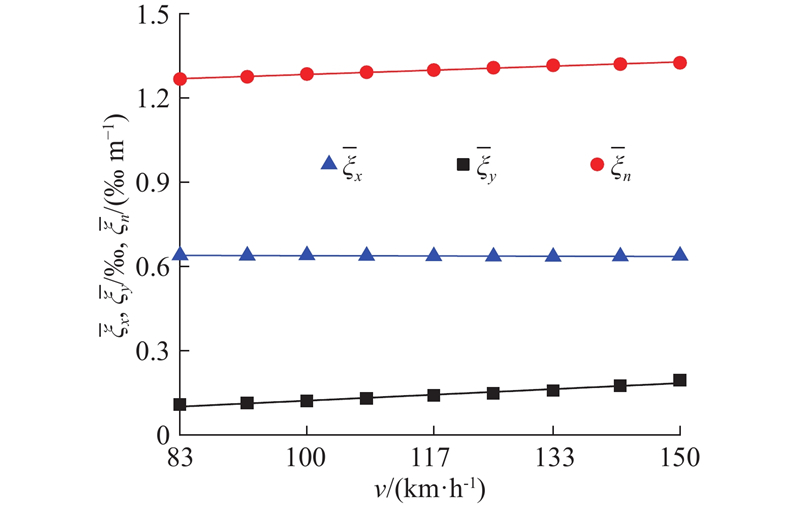
如图13所示统计了不同速度下试验轮轨的蠕滑率水平. 可以看出,在所有速度等级下,自旋蠕滑率都是最高的,纵向蠕滑率次之,横向蠕滑率最小,自旋和横向蠕滑率均随速度的升高而略微增大. 具体而言,速度从83 km/h增大到150 km/h,横向蠕滑率从0.11‰增大到0.19‰,自旋蠕滑率从1.27‰ m−1增大到1.33‰ m−1.
图 13
图 14
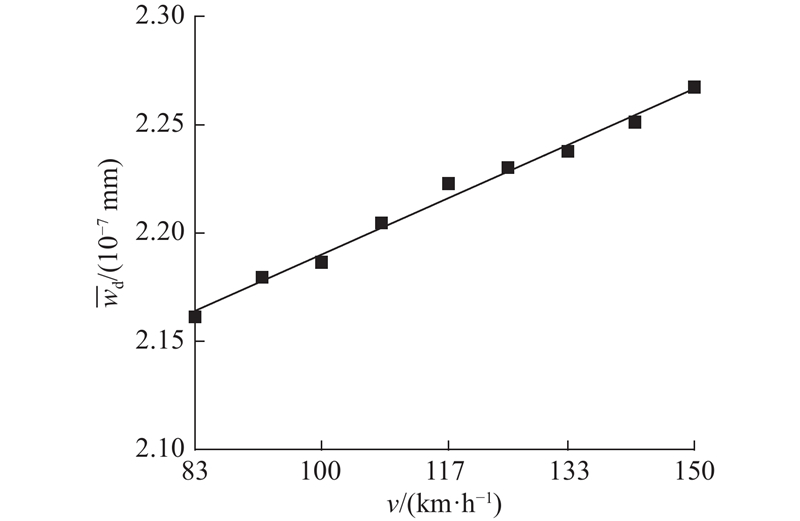
式中:ΔFx、ΔFy、ΔFz分别为轮轨纵、横、垂向力极差,反映其波动幅度;v为轮轨运行速度,取值范围为83~150 km/h.
3. 结 论
(1)经实物试验数据验证与模拟结果论证,所建立的瞬态滚动接触有限元模型能够较准确地模拟缩尺车轮-环轨的滚动接触行为,轮轨垂向力波动的极差约为均值的20%,来源于轮轨结构的高频弹性振动,而非接触表面不平顺激励.
(2)设定垂向载荷为10.58 kN、速度缩比为1∶3、牵引系数相同时,缩尺车轮-环轨在纵向动力学行为和钢轨磨耗深度变化趋势方面能够模拟轴重为17 t的服役轮轨的直线或大半径曲线通过工况.
(3)缩尺车轮-环轨的横向和自旋蠕滑行为较为特殊,具体表现为自由滚动工况下偏高的横向力、横向蠕滑率、自旋蠕滑率、钢轨磨耗深度,分别为1.33 kN、0.16‰、1.33‰ m−1、2.22×10−7 mm,切向接触应力最大值出现在接触斑后沿两侧,这是环轨的极小曲线半径所致.
(4)缩尺车轮-环轨的车轮驱动扭矩主要使轮轨纵向力、纵向蠕滑率、钢轨磨耗深度均值近线性增加,接触斑内滑移区面积增大;轮轨运行速度主要使三向轮轨力的极差、横向和自旋蠕滑率、钢轨磨耗深度均值近线性增加,对接触斑内法、切向应力分布几乎无影响. 上述规律可定量归纳为一组经验公式.
须指出,任何种类的轮轨试件都会在结构几何、接触廓形、边界条件等方面与现场服役轮轨存在一定差距,无论全尺还是缩尺、轨盘还是环轨、整车还是半轮对. 本研究在对缩尺车轮-环轨的瞬态滚动接触行为和磨耗进行仿真分析时设定试验车轮的横移量、侧滚角、冲角均为0,主要是基于高速线路上以直线和大半径曲线线路为主、轮对横移量较小的客观事实. 但考虑到环轨的极小曲线半径以及偏高的轮轨横向蠕滑力/率、自旋蠕滑率、钢轨磨耗量,在利用试验轮轨模拟直线、大半径曲线、小半径曲线运行工况时均须对车轮运动姿态和载荷进行一定的修正. 因此,未来可构建线路服役条件下的车辆-轨道耦合动力学模型或全轮对-轨道瞬态滚动接触有限元模型,并考虑直线和不同曲率半径的轨道,定量得出不同模拟工况下试验车轮的空间运动姿态和试验载荷,以拓宽缩尺车轮-环轨的使用范围.
参考文献
轮轨高频动力作用模拟中接触模型的影响分析
[J].DOI:10.3901/JME.2020.12.124 [本文引用: 2]
Influence of contact modeling on numerical analyses of high frequency wheel-rail interactions
[J].DOI:10.3901/JME.2020.12.124 [本文引用: 2]
Study on the phenomenon of rail corrugation on high-speed rail based on the friction-induced vibration and feedback vibration
[J].
Experimental study on mechanism of rail corrugation using corrugation simulator
[J].
Investigation on rolling contact fatigue of railway wheel steel with surface defect
[J].
干-水态下圆形硌伤对钢轨材料滚动接触疲劳特性影响
[J].
The effect of round defects on rolling contact fatigue characteristics of rail materials under dry-wet conditions
[J].
Predictive maps for the rolling contact fatigue and wear interaction in railway wheel steels
[J].DOI:10.1016/j.wear.2022.204513 [本文引用: 1]
Effects of molybdenum addition on rolling contact fatigue of locomotive wheels under rolling-sliding condition
[J].
Study on the wear and damage behaviors of hypereutectoid rail steel in low temperature environment
[J].DOI:10.1016/j.wear.2020.203365
钢轨滚动接触疲劳裂纹萌生和磨耗共存预测方法验证
[J].
Verification of prediction method for coexistence of rolling contact fatigue crack initiation and wear growth in rail
[J].
新型轮轨关系试验台研究
[J].
Research on a new wheel-rail test rig
[J].
Development of a new downscale setup for wheel-rail contact experiments under impact loading conditions
[J].
On the effect of unsupported sleepers on the dynamic behaviour of a railway track
[J].DOI:10.1080/00423114.2010.524303 [本文引用: 1]
An experimental study on the effects of friction modifiers on wheel-rail dynamic interactions with various angles of attack
[J].DOI:10.1007/s40534-022-00285-y [本文引用: 1]
Scaling strategy of a new experimental rig for wheel-rail contact
[J].
Substantial fatigue similarity of a new small-scale test rig to actual wheel-rail system
[J].
三维高速轮轨瞬态滚动接触有限元模型及其应用
[J].DOI:10.3901/JME.2013.18.001 [本文引用: 2]
3D transient finite element model for high-speed wheel-rail rolling contact and its application
[J].DOI:10.3901/JME.2013.18.001 [本文引用: 2]
单轮对高速滚动试验台的动态有限元模拟研究
[J].
Simulation research of dynamic finite element based on single wheel set high speed rolling test rig
[J].
Rolling-sliding laboratory tests of friction modifiers in dry and wet wheel-rail contacts
[J].
钢轨的安定状态研究
[J].
Research on stable state of rail
[J].
A fast algorithm for the simplified theory of rolling contact
[J].DOI:10.1080/00423118208968684 [本文引用: 1]
Prediction of wheel profile wear–comparisons with field measurements
[J].
Prediction of wheel wear in urban railway transport: comparison of existing models
[J].
Development of a wear prediction tool for steel railway wheels using three alternative wear functions
[J].
Wear mechanisms and transitions in railway wheel steels
[J].
Wear transitions in a wear coefficient model
[J].
On the coupling of the vertical, lateral and longitudinal wheel-rail interactions at high frequencies and the resulting irregular wear
[J].DOI:10.1016/j.wear.2019.05.017
缩尺轮轨模型中钢轨波磨的相似性
[J].
Similarity study of small-scale wheelset-track model for investigation of rail corrugation
[J].
缩尺车轮-环轨试验台轮轨静态接触相似性研究
[J].
Static contact similarity analysis of a scaled test rig wheel on rail track ring
[J].