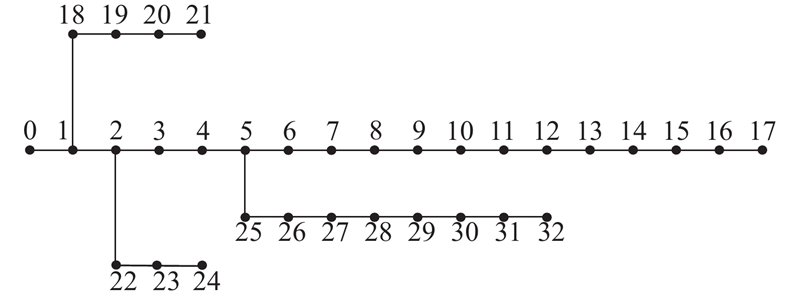对于分布式光伏承载力评估模型的计算方法有试探法[7]、数学解析法[8-9]和智能优化算法[10-11]等,Koirala等[7]使用的随机性方法仅仅针对于约束少、规模小的分布式光伏并网计算. 董昱等[9]针对电力系统的非线性问题建立了线性化方法,将非线性目标函数和约束条件进行线性变换,实现了算法的改进优化,但是数学解析法仍然存在计算复杂性大的问题,只适用于求解小规模问题. 刘科研等[10]对分布式光伏承载力计算提出了利用多种群遗传算法进行求解的方法,陈德炜等[11]对承载力的计算提出了改进花授粉优化算法. 智能优化算法计算速度相对于数学解析法有较大程度的提高,但还是存在精度低与收敛速度较慢的缺点.
针对分布式光伏承载力的评估,本研究建立了全新的中压配电网分布式光伏承载力评估模型,提出改进模拟退火-粒子群(simulated annealing-particle swarm optimization, SA-PSO)算法. 该模型的目标函数选取考虑了分布式光伏并网容量对网络损耗的影响,约束条件聚焦了目前分布式光伏并网所面临的节点电压越限与配电变压器的反向过载问题.
1. 分布式光伏对中压配电网的影响分析
1.1. 分布式光伏并网的中压配电网分析模型
图 1
图 1 含分布式光伏的中压配电网模型
Fig.1 Medium voltage distribution network model with distributed photovoltaic
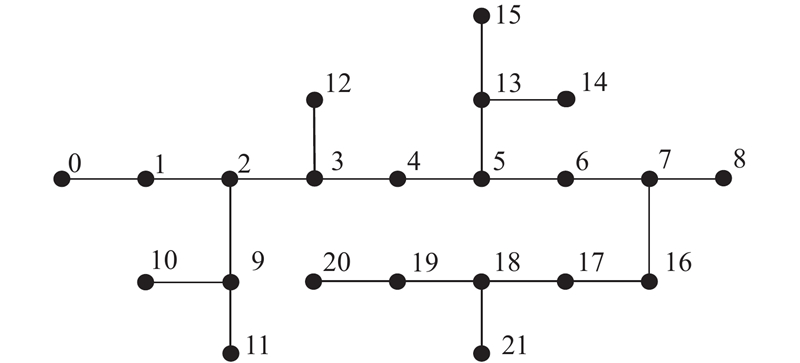
以IEEE33系统为例分析分布式光伏并网对中压配电网的影响. 该系统基准电压为12.66 kV,总负荷为(3715+j2300) kV·A. 系统结构如图2所示. 图中,节点0为电源节点,设置电压标幺值U0=1.05,其他节点看作PQ节点. 除了电源节点外,每个节点都可以进行分布式光伏的并网.
图 2
1.2. 渗透率
分布式光伏渗透率为某时刻线路并网的分布式光伏有功出力总和与负荷的总有功功率之比,即
式中:PPV为分布式光伏有功出力;PL为系统有功负荷.
渗透率代表配电网的分布式光伏承载力,渗透率超过配电网的承受限值会造成配电网运行安全问题[13].
1.3. 电压偏差
电压偏差为电网中电压有效值长时间偏离额定值的情况,对于如图1所示的模型,k点的电压偏差表达式如下:
式中:Uk为节点k电压.
k点电压大小如下:
式中:U0为电源点电压,ΔUi为节点i−1与i之间电压降落,Ri、Xi为节点i−1与i之间的线路电阻和电抗,PL.k、QL.k为节点k的有功、无功负荷,PPV.k、QPV.k为节点k光伏的有功、无功输出功率.
由式(2)、(3)可以看出,在分布式光伏并网后,光伏出力减少了线路的功率流动和电压降落,当分布式光伏的并网容量超过负荷功率并继续增加时,功率会向上级电网反送,出现下级电网电压高于上级电网电压的现象,最终造成节点电压越限.
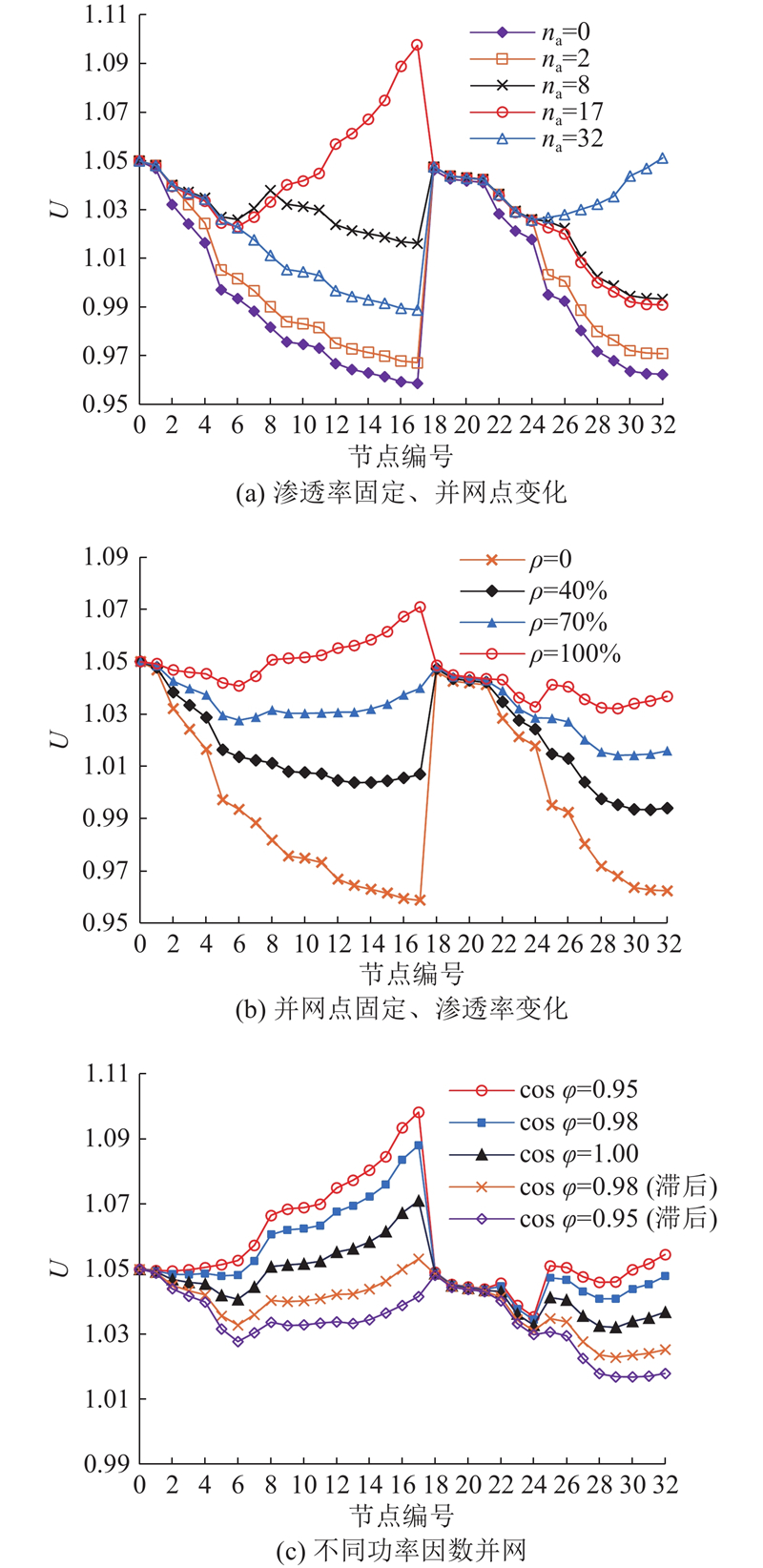
如图3所示为分布式光伏在渗透率固定(30%)而并网点变化、并网点固定(2、8、17、32节点)而渗透率变化、逆变器功率因数变化(并网点2、8、17、32节点,渗透率100%)3种情况下,IEEE33系统节点电压U的变化. 图中,na为光伏接入节点个数,
图 3
图 3 分布式光伏并网对电压的影响
Fig.3 Impact of grid connection of distributed photovoltaics on voltage
1.4. 反向负载率
反向负载率λ是衡量分布式光伏并网对配电变压器运行安全影响的重要指标,定义如下:
式中:Pload为等效用电负荷,即用电负荷减掉分布式电源之外的其他电源出力;Se为变压器实际运行的最大限值.
表 1 反向负载率评估等级
Tab.1
| 评估等级 | 电网状态 | |
| 绿色 | 负荷满足分布式电源就地消纳 | |
| 黄色 | 负荷水平无法满足就地消纳,新增分布式电源发电在满足电网安全稳定约束前提下向上级电网反送 | |
| 红色 | 所在变电站区域内用电负荷已无法满足分布式电源就地就近消纳需求,电网运行安全存在风险 |
我国分布式光伏装机容量在近几年骤增,且大部分新增的分布式光伏在农村地区,因为农村的台区负荷水平较低,在分布式光伏渗透率高、光伏出力较大的时刻易出现配电变压器的功率反向(λ>0),甚至出现反向过载(λ>80%),长时间的反向过载会导致配电变压器的过热损坏.
以某省为例,截至2022年底,全省光伏装机23330 MW,其中分布式光伏装机17810 MW,占比为76%,有16个地市的分布式光伏装机容量超过500 MW,7个地市的分布式光伏装机容量超过1000 MW. 全省分布式光伏台区共16.8万个,渗透率超过100%的台区约1.2万个,占比为7.05%,反向过载的台区有1847个(1.1%). 全省情况最严重的县域的2105个配电台区中,渗透率超过100%的台区有803个(38.18%),反向过载的台区有125个(6%),反向负载率最高达120%. 根据电网公司的统计数据,每季度都会出现因反向过载烧毁配电变压器的情况,配电变压器的烧毁将造成供电质量下降与较大的经济损失.
随着分布式光伏装机容量的增加,配电台区的反向过载现象将越来越严重,届时配电网将面临巨大风险. 因此配电变压器的反向过载问题是制约分布式光伏发展的重要因素,进行分布式光伏承载力评估时必须将其考虑在内.
1.5. 网络损耗与线路载流量
配电网的网络损耗主要为有功损耗,表达式如下:
式中:
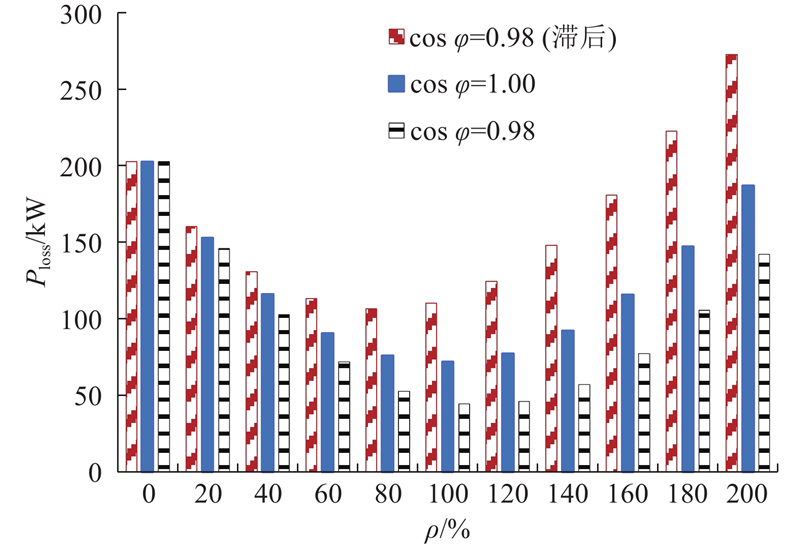
选取光伏并网节点2、10、17、21、23、26、32,分析分布式光伏在不同的功率因数与渗透率ρ下并网时,IEEE33系统网损的变化情况,结果如图4所示. 可以看出,随着渗透率从零开始不断增加,系统的网损呈现先减少后增加的趋势. 当渗透率较小时,分布式光伏的接入能够补偿部分负荷的功率需求,减少线路功率流动,从而减少网损;当渗透率增加到100%时,系统网损达到最小,正向潮流也达到最小;随着渗透率的继续增大,功率发生反送,网损逐渐增加. 在相同渗透率水平下,功率因数滞后时,逆变器进相运行,吸收无功,线路的无功流动增加,网损增加;相反,功率因数超前,网损减少. 此外,根据式(5),线路电流的变化趋势与网损的变化趋势一致,当渗透率不断增加时,线路电流呈现先减少后增加的趋势.
图 4
图 4 分布式光伏并网对网损的影响
Fig.4 Impact of grid connection of distributed photovoltaics on network loss
1.6. 短路容量与短路电流
表 2 不同类型分布式电源的短路电流注入能力
Tab.2
| 分布式电源类型 | 短路电流注入能力 |
| 逆变电源 | 100%~400%,持续时间取决于控制装置 |
| 同步发电机 | 500%~1000%,几个周波后衰减到200%~400% |
| 感应发电机 | 500%~1000%,10个周波衰减至可忽略 |
分布式光伏作为逆变器型分布式电源,向故障点注入的短路电流小于其额定容量的1.5倍[18].
表 3 短路电流计算结果
Tab.3
| PPV/MW | 短路点位置 | Ik/kA | Ik.PV/kA | αk/% |
| 2 | 6 | 2.403 | 0.037 | 1.52 |
| 14 | 1.502 | 0.041 | 2.73 | |
| 28 | 1.321 | 0.015 | 1.14 | |
| 5 | 6 | 2.453 | 0.087 | 3.64 |
| 14 | 1.555 | 0.094 | 6.03 | |
| 28 | 1.339 | 0.033 | 2.53 |
综上所述,配电网的电压偏差、反向负载率以及线路载流量是限制分布式光伏大规模并网的主要因素,可作为承载力评估模型的约束条件.
2. 分布式光伏承载力评估模型
2.1. 目标函数
由1.5节可知,分布式光伏并网会改变配电网的损耗,因此分布式光伏承载力的评估不仅要考虑分布式光伏的并网容量,同时也要考虑分布式光伏所造成的网络损耗. 分布式光伏等效并网容量为两者差值,其最大值为配电网分布式光伏的承载力,因此分布式光伏承载力评估模型的目标函数如下:
式中:NPV为线路中分布式光伏并网数量,
2.2. 约束条件
分布式光伏承载力评估模型的约束条件分为等式与不等式约束.
2.2.1. 等式约束
系统的功率、电压平衡为配电网运行的基础,因此将潮流约束作为系统等式约束:
式中:Pi、Qi为流过节点i的有功和无功功率.
2.2.2. 不等式约束
不等式约束为电压偏差、反向负载率、线路电流,表达式如下:
3. 改进SA-PSO算法
采用改进SA-PSO算法求解分布式光伏承载力评估模型,该方法可以提高模型的计算收敛速度,增强全局搜索能力,从而提高算法的寻优能力.
3.1. 算法原理
3.1.1. PSO算法
PSO算法是基于群体智能的全局优化进化算法,原理如下:假设空间中有m个粒子,向量
式中:Vis,k、Pis,k、Pgs,k、Xis,k为第i个粒子在s维空间中第k次搜索时的速度、个体最优位置、全局最优位置和个体当前位置,
3.1.2. SA算法
SA算法的核心思想是Metropolis准则,即以概率
3.2. 算法改进
3.2.1. 算法改进原理
采用粒子随机衰减因子α,收敛速度β和γ参数对PSO算法进行改进. α随着算法迭代进行更新:αk+1=αkγ,其中αk为第k次迭代时的α,γ为α的迭代更新表达式中的常量. 改进后的粒子位置更新公式如下:
式中:Pbest,k为第k次迭代时粒子位置,gbest为全局最优位置,rand为随机数,S为取值区间大小.
式(10)舍弃了PSO算法中的
本研究提出的分布式光伏承载力评估模型约束条件较多,在算法中增加罚函数项[24],将已有的约束条件转换为惩罚项施加在目标函数上,使迭代值逼近可行域,将问题求解简单化,最终可以加快算法的收敛速度.
3.2.2. 改进算法的实现步骤
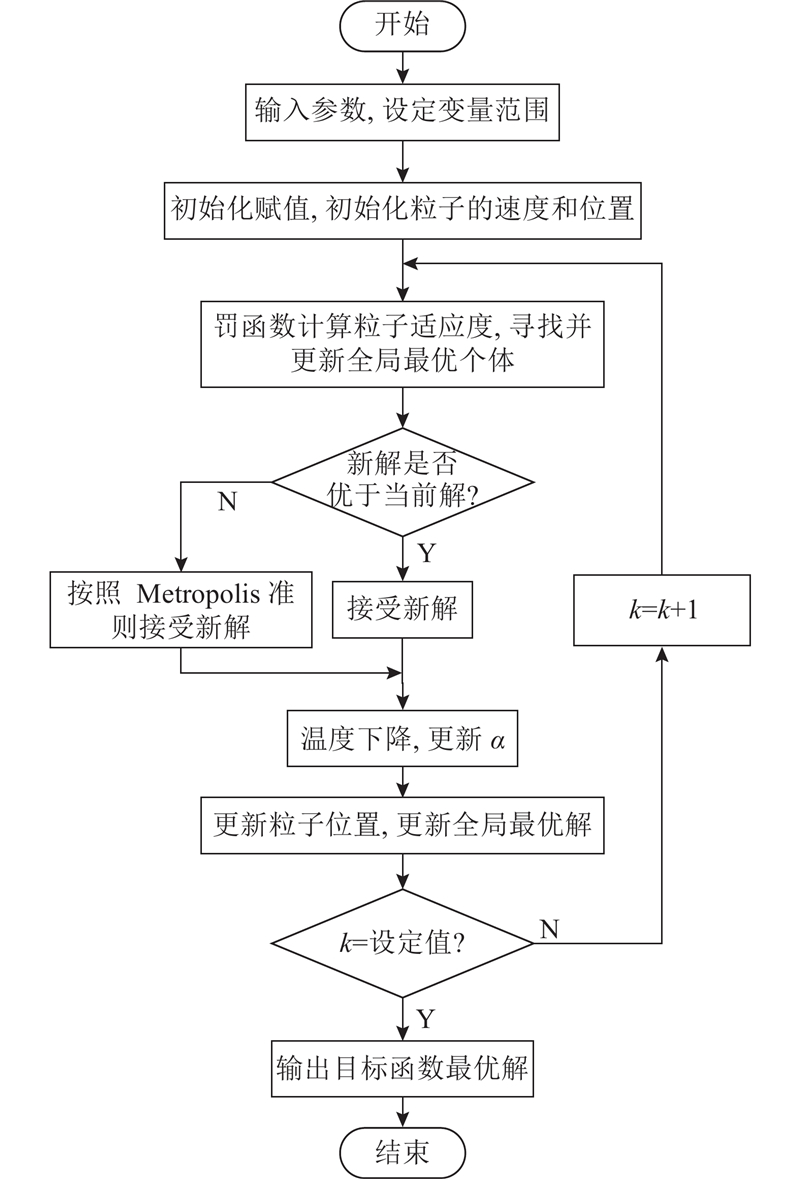
所提出的改进SA-PSO算法流程如图5所示.
图 5
1)输入参数. 输入配电网参数(包括线路阻抗参数、配电网节点拓扑关系、配电网负荷等数据),根据2.2节所列标准设定约束条件(式(7)、(8))的限值.
2)初始化赋值. 设置种群数量为n,最大迭代次数为T(种群数量与迭代次数根据配电网规模与分布式光伏并网节点数目进行选取,粒子种群数量
3)初始化粒子位置与速度. 每个粒子种群代表分布式光伏的一种接入方案,假设分布式光伏的并网数量为m个,每个种群中的粒子就是维度为m的向量,对粒子群进行随机赋值,代入目标函数(式(6)),结合潮流计算,得出初始目标函数值.
4)迭代计算. 利用罚函数法形成具有惩罚项的目标函数值,计算每个粒子群的目标函数值,经过比较得到最优粒子位置.
5)确定全局最优值. 若新的目标函数值优于当前解,则接受新解,否则根据SA算法的Metropolis准则去选择是否接受迭代计算后的较差解.
6)更新迭代参数. 对算法中的退火温度与粒子随机衰减因子α进行更新,更新粒子位置,更新全局最优解.
7)判断是否满足结束条件,若满足则停止迭代并输出最优解,最优解为所求分布式光伏的承载力,否则转至步骤4).
4. 分布式光伏承载力计算
4.1. IEEE33系统
考虑分布式光伏并网的实际情况,线路类型设置为JKLYJ-120线路,台区根据负荷水平设置配电变压器容量,线路拓扑结构如图2所示. 分布式光伏承载力计算分为单节点、多节点、全节点接入.
4.1.1. 单节点分布式光伏并网计算
只考虑单节点光伏并网的情况可以看作线路上大容量分布式光伏电站通过专有变压器并网的选址. 单节点分布式光伏并网对于分布式光伏承载力评估模型来说计算量较低,对每个节点采用二分法(从零开始逐渐增加分布式光伏并网容量,计算是否能满足约束条件,循环迭代,直到得出单节点最大并网容量)可以得出较为精准的结果. 将计算结果与改进SA-PSO算法进行比较,所得结果一致,证明在计算量较小的模型中,改进SA-PSO算法具有较好的收敛性和精准性,并且改进SA-PSO算法相对于二分法的试探求解计算速度有较大提高. 如图6所示为使用二分法与改进SA-PSO算法在IEEE33系统节点单独接入分布式光伏时的承载力情况. 可以看出,当分布式光伏并网位置在系统前端时,系统的光伏承载力较强,随着并网位置的后移,并网点受到电压越限的约束逐渐增加,光伏承载力逐渐降低. 因此在选择单节点并网点时,尽量选择系统前端.
图 6
图 6 单节点接入的分布式光伏承载力
Fig.6 Hosting capacity of distributed photovoltaics with single node
4.1.2. 多节点分布式光伏并网计算
表 4 多节点接入的分布式光伏承载力
Tab.4
| 并网类型 | PPV/kW | Ploss/kW | ρ/% |
| 分散型并网 | 2 088.12 | 82.57 | 56 |
| 紧凑型并网 | 1 286.81 | 61.03 | 34 |
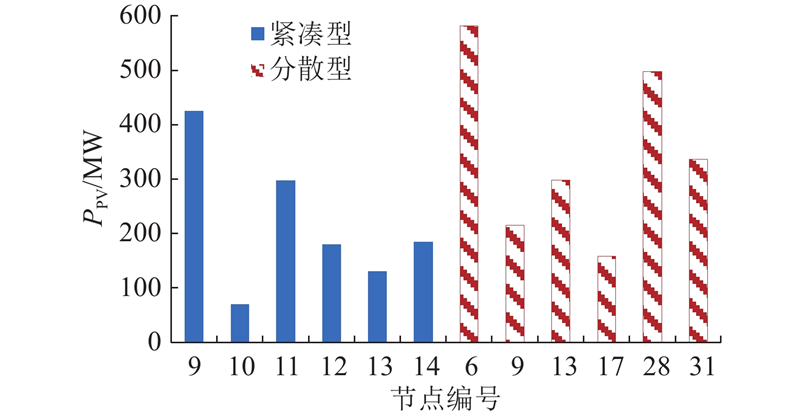
图 7
图 7 多节点接入的分布式光伏承载力
Fig.7 Hosting capacity of distributed photovoltaics with multi nodes
4.1.3. 全节点分布式光伏并网计算
假设所有节点均进行分布式光伏并网,分别对该系统的承载力采用PSO算法、自适应粒子群算法(adaptive particle swarm optimization, APSO)、遗传算法(genetic algorithm, GA)以及改进SA-PSO算法进行计算(种群数量n=50,最大迭代次数T=600). 其中PSO算法在进行承载力计算时容易陷入局部最优,导致每次迭代计算结果差距较大;GA与APSO算法的寻优能力较差,需要500次左右的迭代才能收敛;改进SA-PSO算法的寻优速度相较于其他算法有明显提高,迭代40次左右就已经收敛,对比计算结果如表5所示. 可以看出,改进SA-PSO算法的综合结果最好,所得分布式光伏承载力更高,网损更低.
表 5 IEEE33系统下的算法结果对比
Tab.5
| 算法 | PPV/kW | Ploss/kW | ρ/% | 收敛次数 |
| PSO | — | — | — | — |
| GA | 8 434.31 | 165.30 | 227 | 500 |
| APSO | 8 588.14 | 176.40 | 231 | 500 |
| 改进SA-PSO | 8 653.09 | 159.87 | 233 | 40 |
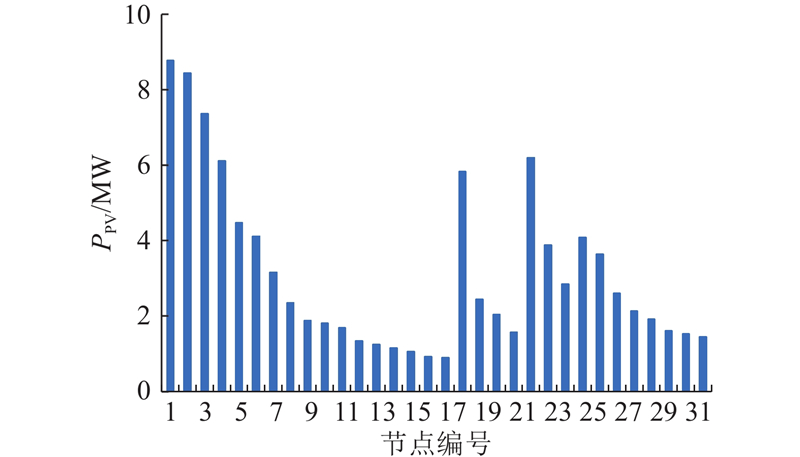
如图8所示为改进SA-PSO算法计算得出的IEEE33系统各节点的光伏承载力. 可以看出,节点10~17位于线路后端,受到节点电压越限约束限制较大,且其节点负荷水平较低,因此分布式光伏并网容量较低;节点18~21负荷与变压器容量相近,且分支线路短,节点距离近使得分布式光伏并网容量近似相同;节点23位于线路前端,且负荷水平较高,配电变压器容量大,因此该节点分布式光伏并网容量为线路最大值.
图 8
图 8 IEEE33系统下的分布式光伏承载力
Fig.8 Hosting capacity of distributed photovoltaic in IEEE33 system
4.2. 实际线路
选取某地市农村地区一条10 kV等级的配电线路进行分布式光伏承载力分析,如图9所示为该线路的拓扑结构.
图 9
图 9 某地市一条10 kV配电线路结构图
Fig.9 Diagram of 10 kV distribution line in certain city
该系统基准电压为10 kV,共含有22个节点,其中节点0为平衡节点,电压标幺值设为1.05,负荷节点为节点1~21,负荷节点全部可以进行分布式光伏的并网,线路类型为JKLYJ-120与JKLYJ-70.
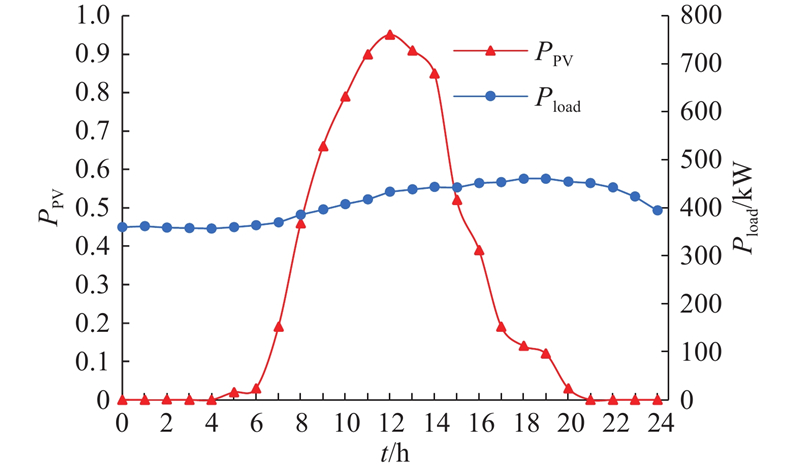
图 10
典型时刻应选择配电系统最容易出现约束条件越限的时刻,即分布式光伏出力与负荷功率比值最大的时刻. 可以看出,分布式光伏出力与负荷功率比值最大的时刻出现在中午时分,因此选取该系统12:00时刻的光伏出力与负荷功率作为分布式光伏承载力计算时刻.
负荷选择同时刻等效用电负荷,即用电负荷减去已并网分布式光伏出力. 其节点在所选时刻的等效用电负荷Pload.j以及线路阻抗Z、配电变压器容量Sj情况如表6所示.
表 6 配电线路参数
Tab.6
| 节点i | 节点j | Z/Ω | Sj/(kV·A) | Pload.j/(kV·A) |
| 0 | 1 | 0.149+j0.047 1 | 100 | 21.95+j4.457 |
| 1 | 2 | 0.203+j0.064 1 | 200 | 34.60+j10.092 |
| 2 | 3 | 0.278+j0.087 9 | 315 | 36.30+j15.464 |
| 3 | 4 | 0.058+j0.018 4 | 100 | 16.80+j2.394 |
| 4 | 5 | 0.240+j0.076 0 | 50 | 31.64+j6.425 |
| 5 | 6 | 0.448+j0.081 0 | 100 | 38.40+j15.177 |
| 6 | 7 | 0.462+j0.083 4 | 100 | 25.65+j10.138 |
| 7 | 8 | 0.243+j0.043 8 | 100 | 13.85+j4.552 |
| 2 | 9 | 0.202+j0.036 4 | 160 | 5.50+j1.996 |
| 9 | 10 | 0.244+j0.044 0 | 100 | 16.60+j4.160 |
| 9 | 11 | 0.233+j0.042 2 | 100 | 31.85+j23.888 |
| 3 | 12 | 0.174+j0.031 4 | 100 | 34.70+j15.810 |
| 5 | 13 | 0.145+j0.026 2 | 200 | 16.55+j2.358 |
| 13 | 14 | 0.363+j0.065 5 | 100 | 18.55+j2.494 |
| 13 | 15 | 0.230+j0.041 6 | 100 | 12.80+j6.199 |
| 7 | 16 | 0.237+j0.042 9 | 200 | 37.95+j5.408 |
| 16 | 17 | 0.284+j0.051 2 | 100 | 10.70+j5.182 |
| 17 | 18 | 0.201+j0.036 3 | 200 | 8.75+j2.876 |
| 18 | 19 | 0.102+j0.018 5 | 100 | 4.70+j0.670 |
| 19 | 20 | 0.128+j0.023 2 | 100 | 13.50+j3.938 |
| 18 | 21 | 0.171+j0.030 9 | 100 | 11.75+j3.427 |
与4.1.3节相同,分别采用不同算法对所选实际线路进行分布式光伏承载力的计算(种群数量n=40,最大迭代次数T=600). 其中PSO算法易陷入局部最优;GA算法的收敛需要600次左右的迭代,APSO算法的收敛需要约500次;改进SA-PSO算法迭代约50次后收敛,计算结果如表7所示.
表 7 实际线路上的算法结果对比
Tab.7
| 算法 | PPV/kW | Ploss/kW | ρ/% | 收敛次数 |
| PSO | — | — | — | — |
| GA | 2 169.37 | 23.34 | 501 | 600 |
| APSO | 2 206.12 | 24.15 | 509 | 500 |
| 改进SA-PSO | 2 283.04 | 22.06 | 527 | 50 |
由表7与4.1节可知,改进SA-PSO算法在对仿真模型与实际线路中的计算相较于其他算法来说收敛速度快,不容易陷入局部最优,所得线路分布式光伏承载力计算结果更高,渗透率更高,网损更低,可见改进SA-PSO算法的寻优能力更好,验证了该算法对于分布式光伏承载力评估模型计算的适用性与优越性.
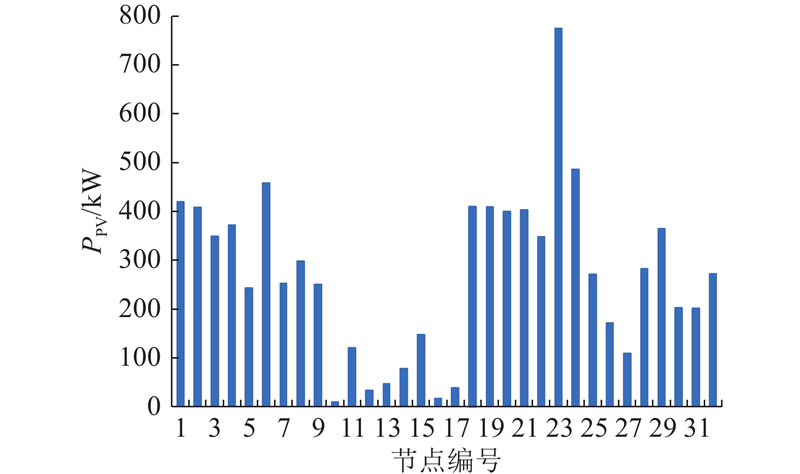
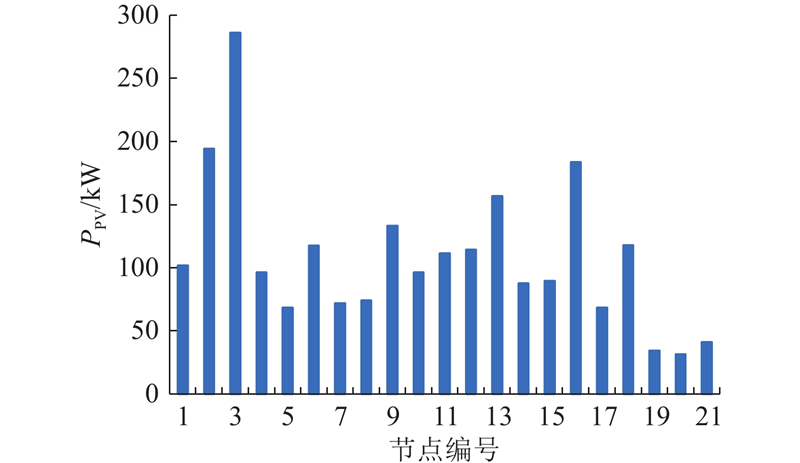
线路各节点的分布式光伏承载力如图11所示.
图 11
图 11 实际线路上的分布式光伏承载力
Fig.11 Hosting capacity of distributed photovoltaic in actual network
4.3. 计算结果分析
上文承载力计算结果可以作为线路分布式光伏并网容量的规划依据. 某些超出承载力计算值的节点在线路渗透率较低的情况下可能并未出现安全问题,但该节点会随着线路整体渗透率的逐渐增加而出现配电变压器反向过载与电压越限问题.
对于光伏并网容量超出承载力计算值的节点,必须降低接入值或者提升节点的光伏承载力,提高光伏承载力必须要了解限制线路中节点分布式光伏容量继续增大的主要原因. 以实际线路中节点6为例,在承载力达到限值时,节点6的节点电压标幺值为1.061,线路电流为37.76 A,配电变压器的反向负载率达到80%的限值,因此若要增加节点6的光伏承载力则须改善该节点配电变压器的反向过载问题.
经归纳,在IEEE33系统与实际线路中,限制各节点分布式光伏容量继续增大的主要原因见表8. 可以看出,分布式光伏承载力的主要限制因素为配电变压器的反向过载与节点电压越限,少量节点被载流量限制. 不同节点的主要限制因素不同,靠近电源的节点容易产生配电变压器的反向过载问题,远离电源的节点容易出现节点电压的越限问题.
表 8 限制各节点分布式光伏容量增大主要因素
Tab.8
| 线路 | 光伏并网点 | 主要限制因素 |
| IEEE 33 | 1、2、5、6、7、8、9、18、20、22、25、26 | 反向负载率越限 |
| 10、11、12、13、14、15、16、17、 20、21、24、27、28、29、30、31、32 | 节点电压越限 | |
| 3、4、19、23 | 支路载流量越限 | |
| 实际线路 | 1、2、3、4、5、9、11、12、13 | 反向负载率越限 |
| 6、7、8、14、15、16、17、18、19、20、21 | 节点电压越限 |
5. 结 论
本研究提出有关中压配电网分布式光伏承载力的评估模型及其计算方法,并以IEEE33系统与实际线路为例进行了验证,结论如下:
(1)分布式光伏的大规模并网给中压配电网带来的主要安全问题为节点电压的越限与配电变压器的反向过载.
(2)所建立的以分布式光伏等效并网容量为目标函数,以配电网潮流、反向负载率、电压偏差、线路载流量为约束建立的评估模型,可以准确反映目前分布式光伏并网带来的节点电压越限与配电变压器的反向过载问题,对于评估分布式光伏承载力与配电网的安全运行具有较强的适用性.
(3)针对分布式光伏承载力评估模型的计算所提出的改进SA-PSO算法,提高了模型的收敛速度与寻优能力.
(4)对于评估模型与改进SA-PSO算法在求解分布式光伏承载力的实际应用效果与准确性,在后续研究中将进行实验验证.
(5)配电变压器的反向过载问题易发生在电源近端节点,节点电压的越限问题易出现在电源远端节点. 为了提升配电网的分布式光伏承载力,后续研究可以根据不同节点的主要约束采取相应改善方案. 例如,针对配电变压器反向过载的现象,可采取变压器的台区联合控制策略;针对电压越限的节点,可利用光伏逆变器的无功调压能力进行电压调整.
参考文献
The impact of PV panel positioning and degradation on the pv inverter lifetime and reliability
[J].DOI:10.1109/JESTPE.2020.3006267 [本文引用: 1]
高比例新能源电网新能源功率优化分配方法
[J].DOI:10.12158/j.2096-3203.2022.03.013 [本文引用: 1]
New energy power optimal distribution method for high proportion new energy power grid
[J].DOI:10.12158/j.2096-3203.2022.03.013 [本文引用: 1]
一种有源配电网分布式光伏消纳能力评估方法
[J].DOI:10.3969/j.issn.1674-3814.2023.02.009 [本文引用: 1]
An assessment method for distributed photovoltaic absorption capacity of active distribution networks
[J].DOI:10.3969/j.issn.1674-3814.2023.02.009 [本文引用: 1]
Dynamic hosting capacity analysis for distributed photovoltaic resources: framework and case study
[J].DOI:10.1016/j.apenergy.2020.115633 [本文引用: 1]
基于改进FPA算法的配电网光伏消纳能力评估
[J].DOI:10.3969/j.issn.1671-5292.2019.02.006 [本文引用: 1]
Evaluation of distributed photovoltaic integration capacity based on improved FPA algorithm
[J].DOI:10.3969/j.issn.1671-5292.2019.02.006 [本文引用: 1]
计及多约束的多分布式电源接入配电网最大承载力分段算法
[J].
Segmentation algorithm for maximum hosting capacity of distributed generator accessing to distribution network considering multiple constraints
[J].
Hosting capacity of photovoltaic systems in low voltage distribution systems: a benchmark of deterministic and stochastic approaches
[J].DOI:10.1016/j.rser.2021.111899 [本文引用: 2]
Probabilistic assessment of PV hosting capacity under coordinated voltage regulation in unbalanced active distribution networks
[J].DOI:10.1109/ACCESS.2022.3163595 [本文引用: 1]
基于线性最优潮流的电力系统新能源承载能力分析
[J].
Renewable energy capacity assessment in power system based on linearized OPF
[J].
基于多种群遗传算法的分布式光伏接入配电网规划研究
[J].
Planning research of distributed photovoltaic source access distribution network based on multi-population genetic algorithm
[J].
基于改进FPA算法的含分布式光伏配电网选址定容多目标优化方法
[J].
Multi-objective optimization method for location and capacity of a distribution network with distributed photovoltaic energy based on an improved FPA algorithm
[J].
考虑合理弃光的配电网光伏最大接入容量研究
[J].
Research on maximum PV access capacity in distribution network considering proper power curtailment
[J].
考虑含光伏接入的配电网故障特性研究
[J].DOI:10.3969/j.issn.1674-3814.2022.12.018 [本文引用: 1]
Research on fault characteristics of the distribution network considering access of photovoltaic
[J].DOI:10.3969/j.issn.1674-3814.2022.12.018 [本文引用: 1]
集中光伏电源接入对低压配电网电压的影响
[J].
Influence of concentrated photovoltaic power supply access on voltage of low voltage distribution network
[J].
A local measurement based protection technique for distribution system with photovoltaic plants
[J].DOI:10.1049/iet-rpg.2019.0996 [本文引用: 1]
基于配电网电流保护约束的分布式光伏电源容量分析
[J].
Capacity analysis of distributed photovoltaic generation based on current protection in distribution network
[J].
数据驱动的配电网分布式光伏承载力评估技术研究
[J].
Data driven assessment of distributed photovoltaic hosting capacity in distribution network
[J].
考虑电压质量与短路容量约束的分布式电源准入容量分析
[J].
Penetration capacity calculation for distributed generation considering voltage quality and short circuit capacity constraints
[J].
多角色多策略多目标粒子群优化算法
[J].
Multi-objective particle swarm optimization algorithm with multi-role and multi-strategy
[J].
Research on power system dispatching operation under high proportion of wind power consumption
[J].DOI:10.3390/en15186819 [本文引用: 1]