出租车是城市交通的重要组成部分,为出行者提供便捷、舒适、通达的交通服务. 然而,在许多城市仍然有大量出租车巡航在城市道路上,以街头叫车的方式寻找乘客[1]. 一方面,出租车空载率高,导致出租车司机运营成本增加的同时收入降低,且一些地方的乘客须等待较长时间才能乘坐出租车,降低了其出行满意度. 例如,上海市出租车的日均时间利用率为59%[2],四川成都出租车的小时时间利用率约为50%[3]. 这意味着出租车须花费大量时间寻找乘客. 另一方面,大量空闲出租车在城市道路上巡航占用了大量的道路空间,加剧了交通拥堵和空气污染[4]. 因此,为出租车推荐路线对提高出租车运营效率、减少交通污染,为乘客提供更高效、便捷的出行服务具有重要意义.
Ge等[11]提出出租车移动顺序推荐(mobile sequential recommendation, MSR)的问题. 该问题通过考虑接载乘客的概率和搜索距离提出潜在行驶距离(potential travel distance, PTD)模型,旨在为空闲出租车提供一系列上客点,减少出租车从当前位置到下一个乘客之间的距离,增加出租车成功接载乘客的可能性. 为了使MSR更好地应用于实际,Ge等[12]进一步改进了MSR提出了宽松假设的路线推荐(route recommendation with relaxed assumptions, RR-RA)和面向目的地的路线推荐(destination-oriented route recommendation, DORR)问题,为出租车司机提供了更为全面的路线推荐建议. 其他学者也对MSR存在的问题开展了研究,使出租车在存在多辆出租车的情况下也能够以较短的距离接载乘客. 如Luo等[13]通过改进PTD模型提出了潜在巡航距离(potential cruising distance, PCD)模型,进一步考虑了出租车根据推荐路线行驶后上客点的容量变化,解决了PTD模型可能为出租车推荐具有较低接客概率的路线及在同一位置存在多辆出租车时的路线推荐的问题. Xiao等[14]针对MSR只能为单个出租车带来有效的解决方案,进一步提出了多用户移动顺序推荐(multi-user mobile sequential recommendation, MMSR)模型,解决了多用户场景下更为复杂的出租车路线推荐问题. 此外,MSR本质上是一个具有高计算复杂度的问题. 为了降低MSR的计算成本,Huang等[15]提出基于动态规划的方法来解决MSR问题,该方法包括离线预处理和在线搜索2个独立阶段. Ye等[16]提出将并行计算和模拟退火算法与全局和局部搜索相结合的新方法,能够实现为空闲出租车实时搜索最佳路线,而无需离线预处理. 然而,上述研究没有考虑到在交通拥堵的情况下,根据推荐路线出租车可能需要长时间行驶才能接载乘客. 因此,Liang等[17]进一步考虑时间因素,提出基于时空矩阵的路线推荐(route recommendation based on temporal-spatial metric, RTS)模型.
综上所述,现有关于出租车移动顺序推荐的研究考虑了接客概率、搜索时间和搜索距离3个因素. 然而,对于出租车司机来说,最关心的问题是如何实现收益最大化,只考虑接客概率、搜索时间和搜索距离为出租车司机推荐一系列上客点,从长远来看无法确保司机更高的收入. 此外,现有研究忽略了上客点中需求大小对空闲出租车成功接载乘客的可能性的影响,会高估一些上客点成功接载乘客的可能性. 针对上述问题,本研究考虑出租车接载下一个乘客的收益及上客点的需求对出租车路线推荐问题进行建模,采用模拟退火算法和贪心算法对出租车路线推荐问题进行求解,最后通过上海市GPS轨迹数据对上述模型进行验证,实验结果验证了本研究所提出的出租车收益路线推荐模型的有效性和优越性.
1. 问题描述和模型构建
1.1. 问题描述
假设空闲出租车当前位置为
设
出租车移动顺序推荐问题区别于传统的旅行商问题和车辆调度问题. 旅行商问题是
图 1
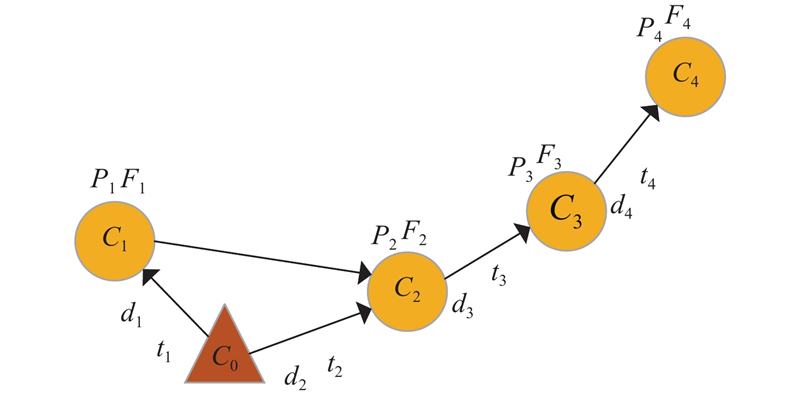
图 1 出租车收益路线推荐示例图
Fig.1 Example diagram of profitable taxi route recommendation
1.2. 潜在出行成本
假设空闲出租车的行驶路线为
例如,若
1.3. 参数估计
1.3.1. 接客概率
在出租车路线推荐中,常用的出租车上客点,即出租车需求热点识别方法有K-means聚类[18]、带噪声的基于密度的空间聚类(density-based spatial clustering of applications with noise, DBSCAN)[19-20]、基于网格的聚类[21]等. 由于DBSCAN方法可以发现任意形状和大小的簇,并且可以有效处理噪声和异常数据,本研究选择DBSCAN方法对乘客上车的位置进行聚类. 簇的质心即为上客点的位置. 为了计算上客点的接客概率,设置簇中乘客上车位置坐标的最大值和最小值为上客点的边界. 因此,上客点
式中:
空闲出租车在上客点
假设所有出租车占用行程接载乘客的数量均为1,
1.3.2. 搜索时间和距离
上客点
式中:
1.3.3. 预期票价
上客点
2. 算法设计
2.1. 出租车路线推荐算法框架
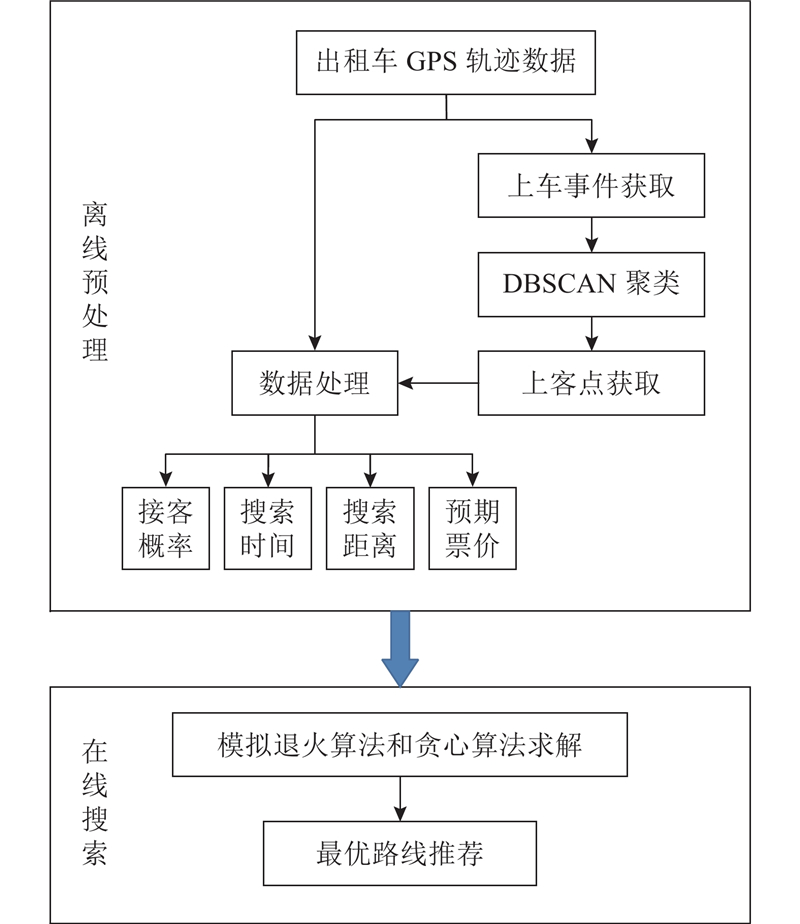
出租车路线推荐算法框架如图2所示. 出租车路线推荐由离线预处理和在线搜索2个阶段组成. 在离线预处理阶段,首先从出租车GPS轨迹数据中提取上车事件,并通过DBSCAN方法对提取的上车事件进行聚类获得一组潜在的上客点. 之后根据上客点的位置进一步处理出租车GPS轨迹数据获得接客概率、搜索时间、搜索距离和预期票价4个参数. 在在线搜索阶段,通过模拟退火算法和贪心算法对出租车收益路线推荐问题进行求解,为出租车推荐最优路线,实现出租车潜在出行成本的最小化.
图 2
当同一地点存在多辆空闲出租车请求路线推荐时,仅根据潜在出行成本的值为出租车推荐路线,同一地点的所有出租车会根据相同的路线行驶,从而导致过载问题. 为了解决该问题,本研究引入循环机制为同一地点的多辆出租车推荐路线,即根据潜在出行成本的值从小到大进行排序,取前k条路线推荐方案,当第1辆空闲出租车请求推荐路线时,为其分配第1条路线推荐方案,第2辆空闲出租车为其分配第2条路线推荐方案,以此类推,第k辆空闲出租车为其分配第k条路线推荐方案;当k小于请求的空闲出租车数量时,第k+1辆空闲出租车分配第1条路线推荐方案,第k+2辆空闲出租车分配第2条路线推荐方案,以此类推,直至所有请求的空闲出租车均分配到路线推荐方案.
2.2. 计算复杂度分析
假设计算一次潜在出行成本
2.3. 出租车路线推荐求解算法
模拟退火(simulated annealing, SA)算法是求解出租车路线推荐问题的常用算法之一[16-17],源于固体退火原理,能够以一定的概率跳出局部最优解并最终趋于全局最优. 因此,本研究选择模拟退火算法对1.1节提出的出租车路线推荐问题进行求解. 算法具体描述如算法1所示. 首先,初始化候选路线
算法1 出租车路线推荐求解算法
输入:出租车当前位置
输出:空闲出租车的最佳行驶路线
1. 初始化路线
2. repeat
3. 从
4. 贪婪选取上客点
5. if
6. temp = rand (0,1)
7.
8. 交换
9.
10. 颠倒
11. else
12. 添加
13. else
14. 替换
15. if
16.
17.
18. until 终止条件满足
19. return
3. 实验结果与分析
3.1. 数据来源
所使用的出租车GPS轨迹数据源于上海市强生出租车公司于2016年8月25日(星期四)—2016年8月31日(星期三)收集的约12000辆出租车的轨迹数据. 出租车GPS轨迹数据约10 s采集一次,包括车机号、空车(0:重车,1:空车)、GPS时间、经度、纬度等有效数据,部分出租车GPS 轨迹数据信息如表1所示. 在删除重复数据、存在缺失值的数据、空车状态异常的数据和不在研究区域的数据后,每天约有1亿条有效的出租车GPS轨迹数据. 在进一步对数据进行可视化分析后,选择出租车需求较为密集的上海市的市中心区域([121.25°E,31.05°N]~[121.70°E,31.35°N])作为本研究的研究区域.
表 1 上海市出租车GPS轨迹数据示例
Tab.1
| 车机号 | 空车 | GPS时间 | 经度/°E | 纬度/°N |
| 3 | 1 | 2016-08-29 07:22:38 | 121.463 930 | 31.256 790 |
| 3 | 1 | 2016-08-29 07:22:48 | 121.464 068 | 31.256 278 |
| 3 | 1 | 2016-08-29 07:22:58 | 121.464 087 | 31.255 910 |
| 21 641 | 0 | 2016-08-29 09:11:11 | 121.604 590 | 31.318 463 |
| 21 641 | 0 | 2016-08-29 09:11:21 | 121.606 452 | 31.318 510 |
上海市出租车的价格计算方法源于2014年发布的《上海市市民价格信息指南》[23],主要与乘客行驶的距离有关,表达式如下:
式中:
实验采用Python语言编写,并在配备Intel(R) Core(TM) i5-1 035G1 CPU和16.00 GB内存的Window 10系统上运行.
3.2. DBSCAN聚类结果
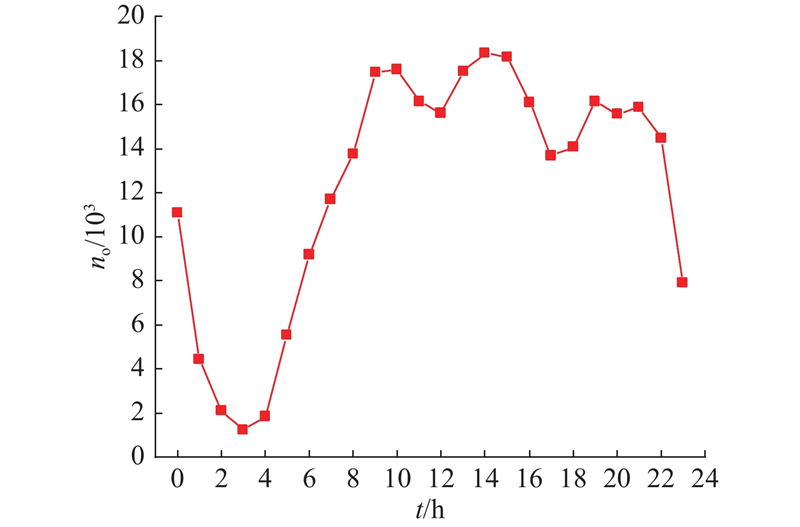
出租车的空车状态为0表示出租车处于占用状态,空车状态为1表示出租车处于空闲状态. 因此,根据出租车GPS轨迹数据的车机号和GPS时间对出租车的轨迹数据进行排序,当出租车的空车状态从1变为0时,即视为发生了一次上车事件,以小时为单位统计这些上车事件,即可获得出租车上车事件的时变特性图. 2016年8月29日出租车上车事件的时变特性图如图3所示. 图中,
图 3
图 3 上车事件数量时变特性图
Fig.3 Time-varying characteristic diagram of number of picking-up
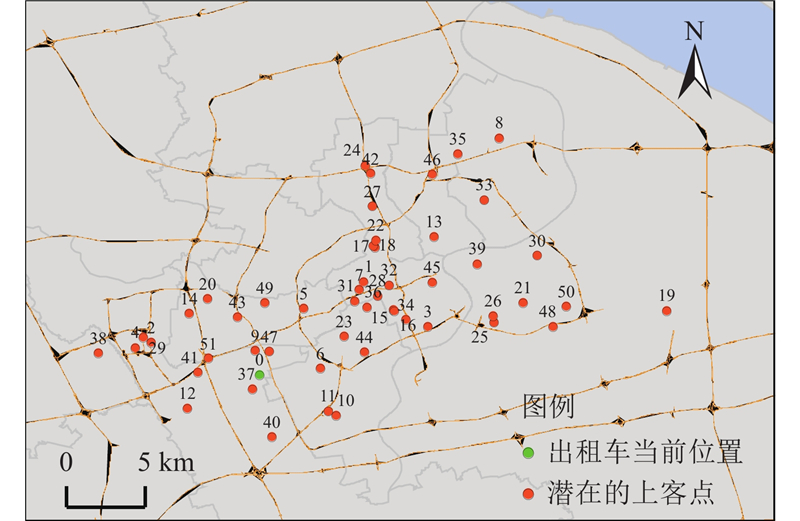
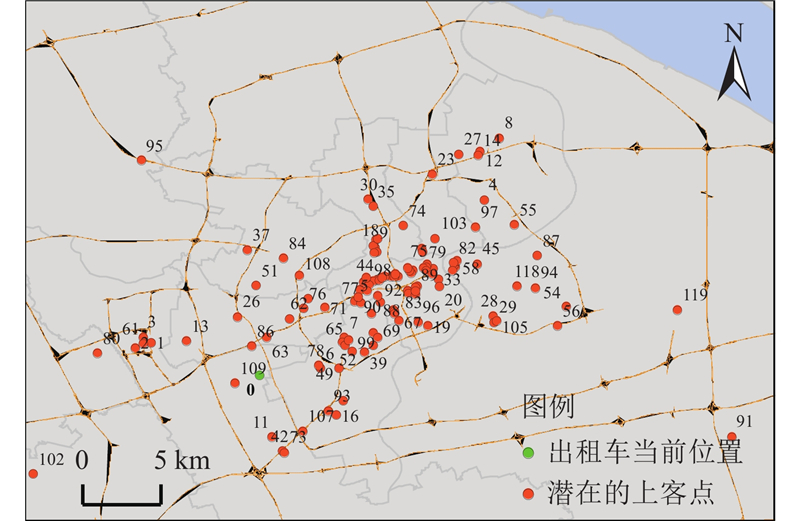
通过DBSCAN对提取的上车事件进行聚类,可以识别出租车需求热点区域,即潜在的上客点,也就是上车事件密度较大的区域. DBSCAN聚类效果取决于Eps半径和MinPts参数的选择. 在本研究中,Eps半径和MinPts参数分别设置为0.5 km和20[19]. 在聚类过程中,可以针对不同时期和区域采取不同粒度的空间挖掘. 2016年8月29日7:00—10:00和13:00—16:00上车事件的聚类结果如图4、5所示. 聚类之后分别获得51和120个潜在的上客点,根据上客点上车事件的数量从大到小为上客点编号,图中绿色的点和红色的点分别为出租车当前位置
图 4
图 4 2016年8月29日7:00—10:00上车事件聚类结果
Fig.4 Clustering results of picking up events during 7:00—10:00 on August 29, 2016
图 5
图 5 2016年8月29日13:00—16:00上车事件聚类结果
Fig.5 Clustering results of picking up events during 13:00—16:00 on August 29, 2016
3.3. 路线推荐结果比较与分析
3.3.1. 效率分析
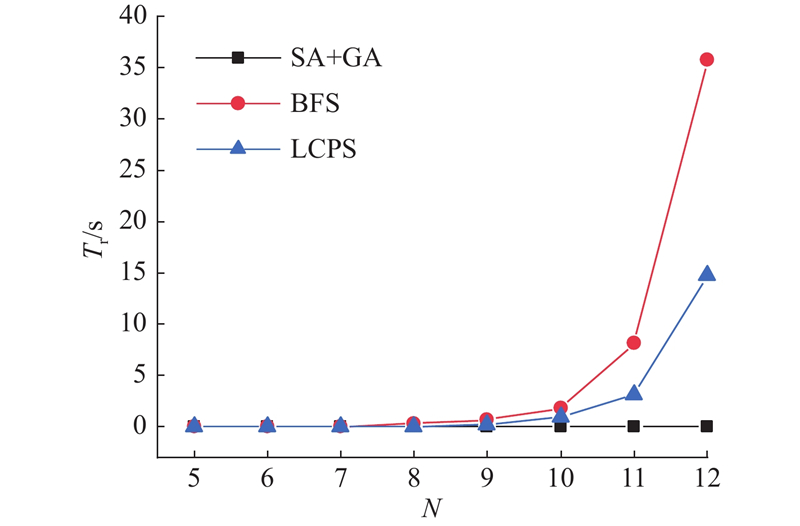
为了验证出租车路径推荐求解算法,即使用模拟退火算法和贪心算法(SA+GA)对出租车路线推荐问题求解的有效性,选择蛮力搜索(brute-force search, BFS)算法和基于路由优势和受限子路由优势的序列剪枝搜索(search with sequence pruning via route dominance and constrained subroute dominance,LCPS)算法为基准模型. BFS搜索
图 6
图 6 潜在上客点数量对SA+GA、BFS和LCPS运行时间的影响
Fig.6 Impact of number of potential picking-up points on running time of SA+GA, BFS and LCPS algorithms
3.3.2. 出租车收益路线推荐结果分析
为了验证本研究所提出的模型的有效性,选择PTD和RTS模型作为基准模型. PTD模型考虑了上客点的接客概率和搜索距离,目标是最小化接载下一个乘客之前的行驶距离. RTS模型考虑了上客点的接客概率、搜索距离和搜索时间,目标是最小化接载下一个乘客之前的行驶距离和时间. RTS模型涉及2个参数
表 2 7:00—10:00 PTD模型路线推荐结果
Tab.2
| 上客点 | Ti/h | Di/km | ||
| 0.095 | 1.761 | 21.738 | 57.643 | |
| 0.243 | 3.344 | 51.332 | 26.591 | |
| 0.120 | 4.861 | 86.188 | 17.506 | |
| 0.051 | 5.493 | 97.403 | 68.778 | |
| 0.546 | 6.670 | 123.784 | 37.570 |
表 3 7:00—10:00 RTS模型路线推荐结果
Tab.3
| 上客点 | Ti/h | Di/km | ||
| 0.243 | 1.417 | 26.794 | 26.591 | |
| 0.095 | 2.733 | 58.234 | 57.643 | |
| 0.120 | 3.681 | 79.277 | 17.506 | |
| 0.051 | 4.313 | 90.491 | 68.778 | |
| 0.233 | 5.899 | 120.290 | 18.650 |
表 4 7:00—10:00 PMSR模型路线推荐结果
Tab.4
| 上客点 | Ti/h | Di/km | ||
| 0.243 | 1.417 | 26.794 | 26.591 | |
| 0.846 | 2.580 | 45.308 | 36.512 | |
| 0.546 | 3.697 | 64.540 | 37.570 | |
| 0.829 | 4.359 | 74.315 | 51.181 | |
| 0.155 | 5.713 | 102.337 | 20.506 |
表 5 13:00—16:00 PTD模型路线推荐结果
Tab.5
| 上客点 | Ti/h | Di/km | ||
| 0.400 | 0.399 | 5.215 | 21.474 | |
| 0.217 | 1.825 | 27.960 | 32.680 | |
| 0.353 | 3.628 | 57.423 | 23.012 | |
| 0.386 | 4.195 | 66.016 | 16.938 | |
| 0.220 | 5.892 | 102.351 | 18.777 |
表 6 13:00—16:00 RTS模型路线推荐结果
Tab.6
| 上客点 | Ti/h | Di/km | ||
| 0.400 | 0.399 | 5.215 | 21.474 | |
| 0.621 | 1.658 | 24.048 | 27.457 | |
| 0.353 | 3.203 | 48.012 | 23.012 | |
| 0.386 | 3.771 | 56.605 | 16.938 | |
| 0.243 | 4.747 | 73.130 | 27.551 |
表 7 13:00—16:00 PMSR模型路线推荐结果
Tab.7
| 上客点 | Ti/h | Di/km | ||
| 0.295 | 0.666 | 9.595 | 22.459 | |
| 0.567 | 1.847 | 26.999 | 17.223 | |
| 0.356 | 3.554 | 57.332 | 20.224 | |
| 0.990 | 4.443 | 69.245 | 38.361 | |
| 0.757 | 4.466 | 69.556 | 29.704 |
由表2~4可知,在7:00—10:00,PTD模型的推荐路线为
同样,由表5~7可知,在13:00—16:00,PTD、RTS和PMSR模型的推荐路线分别为C0→C99→C117→C40→C84→C109、 C0→C99→C8→C40→C84→C86和 C0→C48→C12→C41→C13→C82,其推荐路线上客点的概率分别为0.400、0.217、0.353、0.386、0.220,0.400、0.621、0.353、0.386、0.243和0.295、0.567、0.356、0.990、0.757,PSMR模型推荐路线的接客概率与PTD和RTS模型相比分别平均增加了88.1%和48.0%. 同时,PMSR推荐路线上客点的最低票价也高于PTD和RTS模型(PTD和RTS模型的最低票价均为16.938,PMSR的最低票价为17.223).
上述分析结果表明,PMSR模型能够综合考虑推荐路线的所有上客点的预期票价为空闲出租车推荐接载乘客概率更高的路线,优于PTD和RTS模型.
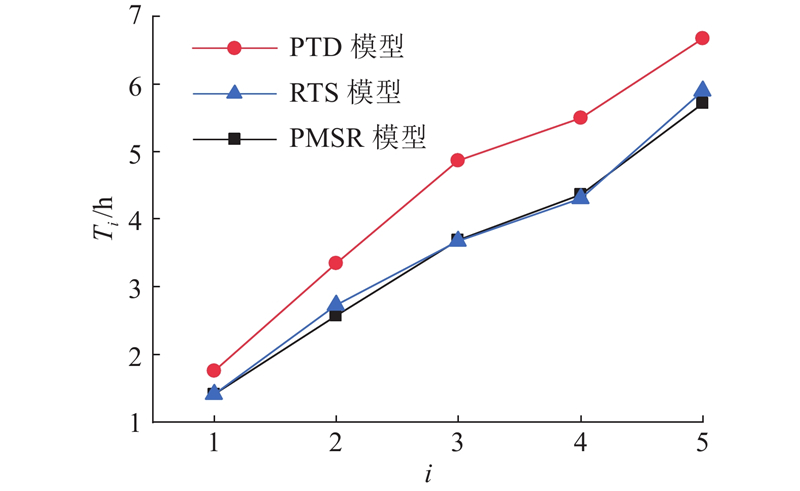
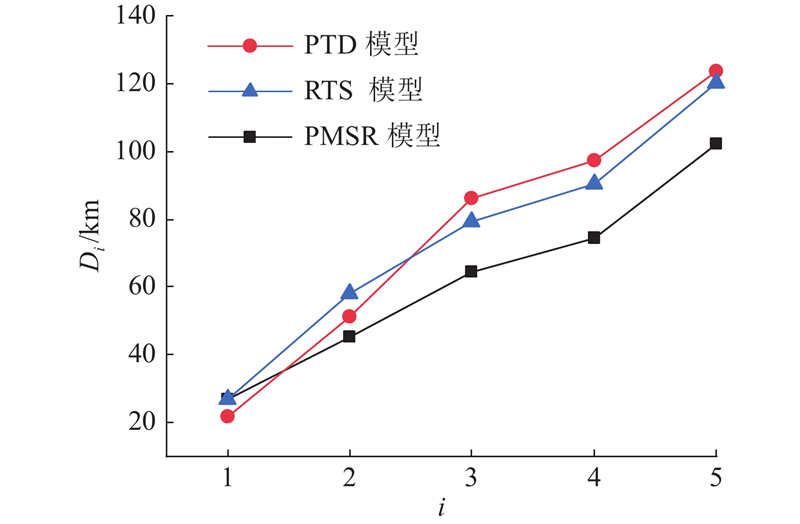
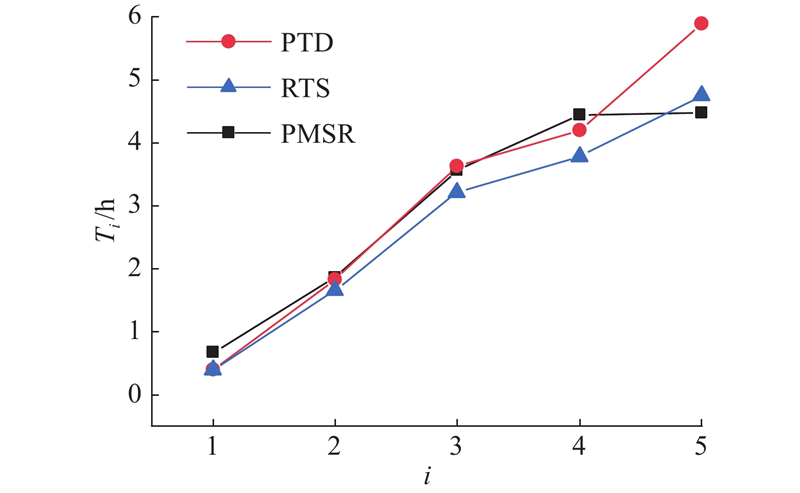
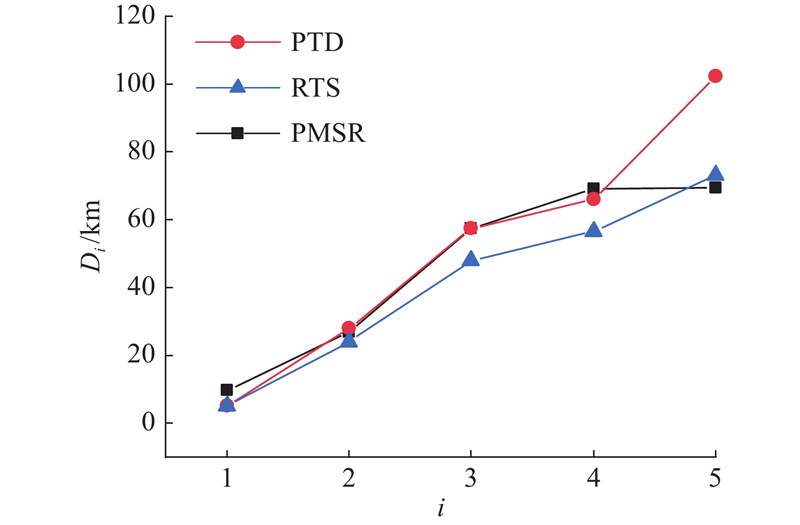
为了进一步探索PTD、RTS和PMSR模型推荐路线的搜索时间和距离的差异,绘制PTD、RTS和PMSR模型推荐路线的搜索时间和搜索距离向量折线图如图7~10所示. 相较于不考虑搜索时间的PTD模型,RTS和PMSR模型推荐路线的搜索时间在7:00—10:00分别平均减少了11.6%、14.3%,在13:00—16:00分别平均减少了19.4%、24.2%. PMSR模型相比RTS在7:00—10:00和13:00—16:00分别平均减少了3.2%和5.9%. 与PTD和RTS模型相比,PMSR模型的推荐路线搜索距离更短,在7:00—10:00平均减少了17.3%和14.9%,在13:00—16:00平均减少了32.0%和4.9%. 上述分析结果表明PMSR模型能够为空闲出租车推荐具有较短搜索时间和距离的路线.
图 7
图 7 7:00—10:00不同模型推荐路线的搜索时间
Fig.7 Search time for recommended routes in different models during 7:00—10:00
图 8
图 8 7:00—10:00不同模型推荐路线的搜索距离
Fig.8 Search distance for recommended routes in different models during 7:00—10:00
图 9
图 9 13:00—16:00不同模型推荐路线的搜索时间
Fig.9 Search time for recommended routes in different models during 13:00—16:00
图 10
图 10 13:00—16:00不同模型推荐路线的搜索距离
Fig.10 Search distance for recommended routes in different models during 13:00—16:00
3.3.3. 考虑需求的路线推荐结果分析
为了验证考虑上客点的出租车需求的出租车收益路线推荐的有效性,在出租车当前位置进一步开展考虑出租车需求的出租车收益路线推荐实验分析,结果如表8、9所示. 在7:00—10:00和13:00—16:00,PMSR-D模型的推荐路线分别为C0→C17→C2→C11→C10→C43和C0→C48→C8→C41→C82→C13,与PMSR模型推荐路线的主要区别均是第2个上客点不同. 在7:00—10:00,PMSR和PMSR-D模型推荐路线中第2个上客点分别为
表 8 7:00—10:00 PMSR-D模型路线推荐结果
Tab.8
| 上客点 | Ti/h | Di/km | ||
| 0.243 | 1.417 | 26.794 | 26.591 | |
| 0.532 | 2.870 | 59.048 | 65.875 | |
| 0.829 | 4.203 | 85.459 | 51.181 | |
| 0.546 | 4.405 | 88.785 | 37.570 | |
| 0.155 | 4.936 | 103.323 | 20.506 |
表 9 13:00—16:00 PMSR-D模型路线推荐结果
Tab.9
| 上客点 | Ti/h | Di/km | ||
| 0.295 | 0.666 | 9.595 | 22.459 | |
| 0.621 | 2.030 | 30.761 | 27.457 | |
| 0.356 | 3.070 | 52.501 | 20.224 | |
| 0.757 | 4.160 | 69.363 | 29.704 | |
| 0.990 | 4.178 | 69.599 | 38.361 |
4. 结 语
本研究通过考虑出租车接载下一个乘客获得的收益及上客点需求对移动顺序推荐问题进行了改进,之后基于上海市GPS轨迹数据,采用DBSCAN算法、模拟退火算法和贪心算法对改进的出租车收益路线推荐模型和考虑需求的出租车收益路线推荐模型进行了验证. 结果表明,相比于PTD和RTS模型,出租车路线收益推荐PMSR模型的推荐路线的搜索时间和搜索距离更小,上客点的最低预期票价也较高. 此外,PMSR模型推荐路线的接客概率与PTD和RTS模型相比在7:00—10:00分别平均提高了148.2%和253.0%,在13:00—16:00分别平均提高了88.1%和48.0%. 考虑需求的出租车路线收益推荐PMSR-D模型能够为出租车推荐需求较大的路线,与PMSR模型相比在7:00—10:00和13:00—16:00分别增加了125和20个潜在的乘客需求,验证了PMSR-D模型的有效性.
本研究主要关注当前出租车根据推荐路线行驶后接载新乘客获得的收入问题,不足之处在于出租车在整个运营周期内的订单布局对其收益的影响尚不清楚,未来可以进一步探索订单布局对出租车收益的影响,从而为出租车提供更精准的路线推荐,增加出租车司机的收入. 此外,探索适用于全市范围的自适应出租车需求热点识别方法也是未来的研究方向之一.
参考文献
An alternative methodology for evaluating the service quality of urban taxis
[J].DOI:10.1016/j.tranpol.2018.05.016 [本文引用: 1]
Does online ride-hailing service improve the efficiency of taxi market? evidence from Shanghai
[J].DOI:10.3390/su14148872 [本文引用: 1]
The analysis of urban taxi operation efficiency based on GPS trajectory big data
[J].DOI:10.1016/j.physa.2019.121456 [本文引用: 1]
Effect of taxis on emissions and fuel consumption in a city based on license plate recognition data: a case study in Nanning, China
[J].DOI:10.1016/j.jclepro.2019.01.123 [本文引用: 1]
出租车超速行为道路因素随机系数空间模型构建
[J].
Group-level random parameter spatial modeling for road factors of taxi speeding behavior
[J].
Exploring the spatial impacts of human activities on urban traffic crashes using multi-source big data
[J].DOI:10.1016/j.jtrangeo.2021.103118
Optimal passenger-seeking policies on e-hailing platforms using Markov decision process and imitation learning
[J].
基于稀疏轨迹数据的出租车载客区域推荐
[J].
Taxi pick-up area recommendation based on sparse trajectory data
[J].
Understanding detour behavior in taxi services: a combined approach
[J].
Modeling taxi driver search behavior under uncertainty
[J].DOI:10.1016/j.tbs.2020.09.008 [本文引用: 1]
Route recommendations for intelligent transportation services
[J].
Dynamic taxi service planning by minimizing cruising distance without passengers
[J].DOI:10.1109/ACCESS.2018.2881419 [本文引用: 1]
Multi-user mobile sequential recommendation for route optimization
[J].
Backward path growth for efficient mobile sequential recommendation
[J].DOI:10.1109/TKDE.2014.2298012 [本文引用: 1]
Applying simulated annealing and parallel computing to the mobile sequential recommendation
[J].DOI:10.1109/TKDE.2018.2827047 [本文引用: 2]
Route recommendation based on temporal-spatial metric
[J].DOI:10.1016/j.compeleceng.2021.107549 [本文引用: 4]
基于网格化的出租车空载寻客路径推荐
[J].
Grid-based route recommendation of no-load taxi
[J].
Environmental benefits mining based on data-driven taxi cruising recommendation strategy
[J].DOI:10.1016/j.jclepro.2021.129376 [本文引用: 3]
基于分时MDP的出租车载客预测推荐技术研究
[J].
Research on forecast and recommendation technology of taxi passengers based on time-varying Markov decision process
[J].
Adaptive passenger-finding recommendation system for taxi drivers with load balancing problem
[J].DOI:10.1016/j.cie.2022.108187 [本文引用: 1]
基于候客点规划的空闲出租车路线推荐算法
[J].
Idle taxi route recommendation algorithm based on waiting point planning
[J].
Recursive decomposition probability model for demand estimation of street-hailing taxis utilizing GPS trajectory data
[J].DOI:10.1016/j.trb.2022.11.014 [本文引用: 1]