管道渗漏是较为粗略的概念,其可以细分为以下3种类型[4]:1)管道内渗:流体沿管道破损处由管道外部进入管道内部;2)管道外渗:管道内部流体经破损处流向管道外部;3)管道周期渗漏:内渗与外渗循环交替发生. 本研究针对管道内渗诱发地面塌陷展开相关研究工作.
目前很多学者采用模型试验与数值模拟的手段对管道内渗诱发的地面塌陷问题进行研究. 在模型试验方面,Guo等[5]基于室内模型试验研究粒径、缺陷尺寸、地下水位高度以及上覆土层厚度对管道内渗侵蚀过程及破坏形态的影响. 郑刚等[6]设计了可以改变缝隙宽度的砂、水渗漏可视化试验装置,对渗漏过程中土拱的形成与破坏进行研究,认为能否形成稳定的土拱对渗漏的发生有重要影响. Sato等[7]探究地下构筑物与管道的相对位置对地面塌陷的影响,试验结果表明地下构筑物的位置会影响局部渗流路径,进而影响地下侵蚀空洞的形成与地面塌陷出现的位置. 张冬梅等[8]研究间断级配砂土中破损管线渗流侵蚀过程中的水土流失变化和侵蚀区域的发展规律. 刘成禹等[9]针对管道满流的情况进行试验研究,发现管道破损诱发的土体渗流侵蚀存在3种模式,分别如下:1)漏水不漏砂;2)漏水漏砂,随后漏砂量减少,破损处上方砂粒形成稳定土拱,砂土停止渗漏,管道上方存在一定厚度的上覆土层;3)漏水漏砂,砂土一直流失,最终管道上方无上覆土层. 钟世英等[10]对砂土在不同相对密实度下的侵蚀破坏过程进行分析,研究发现砂土的相对密实度对侵蚀破坏形态有显著影响. 在数值模拟方面,Zhang等[11]利用有限元方法研究管道渗漏过程中间断级配砂土中细颗粒流失规律. Long等[12]采用离散元与有限差分耦合方法 (discrete element method-finite difference method, DEM-FDM) 探究隧道漏砂过程中的土拱效应. 蔡剑韬等[13]采用离散元与计算流体力学耦合方法(discrete element method-computational fluid dynamics, DEM-CFD) 揭示管道渗漏引发地面塌陷灾害的发展过程.
综上所述,研究了管道缺陷尺寸、颗粒级配、地下水位高度等参数对侵蚀破坏形态及砂水流失速率等方面的影响,但是相关研究主要集中于管(隧)道正上方存在缺陷发生内渗的情况,而鲜有关注管道不同渗漏位置对侵蚀破坏形态以及土拱发展的影响的. 虽然Mohamed等[14]与Tang等[15]研究了管道不同渗漏位置对地层塌陷的影响,但其研究主要集中在管道不同渗漏位置对砂水流失量的影响方面,而缺少对颗粒流失路径及细观机理的研究. 鉴于此,本研究针对富水砂性地层中的排水无压管道内渗进行研究,分析管道不同渗漏位置对水土流失发展规律以及颗粒渗蚀路径的影响,并结合DEM-FDM流固耦合数值模拟手段在细观层面上探究管道不同渗漏位置对地层应力以及渗流侵蚀的影响. 阐明管道不同渗漏位置造成地层塌陷严重性不同的内在原因;分析管道渗漏前后所受水、土压力的改变情况,以及在渗漏过程中因地层应力改变而导致管道所受土压力的变化.
1. 物理模型试验概况
1.1. 试验装置
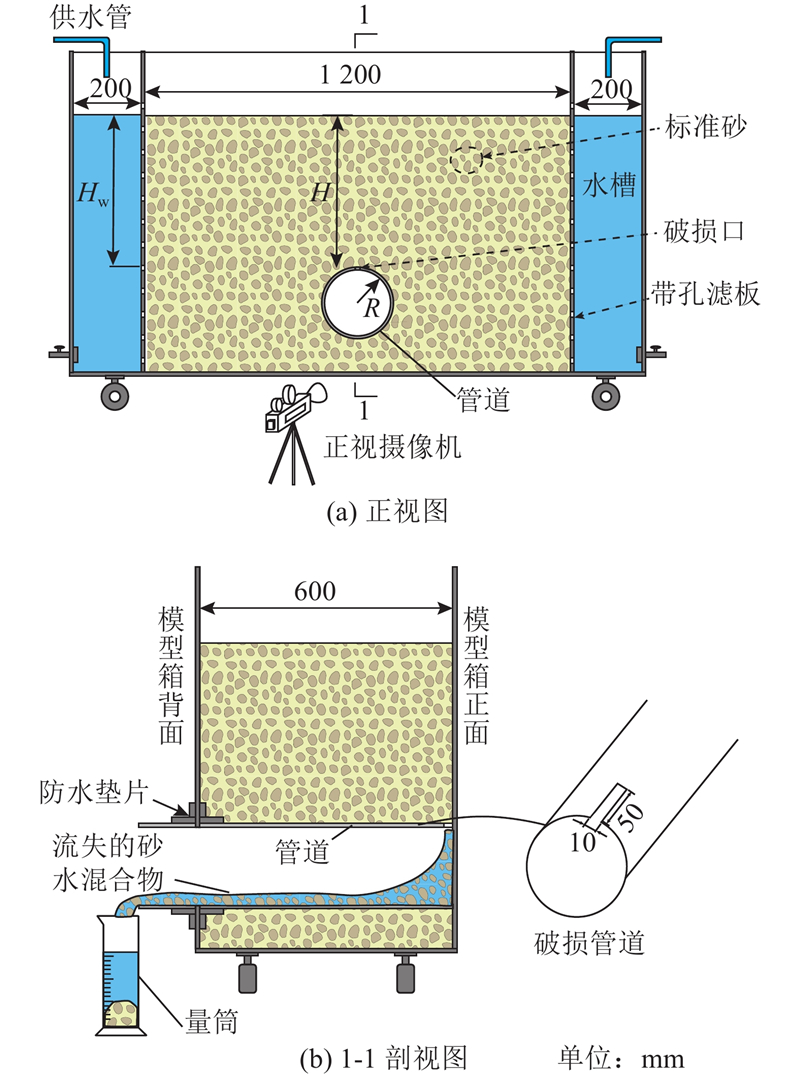
自行设计的模拟管道内渗可视化试验装置如图1所示,其中,图1(a)为正视图,图1(b)为1-1剖视图. 图中,R为PVC管道的半径,R =100 mm;H为管道以上覆土厚度,Hw为管道以上水位高度. 装置由4部分构成:上部供水管、两侧水槽、中部土体箱以及带有破损口的管道. 位于模型箱上部的供水管用来保持管道渗漏过程中两侧水槽的水位稳定;中部的土体箱长为1200 mm,宽为600 mm,高为900 mm;模型箱足够大以消除边界效应的影响[16]. 为了清楚地观察管道渗漏过程中地层侵蚀过程,模型箱正面采用透明的有机玻璃板. 两侧水槽的长度均为200 mm,通过带孔的玻璃滤板可以实现与土体箱之间水的自由传递;为了防止土颗粒流失到水箱中,带孔滤板上覆有一层孔径小于最小砂土粒径的筛网. 本研究基于定性的目的来探究管道不同渗漏位置对地面塌陷程度的影响,因此模型试验在1g重力下进行.
图 1
图 1 管道渗漏侵蚀试验装置示意图
Fig.1 Schematic diagram model test equipment for soil erosion induced by pipe leakage
在模型箱中部,安置了一根半径为100 mm的带有缺陷的PVC管用来模拟破损管道,其中心点距土体箱底部为200 mm. 缺陷设置在管道顶部,其环向尺寸设置为10 mm,纵向尺寸设置为50 mm(见图1(b)),用来模拟管道上存在一条纵向裂缝的情况. 为了观察颗粒流失情况,本试验设置为半模型试验,即将管道带有缺陷的一端紧贴模型箱正面. 因此通过正面有机玻璃板观察到的现象对应于:管道上存在一条宽为10 mm,长为100 mm的纵向裂缝时,其裂缝中点横截面上的渗流侵蚀现象. 同时由于试验模拟的是一条裂缝,可认为紧贴壁面处的土体侵蚀近似为平面问题[11-12]. 缺陷尺寸的设置参考了Zhang等[11]与Long等[12]的试验.
1.2. 试验土样与试验工况
表 1 福建标准砂物理特性参数
Tab.1
| 参数 | Gs | emin | emax | ρmin / (g·cm−3) | ρmax / (g·cm−3) |
| 值 | 2.63 | 0.52 | 0.84 | 1.43 | 1.73 |
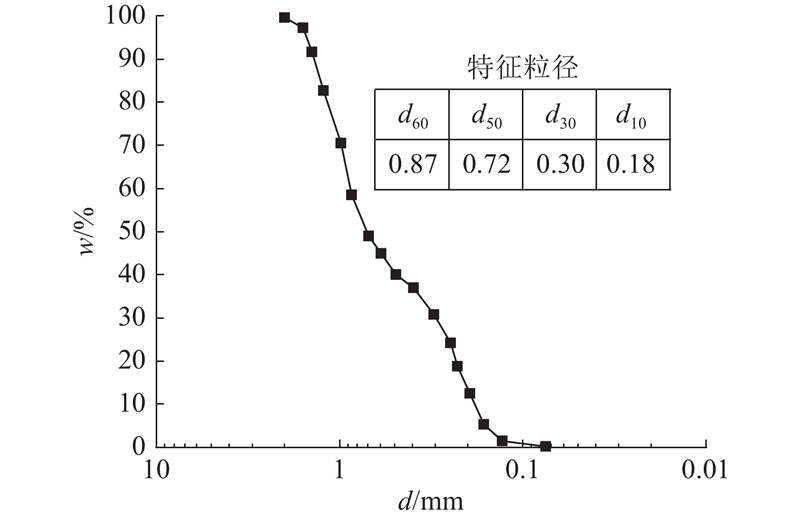
图 2
表 2 管道不同渗漏位置试验方案表
Tab.2
| 试验工况 | H | 管道渗漏 破坏位置 | Hw |
| Case 1 | 4R | 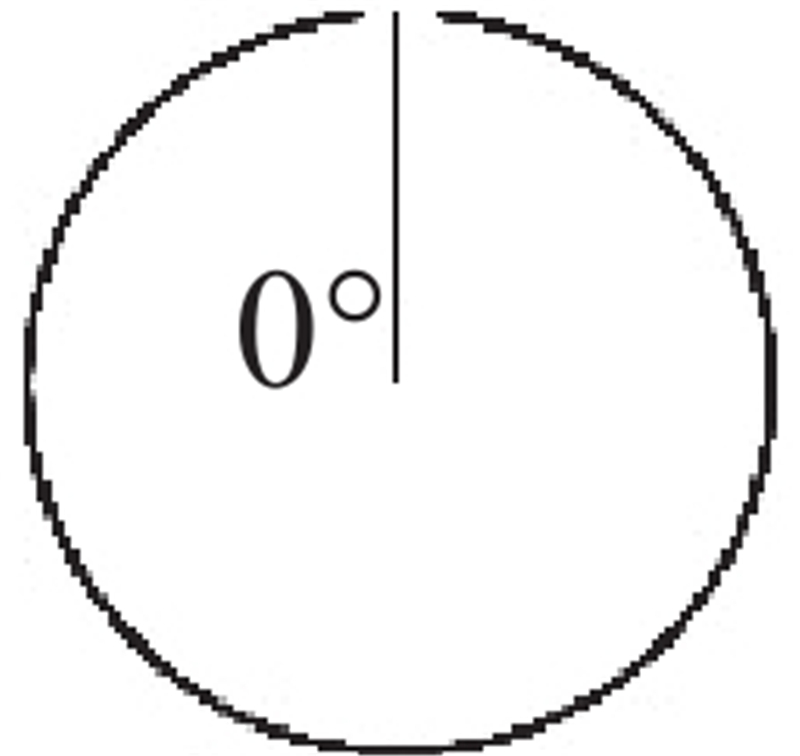 | 4R |
| Case 2 | 4R | 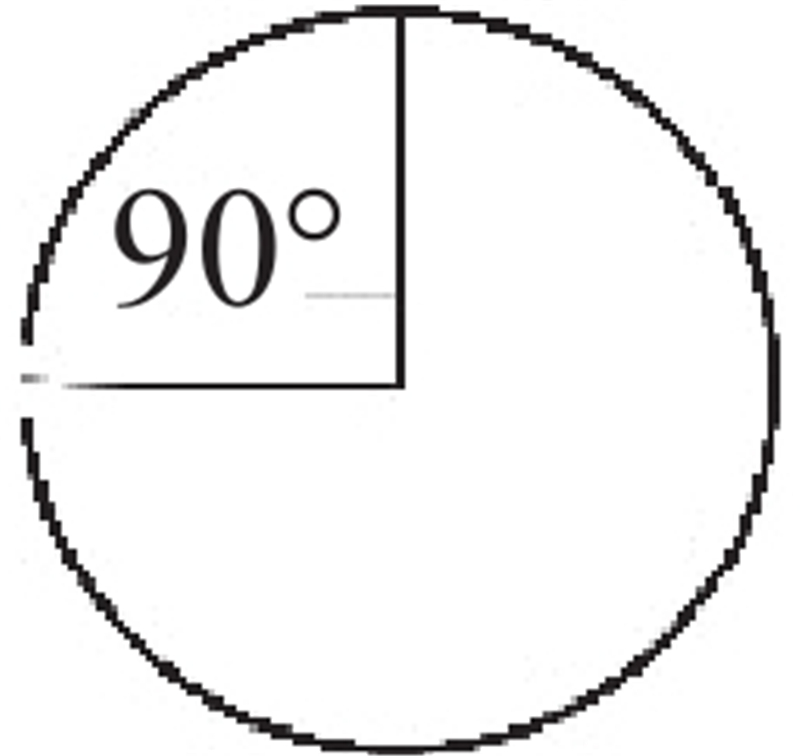 | 4R |
1.3. 试验步骤
1)试验前准备:在装填土样前,将管道按照试验方案中的渗漏位置安装好,使管道前部与土体箱的玻璃板紧密贴合并在贴合处涂上一圈防水胶,同时在发生渗漏的缺陷处提前放置橡胶塞并用防水胶带密封.
2)填埋土体:将预先制备好的一定质量的砂土缓慢导入模型箱中,将土样分层装填并压实,压实度的标准参考给水排水工程管道结构设计规范[19],同时每隔10 cm铺设一层薄的红色砂,试验土体的压实度为94.8%,相对密度为75%,密度为1.64 g/cm3,孔隙比为0.6. 当土体填埋到试验工况指定高度后,打开供水管,将水缓慢加入到土体箱两边的水槽中,直到水刚好淹没土体表面,放置一段时间,使土体充分饱和. 2次试验除了管道渗漏位置不同以外,其他条件均相同.
3)进行试验:拔掉渗漏处的橡胶塞,开始模拟管道的渗漏侵蚀过程. 试验过程中通过供水管来保持两侧水槽内的水位与地表平齐,并不断测量水和砂的流失量,直到渗漏处没有砂土颗粒流失为止.
2. 模型试验结果分析
2.1. 管道不同渗漏位置下土体侵蚀发展规律
Case 1中管道顶部发生渗漏,土体受地下水侵蚀的发展过程如图3所示. 整个渗漏过程可以分为以下3个阶段.
图 3
第1阶段:初步渗漏阶段,如图3(a)所示. 在这个阶段内,土体受侵蚀区域仅在渗漏处上方附近的一个小范围内,尚未发展到地表,因此地表未观察到明显的沉降.
第3阶段:渗漏收敛阶段,如图3(d)所示. 此时砂土颗粒的流失速率迅速减慢,并最终停止渗漏,土体颗粒在模型箱内部达到了一个稳定的状态. 但地下水仍持续从土体中渗出,从破损处流入到管道内部.
Case 2中管道左侧90°发生渗漏,土体受地下水侵蚀的发展过程如图4所示,其渗漏过程也可分为上述3个阶段,但是颗粒侵蚀路径却与管道顶部开孔有较大不同.
图 4
第1阶段:如图4(a)所示. 管道破损处附近的砂土颗粒开始发生渗漏,受侵蚀的区域逐渐向上扩展,但还未延伸到地表. 观察离管道最近一层红线的侵蚀流失路径,可以发现砂土颗粒明显受到地下水作用而绕流到管道左边的渗漏处.
第3阶段:砂土颗粒的流失速度大大减缓,之后停止了渗漏,最终形成了如图4(d)中黑色虚线所示的渗流侵蚀区域,其地层塌陷相较于Case 1中更为严重.
2.2. 砂水流失量
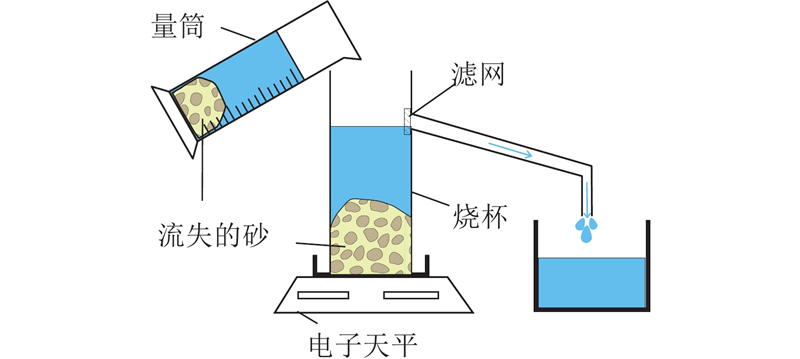
自制的砂水流失测量装置如图5所示,测量装置中滤网的作用是防止砂颗粒的流失.
图 5
砂水流失量的计算过程如下:首先测量一定时间量筒内收集到的砂水混合物总质量,记为∆m,并记录电子天平的初始示数为m1;之后将量筒中收集到的砂水混合物倒入电子天平上的烧杯中,待电子天平的示数稳定后,记录示数为m2,则一定时间内流失的砂质量∆ms与水质量∆mw表达式如下:
式中:ρs与ρw分别为砂的颗粒密度与水的密度,ρs=2.63 g/cm3.
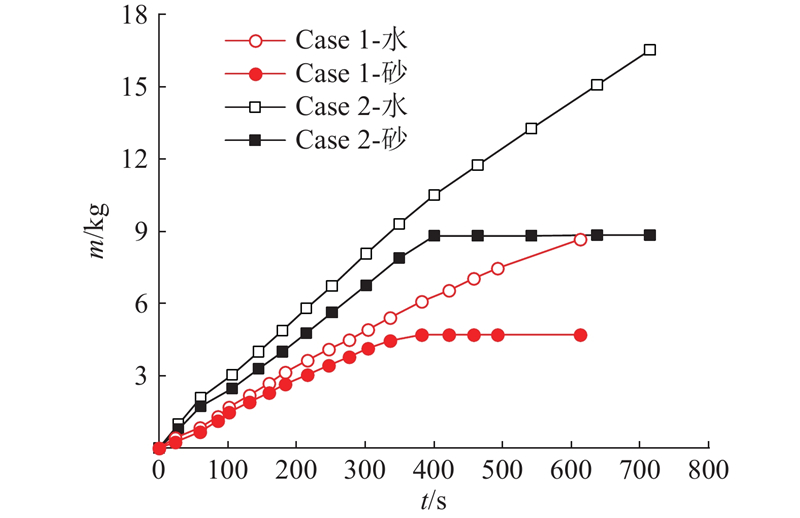
如图6所示为2种工况下的砂水累积流失质量m随时间t的发展过程. 可见,2种工况下砂土的流失量均先呈线性增加,后趋于稳定;水的流失量也随时间呈线性增加,但没有停止的趋势,同时在流失过程中,水的流失量始终大于砂的流失量,图中砂水流失量的变化也反映了Case 1与Case 2中土体侵蚀的发展,即与管道顶部发生渗漏相比,管道腰部发生渗漏时,其砂水流失速率更快,造成的地面塌陷也更严重.
图 6
图 6 不同工况下砂水累积流失量随时间的变化
Fig.6 Discharge of sand and water with time in different cases
表 3 管道不同渗漏位置下砂水流失特性
Tab.3
| 工况 | vs / (g·s−1) | vw / (g·s−1) | msum /g | r |
| Case 1 | 13.3 | 14.1 | 4704.4 | 1.06 |
| Case 2 | 21.9 | 23.6 | 8829.8 | 1.08 |
3. 数值模型的建立
管道渗漏侵蚀问题作为一种典型的颗粒之间作用以接触为主的高密度颗粒流固耦合问题,从实用以及计算精确性角度出发,采用DEM-FDM方法是较合适的,且此方法已经被广泛用于高密度颗粒和流体相互作用的研究中,并取得了较好的结果[12]. 因此,采用DEM-FDM耦合的方法对管道渗漏侵蚀过程进行数值模拟,分析管道渗漏侵蚀过程中的细观规律.
为了更加直观地分析在管道渗漏过程中各种参量的变化规律,采用二维分析,这相当于分析管道上存在的是一条“裂缝”而不是一个“缺口”. 缺陷的长度是宽度的5倍(10×50 mm),可认为在靠近管道缺陷前端近似是一条“裂缝”.
3.1. DEM-FDM耦合基本原理
砂土颗粒采用离散元软件PFC(Particle Flow Code)来进行模拟,流体采用有限差分软件FLAC(Fast Lagrangian Analysis of Continua)进行分析.
在PFC中,颗粒之间的接触采用线性接触模型,颗粒的运动遵循牛顿第二定律,其具体计算原理在文献[21]有详细说明. 流体作用到颗粒上的渗透力通过以下公式计算:
式中:Vi为颗粒的体积,γw为水的重度,
FLAC的计算原理是达西定律,在仅执行流体计算时,其关键参数是渗透系数k的选取. 针对颗粒材料,渗透系数通常是通过颗粒材料的孔隙率转化得到的,其应用最为广泛的是Kozeny-Carman方程[22]:
式中:Cs为颗粒材料的形状因子,Ss为每单位体积颗粒的表面积,T为曲折因素,μ为动力黏度,e为孔隙比. 在含有均匀颗粒粒径的多孔介质中,可以设置Cs=2.5,T=
在PFC中,可以通过测量圆测量孔隙率. 通过孔隙比e与孔隙率n的转换关系,式(4)可以改写为
综上所述,PFC与FLAC进行的DEM-FDM耦合过程可以概括为以下主要步骤:在PFC和FLAC中分别建立相应的地层模型;将PFC中的孔隙率通过式(5)转换为渗透系数,再通过Socket I/O接口传递到FLAC中对应的PFC区域的模型中;当FLAC运行稳定后,将获得的渗流场(每个单元的水力梯度)通过式(3)转化为颗粒的渗透力,并通过Socket I/O口传回到PFC中对应的单元中去,PFC更新颗粒所受到的渗透力,开始颗粒渗流侵蚀过程.
3.2. 土体参数的选取
对于颗粒粒径的选择,若完全按照模型试验中标准砂的粒径大小建立同等大小的地层模型,会生成上千万个颗粒,这远远超出普通计算机的运算能力,因此须对颗粒的大小以及粒径范围进行适当缩放. Kondic[20]在利用离散元采用线性接触模型研究二维料斗颗粒流问题时发现,当料斗出口直径与颗粒粒径的比值为3~6时,会发生物料漏失一段时间之后发生堵塞的现象. 因此将粒径范围限制在2~3 mm,管道破损口大小设置为12.21 mm(对应的圆心角为7°),破损口大小与最大粒径比值为4.07,这样确保能够模拟管道渗漏侵蚀一段时间之后渗漏收敛的情况.
为了保证二维与三维在同等深度处地层有效应力在理论上的一致性,对数值模拟中颗粒密度进行二维与三维的等效转化,其具体过程如下. 当地层饱和时,在相同深度h处的有效应力为
式中:
式中:
结合式(6)、(7)可以得出
式中:
二维与三维孔隙率的转化公式[23]为
式中:
因此结合式(8)、(9)可以计算得出
图 7
图 7 PFC中砂土的内摩擦角标定结果
Fig.7 Calibration results of PFC for internal friction angle
表 4 管道渗漏数值模拟参数取值表
Tab.4
| 单元 | PFC参数 | 数值 |
| 颗粒参数 (ball单元) | 颗粒粒径/mm | 2~3 |
| 颗粒密度/(g·cm−3) | 2.2 | |
| 颗粒摩擦系数 | 0.5 | |
| 颗粒法向刚度/( N·m−1) | 1×106 | |
| 颗粒切向刚度/( N·m−1) | 0.8×106 | |
| 阻尼系数(局部阻尼) | 0.7 | |
| 法向黏滞阻尼系数 | 0.2 | |
| 孔隙率 | 0.15 | |
| 模型箱参数(wall单元) | 墙体法向接触刚度/( N·m−1) | 1.5×108 |
| 墙体切向接触刚度/( N·m−1) | 2.0×108 | |
| 墙体摩擦系数 | 0.0 | |
| 管道参数 (wall单元) | 墙体法向接触刚度/( N·m−1) | 3.0×1011 |
| 墙体切向接触刚度/( N·m−1) | 3.0×1011 | |
| 墙体摩擦系数 | 0.5 |
3.3. 数值模型建立及验证
针对所研究的管道渗漏问题,涉及地层模型的建立和砂土颗粒流失过程,须使用PFC中提供的2种阻尼机制[24],在地层模型创建时,使用局部阻尼来使地层尽快达到静态平衡;在模拟颗粒流失过程时则取消局部阻尼,使用法向黏滞阻尼来考虑颗粒流失这一动态过程中的能量耗散.
地层模型的创建:采用多层压密法[25]生成地层,地层生成后删除安装管道区域的颗粒,同时用一个与管道直径相当的球体来代替管道,之后施加重力以及浮力,模拟土体固结沉降过程. 固结完成之后,删除模拟管道的球体并用720片墙体重新建立管道模型,每片墙体对应的圆心角为0.5°.
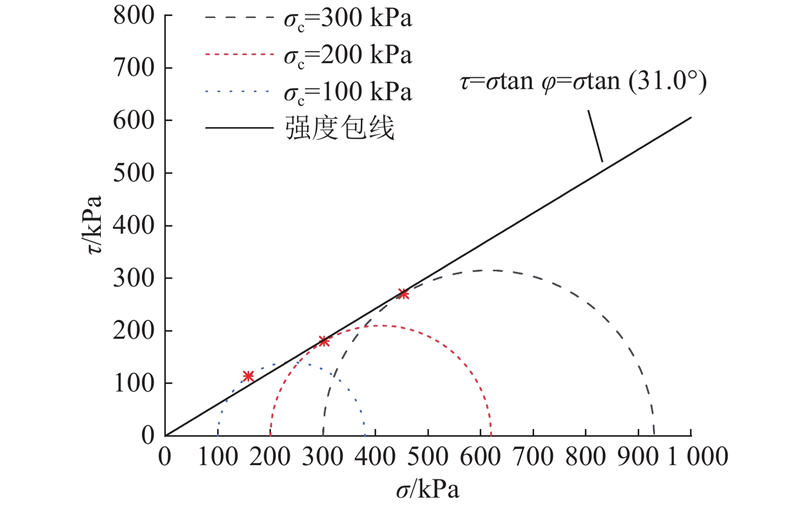
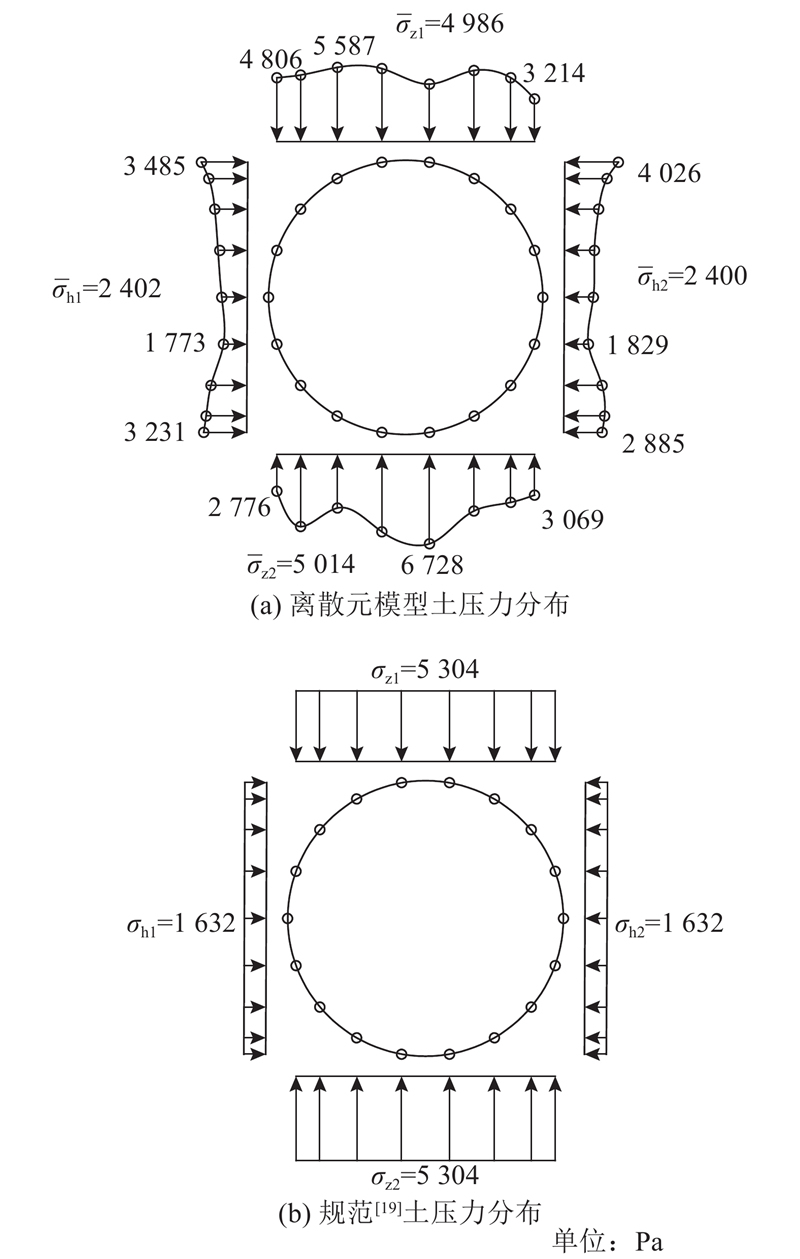
为了验证所建立地层模型的合理性,将管道表面所受到的土压力与规范[19]进行对比,如图8所示. 按照规范中土压力的计算方法,管周土压力分布如图8(b)所示,其中将管道视为无重介质,上埋式管道竖向土压力系数Cc =1.3,土体浮重度γ'=1.02×104 kN/m3,管道侧向土压力系数取朗肯主动土压力系数Ka=0.32 ( Ka=tan2 (45−φ/2) ), φ为土体的内摩擦角,取31o. 图中,σz1为管道顶部土压力,σh1为管道侧向土压力. 由图8(a)可以看出,离散元模型中管道竖向的平均土压力比规范中要小,而管道侧向平均土压力比规范中要大,这是因为规范中高估了管道竖向土压力,低估了管道侧向土压力[26]. 总体而言,离散元模型土压力能够反映管道周围应力分布,说明本研究数值建模以及参数选取的正确性.
图 8
图 8 PFC数值模型土压力与规范土压力对比
Fig.8 Comparison of calculated soil pressure between using PFC model and using code
图 9
4. 管道渗漏过程细观机理分析
4.1. 管道渗漏过程中土体位移发展规律
数值模拟管道渗漏过程如图10所示,分别展示了管道0°渗漏(左)与90°渗漏(右)情况下地层侵蚀的发展过程. 对于0°渗漏,颗粒流失过程总共持续了32万步,对于90°渗漏,颗粒流失过程总共持续了48万步,之后管道渗漏便迅速收敛,不再渗漏. 两者最终流失颗粒质量的比值为1.68. 可以看出,数值模拟结果可以较好地反映管道渗漏造成砂层侵蚀的3个阶段:初步渗漏阶段,侵蚀区土颗粒的位移仅限制在孔口附近,地表无明显沉降;渗漏发展阶段,土颗粒逐层侵蚀,颗粒的位移逐渐发展到地表,地表缓慢沉降;渗漏收敛阶段,孔口处形成稳定的力链,渗漏快速收敛,最终土颗粒不再流失,渗漏达到稳定状态. 同时从数值模拟中得到的渗流侵蚀区域的形态(如图10 (c)中黑色虚线所示)也可以较好地与模型试验中的渗流侵蚀区域相吻合. 这说明采用DEM-FDM耦合的数值模拟方法可以较好地反映管道渗漏侵蚀过程的特征.
图 10
图 10 管道0°与90°渗漏下地层侵蚀的发展
Fig.10 Development of stratum erosion for 0° leaking and 90° leaking
4.2. 渗漏后地层应力及水力梯度的变化
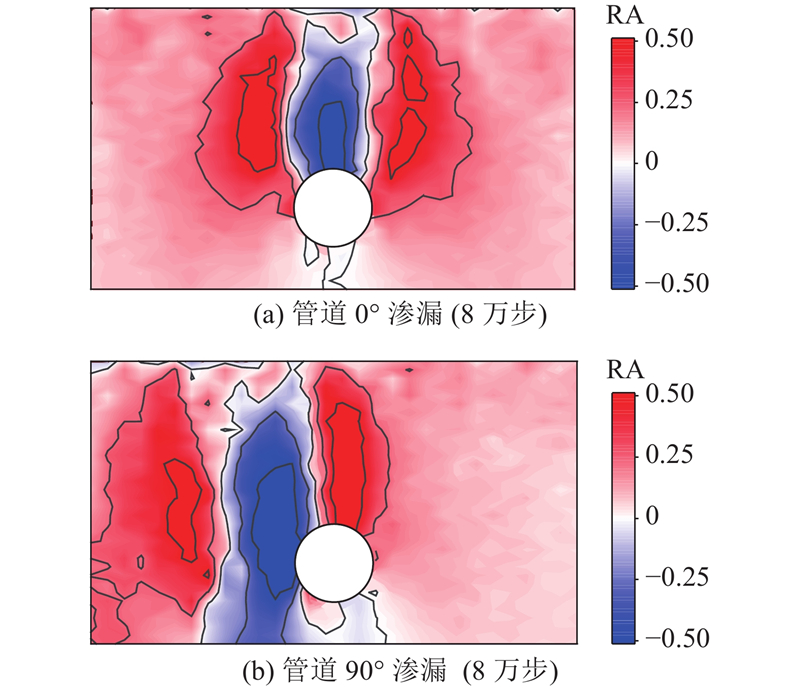
为了从细观层面上探究Case 1与Case 2所造成地面塌陷严重性的不同,研究管道渗漏后地层应力的变化,选择流固耦合计算8万步时地层应力的变化情况,利用PFC中自带的测量圆功能来测量地层中的竖向应力,并定义归一化指标RA来描述竖向应力的改变:
式中:σ0表示渗漏发生前的竖向应力,σi表示渗漏发生后的竖向应力,RA>0,RA<0与RA=0分别表示渗漏侵蚀后的竖向应力增加、减小与不变.
图 11
图 11 管道不同位置渗漏后土体竖向有效应力的变化
Fig.11 Change of vertical effective stress after pipeline leakage under different locations
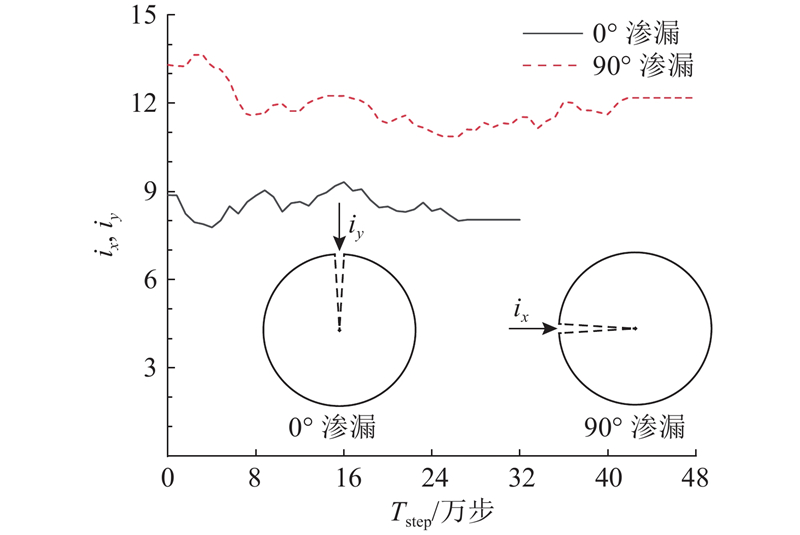
如图12所示为管道不同渗漏位置破损口周围水力梯度 ix、iy随时间步 Tstep 的变化过程,其中0°渗漏代表在渗漏处竖向(如图中iy所示)水力梯度大小的变化情况,90°渗漏代表在渗漏处水平方向上(如图中ix所示)水力梯度大小的变化情况. 水力梯度的计算公式为
图 12
图 12 管道渗漏过程中破损口周围水力梯度的变化
Fig.12 Change of hydraulic gradient near defect during leaking
式中:
可以发现,在管道渗漏侵蚀过程中,90°渗漏处水平方向上的水力梯度要高于0°渗漏处竖向方向上的水力梯度. 这是因为管道90°位置比0°位置低100 mm,由于水位线在地表,在未渗漏时管道90°位置的压力水头更大,而当管道发生渗漏后,渗漏位置处的压力水头瞬间变为0,因此,在管道发生渗漏之后,管道90°渗漏位置处所产生的孔隙水压力梯度更大,计算得到的水力梯度也会更大,从而在管道90°渗漏处的周围土体会受到更大的渗透力,造成更为严重的渗流侵蚀现象.
结合上述分析,之所以管道90°渗漏会造成更多的砂土颗粒流失以及更为严重的地面塌陷现象,其原因是当管道90°渗漏时,管道渗漏处渗透力的方向为水平,这会对地层造成更为剧烈的扰动(见图11),削弱地层稳定,使砂土颗粒更容易被渗透力迁移与移动;同时由于其埋深更深,渗漏后破损口周围土体所受到的渗透力也更大,会受到更为强烈的渗流侵蚀作用. 最终在两者耦合作用下会造成更为严重的地面塌陷现象.
4.3. 渗漏前后管道表面水土压力分布
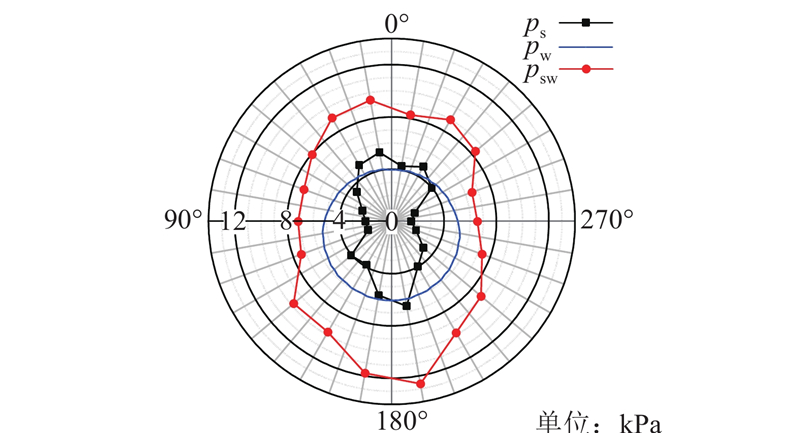
土体应力的重分布会影响作用在管道上的土压力,因此有必要探讨渗漏前后管道所受土压力的变化,采用自行编写的程序对管道渗漏前后管道表面的土压力分布情况进行测量,将圆形管道分为18块,每隔20°为一块,每一块包含40个管道墙体(每个墙体对应的圆心角为0.5°,见3.3节). 如图13所示为计算示意图. 检测并记录作用在每块管道上的总法向作用力,得到其总作用力之后除以每块管道的面积即得到作用在每块管道上的土压力. 作用在管道上的水压力通过提取FLAC中孔隙水压力数据来获得. 由此可以得到作用于管道表面的水、土压力以及总压力在管周360°的分布. 如图14所示为未渗漏时管道表面压力分布. 图中,径向轴表示管道所受压力的大小(单位为kPa);外圆周的角度轴表示管道圆周的位置,计算得到的土压力作用点为每块管道的中心点;ps、pw、psw分别表示土压力、水压力、总压力.
图 13
图 13 管道表面土压力计算示意图
Fig.13 Schematic diagram for calculating soil pressure on pipe surface
图 14
图 14 未渗漏时管道表面压力分布
Fig.14 Distribution of pressure on pipe surface before pipeline leakage
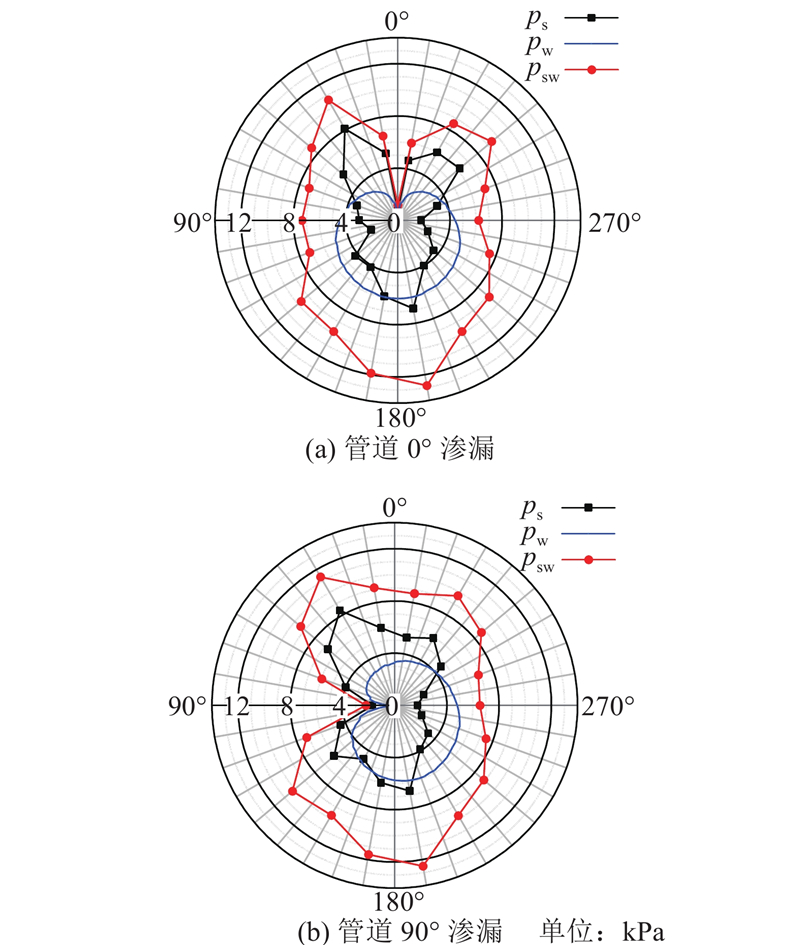
如图15所示为流固耦合计算0.8万步时管道0°与90°渗漏管道表面压力分布情况. 为了更加清楚地观察渗漏前后管周土压力以及水土合力的变化情况,如图16所示对比了管道未渗漏、0°渗漏以及90°渗漏时管道表面土压力以及水土总压力的分布情况. 由图16(a)可以看出,在发生渗漏之后,无论是90°还是0°渗漏,在破损口位置处的土压力都会降低;然而在破损口周围管道表面处土压力则会增加. 对于0°渗漏情况,在渗漏前、后,管片位于30o位置处的土压力由4966 Pa增加到8107 Pa,增幅为63%;对于90°渗漏情况,管片位于110o位置处的土压力由1909 Pa增加到4249 Pa,增幅为123%. 结合图11中管道周围土体竖向应力增加的区域,可以说明管道渗漏之后,在破损口周边形成了土拱,造成管道渗漏处周围表面所受土压力增加.
图 15
图 15 不同位置渗漏后管道表面压力分布情况
Fig.15 Distributions of pressure on pipe surface after pipeline leakage under different leaking locations
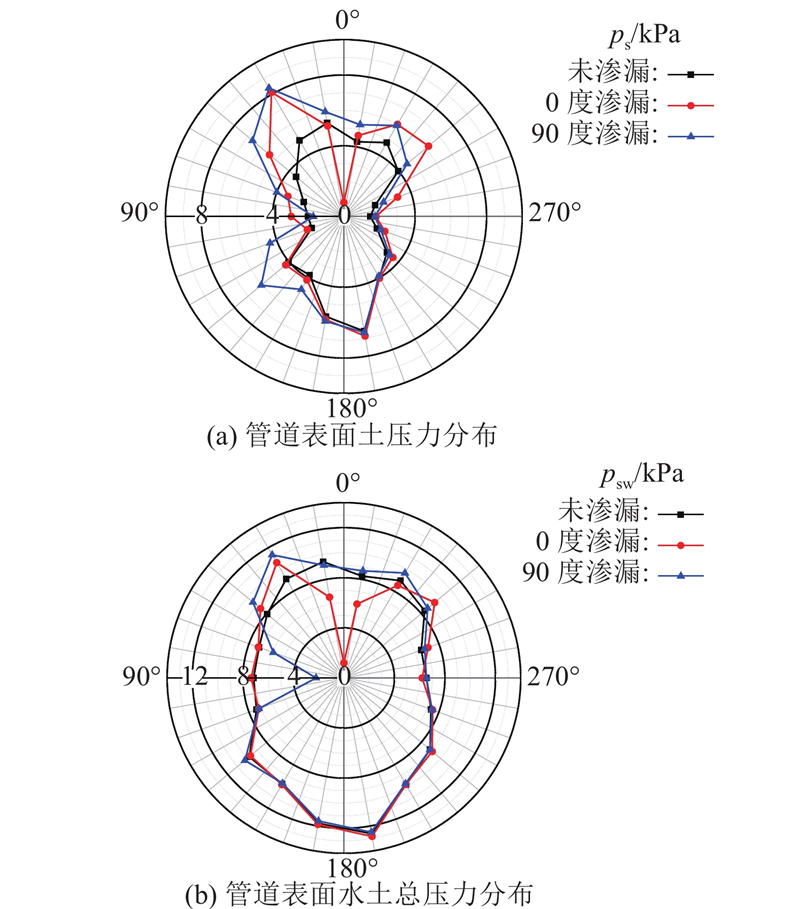
图 16
图 16 不同位置渗漏后管道表面土压力与总压力的对比
Fig.16 Comparison of soil pressure and sum pressure after pipeline leakage under different leaking locations
如图16(b)所示,对比管道未渗漏、0°渗漏以及90°渗漏的管道表面总压力分布情况. 管道表面总压力分布情况表明,除了在破损口位置处管道表面总压会突降,在其他位置管道表面压力没有明显的变化.
结合以上分析可知,在管道渗漏之后,位于破损口处的土压力、水压力以及总压力都会减小;由于土拱效应,管道渗漏处周围表面所受到的土压力会增加,但是作用在其表面上的总压力基本保持不变.
4.4. 渗漏后管道表面土压力发展
如图17所示,分别展示了管道0°以及90°渗漏过程中管道表面土压力的变化过程.
图 17
图 17 不同渗漏位置下管道表面土压力的发展
Fig.17 Developments of soil pressure on pipe surface under different leaking locations
由图17(a)可以看出,对于0°渗漏情况,在管道渗漏之初(0.8万步),破损口周围(管周10o ~30o以及310o ~350o)所受土压力迅速增加,说明管道破损口周围的土拱已经形成;之后随着渗漏的发展,破损口周围土压力不断减小并最终趋于稳定,表明随着渗漏的发展,土拱效应不断减弱,在渗漏收敛后,土拱稳定.
对于90°渗漏情况,如图17(b)所示,当管道渗漏发生之初(0.8万步),破损口周围的土压力迅速增加,相比于0°渗漏,可以发现其形成土拱的范围更大,且管周土压力发展更为复杂:在颗粒流失过程中在破损口附近管周10o ~70o位置的土压力随渗漏的发展而不断降低,在破损口附近管周110o ~170o位置的土压力随渗漏的发展变化不大,而管周310o ~360o位置的土压力则随着渗漏的发展逐渐增加. 这表明在管道渗漏过程中,土拱在管周10o ~70o逐渐削弱;在管周110o ~170o位置基本保持不变,而在管周310o ~360o位置则逐渐增加.
通过以上分析可知,当管道在不同位置发生渗漏后,管道表面土压力的变化是不同的. 对于管道顶部发生渗漏,随着渗漏的发展,破损口周围土压力逐渐减小;对于管道腰部发生渗漏,其土压力在管道不同位置分别展现出增加、减小以及不变3种趋势.
5. 结 论
针对富水砂性地层中不同渗漏位置下管道渗蚀展开物理模型试验与DEM-FDM流固耦合细观研究,结果如下.
(1)对于级配均匀的砂土,当管道渗漏为先漏水漏砂,之后漏砂收敛的模式时,管道渗漏过程可以分为:初步渗漏阶段,侵蚀区土颗粒的位移仅限制在孔口附近,地表无明显沉降;渗漏发展阶段,砂土颗粒逐层侵蚀,颗粒的位移逐渐发展到地表,地表缓慢沉降;渗漏收敛阶段,孔口处形成稳定土拱,渗漏快速收敛,最终土颗粒不再流失,只有水流失,渗漏达到稳定状态.
(2)管道腰部发生渗漏会造成更严重的地面塌陷现象,其原因为当管道腰部渗漏发生时,渗漏处的渗透力方向为水平,会对地层造成更为剧烈的扰动,削弱地层稳定性,使砂土颗粒更容易被渗透力迁移与移动;同时由于其埋深更深,渗漏后破损口周围土体所受到的渗透力也更大,会受到更为强烈的渗流侵蚀作用. 最终在两者耦合作用下会造成更为严重的地面塌陷现象.
(3)管道发生渗漏后,管道渗漏处表面的土压力、水压力以及总压力都会减小;由于土拱效应,管道渗漏处周围表面处土压力会增加,但是作用在其表面上的水土合力基本保持不变.
(4)管道在不同位置发生渗漏时,管道表面土压力的变化是不同的,对于管道顶部发生渗漏,随着渗漏的发展,破损口周围土压力逐渐减小;对于管道腰部发生渗漏,其土压力在管道不同位置则分别展现出了增加、减小以及不变3种趋势.
由于数值模拟中管道建模的限制,本研究仅讨论了管道表面所受土压力的变化发展情况,而没有考虑管道所受力矩的变化,未来可以针对管道在渗漏过程中所受力矩的发展变化进一步研究.
参考文献
近10年中国城市道路塌陷原因及防治对策分析
[J].
Analysis on causes and countermeasures of urban road collapse in recent 10 years in China
[J].
2014—2018年中国城市路面塌陷时空规律与原因分析
[J].
Analysis on spatio-temporal law and causation of urban road collapse in China from 2014 to 2018
[J].
Review of cave-in failures of urban roadways in China: a database
[J].
Visualization of three dimensional failure in sand due to water inflow and soil drainage from defective underground pipe using X-ray CT
[J].DOI:10.3208/sandf.49.959 [本文引用: 1]
Physical modeling on sand erosion around defective sewer pipes under the influence of groundwater
[J].DOI:10.1061/(ASCE)HY.1943-7900.0000785 [本文引用: 2]
地下工程漏水漏砂灾害发展过程的试验研究及数值模拟
[J].
Experiment study and numerical simulation of leaking process of sand and water in underground engineering
[J].
Influence of location of subsurface structures on development of underground cavities induced by internal erosion
[J].DOI:10.1016/j.sandf.2015.06.014 [本文引用: 1]
间断级配砂土中管线破损引起的渗流侵蚀模型试验
[J].DOI:10.11779/CJGE201811020 [本文引用: 2]
Model tests on seepage erosion caused by pipeline damage in gap-grading sand
[J].DOI:10.11779/CJGE201811020 [本文引用: 2]
地下管道破损诱发沉降的预测模型及试验验证
[J].DOI:10.11779/CJGE202103003 [本文引用: 4]
Prediction model for settlement caused by damage of underground pipelines and its experimental verification
[J].DOI:10.11779/CJGE202103003 [本文引用: 4]
不同相对密实度下砂土侵蚀破坏试验研究
[J].DOI:10.12077/sdjz.2022.01.007 [本文引用: 1]
Experimental study on erosion and destruction of sandy soil under different relative compactness
[J].DOI:10.12077/sdjz.2022.01.007 [本文引用: 1]
Experimental and numerical study of internal erosion around submerged defective pipe
[J].DOI:10.1016/j.tust.2019.103256 [本文引用: 3]
Soil arching due to leaking of tunnel buried in water-rich sand
[J].DOI:10.1016/j.tust.2019.103158 [本文引用: 7]
上海浅部砂层管道渗漏引发塌陷的数值模拟
[J].
Numerical simulation of ground collapse induced by pipeline leakage in Shallow sand layer of shanghai area
[J].
Laboratory investigation of ground surface settlement caused by erosion around a leaking pipe
[J].DOI:10.1061/(ASCE)PS.1949-1204.0000629 [本文引用: 1]
Physical and analytical modeling of soil loss caused by a defective sewer pipe with different defect locations
[J].DOI:10.1007/s11440-022-01747-7 [本文引用: 3]
The design of a laboratory facility for evaluating the structural response of small-diameter buried pipes
[J].
The mechanical behaviour of drainage pipeline under traffic load before and after polymer grouting trenchless repairing
[J].DOI:10.1016/j.tust.2018.01.018 [本文引用: 1]
Simulations of two dimensional hopper flow
[J].DOI:10.1007/s10035-013-0462-4 [本文引用: 2]
颗粒流程序(PFC~(2D))中阻尼参数的适用性研究
[J].
Selection of damping parameters used in a particle flow code (PFC 2D)
[J].
An efficient technique for generating homogeneous specimens for DEM studies
[J].DOI:10.1016/S0266-352X(03)00064-8 [本文引用: 1]