浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(6): 1198-1208 doi: 10.3785/j.issn.1008-973X.2024.06.010

土木工程、交通工程

缩尺效应对砂砾石料力学特性及其本构模型的影响

崔熙灿,, 张凌凯,, 王建祥

1. 新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐 830052

2. 新疆水利工程安全与水灾害防治重点实验室，新疆 乌鲁木齐 830052

3. 贵州民族大学 建筑工程学院，贵州 贵阳 550025

Influence of scale effect on mechanical properties and constitutive model of gravel materials

CUI Xican,, ZHANG Lingkai,, WANG Jianxiang

1. College of Hydraulic and Civil Engineering, Xinjiang Agricultural University, Urumqi 830052, China

2. Xinjiang Key Laboratory of Hydraulic Engineering Security and Water Disasters Prevention, Urumqi 830052, China

3. College of Architectural Engineering, Guizhou Minzu University, Guiyang 550025, China

通讯作者: 张凌凯，男，副教授. orcid.org/0000-0002-5290-5309. E-mail: xjau_zlk@163.com

收稿日期: 2023-05-16  

基金资助: 国家自然科学基金青年科学基金资助项目(52109136).

Received: 2023-05-16  

Fund supported: 国家自然科学基金青年科学基金资助项目(52109136).

作者简介 About authors

崔熙灿（1998—），女，硕士生，从事岩土材料多尺度数值模拟研究.orcid.org/0000-0002-6597-8451.E-mail：cuixican0317@qq.com , E-mail：cuixican0317@qq.com

摘要

针对三轴仪受颗粒尺寸的限制而存在缩尺效应的问题，以新疆阿尔塔什筑坝料为研究对象，通过大型三轴数值模拟试验，从宏细观角度开展缩尺效应对砂砾石料力学特性及其非线性本构模型影响的研究. 结果表明，随着围压的增加，试样偏应力极值增大，剪缩程度显著而剪胀特性被抑制；随着试样尺寸的增大，其峰值强度提高，试样由剪缩向剪胀过渡. 随着试样尺寸的增大，邓肯模型的内摩擦角分量、弹性模量参数、体积模量参数均明显增大，其他参数的影响可忽略不计. 砂砾石料的内摩擦角分量与颗粒粒径呈对数型函数关系，弹性模量参数、体积模量参数与颗粒粒径均呈线性函数关系. 随着试样尺寸的增大，变形集中区的范围更广泛，其形式逐渐由“X”型变为“X+x”或“X+x+x”型变形集中区. 初始阶段配位数随着试样尺寸的增大而增加；加载过程中配位数增加，试样以剪缩为主，随着试样尺寸的增大其配位数逐渐呈减小趋势，剪缩性被抑制.

关键词： 砂砾石料 ; 离散元分析 ; 三轴试验模拟 ; 缩尺效应 ; 邓肯模型

Abstract

The triaxial instrument has a scale effect due to the particle size limitation. The Xinjiang Altash dam building materials were taken as the research object, and through the large-scale triaxial numerical simulation test, the influences of scale effect on the mechanical properties and nonlinear constitutive model of gravel materials were studied from the macro and micro perspectives. Results showed that, with the increase of confining pressure, the extreme value of deviatoric stress of the sample increased, the degree of shear shrinkage was significant and the dilatancy characteristics were suppressed. The peak strength was increased with increasing specimen size, and the specimen transitioned from shear shrinkage to shear expansion. With the increase of specimen size, the internal friction angle component, the elastic modulus parameter, and the bulk modulus parameter of Duncan's model parameters were significantly increased, and the effects of other parameters were negligible. The relationship between internal friction angle component and particle size for gravel was expressed as a logarithmic function, and the relationships between elastic modulus parameter, bulk modulus parameter and specimen size were expressed as linear functions. As the size of the specimen increased, the range of the deformation concentration zone was widely expanded, and its form gradually changed from the "X" type to the "X+x" or "X+x+x" type deformation concentration zone. As the specimen size increased, the initial coordination number was increased. During loading, the coordination number increased and the specimen was dominated by shear shrinkage. As the specimen size increased, the coordination number was shown to decrease gradually, and the shear shrinkage was suppressed.

Keywords： gravel ; discrete element analysis ; triaxial test simulation ; scale effect ; Duncan model

PDF (3405KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

崔熙灿, 张凌凯, 王建祥. 缩尺效应对砂砾石料力学特性及其本构模型的影响. 浙江大学学报(工学版)[J], 2024, 58(6): 1198-1208 doi:10.3785/j.issn.1008-973X.2024.06.010

CUI Xican, ZHANG Lingkai, WANG Jianxiang. Influence of scale effect on mechanical properties and constitutive model of gravel materials. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(6): 1198-1208 doi:10.3785/j.issn.1008-973X.2024.06.010

为了实现水资源的综合开发和高效利用，中国西部将建设一批高度约为300 m的高堆石坝. 目前对筑坝料变形的控制常用室内三轴试验测得，但随着堆石坝高度的增加筑坝料的尺寸不断增大，试验设备受限，会存在显著的缩尺效应问题，因此，对高堆石坝变形破坏机制的研究尚不明确.

砂砾石料是高堆石坝主要筑坝料之一，施工现场砂砾石料的尺寸较大，进行原型试验难度较高，常用缩尺手段进行研究，其方式主要有物理试验和数值模拟. 1）物理试验. Hall等[1]在自制三轴仪上首次进行大型三轴试验，发现不同的密度控制标准会造成峰值摩擦角呈现截然相反的规律[2]. 当干密度一定时，低围压下内摩擦角随最大粒径dmax增大而增大，高围压下出现相反的规律[3-4]；在同一干密度下，随着dmax的增大，试样抗剪强度减小，这可以从密实度和颗粒强度上进行解释[5]；在变形上，随着试样尺寸增加，剪缩特性增强[6]；在同一相对密度下，随着颗粒尺寸增大，试样干密度增加，孔隙比减小，故体积模量增大，变形模量减小[5,7]. 在进行物理试验时，超大三轴仪涉及到的问题非常复杂，如试样装样、橡皮膜、测量方法、加载设备等均存在一定试验缺陷易造成数据失真. 离散元颗粒流法在克服以上局限性的同时又可减少工作时间，是探究缩尺效应的有效方式. 2）数值模拟. 从细观角度探究其根本原因，发现堆石料强度的缩尺效应与颗粒的剪胀、破碎和重排列过程中能量变化产生的此消彼长有关[8-9]；采用相似级配法缩尺得到的试样，其初始承力结构与未缩尺前的相似，随尺寸增加其承力结构变得稀疏，有效配位数降速减缓[10]；堆石料缩尺效应的细观机理主要与不同尺寸试样的法向接触力的各向异性有关[11-12]；缩尺效应对堆石体蠕变特性影响显著，随试样尺寸增大其最终变形量明显增加[13-14]；数值模型的峰值强度、弹性模量、泊松比、黏结破裂率等参数的变异系数会随特征长度比L/R的减小而增大[15-16].

目前土体的静本构模型主要有非线性弹性模型和弹塑性模型2类. 非线性弹性模型主要有邓肯模型和K-G模型. Chang等[17]建立了邓肯张E-v模型，而研究发现E-v模型大多应用于标准土，不适合分析粗粒料； Duncan等[18]用体积变形模量B代替E-v模型中的切线泊松比v，提出适用于土石坝工程的邓肯E-B模型； Naylor等[19]考虑球张量与偏张量建立了K-G模型；高莲士等[20-21]在解耦K-G模型参数时，提出了新的清华K-G模型. 弹塑性本构模型大致可分为以下6类. Roscoe等[22]针对土体提出了剑桥模型，从此学者们开始关注土的本构模型； Lade等[23]通过大量的真三轴试验建立了能反映砂土剪胀特性的Lade-Duncan模型；Desai等[24]提出了封闭型的单一屈服面模型，随后又将其改进为考虑非等向硬化规律、非关联流动法则、损伤软化特性的Desai系列弹塑性模型；黄文熙[25]提出的清华模型是在众多弹塑性模型中假设中最少的一个；殷宗泽等[26]基于土体的变形特性提出了椭圆-抛物线模型. 在实际工程中土的应力-变形表现为复杂的非线性，双曲线模型应用广泛. 现有研究对邓肯模型参数进行敏感性分析后发现，参数的取值对不同高度堆石坝的应力和位移影响显著[27].

以上研究表明，学者们通过室内试验和数值模拟2种方式对筑坝料的缩尺效应进行了一定的研究，但由于研究对象、方法、思路等存在差异，得到的结论不同，甚至相反，缺乏完整体系. 因此，有必要对筑坝料缩尺进一步深入研究. 本研究以阿尔塔什水利工程为背景，从宏细观角度开展缩尺效应对砂砾石料力学特性及本构模型的影响的研究，同时对现场超大尺寸的筑坝料进行邓肯模型参数的推演，进一步揭示其缩尺效应产生的变形破坏机理.

1. 细观参数确定及模型构建

1.1. 模型构建依据

在模型构建时，以新疆阿尔塔什水利工程混凝土面板堆石坝的主要筑坝料为研究对象. 标定的物理试验数据由大连理工大学主持研制的高精度大型液压伺服三轴仪所采集；物理试验的试样制备采用20 cm/次或10 cm/次的分层捣鼓法，使用控制密度法成型，试样饱和采用水头饱和法[28].

1.2. 本构模型及参数标定

本构模型采用平行黏结模型PBM，其黏结破坏会使刚度迅速减小，这更符合砂砾石料脆性破坏特征，采用PBM来模拟试样破坏过程中的力学行为较合理.

参数标定主要由宏观指标选取、本构模型确定、细观参数选取以及参数反演等工作完成. 宏观指标根据三轴试验的典型关系曲线选取割线模量、峰值强度2个应力-应变指标和泊松比、剪胀角2个应变-体变指标[29]. 直接取用笔者已发表研究结果[29]：平行黏结模量$ {{\overline E_{\text{c}}}} $=24 GPa、刚度比k=2、平行黏结抗拉强度比$ {\overline \sigma _{\mathrm{b}}} $=10 MPa、平行黏结强度$ \bar c $=52 MPa、颗粒间摩擦系数μ=0.4、平行黏结半径乘子为1.

采用上述值分别对阿尔塔什工程报告中大型三轴试验和超大型三轴试验进行参数标定[29]，结果如图1所示. 图中，σ3为围压，σ1−σ3为轴向偏应力，εa为应变. 在统计学上，一般使用模型的决定系数R2来衡量模型的预测能力，R2的取值范围为0~1.0，R2越大，表示预测效果越好. 各组曲线的拟合程度如表1所示，R2范围为0.976~0.998，说明其拟合效果较好. 以上结果证明所用参数和本构模型对大型三轴数值模拟试验（试样直径D=300 mm）和超大型三轴数值模拟试验（D=800 mm）具有可行性.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

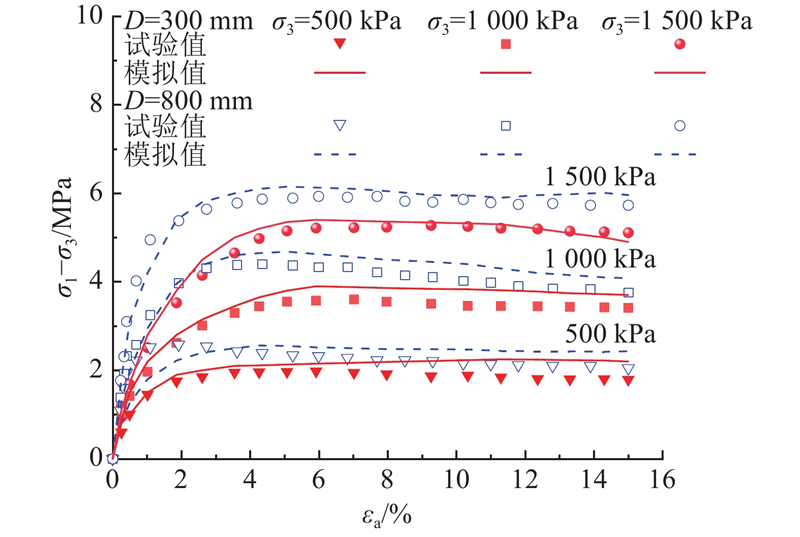
图 1   室内试验与数值模拟试验偏应力-应变曲线

Fig.1   Stress-strain curves of laboratory test and numerical model test


表 1   决定系数统计

Tab.1  Decision coefficient statistics

σ3/kPaR2
D=300 mmD=800 mm
5000.9760.988
1 0000.9930.981
1 5000.9980.987

新窗口打开| 下载CSV


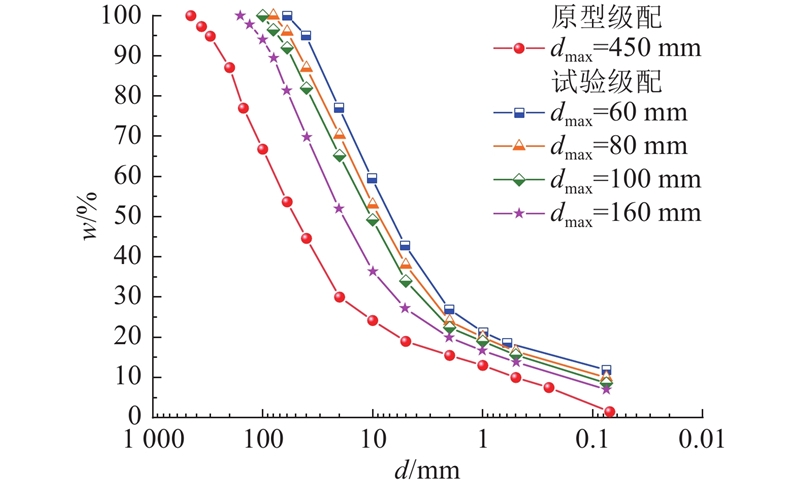
1.3. 缩尺方法的选取

参考规范[30]，常用的缩尺方法主要有以下4种：超粒径剔除法、等量替代法、相似级配法和混合法. 为了开展缩尺效应对砂砾石料的力学特性的研究，以新疆阿尔塔什筑坝料的级配为原型级配，砂砾石料的最大粒径为450 mm. 当粒径小于5 mm颗粒的质量分数为15%~30%时，采用相似级配法对筑坝料力学性质的影响较小[30]，其既能保持不均匀系数Cu和曲率系数Cc不变又不影响材料的力学性能. 原型级配与缩尺后级配曲线如图2所示. 图中，w表示小于某粒径的试样质量占试样总质量的百分比，d表示颗粒粒径.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   原型级配与设计级配曲线（相似级配法）

Fig.2   Prototype gradation and design gradation curves (similar gradation method)


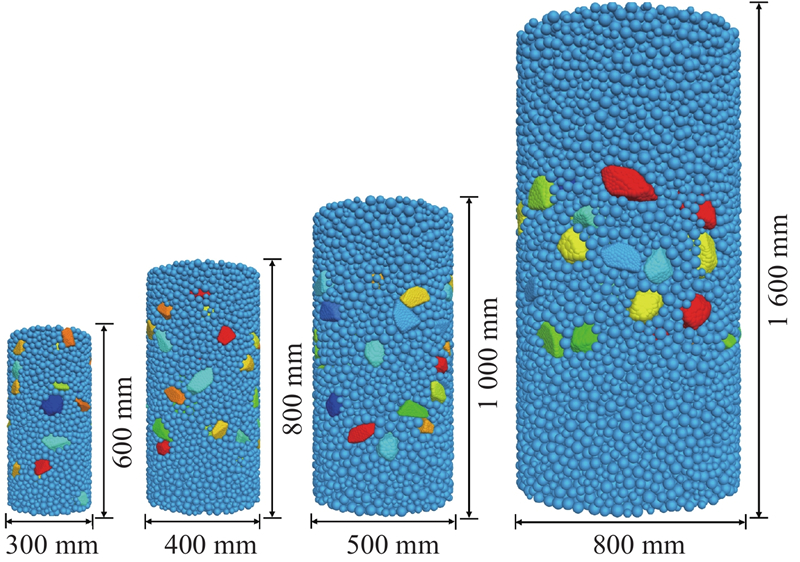
1.4. 试样制备及加载

为了使进行三轴试验时的数值试样能更真实准确地反映原砂砾石的剪切力学特性[31]，通过AutoCAD进行轮廓绘制后，把stl文件导入PFC中，利用Clump template bubblepack算法构建块石颗粒簇，如图3所示. 根据砂砾石的特性对Clump进行相应的参数设定后与土颗粒进行模型重构，得到如图4所示的不同尺寸的数值模型，分别设定模拟试样的尺寸D×H（直径×高度）取300×600、400×800、500×1000、800×1600 mm.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   块石颗粒簇

Fig.3   Clusters of stone particles


图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   不同尺寸的三轴数值模型

Fig.4   Triaxial numerical samples of different sizes


当所研究的试样尺寸不同时，相同直径的块石对试样起到不同的作用. 以块石颗粒d=60 mm为例，当试样尺寸为300×600 mm时，直径为60 mm的块石构成石骨架，起到主要作用；当试样尺寸为800×1600 mm时，直径为60 mm的块石填充在粒径更大的颗粒之间，起到辅助作用. 为了消除上述影响，获得具有代表性的结果，规定试样的直径径比一致，即D/dmax=5，因此各试样所允许的最大粒径dmax分别为60、80、100、160 mm.

不同级配砂砾石料的最大、最小干密度不同，若具有相同孔隙率或干密度的砂砾石料级配不同，其密实程度具有显著差异，采用相对密度Dr=0.9控制不同级配料的密实度更加合理[9]. 高围压下易产生颗粒破碎的影响，对此暂不考虑，故本试验设定的加载围压为100、300、500 kPa. 破坏标准采用剪应力的最大值或轴向应变达15%对应的剪应力.

2. 宏观试验结果与分析

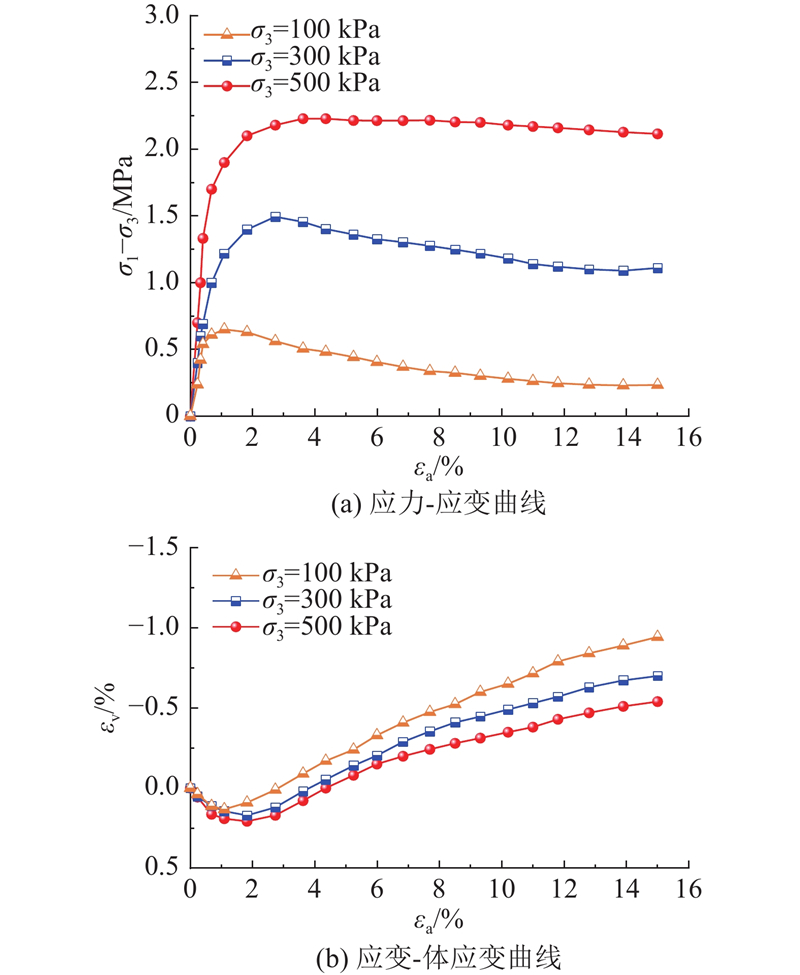
2.1. 轴向偏应力-应变-体应变关系

如图5所示为D=500 mm时不同围压下试样的轴向偏应力（σ1−σ3）-应变（ɛa）-体应变（ɛv）关系曲线. 可以看出，随着围压的增加，试样偏应力极值增大，但初始模量变化相对较稳定；在峰值后，试样在低围压下出现明显的应变软化现象. 低围压下试样以剪胀为主，随着围压的增加，曲线的初始斜率增大，剪缩显著，剪胀特性被抑制，表现出显著的“低压剪胀，高压剪缩”规律.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   不同围压下试样的偏应力-轴向应变-体应变关系曲线

Fig.5   Deviatoric stress-axial strain-volumetric strain relationship curves of specimens under different confining pressures


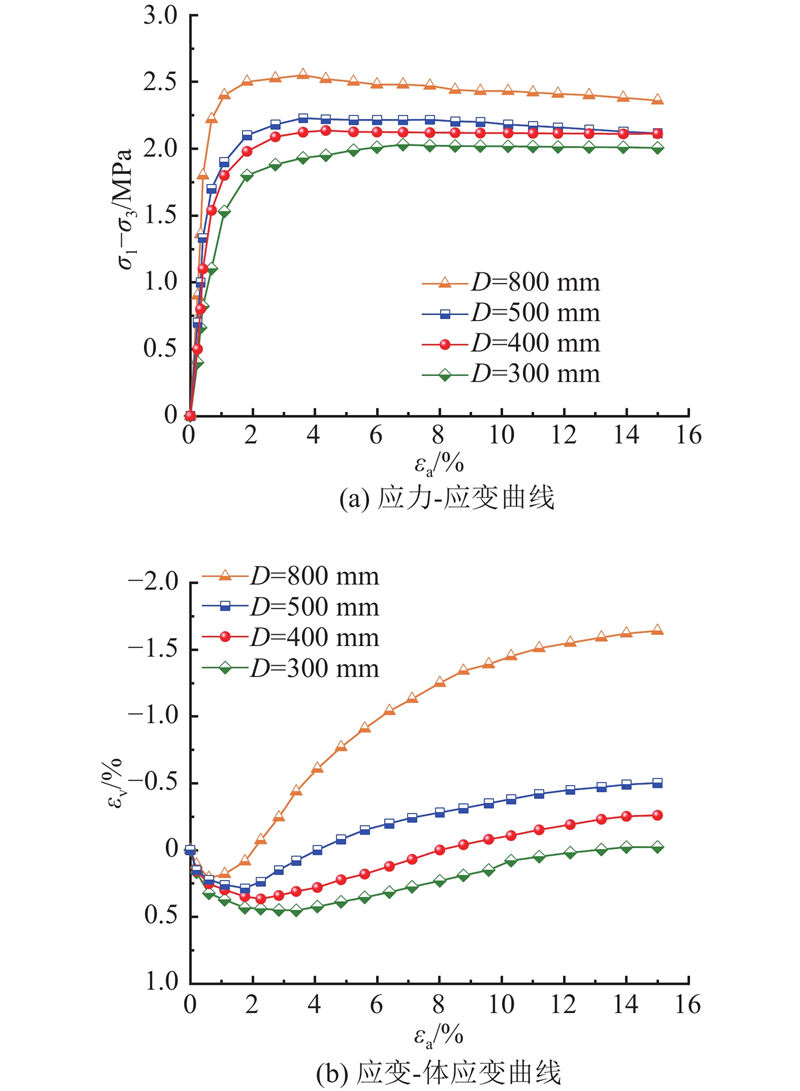
如图6所示为围压为500 kPa时不同尺寸试样的轴向偏应力-应变-体应变关系曲线. 可以看出，试样的偏应力与应变关系曲线的规律相似. 当围压相同时，不同尺寸试样的偏应力-应变-体变曲线并不重合，此现象证明采用相对密度法控制试样时，缩尺效应是客观存在的；随着试样尺寸增大，轴向偏应力-应变曲线的初始模量增加，其峰值强度增大；应变软化现象在超大尺寸（D=800 mm）下更为显著，而残余强度之间的差别相对较小. 随着试样尺寸增大，其变形模量及体积模量均增加，剪缩程度降低，剪胀现象凸显（D=800 mm）. 产生上述现象的主要原因如下：在D=300 mm试样中dmax=60 mm，土石颗粒间的差距较小，细粒能较好地填充在石缝之间，体积变化也较D=800 mm试样更加困难，相应的剪胀现象也因此削弱.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   不同尺寸试样的偏应力-轴向应变-体应变关系曲线

Fig.6   Relationship curves of deviatoric stress-axial strain-volumetric strain for specimens of different sizes


2.2. 邓肯模型参数

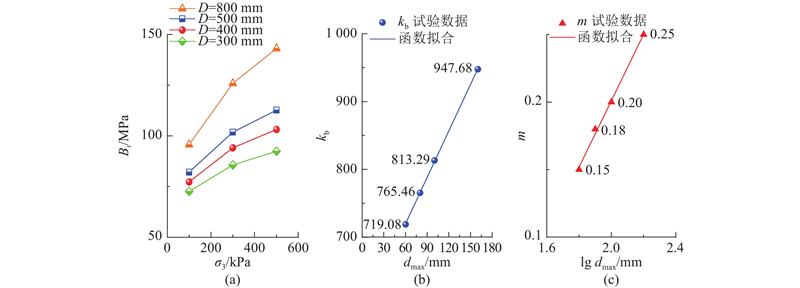
为了更好开展缩尺效应对砂砾石料强度及变形的研究，根据阿尔塔什面板坝筑坝材料的三轴数值模拟试验确定了各尺寸试样的邓肯模型（包括E-B和E-v）参数值，如表2所示. 表中，k为弹性模量参数，n为弹性模量指数，Rf为破坏比，φ0、Δφ为强度指标，kb为体积模量参数，m为体积模量指数，G、F为初始切线泊松比v1的常量参数. 可以看出，邓肯模型参数的缩尺效应主要体现在φ0、k和kb上.

表 2   不同尺寸砂砾石料的邓肯模型参数

Tab.2  Duncan model parameters of gravels with different sizes

D/mmφ0/(°)Δφ/(°)knkbmRfGF
30047.728.181 318.060.45719.080.150.820.52−0.04
40048.858.411 400.620.47765.460.180.830.48−0.11
50049.898.631 489.410.49813.290.200.830.44−0.12
80052.309.091 732.970.52947.680.250.850.41−0.12

新窗口打开| 下载CSV


2.3. 特征指标分析

基于三轴试验，主要以峰值内摩擦角、初始模量、切线体积模量等描述缩尺效应对不同尺寸试样的影响规律.

2.3.1. 峰值内摩擦角

砂砾石料为无黏性材料，其峰值内摩擦角$ \varphi_{\mathrm{p}}$与围压σ3的非线性关系表达式[30]如下：

$ \varphi_{\mathrm{p}}=\varphi_0-\Delta \varphi \lg \;\left(\sigma_3 / P_{\mathrm{a}}\right) . $

式中：Δφ和φ0均为试验常数，其中Δφ能反映非线性程度；Pa为标准大气压，取101 kPa.

如图7所示为非线性强度指标与σ3、dmax的关系曲线，其中，图7(a)为σ3-φp关系图，图7(b)为lg dmax-φ0、lg dmax-Δφ关系图. 由图7(a)可知，随围压的增大峰值内摩擦角减小；在相同围压下，随试样尺寸的增大，峰值内摩擦角增加；最大尺寸试样（D=800 mm）的峰值内摩擦角比最小尺寸试样（D=300 mm）平均高4.58°，约高出9.6%. 这表明砂砾石料峰值强度的缩尺效应较显著.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

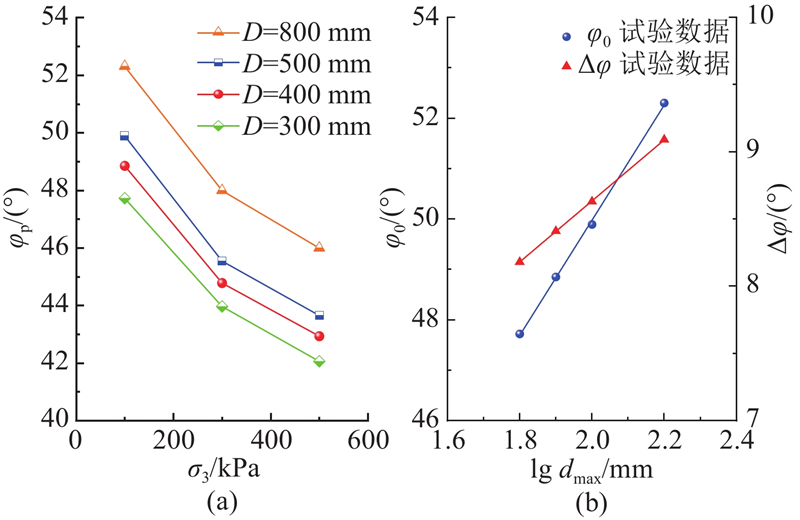
图 7   非线性强度指标与σ3、lg dmax关系曲线

Fig.7   Relationship curves between nonlinear strength indexes and σ3, lg dmax


为了进一步探究峰值内摩擦角的哪个分量对其影响显著，整理试验数据，得到不同尺寸砂砾石料的非线性强度指标随dmax变化曲线，如图7(b)所示. 可以看出，D=300、400、500、800 mm对应的φ0分别为47.72°、48.85°、49.89°、52.30°，Δφ分别为8.18°、8.41°、8.63°、9.09°；φ0、Δφ均随dmax增大而增大，dmax每增大20 mm，Δφ平均增加0.18°，φ0平均增大0.93°，φ0增幅约为Δφ的5倍，dmax变化对φ0影响更显著. 综上，φ0缩尺效应显著，Δφ缩尺效应可忽略不计.

φ0和Δφ与dmax之间的关系均可用对数形式表示：

$ \varphi_0=11.43 \lg\; d_{\max }+27.19, $

$ \Delta \varphi=2.27 \lg\; d_{\max }+4.09 . $

2.3.2. 初始模量

为了定量开展缩尺效应对砂砾石料特性的研究，根据数值试样的常规三轴试验结果，整理出初始模量Ei，其表达式 [30] 如下：

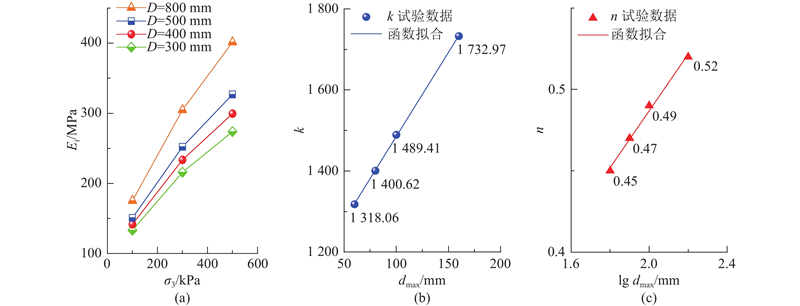
$ E_{\mathrm{i}}=k P_{\mathrm{a}}\left(\sigma_3 / P_{\mathrm{a}}\right)^{{n}}. $

如图8所示为E-B模型中刚度相关指标与σ3、dmax关系曲线，其中，图8(a)为σ3-Ei关系图，图8(b)为dmax-k关系图，图8(c)为lg dmax-n关系图. 由图8(a)可知，初始模量Ei随围压σ3的增加而增大，证明围压的约束作用对颗粒材料刚度存在影响；在相同围压下，随着试样尺寸增大，试样的dmax越大，级配的不均匀系数Cu越大，颗粒间的咬合作用增强，初始模量Ei越大. 综上，砂砾石料变形特性的缩尺效应显著. 现探究Ei式中弹性模量k、变形模量n随试样尺寸的变化规律. 在对数坐标上绘制lg （σ3/Pa）-lg （Ei/Pa）线（x-y），当x=1时可求得k，n为该线的斜率，具体各参数见表3所示. 由表3得到图8(b)、(c)，对图上数据点进行拟合，得到如下公式：

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   刚度相关指标与σ3、lg dmax关系曲线

Fig.8   Relationship curves between stiffness indexes and σ3, lg dmax


$ k=4.15 d_{\max }+1\;070.20, $

$ n=0.17 \lg\; d_{\max }+0.14. $

由图8(b)、(c)可得，k、n均随试样尺寸的增大而增大；砂砾石料弹性模量参数k缩尺效应显著，反映材料的可压缩性，与dmax呈线性函数关系，决定系数R2=0.9998；dmax每增大20 mm，k平均增加82.98；变形模量n与dmax呈对数函数型关系，决定系数R2=0.9968；dmax每增大20 mm，n平均增大0.014，n约为k的1/5927，其缩尺效应可忽略不计. 参数n反映的是Ei受围压影响的大小，主要与砂砾石料本身的密实程度有关，故对试样尺寸的变化影响不大.

表 3   不同尺寸砂砾石料的k、n

Tab.3  k and n values of gravels with different sizes

dmax/mmkn
601 318.060.45
801 400.620.47
1001 489.410.49
1601 732.970.52

新窗口打开| 下载CSV


2.3.3. 泊松比与体积模量

Kulhawy假设轴向应变ɛ1与侧向应变ɛ3之间为双曲线关系，不同σ3作用下的初始切线泊松比计算式如下：

$ \varepsilon_1=\varepsilon_3 /\left(f+D_1 \varepsilon_3\right), $

$ v_{\mathrm{i}}=G-F \lg \;\left(\sigma_3 / P_{\mathrm{a}}\right) . $

式中：f为初始切线泊松比vi，D1为假设的应变ɛ1渐进值的倒数，G、F为vi的2个参数.

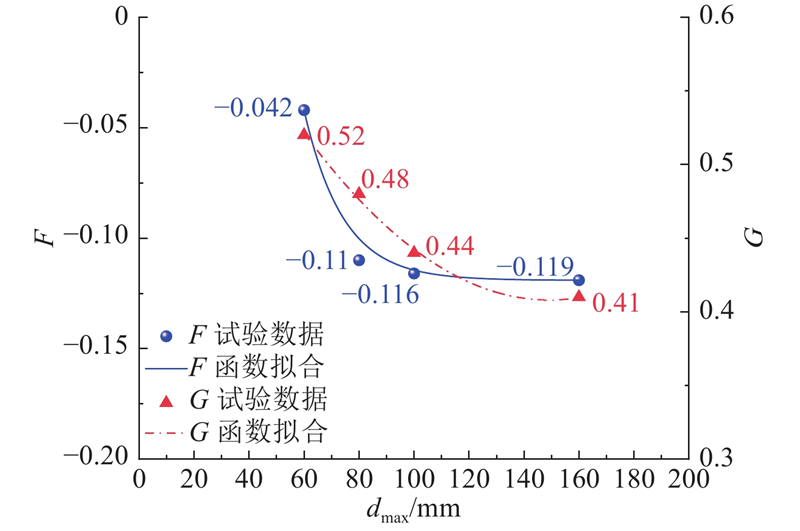
如图9所示为E-v模型中体积变形相关指标G、F与dmax的关系曲线. 可以看出，G、F均随试样尺寸的增大而减小；参数F与dmax呈指数函数型关系，决定系数R2=0.9995；dmax每增大20 mm，F平均减小0.015. 参数G与dmax呈二次函数型关系，决定系数R2=0.9968；dmax每增大20 mm，G平均减小0.022，故在vi中参数F、G的缩尺效应可以忽略. 参数F、G的表达式分别如下：

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   E-v模型中体积变形相关指标G、F与dmax的关系曲线

Fig.9   Relationship curves of deformation indexes G, F and dmax in E-v model


$ F=0.08 \exp\; \left(60-d_{\max }\right) / 14.22-0.12 , $

$ G=1.43 \times 10-5\left(d_{\max }\right)^2-0.004 d_{\max }+0.73 . $

用上述方法确定的切线泊松比与试验实测值存在较大误差，且应力水平越大误差越大. 邓肯发现体积模量与固结围压呈指数型函数关系，为了更好地开展变形对缩尺效应的研究，现对初始体积模量按如下公式进行分析[30]：

$ B_{\mathrm{i}}=k_{\mathrm{b}} P_{\mathrm{a}}\left(\sigma_3 / P_{\mathrm{a}}\right)^{m} . $

如图10所示为E-B模型中体积变形相关指标与σ3、dmax关系曲线，由图10(a)可知，体积模量Bi随围压σ3的增加而增大；因本研究模拟时未考虑颗粒破碎，较低围压下的砂砾石料在剪切时颗粒间易发生翻越和滚动现象，宏观上表现为先剪缩后剪胀；在相同围压下，随试样尺寸增加，体积模量增大，D=800 mm（dmax=160 mm）时体积变形最显著.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   E-B模型中体积变形相关指标与σ3、dmax、lg dmax关系曲线

Fig.10   Relationship curves of deformation indexes and σ3, dmax, lg dmax in E-B model


砂砾石料体积变形的缩尺效应显著，探究Bi表达式中体积模量参数kb、体积模量指数m随试样尺寸的变化规律. 在对数坐标上绘制lg （σ3/Pa）-lg （Bi/Pa）曲线（x-y），当x=1时可求得kb，m为该线的斜率. 具体各参数如表4所示. 由表4可以得到图10(b)、(c)，对图上数据点进行拟合，得到如下公式：

表 4   不同尺寸砂砾石料的kb、m

Tab.4  kb and m values of gravels with different sizes

dmax/mmkbm
60719.080.15
80765.460.18
100813.290.20
160947.680.25

新窗口打开| 下载CSV


$ k_{\mathrm{b}} =2.28 d_{\max }+583.01, $

$ m =0.25 \lg d_{\max }-0.29 . $

由图10(b)、(c)可得，kb、m均随试样尺寸的增大而增大；砂砾石料体积模量参数kb缩尺效应显著，与dmax呈线性关系，决定系数R2=0.9999；dmax每增大20 mm，kb平均增加45.72；体积模量指数m与dmax呈对数函数型关系，决定系数R2=0.9984；dmax每增大20 mm，m平均增大0.02，m增幅约为kb的1/2286，其缩尺效应可忽略不计. m代表体积模量随围压变化的显著程度，故对不同尺寸试样的影响不大.

2.4. 原始级配参数推演

综上分析，砂砾石料的φ0、k和kb均随着试样尺寸的增大而增加，φ0与dmax呈对数型函数关系，k、kb与dmax均呈线性函数关系. D=800 mm的砂砾石料的φ0、k以及kb约为D=300 mm的1.10、1.31、1.32倍. 故缩尺效应的显著程度如下：kb＞k＞φ0. 利用本研究建立的φ0-dmax、k-dmax、kb-dmax函数关系可初步预测缩尺效应对砂砾石料原型级配参数的影响.

新疆阿尔塔什筑坝砂砾料的原始级配如表5所示. 可以看出，在实际工程中，现场筑坝料的尺寸直径最大可达450 mm，即三轴试验试样的直径可达D=2 250 mm，而目前的大型三轴仪器难以实现对其强度及变形的测定. 利用本研究建立的关系可对原型级配中砂砾石料的邓肯模型参数进行预测，预测结果如表6所示. 其可为类似工程施工提供一定的参考.

表 5   砂砾石料的原型级配

Tab.5  Prototype gradation of gravel material

dmax/mmw/%dmax/mmw/%
6053.730094.9
10066.8450100.0
20087.1——

新窗口打开| 下载CSV


表 6   现场筑坝砂砾料的邓肯模型参数推演

Tab.6  Parameter deduction of Duncan model for on-site damming gravels

dmax/mmφ0/(°)Δφ/(°)knkbmRfGF
1）注：表中为建议取值，括号内为计算值.
20053.499.091 900.00
（1 900.20）1）		0.521 040.00
（1 039.01）		0.250.850.41−0.12
30055.509.092 315.00
（2 315.20）		0.521 270.00
（1 267.01）		0.250.850.41−0.12
40056.939.092 730.00
（2 730.20）		0.521 500.00
（1 495.01）		0.250.850.41−0.12

新窗口打开| 下载CSV


3. 细观试验结果与分析

3.1. 欧拉角

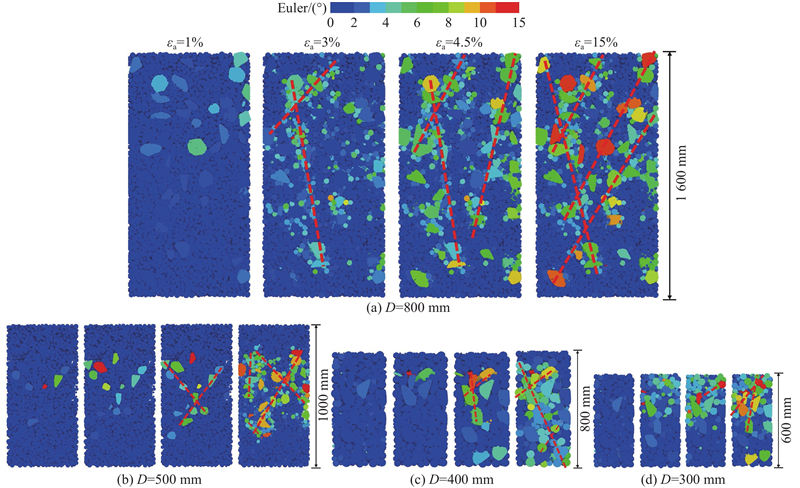
在PFC中常用欧拉角（Euler）来描述颗粒在空间中的旋转行为，颗粒的活跃程度可由欧拉角的大小来体现，以此来反映试样变形集中区的演变形式. 如图11所示为不同尺寸试样在围压为500 kPa时欧拉角的渐进演化过程. 图中，颗粒颜色由蓝至红表示颗粒活跃度增加，旋转欧拉角增大；虚线表示变形集中区. 可以看出，变形集中区的形成可分为2个阶段：应力传导阶段（峰值前）和应力集中阶段（峰值后）. 在应力传导阶段，随着轴向应变的增加，试样的变形集中区从两端向中间传导，在应力传导到达一定程度后，峰值处能形成初步的变形集中区；在应力集中阶段，随着应力间的传递，试样主要经历弹性压缩，应力开始集中在较弱颗粒的表面，但试样整体变形不明显；当进入应力集中阶段后，应力集中区逐渐明显，直至形成变形集中区后试样开始发生破坏，颗粒之间出现翻越、滑移、黏结键断裂等现象.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   不同尺寸试样欧拉角的位置转动云图

Fig.11   Rotation nephograms of specimens with different sizes


当D=300 mm时，dmax仅为60 mm，块石能较好地与土颗粒“镶嵌”，颗粒间相互抱紧贴合，初始结构均匀，内部结构较稳定；在内部应力集中作用的影响下，试样的变形集中区的形式为“X”型. 随着三轴试样尺寸的增大（D=400、500 mm），dmax不断增加，试样内部的土石颗粒间差异化加剧，应力集中现象逐渐凸显，当应力由端部向中间传导时，试样的两端可能会加剧颗粒的转动，而后继续发展成小型应力集中区域，形式为“X”或多“X”型并伴随两端小型变形集中区，呈现“X+x”或“X+x+x”型. 上述现象在D=500 mm下更显著. 随着试样尺寸的进一步增大（D=800 mm），砂砾石颗粒内部微缺陷（微裂缝、孔隙）及应力集中现象加剧，同时土石颗粒尺寸差异性进一步增大[16]；试样变形集中区发展不稳定，颗粒间过早地发生翻越、滑移，表现出显著的缩尺效应，变形集中区域更加广泛.

3.2. 颗粒配位数

配位数，又称平均接触数目，在数值上等于模型中所有的接触之和除以颗粒总数，即

$ Z={2 N_{\mathrm{c}}}/{N_{\mathrm{p}}}. $

式中：Nc为试样中实际接触的量，Np为试样中总颗粒数.

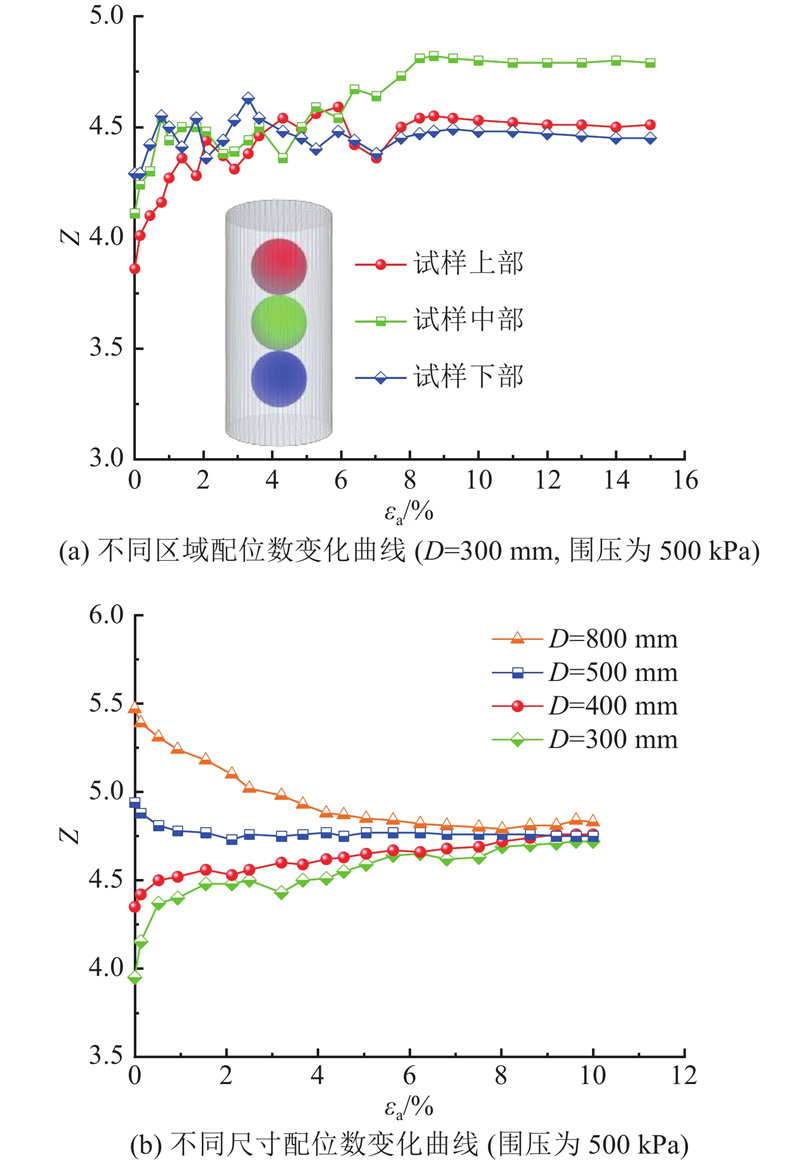
以试样形心为球心，对D=300、400、500、800 mm试样分别设置3个半径为80、100、130、200 mm的测量球，监测试样加载过程中颗粒配位数的变化情况.如图12所示为不同试样在围压为500 kPa时颗粒配位数Z演化过程曲线. 其中因数据较多且规律相似，在不影响机理研究的前提下，图12(a)中选用D=300 mm的试样对不同区域的配位数变化进行分析. 由图12(a)可知，在外荷载的作用下，各测量处的配位数随着轴向应变增加而逐渐增大，但增幅不同，最终趋于稳定，此时可认为达到配位数阈值，即临界配位数. 结合3.1节的结果进行分析，在D=300 mm的试样中，变形集中区位于中上部，颗粒旋转幅度较大，其转动、错动、翻滚、滑移及重组现象显著，因此在试样变形集中区处（中上部）配位数变化幅度较下部大. 由图12(b)可知，在初始阶段，试样尺寸越大其配位数越大，其颗粒间的平均接触越多，这也从细观角度解释了图6(a)中D=800 mm试样具有更高抗剪强度的原因. 随着轴向应变继续增加，试样配位数开始增加或减小，最终趋于阈值. 结合图6(b)中不同尺寸试样的轴向应变-体变曲线可知，当D=300 mm时，试样以剪缩为主，配位数表现为上升趋势；随着尺寸的增大，试样的变形逐渐以剪胀为主，配位数表现为下降的趋势；当配位数达到阈值后，体变也在此时趋于稳定状态.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   颗粒配位数演化过程曲线

Fig.12   Evolution curves of particle coordination number


综上，配位数增加，试样以剪缩为主，配位数减小，试样以剪胀为主；在宏观表现上，试样不会持续处于剪缩或剪胀状态，必定会有一个配位数阈值与稳态相对应；不同尺寸试样间有效配位数分布演化的差异是试样剪胀特性缩尺规律产生的细观机理之一[10]. 这反映了配位数对临界状态下的土力学研究具有重要意义.

4. 结　论

（1）随着围压的增加，试样偏应力极值增大，剪缩程度显著，剪胀特性被抑制；随着试样尺寸的增大，其峰值强度增大，峰后应变软化现象越来越显著，但残余强度间差别较小；在变形方面最大体变均减小，同时剪缩性被抑制、剪胀现象逐渐凸显.

（2）内摩擦角分量φ0、弹性模量参数k、体积模量参数kb均随试样尺寸的增大而增大，其中D=800 mm试样的φ0、kb、k比D=300 mm的约增加10%、32%、31%. 故缩尺效应的显著程度如下：kb＞k＞φ0. φ0与dmax呈对数型函数关系，k、kb与dmax均呈线性函数关系. 用上述函数关系对存在缩尺效应的超大砂砾石邓肯模型主要参数进行预测，建议值如下. dmax=200 mm：kb=1 040、k=1 900、φ0=53.49°；dmax=300 mm：kb=1 270、k=2 315、φ0=55.50°；dmax=400 mm：kb=1 500、k=2 730、φ0=56.93°.

（3）随着试样尺寸的增大，其变形集中区的形式由“X”型变为“X+x”或“X+x+x”型，变形集中区随试样尺寸的增大而更广泛. 初始配位数可解释试样宏观抗剪强度高的原因，其随试样尺寸的增大而增加；配位数变化能反映宏观的体变现象，配位数增加试样以剪缩为主，配位数减小试样以剪胀为主，当配位数达阈值时试样处于稳态.

（4）本研究主要以细观为主，开展了大型、超大型三轴数值模拟试验. 下一步计划开展相关的室内三轴试验，宏细观相结合，在有限的条件中验证邓肯模型参数的准确性.

参考文献

HALL

E B, GORDON B B. Triaxial testing with large-scale high pressure equipment

[J]. Laboratory Shear Testing of Soils, 1963, 361: 315- 328

DOI:10.1061/JSFEAQ.0001433      [本文引用: 1]

VARADARAIAN A, SHARMA K G, VENKATACH -ALAM K, et al

Testing and modeling two rockfill materials

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129 (3): 206- 218

DOI:10.1061/(ASCE)1090-0241(2003)129:3(206)      [本文引用: 1]

凌华, 殷宗泽, 朱俊高, 等

堆石料强度的缩尺效应试验研究

[J]. 河海大学学报: 自然科学版, 2011, 39 (5): 540- 544

[本文引用: 1]

LING Hua, YIN Zongze, ZHU Jungao, et al

Experimental study of scale effect on strength of rockfill materials

[J]. Journal of Hohai University: Natural Sciences, 2011, 39 (5): 540- 544

[本文引用: 1]

郦能惠, 朱铁, 米占宽

小浪底坝过渡料的强度与变形特性及缩尺效应

[J]. 水电能源科学, 2001, 19 (2): 39- 42

[本文引用: 1]

LI Nenghui, ZHU Tie, MI Zhankuan

Strength and deformation properties of transition zone material of Xiaolangdi dam and scale effect

[J]. International Journal Hydroelectric Energy, 2001, 19 (2): 39- 42

[本文引用: 1]

武利强, 朱晟, 章晓桦, 等

粗粒料试验缩尺效应的分析研究

[J]. 岩土力学, 2016, 37 (8): 2187- 2197

[本文引用: 2]

WU Liqiang, ZHU Sheng, ZHANG Xiaohua, et al

Analysis of scale effect of coarse-grained materials

[J]. Rock and Soil Mechanics, 2016, 37 (8): 2187- 2197

[本文引用: 2]

孔宪京, 宁凡伟, 刘京茂, 等

基于超大型三轴仪的堆石料缩尺效应研究

[J]. 岩土工程学报, 2019, 41 (2): 255- 261

[本文引用: 1]

KONG Xianjing, NING Fanwei, LIU Jingmao, et al

Scale effect of rockfill materials using super-large triaxial tests

[J]. Chinese Journal of Geotechnical Engineering, 2019, 41 (2): 255- 261

[本文引用: 1]

NAKATA Y, KATO Y, HYODO M, et al

One dimensional compression behaviour of uniformly graded sand related to single particle crushing strength

[J]. Soils and Foundations, 2001, 41 (2): 39- 51

DOI:10.3208/sandf.41.2_39      [本文引用: 1]

马刚.

周伟, 常晓林, 等. 堆石料缩尺效应的细观机制研究

[J]. 岩石力学与工程学报, 2012, 31 (12): 2473- 2482

[本文引用: 1]

MA Gang, ZHOU Wei, CHANG Xiaolin, et al

Mesoscopic mechanism study of scale effects of rockfill

[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31 (12): 2473- 2482

[本文引用: 1]

周伟, 常晓林, 马刚, 等

堆石体缩尺效应研究进展分析

[J]. 水电与抽水蓄能, 2017, 1: 17- 23

[本文引用: 2]

ZHOU Wei, CHANG Xialin, MA Gang, et al

Analysis on the research development of rockfill scale effect

[J]. Hydropower and Pumped Storage, 2017, 1: 17- 23

[本文引用: 2]

徐琨, 杨启贵, 周伟, 等

基于可破碎离散元法的堆石料应力变形及剪胀特性缩尺效应研究

[J]. 中国农村水利水电, 2022, (3): 200- 206

[本文引用: 2]

XU Kun, YANG Qigui, ZHOU Wei, et al

Research on the scaling effect of the stress deformation feature and the dilatancy characteristics of rockfill material based on the crushable DEM

[J]. China Rural Water and Hydropower, 2022, (3): 200- 206

[本文引用: 2]

李响, 马刚, 周伟, 等

考虑颗粒强度尺寸效应的堆石体缩尺效应研究

[J]. 水力发电学报, 2016, 35: 12- 22

[本文引用: 1]

LI Xiang, MA Gang, ZHOU Wei

et al. Scale effects of rockfill materials considering size effect of particle strength

[J]. Journal of Hydroelectric Engineering, 2016, 35: 12- 22

[本文引用: 1]

常晓林, 马刚, 周伟, 等

颗粒形状及粒间摩擦角对堆石体宏观力学行为的影响

[J]. 岩土工程学报, 2012, 34: 646- 653

[本文引用: 1]

CHANG Xiaolin, MA Gang, ZHOU Wei, et al

Influences of particle shape and inter-particle friction angle on macroscopic response of rockfill

[J]. Chinese Journal of Geotechnical Engineering, 2012, 34: 646- 653

[本文引用: 1]

花俊杰, 周伟, 常晓林, 等

堆石体应力变形的尺寸效应研究

[J]. 岩石力学与工程学报, 2010, 29: 328- 335

[本文引用: 1]

HUA Junjie, ZHOU Wei, CHANG Xiaolin, et al

Study of scale effect on stress and deformation of rockfill

[J]. Journal of Rock Mechanics and Engineering, 2010, 29: 328- 335

[本文引用: 1]

易颖, 周伟, 马刚, 等

基于精确缩尺的颗粒材料流变研究

[J]. 岩土力学, 2016, 37: 1799- 1808

[本文引用: 1]

YI Ying, ZHOU Wei, MA Gang, et al

Study of rheological behaviors of granular materials based on exact scaling laws

[J]. Rock and Soil Mechanics, 2016, 37: 1799- 1808

[本文引用: 1]

ZHOU W, MA G, CHANG X, et al

Influence of particle shape on behavior of rockfill using a three-dimensional deformable DEM

[J]. Journal of Engineering Mechanics, 2013, 139 (12): 1868- 1873

DOI:10.1061/(ASCE)EM.1943-7889.0000604      [本文引用: 1]

宿辉, 杨家琦, 胡宝文, 等

颗粒离散元岩石模型的颗粒尺寸效应研究

[J]. 岩土力学, 2018, 39 (12): 4642- 4650

[本文引用: 2]

SU Hui, YANG Jiaqi, HU Baowen, et al

Study of particle size effect of rock model based on particle discrete element method

[J]. Rock and Soil Mechanics, 2018, 39 (12): 4642- 4650

[本文引用: 2]

CHANG C Y, DUNCAN J M

Analysis of soil movement around a deep excavation

[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96 (5): 1655- 1681

DOI:10.1061/JSFEAQ.0001459      [本文引用: 1]

DUNCAN J M, BYRNE P, WONG K. Strength, stress-strain and bulk modulus parameters for finite element analyses of stresses and movements in soil masses: UCB/GT/80-01 [R]. Berkeley: University of California, 1980.

[本文引用: 1]

NAYLOR D J, KNIGHT D J, DING D

Coupled consolidation analysis of the construction and subsequent performance of Monasavu Dam

[J]. Computers and Geotechnics, 1988, 6 (2): 95- 129

DOI:10.1016/0266-352X(88)90076-6      [本文引用: 1]

高莲士, 汪召华, 宋文晶

非线性解耦K-G模型在高面板堆石坝应力变形分析中的应用

[J]. 水利学报, 2001, (10): 1- 7

[本文引用: 1]

GAO Lianshi, WANG Zhaohua, SONG Wenjing

The application of nonlinear uncoupled K-G model to deformation analysis of high concrete face rockfill dam

[J]. Journal of Hydraulic Engineering, 2001, (10): 1- 7

[本文引用: 1]

高莲士, 蔡昌光, 朱家启

堆石料现场侧限压缩试验解耦K-G模型参数分析方法及在面板坝中的应用

[J]. 水力发电学报, 2006, (6): 26- 33

[本文引用: 1]

GAO Lianshi, CAI Changguang, ZHU Jiaqi

An analysis method for uncoupled K-G model parameters in site confined compression test of rock-fill materials and its application on CFRD

[J]. Journal of Hydroelectric Engineering, 2006, (6): 26- 33

[本文引用: 1]

ROSCOE K H, THURAIRAJAH A, SCHOFIELD A N

Yielding of clays in states wetter than critical

[J]. Géotechnique, 1963, 13 (3): 211- 240

[本文引用: 1]

LADE P V, DUNCAN J M

Elastoplastic stress strain theory for cohesionless soil

[J]. Journal of the Geotechnical Engineering Division, 1975, 101 (10): 1037- 1053

DOI:10.1061/AJGEB6.0000204      [本文引用: 1]

DESAI C S, GALLAGHER R H. Mechanics of engineering materials [M]. London: J Wiley and Sons, 1984.

[本文引用: 1]

黄文熙

土的弹塑性应力-应变模型理论

[J]. 清华大学学报: 自然科学版, 1979, (1): 1- 26

[本文引用: 1]

HUANG Wenxi

Theory of elastoplastic stress-strain models for soils

[J]. Journal of Tsinghua University: Science and Technology, 1979, (1): 1- 26

[本文引用: 1]

殷宗泽, 卢海华, 朱俊高

土体的椭圆-抛物双屈服面模型及其柔度矩阵

[J]. 水利学报, 1996, (12): 23- 28

[本文引用: 1]

YIN Zongze, LU Haihua, ZHU Jungao

The elliptic-parabolic yield surfaces model and its softness matrix

[J]. Journal of Hydraulic Engineering, 1996, (12): 23- 28

[本文引用: 1]

肖化文

邓肯-张E-B模型参数对高面板坝应力变形的影响

[J]. 长江科学院院报, 2004, 21 (6): 41- 44

[本文引用: 1]

XIAO Huawen

Effect of Duncan-Chang E-B model parameters on stress and deformation of high CFRD dam

[J]. Journal of Yangtze River Scientific Research Institute, 2004, 21 (6): 41- 44

[本文引用: 1]

邹德高, 陈楷, 余翔, 等. 筑坝材料特性尺寸效应三轴试验及大坝三维非线性静、动力精细化有限元分析 [R]. 大连: 工程抗震研究所, 2019.

[本文引用: 1]

崔熙灿, 张凌凯, 王建祥

高堆石坝砂砾石料的细观参数反演及三轴试验模拟

[J]. 农业工程学报, 2022, 38 (4): 113- 122

[本文引用: 3]

CUI Xican, ZHANG Lingkai, WANG Jianxiang

Inversion of meso parameters and triaxial test simulation of the gravel materials for high rockfill dam

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2022, 38 (4): 113- 122

[本文引用: 3]

中华人民共和国水利部. 土工试验方法标准:GBT 50123—2019 [S]. 北京: 中国计划出版社, 2019.

[本文引用: 5]

周辉, 程广坦, 朱勇, 等

基于三维扫描和三维雕刻技术的岩石结构面原状重构方法及其力学特性

[J]. 岩土力学, 2018, 39 (2): 417- 425

[本文引用: 1]

ZHOU Hui, CHENG Guangan, ZHU Yong, et al

A new method to originally reproduce rock structural plane by integrating 3D scanning and 3D carving techniques and mechanical characteristics of reproduced structural planes

[J]. Rock and Soil Mechanics, 2018, 39 (2): 417- 425

[本文引用: 1]

/

〈 〉