针对上述问题,本文提出考虑不同设备下能量收集(energy harvesting, EH)技术和用户间社会信任关系的D2D-MEC网络架构,此架构可以有效地降低系统的能量损耗,提高D2D链路的安全性. 设计基于李雅普诺夫的在线决策和资源分配(online decision matching and resource allocation, ODMRA)算法,最小化所有用户的长期平均服务成本,将原始随机优化问题转化为单时隙独立的确定性问题,然后分别求解. 仿真结果验证了ODMRA算法在系统服务成本和队列稳定性方面具有性能优势.
1. 系统模型
如图1所示为能量收集下的D2D辅助MEC网络系统,由物理域和社会域2个部分组成. 其中物理域由一个配备MEC服务器的基站(base station, BS)和多个移动设备组成. 移动设备分为远程发送设备(distant transmitters, DTs)和近端发送设备(nearby receivers, NRs)2种类型,其中DTs的集合为
图 1
图 1 能量收集下的D2D辅助MEC网络系统模型图
Fig.1 System model of D2D-assisted MEC network with energy harvesting
将时间离散为时隙的形式,用
假设DTi在每个时隙产生的计算任务量为
本节阐述了物理域中移动设备的基本关系. 物理域包含队列模型、传输模型、任务计算模型和EH模型,其中每个DT和NR对应社会域中的单个用户. 在社会域中,将用户之间的社会关系量化为社会信任矩阵后,作为D2D匹配过程中决策选择的重要依据. 下面详细介绍各个模型.
1.1. 任务队列模型
由于D2D的传输速率大于本地任务的生成速率,DT生成的任务在本地计算一部分后,剩余部分可以通过D2D快速上传到匹配的NR上.一个NR最多可以接收
式中:
1.2. 传输模型
为了避免不同卸载用户间的严重干扰,系统采用正交频分多址(OFDMA)技术. D2D传输过程中分为N 个相同大小的子信道,从NRj卸载到MEC的可用带宽被划分为K 个相同大小的子信道,N+K 个子信道的带宽均为W Hz. 从DTi到NRj的信道功率增益为
1.3. 任务计算模型
为了确保MEC的可持续使用,搭载MEC的基站通常由电网供电,所以忽略MEC计算过程的能量消耗. 令
D2D链路的传输能耗为
1.4. EH模型
每个移动设备都配备EH装置,可以捕获可再生能源供能. 在时隙开始的时刻,DTi的能量为
采用虚拟电池能量队列来量化DTi和NRj的电池能量水平,在每个时隙开始时,将DTi和NRj的虚拟电池队列记为
两者受到以下能量关系的约束:
DT和NR的虚拟电池能量队列动态模型为
1.5. 社会信任矩阵
在社会域中,社会关系为用户通过社交网络中的连接、交流和互动构建的关系网络,反映了用户间的信任度和亲密程度. 利用贝叶斯技术,将不同社交网络平台下收集到的历史记录进行整合,获得用户之间的社会关系,用社会信任矩阵表示一个时隙内DTi和NRj的社会关系强度. 社会关系的强度越大,移动设备之间越有可能建立D2D通信链接. 社会关系属性在D2D匹配决策中发挥了关键作用.
1.5.1. 社会信任矩阵的获取方案
1.5.2. 社会信任矩阵在本文的应用
在利用上述方案得到多个社交网络的数据整合模型后,社会信任矩阵
2. 问题公式化
2.1. 性能度量
式中:
2.2. 最小化系统服务成本
由于
式中:
不等式(19a)~(19d)表示每个设备的计算频率和发射功率不超过它们的最大值. 式(19e)表示社会信任值的约束. 不等式(19f)、(19g)表示DTs和NRs的电池输出量不超过它们的电池放电约束. 式(19h)保证了任务缓冲队列
2.3. 李雅普诺夫优化框架
为了解决随机优化问题
式中:
引入李雅普诺夫漂移函数:
通过将队列稳定性纳入执行成本性能中,定义李雅普诺夫漂移加惩罚函数来解决上述问题:
式中:V为目标函数对漂移惩罚的权值,可以作为调整系统成本和队列稳定性的控制参数[21].
在每个时隙中,通过最小化
在每个时隙中,对于任意队列积压
证明:将队列积压公式(4)的两边平方,得到
式中:
将式(25)的所有移动设备相加,得到以下不等式:
对2种设备的虚拟能量队列(15)、(16)开展与式(4)相同的操作,如下所示:
将式(26)~(28)相加,可得
将C和式(29)代入式(22),可得漂移加罚函数的上界(23).
根据漂移加罚函数的上界,设计基于李雅普诺夫的在线优化方法. 通过最小化式(23)的右侧,将长期优化问题转化为基于单个时隙的优化问题
3. ODMRA算法的设计
该部分的目标是将长期平均优化问题转化为如下4个单时隙优化问题:1)能量收集;2)计算资源分配;3)发射功率分配;4)D2D匹配决策. 结合凸分解和子模块优化理论,提出基于李雅普诺夫优化的D2D在线决策匹配和资源分配(ODMRA)算法,分别解决这些子问题.
3.1. 收获的最佳能量
通过如下问题求解DTs和NRs收获的能量.
3.2. 最优卸载决策和资源分配
将
3.2.1. 最优的CPU频率
假设发射功率和D2D匹配决策固定,最优的CPU周期频率调度问题为
将
将目标函数
分以下2种情况讨论
情况1:若
情况2:若
其中
将目标函数
式中:
证明:证明过程与
3.2.2. 功率分配问题
通过固定DTs和NRs的CPU循环频率和D2D连接决策,功率分配问题可以写成如下形式:
问题
接下来解决NR到MEC的传输功率问题:
将目标函数
式中:
3.2.3. D2D决策选择问题
给定最优的发射功率和设备的CPU频率,关于社会信任关系的D2D匹配决策问题表述如下:
式中:
利用子模块优化来寻找D2D之间的决策. 具体来说,将约束下的2种移动设备DT和NR之间的决策约束(1)和(2)写为拟阵的形式,严格证明了D2D决策选择的效用函数
定义DTs与NRs匹配决策的地面集合
拟阵
定理1:给定地面集合
证明:因为
令
接下来证明目标函数
式中:
可以看出,
将问题
在拟阵约束的情况下,根据“边际效应递减”性质,结合贪婪算法的思想,设计策略选择算法,解决问题
初始化集合
算法1 策略选择算法
输入 设置集合
输出 D2D决策匹配集合
{Repeat
计算
//计算每个
更新集合
更新集合
{If
}//End if NRj此时不辅助其他任何DT
直到
}//End repeat
3.2.4. ODMRA算法和最优值分析
通过考虑D2D用户卸载决策、CPU-周期频率、传输功率分配和收集的电池能量,将ODMRA算法总结在算法2中. 求解问题
算法2 ODMRA算法
输入 每个时隙开始的时刻,获取
输出
{While
根据式(30)、(31),得到
随机初始化:
{Repeat
给定
给定
给定
给定
给定
在下一次迭代中输出
Until 收敛
输出
}//End repeat
t = t+1
}//End while
4. 仿真分析
考虑半径为200 m的圆形区域,配备了MEC服务器的BS位于该区域的中心. NRs和DTs分别随机分布在半径分别为50~150 m和150~200 m的环状区域内. 仿真参数基于文献[12]和[16]设置. DT生成的任务在
本文的对比算法如下. 1)基线1:只考虑MEC服务器的执行和本地执行,而附近的设备只作为中继设备,无法执行计算任务. 2)基线2:NRs仅用于通过D2D通信卸载任务,不作为中继设备. 3)随机算法:DTs和NRs在D2D中随机匹配的算法. 4) SADLS算法:Long等[12]提出的使用匹配博弈的方法进行D2D的策略选择算法. 5)Q-learning算法.
近端发送设备NR的队列长度随时隙数t变化的图像如图2所示. 随着时间的增加,近端发送设备的队列长度逐渐增加并趋于稳定.这是由于ODMRA算法可以通过最小化目标函数,调整惩罚函数的大小来调整任务到达率和任务处理率之间的动态关系,使得李雅普诺夫漂移项逐渐减小,系统逐渐趋于稳定状态. 仿真图像显示了李雅普诺夫漂移惩罚函数的上界,证明了本文算法的有效性.
图 2
2种设备的虚拟电池队列随着时间变化的图像如图3所示. NRs的计算能力大于DTs,故NRs的电池容量大于DTs. 随着时间的增加,2种设备的虚拟电池队列长度在本文算法的优化下逐渐减小并逐渐稳定在扰动参数
图 3
图 4
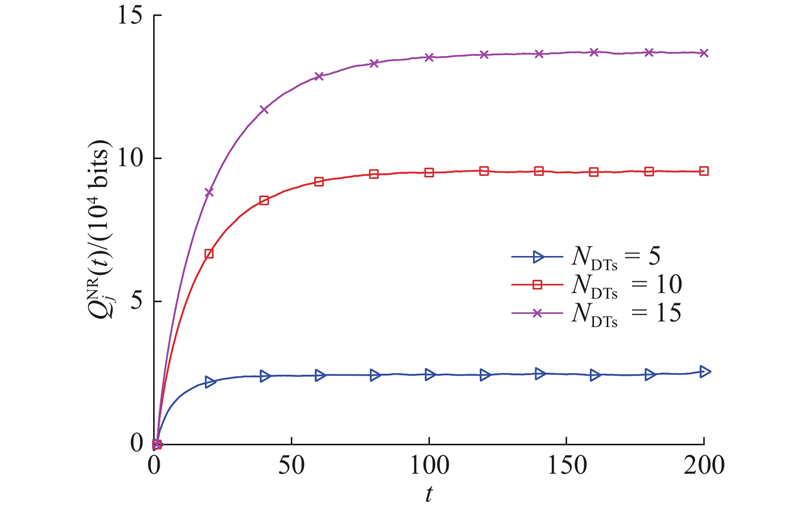
图 4 不同数量DTs下队列长度随时隙数的变化
Fig.4 Change of queue length with number of time slot under different quantities of DTs
图 5
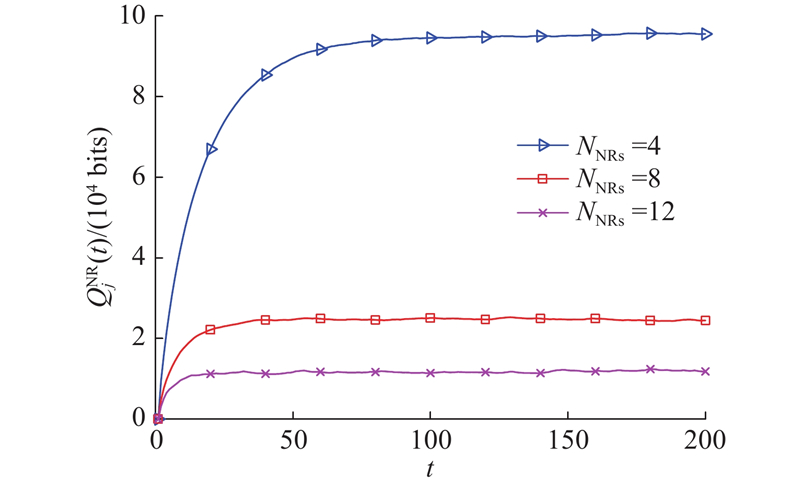
图 5 不同数量NRs下队列长度随时隙数的变化
Fig.5 Change of queue length with number of time slot under different quantities of NRs
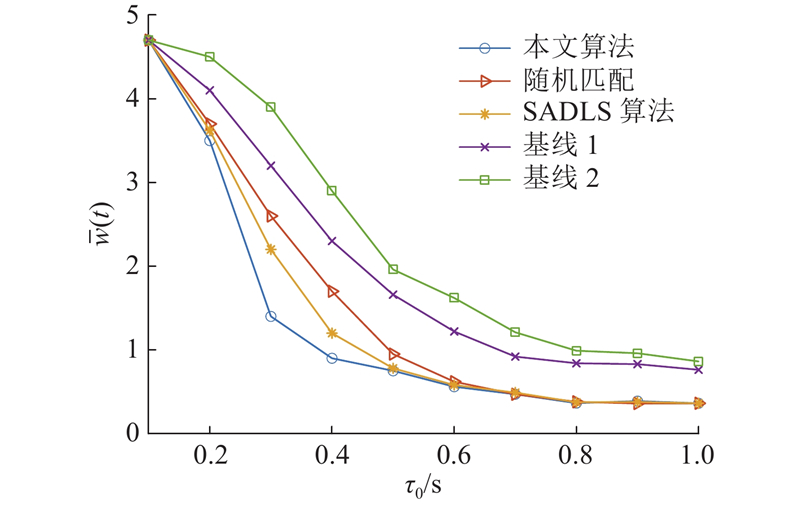
如图6所示为不同算法下时隙长度对系统性能的影响. 可知,执行延迟越长,系统的服务成本越小. 所有算法的系统服务成本都随着
图 6
图 6 平均服务成本随时隙长度的变化
Fig.6 Change of average service cost with length of time slot
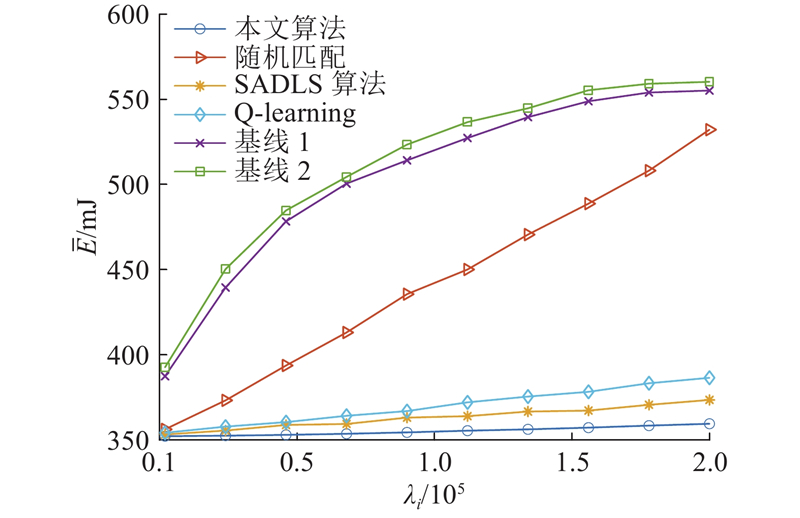
如图7所示为不同算法下平均任务到达率
图 7
图 7 平均能量消耗随平均任务到达率的变化
Fig.7 Change of average energy consumption with average task arrival rate
5. 结 语
本文研究具有社会关系属性的D2D-MEC网络的任务卸载和资源分配框架,即具有空闲计算能力的附近设备发挥中继作用,帮助远程发送设备执行或进一步将其任务转移到MEC服务器.将具有QoS和能量队列稳定性约束的平均服务成本最小化的随机优化问题表述为一系列的短期确定性优化问题. 设计基于李雅普诺夫优化的ODMRA算法解决该问题. 该算法对设备收集的能量、CPU计算频率、发射功率及D2D链路匹配决策进行优化. 仿真结果和理论分析表明,在任务随机到达、系统状态时变的情况下,该算法提高了队列稳定性,减少了能量消耗,且算法复杂度较低,优于其他算法.
参考文献
Toward edge intelligence: multiaccess edge computing for 5G and Internet of Things
[J].DOI:10.1109/JIOT.2020.3004500 [本文引用: 1]
移动边缘计算卸载技术综述
[J].
Survey on mobile edge computing offloading technology
[J].
D2D辅助移动边缘计算下的卸载策略优化
[J].
Optimization of offloading decisions in D2D-assisted MEC networks
[J].
Joint task offloading, D2D pairing, and resource allocation in device-enhanced MEC: a potential game approach
[J].
D2D-assisted multi-user cooperative partial offloading, transmission scheduling and computation allocating for MEC
[J].DOI:10.1109/TWC.2021.3062616 [本文引用: 1]
Dynamic social-aware computation offloading for low-latency communications in IoT
[J].DOI:10.1109/JIOT.2019.2909299 [本文引用: 1]
Dynamic social-aware peer selection for cooperative relay management with D2D communications
[J].DOI:10.1109/TCOMM.2019.2894138 [本文引用: 2]
SERS: social-aware energy-efficient relay selection in D2D communications
[J].DOI:10.1109/TVT.2018.2810162 [本文引用: 3]
Resource management for computation offloading in D2D-aided wireless powered mobile-edge computing networks
[J].
Intelligent task offloading and collaborative computation over D2D communication
[J].DOI:10.23919/JCC.2021.03.020 [本文引用: 1]
Socially-aware energy-efficient task partial offloading in MEC networks with D2D collaboration
[J].DOI:10.1109/TGCN.2022.3153956 [本文引用: 4]
Energy harvesting sensor nodes: survey and implications
[J].
Energy efficiency and delay tradeoff in a MEC-enabled mobile IoT network
[J].DOI:10.1109/JIOT.2022.3153847 [本文引用: 1]
Social network-based content delivery in device-to-device underlay cellular networks using matching theory
[J].DOI:10.1109/ACCESS.2016.2621010 [本文引用: 1]
Mobility-aware offloading and resource allocation in a MEC-enabled IoT network with energy harvesting
[J].DOI:10.1109/JIOT.2021.3081983 [本文引用: 3]
Parallel offloading in green and sustainable mobile edge computing for delay-constrained IoT system
[J].DOI:10.1109/TVT.2019.2944926 [本文引用: 1]
Energy-delay tradeoff for dynamic offloading in mobile-edge computing system with energy harvesting devices
[J].DOI:10.1109/TII.2018.2843365 [本文引用: 1]
Dynamic task offloading and resource allocation for mobile-edge computing in dense cloud RAN
[J].DOI:10.1109/JIOT.2020.2967502 [本文引用: 1]
Dynamic network slicing and resource allocation in mobile edge computing systems
[J].DOI:10.1109/TVT.2020.2992607 [本文引用: 1]
On the convergence of the block nonlinear Gauss–Seidel method under convex constraints
[J].DOI:10.1016/S0167-6377(99)00074-7 [本文引用: 1]
DEBTS: delay energy balanced task scheduling in homogeneous fog networks
[J].DOI:10.1109/JIOT.2018.2823000 [本文引用: 2]
Maximizing submodular set function with connectivity constraint: theory and application to networks
[J].