空间特征是指空间中不同种类的事物,空间实例是这种类别事物在具体空间位置上的出现. 由于空间实例分布的异质性和空间特征实例数量的差异,空间实例通常分布不均,这导致一些同位模式只存在于有限的局部子区域中,于是空间同位模式被分为全局同位模式和区域同位模式. 多级同位模式挖掘指挖掘到全局和区域所有的同位模式.
现有的多级同位模式挖掘研究存在诸多问题. 多级同位模式挖掘方法往往沿用传统同位模式挖掘中实例间的欧氏距离作为其邻近关系的度量准则,未考虑空间数据分布的网格特性. 例如城市网格布局作为城市规划和设计的基本模式,广泛应用于现代城市的管理和规划中;在生态环境中,由于水流和植被分布的相互作用,物种分布呈现网格状分布的现象. 空间实例呈现网格分布的现象在现实中非常普遍,只考虑欧氏距离的度量会忽略网格对角线实例间的邻近关系,可能会遗漏某些有潜在价值的同位模式. 区域划分的目的是通过合理的划分策略,使划分的区域内部具有相同的模式分布. 现有基于点数据聚类的区域划分方法[6-7]存在一系列不足,由于空间数据存在特征实例异质性,只考虑点数据的密度和位置容易忽略特征实例数量的差异,可能导致划分的区域内部缺乏相同的模式分布,使得划分的区域不合理. 现有的多级同位模式挖掘方法采用先挖掘全局同位模式,将全局非频繁同位模式识别为候选区域同位模式,并逐一筛选这些候选区域同位模式,以挖掘区域频繁同位模式. 这种传统的多级模式挖掘方法需要消耗大量的时间与空间,计算模式的全局参与度. 该方法未采用有效的剪枝策略,导致时间复杂度较高.
针对现有的多级同位模式挖掘存在的问题,本文利用网格划分技术重新定义实例之间的邻近关系,利用网格邻近关系和模式参与实例的反单调性提出有效的剪枝策略,使得提出的挖掘算法不仅能够有效地提高挖掘效率,而且挖掘结果更贴合实际应用. 在区域划分阶段,采用网格密度峰值聚类的方法,基于网格中2阶网格空间团定义不同网格的相似性,使得区域划分更合理. 因为多级同位模式挖掘方法旨在挖掘出全局和区域频繁的同位模式,但是通过将全局不频繁的模式作为区域候选模式并逐阶筛选,时间复杂度非常高. 本文考虑模式的分布情况,提出先挖掘区域同位模式再推导全局同位模式的新颖挖掘框架,时间效率得到了很大的提升.
1. 相关工作
Huang等[8]提出空间同位模式的挖掘,定义参与度来衡量同位模式的频繁程度. 基于参与度的反单调特性,提出类Apriori的挖掘方法,即join-based算法[8]. 随后,人们提出各种方法来提高同位模式挖掘算法的效率,例如Partial-join和joinless算法[9]. 由于挖掘同位模式和空间实例的团关系密不可分,人们提出一系列基于团的同位模式挖掘方法,如基于order-cliques的算法[10]、基于极大团的算法[11]. 传统的同位模式挖掘方法只着眼于在全局空间中频繁出现的同位模式,忽略了空间数据分布异质性的存在. 由于一些模式只在局部子区域内频繁出现,而全局同位模式挖掘方法无法发现这些频繁出现的区域模式,忽略了局部区域信息. 区域同位模式挖掘引起了人们的关注,它旨在寻找在局部子区域中频繁存在的同位模式及相应的频繁区域.
区域同位模式的挖掘方法主要可以分为以下2类. 1)基于区域识别的方法,它们通过对空间实例或模式实例进行聚类来识别模式的频繁区域,计算区域内模式的参与度来评价模式的频繁程度. Eick等[12]将具有最大适配度函数的聚类结果作为挖掘同位模式的区域. Mohan等[13]提出基于邻域图的方法,发现区域同位模式的频繁区域. Deng等[14]提出多级挖掘方法,将全局不频繁模式作为候选区域模式,通过Delaunay Triangular自适应聚类方法识别模式的频繁区域. Liu等[15]提出基于自然邻居的多级同位模式挖掘方法,建立新的局部自适应邻近关系,但该方法对空间特征的数量比较敏感. Liu等[16]提出k近邻中加入道路网格约束和启发式的两阶段方法,通过蒙特卡罗模拟方法评估模式的统计意义,识别每个区域同位模式的频繁区域. 2)基于区域划分的方法. 这种方法将整个研究区域划分为多个子区域,分别在每个子区域内挖掘同位模式. 基于区域划分方法的主要挑战在于找到适当的空间划分方案,目前的研究提出了各种划分区域的方法. Celik等[17]提出基于四叉树的结构来挖掘频繁的区域同位模式,但需要大量的先验知识. Ding等[18]使用监督聚类算法,将基于网格的地理空间划分为任意形状的区域. Qian等[19]提出基于k近邻的分区方法,用 k = 1初始化原始区域,利用迭代方法合并具有近似距离阈值和一定比例的同类型模式的区域,得到具有相似数据分布的目标区域. Wang等[20]提出挖掘区域同位模式的频繁主义和贝叶斯框架,开发基于概率扩展的启发式方法,寻找任意形状的区域.
本文引用网格密度峰值聚类方法,通过2阶网格空间团来判断不同网格的相似度进行区域划分. 基于数据分布的网格特性提出有效的剪枝策略,设计高效的多级同位模式挖掘算法,解决了传统多级方法时间效率低的问题. 本文提出从区域同位模式推导出全局同位模式的新挖掘框架,避免了将区域同位模式误判为全局同位模式的情况,显著减少了计算时间. 这些创新使得算法在实际应用中能够更高效地挖掘多级同位模式,得到有意义且可靠的结果.
2. 概念与方法
2.1. 基本概念
给定空间特征集F = {f1, f2
图 1
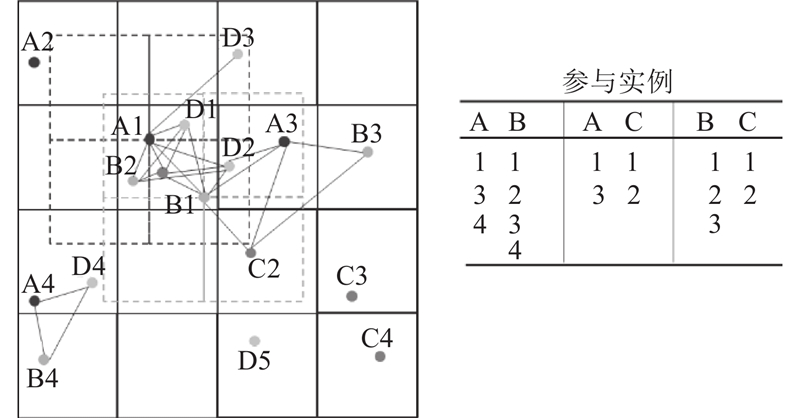
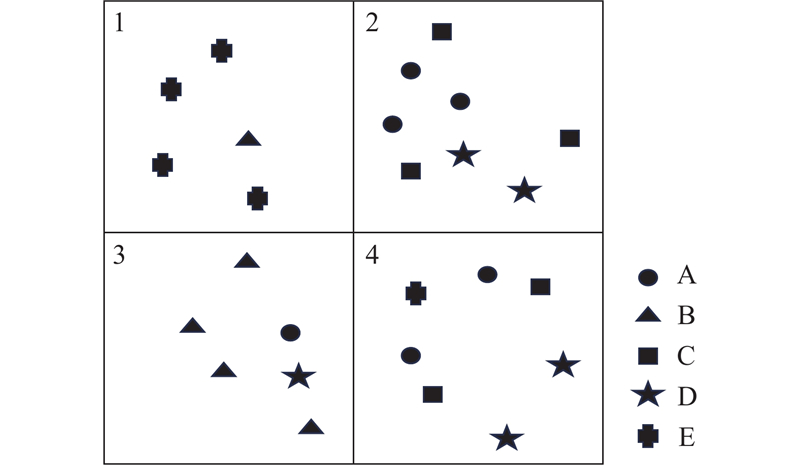
图 1 包含4个空间特征A、B、C、D的区域数据示例(左图)和一些模式的参与实例(右图)
Fig.1 Example of regional data containing four spatial features A, B, C, D (left figure) and some examples of pattern participation instances (right figure)
2.2. 区域划分方法
密度峰值聚类[21]是基于密度的聚类算法,能够自动确定聚类中心点和聚类数目,该聚类算法依据以下2点获取聚类结果. 1)簇中心的局部密度较高;2)簇中心离其他簇中心距离较远. 密度峰值聚类算法中需要设置一些参数,算法对参数较敏感. 本文提出自适应网格密度峰值聚类算法,在簇分配的过程中利用网格中2阶网格空间团,度量网格之间的相似度.
定义1 网格密度. 给定网格g,该网格密度定义为网格内空间实例数量.
式中:Ins (g)为网格内的实例个数.
定义2 网格相对距离. 给定网格g,网格相对距离
式中:
定义3 中心网格. 中心网格gcenter的密度和相对距离经过归一化处理后,密度和距离都大于其阈值.
簇中心满足以下2个条件:1)簇中心的密度大;2)离其他簇的距离较远. 因为密度和距离的单位不一致,对网格密度和相对距离进行归一化处理,
中心网格的密度和距离均同时大于其阈值,即
区域划分的目的是通过合理的划分策略,使划分的区域内存在尽可能相同的区域模式. 为了使具有相同模式的区域尽可能地聚集在一起,在聚类过程中需要进一步考虑网格内部的模式. 在同位模式挖掘中,2阶网格空间团探究的是不同空间位置上对象的属性之间的相关性,通过分析2阶网格空间团可以预测出更高阶模式的潜在联系,所以考虑利用2阶网格空间团度量不同网格的相似度.
定义4 网格相似度. 给定中心网格gcenter和待分配的网格g,2个网格的相似度定义如下:
gcenter和g的2阶模式并集为c={c1,
图 2
Sg(1,2)=
算法1(AG-DPC)将整个研究区域S划分成d
算法1 AG-DPC
输入: S, d;
输出: Clusters;
1. G = Divide(d, S);
2.
3.
4. For g
5. Calculate
6. If
7. Clusterg
8. For g'
9. Clusterg = FindCenterGrid(g');
10. Clusterg
11. Return Clusters;
2.3. 多级同位模式挖掘
图 3
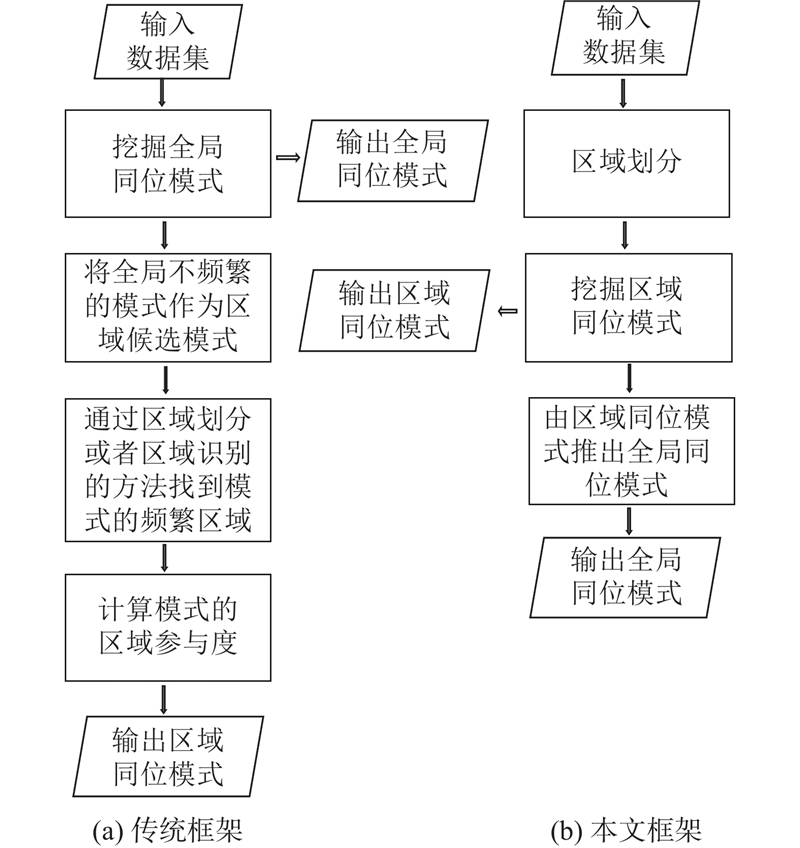
图 3 多级同位模式挖掘框架上的对比
Fig.3 Comparison of multi-level co-location pattern mining framework
定义5 区域参与度PI、区域参与率PR. 给定模式c及其所在区域r,该模式c中特征fi在区域r的区域参与率
式中:R(r, fi)为区域r中特征 fi的实例集合,
定义6 区域同位模式RCP. 给定模式c及其所在区域r,若该模式c在区域r内的参与度
如图1所示,在区域中,假设区域频繁度阈值为0.4,PI(r,{B, C}) = 1/2 > 0.4,则模式{B, C}为区域同位模式.
定义7 全局同位模式GCP. 给定模式c和面积占比阈值
式中:
引理1 区域模式在区域内满足先验性原理. 在区域r中,若区域模式是区域频繁的,则其子模式也是区域频繁的;若区域模式不是区域频繁的,则其超模式也是区域不频繁的.
证明:若模式c在区域r中频繁即满足
引理2 全局模式满足先验性原理. 若全局模式是频繁的,则其子模式也是频繁的;若全局模式不是频繁的,则其超模式也是非频繁模式.
证明:由于本文的全局模式是由区域同位模式推出的,区域同位模式在其频繁区域中满足先验性原理,一个模式在区域中是频繁的,那么其子模式也是区域频繁的(引理1). 子模式subc所占的区域面积一定大于等于该模式c的区域面积,即
即
当计算区域模式的参与度时,不需要再花费大量时间和空间存储模式的表实例,只需要存储表实例中不重复的实例即参与实例. 在区域内从低阶向高阶挖掘区域同位模式,需要进一步考虑高阶的候选参与模式,以减小搜索空间.
定义8 候选参与实例集. 在区域r中,特征f在k(k >2)阶同位模式c中的候选参与实例集是f在模式c的所有包含f的k-1阶子模式中的参与实例集的交集,表示为
式中:
引理3 在
证明:若
引理4 在区域r中,对于区域同位模式c及其特征f (f
证明:根据引理3可知,
基于参与度上界的剪枝策略. 根据引理4可知,若模式c中存在某一特征f的参与度上界
引理5 包含模式c的参与实例的网格为c中所有特征f (f
证明:由引理3可得,模式c的参与实例一定存在于模式c的候选参与实例中,可以得到模式c的参与实例所在的网格一定包含于候选模式参与实例所在的网格范围内. 如果要找到包含模式c的参与实例的网格,那么这些网格一定包含在所有特征的候选参与实例所在的网格的交集中. 如图4所示为区域r的实例分布,(gridX, gridY)为网格的编号. 根据定义8列出模式{A, B, C}的候选参与实例集,显示了候选参与实例所在的网格标号,可以看出网格(1, 2)是模式{A, B, C}的所有特征所在网格的交集,即网格(1, 2)内存在{A, B, C}的网格空间团.
图 4
引理6 若某一网格内包含模式c的所有特征,则这些特征实例o (o. f
证明:由邻近关系的定义可知,实例的邻域范围是以该实例坐标为中心、边长为2d的矩形,则实例的邻域范围一定包括实例所在的网格. 网格内的所有实例都存在邻近关系,即满足团关系,所以只要网格内包含模式c的所有特征,则这些特征实例o (o. f
引理7 在区域r内,若模式c在网格内的区域参与度为
证明:区域模式c存在以下2种情况. 1)模式的网格团关系完全存在于网格内,如图4的团关系(A1, B2, C1). 2)模式的网格团关系存在于网格间,如图4的(A3, B1, C2). 模式的区域参与度由2部分组成:
基于参与度下界的剪枝策略. 根据引理5找到区域模式c完全存在于网格内的情况,可以进一步缩小搜索范围. 根据引理6可知,网格内部的特征实例o (o. f
3. 算法与分析
3.1. 算法描述
提出的算法利用2.2节中网格密度峰值聚类的方法进行区域划分,开展多级同位模式挖掘. 采用先挖掘区域频繁模式再推导出全局频繁模式的多级同位模式挖掘框架,具体算法如下.
算法2 S-ML
输入: d,
输出: RCPs(区域同位模式集合)、GCPs(全局同位模式集合)
1. Regions = AG-DPC(d)
2. RCPs =
3. For r
4. RC1
5. While RLk−1
6. RCk = CandidateGeneration(RLk−1);
7. For c
8. If IsRegionalCo-location(c, r) do:
9. RCPs
10. If c
11. GCPs
12. k++;
13. Return GCPs and RCPs;
在算法2(S-ML)中,根据算法1的网格密度峰值聚类获得划分区域(行1). 在区域划分的基础上,对每个区域进行区域同位模式挖掘(行3~12). 根据区域内上一阶的频繁区域模式生成候选模式(行6),验证每个候选模式是否在区域内频繁(行7~9,具体见算法3). 与传统的多级同位模式挖掘不同,算法2从区域同位模式推出全局模式(行10、11),该全局模式不需要计算参与度,因此不需要存储全局的参与实例集,节省了空间消耗,只需要计算模式c的区域面积与全局空间面积的比值. 若模式c在之前区域中未被判定为频繁全局模式,则计算模式当前频繁区域的面积之和与全局面积的比值
算法3 (IsRegionalCo-location)描述了如何判断模式c在区域r中的频繁性. 在区域中挖掘同位模式先通过模式的参与度上界和下界进行剪枝,根据定义8得到模式中特征的候选参与实例,根据引理4计算得到参与度上界(行2). 若存在某一特征的区域参与度上界未达到频繁度阈值,则说明该模式在区域r中不是频繁的,直接返回False(行3);否则根据引理7计算模式的区域参与度下界,记录网格内模式的参与实例(行4). 若模式的区域参与度下界达到频繁度阈值,直接返回True(行5、6);否则在区域中搜索模式的所有参与实例,计算参与度,判断频繁性(行7~12),具体见算法4.
算法3 IsRegionalCo-location
输入: 模式c,区域r
1. For f
2. If
3. Return false;
4. Calculate PIintra(r, c);
5. If PIintra(r, c)
6. Return true;
7. Else:
8. Search(r, c) and Calculate PI(r, c);
9. If PI(r, c)
10. Return true;
11. Else:
12. Return false;
算法4(Search)描述了如何在区域r中搜索c的参与实例,由引理3可知,在区域模式的候选参与实例集
算法4: Search(r, c)
输入: c,ParticipateIns(参与实例集)
1. For f
2. For o
3. If 计算参与度下界时已经验证了实例o为参与实例 do:
4. Return true;
5. Else:
6. If o.g及其周围8个网格不完全包含c中所有特征实例 do:
7. Return false;
8. Else:
9. 初始化S={o}, X={o}, i=1, flag = False, Oss {f, o'.f}(o'.f ≠ o.f);
10. S= BracktrackingSreaching(S, X, i, flag);
11. If S
12. PariticipateIns记录参与实例;
13. Return true;
14. Return false;
3.2. 算法时间复杂度的分析
分析算法AG-DPC和S-ML的时间复杂度,以下均假设数据集拥有y个特征、m个网格、z个区域.
AG-DPC:提出的基于网格的密度峰值聚类算法将数据分布空间划分为m个网格,假设中心网格数量为g个,每个网格内的特征数量为x个(x<<y),则网格内的2阶网格团的种类有
S-ML:算法S-ML采用分区后逐阶挖掘区域同位模式,该算法仅挖掘区域同位模式,并由区域模式推导出全局模式,不需要计算模式的全局参与度. 最坏情况下区域内的特征数有y个,区域每个特征的实例数最多为n. 在每个区域中从2阶开始逐阶进行区域同位模式挖掘,最坏情况下模式的最高阶数为y (一般情况下,由于邻近关系和频繁度阈值的约束,模式的最高阶数远小于y). 假设每次迭代中搜索的候选区域模式个数为
在推出全局模式时,仅需要考虑模式所在区域面积与全局面积的比值. 在最坏情况下,每个模式都在其最后一个频繁区域中判断出全局频繁性,即在每个区域中的每个模式都需要计算A(c),则推导出全局同位模式的时间复杂度为O (zy×
4. 实验结果与分析
使用真实和合成数据集,评估所提出的多级同位模式挖掘算法的有效性、效率和可扩展性. 实验中的算法均由C++实现的. 硬件环境为Intel Core i7 3.70 GHz CPU、16 GB RAM. 运行环境为Microsoft Windows 10、Clion2021.
4.1. 实验数据集
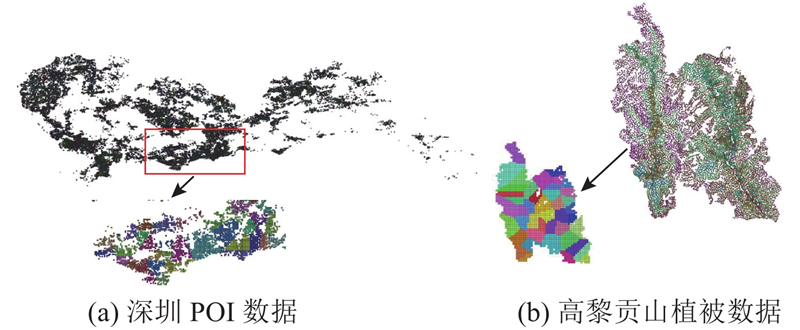
图 5
图 5 真实数据集分布及其分区结果
Fig.5 Distribution of real datasets and their partition results
4.2. 真实数据集上的实验分析
4.2.1. 网格空间团的网格相似性度量方法的有效性
区域划分的目的是通过合理的划分策略使划分的区域内存在尽可能相同的区域模式. 为了验证提出的利用2阶网格空间团获取目标区域的效果,定义区域划分的评估指数EI.
式中:R1、R2为2个相邻的区域;n为区域个数,
表 1 不同方法的EI值
Tab.1
| 方法 | EI | |
| 深圳 | 高黎贡山 | |
| S-ML | 0.9892 | 0.8771 |
| S-ML-2 | 0.8783 | 0.6564 |
| FDPC-RCPM | 0.6532 | 0.6401 |
4.2.2. 挖掘结果的有效性
图 6
图 6 挖掘到的区域模式频繁区域的比较
Fig.6 Comparison of mined prevalent regions of regional co-location patterns
在传统的多级挖掘方法中,全局同位模式是满足全局频繁度阈值的模式,即表示该模式在整个研究空间中频繁出现的模式;本文的全局模式不从参与度的角度考虑,从区域同位模式考虑,频繁的区域同位模式出现在多个区域,且这些区域的面积占整个研究区域面积的比值达到给定阈值时,认为该模式为全局频繁模式. 当挖掘全局模式时,ML方法仅考虑模式的全局参与度,忽略了模式的分布情况,会造成仅分布在局部小区域的模式被误判为全局模式,如图7所示,深色部分表示该模式存在的区域,这些区域面积占比很小,不满足模式在全局范围内频繁共现. 本文挖掘的全局模式在区域模式的基础上考虑了模式的分布情况,从图8可以看出,模式在全局范围内频繁出现(浅色为模式分布的区域).
图 7
图 8
图 8 利用提出方法识别的全局模式的分布
Fig.8 Distribution of global patterns identified by proposed method
通过对比挖掘到的区域模式和全局模式,可知提出的挖掘方法的结果更加合理.
4.2.3. 挖掘效率
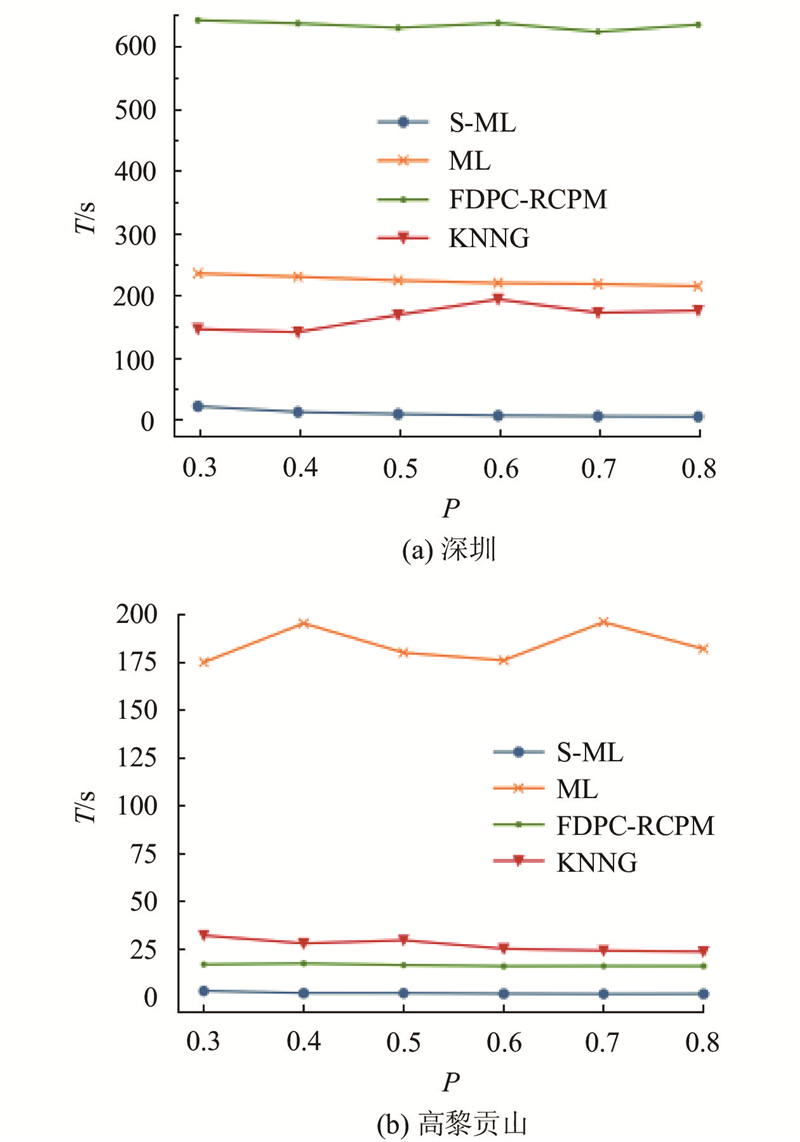
为了对比本文方法与其他多级同位模式挖掘方法的执行效率,对比了3个传统多级同位模式挖掘方法(ML[14]、NN[15]、QGFR[24])和2个仅挖掘区域同位模式的方法(KNNG[19]、FDPC-RCPM[6]). 将深圳POI数据的邻近阈值设置为100,高黎贡山的邻近阈值设置为1 500 (深圳POI属于城市建筑数据,实例之间的距离较近;高黎贡山属于植被数据,实例之间的距离较远. 在考虑数据集内实例的平均距离后分别设置了相对较合理的距离阈值). 其中采用k近邻生成邻近关系的方法(KNNG、FDPC-RCPM),将输入距离阈值的平均邻居个数作为k值. NN方法是基于自然邻居挖掘多级同位模式,建立新的局部自适应邻近关系,对特征数量极其敏感. QGFR方法使用最小正交包围矩形作为模式的区域, 但得到的区域形状固定为正交矩形, 且即使在带有剪枝策略的情况下, 算法的时间复杂度仍极高. 在本实验中仅限于比较方法的时间效率,无法在24 h内获取到NN方法和QGFR方法的实验结果.
如图9所示为在不同的频繁度阈值P下多个方法的运行时间T. 可以看出,在不同的频繁度阈值下,本文方法的时间效率最优. ML方法将全局不频繁的模式全部作为区域候选模式. 随着频繁度阈值的增加,全局同位模式数量减少导致区域候选模式数量增加,ML方法需要对每个候选区域模式计算区域参与度,导致消耗大量的运行时间. KNNG方法需要花费大量的时间验证相似的模式,获取目标区域,计算参与度. FDPC-RCPM方法在每个区域中采用原始的join-less方法进行挖掘,并未优化算法效率. 本文提出的方法采用参与度的上下界进行有效剪枝,只需要对不能剪枝的模式计算区域频繁度,时间效率有了很大的提升,甚至优于仅挖掘区域同位模式方法的时间效率.
图 9
图 9 在不同频繁度阈值下的运行时间对比
Fig.9 Comparison of running time under different prevalent thresholds
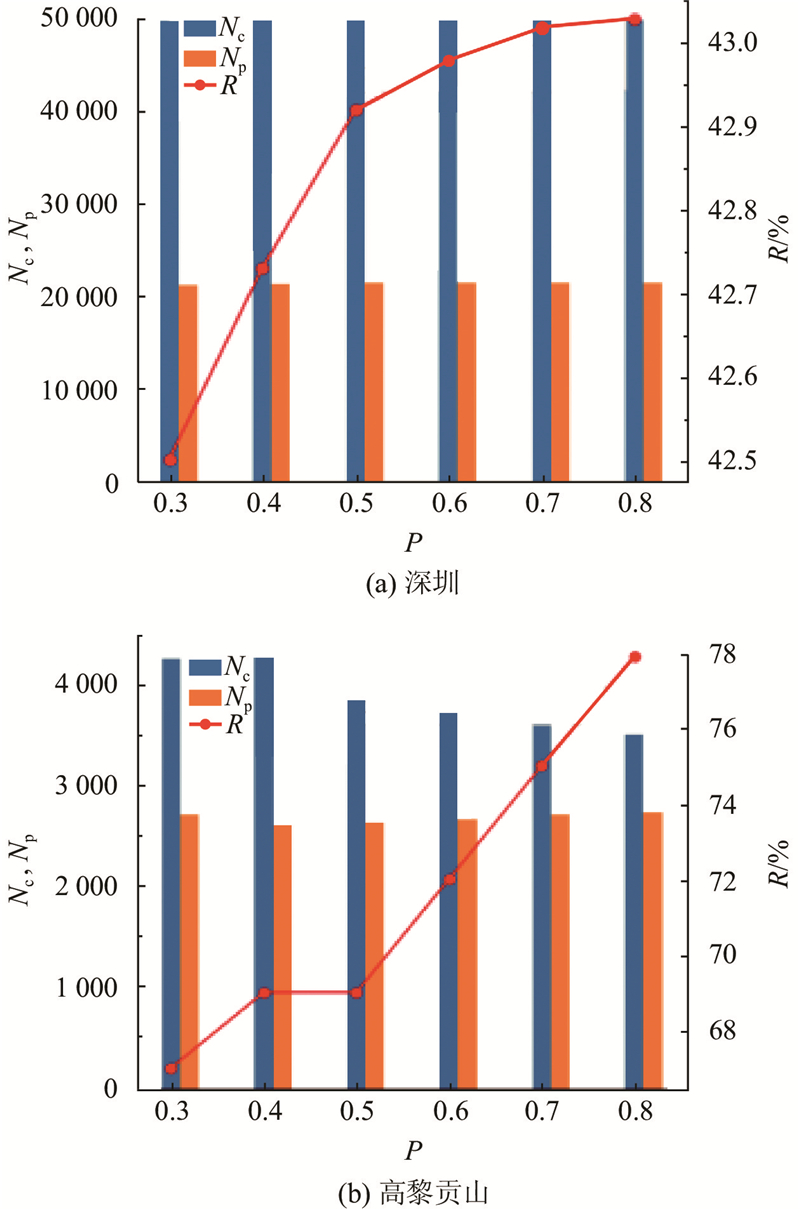
本文方法是新颖的多级同位模式挖掘方法,将其挖掘结果与传统多级方法ML进行对比. 随着频繁度阈值的增大,利用这2个方法挖掘到的模式数量递减. 本文所挖掘到的区域模式数量多于ML方法挖掘到的模式数量,如图10所示. 图中,N为模式数量. 这是因为考虑了实例之间的网格特性,且邻近关系包括对角线可达性,相比于ML方法中的邻近关系,本文的邻近关系更丰富,可以捕捉到更多有潜在价值的模式. 此外,本文避免了将区域模式误判为全局模式,而ML方法存在误判的情况,这导致ML方法挖掘到的区域模式数量较少.
图 10
图 10 在不同频繁度阈值下的区域模式数量对比
Fig.10 Comparison of number of regional patterns under different prevalent thresholds
4.2.4. 剪枝效率
图 11
4.3. 合成数据集上算法的可扩展性分析
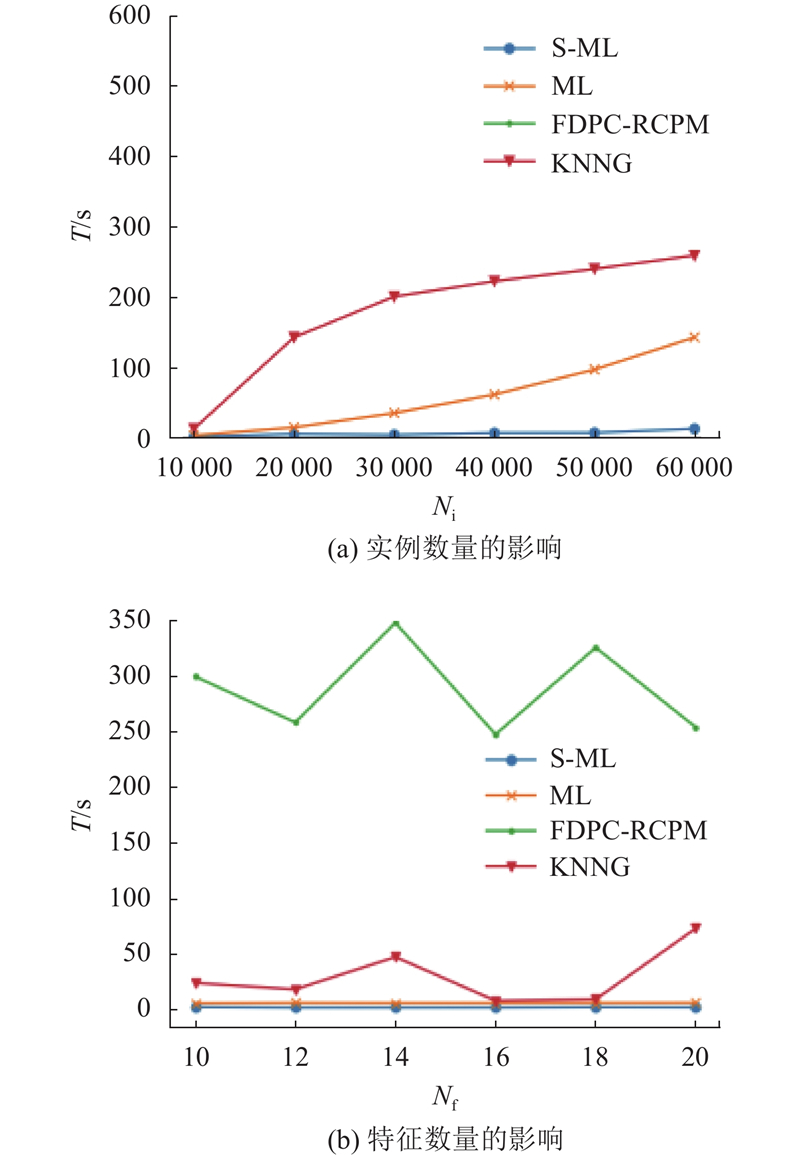
图 12
空间特征数量对同位模式的阶数有着较大的影响. 为了研究特征数量对算法运行效率的影响,合成了5个不同特征数量的数据集,实例数量为10 000. 实验结果如图12(b)所示,S-ML算法的运行效率较高.
综上所述,提出的算法具有良好的时间效率,在处理大规模实例数量时具有更好的可扩展性.
5. 结 语
本文提出基于网格空间团的多级同位模式挖掘方法. 传统的邻近关系定义通常只考虑空间实例之间的欧氏距离,忽略了真实数据普遍的网格化分布. 为了弥补这一不足,采用网格邻近关系来替代传统的基于距离的邻近关系. 在区域划分阶段,针对点聚类划分区域方法的不足,提出优化的网格密度峰值聚类方法,在聚类的基础上进一步考虑网格内模式的相似情况. 在模式挖掘阶段,提出从区域同位模式推导出全局同位模式的挖掘新框架,设计带有剪枝策略的多级同位模式挖掘算法. 该算法不仅避免了将区域同位模式误判为全局同位模式的情况,还减少了计算全局参与度的时间,显著提升了时间效率. 本文的全局模式考虑了模式的分布情况,使得结果更加准确. 通过实验验证了挖掘结果的有效性和合理性,在真实和合成数据集上进行了广泛的实验,验证了本文算法的高效性和可扩展性.
参考文献
Discovering the joint influence of urban facilities on crime occurrence using spatial co-location pattern mining
[J].DOI:10.1016/j.cities.2020.102612 [本文引用: 1]
On discovering co-location patterns in datasets: a case study of pollutants and child cancers
[J].
Mining strong symbiotic patterns hidden in spatial prevalent co-location patterns
[J].DOI:10.1016/j.knosys.2018.02.006 [本文引用: 1]
Understanding the spatial organization of urban functions based on co-location patterns mining: a comparative analysis for 25 Chinese cities
[J].DOI:10.1016/j.cities.2019.102563 [本文引用: 1]
基于模糊密度峰值聚类的区域同位模式并行挖掘算法
[J].
Parallel mining algorithm for regional co-location patterns based on fuzzy density peak clustering
[J].
MLCPM-UC: 一种基于模式实例分布均匀系数的多级 co-location 模式挖掘算法
[J].DOI:10.11896/jsjkx.201000097 [本文引用: 3]
MLCPM-UC: a multi-level co-location pattern mining algorithm based on uniform coefficient of pattern instance distribution
[J].DOI:10.11896/jsjkx.201000097 [本文引用: 3]
Discovering colocation patterns from spatial data sets: a general approach
[J].DOI:10.1109/TKDE.2004.90 [本文引用: 3]
A joinless approach for mining spatial colocation patterns
[J].DOI:10.1109/TKDE.2006.150 [本文引用: 1]
An order-clique-based approach for mining maximal co-locations
[J].DOI:10.1016/j.ins.2009.05.023 [本文引用: 1]
CPM-MCHM: 一种基于极大团和哈希表的空间并置模式挖掘算法
[J].DOI:10.11897/SP.J.1016.2022.00526 [本文引用: 1]
An order-clique-based approach for mining maximal co-locations
[J].DOI:10.11897/SP.J.1016.2022.00526 [本文引用: 1]
Multi-level method for discovery of regional co-location patterns
[J].DOI:10.1080/13658816.2017.1334890 [本文引用: 3]
An adaptive detection of multilevel co-location patterns based on natural neighborhoods
[J].DOI:10.1080/13658816.2020.1775235 [本文引用: 2]
Discovery of statistically significant regional co-location patterns on urban road networks
[J].DOI:10.1080/13658816.2021.1981335 [本文引用: 1]
A framework for regional association rule mining and scoping in spatial datasets
[J].
Mining regional co-location patterns with kNNG
[J].DOI:10.1007/s10844-013-0280-5 [本文引用: 2]
Clustering by fast search and find of density peaks
[J].DOI:10.1126/science.1242072 [本文引用: 1]
Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy
[J].DOI:10.1016/j.knosys.2017.07.010 [本文引用: 1]