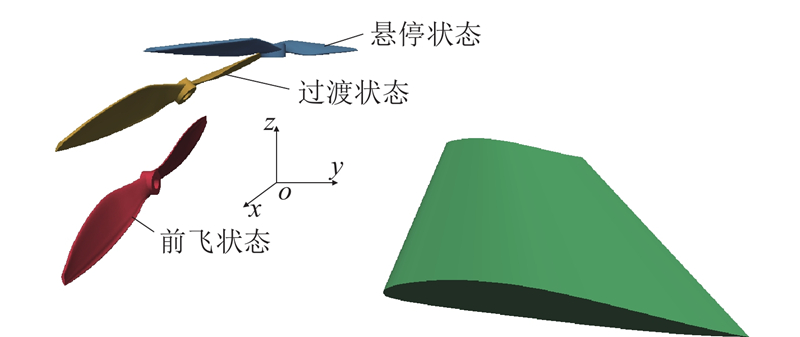
倾转旋翼机在直升机模式和固定翼模式切换时引入的过渡状态,是具有强非线性气动特性的特殊状态,过渡状态气动性能的好坏是决定飞机模式切换过程是否安全可靠、平稳高效的关键因素. 针对过渡状态的气动特性研究主要有试验和数值仿真2种方法. 在试验方法方面,招启军等[4]基于3D-PIV(particle image velocimetry)技术测量悬停和过渡状态倾转旋翼机旋翼/机翼气动干扰特性, 部分揭示了干扰流动的机理. 董凌华等[5]基于倾转旋翼/机翼耦合系统动力学试验模型开展倾转过渡状态下模型机翼的基阶挥舞弯曲/扭转耦合振动的气弹动力学风洞试验研究. Chinwicharnam等[6] 开展MAV VTOL螺旋桨/机翼结构相互作用的低速风洞实验研究,发现螺旋桨滑流不仅能够提高机翼性能,还能够延缓失速角的形成. 由于试验方法花费的时间周期长、成本高、数据测量难度大且数据有限,随着计算机算力的增强,数值仿真方法得以快速发展和广泛应用. 刘佳豪等[7]针对倾转过渡状态旋翼/机翼之间的气动干扰进行高分辨率数值模拟,对比旋翼/机翼组合体悬停状态改进延迟分离涡模拟(improved delayed detached eddy simulation, IDDES)和雷诺平均模拟(Reynolds-averaged Navier-Stokes equations, RANS)计算结果,发现在倾转过程中旋翼产生的诱导滑流对机翼有升力增益效果. 李鹏等[8-9] 提出并建立适合过渡状态气动特性分析的混合桨叶模型(hybrid blade model, HBM)方法. 相对于传统的真实桨叶模型(real blade model, RBM)方法,HBM方法结合虚拟桨叶模型(virtual blade model, VBM)方法的优势,在保证流场模拟精度的基础上进一步提高了计算效率. Garcia等[10]对1∶5模型尺寸的ERICA倾转旋翼机进行高保真的气动计算,评估当前计算流体力学方法在不同飞行状态下预测空气载荷的能力. 杨海涛等[11]研究前飞状态和倾转过渡状态倾转旋翼对机翼的气动干扰的结果表明,当旋翼倾角小于75°时,随着前进比的增大,机翼升力系数由负值逐渐增大,倾转角对机翼气动特性的影响随前进比的增大而降低. 吴伟伟等[12]基于运动嵌套网格和局部坐标系理论提出适合于模拟连续倾转过渡状态非定常流场的数值计算方法,并模拟某型无人倾转旋翼机的连续倾转过渡状态,研究倾转时间、前飞速度和旋翼总距角对旋翼机气动性能的影响.
1. 计算方法
1.1. 重叠网格方法
图 1
在旋翼的常见研究方法中,虚拟桨叶模型和动量源方法旋翼被体积力模型代替,计算结果受到一定程度的影响;滑移网格和多参考系模型方法只能实现单一的运动情况,使得多数学者通过固定倾转角的方法来研究旋翼倾转过渡状态的气动性能,与实际的连续倾转过渡运动情况有出入. 同时,其他常见的动网格计算方法在物体运动幅度过大时会出现网格变形的情况,影响精度和计算结果,甚至导致整个计算发散. 降低这个问题造成的影响,将增加网格量和计算成本. 重叠网格可以实现旋翼的六自由度运动,即旋翼有一定转速旋转并且连续倾转90°,网格不会变形,确保在合适的计算量下实现连续倾转过渡的模拟计算.
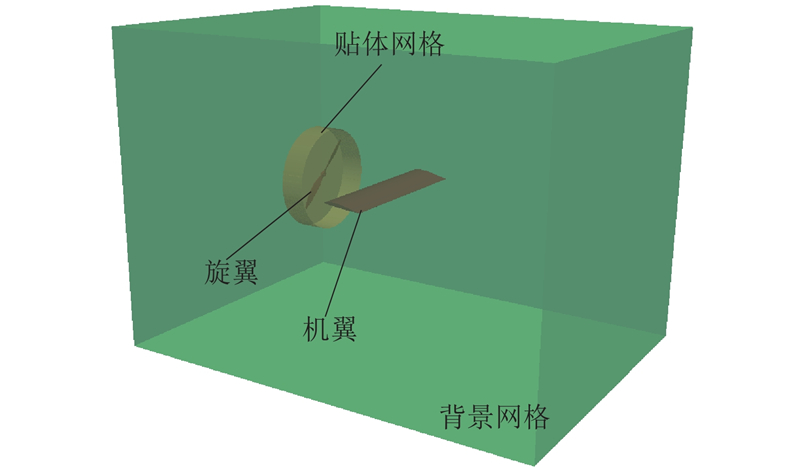
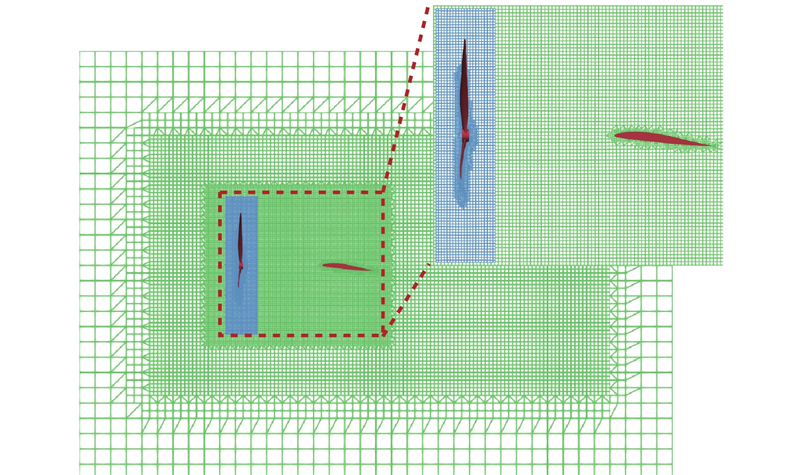
重叠网格(overset mesh)方法对每个运动物体进行单独的网格划分,由于各运动物体网格与背景网格有重叠,通过计算重叠网格的联系信息(domain connectivity information, DCI)进行流场信息交换,能够实现计算域的求解. 网格单元类型分为边界单元(fringe cell)、活动单元(active cell)、贡献单元(donor cell)、洞单元(hole cell)和孤点单元(orphan). 计算首先执行挖洞步骤,即搜寻洞单元,并且将相邻的单元标记为边界单元;之后根据标记的边界单元从另外背景网格中寻找最佳匹配的贡献单元,根据搜寻的边界单元和贡献单元的位置进行贡献单元的插值系数求解;最后对重叠区域的优化,重新搜寻最优的匹配单元,保证最佳的插值关系,去除额外的边界单元,进而减少计算量[15-17]. 有3种典型的贡献单元插值系数求解方法:1)就近原则,2)通过边界单元到贡献单元中心的距离倒数求得插值系数,3)Laplace 算子权重方法. 本研究采用Laplace 算子权重方法,计算域示意图如图2 所示. 旋翼周围网格单独划分,机翼处于背景网格中,网格沿机翼对称面截取示意图如图3所示. 在过渡状态中,旋翼与贴体网格一同以一定转速旋转,同时倾转90°,模拟旋翼从前飞状态倾转至悬停状态.
图 2
图 3
图 3 计算域中沿机翼对称面的网格
Fig.3 Girds along wing's symmetric plane of computational domain
1.2. 控制方程
数值计算工具使用基于有限体积的开源CFD软件OpenFOAM中的overPimpleDyMFoam求解器,重叠网格技术用于实现网格的相对运动以捕捉旋翼的旋转运动和连续倾转运动,并通过重叠区域进行插值与背景网格传递信息. 采用PIMPLE(PISO-SIMPLE)算法求解非定常不可压缩流动的压力速度耦合问题,求解时,将每个时间步长内的流动看作稳态流动,采用SIMPLE算法进行迭代求解,采取低松弛的方法保证方程在每一时间步长内的收敛性. 空间离散格式采用鲁棒性高的二阶迎风差分格式,时间步进采用一阶精度的隐式欧拉格式.
流场控制方程采用雷诺平均方程[18],表达式为
式中:t为时间;E为守恒变量;FI为非黏性通量,FV为黏性通量;Q为源项,是旋翼旋转带来的附加项(由科氏力引起),假设旋翼旋转的角速度为[0,−ω,0],此时源项表达式为
式中:k为湍流动能,Dk为k的有效扩散系数,P为湍流动能产生速率,ε为湍流动能耗散率,Dε为ε的有效扩散系数,u为流场速度,C1、C2、C3为模型系数,Cμ为湍流黏度的模型系数,νt为湍流黏度.
2. 计算验证方法
式中:V∞为前方来流速度;n为旋翼转速;D为旋翼直径,D=0.203 2 m. 在连续倾转过渡过程中,不同倾转时间(t=1 s和t=2 s)系统气动特性随旋翼倾转角增加的变化趋势基本一致[12]. 在计算验证算例时发现,当保持前飞状态计算到0.08 s左右时,机翼升力趋于稳定,说明此时流场达到稳定. 在连续过渡状态研究中,设置计算时间范围为0~1.08 s,前0.08 s旋翼保持前飞状态,在流场达到稳定后开始从前飞状态(倾转角α=0°)到悬停状态(倾转角α=90°)的倾转过渡过程,倾转时间为1 s.
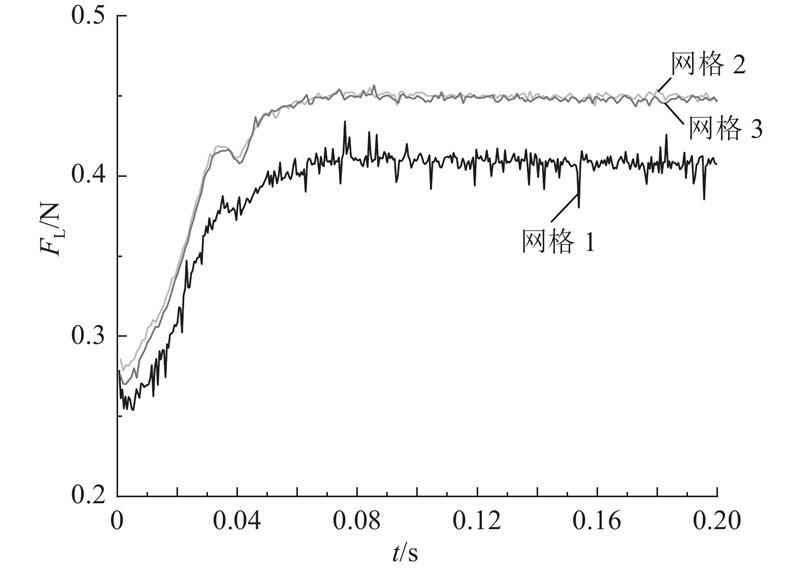
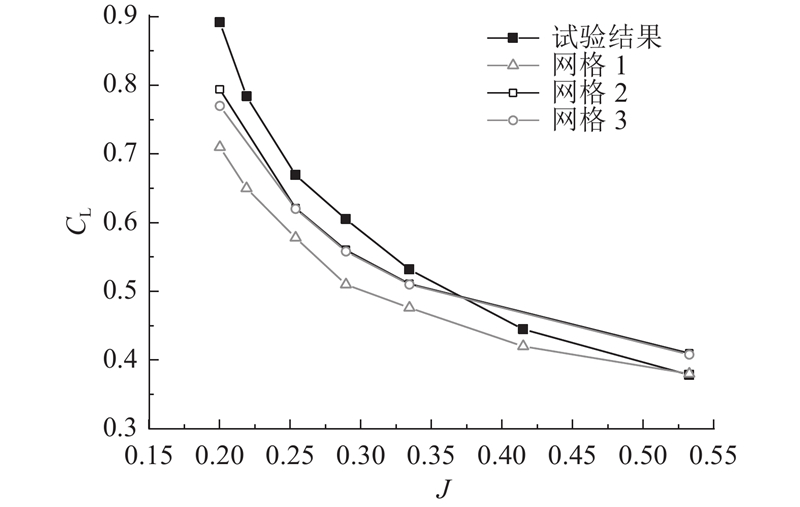
选取J=0.334的工况进行网格无关性对比验证,计算区域大小. 划分网格数量分别为5.14×105(网格1)、1.68×106(网格2)、2.00×106(网格3),计算得到0~0.2 s的机翼升力FL如图4所示. 初始化流场速度为0,前方来流流过整个计算域,这期间机翼升力系数逐渐增大,原因是随着被旋翼加速过的气流流过机翼,机翼升力逐渐增大. 机翼升力的变化趋势在不同网格情况下大体一致,证明了网格无关性. 由于网格1的网格数量较少,该网格计算得到的结果比其他2种网格的小;网格3与网格2的计算结果基本一致,网格数量增加结果变化不明显.
图 4
如图5所示为不同前进比时机翼升力系数CL的风洞试验结果与数值仿真结果对比,数值仿真结果和试验结果吻合较好. 风洞试验和数值仿真均发现: 随着前进比的增加,机翼升力系数降低; 且前进比越小,机翼升力系数减小越快. 证明本研究所提方法合理,适于倾转旋翼连续过渡状态气动特性数值模拟. 上述结果表明,网格数量越多,计算结果越接近试验值,但增大到一定数量后,计算结果改善不明显. 为了节约计算时间,提高计算效率,选取网格2 作为后续研究的网格.
图 5
图 5 仿真结果与试验结果的升力系数-前进比曲线
Fig.5 Lift coefficient-advance ratio curves of simulation results and test results
3. 连续过渡状态旋翼/机翼的气动性能
3.1. 旋翼转速对过渡状态气动性能的影响
为了研究旋翼转速对过渡状态的气动性能影响,设置旋翼/机翼系统前方来流速度为6 m/s,4个计算算例的旋翼转速n和前进比J如表1所示. 本研究的计算流场比较复杂,很难指定满足条件的固定时间步长,为此采用变时间步长,设置最大库郎数 maxCo=1,自动调整时间步. 由于前进比的数值不同,旋翼旋转速度不同,流场变化的剧烈程度也不同,不同前进比和不同来流速度工况下的计算时间步长略有不同,变化范围为2.5×10−6~6.5×10−6,每个虚拟时间步的最大迭代次数的均值为100.
表 1 算例的参数取值
Tab.1
| 算例 | n/(r·s−1) | J | 算例 | n/(r·s−1) | J | |
| 1 | 147.57 | 0.200 | 3 | 88.30 | 0.334 | |
| 2 | 116.33 | 0.254 | 4 | 55.43 | 0.533 |
机翼性能主要由机翼升力系数和机翼阻力系数CD体现,计算式[20]分别为
式中:FL为机翼所受升力;FD为机翼所受阻力;远场动压力
图 6
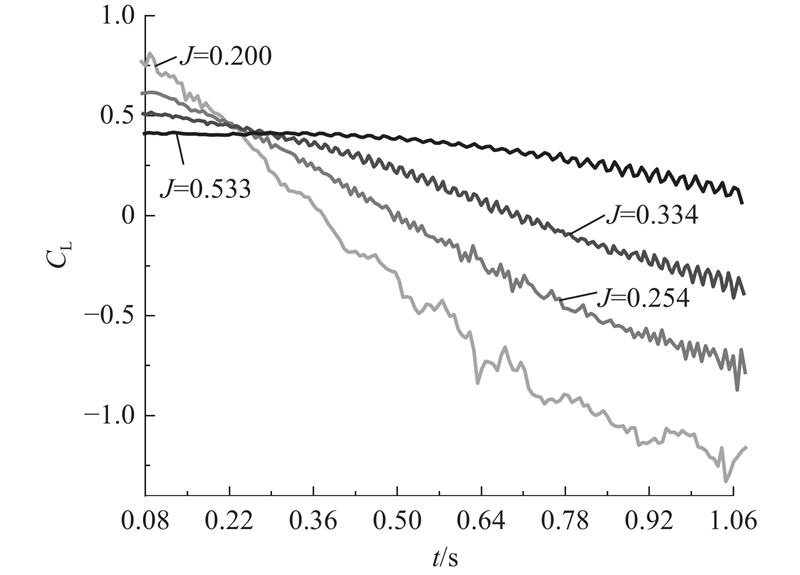
图 6 不同前进比的机翼升力系数-时间曲线
Fig.6 Wing lift coefficient-time curves for different advance ratios
图 7
图 7 yoz截面流场压力云图和流线图(J = 0.2, α=90°)
Fig.7 Pressure contour and streamline of flow field in yoz plane (J=0.2, α=90°)
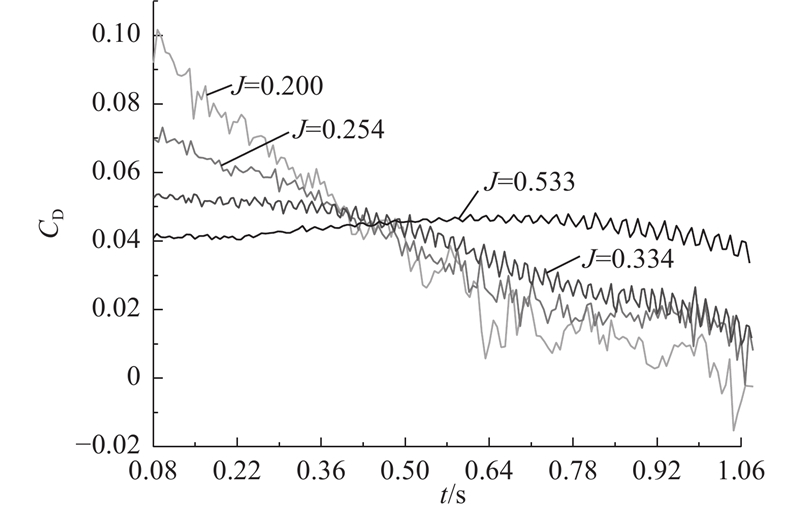
如图8所示为机翼的阻力系数随时间和前进比的变化趋势. 与机翼升力系数变化趋势大体一致,阻力系数随时间变化逐渐减小. 原因是旋翼倾转改变了气流方向,导致沿机翼弦向气流减少,阻力系数减小. 在J=0.2时旋翼倾转到85°后,机翼会产生负阻力,即会使机翼产生向前的力. 原因是此时接近于悬停状态,机翼自带攻角,旋翼产生向下的气流会使机翼有很小的前进的力. 同时,前进比越大,旋翼旋转对气流的作用减弱,阻力系数对倾转角的敏感程度越弱,振荡幅度越小. 和前进比对升力系数的影响相比,前进比对阻力系数的影响更大,最大转速对阻力系数的影响将近是最小转速的20倍,当倾转至24°~30°时,大转速对机翼阻力系数的影响情况开始从优势转变为劣势. 只从阻力系数方面来看,大转速对机翼气动性能是有利影响,但机翼的升力系数对总体性能的影响大于阻力系数,且倾转至悬停状态过程中前飞速度逐渐减小,实际上阻力系数的减小作用不大.
图 8
图 8 不同前进比的机翼阻力系数-时间曲线
Fig.8 Wing drag coefficient-time curves for different advance ratios
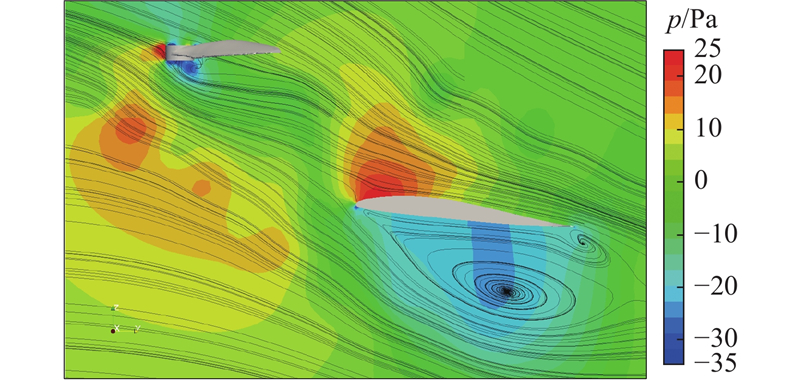
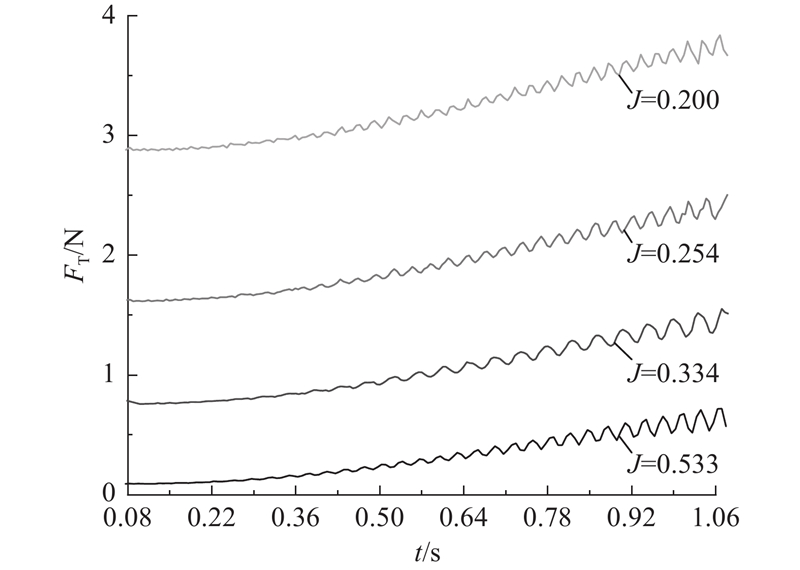
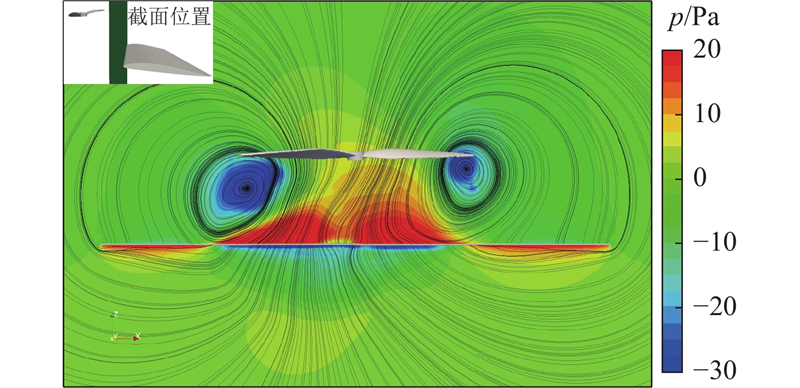
式中:FT为旋翼拉力. 前进比的变化时由转速控制,若采用拉力系数分析旋翼性能会出现2个变量,不够准确,因此分析旋翼拉力随时间和前进比的变化趋势. 如图9所示,随着倾转角的增大,旋翼拉力逐渐增大. 原因是从前飞状态过渡到悬停状态时旋翼的入流不断减少,有效攻角逐渐增加. 此外,尾迹下洗气流被机翼阻挡,使机翼与旋翼之间产生高压区(地面效应),如图10所示. 图中,高压区中间存在一小部分低压区,是气流流过旋翼的桨毂部分造成的. 旋翼拉力的数值随前进比的减小而增大,拉力从倾转开始至倾转结束的变化程度也随前进比的减小而增大,这是因为转速的增加增大了在给定的旋翼攻角下叶片截面所经历的攻角扰动. 拉力的振动幅度基本不随前进比变化,说明拉力的振动幅度与旋翼转速无关.
图 9
图 9 不同前进比的旋翼拉力-时间曲线
Fig.9 Rotor thrust-time curves for different advance ratios
图 10
图 10 旋翼与机翼之间的流场压力云图(J=0.2, α=90°)
Fig.10 Pressure contour of flow field between rotor and wing (J=0.2, α=90°)
在连续倾转过程中选取典型倾转角度绘制流场的Q涡量云图和压力云图. 如图11所示为不同前进比和不同倾转角下流场的涡量图(Q=0.1),随着前进比的减小,机翼下方的涡结构逐渐增多,且向下倾斜的角度逐渐增大,叶片的桨尖涡距离也逐渐减小. 小前进比的情况下机翼上下表面涡结构更多,证明此时旋翼滑流对机翼的影响更大,导致机翼升阻力系数对倾转角的更敏感,振荡幅度也更剧烈. J=0.533时悬停状态旋翼的滑流没有完全包裹住机翼的对应位置部分,因此此时机翼仍可以保持一定前飞状态的气动性能.
图 11
图 11 典型倾转角度和不同前进比下的流场Q涡量云图
Fig.11 Q-vortex structure of flow field at typical tilt angles with different advance ratios
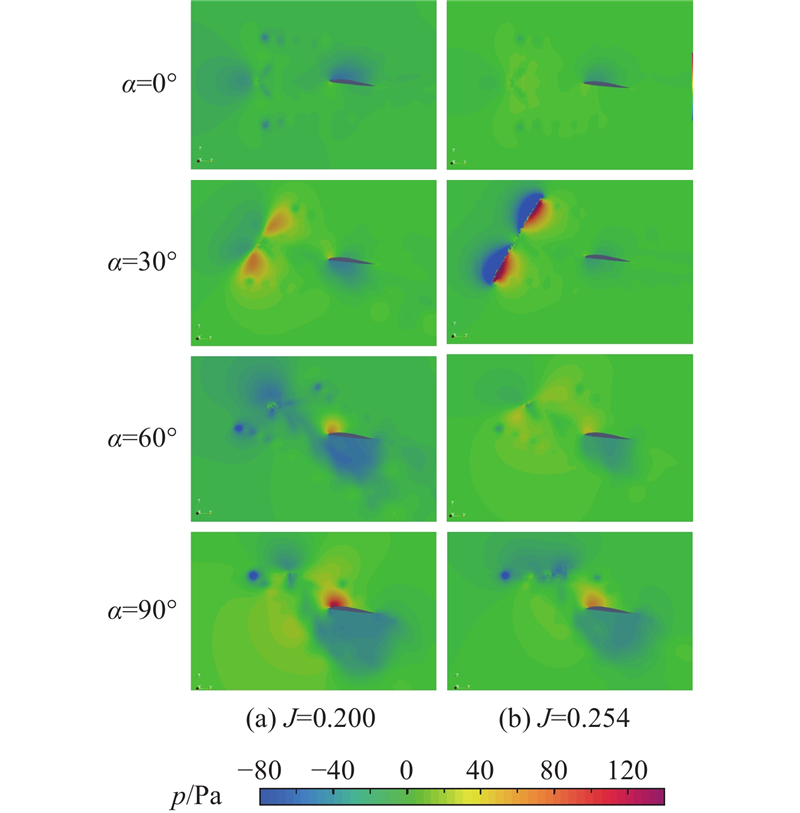
图 12
图 12 典型倾转角度和不同前进比下的流场压力云图
Fig.12 Pressure contour of flow field at typical tilt angles with different advance ratios
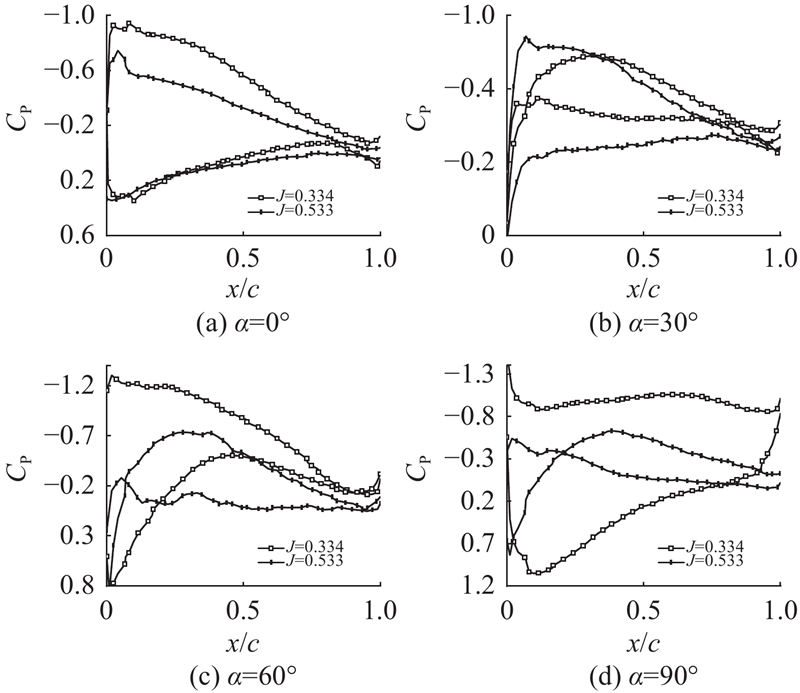
图 13
图 13 典型倾转角度和不同前进比下的机翼压力系数
Fig.13 Pressure coefficient of wing at typical tilt angles with different advance ratios
综上所述,在旋翼从前飞状态倾转至悬停状态过程中,机翼升力系数和阻力系数均减小,旋翼拉力增大. 随着前进比的减小(旋翼转速增大),升阻力系数对倾转角越敏感,当倾转至14°~19°时,大转速对于机翼气动性能的影响由从优势转变为劣势;前进比越小,拉力越大,对倾转角的敏感程度越强.
3.2. 侧风对过渡状态气动性能的影响
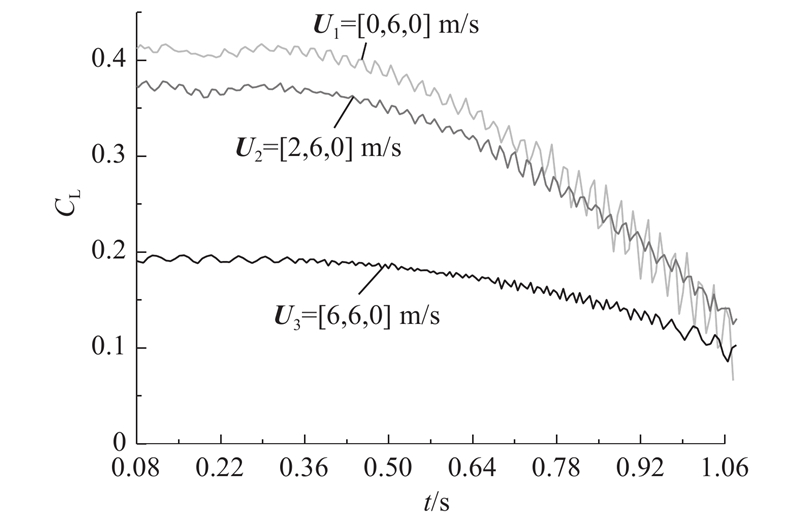
设置旋翼转速为55.43 r/s,在前方来流速度为6 m/s的基础上增加侧向来流,选取3种来流速度U计算,分别为U1=[0, 6, 0] m/s,U2=[2, 6, 0] m/s,U3=[6, 6, 0] m/s. 机翼的升力系数在不同侧风情况下随时间变化情况如图14所示. 旋翼从0.08 s时开始倾转,机翼升力系数随时间逐渐减小,当U2=[2, 6, 0] m/s时,机翼升力对倾转角的敏感程度小于没有侧风的情况,在旋翼倾转到65°左右后,机翼升力系数大于没有侧风的情况. 当侧向风速再增大时,机翼升力系数减小较多,对倾转角的敏感程度降低,原因是侧风风速较小相当于增加了来流速度;当侧风风速过大时,被旋翼加速过的气流不再流经机翼表面的部分较多,机翼上下表面压差减小明显. 当旋翼接近悬停状态时,3种情况机翼升力系数差别不明显,说明此时旋翼气流对机翼升力系数的影响不大,大部分尾迹下洗被机翼阻挡产生地面效应.
图 14
图 14 不同侧风速度的机翼升力系数-时间曲线
Fig.14 Wing lift coefficient-time curves for different crosswind velocities
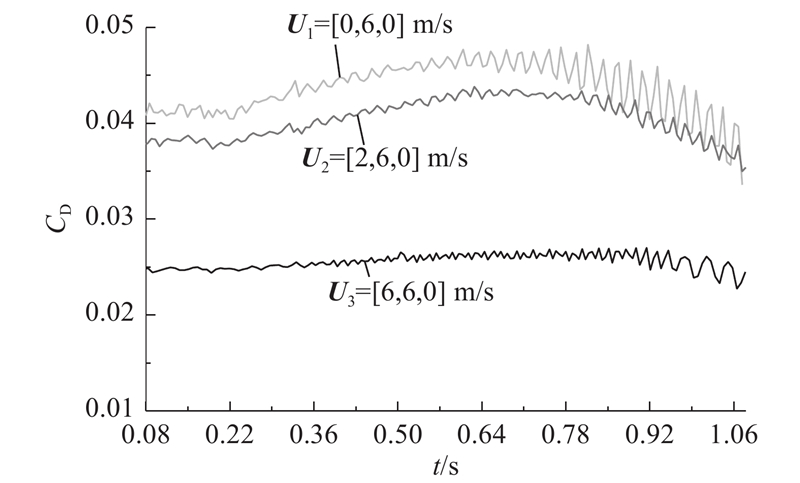
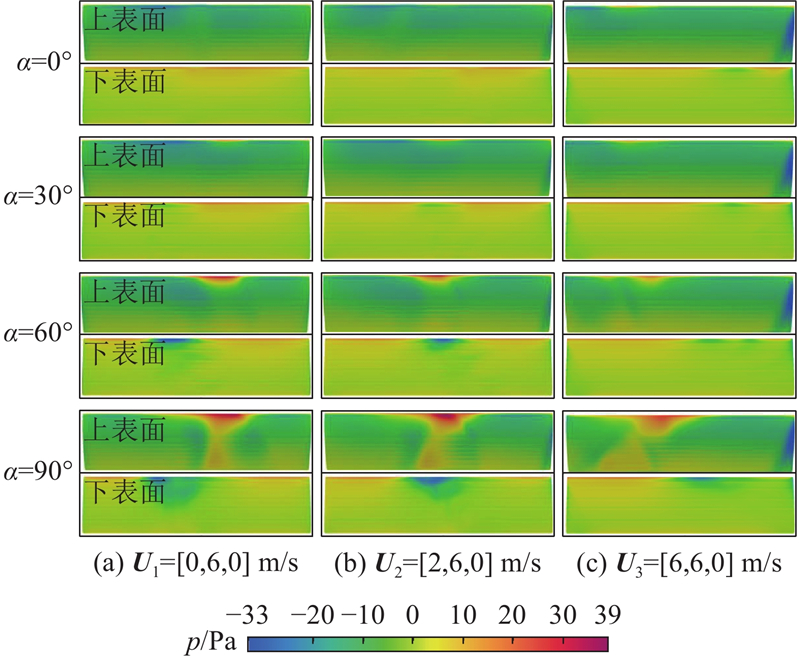
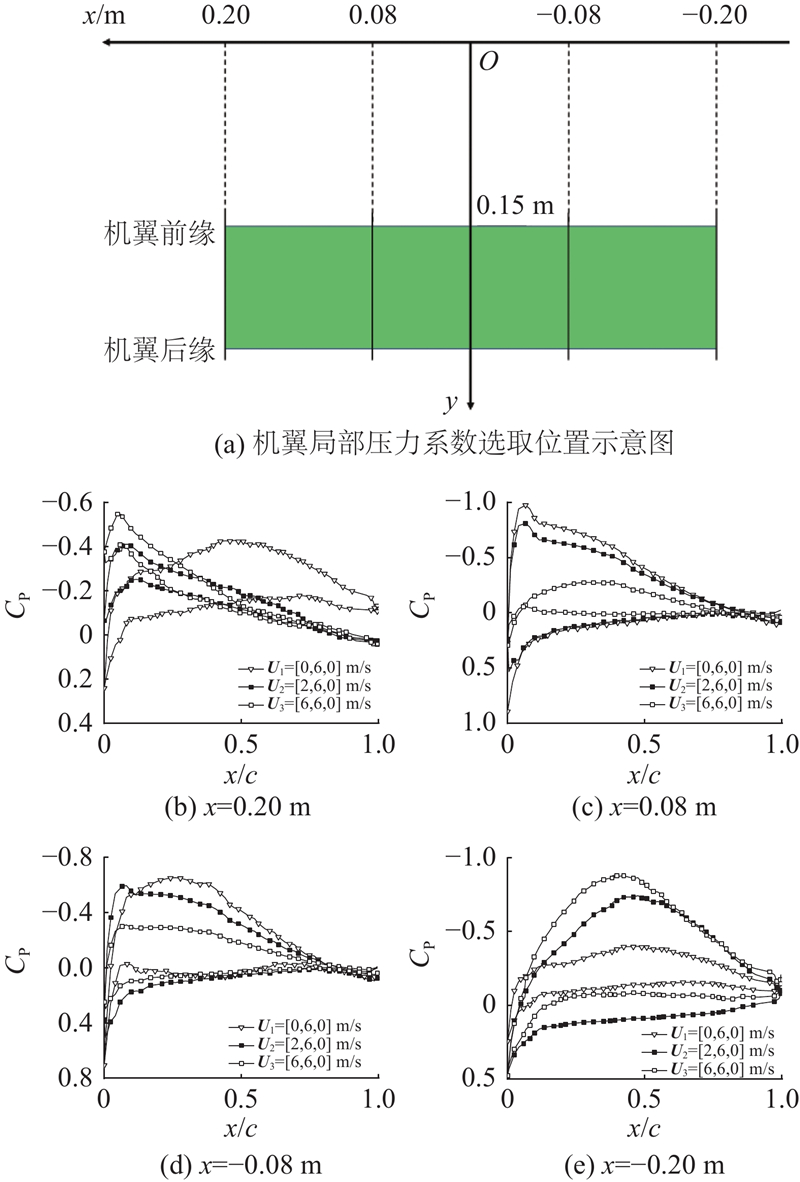
机翼阻力系数变化情况如图15所示. 前方来流或侧风较小时,机翼阻力系数先增大后减小;侧风风速较大时,倾转对阻力系数几乎无影响. 原因是大风速下旋翼滑流的方向改变,对机翼的影响范围缩小. 侧风风速越大,阻力系数越小,且风速大时机翼阻力系数减小是小侧风时的25%. 当U2=[2, 6, 0] m/s时,机翼的升阻力系数整体降低幅度较小,在旋翼倾转到65°后相对于无侧风情况,机翼升力系数增大,阻力系数减小,因此存在风速小的侧风时,倾转过程中机翼气动性能的下降可以改善. 如图16所示为不同倾转角和不同来流速度方向机翼上下表面的压力云图. 旋翼气流对机翼的影响受侧向来流影响向机翼一侧偏移,机翼所受压力分布发生变化:随Ux的增大,作用在机翼上表面的正压范围越大,尤其在机翼靠近后缘处;作用在机翼下表面的负压范围越小;下表面负压范围减小的比例小于上表面正压范围增大的比例,因此机翼升力会不同程度地减小. 由机翼升阻力系数曲线可以看出,在倾转角为30°左右时,不同工况的升阻力系数差别最大. 绘制α=30°时,机翼上下表面不同站位的压力系数分布曲线,如图17所示. 随Ux的增大,机翼上下表面压力系数差值整体呈减小趋势,证明了在小倾转角情况下,侧风使机翼升力减小. 不同风速机翼中段下表面压力系数基本保持一致,Ux增大主要影响机翼上表面的压力系数,由于侧风从机翼翼尖外侧吹来,Ux增大使机翼翼尖x=−0.2 m处主要受来流影响,机翼上下表面压力系数均差别较大,机翼翼根x=0.2 m处主要受旋翼尾迹影响.
图 15
图 15 不同侧风速度的机翼阻力系数-时间曲线
Fig.15 Wing drag coefficient-time curves for different crosswind velocities
图 16
图 16 典型倾转角度和不同来流速度方向下机翼上下表面的压力云图
Fig.16 Pressure contour on upper and lower surfaces of wing at typical tilt angles with different crosswind velocities
图 17
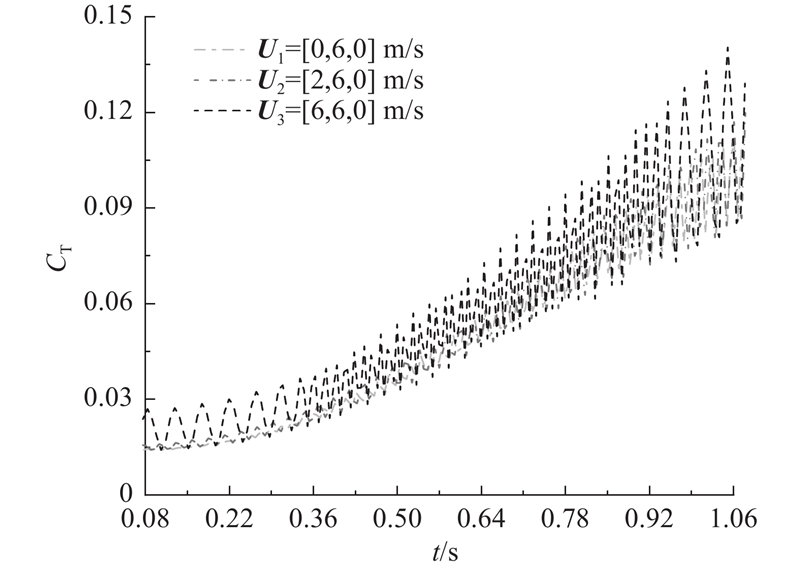
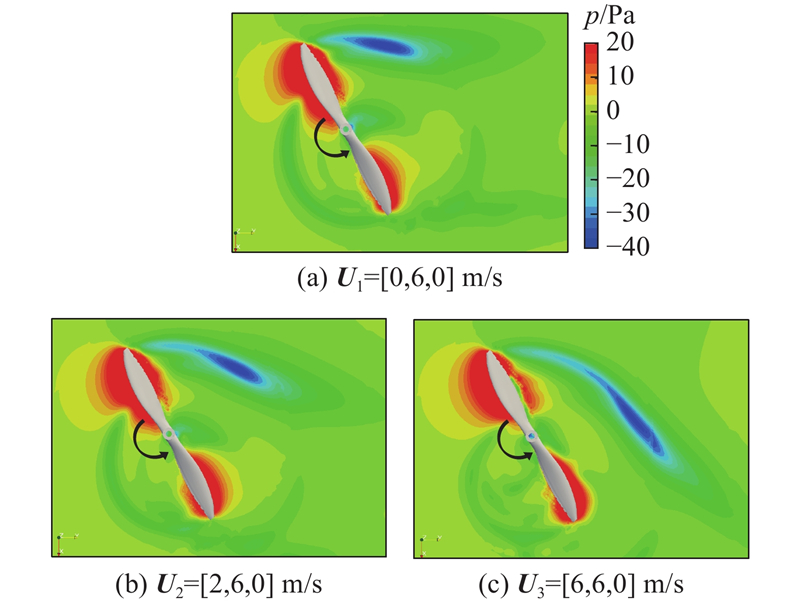
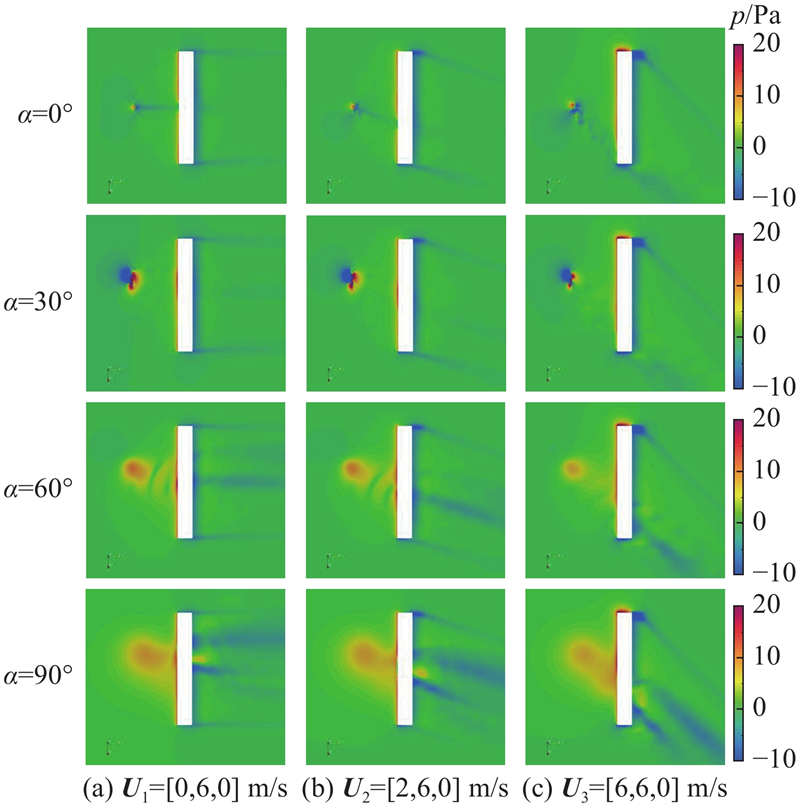
旋翼拉力系数随时间和侧风速度的变化趋势如图18所示. 旋翼拉力系数随时间逐渐增大,受侧风的影响不明显,拉力系数只略微提升,说明旋翼的拉力大小不受风速风向的影响. 当存在小侧风时,旋翼拉力系数振荡幅度增大较少,当风速增加后,振荡幅度增大较明显. 原因是大侧风风速加重了旋翼前、后行桨叶气流的不对称性. 悬停状态下拉力振荡幅度最大,绘制此时旋翼旋转平面的流场压力云图如图19所示. 旋翼尾迹受侧风影响,方向发生改变,且低压区范围变大,说明旋翼前后行桨叶气流愈加不对称,振荡幅度增大. 如图20所示为α=45°时流场的涡量图. 可以发现,存在侧风时,旋翼尾迹沿来流合速度方向发展,当U2=[2, 6, 0] m/s时,旋翼尾迹的影响范围发生变化,由于机翼弦长较短,影响范围变化不大,大部分影响变化在机翼尾迹处,此时机翼气动性能与无侧风情况区别较小. 当U2=[6, 6, 0] m/s时,气流主要作用在机翼翼根处而不流经机翼表面,证明此时旋翼的尾迹对机翼的影响范围较小,对机翼的气动性能影响较小,与无侧风情况的气动性能差别较大. 叶片桨尖涡的直径和间距变大,说明旋翼拉力振荡幅度增大. 截取xoy平面,不同来流速度不同倾转角下流场的压力云图如图21所示. 在侧风影响下,流场来流方向与机翼成一定夹角,受机翼的阻挡,在右侧翼尖旁形成高压区,反映了侧风改变旋翼的尾迹方向及其对机翼的影响范围,改变机翼尾流的压力分布情况,影响旋翼和机翼的气动性能. 由于机翼两边压力分布不均,侧风也会使机翼出现滚转的趋势.
图 18
图 18 不同侧风速度的旋翼拉力系数-时间曲线
Fig.18 Rotor thrust coefficient-time curves for different crosswind velocities
图 19
图 19 旋翼旋转平面的流场压力云图(α=90°)
Fig.19 Pressure contour of flow field in rotor rotation plane (α=90°)
图 20
图 20 不同侧风风速下的流场Q涡量云图(α=45°)
Fig.20 Q-vortex structure of flow field with different crosswind velocities (α=45°)
图 21
图 21 典型倾转角度和不同来流速度方向的流场压力云图
Fig.21 Pressure contour of flow field at typical tilt angles with different crosswind velocities
综上所述,来流速度方向会影响旋翼和机翼尾流的位置分布,使机翼出现滚转趋势. 在小风速时旋翼倾转到65°后,机翼性能相对于没有侧风情况的有所提升,随侧向风的再次增大,升阻力系数减小明显,旋翼的拉力系数变化不明显,但是振荡幅度会增大.
4. 结 语
本研究基于重叠网格提出适用于连续倾转过渡状态模拟的数值计算方法,分析前进比和侧风在旋翼倾转过程中对旋翼/机翼系统气动性能的影响,主要得出以下结论. 1)前进比减小(旋翼转速增大),机翼升力系数对倾转角的敏感程度增加,振荡幅度增大,阻力系数与升力系数变化情况一致,倾转角在14°~19°时,大转速对于机翼气动性能的影响开始从优势转变为劣势;旋翼拉力增大,对倾转角的敏感程度越强,但振荡幅度基本不变. 2)来流存在侧风情况时,机翼升阻力系数均有减小,但在侧风风速较小的情况下倾转角到65°后,升力系数高于没有侧风的情况,机翼性能有一定提升;旋翼的拉力系数变化不明显,但是振荡幅度会增大;侧向风还会影响机翼的滚转趋势和旋翼机翼尾流的位置分布.
本研究分析了前进比和存在侧风对连续倾转过渡状态中旋翼/机翼系统气动性能的影响,单独提取旋翼和机翼作为研究对象,在实际倾转过程中,还有其他影响因素,旋翼对倾转旋翼机的其他部件以及部件之间也存在着相互干扰. 后续研究计划在重叠网格的数值计算方法基础上,继续对其他气动影响因素和部件间的干扰进行分析,为倾转旋翼机的研制提供数据支持.
参考文献
倾转旋翼机的发展与关键技术综述
[J].
A review on development and key technolo-gies of tiltrotor
[J].
飞机垂直/短距起降技术的研究
[J].
Study on V/STOL technology of aircraft
[J].
倾转旋翼机流动机理及气动干扰特性试验
[J].
Experiment on flow mechanism and aerodynamic interaction characteristics of tilt-rotor aircraft
[J].
倾转旋翼/机翼耦合系统过渡状态气弹动力学试验研究
[J].
Experiment on aeroelastic characteristics of tiltrotor aircraft in transition flight
[J].
Aerodynamic characteristics of a low aspect ratio wing and propeller interaction for a tilt-body MAV
[J].DOI:10.1260/1756-8293.5.4.245 [本文引用: 1]
倾转过渡状态旋翼-机翼气动干扰特性
[J].
Rotor-wing aerodynamic interference characteristics in conversion mode
[J].
过渡状态倾转旋翼气动力模拟的高效CFD方法
[J].
Highly-efficient CFD method for predicting aerodynamic force of tiltrotor in conversion mode
[J].
Numerical simulations on the ERICA tiltrotor
[J].DOI:10.1016/j.ast.2017.01.023 [本文引用: 1]
倾转旋翼-机翼气动干扰准定常多重参考系仿真和风洞试验
[J].
Qusi-steady multiple reference frame simulation and wind tunnel test for the aerodynamic interference between tilt-rotors and wings
[J].
倾转旋翼机连续倾转过渡状态数值模拟
[J].
Numerical simulation of continuous tilting transition of tiltrotor aircraft
[J].
侧风作用下无人机旋翼悬停状态气动响应分析
[J].
Aerodynamic response analysis of unmanned aerial vehicle rotor hovering under crosswind influence
[J].
前飞来流和侧风对植保无人机下洗流场影响的数值模拟研究
[J].
Numerical simulation of the effects incoming flow and crosswinds on airflow field of plant protection UAV
[J].
基于滑移网格的倾转旋翼机全机干扰流场研究
[J].
Research on the whole aircraft interference flow field of tilt-rotor aircraft based on sliding grid
[J].
The numerical com-putation of turbulent flows
[J].DOI:10.1016/0045-7825(74)90029-2 [本文引用: 1]
Wingtip-mounted propellers aerodynamic analysis of interaction affects and comparison with conventional layout
[J].DOI:10.2514/1.C034978 [本文引用: 3]