随着家用电器的广泛使用，住宅家庭能源消耗大幅增加. 在家庭能源管理系统中部署分布式可再生能源收集装置，为家庭用电高额能耗问题提供了重要的解决方案^[1-2]. 在电网消纳能源能力有限的情况下，可再生能源随机、海量和多样化地接入电网，给电网的安全和发、输电环节带来挑战^[3-5]. 如何有效实现分布式能源并网、保证供电可靠性成为当前亟须解决的难题^[6]. 需求响应因对提高电网系统的稳定性和实现可再生能源消纳有很大帮助而备受关注^[7-8]. 价格型需求响应作为需求响应方式之一，主要通过电价变化来引导用户改变用电行为^[9]. 时变电价作为价格型需求响应的重要研究方向之一，能够通过电价变化实时给予用户经济信号，引导用户改变用电行为以削减用电费用^[10].

基于价格型需求响应，研究者在家庭用电负荷优化调度方面取得了一些成果. 史林军等^[11]提出的能源管理模型可以对各负荷进行规划与调度，使电器按照制定的计划有序运行. 张彦等^[12]提出混合整数二次规划模型，并应用模型预测控制方法来实现该能源局域网的在线能源管理. 赵冬梅等^[13]针对弹性负荷响应的不确定性构建价格型需求响应的响应量模型. El Rahi等^[14]构造了需求和价格不确定的能源交易模型. 贾雁冰等^[15]制定时变电价引导下的家庭负荷优化策略，并采用情景分析法处理不同家庭用电需求预测的不确定性. 上述研究虽在一定程度上调度了家庭用电负荷，但大多依赖预测未来电价变化和用户用电需求，没有考虑负荷不确定性情况. 研究者为此提出的解决方法包括线性规划法、深度强化学习算法、粒子群算法、李雅普诺夫优化算法等. Deng等^[16]使用线性规划法求解基于耗电量和用户舒适度的多目标优化模型，但该方法只能规划约束线性的问题，且对数据的准确性要求较高. 为了解决负荷不确定性问题，徐弘升等^[17]提出基于深度强化学习的动态能量调度方法，但该方法过度依赖环境，易出现陷入局部最优的状况. 为了解决用户日负荷需求响应调度问题，陆俊等^[18]提出混合粒子群优化算法，但传统的粒子群算法在进行大规模数据运算时速度较慢. 李雅普诺夫优化理论不但具有较快的收敛速度和较好的稳定性，而且不需要先验统计信息^[19]，在电力系统领域被广泛应用. Guo等^[20-21]提出的时变电价下的动态负荷优化策略没有考虑和智能电网的双向贸易. 刘迪迪等^[22]在优化负荷时没有考虑可容忍时延. Qiao等^[23]考虑将剩余的可再生能源存储到储能设备中，在电价高时放电使用，但用户购买的能量只能用于满足自身的负荷需求，不能充电存入储能设备，导致用户的收益能力降低. 范斌涛等^[24]以能源交易和负荷调度为优化目标进行模型研究，但所研究模型的需求响应只到用户层面，没有考虑各电器的实际需求和时延，不能对电器进行针对性的能量分配，可能导致将能量分配给等待时延较小的电器，不利于提高用户的经济性.

本研究针对家庭用电负荷基于李雅普诺夫优化理论提出高效的智能电器能量分配算法，将智能电器作为可调负载，在时变电价引导下，对其使用进行合理地调度和管理. 1）考虑家庭设备层面上的用电负荷响应及调度优化问题，建立典型的家庭用电设备模型. 2）基于李雅普诺夫优化理论提出时变电价下的家庭用户多电器能量分配算法，该算法不需要任何先验统计知识，能够充分考虑到居民响应行为的不确定性. 3）针对不同电器的使用需求和可容忍时延差异，将各电器总积压队列划分为多个能量需求积压队列，针对性地对电器进行能量分配以提高用户收益. 4）通过与不同的算法和模型对比，验证所提算法在经济性和等待时延上的优势.

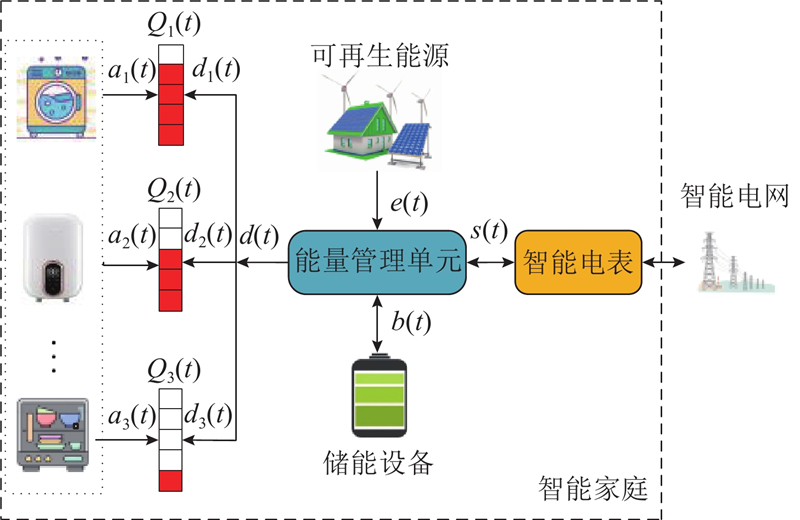
如图1所示为家庭智能用电管理系统模型，其中能源供给侧包括智能电网、可再生能源和储能设备. 3种能源供给侧之间的能量可以通过能量管理单元实现双向流动，智能电网的电能和多余的可再生能源可以存储到储能设备中，由智能电表获取外部时变电价，在电价较高时将可再生能源和储能设备的电能反馈给电网来实现降本增效. 能量管理单元是整个家庭用电结构的控制核心，它可以根据当前能源供给侧的实时情况，决定用户是否从智能电网买/卖能量和是否对储能设备进行充/放电，并确定给各智能电器分配的能量，以实现用户收益最大化.

根据家庭用电负荷是否具有可转移属性，将能量需求分为弹性和非弹性2个类别. 弹性能量需求是指用户允许需求的能量有一定的时延，从而将该类负荷的工作时间段转移到电价较低的时间段以降低用户的用电成本；非弹性能量需求是指用户的能量需求须即时满足（无时延），在本研究中，该类负荷不参与能量调控分配.

家庭用户的智能电器使用差异性，导致各智能电器能量需求的时延限制不尽相同，因此对不同的智能电器使用不同的需求队列. 对于包含G个简单实际队列的系统，每个队列都对应一个延迟时间${T_g}$，$g \in (1,2,\cdots,G)$. 各智能电器g在时隙t的能量需求${a_g}(t)$被存储在各自的能量需求队列中，每个队列的能量需求都以先入先出为基础得到服务. 智能电器的能量需求队列更新公式为

(1)$ {Q_g}(t+1) = \max \;[{Q_g}(t) - {d_g}(t),0]+{a_g}(t). $

式中：${d_g}(t)$为t时分配给智能电器的能量，${Q_g}(t)$为智能电器t时的能量需求积压.

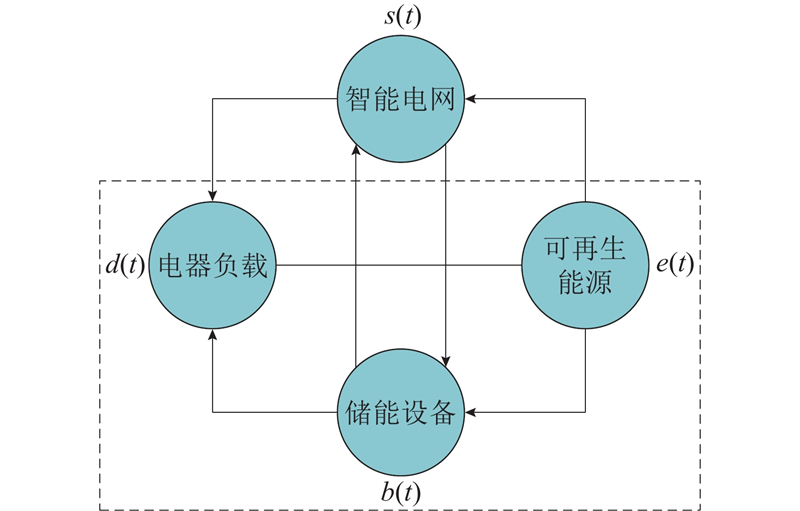
家庭能源管理系统控制能量在电器负载、智能电网、可再生能源、储能设备间流动，如图2所示. 在家庭用户智能用电管理系统中，将可再生能源作为优先供电能源. 当t时收集的可再生能源$e(t)$小于能量管理单元在t时分配给所有智能电器的总能量$d(t) = \sum\nolimits_{g = 1}^G {{d_g}(t)} $时，即当可再生能源不足以满足用户能量需求时，用户可以根据实时电价$p(t)$选择从智能电网购电或利用储能设备放电来满足需求；当$e(t) > d(t)$时，即当可再生能源在满足用户能量需求后还有富余时，用户可以根据$p(t)$选择将过剩的能量存入储能设备或卖给智能电网. 若t时从智能电网买卖的能量$s(t) > 0$，则从电网购买能量；反之，则表示能量被出售. 同样地，若t时储能设备的充/放电量$b(t) > 0$，则表示储能设备放电；反之，则表示储能设备充电. 智能用电管理系统实际上就是对这些能量流动进行调整分配，以实现用户收益最大化. 由能量流动供需平衡，可以得到

(2)$ d(t) = e(t)+s(t)+b(t). $

从实际的角度来看，储能设备的充放电速率受到硬件电路的限制. 储能设备的相关公式如下：

(3)$ B(t+1) = B(t) - b(t)\text{，} $

(4)$ {B_{\min }} \leqslant B(t) \leqslant {B_{\max }}\text{，} $

(5)$ \left| {b(t)} \right| \leqslant {b_{\max }}\text{，} $

(6)$ b(t) < B(t). $

式中：$B(t)$为t时储能设备的电量，${B_{\max }}$为储能设备的最大容量，${B_{\min }}$为储能设备的最低电量下限，${b_{\max }}$为储能设备的最大充/放电速率. 式(3)为储能设备的更新方程式；设置式(4)是为了保证储能设备的电量始终在合理水平，防止储能设备放电深度过大而导致寿命减少，即当$B(t) < {B_{\min }}$时储能设备处于电量枯竭状态，此时储能设备不能再进行放电；式(6)表示储能设备的放电量应小于当前储能设备所剩电量.

进行以下假设，以确保$e(t)$，$a(t)$，$p(t)$有界：

(7)$ 0 \leqslant e(t) \leqslant {e_{\max }},\;0 \leqslant a(t) \leqslant {a_{\max }},\;0 \leqslant p(t) \leqslant {p_{\max }}. $

式中：${e_{\max }}$为可再生能源收集的最大值，${a_{\max }}$为能量需求最大值，${p_{\max }}$为电价的最大值. 进一步假设分配给智能电器的能量最大值${d_{\max }} > {a_{\max }}$，使得需求队列始终稳定. 考虑到能源供应商的收益和部分能量在传输过程中会损失，用户的售电价应低于购电价，设置常数$\;\beta $∈（0, 1.0），当用户从智能电网获取能量时，花费成本：

(8)$ \begin{split} & p(t){(s(t))^+} = p(t){(d(t) - e(t) - b(t))^+}\text{，} \\& {(x)^+}^{\underline{\underline{\rm{\;def\;}}}} \max \;\{ x,0\} .\end{split}$

当用户卖给电网能量时，产生收益：

(9)$ \begin{split} & \beta p(t){(s(t))^ - } = \beta p(t){(d(t) - e(t) - b(t))^ - }, \\&{(x)^ - }^{\underline{\underline{\rm{\;def\;}}}} \max\; \{ - x,0\} .\end{split} $

问题1：用户的平均时间收益最大化，表达式为

(10)$ \begin{split} \mathop {\max }\limits_{{d_g}(t),b(t)} :&\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T {E[\beta p(t){{(d(t) - e(t) - b(t))}^ - }}- \\& p(t){(d(t) - e(t) - b(t))^+}]. \end{split} $

　　　s.t. 式(2)~式(6),

(11)$ \overline {{Q_g}} < \infty , $

(12)$ 0 \leqslant d(t) \leqslant {d_{\max }}, $

(13)$ \overline {Q_{_g}^{'}(t )+{a_g}(t ) - {d_g}(t )} \leqslant 0. $

式中：${Q_g}$的平均值$\overline {{Q_g}} ^{\underline{\underline{\;{\mathrm{def}}\;}}} \mathop {\lim }\limits_{t \to \infty } \sup {t^{-1}}\displaystyle\sum\nolimits_{\tau = 0}^{t - 1} {E\{ {Q_g}(t )\} } $，$Q_{_g}^{'}(t ) = {{{Q_g}(t )}}/{{{T_g}}}$. 设置式(11)是为了保证所有队列均稳定，将式(13)改为

(14)$ \overline {{Q_g}(t )} \leqslant {T_g} \cdot \;\overline {{d_g}(t ) - {a_g}(t )} . $

其中$\overline {{Q_g}(t )} $为队列的平均大小，$\overline {{d_g}(t ) - {a_g}(t )} $为队列大小的平均减少率，因此式(13)对平均服务延迟时间施加了限制. 式(10)是针对家用电器需求调度问题的松弛目标函数. 若每个电器不存在单独的时延约束，则通过求解式(2)~式(6)和式(11)~式(13)可以得到函数的最大收益值. 求解式(10)只反映极端的目标（最大化用户的收益），不包括每个电器的时延约束，也没有考虑到用户的舒适性，因此须进行公式完善.

为了让用户等待电力服务的最大时延不超过可容忍的范围，引入虚拟队列使得式(14)成立. 虚拟队列${Z_g}(t)$的队列更新方程为

(15)$ {Z_g}(t+1) = \max \;[{Z_g}(t) - {d_g}(t)+{\varepsilon _g}{1_{{Q_g}(t) > 0}},0]. $

相比式(1)， ${Z_g}(t)$与真实队列${Q_g}(t)$具有相同的服务速率${d_g}(t)$，区别在于能量到达的过程. 其中${1_{{Q_g}(t) > 0}}$为指示变量，当${Q_g}(t) > 0$时其值为1，否则其值为0；${\varepsilon _g}$为常数，作用是调整虚拟队列的增长率，防止${Q_g}(t)$长时间未得到服务. ${T_g}(t)$为电器g在t时的时延，给定${Q_g}(t)$和${Z_g}(t)$有限上界，就可以保证${Q_g}(t)$中任意时隙能量需求都有有限的最大时延${T_{g,\max }}$，如引理1所示.

引理1　保证${Q_g}(t)$和${Z_g}(t)$均有限上界，即${Q_g}(t) < {Q_{g,\max }}$，${Z_g}(t) < {Z_{g,\max }}$，则

(16)$ {T_{g,\max }} ^{\underline{\underline{\;{\mathrm{def}}\;}}} \frac{{{Q_{g,\max }}+{Z_{g,\max }}}}{{{\varepsilon _g}}}. $

在利用李亚普诺夫优化理论求解问题1之前，为了满足储能设备的约束条件式(4)，定义队列$X(t)$的表达式为

(17)$ X(t) = B(t) - V{p_{\max }} - {b_{\max }}. $

其中V为控制参数，由式(3)得到$X(t)$的更新方程为

(18)$ X(t+1) = X(t) - b(t). $

本研究算法基于李雅普诺夫优化方法提出，其优点是在$(p(t),e(t),a(t))$的概率分布未知的情况下，使式(10)得到渐进最优值. 矢量${\boldsymbol{\theta}} (t)^{\underline{\underline{\rm{\;def\;}}}} [ Q(t), Z(t),X(t) ]$，将李雅普诺夫函数定义如下:

(19)$ L({\boldsymbol{\theta}} (t)) ^{\underline{\underline{\;{\mathrm{def}}\;}}} \frac{1}{2}\left[\sum\limits_{g = 1}^G {Q_g^2(t)+} \sum\limits_{g = 1}^G {Z_g^2(t)+{X^2}(t)} \right]. $

时隙t的李雅普诺夫漂移函数为

(20)$ \Delta L({\boldsymbol{\theta }}(t)) ^{\underline{\underline{\;{\mathrm{def}}\;}}} E\{ L({\boldsymbol{\theta}} (t+1)) - L({\boldsymbol{\theta}} (t))|{\boldsymbol{\theta}} (t)\} . $

优化目标是最大化式(10)，应取负值作为李雅普诺夫惩罚部分. 问题1的求解转化为问题2：最小化每个时隙的漂移加惩罚函数，表达式为

(21)$ \begin{split} \mathop {\min }\limits_{{d_g}(t),b(t)} :&\Delta ({\boldsymbol{\theta}} (t)) - V \cdot E[\beta p(t){(d(t) - e(t) - b(t))^ - } - \\& p(t){(d(t) - e(t) - b(t))^+}\left| {{\boldsymbol{\theta}} (t)} \right.] .\end{split} $

　　　s.t. 式（2）~式（8），

(22)$ \overline {{Q_g}} < \infty ,\;\overline {{Z_g}} < \infty . $

$\Delta ({\boldsymbol{\theta}} (t))$表示队列积压情况，剩余项表示用户的收益情况，权衡参数V用来平衡用户的收益和队列积压大小之间的关系. 若只最小化前者，则队列积压小，用户收益会减少；若只最小化后者，则可实现用户收益最大化，但可能无法保证电器的能量需求在可容忍时延内得到满足. 因此须最小化两者的加权和. 求得漂移加惩罚函数上界，如引理2所示.

引理2　对时隙t，漂移加惩罚函数满足

(23)$ \begin{split}& \Delta ({\boldsymbol{\theta}} (t)) - V \cdot E[\beta p(t){(d(t) - e(t) - b(t))^ - } - \\& \;\;\;\;p(t){(d(t) - e(t) - b(t))^+}\left| {{\boldsymbol{\theta}} (t)} \right.] \leqslant \\& \;\;\;\; S+[X(t)+Vp(t)]E\{ {(d(t) - e(t) - b(t))^+}\left| {{\boldsymbol{\theta}} (t)} \right.\} - \\& \;\;\;\;[X(t)+V\beta p(t)]E\{ {(d(t) - e(t) - b(t))^ - }\left| {{\boldsymbol{\theta}} (t)} \right.\} \; - \\& \;\;\;\;\left[\sum\limits_{g = 1}^G {(X(t)+{Q_g}(t)+{Z_g}(t)} )\right]E\{ {d_g}(t)|{\boldsymbol{\theta}} (t)\}+ \\& \;\;\;\;X(t)E\{ e(t)|{\boldsymbol{\theta}} (t)\} .\end{split} $

(24)$ \begin{split} S =&\sum\limits_{g = 1}^G \left[{{0.5(d_{g,\max }^2+a_{g,\max }^2)}}+{{0.5\max (\varepsilon _g^2,d_{g,\max }^2)}}\right.+ \; \\& \left.{Q_{g,\max }}{a_{g,\max }}+{Z_{g,\max }}{\varepsilon _g}\right]\;+0.5b_{\max }^2. \\[-1pt]\end{split} $

最小化每个时隙的漂移加惩罚函数等价于式(23)的右侧，除去式中的无关项：决策变量${d_g}(t)$、$b(t)$，问题2的求解可以转化为问题3，表达式为

(25)$ \begin{split} \mathop {\min }\limits_{{d_g}(t),b(t)} :\;\;&[X(t)+Vp(t)]{(d(t) - e(t) - b(t))^+}- \\& [X(t)+V\beta p(t)]{(d(t) - e(t) - b(t))^ - }- \\& \sum\limits_{g = 1}^G {(X(t)+{Q_g}(t)+{Z_g}(t)} ){d_g}(t) .\end{split} $

所提算法是比较$ X(t)+Vp(t) $、$ X(t)+ V\beta p(t) $、$ X(t)+ {Q_g}(t)+ {Z_g}(t) $在每个时隙的大小关系，并根据权重做出决策，在不同的情况下，给不同的电器分配不同的能量，使目标式子整体最小化. 1）$ \forall g\;\;{Q_g}(t)+ {Z_g}(t) - Vp(t) > 0 $，表明队列积压量很高或电价很低，须将最大可能的能量分配给$ {d_g}(t) $，即如果可再生能源或者储能设备能量不够，用户要从外部电网购买能量. 2）$ \forall g\;\;V\beta p(t) \leqslant {Q_g}(t)+ {Z_g}(t) \leqslant Vp(t) $，表明队列积压量适中，只使用可再生能源，根据队列顺序分配可用的可再生能源（这里的队列顺序是针对不同的队列g）对系数$ X(t)+{Q_g}(t)+{Z_g}(t) $依大小进行排序，再从大到小分配能量. 从数学角度分析式(25)，当系数$ X(t)+{Q_g}(t)+$$ {Z_g}(t) $越大时，$ {d_g}(t) $越大，可使目标式整体最小化. 详细决策如下.

当$ \forall g\;\;X(t) + {Q_g}(t) + {Z_g}(t) \geqslant 0 $ 时，1)若 $ X(t) + V\beta p(t) \geqslant 0 $，则由式(17)可以得到$ B(t) - {b_{\max }} \geqslant V{p_{\max }} - V\beta p(t) $，表示储能设备中有大量的电量或智能电网的电价很高，将最大可能的放电率分配给$b(t)$，即$ b(t) = {b_{\max }} $. 能量分配：若$ \forall g\;\;{Q_g}(t)+{Z_g}(t) > Vp(t) $，表明$ {Q_g}(t) $积压量很高，将最大可能的能量分配给$ {d_g}(t) $，即$ {d_g}(t) = \min\; ({Q_g}(t),{d_{\max }}) $；若$ \forall g\;\;V\beta p(t) \,\leqslant\, {Q_g}(t)\,+\,$$ {Z_g}(t) \leqslant Vp(t) $，表明$ {Q_g}(t) $积压量适中，根据队列顺序分配可用的可再生能源，即$ {d_g}(t) = \min\; ({Q_g}(t),{e_g}(t)) $；若$ \forall g\;\;{Q_g}(t)+ {Z_g}(t) \leqslant $$ V\beta p(t) $，表明$ {Q_g}(t) $积压量很小，此时$ {d_g}(t) = 0 $. 2)若$ X(t)+Vp(t) \leqslant 0 $，则$ B(t) - {b_{\max }} \leqslant V{p_{\max }} $$ - V\beta p(t) $，表示储能设备中电量很少或智能电网的电价很低，将最大可能的充电率分配给$b(t)$，即$ b(t) = - \min \; ({b_{\max }}, {B_{\max }} - B(t)) $，因为$ \forall g\;\;X(t)+$$ {Q_g}(t) + {Z_g}(t) \geqslant 0 $、$ X(t) + Vp(t) \leqslant 0 $，所以 $ \forall g\;\;{Q_g}(t)+ {Z_g}(t) \geqslant Vp(t) $，此时的队列积压也很高，要将最大可能的能量分配给$ {Q_g}(t) $，即$ {d_g}(t) \,=\, \min \;({Q_g}(t),{d_{\max }}) $. 3)若$ \;X(t)\,+\,V\beta p(t) < 0 < X(t) + Vp(t) $，则$ V{p_{\max }} \,-\, Vp(t) \,<\, B(t) \,-\,{b_{\max }} \,<\, V{p_{\max }} \,- V\beta p(t) $，表示储能设备的电量适中且智能电网的电价中等. 能量分配：若$ \forall g\;\; {Q_g}(t)+ {Z_g}(t) > Vp(t) $，表明此$ {Q_g}(t) $积压量很高，要将最大可能的能量分配给$ {d_g}(t) $，$ {d_g}(t) = \min \;({Q_g}(t),{d_{\max }})， $ $ b(t) = \min\; ({b_{\max }},\min\; ( $$ {B_{\max }} - B(t), d(t) - e(t))) $；若 $ \forall g\;\; V \beta p(t) \leqslant {Q_g}(t)+$$ {Z_g}(t) \leqslant Vp(t) $，表明$ {Q_g}(t) $积压量适中，根据队列顺序分配可用的可再生能源，即$ {d_g}(t) = \min \;({Q_g}(t),{e_g}(t)) $，$ b(t) = 0 $.

当$ \forall g\;\;X(t) + {Q_g}(t) + {Z_g}(t) < 0 $时，1)若$ X(t)+Vp(t) \leqslant 0 $，则$ B(t) - {b_{\max }} \leqslant V{p_{\max }} $$ - V\beta p(t) $，表示储能设备中电量很少或者智能电网的电价很低，将最大可能的充电率分配给$ b(t) $，即$ b(t) = - \min\; ({b_{\max }},{B_{\max }} - B(t)) $. 能量分配：若$\forall g\;\;V\beta p(t) \leqslant {Q_g}(t)+{Z_g}(t) \leqslant Vp(t)$，表明$ {Q_g}(t) $积压量适中，根据队列顺序分配可用的可再生能源，即$ {d_g}(t) = \min\; ({Q_g}(t),{e_g}(t)) $；若$ \forall g\;\;{Q_g}(t)+$$ {Z_g}(t) \leqslant V\beta p(t) $，表明$ {Q_g}(t) $积压量很小， $ {d_g}(t) = 0 $. 2)若$ X(t)+ V\beta p(t) \geqslant 0 $，则$ B(t) - {b_{\max }} \geqslant V{p_{\max }} $$ - V\beta p(t) $且$ \forall g\;\; {Q_g}(t)+ {Z_g}(t) \leqslant V\beta p(t) $，表示储能设备中有大量的电量或智能电网的电价很高，且队列积压也很低，因此$ b(t) = {b_{\max }} $，$ {d_g}(t) = 0 $. 3)若$ X(t)+V\beta p(t) < 0 < X(t)+Vp(t) $，则 $ V{p_{\max }} \,-\, Vp(t) < B(t) \,-\, {b_{\max }} < V{p_{\max }} - V\beta p(t) $，表示储能设备电量适中且智能电网电价中等. 能量分配：若$ \forall g\;\;V\beta p(t) \leqslant {Q_g}(t)+{Z_g}(t) \leqslant Vp(t) $，表明$ {Q_g}(t) $积压量适中，根据队列顺序分配可用的可再生能源，即$ {d_g}(t) = \min\; ({Q_g}(t),{e_g}(t)) $，$ b(t) = 0 $；若$ \forall g\;\;{Q_g}(t)+{Z_g}(t) \leqslant V\beta p(t) $，表明$ {Q_g}(t) $积压量很小，$ {d_g}(t) = 0 $，$ b(t) = 0 $.

定理1　假设$ {d_{g,\max }} > {a_{g,\max }},{Q_g}(0) = 0, {Z_g}(t) = 0, g \in \{ 1,\cdots,G\} $，$ t \in $$ \{ 0, \cdots, T - 1\} $，且对于任意参数V满足$ 0 \leqslant V \leqslant {V_{\max }} $，

(26)$ {V_{\max }} = \frac{{{B_{\max }} - 2{b_{\max }}}}{{{p_{\max }} - {p_{\min }}}} . $

算法对每个队列g具有以下性质.

性质1　在所有时隙t，队列$ {Q_g}(t) $,$ {Z_g}(t) $都有上界：

(27)$ {Q_g}(t) \leqslant V{p_{\max }}+{a_{g,\max }} \text{，} $

(28)$ {Z_g}(t) \leqslant V{p_{\max }}+{\varepsilon _g} \text{，} $

(29)$ {Q_g}(t)+{Z_g}(t) \leqslant V{p_{\max }}+{a_{g,\max }}+{\varepsilon _g} . $

性质2　队列$ g \in \{ 1,\cdots,G\} $的最大时延为

(30)$ {T_{g,\max }} ^{\underline{\underline{\rm{\;def\;}}}} \frac{{2V{p_{\max }}+{a_{g,\max }}+{\varepsilon _g}}}{{{\varepsilon _g}}} . $

性质3　队列$X(t)$在任意时隙t的上下界为

(31)$ - V{p_{\max }} - {b_{\max }} \leqslant X(t) \leqslant {b_{\max }} . $

性质4　所提算法的时间平均预期收益在最优值$ {S /V} $界内，即

(32)$ \begin{split}& \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T {E[\beta p(t){{(d(t) - e(t) - b(t))}^ - }}- \\& \;\;\;\;\; p(t){(d(t) - e(t) - b(t))^+}] \geqslant {C^*} - {S}/{V} .\end{split} $

式中：$ {C^*} $为收益的时间平均最优值. 所提算法渐近等价于最优解$ V \to \infty $（$ {T_{\max }} \to \infty $和$ {B_{\max }} \to \infty $）. 由性质1可知，各队列$ {Q_g}(t) $、$ {Z_g}(t) $在所有时隙都有上界，因此队列积压不会无限大，队列的稳定性得到保证，满足约束式(22). 性质2和性质4表示需求队列中任何需求的最大时延$ {T_{g,\max }} $随V的增大而增大，用户最终收益随V的增大而无限趋于最优值$ {C^*} $，因此须合理调节V值大小，使得分配的能量在满足用户时延需求情况下达到收益最大化. 性质3表示充/放电决策$b(t)$的合理性，使得储能设备的实时电量不会过高或过低，即$ {B_{\min }} \leqslant B(t) \leqslant {B_{\max }} $.

对所提算法的可行性进行仿真验证. 根据用户用电行为假设能量收集和能量需求均服从泊松分布，对于其他统计分布，该算法同样适用. 大多数智能电网的时变电价在0.5~2.0元波动. 设置时隙区间为10 min，共14 400个时隙（100 d）. 该响应时间不仅适用于所有家用电器的操作间隔，也便于进行仿真实验. 参考市面上充电储能设备的容量范围，将其值设置为2 500 kJ.

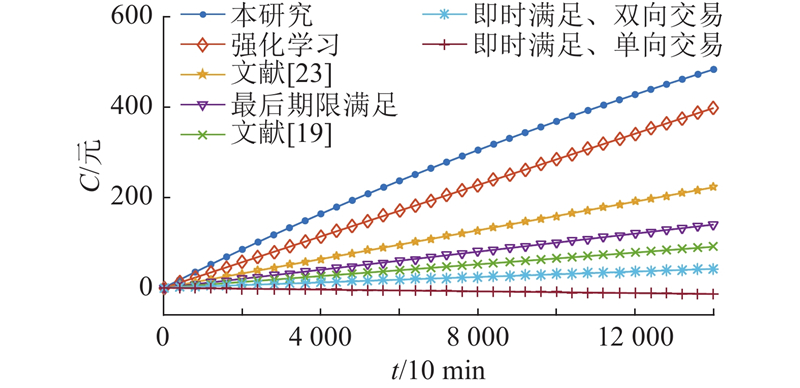
为了验证所提算法的经济性，对比不同算法的累计收益C，结果如图3所示. 其中最后期限满足算法指用户在可容忍期限内只使用可再生能源，若最后期限到达时用户需求仍没有被满足，再从智能电网购电；文献[19]的算法不包含储能设备，即多余的可再生能源无法存储；文献[23]的算法将剩余的可再生能源存储到储能设备中，并在电价高时放电供用户使用，但是不能从电网购电存入储能设备中；其余2种算法（即时满足、双向交易，即时满足、单向交易）均为贪婪算法，即用户的能量需求要立即满足，区别在于前者与智能电网之间的交易是双向的. 可以看出，本研究所提算法在7种算法中累计收益最高，且较最后期限满足算法收益显著提高，原因是所提算法能够充分响应时变电价的波动，使能量管理单元在相对较低的价格购买额外的能源.

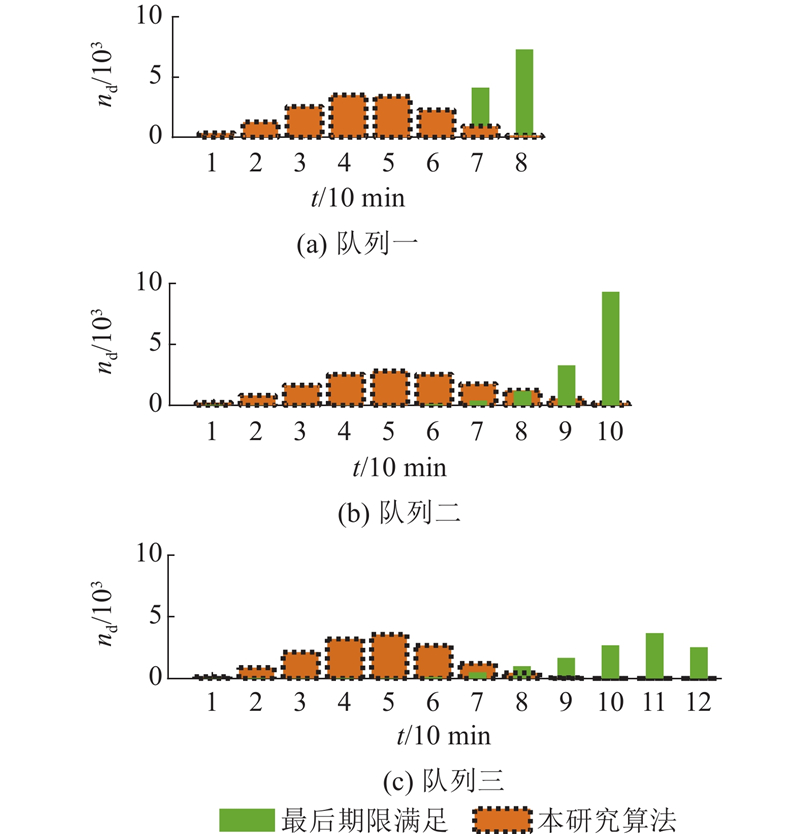
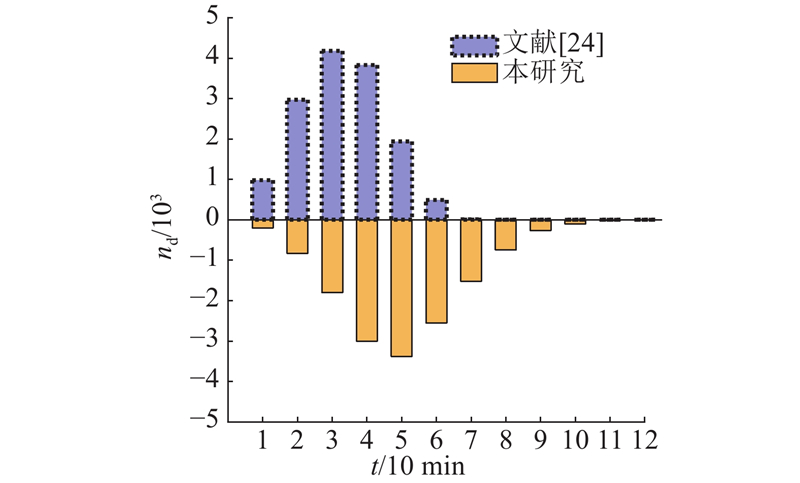
如图4所示，随机显示3个队列所提算法与最后期限满足算法的时延对比情况. 图中，n_d为队列中实时达到的能量需求等待被服务的时延统计. 3个队列的最大时延分别设置为8、10、12个时隙可以看出，在3个队列中，所提算法的时延性均明显优于最后期限满足算法. 比如队列二，所提算法队列中的需求平均等待5个时隙，最后期限满足算法大部分需求要等待9~10个时隙.

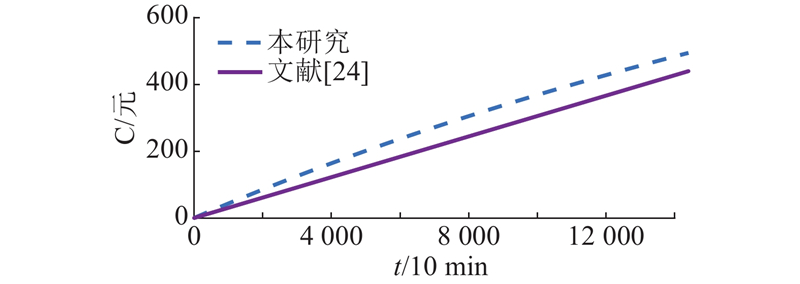
为了对比所提模型的优越性，将所提模型与文献[24]的模型进行比较. 文献[24]的模型的需求响应只涉及用户层面，未考虑各类家电的不同需求和时延差异. 相比之下，本研究所提模型根据用户对每个电器的实际使用情况设置了不同的时延约束，并根据需求有针对性地分配能量. 如图5所示为2种模型的用户在14 400时隙（100 d）的累计收益对比. 可以看出，所提模型明显优于文献[24]的模型，在100 d末，文献[24]模型的用户收益为434元，本研究所提模型用户的收益为489元，提高了11.2%. 如图6所示为2种模型下用户在不超过14 400时隙（100 d）的平均时延对比. 可以看出，2种模型均满足用户时延要求，但所提模型平均时延次于文献[24]的模型，原因是文献[24]的模型没有考虑各电器的时延差异，最大时延须满足各电器的时延需求（取各电器时延最小值作为时延约束）.

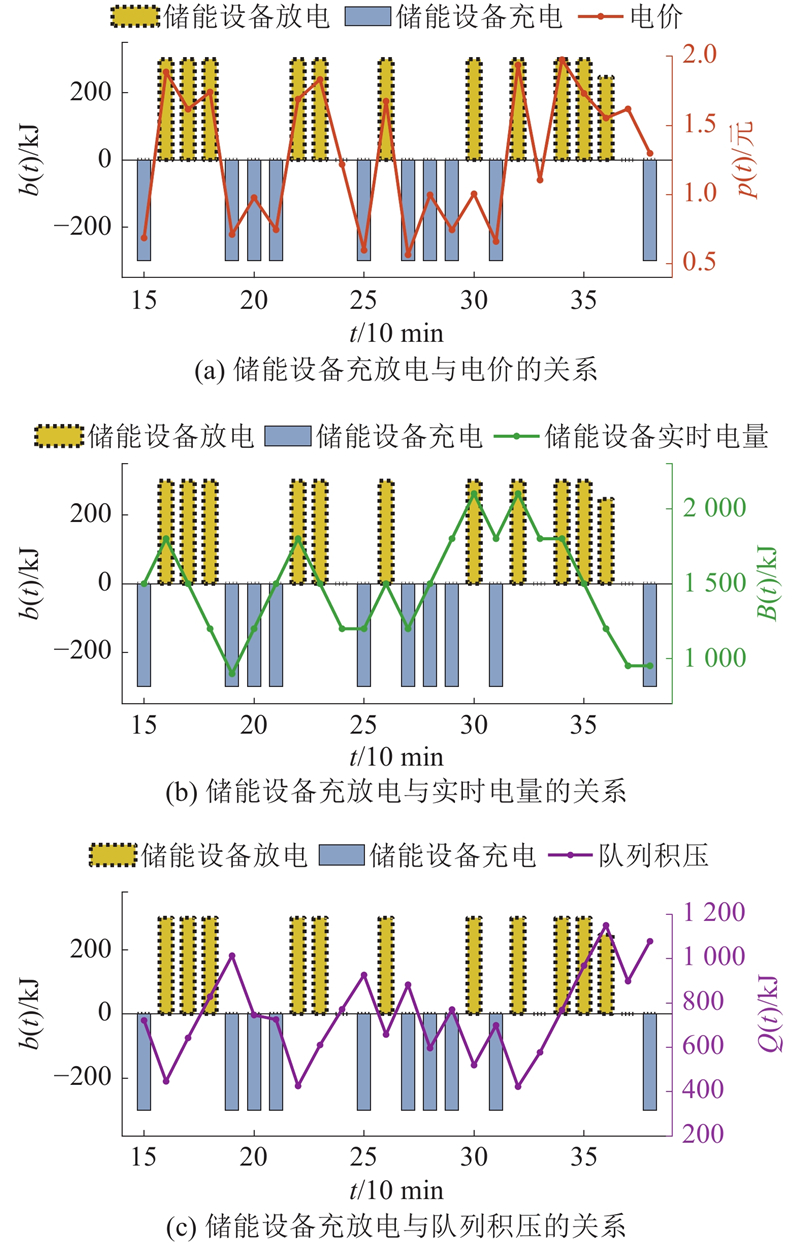
如图7所示，为了研究储能设备充放电特性，分析随机24个时隙（15~38）中储能设备充放电情况与外部电网电价、储能设备实时电量和队列积压的关系. 可以看出，当外部电网电价较高或者储能设备电量较多时，储能设备进行放电，如时隙16（外部电网电价较高）、时隙30（储能设备电量较高）；当外部电网电价较低或者储能设备电量较少时，储能设备进行充电，如时隙19（外部电网电价很低）、时隙38（储能设备电量较低）；当外部电网电价中等且储能设备中有一定的电量时，若此时队列积压很大，储能设备进行放电用于服务，如时隙36. 还可以看到，有些时隙的充放电量为0，如时隙24，原因是外部电网电价中等且储能设备中有一定的电量，队列积压适中，此时将可再生能源按队列积压大小进行能量分配，用于服务电器的需求.

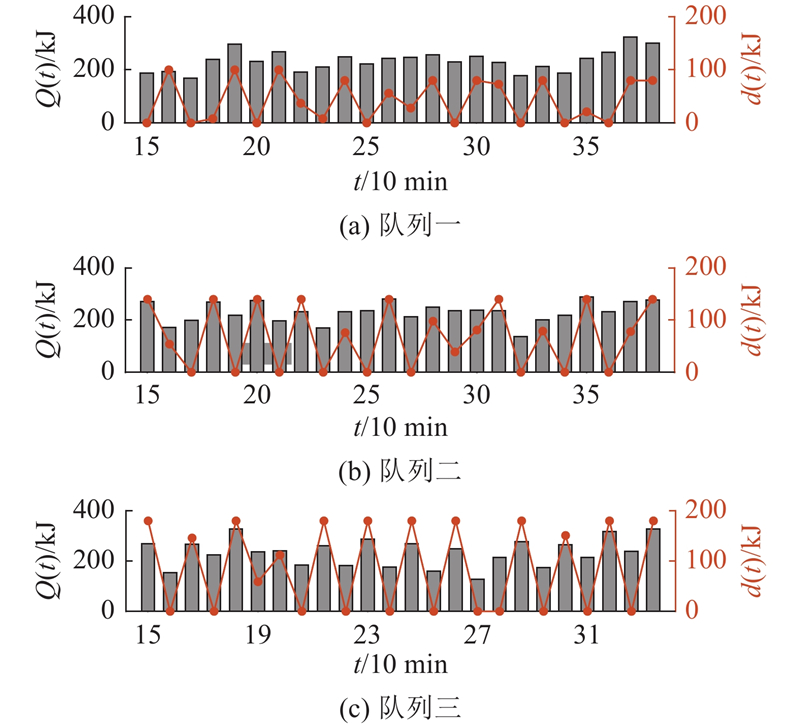
如图8所示，为了验证所提动态能量分配算法的可行性，分析24个时隙（15~38）不同电器队列积压下分配的能量结果. 可以看出，各电器分配的能量与队列积压大小有关. 当队列积压量较高时，须分配最大可能的能量，如果可再生能源发电量不够，则从储能设备中放电或从电网购电. 如时隙15，此时队列2和队列3积压量较高，要分配最大可能的能量，此时可再生能源发电量不够，而电价较低，应从电网购电来满足用户需求. 当队列积压量适中时，按照队列顺序分配可再生能源，如时隙21，此时队列1积压量最高，分配最大可能的能量，再将剩余的可再生能源分配给积压量较大的队列3. 当队列积压量较小时，不需要分配能量，如时隙32，此时给积压量较高的队列3分配最大可能的能量后，可再生能源还有富余，但队列1和队列2的积压量较小，此时电价较高、储能设备实时电量较多，应将多余的能量卖给电网以营利，故电器1和电器2分配的能量均为0.

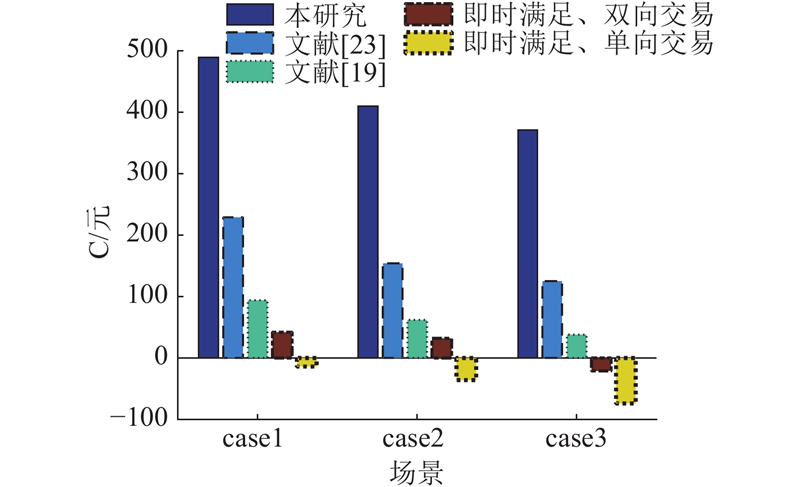
不同季节可再生能源出力差异以及家用电器的使用可能不完全相同（夏季可再生能源出力较多，冬季如热水器的弹性负荷使用量较大），为此针对不同季节设置3种场景：case1代表夏季，case2代表春秋季，case3代表冬季. 基于5种算法在不同场景下百天的累计收益对比如图9所示. 可以看出，所提算法在3种场景中均达到最大收益值，表明所提算法具有较好的普适性，能够在满足用户各电器能量需求的情况下取得渐进最优的收益.

本研究集成家用电器、可再生能源和智能电网，形成绿色和高效的能源枢纽，并基于李雅普诺夫优化方法提出时变电价下的家庭用户多电器能量分配算法. 通过算例分析和仿真结果得到以下结论. 1）所提算法能够保障算法的稳定性与收敛性，使时间平均预期收益在最优值界内；2）所提算法能够促进可再生能源的消纳，提高能源效率；3）所提多队列模型纳入不同电器的能量需求和最大时延，能够有效满足不同电器的实际使用情况，进一步证明了所提算法既能保证用户的使用舒适度，还能显著提高用户收益. 本研究主要考虑单用户家庭模型，能够为社区级用户模型提供重要基础，未来计划针对社区级模型开展研究.