[1]
杨荣悦, 张鹏洲, 宋卿 基于5G技术的智能车联网研究与展望
[J]. 电信科学 , 2020 , 36 (5 ): 106 - 114
[本文引用: 1]
YANG Rongyue, ZHANG Pengzhou, SONG Qing Research and prospect of intelligent internet of vehicles based on 5G technology
[J]. Telecommunications Science , 2020 , 36 (5 ): 106 - 114
[本文引用: 1]
[2]
JU Z, ZHANG H, LI X, et al A survey on attack detection and resilience for connected and automated vehicles: from vehicle dynamics and control perspective
[J]. IEEE Transactions on Intelligent Vehicles , 2022 , 7 (4 ): 815 - 837
DOI:10.1109/TIV.2022.3186897
[本文引用: 1]
[3]
HE Q, DAN G, FODOR V. Minimizing age of correlated information for wireless camera networks [C]// IEEE INFOCOM 2018-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS) . Honolulu: IEEE, 2018: 547–552.
[本文引用: 1]
[4]
LI B, FEI Z, ZHANG Y UAV communications for 5G and beyond: recent advances and future trends
[J]. IEEE Internet of Things Journal , 2019 , 6 (2 ): 2241 - 2263
DOI:10.1109/JIOT.2018.2887086
[本文引用: 1]
[5]
BURHANUDDIN L A B, LIU X, DENG Y, et al QoE optimization for live video streaming in UAV-to-UAV communications via deep reinforcement learning
[J]. IEEE Transactions on Vehicular Technology , 2022 , 71 (5 ): 5358 - 5370
DOI:10.1109/TVT.2022.3152146
[本文引用: 1]
[6]
HABIBZADEH H, DINESH K, SHISHVAN O R, et al A survey of healthcare internet-of-things (HIoT): a clinical perspective
[J]. IEEE Internet Things Journal , 2020 , 7 (1 ): 53 - 71
DOI:10.1109/JIOT.2019.2946359
[本文引用: 1]
[7]
SONG H, GAO S, LI Y, et al Train-centric communication based autonomous train control system
[J]. IEEE Transactions on Intelligent Vehicles , 2023 , 8 (1 ): 721 - 731
DOI:10.1109/TIV.2022.3192476
[本文引用: 1]
[8]
KAUL S, GRUTESER M, RAI V, et al. Minimizing age of information in vehicular networks [C]// 2011 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks . Salt Lake City: IEEE, 2011: 350–358.
[本文引用: 1]
[9]
KAUL S, YATES R, GRUTESER M. Real-time status: how often should one update? [C]// 2012 Proceedings IEEE INFOCOM . Orlando: IEEE, 2012: 2731–2735.
[本文引用: 1]
[10]
YATES R D, SUN Y, BROWN D R, et al Age of information: an introduction and survey
[J]. IEEE Journal on Selected Areas in Communications , 2021 , 39 (5 ): 1183 - 1210
DOI:10.1109/JSAC.2021.3065072
[本文引用: 1]
[11]
WANG Q, CHEN H, ZHAO C, et al Optimizing information freshness via multiuser scheduling with adaptive NOMA/OMA
[J]. IEEE Transactions on Wireless Communications , 2022 , 21 (3 ): 1766 - 1778
DOI:10.1109/TWC.2021.3106778
[12]
CHIARIOTTI F, HOLM J, KALØR A E, et al Query age of information: freshness in pull-based communication
[J]. IEEE Transactions on Communications , 2022 , 70 (3 ): 1606 - 1622
DOI:10.1109/TCOMM.2022.3141786
[本文引用: 1]
[13]
DONG Y, CHEN Z, LIU S, et al. Age of information upon decisions [C]// 2018 IEEE 39th Sarnoff Symposium . Newark: IEEE, 2018: 1–5.
[本文引用: 4]
[14]
DONG Y, FAN P. Age upon decisions with general arrivals [C]// 2018 9th IEEE Annual Ubiquitous Computing, Electronics and Mobile Communication Conference . New York: IEEE, 2018: 825–829.
[本文引用: 1]
[15]
DONG Y, CHEN Z, LIU S, et al Age-upon-decisions minimizing scheduling in Internet of Things: to be random or to be deterministic?
[J]. IEEE Internet of Things Journal , 2020 , 7 (2 ): 1081 - 1097
DOI:10.1109/JIOT.2019.2950054
[本文引用: 1]
[16]
BAO Z, DONG Y, CHEN Z, et al Age-optimal service and decision processes in Internet of Things
[J]. IEEE Internet of Things Journal , 2021 , 8 (4 ): 2826 - 2841
DOI:10.1109/JIOT.2020.3020875
[本文引用: 1]
[17]
CHEN S, ZHANG T, CHEN Z, et al Minimizing age-upon-decisions in bufferless system: service scheduling and decision interval
[J]. IEEE Transactions on Vehicular Technology , 2023 , 72 (1 ): 1017 - 1031
DOI:10.1109/TVT.2022.3202790
[本文引用: 1]
[18]
DONG Y, FAN P, LETAIEF K B Energy harvesting powered sensing in IoT: timeliness versus distortion
[J]. IEEE Internet of Things Journal , 2020 , 7 (11 ): 10897 - 10911
DOI:10.1109/JIOT.2020.2990715
[本文引用: 4]
[19]
DONG Y Distributed sensing with orthogonal multiple access: to code or not to code?
[J]. IEEE Transactions on Signal Processing , 2020 , 68 : 1315 - 1330
DOI:10.1109/TSP.2020.2971203
[本文引用: 2]
[20]
ORNEE T Z, SUN Y. Sampling for remote estimation through queues: age of information and beyond [C]// International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks . Avignon: IEEE, 2019: 1–8.
[本文引用: 1]
[21]
BASTOPCU M, ULUKUS S. Age of information for updates with distortion [C]// 2019 IEEE Information Theory Workshop (ITW) . Visby: IEEE, 2019: 1–5.
[本文引用: 2]
[22]
QIAO L, ZHOU Y Timely split inference in wireless networks: an accuracy-freshness tradeoff
[J]. IEEE Transactions on Vehicular Technology , 2023 , 72 (12 ): 16817 - 16822
DOI:10.1109/TVT.2023.3294494
[本文引用: 2]
[23]
HUANG Y, ZHANG W. Research on the methods of data mining based on the edge computing for the IoT [C]// IEEE International Conference on Integrated Circuits and Communication Systems . Raichur: IEEE, 2023: 1–6.
[本文引用: 1]
[24]
CUI S, XIAO J J, GOLDSMITH A J, et al Estimation diversity and energy efficiency in distributed sensing
[J]. IEEE Transactions on Signal Processing , 2007 , 55 (9 ): 4683 - 4695
DOI:10.1109/TSP.2007.896019
[本文引用: 1]
[25]
田乃硕, 徐秀丽, 马占友. 离散时间排队论[M]. 北京: 科学出版社, 2008: 38–49.
[本文引用: 2]
基于5G技术的智能车联网研究与展望
1
2020
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
基于5G技术的智能车联网研究与展望
1
2020
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
A survey on attack detection and resilience for connected and automated vehicles: from vehicle dynamics and control perspective
1
2022
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
1
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
UAV communications for 5G and beyond: recent advances and future trends
1
2019
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
QoE optimization for live video streaming in UAV-to-UAV communications via deep reinforcement learning
1
2022
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
A survey of healthcare internet-of-things (HIoT): a clinical perspective
1
2020
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
Train-centric communication based autonomous train control system
1
2023
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
1
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
1
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
Age of information: an introduction and survey
1
2021
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
Optimizing information freshness via multiuser scheduling with adaptive NOMA/OMA
0
2022
Query age of information: freshness in pull-based communication
1
2022
... 时延敏感应用包括智能车联网[1 -2 ] 、无线智能相机网络[3 ] 、无人机网络通信[4 -5 ] 、工业4.0、智慧医疗[6 ] 和智慧城市[7 ] 等,这些应用的关键环节涉及系统状态信息的收集、处理以及使用,要求及时有效的信息交付. 传统性能指标(如时延和吞吐量)以数据为中心,主要关注信息传输环节的时延,不能有效衡量信息的时效性. 作为一种新的时效性指标,信息年龄(age of information,AoI)[8 -9 ] 被定义为接收机最新可用数据包的年龄,即数据包在源节点生成以来所经过的时间. Yates等[10 -12 ] 总结了使用AoI表征信息新鲜度的相关研究. ...
4
... 特定时刻上可用信息的时效性直接影响网络/系统的控制,因而备受物联网应用研究者的关注. 例如,在车联网中,收集车辆状态信息更关注车辆接近路口或发生紧急情况的时刻,即状态信息用于动态规划路线或调整行驶速度的时刻;在工业4.0现代工厂中,终端处理人员收集设备故障时的状态信息,以便做出合理调整. Dong等[13 ] 引入决策信息年龄(age upon decisions,AuD)来表征所接收的数据包在决策时刻的信息新鲜度. AuD比其他时效性度量指标更关注特定时刻的新鲜度,这些时刻的信息对于物联网应用的实时决策更有价值. 更新决策系统根据接收到的数据包做出随机决策,面向实时决策的物联网更新系统将接收到的数据包用于决策,因而决策时刻信息的时效性至关重要. 学者研究了不同排队模型下的系统平均AuD. Dong等[13 ] 提出使用AuD表征决策时刻的信息新鲜度,研究了M/M/1/M排队策略下更新决策系统的AuD. 沿着相似的路线,Dong等[14 ] 进一步推导了G/G/1/M和G/M/1/M排队策略下更新决策系统平均AuD的闭式解. Dong等[15 ] 通过优化数据的生成过程来降低泊松决策系统的平均AuD,分析了周期性决策系统D/M/1/D的平均AuD. Bao等[16 ] 探讨了不同服务时间分布对M/G/1/M和M/G/1/D更新决策系统时效性的影响. Chen等[17 ] 研究了无缓冲队列更新决策系统的AuD,从服务调度和决策过程两方面对系统性能进行了优化. ...
... [13 ]提出使用AuD表征决策时刻的信息新鲜度,研究了M/M/1/M排队策略下更新决策系统的AuD. 沿着相似的路线,Dong等[14 ] 进一步推导了G/G/1/M和G/M/1/M排队策略下更新决策系统平均AuD的闭式解. Dong等[15 ] 通过优化数据的生成过程来降低泊松决策系统的平均AuD,分析了周期性决策系统D/M/1/D的平均AuD. Bao等[16 ] 探讨了不同服务时间分布对M/G/1/M和M/G/1/D更新决策系统时效性的影响. Chen等[17 ] 研究了无缓冲队列更新决策系统的AuD,从服务调度和决策过程两方面对系统性能进行了优化. ...
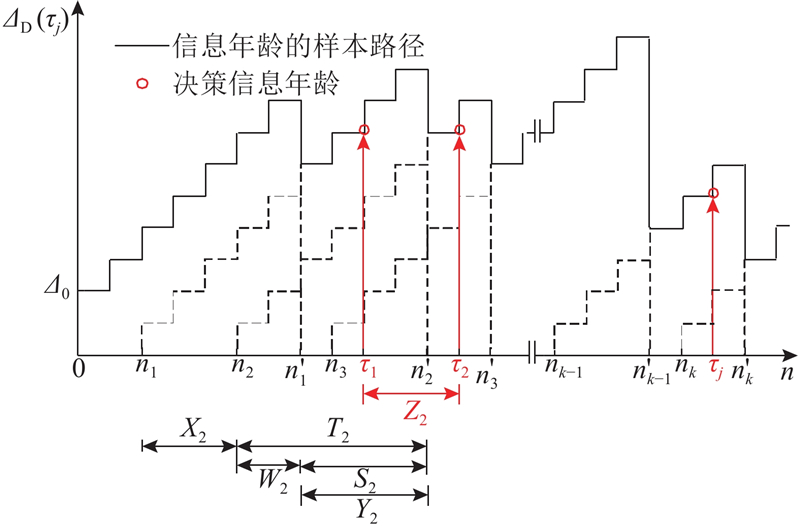
... 与AoI度量中系统会度量数据包在接收后的每个时刻上的新鲜度不同,本研究通过AuD度量接收到的数据包在决策时刻的新鲜度. 具体来说,第$j$ ${\tau _j}$ $U\left( {{\tau _j}} \right)$ [13 ] : ...
... 其中$E\left[ {{Y_k}} \right] = E\left[ {{X_k}} \right] = {1 \mathord{\left/ {\vphantom {1 \lambda }} \right. } \lambda }$ . 根据文献[13 ]中决策年龄的定义,结合式(18)、式(33)、式(34)和式(4),系统的平均决策年龄可以表示为 ...
1
... 特定时刻上可用信息的时效性直接影响网络/系统的控制,因而备受物联网应用研究者的关注. 例如,在车联网中,收集车辆状态信息更关注车辆接近路口或发生紧急情况的时刻,即状态信息用于动态规划路线或调整行驶速度的时刻;在工业4.0现代工厂中,终端处理人员收集设备故障时的状态信息,以便做出合理调整. Dong等[13 ] 引入决策信息年龄(age upon decisions,AuD)来表征所接收的数据包在决策时刻的信息新鲜度. AuD比其他时效性度量指标更关注特定时刻的新鲜度,这些时刻的信息对于物联网应用的实时决策更有价值. 更新决策系统根据接收到的数据包做出随机决策,面向实时决策的物联网更新系统将接收到的数据包用于决策,因而决策时刻信息的时效性至关重要. 学者研究了不同排队模型下的系统平均AuD. Dong等[13 ] 提出使用AuD表征决策时刻的信息新鲜度,研究了M/M/1/M排队策略下更新决策系统的AuD. 沿着相似的路线,Dong等[14 ] 进一步推导了G/G/1/M和G/M/1/M排队策略下更新决策系统平均AuD的闭式解. Dong等[15 ] 通过优化数据的生成过程来降低泊松决策系统的平均AuD,分析了周期性决策系统D/M/1/D的平均AuD. Bao等[16 ] 探讨了不同服务时间分布对M/G/1/M和M/G/1/D更新决策系统时效性的影响. Chen等[17 ] 研究了无缓冲队列更新决策系统的AuD,从服务调度和决策过程两方面对系统性能进行了优化. ...
Age-upon-decisions minimizing scheduling in Internet of Things: to be random or to be deterministic?
1
2020
... 特定时刻上可用信息的时效性直接影响网络/系统的控制,因而备受物联网应用研究者的关注. 例如,在车联网中,收集车辆状态信息更关注车辆接近路口或发生紧急情况的时刻,即状态信息用于动态规划路线或调整行驶速度的时刻;在工业4.0现代工厂中,终端处理人员收集设备故障时的状态信息,以便做出合理调整. Dong等[13 ] 引入决策信息年龄(age upon decisions,AuD)来表征所接收的数据包在决策时刻的信息新鲜度. AuD比其他时效性度量指标更关注特定时刻的新鲜度,这些时刻的信息对于物联网应用的实时决策更有价值. 更新决策系统根据接收到的数据包做出随机决策,面向实时决策的物联网更新系统将接收到的数据包用于决策,因而决策时刻信息的时效性至关重要. 学者研究了不同排队模型下的系统平均AuD. Dong等[13 ] 提出使用AuD表征决策时刻的信息新鲜度,研究了M/M/1/M排队策略下更新决策系统的AuD. 沿着相似的路线,Dong等[14 ] 进一步推导了G/G/1/M和G/M/1/M排队策略下更新决策系统平均AuD的闭式解. Dong等[15 ] 通过优化数据的生成过程来降低泊松决策系统的平均AuD,分析了周期性决策系统D/M/1/D的平均AuD. Bao等[16 ] 探讨了不同服务时间分布对M/G/1/M和M/G/1/D更新决策系统时效性的影响. Chen等[17 ] 研究了无缓冲队列更新决策系统的AuD,从服务调度和决策过程两方面对系统性能进行了优化. ...
Age-optimal service and decision processes in Internet of Things
1
2021
... 特定时刻上可用信息的时效性直接影响网络/系统的控制,因而备受物联网应用研究者的关注. 例如,在车联网中,收集车辆状态信息更关注车辆接近路口或发生紧急情况的时刻,即状态信息用于动态规划路线或调整行驶速度的时刻;在工业4.0现代工厂中,终端处理人员收集设备故障时的状态信息,以便做出合理调整. Dong等[13 ] 引入决策信息年龄(age upon decisions,AuD)来表征所接收的数据包在决策时刻的信息新鲜度. AuD比其他时效性度量指标更关注特定时刻的新鲜度,这些时刻的信息对于物联网应用的实时决策更有价值. 更新决策系统根据接收到的数据包做出随机决策,面向实时决策的物联网更新系统将接收到的数据包用于决策,因而决策时刻信息的时效性至关重要. 学者研究了不同排队模型下的系统平均AuD. Dong等[13 ] 提出使用AuD表征决策时刻的信息新鲜度,研究了M/M/1/M排队策略下更新决策系统的AuD. 沿着相似的路线,Dong等[14 ] 进一步推导了G/G/1/M和G/M/1/M排队策略下更新决策系统平均AuD的闭式解. Dong等[15 ] 通过优化数据的生成过程来降低泊松决策系统的平均AuD,分析了周期性决策系统D/M/1/D的平均AuD. Bao等[16 ] 探讨了不同服务时间分布对M/G/1/M和M/G/1/D更新决策系统时效性的影响. Chen等[17 ] 研究了无缓冲队列更新决策系统的AuD,从服务调度和决策过程两方面对系统性能进行了优化. ...
Minimizing age-upon-decisions in bufferless system: service scheduling and decision interval
1
2023
... 特定时刻上可用信息的时效性直接影响网络/系统的控制,因而备受物联网应用研究者的关注. 例如,在车联网中,收集车辆状态信息更关注车辆接近路口或发生紧急情况的时刻,即状态信息用于动态规划路线或调整行驶速度的时刻;在工业4.0现代工厂中,终端处理人员收集设备故障时的状态信息,以便做出合理调整. Dong等[13 ] 引入决策信息年龄(age upon decisions,AuD)来表征所接收的数据包在决策时刻的信息新鲜度. AuD比其他时效性度量指标更关注特定时刻的新鲜度,这些时刻的信息对于物联网应用的实时决策更有价值. 更新决策系统根据接收到的数据包做出随机决策,面向实时决策的物联网更新系统将接收到的数据包用于决策,因而决策时刻信息的时效性至关重要. 学者研究了不同排队模型下的系统平均AuD. Dong等[13 ] 提出使用AuD表征决策时刻的信息新鲜度,研究了M/M/1/M排队策略下更新决策系统的AuD. 沿着相似的路线,Dong等[14 ] 进一步推导了G/G/1/M和G/M/1/M排队策略下更新决策系统平均AuD的闭式解. Dong等[15 ] 通过优化数据的生成过程来降低泊松决策系统的平均AuD,分析了周期性决策系统D/M/1/D的平均AuD. Bao等[16 ] 探讨了不同服务时间分布对M/G/1/M和M/G/1/D更新决策系统时效性的影响. Chen等[17 ] 研究了无缓冲队列更新决策系统的AuD,从服务调度和决策过程两方面对系统性能进行了优化. ...
Energy harvesting powered sensing in IoT: timeliness versus distortion
4
2020
... 时效性是基于物联网的传感系统的重要性能指标. 在提高信息新鲜度的过程中,如果系统的失真增大,恢复信号将无法准确地描述现象,可能导致错误的决策. 因此,在考虑系统时效性的同时,还必须考虑状态更新系统的失真性能[18 ] . 通常采用解码(或估计)信号的均方误差(MSE)来度量信号的失真. 例如,对具有有限节点分布式的传感器系统,常将传感器观测值与最佳线性无偏估计量(best linear unbiased estimator, BLUE)结合来估计信号源的失真[19 ] . Ornee等[20 ] 提出在远程估计中生成及时更新的问题,研究了通过队列估计维纳过程的MSE最优策略和AoI最优策略. Bastopcu等[21 ] 讨论的信息更新系统权衡了服务性能和信息新鲜度,在给定的更新质量约束下,通过数据处理降低了信息年龄. 为了实现及时准确的边缘推断,在平均推理失真约束条件下,Qiao等[22 ] 提出优化边缘推理系统准确性和新鲜度之间权衡的框架. Bastopcu等[21 -22 ] 都是在给定阈值下进行新鲜度和失真的权衡,以最小化信息年龄. ...
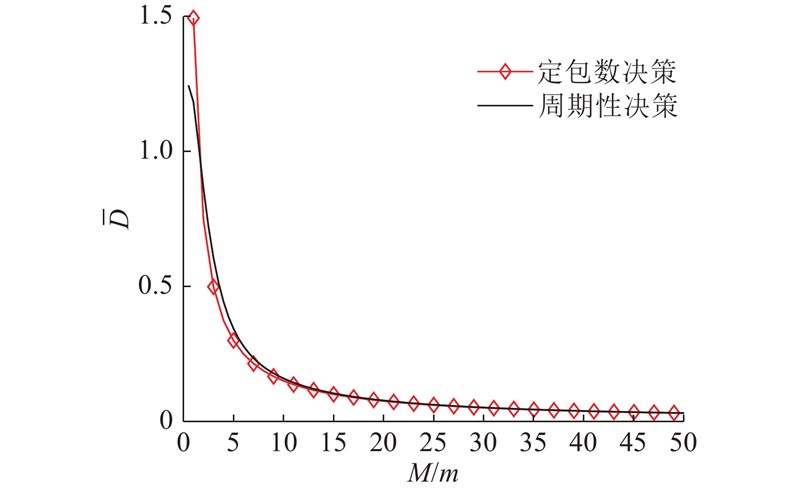
... 如图7 所示为不同决策过程下数据包个数$M$ $ \overline D $ $\lambda = 0.5$ $ \sigma _\theta ^2 = 1.0 $ ${\gamma _{{\text{ob}}}} = 2$ ${\gamma _{{\text{ch}}}} = 1.5$ [18 ] . 可以看出,系统的平均失真随$M$
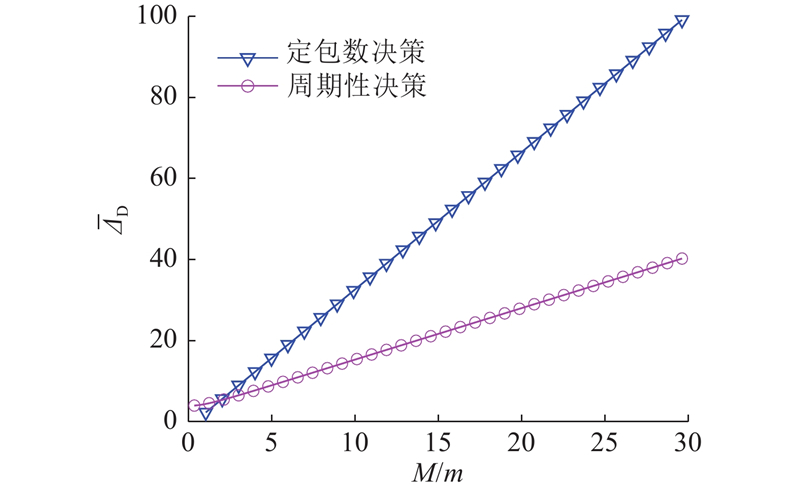
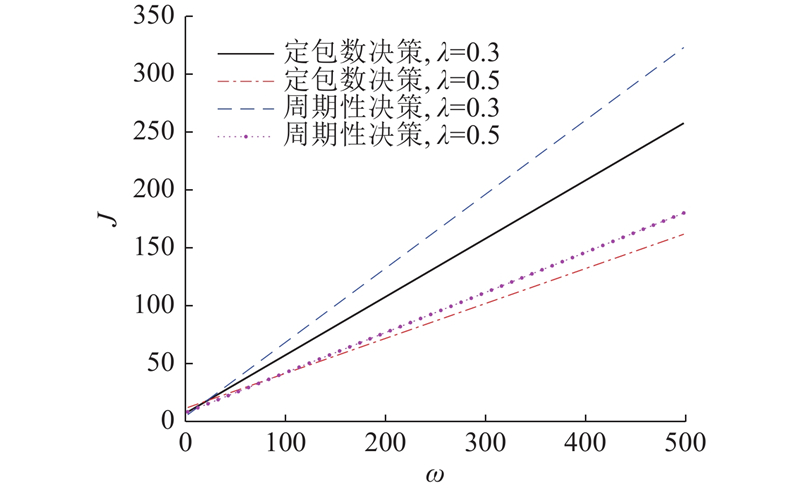
... 如图8 所示为2种决策方式在不同到达率下权重$\omega $ $ \mu = 0.6 $ $ \sigma _\theta ^2 = 1.0 $ $ {\gamma _{{\text{ob}}}} = 2.0 $ $ {\gamma _{{\text{ch}}}} = 1.5 $ [18 ] . 由图可知,随着$\omega $ $J = \left( {{{\overline \varDelta }_{\text{D}}}+\omega \overline D} \right)$ $\omega $ $J$ $\lambda $ $J$ $J$
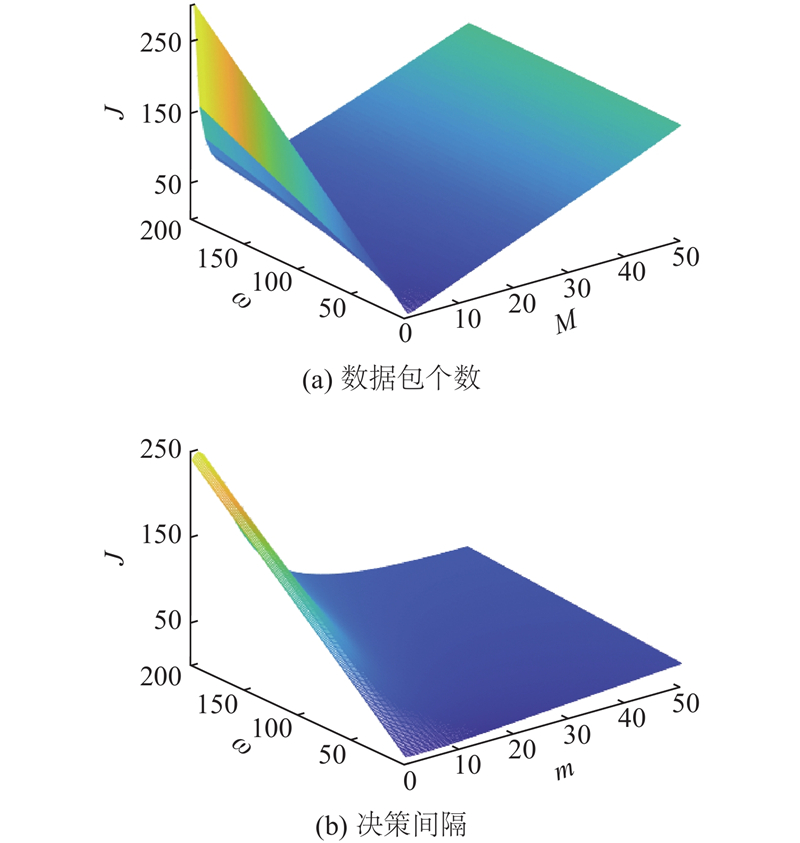
... 如图9 所示的三维图像更加直观地反映了决策过程参数与权重$\omega $ $\lambda = 0.3$ $ \mu = 0.6 $ $ \sigma _\theta ^2 = 1.0 $ $ {\gamma _{{\text{ob}}}} = 2.0 $ $ {\gamma _{{\text{ch}}}} = 1.5 $ [18 ] . 图9 (a)和图9 (b)分别表示系统在定包数$M$ $m$ $J$ 图9 (a)中可以看出,当$\omega $ $J$ $M$ $M = 1$ . 随着$\omega $ $J$ $M$ $J$ $M$ 图9 (b)可以看出,当$\omega \to 0$ $m = 1$ $J$ $\omega $ $J$ $m$ $\omega $ $J$ $J$ $m$
Distributed sensing with orthogonal multiple access: to code or not to code?
2
2020
... 时效性是基于物联网的传感系统的重要性能指标. 在提高信息新鲜度的过程中,如果系统的失真增大,恢复信号将无法准确地描述现象,可能导致错误的决策. 因此,在考虑系统时效性的同时,还必须考虑状态更新系统的失真性能[18 ] . 通常采用解码(或估计)信号的均方误差(MSE)来度量信号的失真. 例如,对具有有限节点分布式的传感器系统,常将传感器观测值与最佳线性无偏估计量(best linear unbiased estimator, BLUE)结合来估计信号源的失真[19 ] . Ornee等[20 ] 提出在远程估计中生成及时更新的问题,研究了通过队列估计维纳过程的MSE最优策略和AoI最优策略. Bastopcu等[21 ] 讨论的信息更新系统权衡了服务性能和信息新鲜度,在给定的更新质量约束下,通过数据处理降低了信息年龄. 为了实现及时准确的边缘推断,在平均推理失真约束条件下,Qiao等[22 ] 提出优化边缘推理系统准确性和新鲜度之间权衡的框架. Bastopcu等[21 -22 ] 都是在给定阈值下进行新鲜度和失真的权衡,以最小化信息年龄. ...
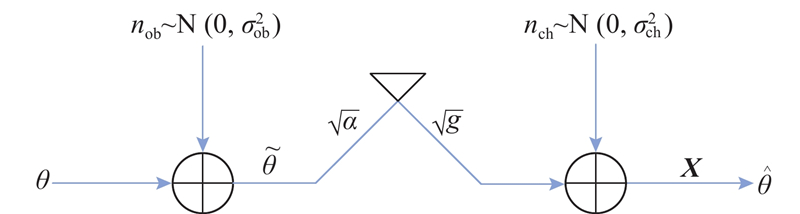
... 在传输过程中,传感器上的观测结果$\tilde \theta $ ${n_{{\text{ob}}}}$ $\tilde \theta = \theta +{n_{{\text{ob}}}}$ ${n_{{\text{ob}}}}$ $\sigma _{{\text{ob}}}^2$ ${n_{{\text{ob}}}} \sim {\text{N}}\left( {0,\sigma _{{\text{ob}}}^2} \right)$ . 在此基础上,定义传感器的局部观测信噪比${\gamma _{{\text{ob}}}} = {{\sigma _\theta ^2} \mathord{\left/ {\vphantom {{\sigma _\theta ^2} \sigma }} \right. }} \sigma _{{\text{ob}}}^2$ . 本研究采用非编码方案[19 ] ,$\tilde \theta $ $\tilde \theta $ $\alpha $ $\alpha = {{{P_{\text{t}}}} \mathord{\left/ {\vphantom {{{P_{\text{t}}}} {\left( {\sigma _\theta ^2+\sigma _{{\text{ob}}}^2} \right)}}} \right. } {\left( {\sigma _\theta ^2+\sigma _{{\text{ob}}}^2} \right)}}$ ${P_{\text{t}}}$ $\tilde \theta $ $\sigma _{{\text{ch}}}^2$ $g = 1$ $ {\gamma _{{\text{ch}}}} = {g \mathord{\left/ {\vphantom {g {\sigma _{{\text{ch}}}^2}}} \right. } {\sigma _{{\text{ch}}}^2}} $ . 在$K$ ${\boldsymbol{X}}$ $\theta $ ${\boldsymbol{X}} = {\boldsymbol{h}}\theta +{\boldsymbol{w}}$ $ \boldsymbol{h}=\left[\sqrt{\alpha g},\sqrt{\alpha g},\cdots,\sqrt{\alpha g}\right]^{\text{T}} $ $K$ $ \boldsymbol{w} $ $K \times 1$ ${n_{{\text{ob}}}}$ ${n_{{\text{ch}}}}$ [24 ] 计算式为 ...
1
... 时效性是基于物联网的传感系统的重要性能指标. 在提高信息新鲜度的过程中,如果系统的失真增大,恢复信号将无法准确地描述现象,可能导致错误的决策. 因此,在考虑系统时效性的同时,还必须考虑状态更新系统的失真性能[18 ] . 通常采用解码(或估计)信号的均方误差(MSE)来度量信号的失真. 例如,对具有有限节点分布式的传感器系统,常将传感器观测值与最佳线性无偏估计量(best linear unbiased estimator, BLUE)结合来估计信号源的失真[19 ] . Ornee等[20 ] 提出在远程估计中生成及时更新的问题,研究了通过队列估计维纳过程的MSE最优策略和AoI最优策略. Bastopcu等[21 ] 讨论的信息更新系统权衡了服务性能和信息新鲜度,在给定的更新质量约束下,通过数据处理降低了信息年龄. 为了实现及时准确的边缘推断,在平均推理失真约束条件下,Qiao等[22 ] 提出优化边缘推理系统准确性和新鲜度之间权衡的框架. Bastopcu等[21 -22 ] 都是在给定阈值下进行新鲜度和失真的权衡,以最小化信息年龄. ...
2
... 时效性是基于物联网的传感系统的重要性能指标. 在提高信息新鲜度的过程中,如果系统的失真增大,恢复信号将无法准确地描述现象,可能导致错误的决策. 因此,在考虑系统时效性的同时,还必须考虑状态更新系统的失真性能[18 ] . 通常采用解码(或估计)信号的均方误差(MSE)来度量信号的失真. 例如,对具有有限节点分布式的传感器系统,常将传感器观测值与最佳线性无偏估计量(best linear unbiased estimator, BLUE)结合来估计信号源的失真[19 ] . Ornee等[20 ] 提出在远程估计中生成及时更新的问题,研究了通过队列估计维纳过程的MSE最优策略和AoI最优策略. Bastopcu等[21 ] 讨论的信息更新系统权衡了服务性能和信息新鲜度,在给定的更新质量约束下,通过数据处理降低了信息年龄. 为了实现及时准确的边缘推断,在平均推理失真约束条件下,Qiao等[22 ] 提出优化边缘推理系统准确性和新鲜度之间权衡的框架. Bastopcu等[21 -22 ] 都是在给定阈值下进行新鲜度和失真的权衡,以最小化信息年龄. ...
... [21 -22 ]都是在给定阈值下进行新鲜度和失真的权衡,以最小化信息年龄. ...
Timely split inference in wireless networks: an accuracy-freshness tradeoff
2
2023
... 时效性是基于物联网的传感系统的重要性能指标. 在提高信息新鲜度的过程中,如果系统的失真增大,恢复信号将无法准确地描述现象,可能导致错误的决策. 因此,在考虑系统时效性的同时,还必须考虑状态更新系统的失真性能[18 ] . 通常采用解码(或估计)信号的均方误差(MSE)来度量信号的失真. 例如,对具有有限节点分布式的传感器系统,常将传感器观测值与最佳线性无偏估计量(best linear unbiased estimator, BLUE)结合来估计信号源的失真[19 ] . Ornee等[20 ] 提出在远程估计中生成及时更新的问题,研究了通过队列估计维纳过程的MSE最优策略和AoI最优策略. Bastopcu等[21 ] 讨论的信息更新系统权衡了服务性能和信息新鲜度,在给定的更新质量约束下,通过数据处理降低了信息年龄. 为了实现及时准确的边缘推断,在平均推理失真约束条件下,Qiao等[22 ] 提出优化边缘推理系统准确性和新鲜度之间权衡的框架. Bastopcu等[21 -22 ] 都是在给定阈值下进行新鲜度和失真的权衡,以最小化信息年龄. ...
... -22 ]都是在给定阈值下进行新鲜度和失真的权衡,以最小化信息年龄. ...
1
... 在实际应用中,边缘计算应用于物联网能够在一定程度上提高系统的时效和失真性能. 例如,在自动驾驶车联网中,各个车载传感器感知内外部环境,并生成位置、速度、道路拥堵情况等信息. 传输主路侧单元对数据信息进行计算并传输至车载控制器,控制器根据接收到的数据包做出驾驶决策(如控制车辆转向、减速或停止等),实时传输的数据可带有部分可接受的失真[23 ] . 信息的时效性对于监测中心非常重要,数据收集和传输的延迟、数据源的准确性等因素可能会导致交通信息的失真. 为了平衡信息新鲜度和失真,车联网系统通过多源数据融合、实时数据处理和数据验证机制,以提供尽可能准确和及时的交通信息. 在面向实时决策的物联网更新系统中,频繁实施决策即降低AuD会导致恢复信号的失真增大;决策频率适当降低,在一定的决策间隔内接收到的数据包增多,失真的减小可能会使AuD增大. 本研究针对如何在决策过程中同时提高信息的时效与失真性能问题,通过优化平均AuD和平均失真的加权,平衡面向实时决策的物联网更新系统时效性和失真. ...
Estimation diversity and energy efficiency in distributed sensing
1
2007
... 在传输过程中,传感器上的观测结果$\tilde \theta $ ${n_{{\text{ob}}}}$ $\tilde \theta = \theta +{n_{{\text{ob}}}}$ ${n_{{\text{ob}}}}$ $\sigma _{{\text{ob}}}^2$ ${n_{{\text{ob}}}} \sim {\text{N}}\left( {0,\sigma _{{\text{ob}}}^2} \right)$ . 在此基础上,定义传感器的局部观测信噪比${\gamma _{{\text{ob}}}} = {{\sigma _\theta ^2} \mathord{\left/ {\vphantom {{\sigma _\theta ^2} \sigma }} \right. }} \sigma _{{\text{ob}}}^2$ . 本研究采用非编码方案[19 ] ,$\tilde \theta $ $\tilde \theta $ $\alpha $ $\alpha = {{{P_{\text{t}}}} \mathord{\left/ {\vphantom {{{P_{\text{t}}}} {\left( {\sigma _\theta ^2+\sigma _{{\text{ob}}}^2} \right)}}} \right. } {\left( {\sigma _\theta ^2+\sigma _{{\text{ob}}}^2} \right)}}$ ${P_{\text{t}}}$ $\tilde \theta $ $\sigma _{{\text{ch}}}^2$ $g = 1$ $ {\gamma _{{\text{ch}}}} = {g \mathord{\left/ {\vphantom {g {\sigma _{{\text{ch}}}^2}}} \right. } {\sigma _{{\text{ch}}}^2}} $ . 在$K$ ${\boldsymbol{X}}$ $\theta $ ${\boldsymbol{X}} = {\boldsymbol{h}}\theta +{\boldsymbol{w}}$ $ \boldsymbol{h}=\left[\sqrt{\alpha g},\sqrt{\alpha g},\cdots,\sqrt{\alpha g}\right]^{\text{T}} $ $K$ $ \boldsymbol{w} $ $K \times 1$ ${n_{{\text{ob}}}}$ ${n_{{\text{ch}}}}$ [24 ] 计算式为 ...
2
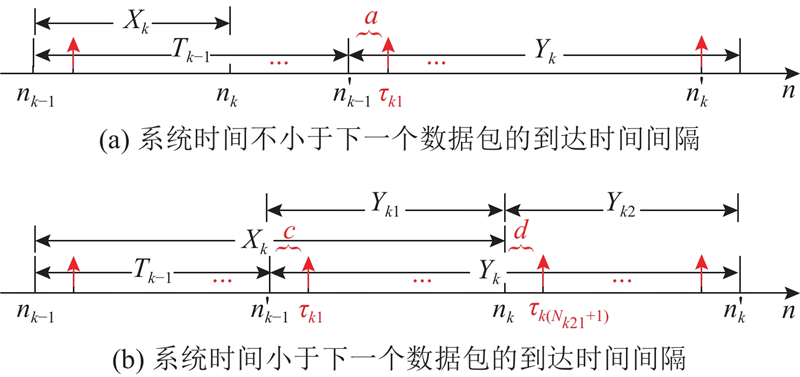
... 式中: ${X_{jk}}$ $j$ $k$ $\lambda $ $\mu $ ${X_{jk}}$ $P\left\{ {{X_{jk}} = i} \right\} = \lambda {\left( {1 - \lambda } \right)^{i - 1}},其中{\text{ }}i = 1,2, \cdots ,\infty $ $E\left[ {{X_{jk}}} \right] = {1 \mathord{\left/ {\vphantom {1 \lambda }} \right. } \lambda }$ . 数据包传输的系统时间${T_{jk}}$ $\left( {1 - p} \right)$ [25 ] ,即 ...
... 假设在时间间隔$m$ $N$ $N$ 25 ]以及排队模型的统计特性分析可知, $N$ $m$ $\lambda $ $ N \sim {\text{B}}\left( {m,\lambda } \right) $