随着上部建构筑物的日益饱和,城市地铁隧道在修建过程中遇到越来越多穿越既有建构筑物的情形. 其中,既有桥梁作为沉降控制较严格的结构,当有地铁盾构隧道邻近侧穿时,应格外关注其变形.
已有较多专家学者针对盾构隧道侧穿施工对邻近桩基的影响展开研究. 其中,在隧道盾构侧穿、斜穿既有桩基的影响性分析中,应用较为普遍的是数值模拟和理论分析方法. 对于数值模拟方法,主要采用不同的有限元软件分析盾构穿越桥梁桩基施工过程中的桩基变形和力学响应机制[1-3]. 数值模拟方法无法有效定量反映桩基变形规律及机理,为此还须采用理论分析的方法加以探讨. 黄戡等[4]利用Pasternak地基模型推导分层地基中盾构施工引起的邻近桩基竖向和水平位移的理论解. 冯国辉等[5]利用Kerr地基模型建立被动桩的水平挠度控制方程,并利用差分法求得被动桩的水平变形位移半解析解. 程康等[6]利用两阶段法,建立桩周邻近开挖扰动影响下的单桩水平方向位移控制方程. 熊巨华等[7]利用荷载传递法和Winkler地基模型,通过两阶段分析法,推导隧道开挖与邻近单桩相互作用的弹塑性解. 综上,盾构穿越桩基的相关理论方法较多,且根据桥梁桩基特点大多采用两阶段法,但其中多数是关于隧道盾构正交侧穿施工引起的桩基变形计算分析,而关于隧道盾构近接斜交侧穿桥梁桩基施工过程中桩基变形规律的理论分析则相对较少,且现有方法大多仅能解决桥梁桩基的水平或竖向其中一项的变形计算问题,不利于工程设计. 因此,有必要针对隧道盾构近接斜交侧穿既有桥梁桩基施工引起桩基变形的问题开展相关研究.
本研究以隧道盾构近接斜交侧穿既有桥梁桩基的实际工程为例,考虑桥梁桩基与隧道盾构斜交角和地层损失率变化的影响,修正传统Loganathan公式,并基于文克尔弹性地基梁模型、m法计算理论和荷载传递法,推导并建立盾构隧道近接斜交侧穿既有桥梁桩基施工引起桩基变形的计算方法,并对隧道轴心与桩基中心轴线水平距离、隧道盾构侧穿斜交角2种因素对桩身水平挠曲变形的影响进行分析,通过现场监测结果验证计算方法的工程适用性.
1. 文克尔弹性地基梁模型及m法计算理论
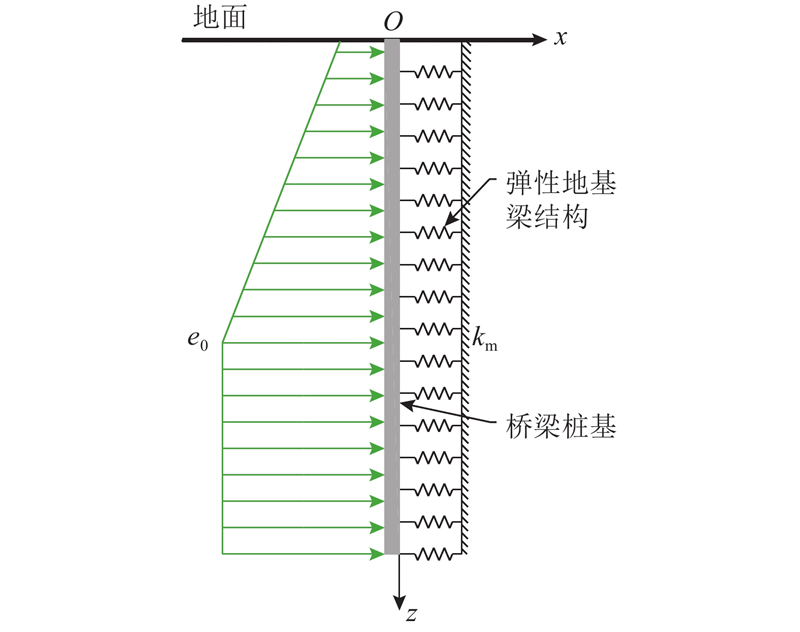
采用弹性地基梁法不仅能计算桩的位移,也能有效反映桩身的变形,因此可将桥梁桩基视为文克尔弹性地基梁,如图1所示. 图中,km为弹簧的弹性系数,e0为主动土压力. 取单位宽度的桥梁桩基作为竖直放置的弹性地基梁,在无外荷载影响的情况下,桥梁桩基外侧土体产生的主动土压力e0可视为作用在桩身的水平荷载,而土体抗力作用在桩基内侧,与之平衡. 在文克尔弹性地基梁模型中,土体水平抗力与桩侧土体压缩量成正比,且桩侧土体压缩量与桩身水平位移相等,由此可以得到桩侧土体水平抗力. 桩侧土体水平抗力表达式如下:
图 1
图 1 桥梁桩基的文克尔弹性地基梁模型示意图
Fig.1 Schematic diagram of Winkel elastic foundation beam model for bridge pile foundations
式中:μ为地基反力系数,δ为桩身水平位移,l'为桥梁桩基的计算宽度.
综上所述,可以根据文克尔弹性地基梁理论提出计算桥梁桩基变形时应满足的假设条件:1)将桩身视为竖向布置的弹性梁,沿深度方向将梁的中心线设为z轴,梁的挠曲面为xOz平面,O点为x轴与z轴在梁中心线上的交点;2)不考虑桩身沿中心轴线产生的压缩变形以及水平方向的挤压变形;3)变形前垂直于中心线的平面在变形后仍保持为平面,但不一定垂直于挠曲线;4)忽略弹性梁截面的剪切转角沿中心轴线关于
式中:q为弹性梁截面剪力;
利用文克尔弹性地基梁模型对盾构近接施工侧穿既有桥梁桩基引起的桩基变形问题进行求解,根据上述弹性地基梁的假设条件,可采用m法计算理论对弹性桩进行分析. 须满足m法的基本假定[8]:1)桩基所处地层土体为弹性体,地基系数从地表至地层深处由零开始按正比例函数关系递增;2)桩基挠曲变形时的土体抗力不受桩基与土之间的摩阻力和黏结力2种因素的影响,并将桩基周围土体受力形成的弹性压缩变形利用地基系数来计算;3)当桩基入土深度与其变形系数的乘积不超过2.5时,可将桩基视为刚性桩进行计算,反之,则将桩基视为弹性桩进行计算.
综上,将桥梁桩基视为文克尔弹性地基梁,根据上述弹性桩m法的计算假定可以得到沿桩身分布的水平荷载作用下桥梁桩基的力学平衡方程:
式中:n为桩侧水平力分布系数,c'为桩基侧面宽度.
引入桥梁桩基变形系数,则式(3)可以改写为
式中:a为桥梁桩基变形系数.
将桩侧水平位移以级数形式表示,得到桩侧水平位移级数解:
综上,由式(2)、(6)可以得到桥梁桩基的抗弯刚度W、转角ψ、弯矩M和剪力Q的级数表达式:
联立式(6),采用初参数法,以桩顶为研究对象,令z=0,则可以求得桥梁桩基桩顶的初始挠度ω0、转角ψ0、弯矩M0和剪力Q0,由此可进一步求得桩侧水平位移级数解的系数b0、b1、b2、b3.
式中:E为桩身弹性模量,I为桩身截面惯性矩.
将式(8)代入式(6),按j=3展开后得到以桩顶初始参数表示的桥梁桩基沿桩身变化的挠曲变形:
式中:A1(z)、B1(z)、C1(z)、D1(z)均为不考虑剪切变形影响时的弹性梁挠曲变形计算所需无量纲参数的函数表达式,可由文献[9]获得.
2. 桩基变形计算方法建立
2.1. 桩身水平挠曲变形
图 2
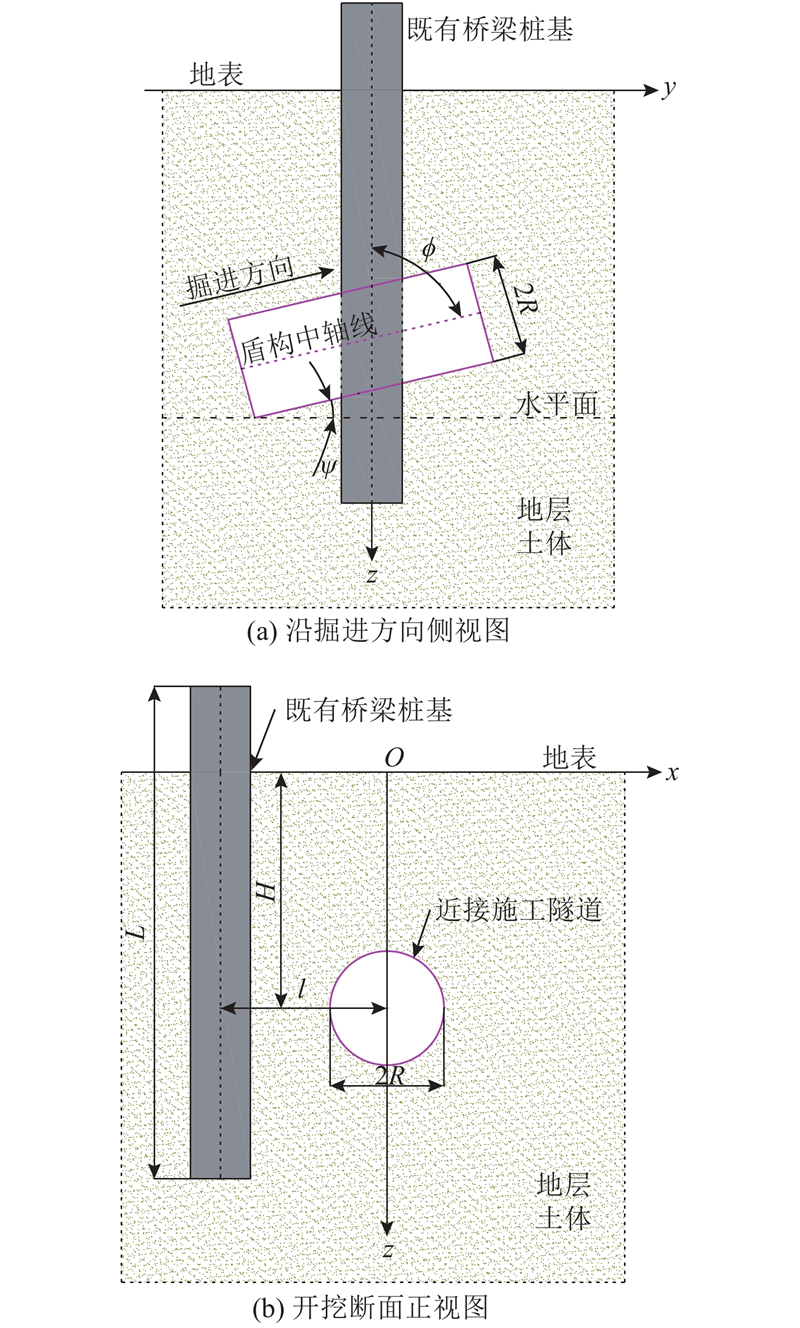
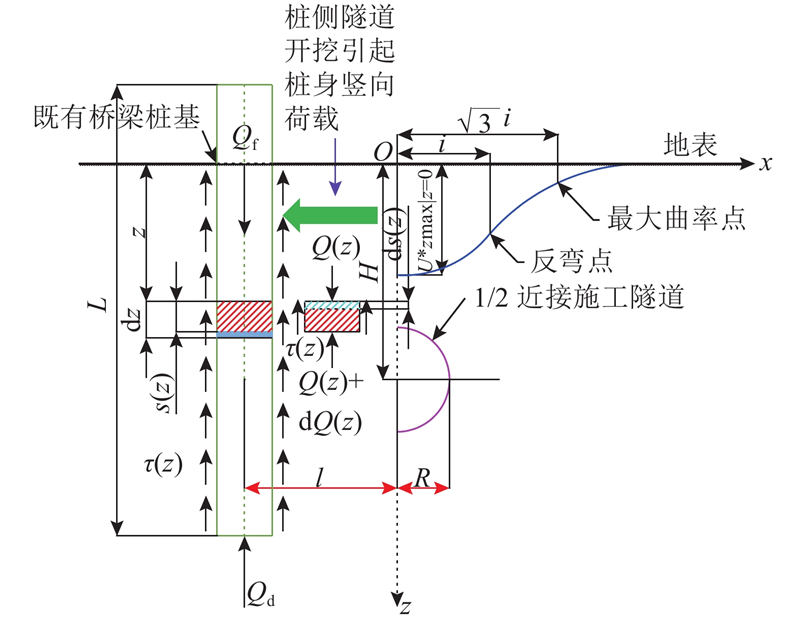
图 2 盾构隧道近接斜交侧穿桥梁桩基施工布置示意图
Fig.2 Layout diagram of shield tunnel construction for diagonal intersection with side penetration of adjacent existing bridge pile foundation
图 3
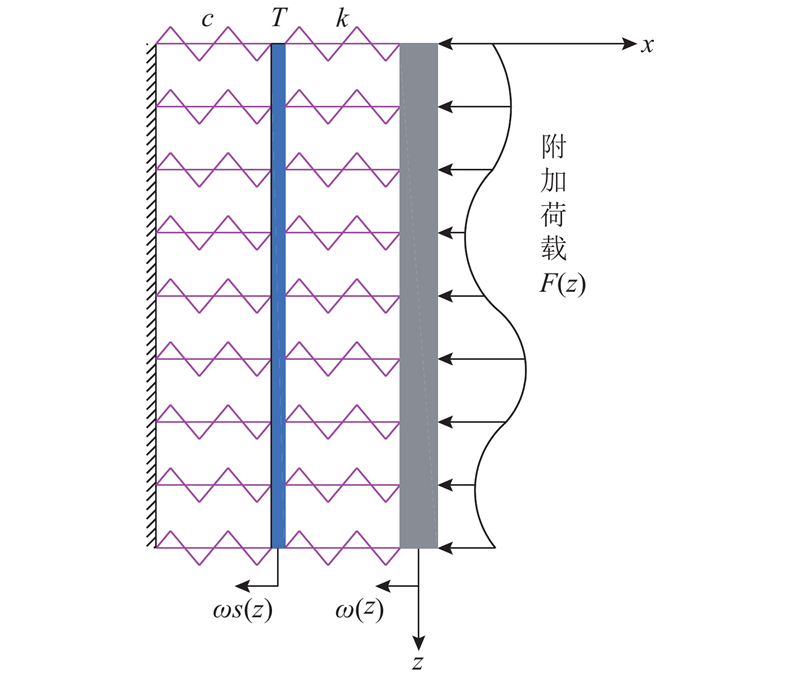
图 3 隧道盾构斜交侧穿时桥梁桩基的桩-土相互作用模型
Fig.3 Pile-soil interaction model of bridge pile foundation during diagonal interaction with side penetration of tunnel shield
式中:R为隧道开挖半径;f、g、h、f'、g'、h'、d、V均为函数变量;ε'为考虑掘进过程中土体损失率变化、盾构坡角ψ和地层损失共同影响的修正土体竖向损失. 表达式如下:
式中:H为隧道中心埋深,z为土体任一点的地层深度,v为泊松比,φ为地层土体内摩擦角.
ε'表达式如下:
式中:Vloss为未考虑土体回弹变形影响的地层损失;cs为地层土体黏聚力;K为地层土体的主动土压力系数,K=tan2 (45°−φ/2), φ为地层土体内摩擦角;γ为地层土体重度; Es为隧道拱顶地层土体回弹模量.
d'表达式如下:
根据修正后的Loganathan公式,求得隧道与桥梁桩基斜交情况下近接施工引起的桩侧土体水平位移,则由如图3所示的桩基受力情况可以求得盾构隧道斜交侧穿施工时的桩基附加水平荷载:
式中:Ux(z)为修正后Loganathan公式得出的隧道开挖引起的土体水平位移,
式中:B'、B''均为Ux(z)二阶导数式中的多项式.
根据如图3所示的桩-土相互作用关系,考虑剪切变形的影响,可以求得附加荷载F(z)作用下的桩身挠曲变形:
式中:ωs(z)为桩基剪切层的弹簧变形,ωe(z)为桩身弹簧变形.
由此可以分别求得桩身及剪切层的弹性应力:
式中:k为桩身弹簧的地基反力系数[12].
桥梁桩基剪切层变形的应力平衡微分方程如下:
联立式(26)中的第1个公式和式(27)可以得到桩身挠曲变形:
引入附加水平荷载作用下的桥梁桩基平衡方程:
式中:r为桥梁桩基横截面半径.
将式(4)、(21)、(27)、(28)代入式(29),得到盾构隧道近接侧穿桥梁桩基引起桩身挠曲变形的控制方程:
进一步简化,得到
式中:Es为地层土体弹性模量;t为桥梁桩基周围土体剪切层厚度,且t=11r[13];vs为桥梁桩基周围土体泊松比.
针对式(31)的求解,如图4所示,可以采用差分进化算法实现:
图 4
式中:n为差分进化算法的种群数, n为大于0的自然数.
结合桩基边界条件,可以求得盾构隧道近接侧穿桥梁桩基引起的桩身挠曲变形方程,由此建立盾构隧道近接侧穿施工引起的桩身挠曲变形计算方法.
式中:Fn为盾构隧道侧穿施工时的桩基附加水平荷载; K−1为逆矩阵,包含桩身挠曲变形方程中的各项系数.
2.2. 桩基竖向位移
图 5
图 5 桥梁桩身竖向荷载传递的力学模型
Fig.5 Mechanical model for transmission of vertical load of bridge pile body
式中:dQ(z)为传递到桩基单元体上的竖向荷载增量;z为地层深度,也可以表示桩身上某点在地层中的埋深.
按照材料力学中的纵向变形公式,可以得到桩基单元体的纵向变形:
式中:Ep为桩身材料弹性模量.
将式(39)代入式(38),得到桩基单元体的力学平衡方程:
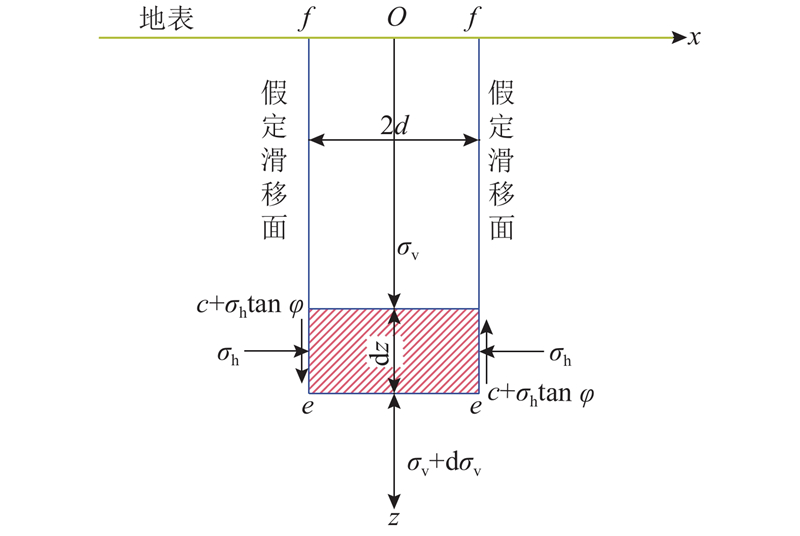
综上所述,考虑盾构隧道近接侧穿桥梁桩基施工将引起桩基周围地层土体产生沉降,同时考虑到隧道开挖后的土拱效应使得拱顶区域内每个微小土体单元上的剪应力合力dq和土体重力的作用力方向相反,从而导致土体卸荷回弹现象的产生,如图6所示. 取一微小土体单元,则作用在该微小土体单元上的剪应力合力为
图 6
图 6 土体卸荷回弹状态下隧道拱顶剪应力计算模型
Fig.6 Calculation model of shear stress in tunnel vault under soil unloading and rebound
式中:σn、σv分别为微小土体单元上的水平侧向应力和竖向应力.
根据图6,隧道拱顶上覆土层厚度为H−R/cos ψ,则受土拱效应影响的隧道拱顶上覆地层土体卸荷总量表达式为
综上所述,地层土体卸荷回弹会导致地层损失减小:
将式(43)代入式(19),可以得到土体卸荷回弹影响下的地层损失率:
将式(44)代入式(10)中第2个公式,使得修正后的Loganathan公式可以计算土体卸荷回弹影响下的竖向位移:
式中:x为隧道周围任一点土体关于隧道中心轴线的横坐标,l为隧道轴心与桩基中心轴线的水平距离.
将式(46)代入式(45),可以得到考虑土体卸荷回弹影响时隧道开挖引起的桩侧土体竖向位移:
当λ(x)=r时,可以得到桩周土体负摩阻力:
由桩侧力学相互作用可知桩侧负摩阻力f(z)在值上与桩侧剪应力τ(z)相等,则由式(39)可得桩侧隧道开挖引起深度z处桩基单元体上的竖向荷载:
根据文献[14],采用修正后的Boussinesq解计算桩身的纵向变形:
式中:η为桥梁桩基埋入土中深度的影响系数,G为桩侧土体剪切模量.
在盾构隧道近接斜交侧穿桥梁桩基施工时,单桩桩周单位厚度土的等效刚度系数可以按照文献[15]中的方法计算:
式中:ρ为桩身中部和桩端处的土体剪切模量之比有关的不均匀系数[15].
将式(54)、(55)代入式(39),且不考虑桩-土界面滑移的影响[16],可以得到盾构隧道近接斜交侧穿桥梁桩基引起桩基沉降的微分方程:
综上,根据桥梁桩基在近接隧道轴心深度处和桩端位置处的纵向力学平衡条件,可以得到式(56)的边界条件为
由此可以解得盾构隧道近接斜交侧穿桥梁桩基引起的桩基沉降:
综上,可分别通过式(36)、(58)计算得到盾构隧道近接斜交侧穿既有桥梁桩基施工引起的桩身挠曲变形和桩基沉降,建立盾构隧道近接斜交侧穿既有桥梁桩基变形计算方法.
3. 模型验证
3.1. 工程概况
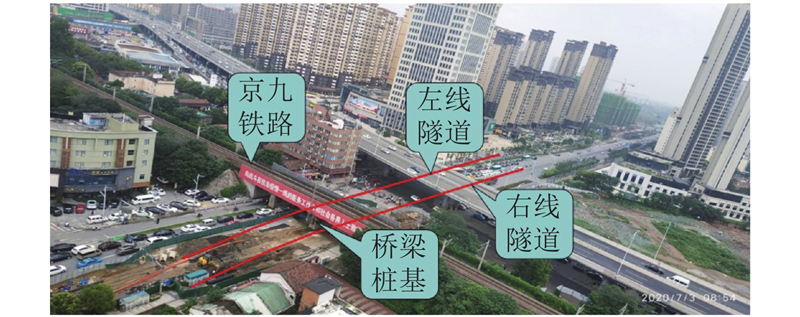
南昌市轨道交通4号线起凤路站~七里站区间隧道双线隧道间距范围为12.0~18.3 m,隧道拱顶埋深范围为9.5~18.5 m. 区间正线采用盾构法施工,且于里程ZDK43+136-ZDK43+180、YDK43+140-YDK43+182处下穿京九铁路正线,如图7所示. 区间线路与既有铁路桥梁桩基在同一平面上的斜交角ϕ≈89°,下穿处隧道拱顶覆土厚度为17.5 m,且盾构隧道左右线间距约为15.5 m. 其中,右线隧道以半径R=1 200 m近接侧穿京九铁路桥梁桩基,侧穿处右线隧道中心轴线与京九铁路桥梁桩基轴线的水平间距约为6.5 m. 该区域地层从上至下依次为杂填土、粉质黏土、粗砂、砾砂、强风化泥质粉砂岩、中风化泥质粉砂岩,各层土体物理力学参数如表1所示. 表中,Γ为层厚,γ为天然重度,cs为黏聚力,φ为内摩擦角,Es为各层土体的压缩模量.
图 7
图 7 盾构隧道近接侧穿既有铁路桥梁桩基施工现场
Fig.7 Site of shield tunnel construction for diagonal intersection with side penetration of adjacent existing railway bridge pile foundation
表 1 土体物理力学参数取值情况统计表
Tab.1
| 岩土层名称 | Γ / m | γ / (kN∙m−3) | cs / kPa | φ / (°) | Es / MPa | ν |
| 杂填土 | 1.8 | 17.8 | 5.5 | 16.5 | — | — |
| 粉质黏土 | 5.4 | 17.6 | 25.2 | 24.4 | 8.5 | 0.35 |
| 粗砂 | 3.2 | 20.2 | 0 | 22.3 | 12.6 | 0.29 |
| 砾砂 | 14.2 | 22.5 | 0 | 23.6 | 16.3 | 0.25 |
| 强风化泥质粉砂岩 | 2.6 | 23.2 | 10.2 | 20.2 | 22.5 | 0.21 |
| 中风化泥质粉砂岩 | 20.8 | 23.6 | 13.6 | 21.8 | 25.3 | 0.18 |
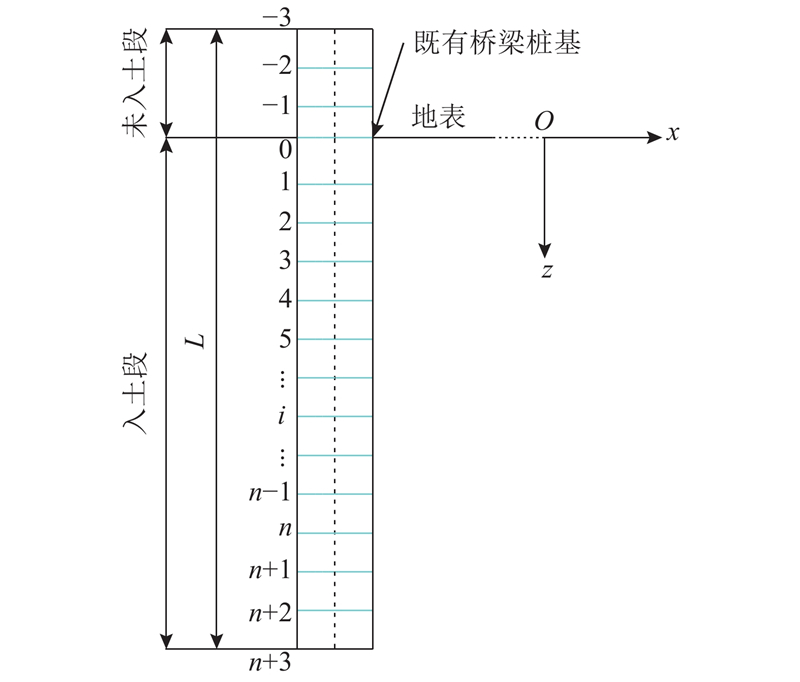
以YDK43+140-YDK43+182里程处的右线隧道近接侧穿既有铁路桥梁桩基为研究对象,则沿掘进方向的隧道盾构侧向先后穿越的2个既有铁路桥梁桩基的桩长均为42.0 m,其中未入土段桩长L'=6.0 m,入土段桩长L''=36.0 m,桥梁桩基模量Ec=30 GPa,桩截面为圆形,直径为3.0 m. 为了便于研究,对前后2个铁路桥梁桩基分别编号为桩1#和桩2#,具体位置关系详见图8,且盾构机在穿越段沿直线掘进. 隧道中心轴线至桥梁桩基边界的最近水平距离均约为5.0 m,盾构掘进开挖过程中的地层损失率ε0≈1%.
图 8
图 8 既有铁路桥梁桩基与盾构隧道位置关系示意图
Fig.8 Schematic diagram of relationship between pile foundation of existing railroad bridge and location of shield tunnel
3.2. 对比验证
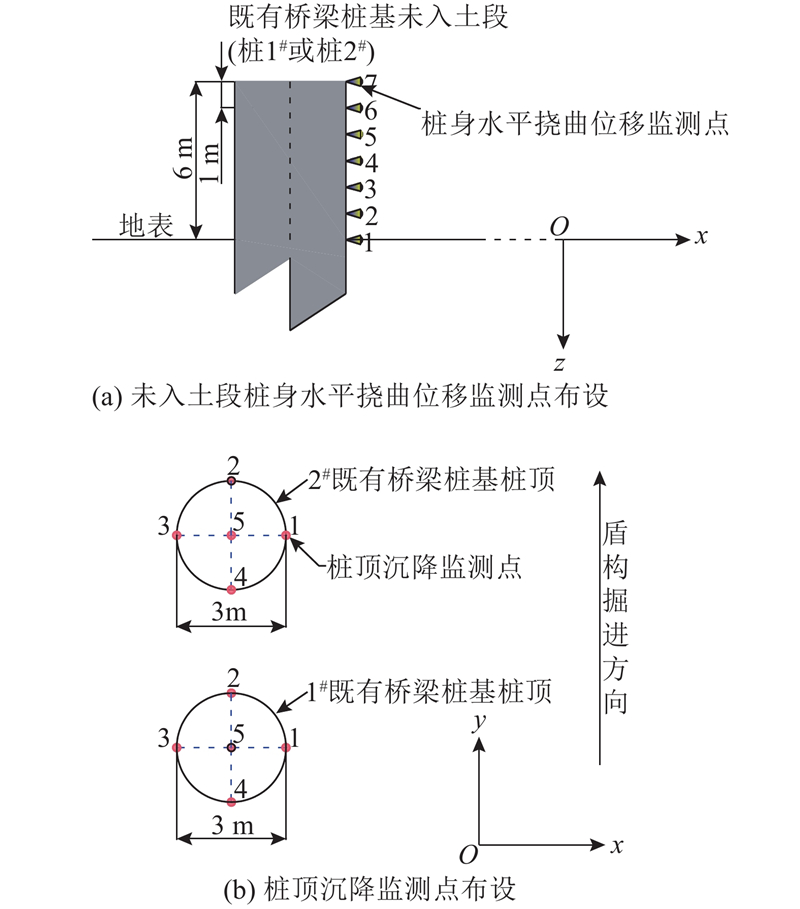
根据工程现场的实际情况,选择右线隧道先后近接斜交侧穿的桩1#和桩2#作为监测对象,在桩身和桩顶分别布置变形监测所需的应变片,以分别对未入土段桥梁桩基的水平位移和沉降进行测量,具体监测点布设情况如图9所示.
图 9
图 9 未入土段铁路桥梁桩基变形监测点布置示意图
Fig.9 Layout of pile foundation deformation monitoring points of railroad bridges in unincorporated section
综上,将桩1#和桩2#的未入土段桩身水平位移和桩顶沉降的监测结果与其理论计算结果进行对比分析,如图10所示. 由于桩身变形的连续性,若未入土段桩身水平及竖向变形的理论计算结果与监测结果拟合良好,则可证明本研究计算方法的工程适用性.
图 10
图 10 未入土段桩基位移结果对比图
Fig.10 Comparison of pile displacement results for unincorporated section
由图10可知,未入土段的桩身水平位移和桩顶竖向位移的理论计算结果均与现场监测结果拟合良好,且桩1#和桩2#未入土段的桩身水平位移的理论计算结果与监测结果之间的最大误差分别为14.6%、10.5%;桩顶竖向位移的理论计算结果与监测结果之间的最大误差分别为2.7%、2.7%,均小于工程经验允许的20%误差要求. 理论值曲线整体上与监测结果的变化趋势一致,监测结果较稳定地分布在桩身水平位移理论值曲线和桩顶竖向位移理论计算结果等值线的附近区域,均在曲线上下微小范围内浮动,故既有桥梁桩基在未入土段的桩身水平位移和桩顶竖向位移的理论计算结果均与现场监测结果整体变化趋势相契合,在一定程度上证明本研究方法的计算精度较高,并具有良好的工程适用性.
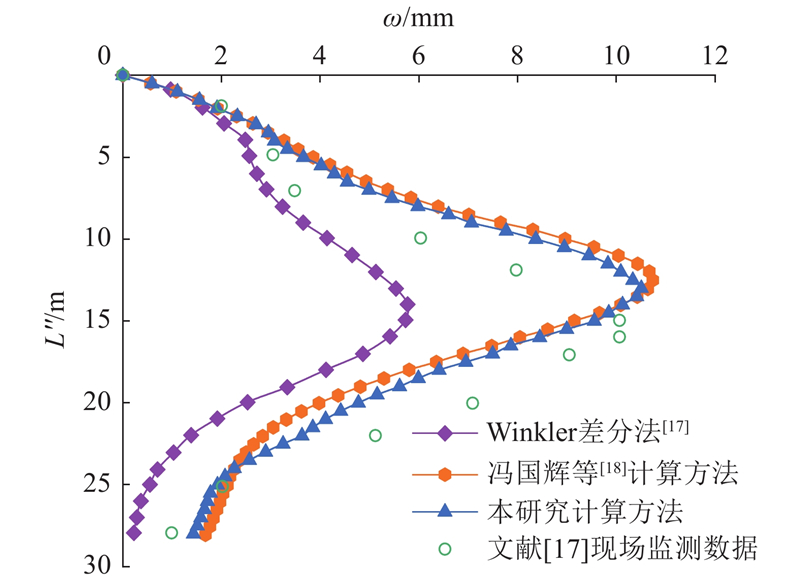
图 11
图 11 不同方法所得入土段桩身水平位移结果对比图
Fig.11 Comparison of horizontal displacement of pile body obtained by different methods
3.3. 影响因素分析
3.3.1. 隧道轴心与桩基中心轴线水平距离
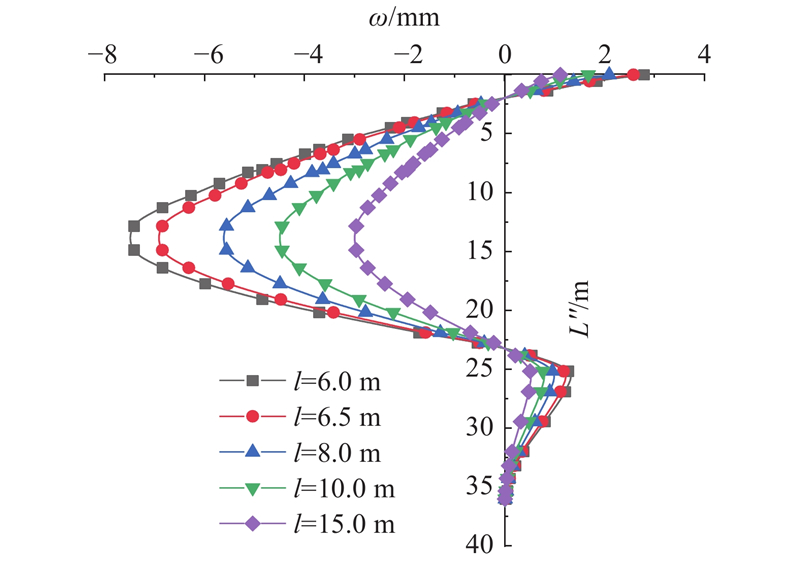
侧穿时隧道与既有桥梁桩基的距离对桩基变形影响较大,采用控制变量法分析隧道轴心与桩基中心轴线水平距离l对桩身水平挠曲变形的影响规律. 基于前述工程案例,依次选取l=6.0、6.5、8.0、10.0、15.0 m,在控制其他因素不变的条件下,通过本研究所建立的桩基变形计算方法计算各组工况下入土段桩基在水平方向上的桩身挠曲变形,计算结果如图12所示. 可以看出,入土段桩身水平挠曲程度随其与隧道净距的减小而逐渐增大,且在盾构侧穿过程中,桩身靠近地表区段向隧道开挖一侧产生水平位移. 隧道盾构近接侧穿区域的桩身水平挠曲变形较大. 在水平侧穿距离l= 6.0 m工况条件下,入土段桩身水平挠曲变形达到最大值7.4 mm;该位置埋深约为15 m,且桩身挠曲变形沿桩身向桩基靠近地表区段和桩基底部逐渐减小;埋深约为2、23 m位置处于桩身水平挠曲变形的反弯点,埋深在2个反弯点区间[2, 23] m以外的桩身水平挠曲变形开始逐渐趋向于隧道开挖一侧,且埋深在[0, 2) m的桩身水平位移逐渐缓慢增大,直至达到地表,而埋深在(23, 36] m的桩身水平位移先增大后减小,且在桩基底部逐渐趋近于零.
图 12
图 12 隧道轴心与桩基中心轴线水平距离影响下的桩身水平挠曲变形曲线
Fig.12 Horizontal deflection curve of pile body under influence of horizontal distance between tunnel axis and pile center axis
对比不同工况下的桩身挠曲变形可知,随着隧道轴心与桩基中心轴线水平距离的增大,桩身水平挠曲变形逐渐减小,并趋于稳定,且当两者之间的水平距离相距较大时,侧穿对桥梁桩基挠曲变形的影响可以完全忽略. 表明隧道轴心与桩基中心轴线水平距离是盾构侧穿桥梁桩基引起桩身挠曲变形的主要影响因素之一,实际工程中应控制盾构隧道与既有桥梁桩基的安全穿越距离,以减轻穿越施工对桥梁桩基造成的变形之类的不良影响.
3.3.2. 隧道盾构侧穿斜交角
基于前述工程案例,仍采用控制变量法分析隧道盾构侧穿斜交角ϕ的影响规律,依次选取ϕ=90.0°、89.8°、89.5°、89.0°、88.0°、85.0°、80.0°、70.0°,在控制其他因素不变的条件下,通过本研究所建立的桩基变形计算方法计算各组工况下入土段桩基在水平方向上的桩身挠曲变形,计算结果如图13所示. 可以看出,入土段桩身水平挠曲程度随隧道侧穿斜交角的减小而逐渐增大;在盾构侧穿过程中,桩身靠近地表区段的水平挠曲位移随盾构侧穿斜交角的减小逐渐由靠近隧道开挖一侧向远离隧道开挖一侧移动;入土段桩身产生最大水平挠曲位移的埋深也逐渐减小,向靠近地表方向移动;在隧道盾构侧穿斜交角ϕ=70.0°条件下,各组工况中入土段桩身的最大水平挠曲位移为15.4 mm,该点的埋深约为9 m. 入土段桩身的最大水平挠曲位移也随隧道盾构侧穿斜交角的减小而逐渐增大;桩身挠曲变形均从各组工况下的最大值位置处沿桩身向桩基靠近地表区段和桩基底部逐渐减小;桩基底部的桩身水平挠曲变形均从远离隧道开挖一侧逐渐转向为隧道开挖一侧. 随着隧道盾构侧穿斜交角的逐渐减小,靠近地表区段桩身水平挠曲变形的反弯点将逐渐消失,而接近桩基底部区段桩身水平挠曲变形的反弯点的埋深将逐渐减小;靠近桩基底部区段的桩身各点在通过反弯点后的水平位移向隧道开挖一侧先增大后减小,且在桩基底部逐渐趋近于零. 对比不同工况下的桩身挠曲变形可知,水平方向上的桩身挠曲变形同隧道盾构侧穿斜交角呈负相关,且当隧道盾构侧穿斜交角逐渐减小时,侧穿对桥梁桩基挠曲变形的影响程度也逐渐增大,且桩身水平挠曲变形曲线的分布形式也随隧道盾构侧穿斜交角而逐渐变化. 表明隧道盾构侧穿斜交角是盾构侧穿桥梁桩基引起桩身挠曲变形的主要影响因素之一,在盾构侧穿施工中也须合理控制穿越角度,以减轻施工过程对桥梁桩基造成的变形之类的不良影响.
图 13
图 13 盾构侧穿斜交角影响下的桩身水平挠曲变形曲线
Fig.13 Horizontal deflection deformation curve of pile body under influence of oblique intersection angle of shield side penetration
4. 结 论
(1)修正后的Loganathan公式考虑了盾构隧道近接侧穿斜交角和地层损失率沿掘进路径变化的综合影响,可以求得近接隧道盾构斜交侧穿开挖卸荷作用下桥梁桩基和隧道周围的土体位移以及桩基附加荷载.
(2)推导并建立的盾构隧道近接斜交侧穿既有桥梁桩基时桥梁桩基的变形计算方法,不仅可以解决正交侧穿时桥梁桩基的变形计算问题,也适用于解决斜交侧穿的工况,并且可以同时计算隧道近接侧穿时桥梁桩基的水平位移和竖向位移,方法适用范围较大,具有良好的工程适用性.
(3)近接斜交侧穿盾构隧道中心埋深附近的桥梁桩身水平位移取得最大值;隧道轴心与桩基中心轴线水平距离、隧道盾构侧穿斜交角均为桩基水平挠曲变形的主要影响因素,并关于桩身水平挠曲最大变形量呈负相关. 在实际施工中应重点控制近接侧穿深度附近区域桥梁桩基的安全穿越距离和盾构侧穿斜交角,以控制桩身水平位移值在合理区间,减轻穿越施工造成的桥梁桩基变形影响,保证既有桥梁的安全性.
(4)所提计算方法仅适用于盾构隧道近接施工过程中单桩变形计算,尚未考虑群桩效应;以地层参数的加权平均值代替桩周土体的分层特性,存在一定的计算误差;对本研究方法在盾构侧穿的其他空间位置场景下的适用性也未做具体讨论. 在后续研究中还应考虑更多斜交侧穿空间位置场景及其他因素的影响,以构建精度更高、适用范围更广的盾构隧道近接斜交侧穿既有桥梁桩基时桥梁桩基的变形计算方法.
参考文献
盾构近距离侧穿桥梁及下穿公路变形规律与控制技术研究
[J].
Research on deformation law and control technology of shield close side crossing bridge and underpassing highway
[J].
盾构法施工对近距离侧穿桥梁桩基的影响分析
[J].
Analysis on the influence of shield construction on lateral and closely cross bridge pile foundation
[J].
Analysis of construction impact of a large diameter shield tunneling side-crossing viaduct pile foundations in short distance
[J].DOI:10.1007/s10706-021-01846-4 [本文引用: 1]
基于渗流应力耦合的盾构隧道开挖对邻近桥梁桩基的影响
[J].
Influence of shield tunneling on pile foundation of adjacent bridge using fluid-soil coupling theory
[J].
隧道开挖引起水平向位移被动桩的简化计算方法
[J].
Simplified calculation method for lateral displacement of passive pile caused by tunneling
[J].
既有单桩在邻近基坑开挖下的水平向响应简化分析
[J].
Simplified analysis method for evaluating horizontal deformation of single pile due to adjacent foundation pit excavation
[J].
隧道开挖对邻近单桩竖向受力特性影响
[J].DOI:10.16285/j.rsm.2013.02.033 [本文引用: 1]
Effects of tunneling on vertical bearing behaviors of adjacent single pile
[J].DOI:10.16285/j.rsm.2013.02.033 [本文引用: 1]
滑体段采用m法模型的抗滑桩计算方法
[J].
An improved method for stabilising pile by using m-method model to the whole pile
[J].
考虑剪切变形影响的桩基m法计算理论
[J].
Calculating theory of m method assumption for piles with shear deformation effect
[J].
Analytical prediction for tunneling-induced ground movement in clays
[J].DOI:10.1061/(ASCE)1090-0241(1998)124:9(846) [本文引用: 1]
基于Loganathan & Poulos、Clough修正公式的浅埋超大直径盾构隧道地面沉降预测
[J].
Ground settlement prediction of shallow-buried super-large-diameter shield tunnel based on Loganathan and Poulos and Clough modified formulas
[J].
对“考虑桩侧土体三维效应和地基剪切变形的隧道开挖对邻近桩基影响分析”讨论的答复
[J].DOI:10.11779/CJGE201807026 [本文引用: 1]
Reply to discussion on “influence of tunneling on deflection of adjacent piles considering shearing deformation of foundation and 3D effects of lateral soils beside piles”
[J].DOI:10.11779/CJGE201807026 [本文引用: 1]
Analysis of deformation of vertically load piles
[J].
基于荷载传递法的高承台桩基沉降计算方法研究
[J].
Settlement calculation of pile foundations with elevated caps by load transfer method
[J].
岩土抗拉模量值修正与桩土作用理论解答研究
[J].
Research of constitutive relation correction of geotechnical materials and theoretical solution due to pile-soil interaction
[J].
Simplified solution for tunnel-soil-pile interaction in Pasternak’s foundation model
[J].
盾构掘进引起的邻近群桩水平位移解析研究
[J].
Analytical study of horizontal displacement of adjacent pile group caused by shield tunneling
[J].