结构动力特性对结构动力设计和振动分析有重要意义,它反映了结构系统刚度、质量分布及边界条件等信息. 由于构件制造误差、老化损伤及自身固有的随机性等因素影响,结构参数具有不确定性,从而导致结构动力特性具有随机性[1]. 为了提供更准确的结构动力信息[2-3],须定量计算结构参数传递到结构动力的不确定性. 蒙特卡罗模拟法(Monte Carlo simulation, MCS)是结构动力不确定性量化常用的方法,其通过大量的有限元模型计算得到动力响应的统计特性[4],不足之处在于计算成本过高. 为了克服MCS方法的不足,代理模型方法构建用于替代结构有限元模型的近似数学模型. 不确定性量化的代理模型包括响应面[5-6]、多项式混沌展开[7]、高斯过程模型(Gaussian process model, GPM)[8]等. 高斯过程模型是一种非参数概率模型,广泛用于不确定性量化[9-11],具有模拟灵活性和预测不确定性定量等优点.
本研究提出基于序贯设计和高斯过程模型的结构动力不确定性量化方法. 基于GPM的预测方差(mean squared error, MSE)信息,通过最大化预测方差(maximizing mean squared error, MMSE)[19]依次选择最佳设计点,逐步自适应地更新GPM. 基于建立的自适应GPM,动力特性统计矩的复杂高维积分可以转化为简单一维积分,进而可以解析计算出结构动力特性统计矩.
1. 高斯过程模型与序贯设计
1.1. 高斯过程模型
式中:η2为协方差函数的变化尺度;d为输入参数的维度;xk为参数x的第k个元素;lk为协方差函数的变化速率;协方差函数的参数
假设有n个观测值的样本点集
待预测点
根据贝叶斯原理,预测值
将式(2)、(3)代入式(4),得到
式中:
式中:
GPM的超参数
1.2. 序贯设计
序贯设计是基于样本填充准则,依次选择最有用的样本点填充至初始样本集中,不断地通过新样本点更新代理模型. 序贯设计的关键是如何根据样本点和当前代理模型选择新的样本点,即如何定义样本填充准则. GPM能够提供预测方差信息(mean squared error, MSE),MSE反映GPM与原始物理模型之间的差异. MSE越大,表明GPM的预测误差越大. 在预测方差最大处增加样本点,能够减小GPM的预测误差. 因此提出基于最大化预测方差的样本填充准则,计算式为
式中:
样本迭代采用的停止准则[20]为
式中:r为比例系数,取值为0.01%~1.00%;
通过MMSE填充准则的动态序贯设计,构建自适应GPM,由于包含最优设计点,可以有效地提高GPM的预测精度. 建立自适应GPM的具体步骤如下.
1) 获取初始训练样本点X;
2) 以X作为输入值计算有限元模型,得到相应的响应输出值Y;
3) 得到初始样本集
4)
5) 以
6) 更新初始样本集
7) 利用步骤6) 中的样本集
8) 判断是否满足停止准则
2. 动力特性统计矩的解析计算
将结构动力特性的输入参数x与输出响应y的关系用自适应GPM来表达,其中输入参数x的概率分布函数为
利用平方指数协方差函数的分离特性,式(6)、(7)可以转换为
将式(13)、(14)代入式(11)、(12),得到
式中:
当参数
当参数
式中:
3. 自适应高斯过程模型拟合过程展示
采用一维函数
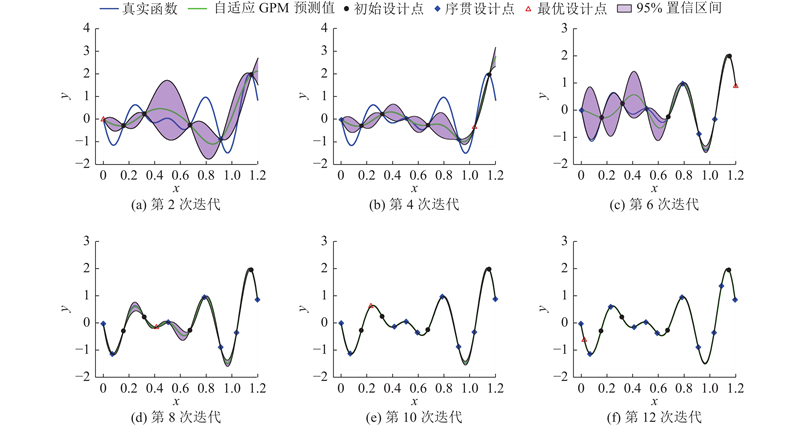
初始样本设为4个,根据MMSE填充准则,在每次迭代过程中选择最优的设计点填充至初始样本集中,并更新当前的GPM,停止准则的比例系数r=0.02%. 整个迭代建模的部分动态过程如图1所示,可以看出,随着迭代次数的增加,GPM的预测均值与真实函数曲线的拟合程度越来越高;GPM的预测方差逐渐减小,即图中95%的置信区间面积不断减小,表明所建立的GPM精度越来越高.
图 1
图 1 一维函数自适应GPM的迭代过程
Fig.1 Evolution of adaptive GPM for a one-dimensional test function
二维函数
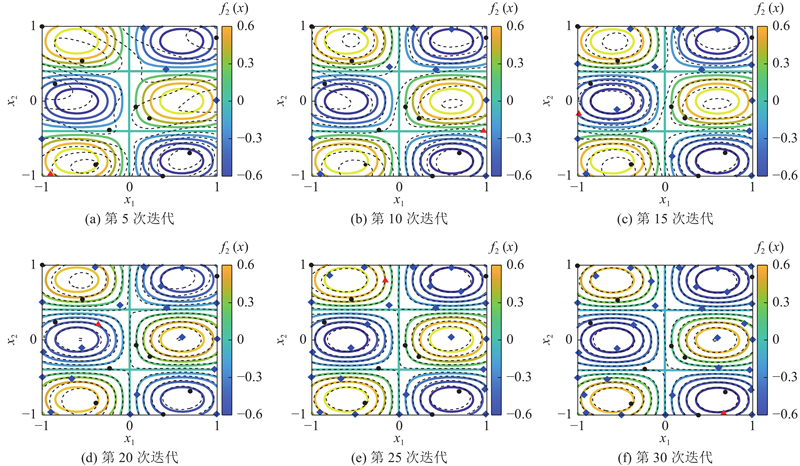
初始样本设为10个,停止准则的比例系数r=0.02%. 在每次迭代过程中,通过MMSE选择最佳设计点,迭代过程如图2所示. 图中,实线为真实函数,虚线为自适应GPM预测值,圆点为初始设计点,菱形为序贯设计点,正三角形为最优设计点. 对于二维函数,以等高线图呈现拟合程度来提高可视化. 与一维函数类似,随着迭代次数增加,GPM的预测曲线与真实函数曲线之间的拟合优度提高.
图 2
图 2 二维函数自适应GPM的迭代过程
Fig.2 Evolution of adaptive GPM for a two-dimensional test function
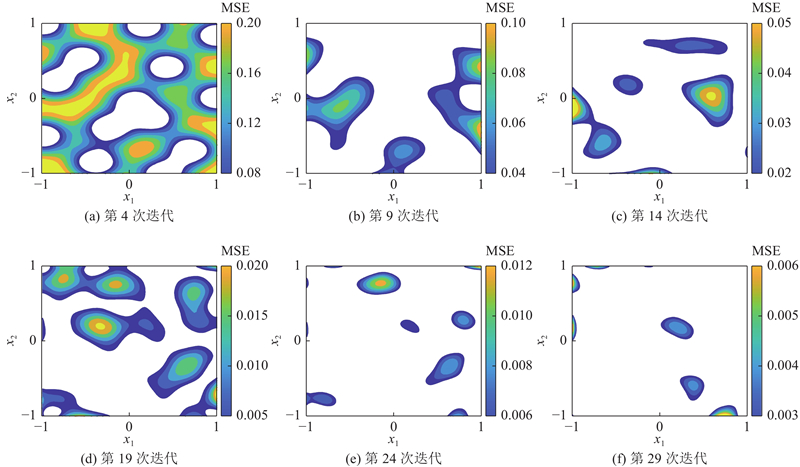
为了更清晰地说明基于MMSE的样本填充机制,迭代过程的部分预测方差如图3所示. 可以看出,随着迭代次数的增加,GPM的预测方差明显减小,进一步表明基于MMSE填充准则建立的自适应GPM可以有效地提高模型预测精度.
图 3
图 3 二维函数自适应GPM迭代过程的MSE
Fig.3 MSE against number of iterations for a two-dimensional test function
4. 方法验证
图 4
图 5
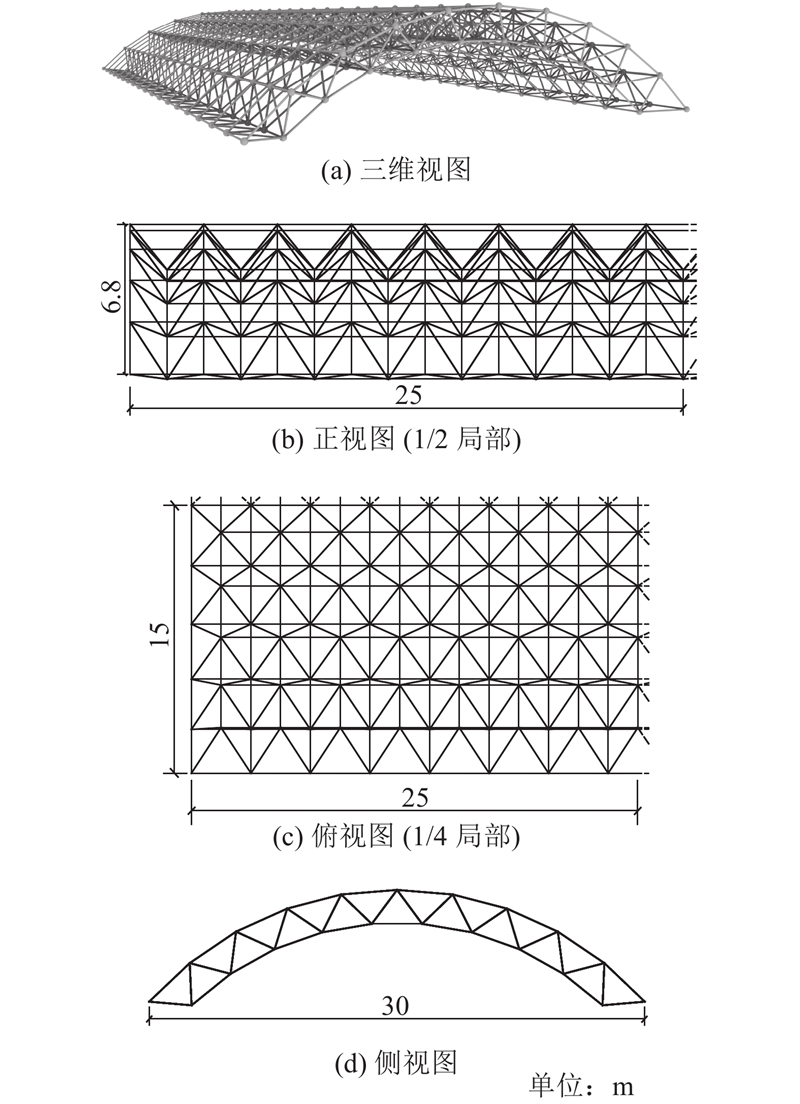
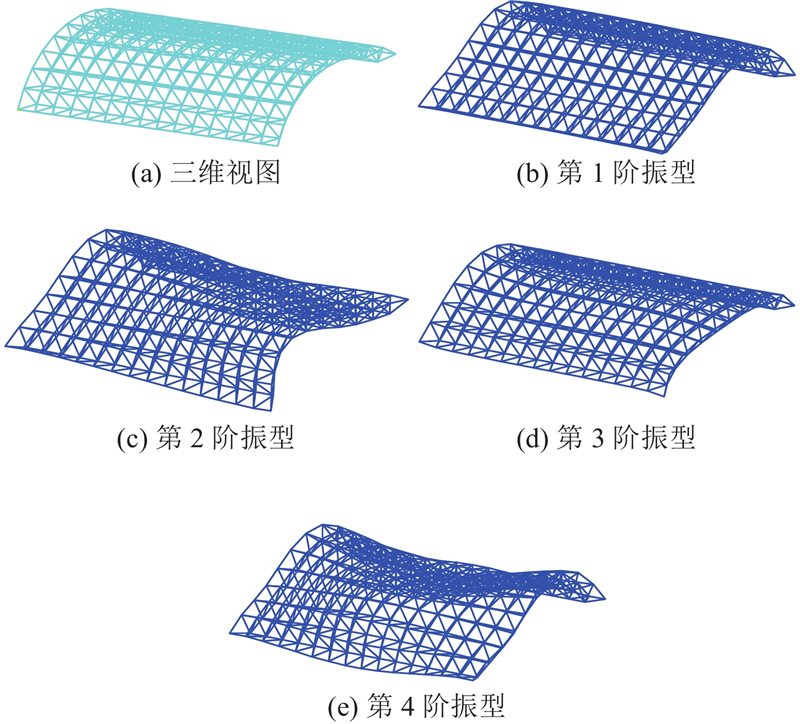
图 5 双层柱面网壳有限元模型和前4阶振型
Fig.5 Finite element model and first-four-order vibration modes of double layer cylindrical reticulated shell
假定钢管半径、钢材密度和弹性模量为不确定性参数(见表1),以网壳的前4阶固有频率为分析对象,计算不确定性参数下该结构固有频率的统计特性. 基于MMSE建立自适应GPM用于结构固有频率的统计矩计算.与传统GPM方法对比,大量次数(
表 1 不确定性参数的统计特征
Tab.1
| 不确定参数 | 分布 | 均值 | 变异系数 |
| 钢管半径 | 均匀分布 | 40 mm | 0.05 |
| 钢材密度 | 正态分布 | 7 850 kg/m3 | 0.10 |
| 钢材弹性模量 | 对数正态分布 | 210 GPa | 0.10 |
表 2 自适应GPM、GPM和MCS法的均值和方差计算结果对比(第1阶固有频率)
Tab.2
| 方法 | 均值 | 方差 | 均值相对误差/% | 方差相对误差/% | 计算时间/s |
| 1)注:括号内的数字“27”、“44”分别指自适应GPM和GPM建模所需的样本个数. | |||||
| 自适应GPM (27)1) | 22.424 4 | 2.564 1 | 0.003 7 | 0.361 5 | 14.3 |
| GPM (44) | 22.424 4 | 2.559 0 | 0.003 6 | 0.561 4 | 20.1 |
| MCS | 22.425 2 | 2.573 4 | — | — | 1 789.2 |
表 3 自适应GPM、GPM和MCS法的均值和方差计算结果对比(第2阶固有频率)
Tab.3
| 方法 | 均值 | 方差 | 均值相对误差/% | 方差相对误差/% | 计算时间/s |
| 自适应GPM (27) | 24.447 6 | 3.047 5 | 0.003 7 | 0.361 6 | 14.3 |
| GPM (44) | 22.447 7 | 3.041 5 | 0.003 6 | 0.561 4 | 20.1 |
| MCS | 24.448 5 | 3.058 7 | — | — | 1 789.2 |
表 4 自适应GPM、GPM和MCS法的均值和方差计算结果对比(第3阶固有频率)
Tab.4
| 方法 | 均值 | 方差 | 均值相对误差/% | 方差相对误差/% | 计算时间/s |
| 自适应GPM (27) | 27.237 0 | 3.782 8 | 0.003 7 | 0.361 6 | 14.3 |
| GPM (44) | 27.237 1 | 3.775 2 | 0.003 6 | 0.561 5 | 20.1 |
| MCS | 27.238 0 | 3.796 5 | — | — | 1 789.2 |
表 5 自适应GPM、GPM和MCS法的均值和方差计算结果对比(第4阶固有频率)
Tab.5
| 方法 | 均值 | 方差 | 均值相对误差/% | 方差相对误差/% | 计算时间/s |
| 自适应GPM (27) | 29.896 9 | 4.557 6 | 0.003 3 | 0.362 2 | 14.3 |
| GPM (44) | 29.896 8 | 4.548 5 | 0.003 8 | 0.561 7 | 20.1 |
| MCS | 29.897 9 | 4.574 2 | — | — | 1 789.2 |
5. 结 论
(1) 所提自适应GPM方法可以通过较少样本数量达到较高的预测精度,均值和方差的相对误差均较低,而传统GPM则需要较多样本点才能达到相当的计算精度,表明所提方法能够明显降低计算成本.
(2) 迭代过程中统计矩的相对误差的变化表明,所提自适应GPM法的相对误差在几次迭代后明显降低,而传统GPM的相对误差在增加大量样本后仍然较高,表明所提自适应GPM法相对于传统GPM法具有高效率的优势.
(3) 所提自适应高斯过程模型方法只涉及一种样本填充准则,可进一步研究其他序贯抽样方法,如最大熵准则、整体均方误差准则,比较几种抽样方法的计算结果,得到不同抽样准则的使用范围。
参考文献
Uncertainty in structural dynamics
[J].DOI:10.1016/j.jsv.2005.07.014 [本文引用: 1]
基于动态贝叶斯网络的变幅载荷下疲劳裂纹扩展预测方法
[J].
Fatigue crack growth prediction method under variable amplitude load based on dynamic Bayesian network
[J].
自助法的改进及在结构参数不确定性量化和传递分析中的应用
[J].DOI:10.16385/j.cnki.issn.1004-4523.2020.04.005 [本文引用: 1]
The improvement of Bootstrap method and its application in structure parameter uncertainty quantification and propagation
[J].DOI:10.16385/j.cnki.issn.1004-4523.2020.04.005 [本文引用: 1]
Computational procedure for a fast calculation of eigenvectors and eigenvalues of structures with random properties
[J].DOI:10.1016/S0045-7825(01)00290-0 [本文引用: 1]
基于响应面的柔轮应力和刚度分析
[J].
Analysis of stress and stiffness of flexspline based on response surface method
[J].
Uncertainty quantification and seismic fragility of base-isolated liquid storage tanks using response surface models
[J].DOI:10.1016/j.probengmech.2015.10.008 [本文引用: 1]
Data-driven polynomial chaos expansions: a weighted least-square approximation
[J].DOI:10.1016/j.jcp.2018.12.020 [本文引用: 1]
Uncertainty propagation of frequency response functions using a multi-output Gaussian Process model
[J].
桥梁结构固有频率不确定性量化的高斯过程模型方法
[J].DOI:10.1360/N092016-00191 [本文引用: 3]
Gaussian process model-based approach for uncertainty quantification of natural frequencies of bridge
[J].DOI:10.1360/N092016-00191 [本文引用: 3]
An efficient metamodeling approach for uncertainty quantification of complex systems with arbitrary parameter probability distributions
[J].DOI:10.1002/nme.5305 [本文引用: 1]
Gradient-based methods for uncertainty quantification in hypersonic flows
[J].DOI:10.1016/j.compfluid.2012.09.003 [本文引用: 1]
Sampling strategies for computer experiments: design and analysis
[J].
A comparison of three methods for selecting values of input variables in the analysis of output from a computer code
[J].DOI:10.1080/00401706.2000.10485979 [本文引用: 1]
基于随机 Pushdown 方法的钢筋混凝土框架结构抗连续倒塌能力概率评估
[J].
Probabilistic assessment of structural resistance of RC frame structures against progressive collapse using random Pushdown analysis
[J].
Parameter selection in finite-element-model updating by global sensitivity analysis using Gaussian process meta-model
[J].DOI:10.1061/(ASCE)ST.1943-541X.0001108 [本文引用: 1]
An efficient sampling technique for off-line quality control
[J].DOI:10.1080/00401706.1997.10485122 [本文引用: 1]
Design and analysis of computer experiments
[J].
Sequential kriging optimization using multiple-fidelity evaluations
[J].DOI:10.1007/s00158-005-0587-0 [本文引用: 1]