同一区域配电网下的多个微电网通过微电网群运营商(microgrid cluster operator,MGCO)实现协同运行[12]. 本文提出将氢储能配置在MGCO侧,在减少氢储能建设成本的同时,实现多微网共享共济. 考虑利益诉求和能源市场的动态特征,提出基于主从博弈的多微网共享氢储能交易定价机制. 研究共享氢储能的容量规划,降低 MGCO的氢储能投资成本,保证共享收益. 通过算例,验证所提策略能够兼顾MGCO和多微网的利益,实现可持续、高效和经济的能源管理和运营.
1. 多类型微网能源交易架构
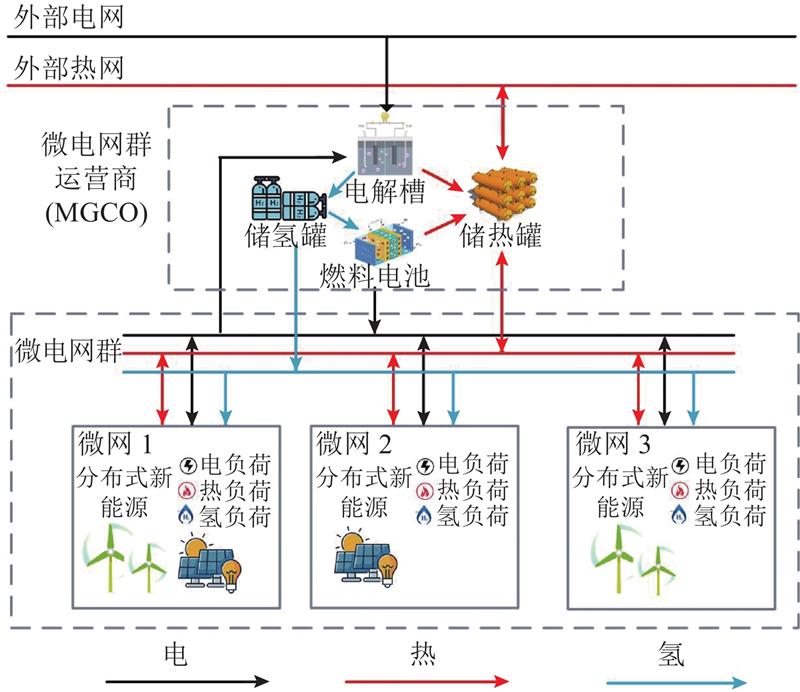
建立微电网群共享氢储能的系统架构,如图1所示. MGCO负责管理和协调各个微网之间的能源交互和协作,为微网内部的用户提供可靠的能源供应. MGCO能够根据整体电网的能源需求和供给情况,灵活地调整微网之间的能量流动,以实现电网的稳定运行. 在MGCO侧配置氢储能系统后,MGCO可以通过优化内部购售能价格,提高系统的能源利用率,进而最大化微电网群的共享效益.
图 1
图 1 微电网群共享氢储能系统的架构
Fig.1 Architecture of microgrid cluster shared hydrogen energy storage system
下层微网1、微网2、微网3为同一区域配电网下分散接入的3个异质微电网,通过MGCO满足负荷需求. 多微网的异质性体现在微网内部新能源发电形式不同及热电需求不同. 微网1是含掺氢运行的燃气轮机的工业微网,新能源出力设备为风机(wind turbine,WT)、光伏(photovoltaic,PV);微网2为热负荷占比较高的居民微网,PV为唯一新能源出力设备;微网3为热负荷需求较低的商业微网设备,WT为唯一新能源出力设备.
氢储能系统由能量转换装置及能量存储装置构成. 其中能量转换装置包括电解槽、燃料电池,分别用ele、fue表示;能量存储设备为储氢罐,用H2表示. 氢储能系统为传统的以电定热的强耦合模式,为了分析氢储能配置的影响,不考虑成本较低的储热装置容量配置,在MGCO和下层微网都采用固定容量的储热装置.
2. 多类型微网共享氢储能容量规划
2.1. 基于主从博弈的两阶段氢储能规划模型
从配置共享氢储能角度出发,在MGCO配置一定容量的氢储能系统后,增强了MGCO能源供需平衡的调控能力. 微网可以向MGCO买额外的能源来弥补缺口;当负荷无法完全消纳时,可以考虑将能源售给上级MGCO,从中获得收益;其中氢储能的配置起到关键作用. 在实际场景中,为了降低MGCO氢储能投资成本并保证MGCO共享收益,提出考虑主从博弈的两阶段氢储能容量规划方法.
第1阶段:氢储能容量配置策略. MGCO根据下层能量交互需求变动,并兼顾自身收益对氢储能配置容量进行滚动优化,通过最小化氢储能投资成本与第2阶段的误差项,确定氢储能的配置容量.
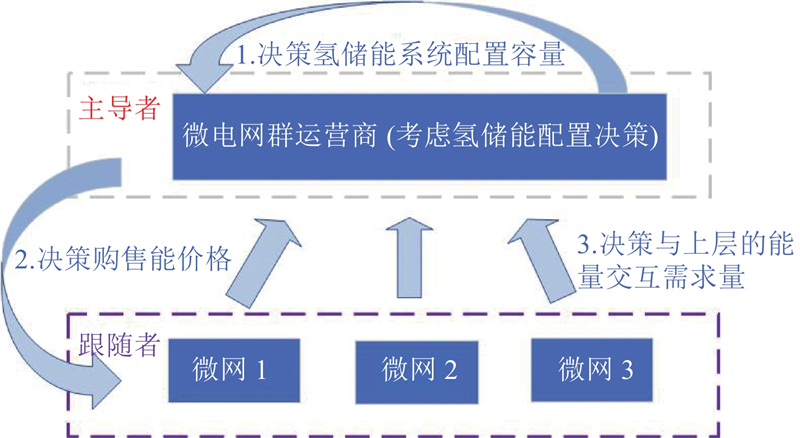
第2阶段:建立基于主从博弈的典型日运行调度模型. MGCO作为领导者进行价格决策,以实现收益最大化. 下层微网作为跟随者,将第1阶段传达的氢储能容量作为边界条件,根据价格信号调整自身的用能行为,以用能成本最小为目标参与主从博弈,如此反复,直至达到博弈均衡状态. 将所求的能量交互需求量返回至第1阶段,为下一轮优化提供参考. 博弈参与者的互动关系如图2所示.
图 2
2.2. 主从博弈的基本元素
MGCO作为主从博弈的领导者,跟随者为3个异质微网,stackelberg博弈的标准形式如下:
上述模型由参与者、策略和效益函数3个要素构成,具体表示如下.
参与者:
策略:MGCO的策略分为规划策略
效益函数:每个参与者的收益分别对应各自的目标函数,即
2.3. 微电网群运营商模型
2.3.1. 运行控制策略
MGCO作为微网的氢负荷供应及电热能调度中心,与内部氢储能构建多能耦合系统. 氢气作为中间能量的存储媒介,实现了风、光可再生能源的可调、可控. 由于电-气-电的二次转换会产生能量的梯阶损耗造成浪费,为了提高能源的利用效率,将氢负荷供应保持在较高优先级,避免了电转氢之后再次将氢能转化为其他能量导致的损耗. 考虑回收电解槽和燃料电池工作时产生的热能,提高能量转换时的综合效率. MGCO通过氢储能系统将新能源过剩出力和外部电网谷时电转换为氢气进行存储,以供应微网的氢负荷需求. 当微网产生电缺额或电价峰时,考虑将存储的氢能转换为电能获利. 上述电-氢-电转换过程中产生的热能利用储热罐进行存储,配合外部热网以满足微网热负荷的需求.
2.3.2. 氢储能系统的数学模型
在氢储能系统中,电解槽通过电解水将富裕的电能转化为氢能和热能,氢能可以出售给下层微网获利,热能参与到热循环中. 燃料电池可以将氢能转化为电能和热能,为系统电热负荷提供支撑. 储氢罐作为储能装置,可以在需要时提供稳定的氢能供应,增强系统的可调度性.
氢储能系统由于储氢罐的存在,使得电解槽和燃料电池之间没有制约关系,因此它们可以独立配置. 氢储能系统的能量转换模型[13]如下:
式中:
2.3.3. 目标函数
MGCO引入共享氢储能后,需要依据下层微网的能量需求进行氢储能优化配置,因而收益模型中须考虑氢储能日化投资成本
式中:
2.3.4. 约束条件
1)系统管网约束.
考虑到实际能量网络的容量约束,MGCO向外部电网购电量、外部热网购热量均应保持在一定的范围内. 本文的研究重点为氢储能在不同配置情况下微网的经济性. 为了简化模型的复杂程度,当区域热网利用热媒循环进行能量传递时,不考虑区域热网的管道热延迟.
式中:
2)设备运行约束.
考虑任意时刻电解槽的耗电功率和燃料电池的发电功率不能超过允许的容量上限. 储氢罐在各个时刻的储氢量应小于其配置容量. 为了确保氢储能在每个调度周期的可持续性,给定氢储能的初始容量. 现有研究中,储能初始容量一般设置为容量的0.25~0.45倍,选取0.4作为氢储能的初始容量系数,以确保在MGCO决策初期时对系统进行供能,并确保一个调度周期内的始末状态
式中:
3)价格约束.
为了防止MGCO故意提高向微网出售的能源价格以获取高额利润,基于分时角度对能源价格进行调控. 根据外界电力、热能和氢气价格,设定基准电价、热价及氢价,确保MGCO定价不高于基线价格.
式中:
4)功率平衡约束.
式中:
2.4. 微电网模型
2.4.1. 运行控制策略
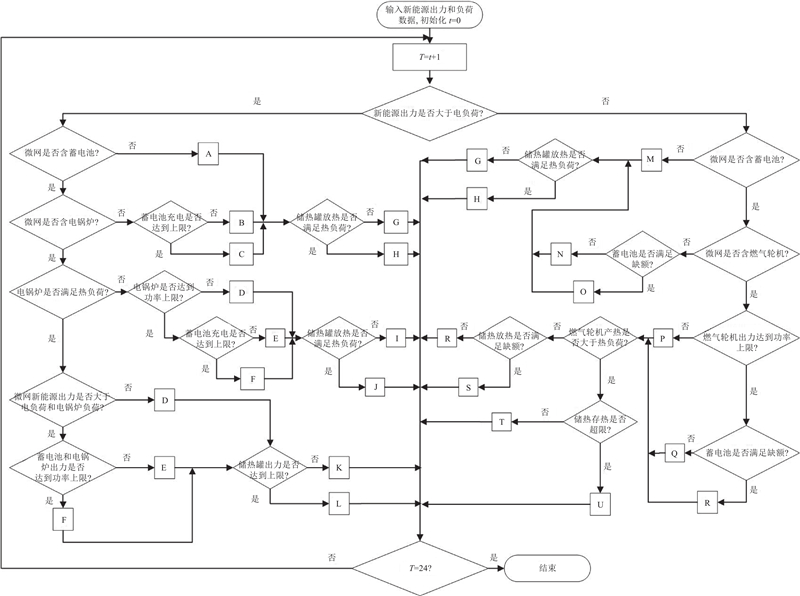
对于微电网而言,微网的运行控制策略不仅决定微网内部能量分配的原则,而且影响配置方案的经济性. 微网控制运行策略的具体流程如图3所示. 微网的氢负荷由MGCO全额提供,故不同微网只存在热电能量管理的差异.
图 3
1)新能源出力大于电负荷.
A:当微网新能源发电装置在满足负荷后仍有剩余,剩余功率直接向上级售卖.
B:当微网新能源发电装置在满足负荷后仍有剩余,剩余功率全部用于对蓄电池充电.
C:当微网新能源发电装置在满足负荷后仍有剩余,剩余功率一部分用于对蓄电池充电,另一部分向上级售卖.
D:当微网新能源发电装置在满足负荷后仍有剩余,剩余功率全部用于对电锅炉制热.
E:当微网新能源发电装置在满足负荷后仍有剩余,剩余功率一部分用于对电锅炉制热,一部分用于对蓄电池充电.
F:当微网新能源发电装置在满足负荷后仍有剩余,剩余功率一部分用于对电锅炉制热和蓄电池充电,剩余部分向上级MGCO进行售卖.
G:热负荷由储热罐负责供给,热负荷缺额由微网向上级MGCO购买.
H:热负荷由储热罐负责供给.
I:热负荷由储热罐和电锅炉负责供给,热负荷缺额由微网向上级MGCO购买.
J:热负荷由储热罐和电锅炉负责供给.
K:热负荷由电锅炉负责供给,电锅炉多余的产热由储热罐进行存储.
L:热负荷由电锅炉负责供给,电锅炉多余的产热一部分由储热罐进行存储,一部分向上级MGCO进行售卖.
2)新能源出力小于电负荷.
M:微网缺额电功率全部向上级MGCO进行购买.
N:蓄电池放电提供一部分电功率缺额,剩余部分向上级MGCO进行购买.
O:蓄电池放电提供电功率缺额.
P:蓄电池放电提供一部分电功率缺额,剩余部分由燃气轮机负责供给.
Q:蓄电池放电和燃气轮机提供一部分电功率缺额,剩余部分向上级MGCO进行购买.
R: 热负荷一部分由储热罐和燃气轮机进行供给,剩余部分由微网向上级MGCO购买.
S:热负荷一部分由储热罐和燃气轮机进行供给,
T:燃气轮机产热以满足热负荷,剩余部分由储热罐进行存储.
U:燃气轮机产热以满足热负荷,剩余一部分由储热罐进行存储,一部分向上级MGCO进行售卖.
2.4.2. 微电网系统内设备的数学模型
1)掺氢燃气轮机模型.
为了充分利用氢能的低碳效益,微网1考虑细化氢能的利用途径,通过燃气轮机引入混氢天然气,进一步提高氢能利用率,降低系统碳排放. 当混氢天然气的氢体积分数为0%~23%时,不需要对燃气轮机进行升级改造[15]. 微网1的掺氢体积比取20%. 燃气轮机设备模型如下.
式中:
2)电热综合需求响应.
将电热负荷分为刚性负荷和柔性负荷,探讨下层微网如何根据MGCO提供的能源价格,灵活地调整内部的电热负荷需求,实现电热综合需求响应.
式中:
2.4.3. 各微网的目标函数及约束
各微网的优化目标是实现日化运行成本最小,如下所示.
式中:
1)设备出力约束.
以MT为例,其余设备出力约束类似.
式中:
2)系统管网约束.
式中:
3)微网1的功率平衡约束.
微网1的设备包括:WT、PV、蓄电池(battery, Bat)、电锅炉(electric boiler, EB)、储热罐(heat storage, HS)及考虑掺氢的微型燃气轮机(micro-gas turbine, MT).
式中:
4)微网2的功率平衡约束.
微网2设备:PV、HS.
5)微网3的功率平衡约束.
微网3设备:WT、EB、Bat及HS.
3. 算例分析
3.1. 算例参数
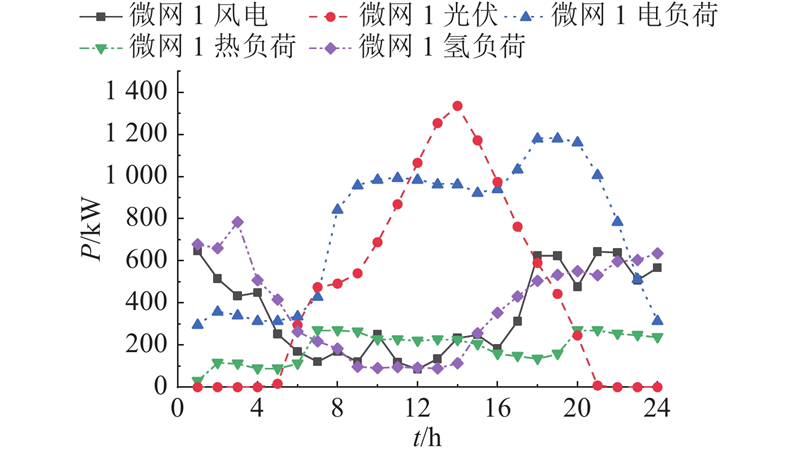
图 4
图 4 微网 1 的基准日负荷和新能源出力曲线
Fig.4 Base day load and new energy output curve of microgrid 1
图 5
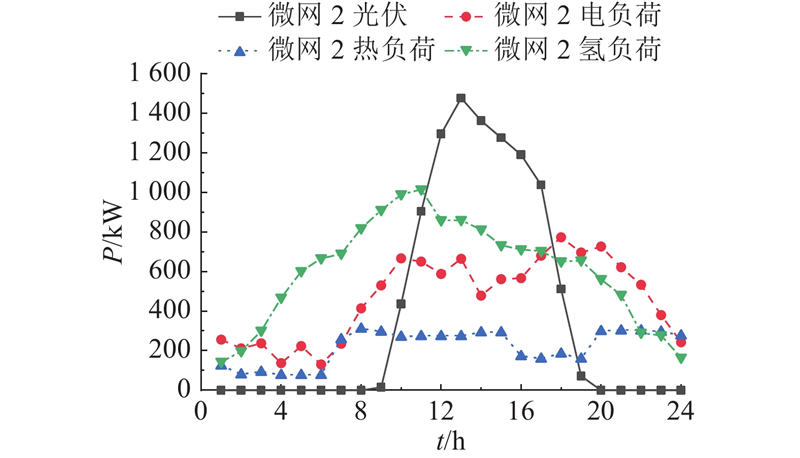
图 5 微网2的基准日负荷和新能源出力曲线
Fig.5 Base day load and new energy output curve of microgrid 2
图 6
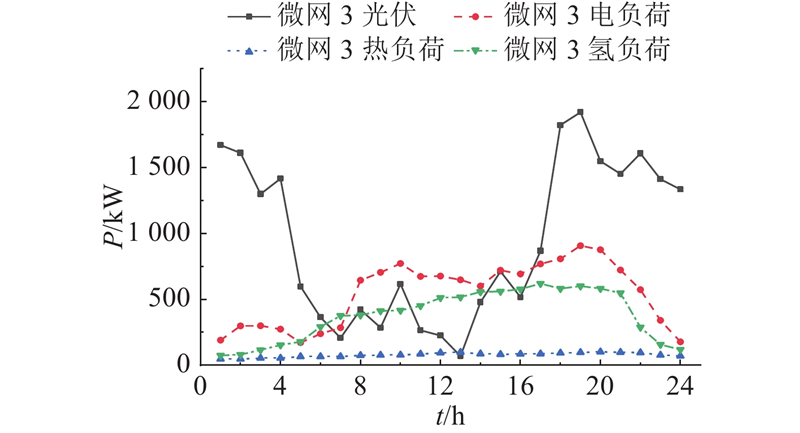
图 6 微网3的基准日负荷和新能源出力曲线
Fig.6 Base day load and new energy output curve of microgrid 3
表 1 氢储能配置成本及效率参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 2850 | 10 | |||
| 3800 | L/a | 20 | ||
| 330 | 3.622×107 | |||
| 98 | 1.246×107 | |||
| 60 | 30 | |||
| 88 | 60 |
3.2. 模型验证
为了验证基于主从博弈的两阶段氢储能容量规划模型的合理性和优越性,设置以下场景进行对比分析.
场景1:MGCO按所提的基于主从博弈的两阶段容量规划模型进行氢储能容量配置和定价.
场景2:MGCO采用传统两阶段氢储能容量配置方法,无主从博弈定价过程,价格直接固定给出.
为了进一步评估在MGCO侧配置共享氢储能的可行性,增设场景3作为对比.
场景3:MGCO不配置氢储能并按传统盈利方式参与博弈定价,氢储能由各微网自建.
表 2 氢储能系统的容量配置结果对比
Tab.2
| 场景 | 主体 | Qele/kW | Qfue/kW | |
| 场景1 | MGCO | 3265 | 653 | 10611 |
| 场景2 | MGCO | 3446 | 689 | 11609 |
| 场景3 | 微网1 | 1057 | 263 | 4822 |
| 微网2 | 1884 | 0 | 1585 | |
| 微网3 | 1173 | 1007 | 6936 | |
| 总和 | 4114 | 1270 | 13343 |
表 3 氢储能系统的设备利用率对比
Tab.3
| 场景 | 主体 | Uele/% | Ufue/% | |
| 场景1 | MGCO | 71.51 | 38.28 | 68.9 |
| 场景2 | MGCO | 68.69 | 37.92 | 69.51 |
| 场景3 | 微网1 | 58.66 | 34.22 | 52.72 |
| 微网2 | 59.43 | — | 63.73 | |
| 微网3 | 59.28 | 29.79 | 65.61 | |
| 总和 | 59.19 | 30.7 | 60.72 |
表 4 各主体的收益结果对比
Tab.4
| 场景 | MGCO | |||||||||
| 场景1 | 4638.77 | 14543.14 | 2188.53 | 20704.64 | −9073.98 | 4582.03 | 14543.14 | 2188.53 | 4919.71 | 4763.33 |
| 场景2 | 3704.82 | 12010.34 | 1924.22 | 19746.74 | −9691.62 | 2796.912 | 12010.33 | 1924.22 | 5236.23 | 1440.01 |
| 场景3 | 5129.18 | 16819.31 | 2689.24 | 18209.54 | −9041.28 | 2567.79 | 11225.31 | −310.28 | 0 | 4314.56 |
3.2.1. 氢储能容量规划方法的分析
比较场景1和场景2可知,提出的基于主从博弈的两阶段氢储能容量规划模型相较于传统两阶段氢储能容量配置方法,在氢储能系统的配置容量和设备利用率方面影响不大. 在利益分配方面,采用主从博弈定价机制(场景1)的模型对MGCO与下级微网之间的能量交互收益产生显著影响. 与固定能源价格相比,采用主从博弈定价机制,使上级MGCO的总收益增加了2 923.32 元. 这种定价机制可以激励MGCO投建氢储能,并使氢储能的投资回收年限缩短2.36 a.
3.2.2. MGCO 配置共享氢储能的可行性分析
比较场景1和场景3可知,与各微网自建氢储能相比,将氢储能系统配置在MGCO侧并通过共享来满足微网用能需求,可以分别将电解槽、燃料电池和储氢罐的总配置容量降低20.64%、48.58%和20.48%. 设备利用率相应提高12.32%、7.58%和8.21%,其中投资成本相对最高的燃料电池配置容量减少得尤为显著. 这些数据表明,利用提出的MGCO配置共享氢储能的模式,可以有效地提高设备利用率,得到更加经济的容量配置方案.
相较于各微网自建氢储能,利用所提的共享交易机制,不仅可以将各微网的总用能成本减少13.26%,还可以将MGCO收益提升10.4%. 对于MGCO而言,配置氢储能后,其与下层微网间的能量交互收益显著增加,其中微网3与MGCO的能源交互收益由负数转变为正数. 这是因为在自建模式下,微网3可以将夜间风电出力盈余转换为氢能进行存储,在电价峰时通过微网3配置的燃料电池将氢能转化为电能,以减小峰时的购能成本.考虑将多余能量向上级销售以盈利,因此自建模式下的微网3总体处于向上层售能的状态. 在共享模式下,考虑风电出力的特性,微网3只能选择在夜间风力盈余时向MGCO售能,此时电价处于谷时,利润较小. 在电价峰时,风电出力较小且电负荷需求较大,微网3需要向MGCO购能以满足负荷需求,成本较高. 微网3在自建模式下向MGCO的购能成本明显低于场景1. 在自建模式下微网3需要承担极高的氢储能投资建设成本,因此总体上微网3的自建总成本高于共享模式下的总成本.
3.3. 共享氢储能对各博弈主体的影响
3.3.1. 共享氢储能对 MGCO 行为的影响
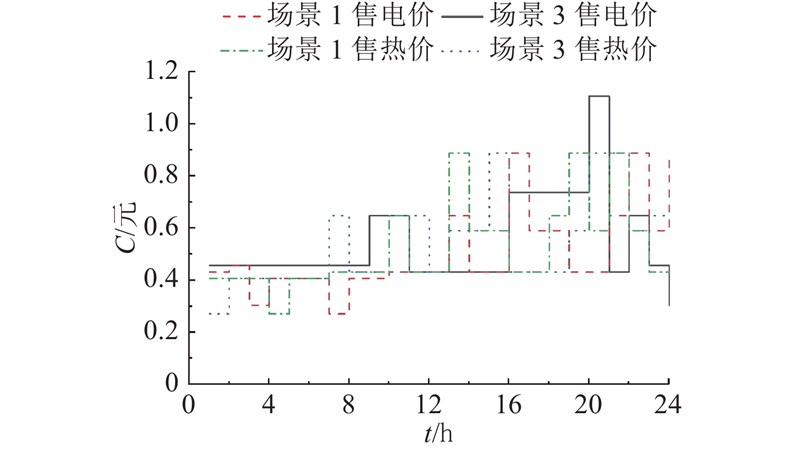
假设各微网在同一时刻从MGCO处购、售能的价格相同. 鉴于篇幅原因,以电价、热价为例,采用分时定价方式得到的能量交易价格C曲线如图7所示.
图 7
图7中,观察到场景1和场景3在用电高峰时段(16:00—20:00)的平均售电价分别为0.8114 元/(kW·h)和1.004 元/(kW·h),两者之间存在明显差异,相差0.192 6元/(kW·h),且自建模式下 MGCO制定的售电价明显高于共享模式(MGCO向下级微网的购电电价跟随售电电价变化,其值为0.8倍售电价格). 这是因为共享模式下,微网在该时段内新能源出力盈余且无氢储能系统,故MGCO可以适当地选择以较低电价从微网购电,然后以电网峰价售出电能,实现利润最大化. 在自建模式下,整体系统向外界售能. 此时,微网向MGCO售电电价均值为0.803 2 元/(kW· h),低于MGCO向外部电网售电电价的均值0.8298元/(kW·h),这意味着MGCO在售电交易中存在一定的盈利空间. 在自建模式下,MGCO会决策较高的电价,以激励各微网增大售电功率. 以上分析表明:在共享氢储能模式下,MGCO具有更大的价格调节范围,无须过度提高购电价格来刺激微网向其售电.
热价分析与电价基本类似,但是由于氢储能系统只能产热,不能消纳热,对热能的调节能力有限. 缺热的时候,还是要依赖上层储热系统及外部热网供热. 不同场景对MGCO热能定价的影响不大.
综上所述,通过配置氢储能系统,MGCO不仅能够灵活地调整能量价格,减轻系统能量供需平衡的压力,而且能够使其更好地掌握能量调度的主动权,获得更大的收益. 领导者MGCO在共享模式下具有较大的定价灵活性和盈利潜力.
3.3.2. 共享氢储能对各微网行为的影响
在场景1和场景3中,在微电网总电负荷需求响应量分别为4 246.28和3 872.53 kW·h,共享模式的电负荷需求响应量较自建模式略有增加,这主要是因为电价设定的差异. 共享模式下,上层MGCO拥有更大的自主权,可以根据电负荷需求的变化来灵活调整电价. 当电负荷需求较高时,上层可以通过提高电价来激励微网进行电负荷响应,以平衡供需关系. 共享模式下的电价调控机制能够促使微网更积极地参与电负荷需求响应. 自建模式微网拥有独立的氢储能系统,电价设定较稳定,故电负荷需求响应相对较少.
在场景1和场景3中,微电网总热负荷需求响应量分别为867.41和885.81 kW·h,共享模式下的热负荷需求响应相对于自建模式有所降低. 这是因为在自建模式下,微网为了更好地利用氢储能系统的热能副产品,即通过电解槽氢热联产和燃料电池热电联供来满足热负荷需求,需要更加灵活地调整热负荷的供应时段. 相对于共享模式下的微网,自建模式下的热负荷需求响应量略有增加.
3.4. 博弈主体能量的交互分析
图 8
图 8 各微网自配氢储能模式下的能量交互
Fig.8 Energy interaction in each micro-grid self-assigned hydrogen storage mode
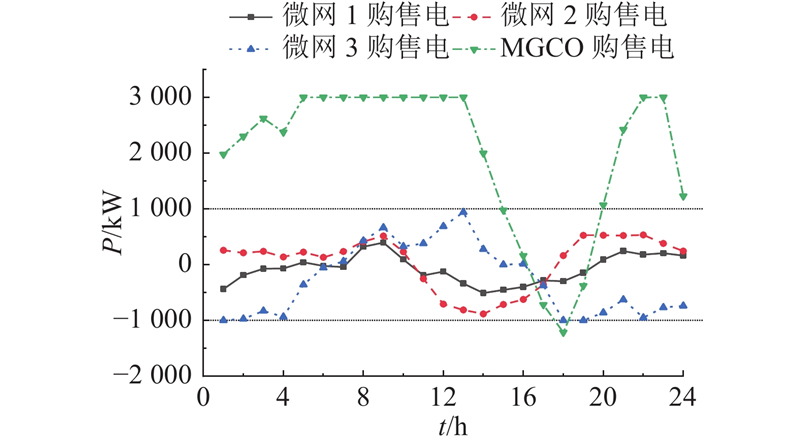
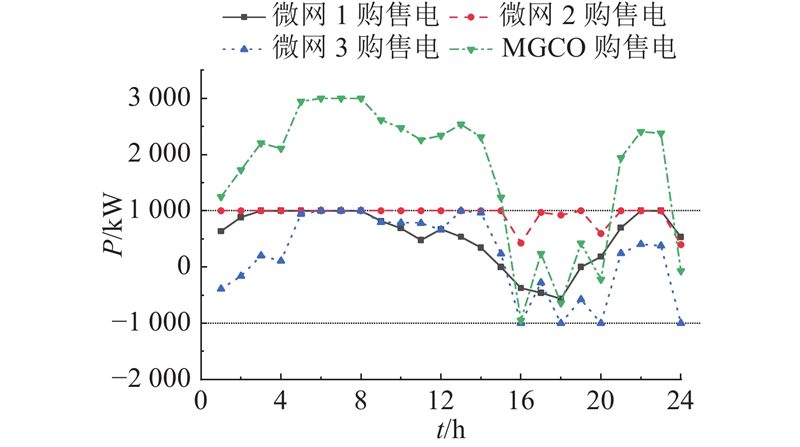
图 9
图 9 各微网共享氢储能模式下的能量交互
Fig.9 Energy interaction in shared hydrogen storage mode across microgrids
从图8可知,在自建模式下,MGCO无电能存储与转换设备,因此其向电网购售的电功率由3个微网的购售能功率总和所决定. 各微网系统独立制定电能购需计划,MGCO仅通过调整电价来对下级微网进行调度以优化能量平衡,然而由于缺乏电能存储和转换设备,MGCO的跨时段调节能力有限.
从图9可知,在(23:00—8:00)时段内,共享模式在电网电价谷时向外界购能21 961 kW·h,较自建模式提高了2 524.4 kW·h,在(16:00—20:00)时段内,共享模式在电网电价峰时向外界售能 2 312.9 kW·h,较自建模式提高了503 kW·h. 通过数据分析可知,在共享氢储能模式下,上层可以直接调控大规模的共享氢储能系统,采取低储高发策略,从而具备更大的跨时段调度灵活性. 共享模式能够在外部电网中起到削峰填谷作用,优化了外部电网的供需曲线,显著提高了MGCO的整体利益.
4. 结 论
(1)通过配置氢储能系统,MGCO可以获得更大的定价灵活性和盈利潜力,从而更好地实现跨时段能源调度,减轻系统能量供需平衡的压力.
(2)利用主从博弈定价机制,MGCO的总收益增加了2 923.32 元,氢储能的投资回收周期从6.68 a缩短到4.32 a,这促使MGCO更有动力投资氢储能.
(3)利用共享交易机制,能够显著地降低电解槽、燃料电池和储氢罐的总配置容量,将设备利用率提高约9.11 %. 此外,它还能将微网总用能成本减少约13.26 %,MGCO收益增加10.4 %. 共享交易机制在实现微网群经济用能方面具有重要的贡献.
(4)MGCO通过灵活地调度共享氢储能系统,在电网负荷高峰期向电网供应额外能量,减轻电网负荷压力;在负荷低谷期储存多余能量,避免能源浪费. 所提出的共享交易机制不仅能够实现微网经济用能,还能够为外部电网提供支撑.
为了进一步推动共享氢储能系统的工程实践和可持续发展,后续研究将致力于探索微网内部发电能力与用能需求之间的协调关系,提高共享氢储能系统的经济性和可行性.
参考文献
交直流混合独立微网互联变换器自适应双向下垂控制策略
[J].
Adaptive bidirectional droop control strategy for the interlinking converter in the islanding hybrid AC/DC microgrid
[J].
考虑源-荷波动的电力系统灵活性运行域研究
[J].
Study on flexible operation region of power system considering source and load fluctuation
[J].
考虑电热气耦合特性的低碳园区综合能源系统氢储能优化配置
[J].
Optimal configuration of hydrogen energy storage in low-carbon park integrated energy system considering electricity-heat-gas coupling characteristics
[J].
含制氢储能的混合传动风电系统建模与运行特性分析
[J].
Modeling andoperation performance analysis of hybrid drive wind powergeneration system with hydrogen energy storage
[J].
考虑电氢耦合的混合储能微电网容量配置优化
[J].
Capacity optimization of hybrid energy storage microgrid considering electricity-hydrogen coupling
[J].
用于电网调节能力提升的 电热氢多源协调储能系统模型
[J].
A model and coordinated optimization for the multi energy storage system of electricity heat hydrogen to regulation enhancement of power grid
[J].
A bargaining game-based profit allocation method for the wind-hydrogen-storage combined system
[J].DOI:10.1016/j.apenergy.2021.118472 [本文引用: 1]
考虑不确定性的电-热-氢综合能源系统规划
[J].
Planning of electricity-heat-hydrogen integrated energy system considering uncertainties
[J].
面向低碳供能的多园区共享氢储能系统容量规划
[J].
Capacity planning of mul-tiple parks shared hydrogen energy storage system for low-carbon energy supply
[J].
Community energy cooperation with the presence of cheating behaviors
[J].DOI:10.1109/TSG.2020.3022792 [本文引用: 1]
考虑电价机制的微电网群主从博弈优化方法
[J].
Stackelberg game optimization method for microgrid cluster considering electricity price mechanism
[J].
基于分布鲁棒的风−氢混合系统氢储能容量优化配置
[J].
Optimal capacity allocation of hydrogen energy storage in wind-hydrogen hybrid system based on distributionally robust
[J].
基于主从博弈的工业园区综合能源系统氢储能优化配置
[J].
Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game
[J].
利用天然气管道掺混输送氢气的可行性分析
[J].
Feasibility analysis of hydrogen transport in natural gas pipeline
[J].
区域综合能源系统两阶段鲁棒博弈优化调度
[J].
Bi-level robust game optimal scheduling of regional comprehensive energy system based on Copula-RCVaR model
[J].
Hierarchical stochastic scheduling of multi-community integrated energy systems in uncertain environments via stackelberg game
[J].DOI:10.1016/j.apenergy.2021.118392 [本文引用: 1]
基于综合需求响应和主从博弈的多微网综合能源系统优化调度策略
[J].
Optimal dispatch of multi-microgrids integrated energy system based on integrated demand response and stackelberg game
[J].