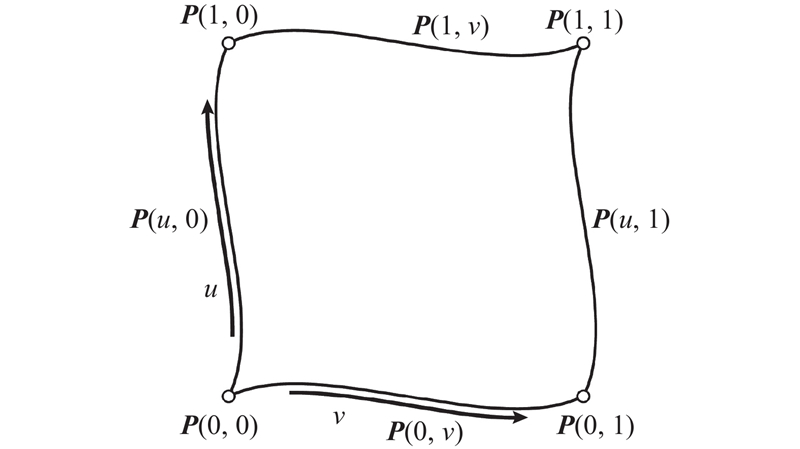
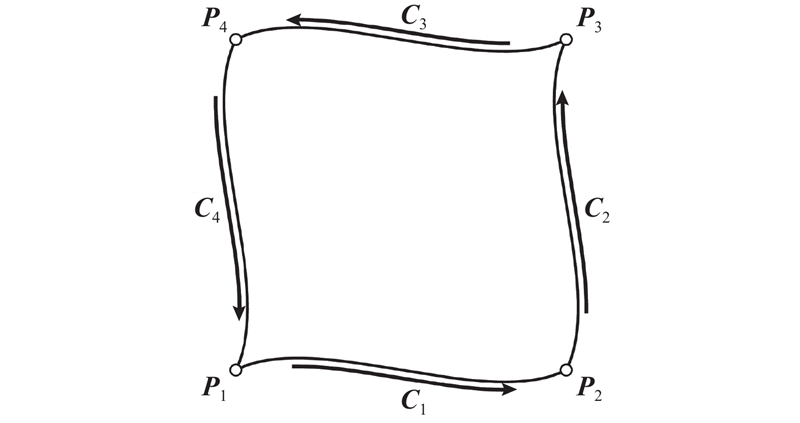
给定一张四边面片,4条边界曲线分别为 ${\boldsymbol{P}}\left( {u,0} \right)、 {\boldsymbol{P}}\left( {u,1} \right)、{\boldsymbol{P}}(0,v)、{\boldsymbol{P}}(1,v),\; u、v \in \left[ {0,1.0} \right],$ $ {\boldsymbol{P}}(0,0)、{\boldsymbol{P}}(0,1)、{\boldsymbol{P}}(1,0)、{\boldsymbol{P}}(1,1),$ 图1 所示.
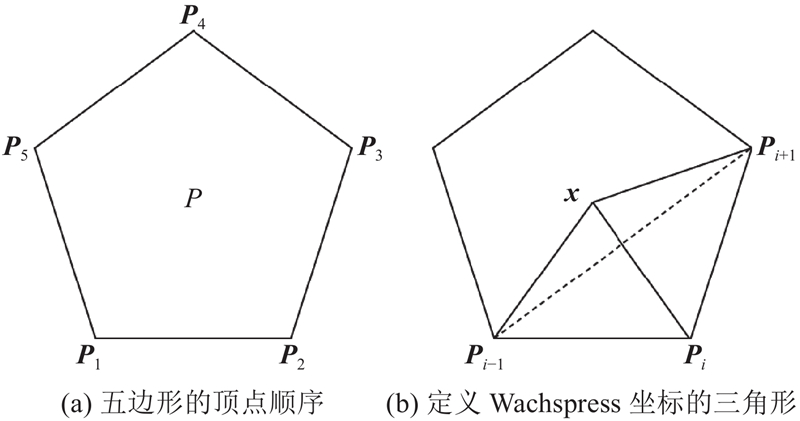
$ {w_i}({\boldsymbol{x}}) = \frac{{A({{\boldsymbol{P}}_{i - 1}},{{\boldsymbol{P}}_i},{{\boldsymbol{P}}_{i+1}})}}{{A({\boldsymbol{x}},{{\boldsymbol{P}}_{i - 1}},{{\boldsymbol{P}}_i})A({\boldsymbol{x}},{{\boldsymbol{P}}_i},{{\boldsymbol{P}}_{i+1}})}}{\text{. }} $
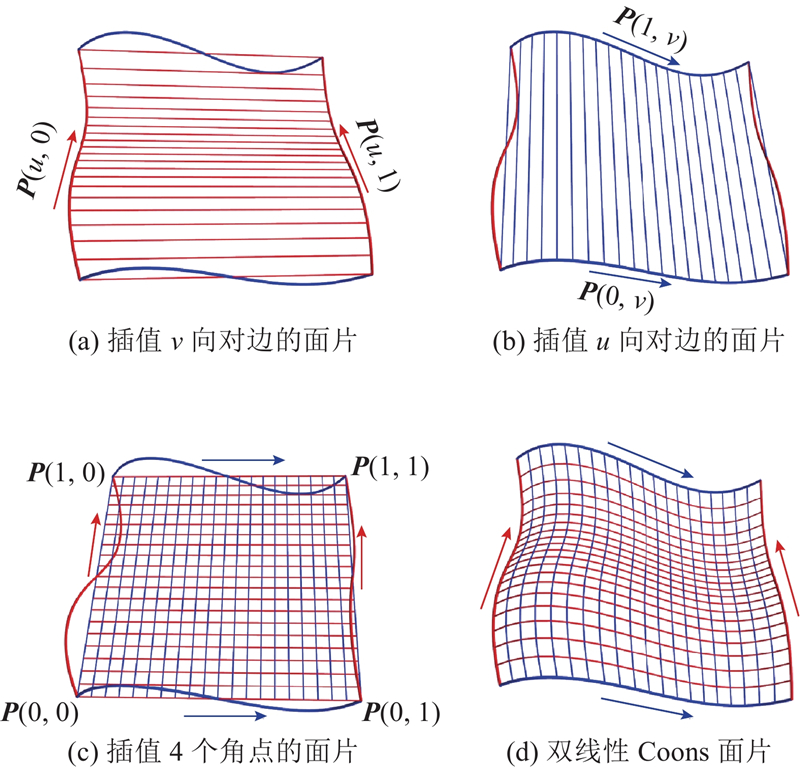
(8) $ \begin{split} {{\boldsymbol{Q}}_1}(u,v) = &{\boldsymbol{P}}(u,0)(1 - v)+{\boldsymbol{P}}(u,1)v = \\ &{\boldsymbol{P}}({\lambda _3}+{\lambda _4},0)({\lambda _4}+{\lambda _1})+{\boldsymbol{P}}({\lambda _3}+{\lambda _4},1)({\lambda _2}+{\lambda _3}),{\text{ }}\end{split}$
(9) $ \begin{split} {{\boldsymbol{Q}}_2}(u,v) =& {\boldsymbol{P}}(0,v)(1 - u)+{\boldsymbol{P}}(1,v)u = \\ &{\boldsymbol{P}}(0,{\lambda _2}+{\lambda _3})({\lambda _1}+{\lambda _2})+{\boldsymbol{P}}(1,{\lambda _2}+{\lambda _3})({\lambda _3}+{\lambda _4}),\end{split} $
(10) $ \begin{split} {{\boldsymbol{Q}}_3}(u,v) = &[{\boldsymbol{P}}(0,0)(1 - u)+{\boldsymbol{P}}(1,0)u](1 - v)+ \\ &[{\boldsymbol{P}}(0,1)(1 - u)+{\boldsymbol{P}}(1,1)u]v = \\ &{\lambda _1}{{\boldsymbol{P}}_1}+{\lambda _2}{{\boldsymbol{P}}_2}+{\lambda _3}{{\boldsymbol{P}}_3}+{\lambda _4}{{\boldsymbol{P}}_4}.\end{split} $
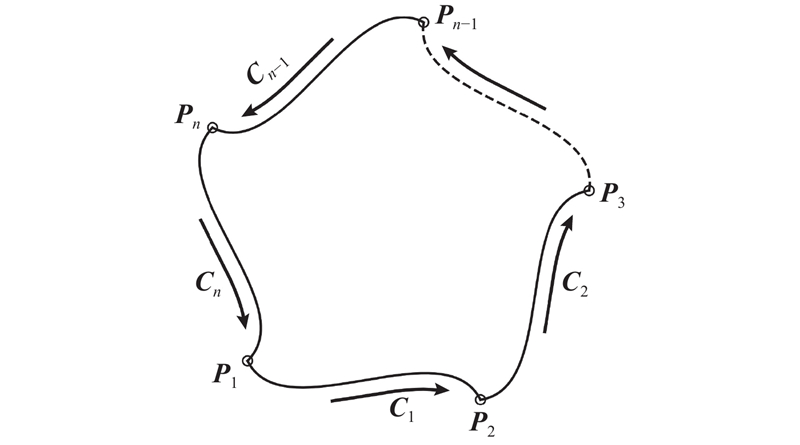
定义2.1 给定n 条 (n > 3) 定义在[0,1.0]上的边界曲线$ {{\boldsymbol{C}}_1},{{\boldsymbol{C}}_2},\cdots ,{{\boldsymbol{C}}_n} $ n 个角点为$ {{\boldsymbol{P}}_1},{{\boldsymbol{P}}_2},\cdots ,{{\boldsymbol{P}}_n} $
$ \begin{split} &{\boldsymbol{Q}}(0, \cdots ,0,{\lambda _k},{\lambda _{k+1}},0, \cdots ,0) = {\lambda _k}{{\boldsymbol{C}}_{k - 1}}(1)+ \\ &{\text{ }}{{\boldsymbol{C}}_k}({\lambda _{k+1}})+{\lambda _{k+1}}{{\boldsymbol{C}}_{k+1}}(0) - {\lambda _k}{{\boldsymbol{P}}_k} - {\lambda _{k+1}}{{\boldsymbol{P}}_{k+1}} = {\text{ }} \\ &{\text{ }}{{\boldsymbol{C}}_k}({\lambda _{k+1}}). \end{split}$
[1]
刘海燕, 朱春钢, 李彩云. 基于边界曲线的N边域toric曲面片生成[C]// 第5届全国几何设计与计算学术会议论文集. 广州: [s. n. ], 2011.
[本文引用: 1]
LIU Haiyan, ZHU Chungang, LI Caiyun. Constructing N-sided toric surface patches from boundary curves [C]// Proceedings of the 5th National Conference on Geometric Design and Computing . Guangzhou: [s. n. ], 2011.
[本文引用: 1]
[2]
COONS S A. Surfaces for computer aided design of space forms [EB/OL]. [2023-07-15]. https://dspace.mit.edu/handle/1721.1/149362.
[本文引用: 2]
[3]
FARIN G. Curves and surfaces for computer-aided geometric design: a practical guide [M]. [S. l. ]: Elsevier, 2014.
[本文引用: 2]
[4]
GREGORY J A, ZHOU J Irregular C2 surface construction using bi-polynomial rectangular patches
[J]. Computer Aided Geometric Design , 1999 , 16 (5 ): 423 - 435
DOI:10.1016/S0167-8396(99)00011-4
[本文引用: 1]
[5]
SHI K L, YONG J H, SUN J G, et al Filling n-sided regions with G1 triangular Coons B-spline patches
[J]. The Visual Computer , 2010 , 26 (6 ): 791 - 800
[6]
YANG Y J, YONG J H, ZHANG H, et al A rational extension of Piegl’s method for filling n-sided holes
[J]. Computer-Aided Design , 2006 , 38 (11 ): 1166 - 1178
DOI:10.1016/j.cad.2006.07.001
[本文引用: 1]
[7]
LAI S, CHENG F Explicit construction of C2 surfaces for meshes of arbitrary topology
[J]. Computer-Aided Design and Applications , 2017 , 14 (6 ): 805 - 814
DOI:10.1080/16864360.2017.1288366
[本文引用: 1]
[8]
VÁRADY T, SALVI P, KARIKÓ G. A multi-sided Bézier patch with a simple control structure [C]//Computer Graphics Forum . [S. l. ]: Wiley, 2016: 307-317.
[本文引用: 2]
[10]
HAMANN B, TSAI P Y A tessellation algorithm for the representation of trimmed NURBS surfaces with arbitrary trimming curves
[J]. Computer-Aided Design , 1996 , 28 (6/7 ): 461 - 472
[本文引用: 1]
[11]
VÁRADY T, SALVI P, ROCKWOOD A Transfinite surface interpolation with interior control
[J]. Graphical Models , 2012 , 74 (6 ): 311 - 320
DOI:10.1016/j.gmod.2012.03.003
[本文引用: 1]
[13]
SABIN M. Transfinite surface interpolation [C]// IMA Conference on the Mathematics of Surfaces . New York: Oxford University Press, 1996: 517-534.
[本文引用: 1]
[14]
GORDON W J. Spline-blended surface interpolation through curve networks [J]. Journal of Mathematics and Mechanics , 1969: 931-952.
[本文引用: 1]
[15]
GORDON W J Blending-function methods of bivariate and multivariate interpolation and approximation
[J]. SIAM Journal on Numerical Analysis , 1971 , 8 (1 ): 158 - 177
DOI:10.1137/0708019
[本文引用: 2]
[16]
GREGORY J A, LAU V K H, ZHOU J. Smooth parametric surfaces and n-sided patches [EB/OL]. [2023-07-10]. https://doi.org/10.1007/978-94-009-2017-0_14.
[本文引用: 1]
[17]
VÁRADY T, ROCKWOOD A, SALVI P Transfinite surface interpolation over irregular n-sided domains
[J]. Computer-Aided Design , 2011 , 43 (11 ): 1330 - 1340
DOI:10.1016/j.cad.2011.08.028
[本文引用: 2]
[19]
VÁRADY T, SALVI P, VAITKUS M, et al Multi-sided Bézier surfaces over curved, multi-connected domains
[J]. Computer Aided Geometric Design , 2020 , 78 : 101828
DOI:10.1016/j.cagd.2020.101828
[本文引用: 1]
[20]
QIN K, LI Y, DENG C Blending Bézier patch for multi-sided surface modeling
[J]. Computer Aided Geometric Design , 2023 , 105 : 102222
DOI:10.1016/j.cagd.2023.102222
[本文引用: 1]
[21]
SALVI P. A multi-sided generalization of the C0 Coons patch [EB/OL]. [2023-07-15]. https://arxiv.org/abs/2002.11347.
[本文引用: 4]
[24]
WACHSPRESS E L. A rational finite element basis [M]. New York: Academic Press, 1975.
[本文引用: 1]
[25]
WARREN J Barycentric coordinates for convex polytopes
[J]. Advances in Computational Mathematics , 1996 , 6 (1 ): 97 - 108
DOI:10.1007/BF02127699
[本文引用: 1]
[27]
JOSHI P, MEYER M, DEROSE T, et al Harmonic coordinates for character articulation
[J]. ACM Transactions on Graphics , 2007 , 26 (3 ): 71 - 81
[本文引用: 1]
[28]
DENG C, CHANG Q, HORMANN K Iterative coordinates
[J]. Computer Aided Geometric Design , 2020 , 79 : 101861
DOI:10.1016/j.cagd.2020.101861
[本文引用: 1]
1
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
1
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
2
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
2
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
... Farin[3 ] 给出双线性Coons面片的定义和构造方式. 给定2条边界曲线$ {\boldsymbol{P}}(u,0) $ $ {\boldsymbol{P}}(u,1) $ $ {{\boldsymbol{Q}}_1}(u,v) $
Irregular C2 surface construction using bi-polynomial rectangular patches
1
1999
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
Filling n-sided regions with G1 triangular Coons B-spline patches
0
2010
A rational extension of Piegl’s method for filling n-sided holes
1
2006
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
Explicit construction of C2 surfaces for meshes of arbitrary topology
1
2017
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
2
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
Ribbon-based transfinite surfaces
2
2014
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
A tessellation algorithm for the representation of trimmed NURBS surfaces with arbitrary trimming curves
1
1996
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
Transfinite surface interpolation with interior control
1
2012
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
Generation of n-sided surface patches with holes
1
1991
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
1
... 在自由曲面造型领域往往需要拼接多张曲面片,在这个过程中容易产生一些 “洞”,因此曲面 “补洞”问题是计算机辅助几何设计(CAGD)研究的一项重要工作,解决曲面 “补洞” 问题的首要任务是构造插值边界曲线的曲面片[1 ] . 目前已有很多方法处理插值3条或4条边界曲线的问题,如Coons等[2 -3 ] 提出的方法. 对于插值5条及5条以上边界曲线的问题,目前有以下5种主要的方法. 1)中心分割法,把参数域从中心分割成三角形域或四边形域,再用相应的面片来插值边界曲线,如Gregory等[4 -6 ] 提出的方法. 2)细分法,利用细分产生的极限曲面来补洞,如Lai等[7 ] 提出的方法. 3)控制网格法,利用边界条件和连续性条件计算控制网格,生成多边面片,如Várady等[8 -9 ] 提出的方法. 4)裁剪曲面法,利用三角形或四边形面片裁剪成多边面片,如Hamann等[10 ] 提出的方法. 5)超限插值曲面法,利用边界曲线及其各阶导矢和混合函数构造多边面片,如Várady等[11 -13 ] 提出的方法. ...
1
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
Blending-function methods of bivariate and multivariate interpolation and approximation
2
1971
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
... 下面以一些四边网格模型为例,探讨本文所述方法和前人方法在 “补洞” 效果以及计算效率方面的差异. 在四边网格中,度为4的点称为非奇异点,其他点称为奇异点. 以四边网格中$6 \times 6$ [15 ] 填充;对于四边以上的 “洞”,采用本文方法和Salvi[21 ] 提出的方法填补. 将提出的多边形域Coons面片和Salvi[21 ] 给出的边界处$ {G^0} $ 图7 、8 所示. 利用2种方法生成的多边面片与周围面片在边界处都是$ {G^0} $ 图9 可以看出,利用2种方法生成的多边面片在曲率分布方面略有不同. 因为2种面片的构造方法不同,计算效率有较大差异. MC面片是利用三边混合方法构建多边面片,对每组相连的3条边界曲线都构造一张矩形域上的双线性Coons面片,其中3条待插值边界曲线是给定的,另一条边界曲线是根据边界信息计算得到的. n 边MC面片涉及4n 条边和4n 个角点的计算; 本文方法只涉及n 条边和n 个角点的计算,且MC面片需要预先计算有理局部参数,增加了计算量. 理论上MGC面片的计算效率高于MC面片,2种方法的计算时间t c 对比如表1 所示,表中数据均在CPU基准速度为3.2 GHz的机器上运行得到,5边和6边面片的采样点数分别为18 602和20 439. ...
1
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
Transfinite surface interpolation over irregular n-sided domains
2
2011
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
... 多边形参数域可以由n 个角点投影到二维平面后顺次连接得到,但该方法在某些情况下可能会生成凹多边形参数域. Várady等[17 ] 针对这种可能出现的情况,提出基于边长度/角生成凸多边形参数域的方法,利用该方法解决了参数域可能出现非凸多边形的问题. ...
Multi-sided Bézier surfaces over concave polygonal domains
1
2018
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
Multi-sided Bézier surfaces over curved, multi-connected domains
1
2020
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
Blending Bézier patch for multi-sided surface modeling
1
2023
... 超限曲面插值最早可以追溯到20世纪60年代,Coons[2 ] 构造出插值型曲面,称为Coons曲面. Gordon[14 ] 利用三次Hermite基函数构造出双三次Coons面片,将Coons曲面解释为布尔和曲面,提出超限插值的概念. Gordon[15 ] 将该方法推广到三角形域上,提出三角形域上Coons面片的构造方法. Gregory[16 ] 提出在正多边形域上构造多边面片的角混合方法,本质上是对多边形的每个角 (相邻的两条边) 构造插值这个角的面片,结合混合函数构造多边面片. Kato[12 ] 提出边混合方法,对每一条边构造插值该边所对应边界曲线的面片,计算效率比角混合方法高. Várady等[17 ] 将角混合和边混合方法中规则的正多边形域推广到不规则域. Salvi等[9 ] 提出三边混合方法,核心是对每一组相连的3条边界曲线构造插值这3条边界曲线及其跨界导矢的面片,结合相应的混合函数得到多边面片,该方法使得多边面片在边界处的曲率过渡更自然. Várady等[8 ] 提出GB面片,这是结合超限插值曲面法和控制网格法构造的多边Bezier面片,GB面片在边界处可以达到$ {G^1} $ [18 ] 将GB面片的凸多边形参数域推广到一般多边形参数域. Várady等[19 ] 将一般多边形参数域推广到曲边多边形参数域,这种参数域更接近输入的三维边界曲线围成的形状,可以解决输入复杂边界曲线构造多边面片时失真的问题. Qin等[20 ] 提出BB面片,这是张量积Bezier曲面在多边形域上的推广,在边界处能够达到$ {G^2} $
4
... 通常相邻面片在边界曲线处至少需要达到切线$ {G^1} $ $ {G^0} $ ) ,或者在边界曲线处法向量和跨界导矢信息缺失的情况下只能达到$ {G^0} $ [21 ] . Salvi[21 ] 提出简单的三边混合方法,构造边界处$ {G^0} $ $ {G^0} $
... [21 ]提出简单的三边混合方法,构造边界处$ {G^0} $ $ {G^0} $
... 下面以一些四边网格模型为例,探讨本文所述方法和前人方法在 “补洞” 效果以及计算效率方面的差异. 在四边网格中,度为4的点称为非奇异点,其他点称为奇异点. 以四边网格中$6 \times 6$ [15 ] 填充;对于四边以上的 “洞”,采用本文方法和Salvi[21 ] 提出的方法填补. 将提出的多边形域Coons面片和Salvi[21 ] 给出的边界处$ {G^0} $ 图7 、8 所示. 利用2种方法生成的多边面片与周围面片在边界处都是$ {G^0} $ 图9 可以看出,利用2种方法生成的多边面片在曲率分布方面略有不同. 因为2种面片的构造方法不同,计算效率有较大差异. MC面片是利用三边混合方法构建多边面片,对每组相连的3条边界曲线都构造一张矩形域上的双线性Coons面片,其中3条待插值边界曲线是给定的,另一条边界曲线是根据边界信息计算得到的. n 边MC面片涉及4n 条边和4n 个角点的计算; 本文方法只涉及n 条边和n 个角点的计算,且MC面片需要预先计算有理局部参数,增加了计算量. 理论上MGC面片的计算效率高于MC面片,2种方法的计算时间t c 对比如表1 所示,表中数据均在CPU基准速度为3.2 GHz的机器上运行得到,5边和6边面片的采样点数分别为18 602和20 439. ...
... [21 ]给出的边界处$ {G^0} $ 图7 、8 所示. 利用2种方法生成的多边面片与周围面片在边界处都是$ {G^0} $ 图9 可以看出,利用2种方法生成的多边面片在曲率分布方面略有不同. 因为2种面片的构造方法不同,计算效率有较大差异. MC面片是利用三边混合方法构建多边面片,对每组相连的3条边界曲线都构造一张矩形域上的双线性Coons面片,其中3条待插值边界曲线是给定的,另一条边界曲线是根据边界信息计算得到的. n 边MC面片涉及4n 条边和4n 个角点的计算; 本文方法只涉及n 条边和n 个角点的计算,且MC面片需要预先计算有理局部参数,增加了计算量. 理论上MGC面片的计算效率高于MC面片,2种方法的计算时间t c 对比如表1 所示,表中数据均在CPU基准速度为3.2 GHz的机器上运行得到,5边和6边面片的采样点数分别为18 602和20 439. ...
Birational quadrilateral maps
1
2015
... Sederberg等[22 -23 ] 研究双线性映射及其逆映射. 双线性坐标可以定义为:设四边形的4个顶点分别是$ {{\boldsymbol{P}}_1}、{{\boldsymbol{P}}_2}、{{\boldsymbol{P}}_3}、{{\boldsymbol{P}}_4} $ ${\boldsymbol{P}}$
The inverse of a rational bilinear mapping
1
2015
... Sederberg等[22 -23 ] 研究双线性映射及其逆映射. 双线性坐标可以定义为:设四边形的4个顶点分别是$ {{\boldsymbol{P}}_1}、{{\boldsymbol{P}}_2}、{{\boldsymbol{P}}_3}、{{\boldsymbol{P}}_4} $ ${\boldsymbol{P}}$
1
... Wachspress坐标是广义重心坐标中的一种,由Wachspress[24 ] 提出,Warren[25 ] 改进. Wachspress坐标定义为 ...
Barycentric coordinates for convex polytopes
1
1996
... Wachspress坐标是广义重心坐标中的一种,由Wachspress[24 ] 提出,Warren[25 ] 改进. Wachspress坐标定义为 ...
Mean value coordinates
1
2003
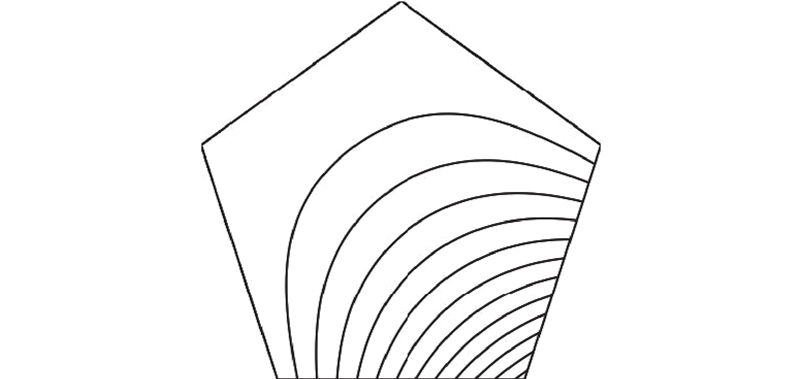
... 仅以Wachspress坐标为例,介绍多边形域Coons面片的构造方法,实际上任何能应用于凸多边形域上的广义重心坐标都能应用于多边形域Coons面片,如均值坐标[26 ] 、调和坐标[27 ] 、迭代坐标[28 ] 等. ...
Harmonic coordinates for character articulation
1
2007
... 仅以Wachspress坐标为例,介绍多边形域Coons面片的构造方法,实际上任何能应用于凸多边形域上的广义重心坐标都能应用于多边形域Coons面片,如均值坐标[26 ] 、调和坐标[27 ] 、迭代坐标[28 ] 等. ...
Iterative coordinates
1
2020
... 仅以Wachspress坐标为例,介绍多边形域Coons面片的构造方法,实际上任何能应用于凸多边形域上的广义重心坐标都能应用于多边形域Coons面片,如均值坐标[26 ] 、调和坐标[27 ] 、迭代坐标[28 ] 等. ...