[1]
ARYAN M, MURARI M, PRATIK N, et al ReViewNet: a fast and resource optimized network for enabling safe autonomous driving in hazy weather conditions
[J]. IEEE Transactions on Intelligent Transportation Systems 2021 , 22 : 4256 - 4266
DOI:10.1109/TITS.2020.3013099
[本文引用: 1]
[2]
CAO Z, QIN Y, JIA L, et al Haze removal of railway monitoring images using multi-scale residual network
[J]. IEEE Transactions on Intelligent Transportation Systems 2020 , 22 (12 ): 7460 - 7473
[本文引用: 1]
[3]
BAI H, PAN J, XIANG X, et al Self-guided image dehazing using progressive feature fusion
[J]. IEEE Transactions on Image Processing 2022 , 31 : 1217 - 1229
DOI:10.1109/TIP.2022.3140609
[本文引用: 11]
[4]
WU H, QU Y, LIN S, et al. Contrastive learning for compact single image dehazing [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . [S. l. ]: IEEE, 2021: 10551-10560.
[本文引用: 2]
[5]
LI H, LI J, ZHAO D, et al. Dehazeflow: multi-scale conditional flow network for single image dehazing [C]// Proceedings of the 29th ACM International Conference on Multimedia . New York: ACM, 2021: 2577-2585.
[本文引用: 5]
[6]
QIN X, WANG Z, BAI Y, et al. FFA-Net: feature fusion attention network for single image dehazing [C]// Proceedings of the AAAI Conference on Artificial Intelligence . New York: AAAI, 2020: 11908-11915.
[本文引用: 6]
[7]
MA L, MA T, LIU R, et al. Toward fast, flexible, and robust low-light image enhancement [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 5637-5646.
[本文引用: 1]
[8]
ARJOVSKY M, BOTTOU L, GULRAJANI I, et al. Invariant risk minimization [EB/OL]. (2019-07-05). https://arxiv.org/pdf/1907.02893.pdf.
[本文引用: 2]
[9]
WANG J, LAN C, LIU C, et al Generalizing to unseen domains: a survey on domain generalization
[J]. IEEE Transactions on Knowledge and Data Engineering 2023 , 35 (8 ): 8052 - 8072
[本文引用: 1]
[10]
MUANDET K, BALDUZZI D, SCHÖLKOPF B. Domain generalization via invariant feature representation [C]/ /International Conference on Machine Learning . Atlanta: ACM, 2013: 10-18.
[本文引用: 2]
[11]
KUANG K, CUI P, ATHEY S, et al. Stable prediction across unknown environments [C]// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . London: ACM, 2018: 1617-1626.
[本文引用: 4]
[12]
KUANG K, XIONG R, CUI P, et al. Stable prediction with model misspecification and agnostic distribution shift [C]// Proceedings of the AAAI Conference on Artificial Intelligence . New York: AAAI, 2020: 4485-4492.
[本文引用: 2]
[13]
ZHANG X, CUI P, XU R, et al. Deep stable learning for out-of-distribution generalization [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition .[S. l. ]: IEEE, 2021: 5372-5382.
[本文引用: 2]
[14]
HE K, SUN J, TANG X Single image haze removal using dark channel prior
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence 2010 , 33 (12 ): 2341 - 2353
[本文引用: 2]
[15]
FATTAL R Dehazing using color-lines
[J]. ACM Transactions on Graphics 2014 , 34 (1 ): 1 - 14
[本文引用: 3]
[16]
BERMAN D, AVIDAN S. Non-local image dehazing [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 1674-1682.
[本文引用: 2]
[17]
LI B, REN W, FU D, et al Benchmarking single-image dehazing and beyond
[J]. IEEE Transactions on Image Processing 2018 , 28 (1 ): 492 - 505
[本文引用: 4]
[18]
LIU X, MA Y, SHI Z, et al. Griddehazenet: attention-based multi-scale network for image dehazing [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2019: 7314-7323.
[本文引用: 3]
[19]
DONG H, PAN J, XIANG L, et al. Multi-scale boosted dehazing network with dense feature fusion [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 2157-2167.
[本文引用: 12]
[20]
KIM G, KWON J Deep illumination-aware dehazing with low-light and detail enhancement
[J]. IEEE Transactions on Intelligent Transportation Systems 2021 , 23 (3 ): 2494 - 2508
[本文引用: 5]
[21]
JU M, DING C, REN W, et al IDE: image dehazing and exposure using an enhanced atmospheric scattering model
[J]. IEEE Transactions on Image Processing 2021 , 30 : 2180 - 2192
DOI:10.1109/TIP.2021.3050643
[本文引用: 7]
[22]
CHEN Z, WANG Y, YANG Y, et al. PSD: principled synthetic-to-real dehazing guided by physical priors [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . [S. l. ]: IEEE, 2021: 7180-7189.
[本文引用: 8]
[23]
SHAO Y, LI L, REN W, et al. Domain adaptation for image dehazing [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 2808-2817.
[本文引用: 3]
[24]
LIANG Y, WANG B, ZUO W, et al. Self-supervised learning and adaptation for single image dehazing [C]// Proceedings of the 31st International Joint Conference on Artificial Intelligence . Vienna: Morgan Kaufmann, 2022: 1-15.
[本文引用: 5]
[25]
LI R, PAN J, LI Z, et al. Single image dehazing via conditional generative adversarial network [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 8202-8211.
[本文引用: 1]
[27]
YANG W, WANG W, HUANG H, et al Sparse gradient regularized deep Retinex network for robust low-light image enhancement
[J]. IEEE Transactions on Image Processing 2021 , 30 : 2072 - 2086
DOI:10.1109/TIP.2021.3050850
[本文引用: 1]
[28]
ZEILER M D, FERGUS R. Visualizing and understanding convolutional networks [C]// European Conference Computer Vision . Zurich: Springer, 2014: 818-833.
[本文引用: 1]
[29]
GRAY R M, GOODMAN J W. Fourier transforms: an introduction for engineers [M]. Berlin: Springer, 2012: 53-113.
[本文引用: 1]
[30]
LI L, DONG Y, REN W, et al Semi-supervised image dehazing
[J]. IEEE Transactions on Image Processing 2019 , 29 : 2766 - 2779
[本文引用: 3]
[31]
YANG Y, WANG C, LIU R, et al. Self-augmented unpaired image dehazing via density and depth decomposition [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 2037-2046.
[本文引用: 9]
[32]
GU K, TAO D, QIAO J F, et al Learning a no-reference quality assessment model of enhanced images with big data
[J]. IEEE Transactions on Neural Networks and Learning Systems 2017 , 29 (4 ): 1301 - 1313
[本文引用: 3]
[33]
GU K, QIAO J, LI X Highly efficient picture-based prediction of PM2.5 concentration
[J]. IEEE Transactions on Industrial Electronics 2018 , 66 (4 ): 3176 - 3184
[本文引用: 3]
[34]
TALEBI H, MILANFAR P NIMA: neural image assessment
[J]. IEEE Transactions on Image Processing 2018 , 27 (8 ): 3998 - 4011
DOI:10.1109/TIP.2018.2831899
[本文引用: 3]
ReViewNet: a fast and resource optimized network for enabling safe autonomous driving in hazy weather conditions
1
2021
... 雾霾是常见的大气现象,由微小的漂浮颗粒吸收和散射其传播方向的光而产生.由于大气光衰减和散射的影响,拍摄的图像亮度和对比度会降低,颜色衰减纹理变得模糊,这给一些基于户外场景的计算机视觉应用带来困难,如户外场景的自动驾驶、行人检测和目标检测等[1 -2 ] . 这些视觉应用对光照和天气状况极其敏感,雾和低光照使得这些应用算法的性能降低,而去雾是提高这些视觉应用性能的重要一步. ...
Haze removal of railway monitoring images using multi-scale residual network
1
2020
... 雾霾是常见的大气现象,由微小的漂浮颗粒吸收和散射其传播方向的光而产生.由于大气光衰减和散射的影响,拍摄的图像亮度和对比度会降低,颜色衰减纹理变得模糊,这给一些基于户外场景的计算机视觉应用带来困难,如户外场景的自动驾驶、行人检测和目标检测等[1 -2 ] . 这些视觉应用对光照和天气状况极其敏感,雾和低光照使得这些应用算法的性能降低,而去雾是提高这些视觉应用性能的重要一步. ...
Self-guided image dehazing using progressive feature fusion
11
2022
... 由于真实的成对有雾图像难以得到,研究人员采用大气光散射模型(atmospheric scattering model, ASM)合成数据并训练模型. 目前,在合成数据上的去雾方法性能得到了极大的提升[3 -5 ] .然而,当将这些性能先进的去雾算法应用在真实数据上时,去雾结果会出现雾残留和亮度衰减的质量干扰. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如图4 所示为不同方法在Fattal数据上的去雾结果. DCP和NLD的去雾性能明显优于其他监督方法,但是它们的去雾结果亮度损失,NLD的结果出现颜色混乱,这说明真实情况违背了他们的先验假设. 有监督方法DehazeFlow[5 ] 和FFA[6 ] 的去雾能力不足,在所有结果中有大量的雾残余,甚至去雾无效. 虽然GridDehazeNet[18 ] 、MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 有一定的去雾能力,但无法有效去雾,纹理模糊. 上述方法的结果出现亮度损失. 造成这种现象的原因是这些方法未考虑真实数据集的复杂情形,与真实数据存在域漂移,尤其是忽略了暗光的影响,缺乏稳定性. 利用本文方法,可以有效地去雾,增加图像亮度,颜色没发生变异且纹理清晰. 这是因为本文方法不仅考虑了低光,而且使用不变学习,可以应对真实的雾霾情况. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
... 如图7 所示为3个具有代表性的方法在SOTS和DarkHaze数据集上的去雾结果. 在SOTS数据集上,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 的去雾图和真实值非常相近.真实值的方框2内存在雾,这导致MSBDN[19 ] 和SGID[3 ] 的结果只能逼近真实值,却无法将方框2的雾去除. 此外,这3个方法均未考虑低光照的情况,真实值存在弱光区域,这导致方框1内去雾亮度存在损失. 利用本文方法,不仅可以有效地去除方框2中的雾,而且可以增大方框1内去雾后的亮度.真实值是MSBDN[19 ] 和SGID[3 ] 的去雾上界,它们无法突破此上界,本文的方法则不然,如图7 中方框1和方框2内所示. 在DarkHaze去雾结果中,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... [3 ]的结果只能逼近真实值,却无法将方框2的雾去除. 此外,这3个方法均未考虑低光照的情况,真实值存在弱光区域,这导致方框1内去雾亮度存在损失. 利用本文方法,不仅可以有效地去除方框2中的雾,而且可以增大方框1内去雾后的亮度.真实值是MSBDN[19 ] 和SGID[3 ] 的去雾上界,它们无法突破此上界,本文的方法则不然,如图7 中方框1和方框2内所示. 在DarkHaze去雾结果中,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... [3 ]的去雾上界,它们无法突破此上界,本文的方法则不然,如图7 中方框1和方框2内所示. 在DarkHaze去雾结果中,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... [3 ]和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... 如表2 所示为MSBDN[19 ] 、SGID[3 ] 、D4[31 ] 和本文方法在SOTS和DarkHaze测试集上的PSNR和SSIM的平均值,本文在这2个数据集上获得了最稳定的PSNR和SSIM.可以发现,当环境变化时,这3种方法的平均PSNR和SSIM显著减小,说明了这3种方法的去雾性能不稳定,而本文方法在2个数据集上的平均PSNR和SSIM变化很小,这是因为本文使用了不变学习,消除了特征之间的虚假相关性,使得网络获得了可以提取跨域本质特征的能力. ...
... PSNR and SSIM of different methods on DarkHaze and SOTS test datasets
Tab.2 方法 DarkHaze SOTS PSNR/dB SSIM PSNR/dB SSIM MSBDN[19 ] 16.05 0.7330 30.93 0.9780 SGID[3 ] 17.02 0.7536 30.20 0.9754 D4[31 ] 16.16 0.6756 25.82 0.9445 本文方法 26.83 0.9301 26.04 0.9511
本文挑选出有代表性的去雾方法,在分辨率为$ 3 \times 224 \times 224 $ 表3 所示为不同方法的参数量 N p 和每秒浮点运算次数FLOPs. 从表3 可以看出,与这些代表性的去雾方法相比,本文所提出的方法在保证真实去雾性能的同时,能够将模型的参数量和计算复杂度保持在合理的范围内. ...
... Complexity comparison of different methods
Tab.3 方法 N p /106 FLOPs/109 MSBDN[19 ] 36.85 137.90 PSD[22 ] 33.11 220.60 SGID[3 ] 13.87 108.40 D4[31 ] 10.70 2.25 本文方法 31.40 34.17
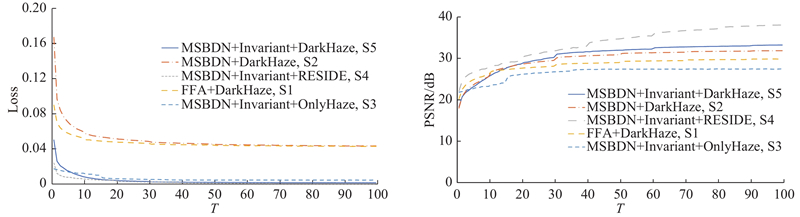
5. 消融实验 在消融实验中,本文要验证所提出的数据集和方法的作用. 1)其他去雾方法使用DarkHaze,能够避免去雾结果出现质量损失.2)提出的数据集和采用的方法起作用的程度.为了验证数据和模型的作用,本文给出5种不同的模型设定.使用DarkHaze来训练FFA[4 ] 模型(FFA+DarkHaze,记为S1). 类似地,将不变学习从提出的模型中移除,使用DarkHaze来训练模型(MSBDN+DarkHaze,S2). 去除Gamma变换,仅使用ASM来合成有雾数据集(OnlyHaze),大气光值$ A $ $ \beta $ [17 ] 来训练提出的方法(MSBDN+Invariant+RESIDE,S4). 将这些不同的设定与本文提出的方法(MSBDN+Invariant+DarkHaze,S5)进行比较. ...
2
... 在消融实验中,本文要验证所提出的数据集和方法的作用. 1)其他去雾方法使用DarkHaze,能够避免去雾结果出现质量损失.2)提出的数据集和采用的方法起作用的程度.为了验证数据和模型的作用,本文给出5种不同的模型设定.使用DarkHaze来训练FFA[4 ] 模型(FFA+DarkHaze,记为S1). 类似地,将不变学习从提出的模型中移除,使用DarkHaze来训练模型(MSBDN+DarkHaze,S2). 去除Gamma变换,仅使用ASM来合成有雾数据集(OnlyHaze),大气光值$ A $ $ \beta $ [17 ] 来训练提出的方法(MSBDN+Invariant+RESIDE,S4). 将这些不同的设定与本文提出的方法(MSBDN+Invariant+DarkHaze,S5)进行比较. ...
... 倘若将图像先增强再去雾,或者先去雾后增强,这种顺序操作仍难以解决去雾结果质量干扰的问题. 本文选择伽玛校正对图像进行增强,设定伽玛值为1.4,选择FFA[4 ] 对增强的图像进行去雾.如图10 第1行所示为对图像先进行增强再进行去雾的结果. 可以看出,先增强虽然可以增强亮度,但是会使得图像雾浓度明显增大,再使用去雾方法不能将雾去除,会出现大量的雾霾残余.如图10 第2行所示为对图像先去雾再增强的结果.可以看出,先去雾后图像亮度出现损失,图像中雾霾减少,再使用增强方法后图像确实变亮,但雾霾被去除的区域重新出现雾. 以上2组实验说明图像去雾和图像增强顺序操作会得到适得其反的作用,需要同时考虑才能获得良好的结果. ...
5
... 由于真实的成对有雾图像难以得到,研究人员采用大气光散射模型(atmospheric scattering model, ASM)合成数据并训练模型. 目前,在合成数据上的去雾方法性能得到了极大的提升[3 -5 ] .然而,当将这些性能先进的去雾算法应用在真实数据上时,去雾结果会出现雾残留和亮度衰减的质量干扰. ...
... ASM忽略了真实场景中的复合情形,例如低光照雾会吸收光,因此雾与弱光总是相伴而生的. 虽然图像去雾[5 -6 ] 和低光照图像增强[7 ] 的研究不断在发展,但真实有雾且低光照的图像图及其对应的无雾图难以得到,这限制了二者结合的研究. 一种直接的方式是将图像去雾和低光增强组合,即先增强后去雾或者先去雾后增强,本文在消融实验部分证明这二种方式不可行. 雾霾的形成受多种因素的影响,真实数据与合成数据的分布不同,这破坏了经典学习理论中的独立同分布假设. 有监督学习方法往往是通过最小化经验风险误差来优化,经验最小化误差会贪婪地吸收数据中发现的所有相关性来进行预测[8 ] . 在独立同分布假设下的所有相关性可能是有效的,但在分布漂移时先前的相关性在未知的测试分布中很难保持不变. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如图4 所示为不同方法在Fattal数据上的去雾结果. DCP和NLD的去雾性能明显优于其他监督方法,但是它们的去雾结果亮度损失,NLD的结果出现颜色混乱,这说明真实情况违背了他们的先验假设. 有监督方法DehazeFlow[5 ] 和FFA[6 ] 的去雾能力不足,在所有结果中有大量的雾残余,甚至去雾无效. 虽然GridDehazeNet[18 ] 、MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 有一定的去雾能力,但无法有效去雾,纹理模糊. 上述方法的结果出现亮度损失. 造成这种现象的原因是这些方法未考虑真实数据集的复杂情形,与真实数据存在域漂移,尤其是忽略了暗光的影响,缺乏稳定性. 利用本文方法,可以有效地去雾,增加图像亮度,颜色没发生变异且纹理清晰. 这是因为本文方法不仅考虑了低光,而且使用不变学习,可以应对真实的雾霾情况. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
6
... ASM忽略了真实场景中的复合情形,例如低光照雾会吸收光,因此雾与弱光总是相伴而生的. 虽然图像去雾[5 -6 ] 和低光照图像增强[7 ] 的研究不断在发展,但真实有雾且低光照的图像图及其对应的无雾图难以得到,这限制了二者结合的研究. 一种直接的方式是将图像去雾和低光增强组合,即先增强后去雾或者先去雾后增强,本文在消融实验部分证明这二种方式不可行. 雾霾的形成受多种因素的影响,真实数据与合成数据的分布不同,这破坏了经典学习理论中的独立同分布假设. 有监督学习方法往往是通过最小化经验风险误差来优化,经验最小化误差会贪婪地吸收数据中发现的所有相关性来进行预测[8 ] . 在独立同分布假设下的所有相关性可能是有效的,但在分布漂移时先前的相关性在未知的测试分布中很难保持不变. ...
... 由于先验方法的局限性,大量的研究人员转向深度学习领域. 利用RESIDE数据集[17 ] ,Qin等[6 ,18 ] 采用端到端的方式进行去雾. Dong等[19 ] 提出基于U-Net架构的多尺度提升方法. 虽然一些研究者考虑了暗雾去除的问题,但非稳健的特征导致了糟糕的结果. Kim等[20 ] 设计两阶段网络,将去雾和低照度增强统一起来,但该方法需要估计亮度图而非端到端,结果会出现局部过曝光和雾残留. Ju等[21 ] 将ASM修改为带有灰色世界假设的增强ASM,这导致在单色场景区域内产生颜色混乱. Chen等[22 ] 使用对比度适应的直方图均衡化来产生伪标签,但伪标签会导致过度饱和并重新加雾. 在领域适应方法中,Shao等[6 ] 采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... [6 ]采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如图4 所示为不同方法在Fattal数据上的去雾结果. DCP和NLD的去雾性能明显优于其他监督方法,但是它们的去雾结果亮度损失,NLD的结果出现颜色混乱,这说明真实情况违背了他们的先验假设. 有监督方法DehazeFlow[5 ] 和FFA[6 ] 的去雾能力不足,在所有结果中有大量的雾残余,甚至去雾无效. 虽然GridDehazeNet[18 ] 、MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 有一定的去雾能力,但无法有效去雾,纹理模糊. 上述方法的结果出现亮度损失. 造成这种现象的原因是这些方法未考虑真实数据集的复杂情形,与真实数据存在域漂移,尤其是忽略了暗光的影响,缺乏稳定性. 利用本文方法,可以有效地去雾,增加图像亮度,颜色没发生变异且纹理清晰. 这是因为本文方法不仅考虑了低光,而且使用不变学习,可以应对真实的雾霾情况. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
1
... ASM忽略了真实场景中的复合情形,例如低光照雾会吸收光,因此雾与弱光总是相伴而生的. 虽然图像去雾[5 -6 ] 和低光照图像增强[7 ] 的研究不断在发展,但真实有雾且低光照的图像图及其对应的无雾图难以得到,这限制了二者结合的研究. 一种直接的方式是将图像去雾和低光增强组合,即先增强后去雾或者先去雾后增强,本文在消融实验部分证明这二种方式不可行. 雾霾的形成受多种因素的影响,真实数据与合成数据的分布不同,这破坏了经典学习理论中的独立同分布假设. 有监督学习方法往往是通过最小化经验风险误差来优化,经验最小化误差会贪婪地吸收数据中发现的所有相关性来进行预测[8 ] . 在独立同分布假设下的所有相关性可能是有效的,但在分布漂移时先前的相关性在未知的测试分布中很难保持不变. ...
2
... ASM忽略了真实场景中的复合情形,例如低光照雾会吸收光,因此雾与弱光总是相伴而生的. 虽然图像去雾[5 -6 ] 和低光照图像增强[7 ] 的研究不断在发展,但真实有雾且低光照的图像图及其对应的无雾图难以得到,这限制了二者结合的研究. 一种直接的方式是将图像去雾和低光增强组合,即先增强后去雾或者先去雾后增强,本文在消融实验部分证明这二种方式不可行. 雾霾的形成受多种因素的影响,真实数据与合成数据的分布不同,这破坏了经典学习理论中的独立同分布假设. 有监督学习方法往往是通过最小化经验风险误差来优化,经验最小化误差会贪婪地吸收数据中发现的所有相关性来进行预测[8 ] . 在独立同分布假设下的所有相关性可能是有效的,但在分布漂移时先前的相关性在未知的测试分布中很难保持不变. ...
... 最近,分布偏移问题在域泛化文献中得到了深入研究[9 -10 ] . 域泛化的基本思想是将一个类别划分为多个域,提取的混杂特征在不同域之间变化,而本质特征保持不变. 利用神经网络从数据中学习出跨域的不变特征成为关键. 不变学习[11 -13 ] 被提出用来解决域泛化问题. 不变学习认为神经网络提取的特征中的无关特征与本质特征之间的虚假相关是跨域性能下降的关键原因[8 -11 ] ,通过抑制不相关特征的负面影响,在分布变化下具有更好的泛化能力. 去除特征中的虚假相关性成为关键. ...
Generalizing to unseen domains: a survey on domain generalization
1
2023
... 最近,分布偏移问题在域泛化文献中得到了深入研究[9 -10 ] . 域泛化的基本思想是将一个类别划分为多个域,提取的混杂特征在不同域之间变化,而本质特征保持不变. 利用神经网络从数据中学习出跨域的不变特征成为关键. 不变学习[11 -13 ] 被提出用来解决域泛化问题. 不变学习认为神经网络提取的特征中的无关特征与本质特征之间的虚假相关是跨域性能下降的关键原因[8 -11 ] ,通过抑制不相关特征的负面影响,在分布变化下具有更好的泛化能力. 去除特征中的虚假相关性成为关键. ...
2
... 最近,分布偏移问题在域泛化文献中得到了深入研究[9 -10 ] . 域泛化的基本思想是将一个类别划分为多个域,提取的混杂特征在不同域之间变化,而本质特征保持不变. 利用神经网络从数据中学习出跨域的不变特征成为关键. 不变学习[11 -13 ] 被提出用来解决域泛化问题. 不变学习认为神经网络提取的特征中的无关特征与本质特征之间的虚假相关是跨域性能下降的关键原因[8 -11 ] ,通过抑制不相关特征的负面影响,在分布变化下具有更好的泛化能力. 去除特征中的虚假相关性成为关键. ...
... 当训练数据与测试数据的分布不一致时,Kuang等[10 ] 提出稳定学习,稳定学习希望在不同的环境中学习出跨域的本质特征,因此稳定学习预测具有不变性. Kuang等[11 ] 提出新的去相关加权回归算法,该算法联合优化了变量去相关正则项和加权回归模型. 虽然上述方法在不同环境分类中获得不错的性能,但上述方法多利用线性模型进行研究,不适用于深度学习提取的非线性特征. Zheng等[12 ] 采用随机傅里叶特征加权去相关算法,将此类方法扩展到了神经网络的非线性表征空间中,并在分类域漂移问题上获得了不错的性能. 域适应方法一般使用测试集中的数据,稳定学习只需要在训练集中学习鲁棒的特征. 本文方法利用不变学习,结合稳定学习与图像去雾,获得更好的性能. ...
4
... 最近,分布偏移问题在域泛化文献中得到了深入研究[9 -10 ] . 域泛化的基本思想是将一个类别划分为多个域,提取的混杂特征在不同域之间变化,而本质特征保持不变. 利用神经网络从数据中学习出跨域的不变特征成为关键. 不变学习[11 -13 ] 被提出用来解决域泛化问题. 不变学习认为神经网络提取的特征中的无关特征与本质特征之间的虚假相关是跨域性能下降的关键原因[8 -11 ] ,通过抑制不相关特征的负面影响,在分布变化下具有更好的泛化能力. 去除特征中的虚假相关性成为关键. ...
... -11 ],通过抑制不相关特征的负面影响,在分布变化下具有更好的泛化能力. 去除特征中的虚假相关性成为关键. ...
... 当训练数据与测试数据的分布不一致时,Kuang等[10 ] 提出稳定学习,稳定学习希望在不同的环境中学习出跨域的本质特征,因此稳定学习预测具有不变性. Kuang等[11 ] 提出新的去相关加权回归算法,该算法联合优化了变量去相关正则项和加权回归模型. 虽然上述方法在不同环境分类中获得不错的性能,但上述方法多利用线性模型进行研究,不适用于深度学习提取的非线性特征. Zheng等[12 ] 采用随机傅里叶特征加权去相关算法,将此类方法扩展到了神经网络的非线性表征空间中,并在分类域漂移问题上获得了不错的性能. 域适应方法一般使用测试集中的数据,稳定学习只需要在训练集中学习鲁棒的特征. 本文方法利用不变学习,结合稳定学习与图像去雾,获得更好的性能. ...
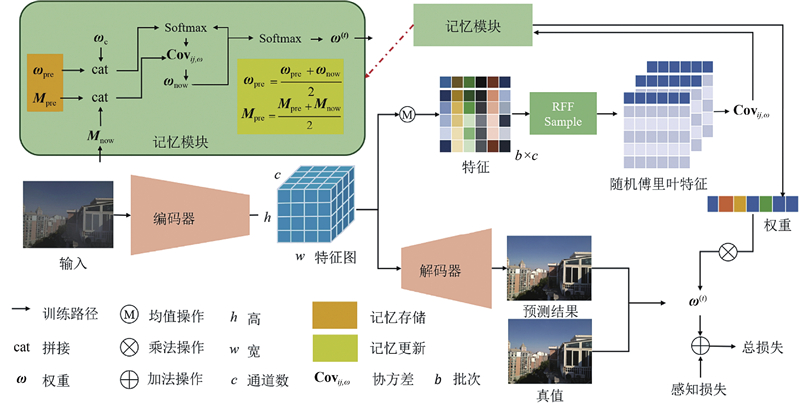
... 由于高斯核为正定核,$ \left\| {{\mathrm{Cov}}} \left( {{u}}\left( {{{\boldsymbol{Z}}_{:,{{i}}}}}\right) , {{v}}\left( {{{\boldsymbol{Z}}_{:,{{j}}}}} \right) \right) \right\|{\mathrm{_F}}^2 $ $ \left\| {{\mathrm{Cov}}}\left( {{u}}\left( {{{\boldsymbol{Z}}_{:,{{i}}}}}\right) , {{v}}\left( {{{\boldsymbol{Z}}_{:,{{j}}}}} \right) \right) \right\|{\mathrm{_F}}^2 $ $ {{\boldsymbol{Z}}_{:,{{i}}}} $ $ {{\boldsymbol{Z}}_{:,j}} $ [11 -12 ] 的研究表明,通过将在表示空间中学习到的每个特征作为处理变量,并学习权重以平衡源数据在每个学习到的特征表示方面的分布,可以学习到新的域,在这个域中只有本质特征与结果相关,使用样本权重$ {\boldsymbol{\omega}} $ $ {{\boldsymbol{Z}}_{:,{{i}}}} $ $ {{\boldsymbol{Z}}_{:,j}} $ $ {\mathrm{Cov}}\left( {{u}}\left( {{{\boldsymbol{Z}}_{:,{{i}}}}}\right) , {{v}}\left( {{{\boldsymbol{Z}}_{:,{{j}}}}} \right) \right) $
2
... 当训练数据与测试数据的分布不一致时,Kuang等[10 ] 提出稳定学习,稳定学习希望在不同的环境中学习出跨域的本质特征,因此稳定学习预测具有不变性. Kuang等[11 ] 提出新的去相关加权回归算法,该算法联合优化了变量去相关正则项和加权回归模型. 虽然上述方法在不同环境分类中获得不错的性能,但上述方法多利用线性模型进行研究,不适用于深度学习提取的非线性特征. Zheng等[12 ] 采用随机傅里叶特征加权去相关算法,将此类方法扩展到了神经网络的非线性表征空间中,并在分类域漂移问题上获得了不错的性能. 域适应方法一般使用测试集中的数据,稳定学习只需要在训练集中学习鲁棒的特征. 本文方法利用不变学习,结合稳定学习与图像去雾,获得更好的性能. ...
... 由于高斯核为正定核,$ \left\| {{\mathrm{Cov}}} \left( {{u}}\left( {{{\boldsymbol{Z}}_{:,{{i}}}}}\right) , {{v}}\left( {{{\boldsymbol{Z}}_{:,{{j}}}}} \right) \right) \right\|{\mathrm{_F}}^2 $ $ \left\| {{\mathrm{Cov}}}\left( {{u}}\left( {{{\boldsymbol{Z}}_{:,{{i}}}}}\right) , {{v}}\left( {{{\boldsymbol{Z}}_{:,{{j}}}}} \right) \right) \right\|{\mathrm{_F}}^2 $ $ {{\boldsymbol{Z}}_{:,{{i}}}} $ $ {{\boldsymbol{Z}}_{:,j}} $ [11 -12 ] 的研究表明,通过将在表示空间中学习到的每个特征作为处理变量,并学习权重以平衡源数据在每个学习到的特征表示方面的分布,可以学习到新的域,在这个域中只有本质特征与结果相关,使用样本权重$ {\boldsymbol{\omega}} $ $ {{\boldsymbol{Z}}_{:,{{i}}}} $ $ {{\boldsymbol{Z}}_{:,j}} $ $ {\mathrm{Cov}}\left( {{u}}\left( {{{\boldsymbol{Z}}_{:,{{i}}}}}\right) , {{v}}\left( {{{\boldsymbol{Z}}_{:,{{j}}}}} \right) \right) $
2
... 最近,分布偏移问题在域泛化文献中得到了深入研究[9 -10 ] . 域泛化的基本思想是将一个类别划分为多个域,提取的混杂特征在不同域之间变化,而本质特征保持不变. 利用神经网络从数据中学习出跨域的不变特征成为关键. 不变学习[11 -13 ] 被提出用来解决域泛化问题. 不变学习认为神经网络提取的特征中的无关特征与本质特征之间的虚假相关是跨域性能下降的关键原因[8 -11 ] ,通过抑制不相关特征的负面影响,在分布变化下具有更好的泛化能力. 去除特征中的虚假相关性成为关键. ...
... 式中:$ g( \cdot ) $ $ {{{\omega}} _{{i}}} $ $ {\boldsymbol{\omega}} $ [13 ] 作为网络架构,$ t $ $ {{\psi }} $ $ {\lambda _{\mathrm{p}}} $ $ \hat {\boldsymbol{y}}_i = g({{\boldsymbol{x}}_i}) $ $ {{\boldsymbol{y}}_i} $ $ {{\boldsymbol{\omega}} ^0} $ $ [1,1, \cdots ,1] $ . 式(14)是典型的二重优化问题,在计算时,先优化网络参数,再在表征空间中优化权重$ {\boldsymbol{\omega}} $ . ...
Single image haze removal using dark channel prior
2
2010
... 图像除雾方法可以分为基于先验的方法和基于学习的方法. 利用基于先验的方法,估计透射图和全局大气光,根据大气散射模型获得去雾结果. 代表性的方法包括暗通道(DCP)[14 ] 、局部颜色线[15 ] 和全局雾线(NLD)[16 ] . 尽管这些先验的方法获得了良好的结果,但复杂的真实场景会违背这些先验假设,使得这些方法不稳健. 此外,上述方法的去雾结果出现亮度衰减. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
Dehazing using color-lines
3
2014
... 图像除雾方法可以分为基于先验的方法和基于学习的方法. 利用基于先验的方法,估计透射图和全局大气光,根据大气散射模型获得去雾结果. 代表性的方法包括暗通道(DCP)[14 ] 、局部颜色线[15 ] 和全局雾线(NLD)[16 ] . 尽管这些先验的方法获得了良好的结果,但复杂的真实场景会违背这些先验假设,使得这些方法不稳健. 此外,上述方法的去雾结果出现亮度衰减. ...
... 利用数据集RESIDE OTS[17 ] 提供的2 061幅图像及其深度图来合成暗雾图,大气光值$ A $ $ \beta $ $ \left[ {0.75,{\text{ }}0.9} \right] $ $ \left[ {0.1,{\text{ }}0.6} \right] $ $ \gamma $ $ \left[ {1.25,5} \right] $ [17 ] 的子集RTTS和URHI来验证所提出的方法,这2个子集十分复杂,分别包含4 322和4 708幅真实的雾霾图像. 本文还收集32幅Fattal[15 ] 真实雾霾图进行测试. ...
... 如表1 所示为利用无参考图评价方法计算在RTTS上的去雾性能.可以看出,本文所提方法在多数评价指标上获得了最好的性能. 除了本文的方法外,方法IDE[21 ] 、SLA[24 ] 、PSD[22 ] 和LED2Net[20 ] 也考虑了图像去雾后亮度损失问题,因此在真实数据上对比他们的结果是十分必要的.本文在Fattal[15 ] 数据集上进行测试,结果如图6 所示. 从图中的方框区域可以看出,IDE[21 ] 和PSD[22 ] 的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
2
... 图像除雾方法可以分为基于先验的方法和基于学习的方法. 利用基于先验的方法,估计透射图和全局大气光,根据大气散射模型获得去雾结果. 代表性的方法包括暗通道(DCP)[14 ] 、局部颜色线[15 ] 和全局雾线(NLD)[16 ] . 尽管这些先验的方法获得了良好的结果,但复杂的真实场景会违背这些先验假设,使得这些方法不稳健. 此外,上述方法的去雾结果出现亮度衰减. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
Benchmarking single-image dehazing and beyond
4
2018
... 由于先验方法的局限性,大量的研究人员转向深度学习领域. 利用RESIDE数据集[17 ] ,Qin等[6 ,18 ] 采用端到端的方式进行去雾. Dong等[19 ] 提出基于U-Net架构的多尺度提升方法. 虽然一些研究者考虑了暗雾去除的问题,但非稳健的特征导致了糟糕的结果. Kim等[20 ] 设计两阶段网络,将去雾和低照度增强统一起来,但该方法需要估计亮度图而非端到端,结果会出现局部过曝光和雾残留. Ju等[21 ] 将ASM修改为带有灰色世界假设的增强ASM,这导致在单色场景区域内产生颜色混乱. Chen等[22 ] 使用对比度适应的直方图均衡化来产生伪标签,但伪标签会导致过度饱和并重新加雾. 在领域适应方法中,Shao等[6 ] 采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... 利用数据集RESIDE OTS[17 ] 提供的2 061幅图像及其深度图来合成暗雾图,大气光值$ A $ $ \beta $ $ \left[ {0.75,{\text{ }}0.9} \right] $ $ \left[ {0.1,{\text{ }}0.6} \right] $ $ \gamma $ $ \left[ {1.25,5} \right] $ [17 ] 的子集RTTS和URHI来验证所提出的方法,这2个子集十分复杂,分别包含4 322和4 708幅真实的雾霾图像. 本文还收集32幅Fattal[15 ] 真实雾霾图进行测试. ...
... [17 ]的子集RTTS和URHI来验证所提出的方法,这2个子集十分复杂,分别包含4 322和4 708幅真实的雾霾图像. 本文还收集32幅Fattal[15 ] 真实雾霾图进行测试. ...
... 在消融实验中,本文要验证所提出的数据集和方法的作用. 1)其他去雾方法使用DarkHaze,能够避免去雾结果出现质量损失.2)提出的数据集和采用的方法起作用的程度.为了验证数据和模型的作用,本文给出5种不同的模型设定.使用DarkHaze来训练FFA[4 ] 模型(FFA+DarkHaze,记为S1). 类似地,将不变学习从提出的模型中移除,使用DarkHaze来训练模型(MSBDN+DarkHaze,S2). 去除Gamma变换,仅使用ASM来合成有雾数据集(OnlyHaze),大气光值$ A $ $ \beta $ [17 ] 来训练提出的方法(MSBDN+Invariant+RESIDE,S4). 将这些不同的设定与本文提出的方法(MSBDN+Invariant+DarkHaze,S5)进行比较. ...
3
... 由于先验方法的局限性,大量的研究人员转向深度学习领域. 利用RESIDE数据集[17 ] ,Qin等[6 ,18 ] 采用端到端的方式进行去雾. Dong等[19 ] 提出基于U-Net架构的多尺度提升方法. 虽然一些研究者考虑了暗雾去除的问题,但非稳健的特征导致了糟糕的结果. Kim等[20 ] 设计两阶段网络,将去雾和低照度增强统一起来,但该方法需要估计亮度图而非端到端,结果会出现局部过曝光和雾残留. Ju等[21 ] 将ASM修改为带有灰色世界假设的增强ASM,这导致在单色场景区域内产生颜色混乱. Chen等[22 ] 使用对比度适应的直方图均衡化来产生伪标签,但伪标签会导致过度饱和并重新加雾. 在领域适应方法中,Shao等[6 ] 采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如图4 所示为不同方法在Fattal数据上的去雾结果. DCP和NLD的去雾性能明显优于其他监督方法,但是它们的去雾结果亮度损失,NLD的结果出现颜色混乱,这说明真实情况违背了他们的先验假设. 有监督方法DehazeFlow[5 ] 和FFA[6 ] 的去雾能力不足,在所有结果中有大量的雾残余,甚至去雾无效. 虽然GridDehazeNet[18 ] 、MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 有一定的去雾能力,但无法有效去雾,纹理模糊. 上述方法的结果出现亮度损失. 造成这种现象的原因是这些方法未考虑真实数据集的复杂情形,与真实数据存在域漂移,尤其是忽略了暗光的影响,缺乏稳定性. 利用本文方法,可以有效地去雾,增加图像亮度,颜色没发生变异且纹理清晰. 这是因为本文方法不仅考虑了低光,而且使用不变学习,可以应对真实的雾霾情况. ...
12
... 由于先验方法的局限性,大量的研究人员转向深度学习领域. 利用RESIDE数据集[17 ] ,Qin等[6 ,18 ] 采用端到端的方式进行去雾. Dong等[19 ] 提出基于U-Net架构的多尺度提升方法. 虽然一些研究者考虑了暗雾去除的问题,但非稳健的特征导致了糟糕的结果. Kim等[20 ] 设计两阶段网络,将去雾和低照度增强统一起来,但该方法需要估计亮度图而非端到端,结果会出现局部过曝光和雾残留. Ju等[21 ] 将ASM修改为带有灰色世界假设的增强ASM,这导致在单色场景区域内产生颜色混乱. Chen等[22 ] 使用对比度适应的直方图均衡化来产生伪标签,但伪标签会导致过度饱和并重新加雾. 在领域适应方法中,Shao等[6 ] 采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... 在Ubuntu系统上进行实验,该系统装载的显卡为NVIDIA GeForce GTX 3090 GPU. 使用PyTorch 1.7.0框架训练本文的模型,输入网络图像的大小被设置为$ 256 \times 256 $ $ b = 28 $ $ c = 128 $ $ h = w = 16 $ . 训练时,通过随机旋转和水平翻转来增强样本,总共训练模型100轮.使用Adam优化器训练本文的方法.设置初始学习率为0.000 1,每20个周期学习率衰减为原来的一半. 以MSBDN[19 ] 网络为基准框架,将提出的不变学习理论与MSBDN网络相结合. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如图4 所示为不同方法在Fattal数据上的去雾结果. DCP和NLD的去雾性能明显优于其他监督方法,但是它们的去雾结果亮度损失,NLD的结果出现颜色混乱,这说明真实情况违背了他们的先验假设. 有监督方法DehazeFlow[5 ] 和FFA[6 ] 的去雾能力不足,在所有结果中有大量的雾残余,甚至去雾无效. 虽然GridDehazeNet[18 ] 、MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 有一定的去雾能力,但无法有效去雾,纹理模糊. 上述方法的结果出现亮度损失. 造成这种现象的原因是这些方法未考虑真实数据集的复杂情形,与真实数据存在域漂移,尤其是忽略了暗光的影响,缺乏稳定性. 利用本文方法,可以有效地去雾,增加图像亮度,颜色没发生变异且纹理清晰. 这是因为本文方法不仅考虑了低光,而且使用不变学习,可以应对真实的雾霾情况. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
... 如图7 所示为3个具有代表性的方法在SOTS和DarkHaze数据集上的去雾结果. 在SOTS数据集上,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 的去雾图和真实值非常相近.真实值的方框2内存在雾,这导致MSBDN[19 ] 和SGID[3 ] 的结果只能逼近真实值,却无法将方框2的雾去除. 此外,这3个方法均未考虑低光照的情况,真实值存在弱光区域,这导致方框1内去雾亮度存在损失. 利用本文方法,不仅可以有效地去除方框2中的雾,而且可以增大方框1内去雾后的亮度.真实值是MSBDN[19 ] 和SGID[3 ] 的去雾上界,它们无法突破此上界,本文的方法则不然,如图7 中方框1和方框2内所示. 在DarkHaze去雾结果中,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... [19 ]和SGID[3 ] 的结果只能逼近真实值,却无法将方框2的雾去除. 此外,这3个方法均未考虑低光照的情况,真实值存在弱光区域,这导致方框1内去雾亮度存在损失. 利用本文方法,不仅可以有效地去除方框2中的雾,而且可以增大方框1内去雾后的亮度.真实值是MSBDN[19 ] 和SGID[3 ] 的去雾上界,它们无法突破此上界,本文的方法则不然,如图7 中方框1和方框2内所示. 在DarkHaze去雾结果中,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... [19 ]和SGID[3 ] 的去雾上界,它们无法突破此上界,本文的方法则不然,如图7 中方框1和方框2内所示. 在DarkHaze去雾结果中,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... [19 ]、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... 如表2 所示为MSBDN[19 ] 、SGID[3 ] 、D4[31 ] 和本文方法在SOTS和DarkHaze测试集上的PSNR和SSIM的平均值,本文在这2个数据集上获得了最稳定的PSNR和SSIM.可以发现,当环境变化时,这3种方法的平均PSNR和SSIM显著减小,说明了这3种方法的去雾性能不稳定,而本文方法在2个数据集上的平均PSNR和SSIM变化很小,这是因为本文使用了不变学习,消除了特征之间的虚假相关性,使得网络获得了可以提取跨域本质特征的能力. ...
... PSNR and SSIM of different methods on DarkHaze and SOTS test datasets
Tab.2 方法 DarkHaze SOTS PSNR/dB SSIM PSNR/dB SSIM MSBDN[19 ] 16.05 0.7330 30.93 0.9780 SGID[3 ] 17.02 0.7536 30.20 0.9754 D4[31 ] 16.16 0.6756 25.82 0.9445 本文方法 26.83 0.9301 26.04 0.9511
本文挑选出有代表性的去雾方法,在分辨率为$ 3 \times 224 \times 224 $ 表3 所示为不同方法的参数量 N p 和每秒浮点运算次数FLOPs. 从表3 可以看出,与这些代表性的去雾方法相比,本文所提出的方法在保证真实去雾性能的同时,能够将模型的参数量和计算复杂度保持在合理的范围内. ...
... Complexity comparison of different methods
Tab.3 方法 N p /106 FLOPs/109 MSBDN[19 ] 36.85 137.90 PSD[22 ] 33.11 220.60 SGID[3 ] 13.87 108.40 D4[31 ] 10.70 2.25 本文方法 31.40 34.17
5. 消融实验 在消融实验中,本文要验证所提出的数据集和方法的作用. 1)其他去雾方法使用DarkHaze,能够避免去雾结果出现质量损失.2)提出的数据集和采用的方法起作用的程度.为了验证数据和模型的作用,本文给出5种不同的模型设定.使用DarkHaze来训练FFA[4 ] 模型(FFA+DarkHaze,记为S1). 类似地,将不变学习从提出的模型中移除,使用DarkHaze来训练模型(MSBDN+DarkHaze,S2). 去除Gamma变换,仅使用ASM来合成有雾数据集(OnlyHaze),大气光值$ A $ $ \beta $ [17 ] 来训练提出的方法(MSBDN+Invariant+RESIDE,S4). 将这些不同的设定与本文提出的方法(MSBDN+Invariant+DarkHaze,S5)进行比较. ...
Deep illumination-aware dehazing with low-light and detail enhancement
5
2021
... 由于先验方法的局限性,大量的研究人员转向深度学习领域. 利用RESIDE数据集[17 ] ,Qin等[6 ,18 ] 采用端到端的方式进行去雾. Dong等[19 ] 提出基于U-Net架构的多尺度提升方法. 虽然一些研究者考虑了暗雾去除的问题,但非稳健的特征导致了糟糕的结果. Kim等[20 ] 设计两阶段网络,将去雾和低照度增强统一起来,但该方法需要估计亮度图而非端到端,结果会出现局部过曝光和雾残留. Ju等[21 ] 将ASM修改为带有灰色世界假设的增强ASM,这导致在单色场景区域内产生颜色混乱. Chen等[22 ] 使用对比度适应的直方图均衡化来产生伪标签,但伪标签会导致过度饱和并重新加雾. 在领域适应方法中,Shao等[6 ] 采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... 与上述方法不同的是,本文方法是端到端的稳定性去雾网络. 上述方法很少考虑到图像去雾之后的亮度保真问题. 即便考虑了亮度损失问题[20 -25 ] ,但他们没有解释出现亮度损失的原因且结果出现去雾残留和过饱和. 本文在理论上证明使用ASM必然导致图像亮度损失,并对此提出改进. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... [20 ]、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如表1 所示为利用无参考图评价方法计算在RTTS上的去雾性能.可以看出,本文所提方法在多数评价指标上获得了最好的性能. 除了本文的方法外,方法IDE[21 ] 、SLA[24 ] 、PSD[22 ] 和LED2Net[20 ] 也考虑了图像去雾后亮度损失问题,因此在真实数据上对比他们的结果是十分必要的.本文在Fattal[15 ] 数据集上进行测试,结果如图6 所示. 从图中的方框区域可以看出,IDE[21 ] 和PSD[22 ] 的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
IDE: image dehazing and exposure using an enhanced atmospheric scattering model
7
2021
... 由于先验方法的局限性,大量的研究人员转向深度学习领域. 利用RESIDE数据集[17 ] ,Qin等[6 ,18 ] 采用端到端的方式进行去雾. Dong等[19 ] 提出基于U-Net架构的多尺度提升方法. 虽然一些研究者考虑了暗雾去除的问题,但非稳健的特征导致了糟糕的结果. Kim等[20 ] 设计两阶段网络,将去雾和低照度增强统一起来,但该方法需要估计亮度图而非端到端,结果会出现局部过曝光和雾残留. Ju等[21 ] 将ASM修改为带有灰色世界假设的增强ASM,这导致在单色场景区域内产生颜色混乱. Chen等[22 ] 使用对比度适应的直方图均衡化来产生伪标签,但伪标签会导致过度饱和并重新加雾. 在领域适应方法中,Shao等[6 ] 采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... [21 ]、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 从RTTS和URHI中挑选出更有挑战性的浓雾数据,而不是选择简单的薄雾数据. 如图5 所示为去雾结果. SSID[30 ] 的去雾结果亮度存在损失,有大量的雾残留. IDE[21 ] 的去雾能力有限,有大量的雾残余,虽然解决了去雾亮度损失的问题,但结果产生了颜色变异,这是因为IDE采用灰色世界假说,当图像中出现大面积单色场景时会违反灰色世界假设. DAD[23 ] 的方法本质上是利用域对抗方法来接近真实的数据,可以解决亮度损失的问题,但会出现颜色变异,在黑暗物体边缘会产生模糊. PSD[22 ] 的去雾结果明亮,对比度大,饱和度过高,去雾能力不足. 这是因为PSD采用增强方法作为伪标签,导致去雾后重新加雾. D4[31 ] 的去雾能力不足. 本文提出的方法没有出现上述问题,且去雾能力强,亮度未出现损失. ...
... 如表1 所示为利用无参考图评价方法计算在RTTS上的去雾性能.可以看出,本文所提方法在多数评价指标上获得了最好的性能. 除了本文的方法外,方法IDE[21 ] 、SLA[24 ] 、PSD[22 ] 和LED2Net[20 ] 也考虑了图像去雾后亮度损失问题,因此在真实数据上对比他们的结果是十分必要的.本文在Fattal[15 ] 数据集上进行测试,结果如图6 所示. 从图中的方框区域可以看出,IDE[21 ] 和PSD[22 ] 的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
... [21 ]和PSD[22 ] 的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
8
... 由于先验方法的局限性,大量的研究人员转向深度学习领域. 利用RESIDE数据集[17 ] ,Qin等[6 ,18 ] 采用端到端的方式进行去雾. Dong等[19 ] 提出基于U-Net架构的多尺度提升方法. 虽然一些研究者考虑了暗雾去除的问题,但非稳健的特征导致了糟糕的结果. Kim等[20 ] 设计两阶段网络,将去雾和低照度增强统一起来,但该方法需要估计亮度图而非端到端,结果会出现局部过曝光和雾残留. Ju等[21 ] 将ASM修改为带有灰色世界假设的增强ASM,这导致在单色场景区域内产生颜色混乱. Chen等[22 ] 使用对比度适应的直方图均衡化来产生伪标签,但伪标签会导致过度饱和并重新加雾. 在领域适应方法中,Shao等[6 ] 采用领域对抗方法,但他们的结果在黑色物体的边缘总会出现颜色混乱. ...
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... [22 ]和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 从RTTS和URHI中挑选出更有挑战性的浓雾数据,而不是选择简单的薄雾数据. 如图5 所示为去雾结果. SSID[30 ] 的去雾结果亮度存在损失,有大量的雾残留. IDE[21 ] 的去雾能力有限,有大量的雾残余,虽然解决了去雾亮度损失的问题,但结果产生了颜色变异,这是因为IDE采用灰色世界假说,当图像中出现大面积单色场景时会违反灰色世界假设. DAD[23 ] 的方法本质上是利用域对抗方法来接近真实的数据,可以解决亮度损失的问题,但会出现颜色变异,在黑暗物体边缘会产生模糊. PSD[22 ] 的去雾结果明亮,对比度大,饱和度过高,去雾能力不足. 这是因为PSD采用增强方法作为伪标签,导致去雾后重新加雾. D4[31 ] 的去雾能力不足. 本文提出的方法没有出现上述问题,且去雾能力强,亮度未出现损失. ...
... 如表1 所示为利用无参考图评价方法计算在RTTS上的去雾性能.可以看出,本文所提方法在多数评价指标上获得了最好的性能. 除了本文的方法外,方法IDE[21 ] 、SLA[24 ] 、PSD[22 ] 和LED2Net[20 ] 也考虑了图像去雾后亮度损失问题,因此在真实数据上对比他们的结果是十分必要的.本文在Fattal[15 ] 数据集上进行测试,结果如图6 所示. 从图中的方框区域可以看出,IDE[21 ] 和PSD[22 ] 的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
... [22 ]的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
... Complexity comparison of different methods
Tab.3 方法 N p /106 FLOPs/109 MSBDN[19 ] 36.85 137.90 PSD[22 ] 33.11 220.60 SGID[3 ] 13.87 108.40 D4[31 ] 10.70 2.25 本文方法 31.40 34.17
5. 消融实验 在消融实验中,本文要验证所提出的数据集和方法的作用. 1)其他去雾方法使用DarkHaze,能够避免去雾结果出现质量损失.2)提出的数据集和采用的方法起作用的程度.为了验证数据和模型的作用,本文给出5种不同的模型设定.使用DarkHaze来训练FFA[4 ] 模型(FFA+DarkHaze,记为S1). 类似地,将不变学习从提出的模型中移除,使用DarkHaze来训练模型(MSBDN+DarkHaze,S2). 去除Gamma变换,仅使用ASM来合成有雾数据集(OnlyHaze),大气光值$ A $ $ \beta $ [17 ] 来训练提出的方法(MSBDN+Invariant+RESIDE,S4). 将这些不同的设定与本文提出的方法(MSBDN+Invariant+DarkHaze,S5)进行比较. ...
3
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 从RTTS和URHI中挑选出更有挑战性的浓雾数据,而不是选择简单的薄雾数据. 如图5 所示为去雾结果. SSID[30 ] 的去雾结果亮度存在损失,有大量的雾残留. IDE[21 ] 的去雾能力有限,有大量的雾残余,虽然解决了去雾亮度损失的问题,但结果产生了颜色变异,这是因为IDE采用灰色世界假说,当图像中出现大面积单色场景时会违反灰色世界假设. DAD[23 ] 的方法本质上是利用域对抗方法来接近真实的数据,可以解决亮度损失的问题,但会出现颜色变异,在黑暗物体边缘会产生模糊. PSD[22 ] 的去雾结果明亮,对比度大,饱和度过高,去雾能力不足. 这是因为PSD采用增强方法作为伪标签,导致去雾后重新加雾. D4[31 ] 的去雾能力不足. 本文提出的方法没有出现上述问题,且去雾能力强,亮度未出现损失. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
5
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... [24 ]方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如表1 所示为利用无参考图评价方法计算在RTTS上的去雾性能.可以看出,本文所提方法在多数评价指标上获得了最好的性能. 除了本文的方法外,方法IDE[21 ] 、SLA[24 ] 、PSD[22 ] 和LED2Net[20 ] 也考虑了图像去雾后亮度损失问题,因此在真实数据上对比他们的结果是十分必要的.本文在Fattal[15 ] 数据集上进行测试,结果如图6 所示. 从图中的方框区域可以看出,IDE[21 ] 和PSD[22 ] 的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
... [24 ]去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
1
... 与上述方法不同的是,本文方法是端到端的稳定性去雾网络. 上述方法很少考虑到图像去雾之后的亮度保真问题. 即便考虑了亮度损失问题[20 -25 ] ,但他们没有解释出现亮度损失的原因且结果出现去雾残留和过饱和. 本文在理论上证明使用ASM必然导致图像亮度损失,并对此提出改进. ...
Vision and the atmosphere
1
2002
... 有雾图像的形成可以用大气散射模型[26 ] 表示: ...
Sparse gradient regularized deep Retinex network for robust low-light image enhancement
1
2021
... 如图2 所示为以ASM合成数据的对比. 可以看出,真值的方框1内是低光区,方框1上的数值为框1内的大气光值,方框2内存在雾,在此数据上训练的模型是有偏移的模型.使用ASM合成之后可以发现方框1区域变亮,这说明ASM提升了图像的亮度. 根据Retinex理论[27 ] 可知,图像由照度图像与反射图像组成,因此式(1)中的$ J $ $ AR $ . 将合成图像$ I $ $ J $
1
... 采用端到端有监督的方式来解决真实数据雾霾去除的问题,如图3 所示为基于不变学习的去雾网络结构图. 给定配对的合成雾数据集$ D = \{ {x_i},{y_i}\} _{i = 1}^n $ . 将数据输入神经网络,可以提取到所有数据的特征图$ {\boldsymbol{Z}} \in {{\bf{R}}^{n \times c \times h \times w}} $ $ n、c、h、w $ [28 ] ,则可将每个通道视为一个随机变量. 在表征空间中消除任意2个变量的相关性,使得变量之间独立. 对于每个通道为$ h \times w $ $ {\boldsymbol{Z}} $ $ n \times c $ $ {\boldsymbol{Z}} \in {{ {\bf{R}}}}^{n \times c} $ . ...
1
... 在得到$ {\boldsymbol{Z}} $ $ {\boldsymbol{Z}} $ $ {{\boldsymbol{Z}}_{:,{{i}}}} $ $ {{\boldsymbol{Z}}_{:,{{j}}}} $ $ {\boldsymbol{Z}} $ $ {\boldsymbol{Z}} $ [29 ] 可知,当且仅当核函数是非负测度的傅里叶变换时,具有平移不变性的高斯核函数在原始隐式空间上是正定的.协方差的定义公式为 ...
Semi-supervised image dehazing
3
2019
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 从RTTS和URHI中挑选出更有挑战性的浓雾数据,而不是选择简单的薄雾数据. 如图5 所示为去雾结果. SSID[30 ] 的去雾结果亮度存在损失,有大量的雾残留. IDE[21 ] 的去雾能力有限,有大量的雾残余,虽然解决了去雾亮度损失的问题,但结果产生了颜色变异,这是因为IDE采用灰色世界假说,当图像中出现大面积单色场景时会违反灰色世界假设. DAD[23 ] 的方法本质上是利用域对抗方法来接近真实的数据,可以解决亮度损失的问题,但会出现颜色变异,在黑暗物体边缘会产生模糊. PSD[22 ] 的去雾结果明亮,对比度大,饱和度过高,去雾能力不足. 这是因为PSD采用增强方法作为伪标签,导致去雾后重新加雾. D4[31 ] 的去雾能力不足. 本文提出的方法没有出现上述问题,且去雾能力强,亮度未出现损失. ...
... 如表1 所示为利用无参考图评价方法计算在RTTS上的去雾性能.可以看出,本文所提方法在多数评价指标上获得了最好的性能. 除了本文的方法外,方法IDE[21 ] 、SLA[24 ] 、PSD[22 ] 和LED2Net[20 ] 也考虑了图像去雾后亮度损失问题,因此在真实数据上对比他们的结果是十分必要的.本文在Fattal[15 ] 数据集上进行测试,结果如图6 所示. 从图中的方框区域可以看出,IDE[21 ] 和PSD[22 ] 的颜色过饱和,过曝光. SLA[24 ] 去雾能力不佳且没有抑制过曝光. LED2Net[30 ] 的结果中有雾残留和过曝光现象. 相比而言,在所有的结果中,本文的方法未出现上述问题. ...
9
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... 如图4 所示为不同方法在Fattal数据上的去雾结果. DCP和NLD的去雾性能明显优于其他监督方法,但是它们的去雾结果亮度损失,NLD的结果出现颜色混乱,这说明真实情况违背了他们的先验假设. 有监督方法DehazeFlow[5 ] 和FFA[6 ] 的去雾能力不足,在所有结果中有大量的雾残余,甚至去雾无效. 虽然GridDehazeNet[18 ] 、MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 有一定的去雾能力,但无法有效去雾,纹理模糊. 上述方法的结果出现亮度损失. 造成这种现象的原因是这些方法未考虑真实数据集的复杂情形,与真实数据存在域漂移,尤其是忽略了暗光的影响,缺乏稳定性. 利用本文方法,可以有效地去雾,增加图像亮度,颜色没发生变异且纹理清晰. 这是因为本文方法不仅考虑了低光,而且使用不变学习,可以应对真实的雾霾情况. ...
... 从RTTS和URHI中挑选出更有挑战性的浓雾数据,而不是选择简单的薄雾数据. 如图5 所示为去雾结果. SSID[30 ] 的去雾结果亮度存在损失,有大量的雾残留. IDE[21 ] 的去雾能力有限,有大量的雾残余,虽然解决了去雾亮度损失的问题,但结果产生了颜色变异,这是因为IDE采用灰色世界假说,当图像中出现大面积单色场景时会违反灰色世界假设. DAD[23 ] 的方法本质上是利用域对抗方法来接近真实的数据,可以解决亮度损失的问题,但会出现颜色变异,在黑暗物体边缘会产生模糊. PSD[22 ] 的去雾结果明亮,对比度大,饱和度过高,去雾能力不足. 这是因为PSD采用增强方法作为伪标签,导致去雾后重新加雾. D4[31 ] 的去雾能力不足. 本文提出的方法没有出现上述问题,且去雾能力强,亮度未出现损失. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
... 如图7 所示为3个具有代表性的方法在SOTS和DarkHaze数据集上的去雾结果. 在SOTS数据集上,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 的去雾图和真实值非常相近.真实值的方框2内存在雾,这导致MSBDN[19 ] 和SGID[3 ] 的结果只能逼近真实值,却无法将方框2的雾去除. 此外,这3个方法均未考虑低光照的情况,真实值存在弱光区域,这导致方框1内去雾亮度存在损失. 利用本文方法,不仅可以有效地去除方框2中的雾,而且可以增大方框1内去雾后的亮度.真实值是MSBDN[19 ] 和SGID[3 ] 的去雾上界,它们无法突破此上界,本文的方法则不然,如图7 中方框1和方框2内所示. 在DarkHaze去雾结果中,MSBDN[19 ] 、SGID[3 ] 和D4[31 ] 均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... [31 ]均存在去雾结果亮度损失和有雾霾残留的问题. 这主要是由于它们考虑的环境单一,未考虑真实情况. 当环境稍微发生变化时,这些方法便会失去作用,而本文的方法不仅考虑了弱光情况,而且使用不变学习来获得跨域特征. ...
... 如表2 所示为MSBDN[19 ] 、SGID[3 ] 、D4[31 ] 和本文方法在SOTS和DarkHaze测试集上的PSNR和SSIM的平均值,本文在这2个数据集上获得了最稳定的PSNR和SSIM.可以发现,当环境变化时,这3种方法的平均PSNR和SSIM显著减小,说明了这3种方法的去雾性能不稳定,而本文方法在2个数据集上的平均PSNR和SSIM变化很小,这是因为本文使用了不变学习,消除了特征之间的虚假相关性,使得网络获得了可以提取跨域本质特征的能力. ...
... PSNR and SSIM of different methods on DarkHaze and SOTS test datasets
Tab.2 方法 DarkHaze SOTS PSNR/dB SSIM PSNR/dB SSIM MSBDN[19 ] 16.05 0.7330 30.93 0.9780 SGID[3 ] 17.02 0.7536 30.20 0.9754 D4[31 ] 16.16 0.6756 25.82 0.9445 本文方法 26.83 0.9301 26.04 0.9511
本文挑选出有代表性的去雾方法,在分辨率为$ 3 \times 224 \times 224 $ 表3 所示为不同方法的参数量 N p 和每秒浮点运算次数FLOPs. 从表3 可以看出,与这些代表性的去雾方法相比,本文所提出的方法在保证真实去雾性能的同时,能够将模型的参数量和计算复杂度保持在合理的范围内. ...
... Complexity comparison of different methods
Tab.3 方法 N p /106 FLOPs/109 MSBDN[19 ] 36.85 137.90 PSD[22 ] 33.11 220.60 SGID[3 ] 13.87 108.40 D4[31 ] 10.70 2.25 本文方法 31.40 34.17
5. 消融实验 在消融实验中,本文要验证所提出的数据集和方法的作用. 1)其他去雾方法使用DarkHaze,能够避免去雾结果出现质量损失.2)提出的数据集和采用的方法起作用的程度.为了验证数据和模型的作用,本文给出5种不同的模型设定.使用DarkHaze来训练FFA[4 ] 模型(FFA+DarkHaze,记为S1). 类似地,将不变学习从提出的模型中移除,使用DarkHaze来训练模型(MSBDN+DarkHaze,S2). 去除Gamma变换,仅使用ASM来合成有雾数据集(OnlyHaze),大气光值$ A $ $ \beta $ [17 ] 来训练提出的方法(MSBDN+Invariant+RESIDE,S4). 将这些不同的设定与本文提出的方法(MSBDN+Invariant+DarkHaze,S5)进行比较. ...
Learning a no-reference quality assessment model of enhanced images with big data
3
2017
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... [32 ]用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
Highly efficient picture-based prediction of PM2.5 concentration
3
2018
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... [33 ]用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...
NIMA: neural image assessment
3
2018
... 选择以下14种去雾方法进行对比:先验方法DCP[14 ] 、NLD[16 ] 和IDE[21 ] ,有监督方法SGID[3 ] 、DehazeFlow[5 ] 、FFA[6 ] 、GridDehazeNet[18 ] 、MSBDN[19 ] 和LED2Net[20 ] ,半监督方法SSID[30 ] ,无监督方法PSD[22 ] 和SLA[24 ] ,对抗域适应方法DAD[23 ] 和D4[31 ] . 其中,利用IDE[21 ] 、LED2Net[20 ] 、PSD[22 ] 和SLA[24 ] 方法,可以解决图像去雾亮度损失的问题. 使用峰值信噪比(PSNR)和结构相似性(SSIM)来评价在合成数据上的去雾性能,使用无参考图评价指标BIQME[32 ] 、PM2.5[33 ] 和NIMA[34 ] 来客观度量在真实有雾图上去雾的性能. NIMA[34 ] 用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... [34 ]用于度量图像的美学质量,BIQME[32 ] 用于对图像进行综合评价,PM2.5[33 ] 用于评价图像的雾霾浓度. NIMA和BIQME越大越好,PM2.5越小越好. ...
... No-reference image quality evaluation of different dehazing results methods on RTTS dataset
Tab.1 方法 NIMA[34 ] BIQME[32 ] PM2.5[33 ] 输入 4.325 0.504 198.250 MSBDN[19 ] 4.140 0.548 166.783 FFA[6 ] 3.718 0.524 189.193 DehazeFlow[5 ] 4.687 0.530 177.369 SGID[3 ] 3.694 0.545 178.359 DAD[23 ] 4.005 0.561 108.403 D4[31 ] 4.631 0.555 163.386 IDE[21 ] 4.586 0.553 150.240 PSD[22 ] 4.345 0.514 151.900 SLA[24 ] 4.598 0.524 138.242 本文方法 4.703 0.577 137.436
图 6 去雾时考虑图像亮度损失方法的去雾结果对比 ...