在压缩载荷下,开孔层合板的最终失效由分层损伤及扭结带的不稳定传播主导[9]. 分层损伤常常先于面内纤维失效[10],导致结构提前失效. 为了提高层合板的层间韧性,常采用厚度方向增强的工艺优化方法[11–13]. 其中,Z-pin技术对Ⅰ型层间断裂韧性的增强效果可以达到10~15 kJ/m2[14],为三维编织和缝合技术的2.0~3.0倍[14–17]. 此外,Z-pin技术还具有适用于预浸料铺放的工艺体系、易于自动化、加工效率高等优点[18-19]. 植入Z-pin会对层合板引入损伤,对面内性能产生负面影响. Z-pin直径越小,引入的面内损伤越少[20]. Fei等[21]研究发现,植入体积分数为0.1%的微细Z-pin,可以将Ⅰ型层间韧性提高11倍,面内拉伸和压缩性能仅下降1.31%和3.46%.
针对开孔板的压缩性能及Z-pin对层合板力学性能的影响,国内外学者作了一定的研究. Zhou等[8]提出开孔层合板的有限元模型,有效模拟了开孔层合板在压缩载荷下的渐进失效行为.孙一凡等[22]研究直径为0.5 mm的碳纤维Z-pin对开孔板压缩性能的影响,发现植入Z-pin后,抗压性能最大提高了23.06%,仿真计算的最大相对误差为17.08%. Mouritz[23]研究Z-pin对开孔板拉伸和压缩性能的影响发现,当植入体积分数为0.5%~4%时,拉伸强度降低了4.20%~15.40%,压缩强度降幅为0.67%~11.15%. Gao等[24]的研究表明,微细Z-pin可以改善孔边的应力集中现象,分层区域的面积减小了54.1 %.
目前缺少有关微细Z-pin对开孔板压缩性能影响的研究. 相关有限元模型的预测精度较低,难以实现对结构失效行为的多尺度分析. 本文通过不同植入体积分数和排布方式下的Z-pin开孔层合板压缩试验和多尺度有限元模型,探究微细Z-pin对开孔板压缩力学性能和失效行为的影响机制.
1. 材料及试验方法
1.1. 试验材料和试验矩阵
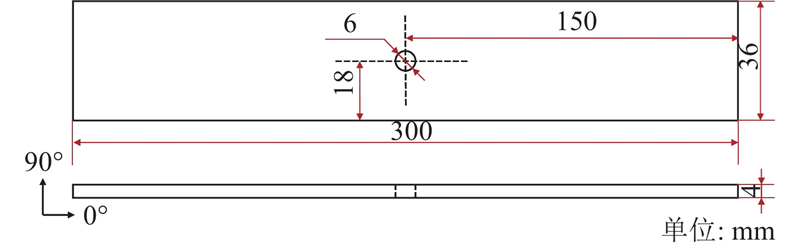
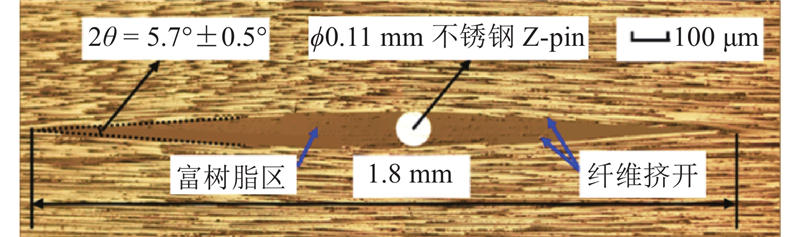
选用山东威海光威复合材料有限公司的T700/7901预浸料,牌号为USN25000,单层名义厚度为0.25 mm. 考虑到压缩载荷作用时相邻子层错位在层间界面产生的剪切作用,Z-pin材料选用延展性较好的304不锈钢丝束,直径为0.11 mm.
图 1
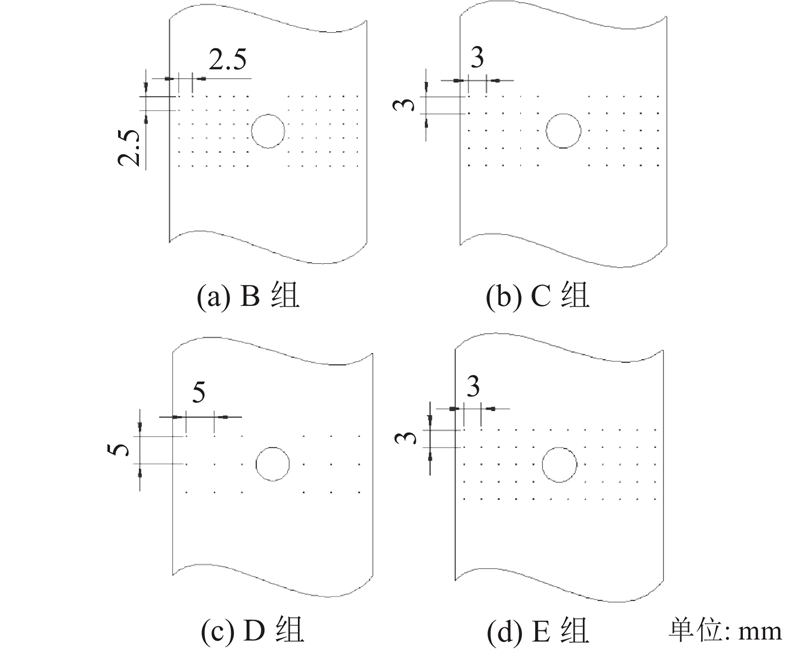
记空白组试样为A组试样,其余配置及对应编号如图2所示,各植入方案中Z-pin点阵均关于开孔处对称排布. 针对Z-pin的体积分数,对比分析A、B、C、D 4组试样;针对Z-pin的排布方式,对比分析C和E 2组配置. 基于空白组试样的测试结果,结构损伤集中于试样长度方向中间部位,以对称轴为中心[−8 mm, +8 mm]范围内,因此确定Z-pin植入区域长度方向尺寸为16 mm,宽度方向与试样等宽. 试验设计以下2种Z-pin排布方式:一种沿试样宽度方向开孔两侧植入,另一种在开孔周围回型区域内植入.
图 2
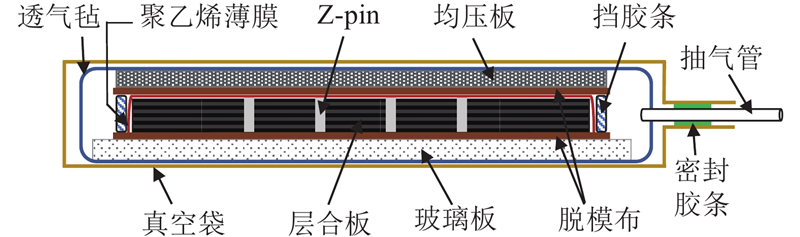
1.2. 试样制备
图 3
图 4
1.3. 试验过程
试验在Instron 5985电子万能试验机上进行. 采用ASTM D6484专用夹具将试样夹持于夹具中心,将试样-夹具装配体置于试验机压盘上,先用23 N的力对装配体预加载,保证试样与夹具、压盘各表面接触对中,然后对设备调零. 利用英视OSG030-815UM工业相机,记录试样失效的过程. 设置试验机加载头的加载速率为2 mm/min. 开孔压缩试验环境如图5所示.
图 5
2. 试验结果讨论
2.1. 力学性能
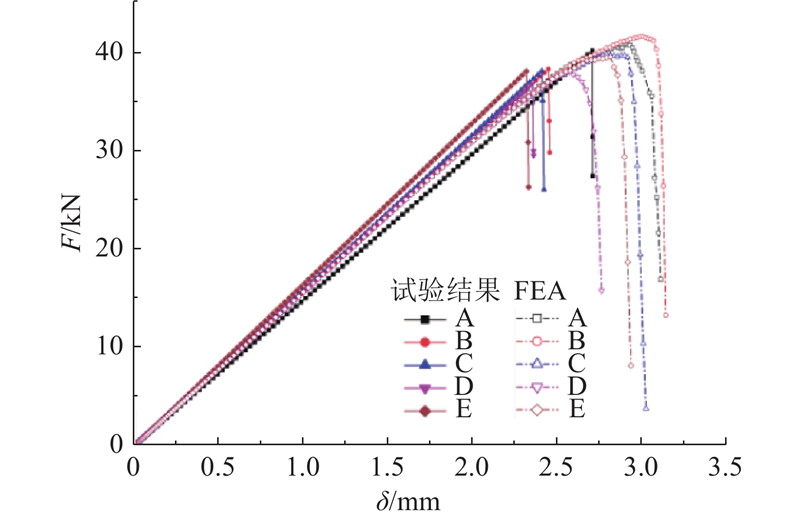
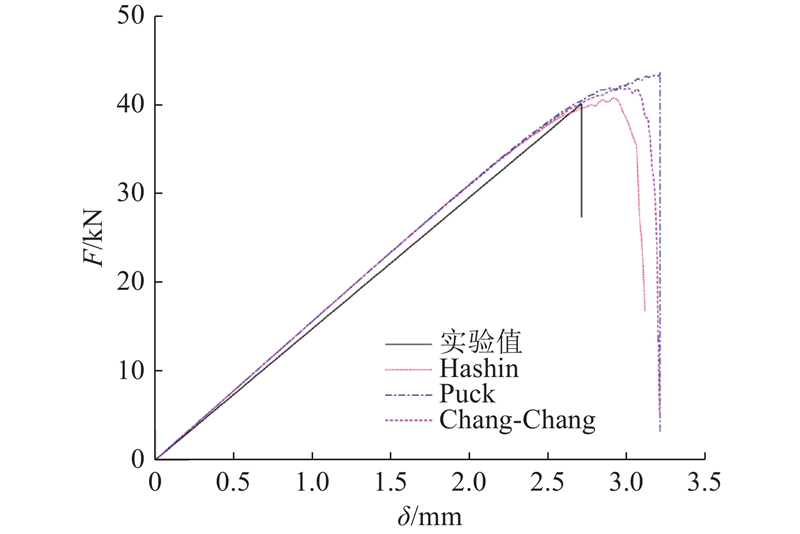
试样的载荷F-位移
图 6
各组试样的压缩强度统计数据如表1所示. 表中,括号内为植入组力学性能相对空白组的变化程度,
表 1 开孔压缩试验结果
Tab.1
| 试验编号 | | | |
| A | 0.00 | 335.25 | 3.63 |
| B | 0.15 | 319.65 (−4.65%) | 4.62 |
| C | 0.11 | 317.86 (−5.19%) | 4.63 |
| D | 0.04 | 307.26 (−8.35%) | 2.49 |
| E | 0.11 | 317.76 (−5.22%) | 3.50 |
图 7
2.2. 失效行为
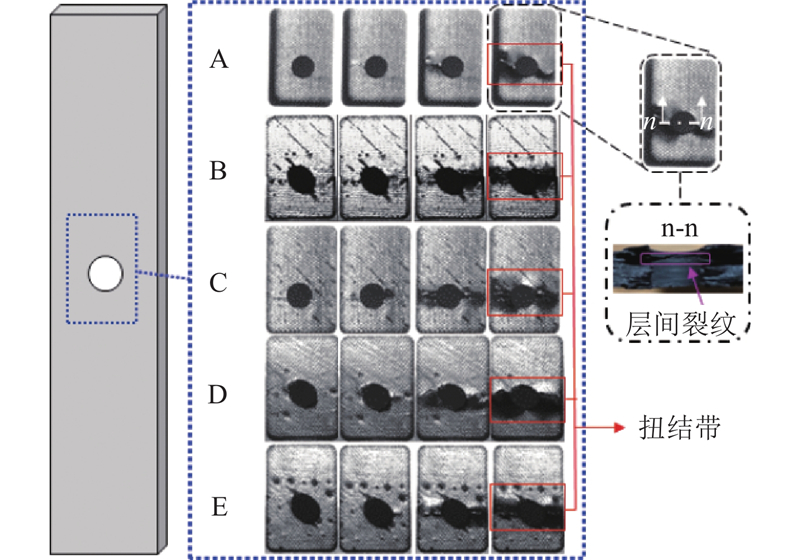
如图8所示为开孔压缩试样的损伤扩展过程,5组试样均可以观察到明显的扭结带现象. 扭结带起始于孔边横向两侧,随后沿试样宽度方向,向两侧逐步不稳定扩展,直至失效. 在开孔纵向两侧,由于初始层间裂纹的逐步扩展,裂纹尖端处应力增大,导致开孔纵向产生靠近试样表面的层间裂纹,如图中n-n截面所示. 对比各组试样的损伤扩展过程可以发现,Z-pin植入没有改变扭结带的产生和扩展形式.
图 8
通过图9中对试样厚度方向破坏形貌的观察可以发现,厚度方向存在分层、纤维微屈曲和纤维断裂等多种失效形式,层间裂纹多出现于靠近试样表面的0°层附近. 对照组试样因扭结带的扩展,在厚度方向产生了明显的鼓包. 随着Z-pin植入体积分数的增加,试样厚度方向的鼓包程度降低,Z-pin对分层扩展起到抑制作用.
图 9
Z-pin减缓了0°层纤维的微屈曲程度,C、D、E组试样的压缩断裂角度没有出现明显变化. 当体积分数达到0.15%(B组)时,作为主要承载层的0°层纤维产生交叉压入断裂后,在试样厚度方向自由剪切边缘,层间裂纹和断裂裂纹的损伤程度较对照组明显减缓,B组试样的断裂角较其余试验配置明显减小,结构的分层失效现象得到一定的改善.
3. 多尺度模型建立
3.1. 仿真模型配置
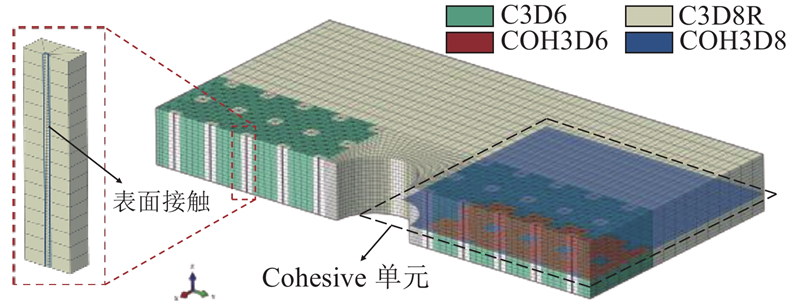
图 10
Z-pin和层合板采用实体单元建模,单元类型为C3D8R和C3D6. 为了避免求解时产生非物理零能变形,对网格单元施加增强型沙漏控制,通过在层间插入0厚度Cohesive单元,模拟开孔板的层间界面属性,对应的单元类型为COH3D8和COH3D6. 通过参考点耦合试样长度方向的两端面,约束一侧端面,另一侧通过Smooth Step方式施加准静态压缩位移. 为了提高计算效率和收敛性,模拟结构在压缩载荷作用下的瞬态失效响应,采用Dynamic Explicit求解器求解,计算过程中调用VUMAT子程序更新损伤变量和刚度矩阵.
3.2. 面内失效
图 11
图 11 不同失效准则的开孔压缩有限元模型计算结果
Fig.11 OHC FE model results for different failure criterions
纤维拉伸失效 (
纤维压缩失效(
基体拉伸失效(
基体压缩失效(
式中:
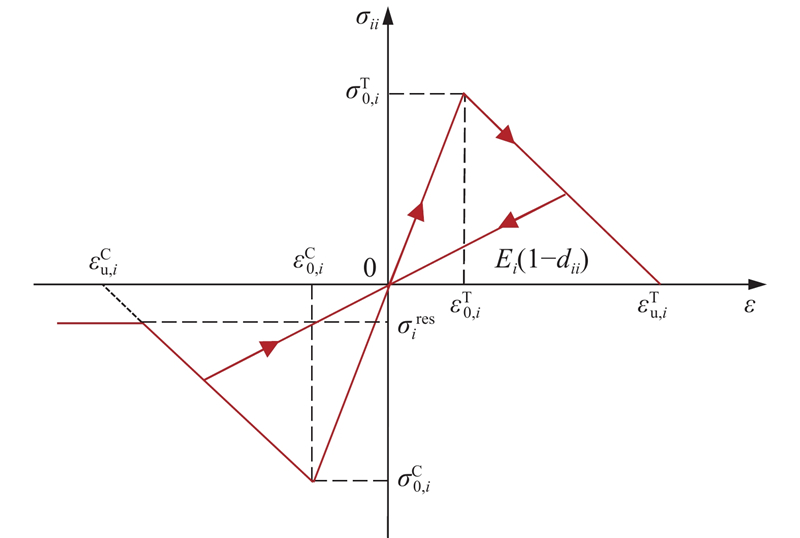
若满足式(1)~(4)中的任一条件,则判断材料发生起始损伤. 在起始损伤发生后,需要更新材料刚度矩阵来模拟复合材料的退化行为,本文采用基于断裂韧性的刚度系数退化方式. 复合材料的含损伤本构关系可以表示为
式中:
式中:
图 12
各种失效模式对应的损伤变量计算公式为
式中:
其中
仿真模型中所用到的层合板单层材料性能参数如表2所示. 表中,
| 参数 | 参数值 | 参数 | 参数值 | |
| | 90 | | 1700 | |
| | 7.1 | | 900 | |
| | 7.1 | | 55 | |
| | 0.34 | | 100 | |
| | 0.34 | | 55 | |
| | 0.4 | | 100 | |
| | 2700 | | 100 | |
| | 2700 | | 100 | |
| | 2500 | | 55 |
3.3. 界面失效
模型通过创建Cohesive行为,模拟材料不同组分之间的界面接触属性. 复合材料界面处的应力-位移关系用3个分量表示:
式中:
选用二次应力准则判断界面起始损伤:
式中:
起始损伤产生后,界面刚度依照双线性内聚区域模型(cohesive zone model)进行退化. 界面的最终失效判据选用Benzeggagh-Kenane准则[32],模拟界面的混合断裂模式下的失效行为.
式中:
层间Cohesive单元和Z-pin与层合板之间的Cohesive接触属性参数如表3所示.
| 参数 | 参数值 | |
| Cohesive单元 | Z-pin Cohesive接触 | |
| | 5×104 | 2188.8 |
| | 5×104 | 10944.1 |
| | 30 | 273.6 |
| | 70 | 789.2 |
| | 0.6 | 1103.5 |
| | 1.2 | 1325.5 |
3.4. 参数化有限元模型算法和模型验证
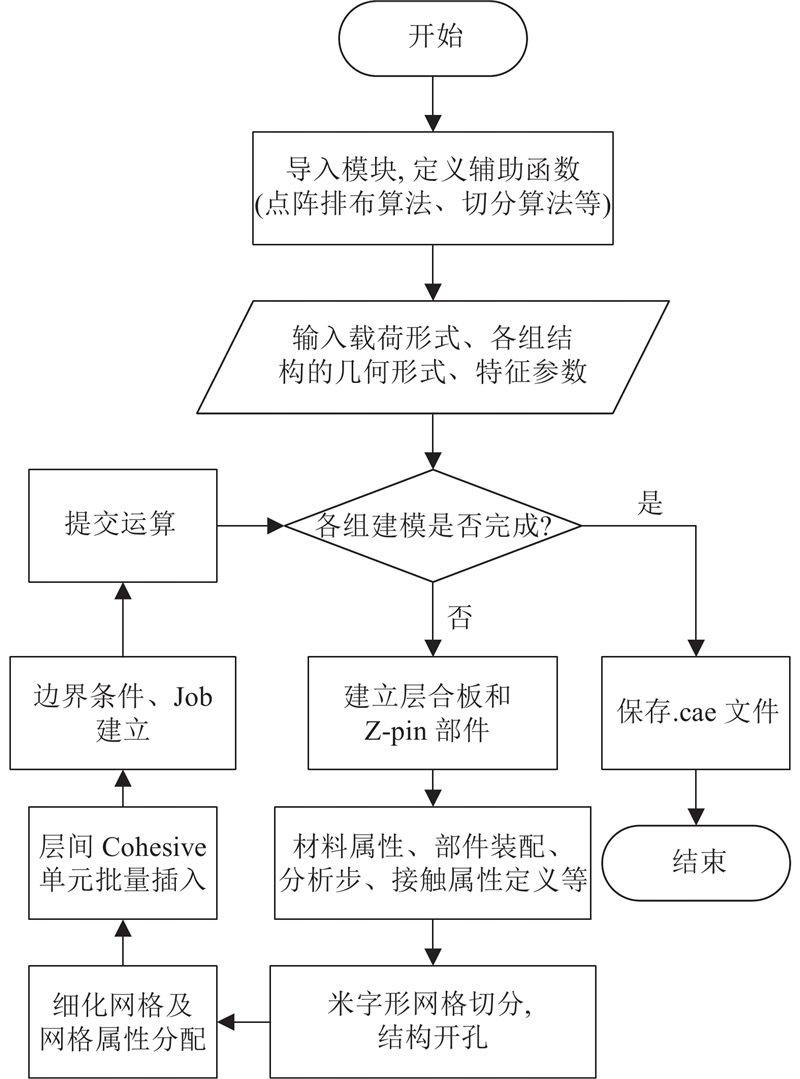
采用用户图形界面进行前处理建模时,需要人工进行大量的重复性操作,存在建模效率低下,同类结构形式、不同尺寸参数的模型无法通用的弊端. 利用Python语言,在ABAQUS平台上开发Z-pin开孔板结构的参数化建模算法,算法流程图如图13所示. 算法输入模块通过给定的载荷形式、Z-pin的排布方式和植入间距等参数,实现不同建模方案的批量参数化建模,并自动提交求解器求解计算,完成后自动保存对应的模型文件.
图 13
图 13 Z-pin开孔层合板建模算法的流程图
Fig.13 Flowchart of Z-pin open-hole laminates modelling algorithm
从图6的试验曲线与仿真曲线可以看出,仿真曲线的载荷-位移关系变化趋势与试验结果相符,整体上近于线性增加,在达到结构承载极限后急剧掉载. 其中,仿真曲线由于采用渐进失效模型,随着压缩载荷的增加,结构刚度逐步衰减. 由于模型对植入工艺的微观损伤进行了简化,导致仿真分析结果延后了失效位移.
如表4所示为各组试验与仿真模型的压缩强度,括号内为植入组计算结果较对照组的变化情况,
表 4 开孔板的试验与仿真压缩强度
Tab.4
| 试验组别 | | | |
| A | 335.25 | 340.83 | 1.67 |
| B | 319.65 | 347.17 | 8.61 |
| C | 317.86 | 332.17 | 4.50 |
| D | 307.26 | 317.00 | 3.17 |
| E | 317.76 | 330.25 | 3.93 |
4. 失效机理分析
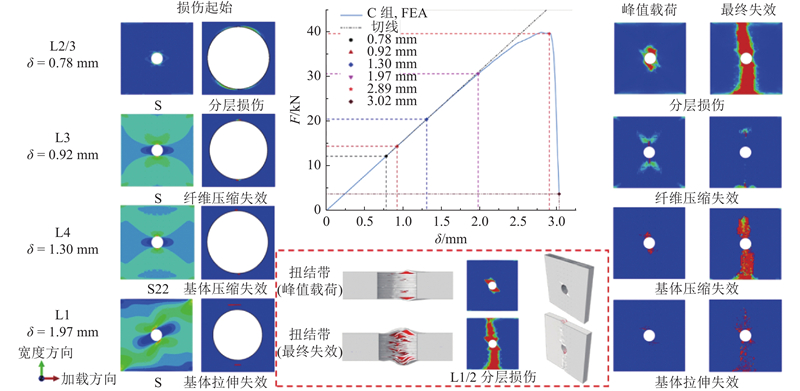
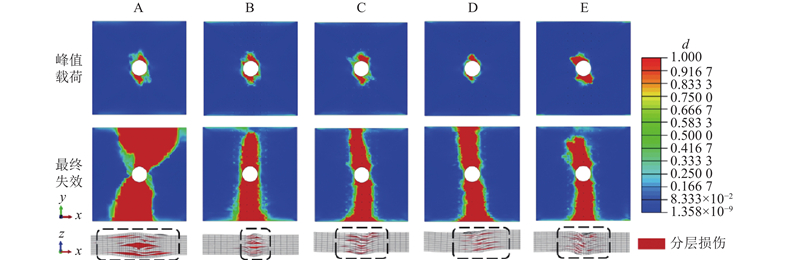
取C组试样的有限元计算结果,分析Z-pin开孔层合板的典型失效过程,如图14所示. 试样的各类起始损伤均出现于开孔横向两侧. 因为0°层是主要承载层,在孔边具有显著的应力集中现象,邻近厚度方向外表面的子层在法向应力作用下更容易产生层间损伤,因此当压缩位移达到0.78 mm时,在第2层和第3层层间界面最先出现分层损伤. 当压缩位移增至0.92 mm时,0°层的孔边应力达到材料纵向压缩强度,出现纤维断裂失效. 在孔边0°层纤维断裂失效后,对应区域的压缩载荷需要由其他子层承担,当孔边横向两侧应力状态达到Hashin损伤的起始条件时,先后出现基体压缩失效和基体拉伸失效,对应的压缩位移分别为1.30和1.97 mm. 结合模型的载荷位移曲线可以发现,各类起始损伤出现时,开孔层合板结构刚度无显著变化. 在孔边各方向铺层均出现损伤后,多种形式的损伤沿宽度方向不断扩张,结构刚度逐渐降低. 由于试样厚度方向外表面缺少约束,表面层在压缩载荷作用下出现纤维微屈曲现象,使得第1层和第2层层间裂纹沿表面层纤维横向(−45°)进一步扩展,在试样表面产生了扭结带. 在表面层的层间约束作用减弱后,扭结带在开孔区域厚度方向急速鼓胀,结构承载能力达到峰值,各类损伤集中于开孔横向局部区域内. 在扭结现象产生后,各类损伤沿试样宽度方向迅速扩展,开孔板承载能力骤降,当扭结带扩张至自由剪切边缘时,结构压溃. 如图15所示为各组试样达到承载极限和最终失效时,第2层(−45°)和第3层(0°)层间界面以及试样厚度方向的损伤状态. 图中,d为损伤变量. 当开孔板载荷达到极限载荷时,各组实验配置下的分层损伤状态均位于开孔横向两侧,随后沿宽度方向扩张. 当结构完全失效时,对照组分层损伤区域呈沙漏状,损伤范围较广. 在植入Z-pin后,最终失效时的分层损伤被锁止于植入区域内,扭结带的鼓包程度出现了明显改善,与图8的试验观察相符. 当植入体积分数为0.04%时损伤面积较对照组减少了58%,当体积分数为0.11%和0.15%时损伤区域面积均减少了67%,增大Z-pin体积分数可以有效地减小分层损伤面积. 随着植入体积分数的增大,单位面积内Z-pin对层间韧性的增强作用提升,阻碍了层间损伤的扩展,扭结区域长度不断缩短. 当采用不同的排布方式时,扭结带长度几乎一致.
图 14
图 15
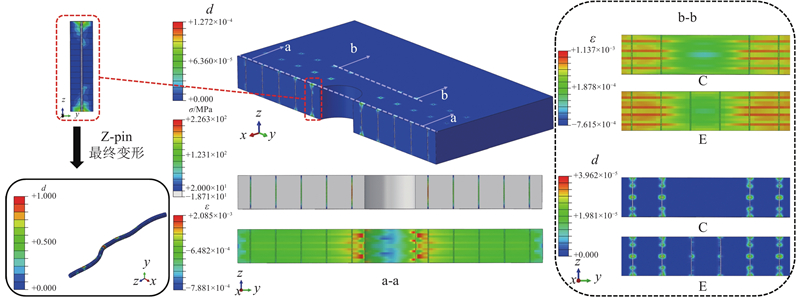
如图16所示为C组和E组试样Z-pin与层合板间界面的Cohesive接触行为有限元分析结果,利用模型可以观察到不同点位Z-pin与层合板之间接触作用的差异. 观察a-a截面厚度方向的应力-应变关系可以发现,由于孔边存在应力集中的现象,试样宽度方向距离开孔区域越近,厚度方向的应力(S33)与应变(LE33)更大,Z-pin与pin孔之间界面的黏聚作用(CSQUADSCRT)越突出. 开孔横向两侧的Z-pin受载过程中的接触界面行为如图16左侧的局部放大图所示. 在试样厚度方向上,由于表面层的层间约束作用较弱,孔边扭结带的扩展使得靠近表面处的Z-pin接触面吸收了更多的应变能,该处Z-pin在靠近层合板上、下表面的位置接触属性体现得更加明显. 如图16所示为结构失效时该处Z-pin的最终形貌. 可以看出,Z-pin在三维应力状态下产生了明显的变形. 综合开孔板应力状态与Z-pin桥联行为分析结果,在设计植入方案时,对层间应力较大的点位及扭结现象严重的区域进行关键增强.
图 16
图 16 Z-pin接触行为的有限元分析结果
Fig.16 Finite element analysis results of Z-pin contact behavior
如图16所示为采用不同排布方式(C组和E组)时Z-pin与层合板界面的黏聚行为. 对比E组模型与C组模型的b-b截面图可以发现,开孔区域纵向的Z向应变(LE33)相对其余点位较小,使得该区域Z-pin增加的黏聚作用有限. 回型区域排布的E组试样与采用横向两侧植入的C组试样相比,沿孔边纵向增加的Z-pin难以为结构提供与横向排布的Z-pin水平相近的桥联作用,开孔板的压缩强度无显著变化.
5. 结 论
(1) 微细Z-pin引入的工艺缺陷和桥联作用共同影响开孔板的压缩强度. 各植入组的开孔板压缩强度较对照组均出现了降低. 随着植入体积分数的增加,Z-pin的桥联作用增强,改善了缺陷对结构压缩强度的降低效果. 在相同的体积分数下,横向排布与回型排布方式对压缩强度无显著影响. 植入Z-pin可以改善厚度方向的损伤形貌,减缓扭结程度.
(2) 开发Z-pin开孔层合板的多尺度参数化建模算法,模型强度预测结果与试验数据的最大相对误差为8.61%. 利用该模型,可以模拟试样损伤扩展过程中扭结现象的不稳定扩展行为和结构内部损伤的扩展情况,能够实现各点位Z-pin桥联行为的多尺度分析,为植入点位的布置提供参考.
参考文献
Modelling and simulation methodology for unidirectional composite laminates in a virtual test lab framework
[J].DOI:10.1016/j.compstruct.2018.02.016 [本文引用: 1]
In situ formation of a carbon nanotube buckypaper for improving the interlaminar properties of carbon fiber composites
[J].DOI:10.1016/j.matdes.2021.109535 [本文引用: 1]
Analysis of the fatigue behaviour of laminated composite holes subjected to pin-bearing loads
[J].DOI:10.1016/j.ijfatigue.2017.05.025 [本文引用: 1]
Investigating the effect of machining processes on the mechanical behavior of composite plates with circular holes
[J].DOI:10.1016/j.compositesa.2013.09.002
碳纤维增强树脂基复合材料制孔技术研究现状与展望
[J].
Review and prospect of drilling technologies for carbon fiber reinforced polymer
[J].
Progressive failure analysis of bolted single-lap composite joint based on extended finite element method
[J].DOI:10.1016/j.matdes.2011.08.039 [本文引用: 1]
Progressive damage simulation of scaling effects on open-hole composite laminates under compression
[J].DOI:10.1177/0731684417708614 [本文引用: 2]
Experimental and numerical study on progressive damage and failure in composite laminates during open-hole compression tests
[J].DOI:10.1016/j.compositesa.2021.106300 [本文引用: 1]
Effect of stitching on plain and open-hole strength of CFRP laminates
[J].DOI:10.1016/S1000-9361(11)60411-1 [本文引用: 1]
Simulation of the forming of tufted multilayer composite preforms
[J].DOI:10.1016/j.compositesb.2021.108981
Review of z-pinned laminates and sandwich composites
[J].DOI:10.1016/j.compositesa.2020.106128 [本文引用: 1]
A review on the multi-scale simulation of Z-pinned composite laminates
[J].DOI:10.1016/j.compstruct.2022.115834 [本文引用: 3]
Interlaminar toughness characterisation of 3D woven carbon fibre composites
[J].DOI:10.1179/1743289812Y.0000000036
Experimental determination of the mode I delamination fracture and fatigue properties of thin 3D woven composites
[J].DOI:10.1016/j.compositesa.2016.02.008
Further validation of the Jain and Mai models for interlaminar fracture of stitched composites
[J].DOI:10.1016/S0266-3538(99)00027-5 [本文引用: 1]
Strengthening of composite T-joints using Ø 0.11 mm Z-pins via an ultrasound-guided insertion process
[J].DOI:10.1016/j.jcomc.2022.100268 [本文引用: 3]
Tuning interlaminar fracture toughness of fine z-pin reinforced polymer composite
[J].
Effect of Ø0.11 mm Z-pinning on the properties of composite laminates via an ultrasound guided insertion process
[J].DOI:10.1016/j.compscitech.2021.108906 [本文引用: 1]
Z-pin增强复合材料开孔层合板压缩性能
[J].
Compression performance of open-hole composite laminates reinforced by Z-pin
[J].
Review of z-pinned composite laminates
[J].DOI:10.1016/j.compositesa.2007.08.016 [本文引用: 1]
Enhancement of composite open-hole tensile strength via fine Z-pins arrangements
[J].DOI:10.1016/j.ijmecsci.2022.107752 [本文引用: 2]
Failure criteria for unidirectional fiber composites
[J].DOI:10.1115/1.3153664 [本文引用: 1]
Progressive damage behaviour analysis and comparison with 2D/3D Hashin failure models on carbon fibre–reinforced aluminium laminates
[J].DOI:10.3390/polym14142946 [本文引用: 1]
Finite element analysis of dynamic progressive failure of carbon fiber composite laminates under low velocity impact
[J].DOI:10.1016/j.compstruct.2016.04.012 [本文引用: 2]
On design of carbon fiber reinforced plastic (CFRP) laminated structure with different failure criteria
[J].DOI:10.1016/j.ijmecsci.2020.106251 [本文引用: 1]
Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus
[J].DOI:10.1016/0266-3538(96)00005-X [本文引用: 1]
Experimental and numerical simulation studies of failure behaviour of carbon fibre reinforced aluminum laminates under transverse local quasi-static loading
[J].DOI:10.1088/1742-6596/1624/2/022042 [本文引用: 1]
Finite element modelling of z-pinned composite T-joints
[J].DOI:10.1016/j.compscitech.2012.09.008 [本文引用: 1]