结构服役行为研究的关键点是建立损伤与宏观物理量的映射关系,变形是结构劣化历程较理想的宏观表征量. 混凝土结构服役过程中的变形包含应变和裂缝,呈现出不连续的特点. 传统的用于混凝土应变和裂缝监测的传感器和技术主要有金属电阻应变片[4]、光栅光纤[5-6]、振弦式应变计[7]、压电陶瓷[8-9]、数字图像技术[10-12]、声发射技术[13-14]等. 电阻应变片只能对混凝土未开裂前的应变进行短期监测,在混凝土开裂后损坏. 其他传感器存在造价高、耐疲劳性差、不能跨裂缝连续工作、与混凝土结构兼容性不好等问题. 因此,急须研制大量程、高灵敏性、低成本、耐疲劳性能好且能适应混凝土非连续变形特点的新型传感器.
近些年来,力敏复合材料在传感领域中表现出巨大的应用价值和发展潜力. Liu等[15]采用絮凝-热压方法,制备了石墨烯/聚氨酯弹性体. Lu等[16]基于溶液共混法,制备了石墨烯/环氧树脂复合材料. Jeong等[17]在泡沫镍上制得石墨烯泡沫,经粉碎、成膜和硅橡胶填充后,制备了泡沫石墨烯/硅橡胶复合薄膜,均表现出良好的力敏性能,但石墨烯分散困难,与聚合物复合的工艺较复杂,由于基体材料属性的限制,弹性变形范围较小. Liu等[18]将石墨烯薄膜直接黏附在不同拉伸状态的弹性胶带基底上,制备具有鱼鳞状石墨烯传感层的复合薄膜. Bonavolontà等[19]将纳米石墨胶体涂敷在聚甲基丙烯酸甲酯基体上,在切应力作用下,石墨纳米晶在基底表面形成均匀连续的多层石墨烯涂层,对于较大的应变具有良好的电阻响应,但传感层与基底层间的结合较弱,在重复拉伸下容易损坏.
本文以纳米纤维素为分散剂,搭载石墨烯,解决石墨烯不易分散的问题. 选用具有优异弹性变形能力的聚二甲基硅氧烷为基底层,通过化学溶胀和孔隙填充,在基底层上构建与之能够紧密结合的传感层,制备石墨烯力敏感应元件. 对感应元件的力学、电学和力敏性能进行试验研究,分析感应元件的变形能力和导电逾渗行为,讨论石墨烯分布密度、应变幅值、应变率效应对感应元件应变电阻响应行为的影响,建立感应元件电阻变化率与应变之间的定量关系.
1. 石墨烯感应元件的设计与制备
1.1. 感应元件的设计构思
当石墨烯均匀分散于聚合物基体中形成导电网络时,随着基体的变形,内部石墨烯导电网络发生变化,导致复合材料的电学性能发生改变. 利用材料电阻变化与应变之间的关系,可以通过测量电信号的变化来实现对变形的监测. 这种具有良好力敏性能的聚合物基石墨烯复合材料能够用于制备感应元件,监测混凝土的变形.
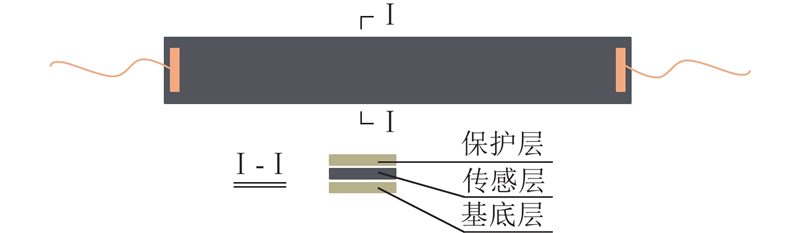
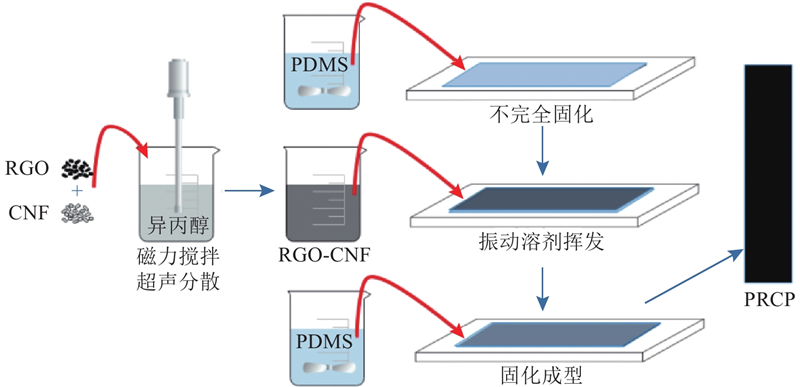
聚合物基石墨烯复合材料的模量一般远低于混凝土,通常制成薄膜形式布设在结构表面. 石墨烯感应元件的长度宜大于混凝土粗骨料直径的3倍,但长度过长,不利于粘贴且浪费材料. 考虑到剪力滞后效应的影响,感应元件宽度不宜过大,综合利弊并参考电阻应变片的尺寸,选择石墨烯感应元件的长×宽为100 mm×10 mm. 混凝土变形通过聚合物基体传递至石墨烯网络,为了避免石墨烯网络受外界影响,感应元件沿厚度方向由基底层、传感层和保护层组成. 为了减小应变传递过程中的损耗,厚度应尽量小,初步设定为1 mm. 石墨烯感应元件的结构组成如图1所示.
图 1
1.2. 感应元件的应变电阻响应模型
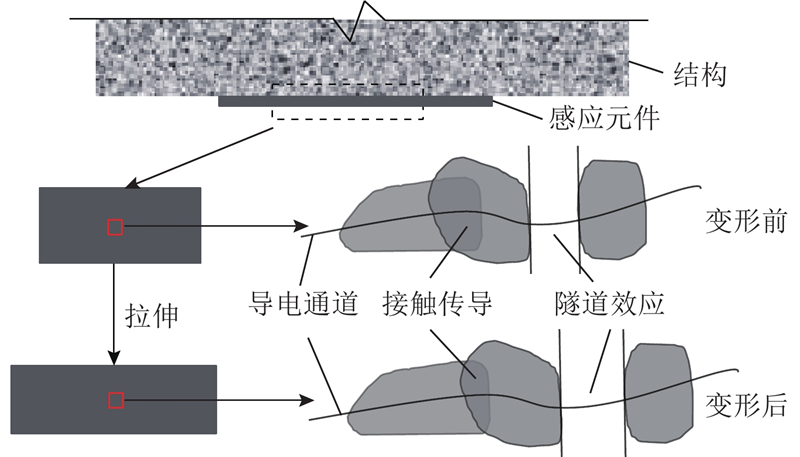
将石墨烯感应元件粘贴于结构表面后,结构受力产生的应变通过剪切作用传递至感应元件的传感层. 宏观上表现为感应元件随结构协调变形,微观上表现为传感层内部的石墨烯导电网络的变化,如图2所示.
图 2
图 2 石墨烯感应元件的应变电阻响应示意图
Fig.2 Diagrammatic sketch of strain resistance response of graphene sensor
当石墨烯的体积分数较小时,无法形成接触传导导电通路,隧道效应机制占主导地位. 此时,石墨烯感应元件的电阻由石墨烯电阻Rg和隧道效应电阻Rm决定. 感应元件的初始电阻为
式中:N0为感应元件中平行于电流方向的初始导电通道数,l为平行于电流方向每个导电通道中石墨烯的平均数目.
根据Simmons隧道效应模型[21],可得
式中:U为电压;J为隧道电流密度;Sp为相邻石墨烯间聚合物隔离层的有效面积;m为电子质量;e为电子电荷量;h为普朗克常量;φ为相邻石墨烯间的势垒;d0为相邻石墨烯的初始间距,与石墨烯的体积分数有关. 将式(2)代入式(1),可得感应元件的初始电阻为
当感应元件发生应变ε时,相邻石墨烯的间距d可以表示为
ε可以反映感应元件内部石墨烯导电网络随基体长度变化而发生破坏的程度,导电通路数N可以表示为[22]
式中:A、B、C、D为与石墨烯分布状态及变形速率有关的常量.
感应元件发生应变ε时的电阻R为
则感应元件应变电阻响应模型可由下式表示:
式中:K为灵敏系数,ΔR为发生应变ε时的电阻变化量.
当石墨烯体积分数较大时,石墨烯之间相互接触,接触传导机制占主导地位. 由于聚合物基体绝缘,电阻率远远大于石墨烯的电阻率,可以忽略聚合物分子间的电流,感应元件的电阻主要由电极间石墨烯电阻和导电通道数目决定. 感应元件应变电阻响应模型可由下式[20]表示:
式中:b为与石墨烯初始接触状态相关的常数.
从式(8)、(10)可以看出,石墨烯感应元件的应变电阻响应与石墨烯间距、势垒、接触面积和应变程度等有关. 随着变形程度的不断加大,感应元件电阻呈现指数变化趋势,相应的灵敏系数接近指数增大. 从式(9)、(11)可以看出,当应变较小时,感应元件的灵敏系数近似于常数,即电阻变化率与应变之间呈线性变化趋势,灵敏系数与石墨烯的初始相对位置有关. 当隧道效应的导电机制占主导地位时,灵敏系数主要取决于相邻石墨烯的初始隧道间距,可以通过增大初始间距(即减小石墨烯体积分数)来提高灵敏系数,前提是保证石墨烯间距足够发生隧道效应. 当石墨烯体积分数较小时,感应元件的电阻较大,不利于实际应用时响应信号的测量和获取. 较大的体积分数会导致感应元件的力学性能显著变化,聚合物基体优异的柔韧性无法得到发挥,感应元件的电阻变化率及灵敏系数变小,因此需要在一定范围内研究石墨烯体积分数对感应元件应变电阻响应的影响.
1.3. 感应元件的制备
还原氧化石墨烯(reduced graphene oxide, RGO),质量分数 > 98%,黑色粉末,厚度为1~5 nm,片层直径为0.5~5 μm. 纳米纤维素(cellulose nanofiber, CNF)为白色粉末,质量分数 > 99%,直径为4~10 nm,长度为1~3 μm. 聚乙烯吡咯烷酮(polyvinylpyrrolidone, PVP)为分析纯,硅烷偶联剂(silane coupling agent, SCA)为分析纯,异丙醇(isopropanol, IPA)为分析纯,聚二甲基硅氧烷(polydimethylsiloxane, PDMS)为分析纯.
1.3.1. 石墨烯分散试验
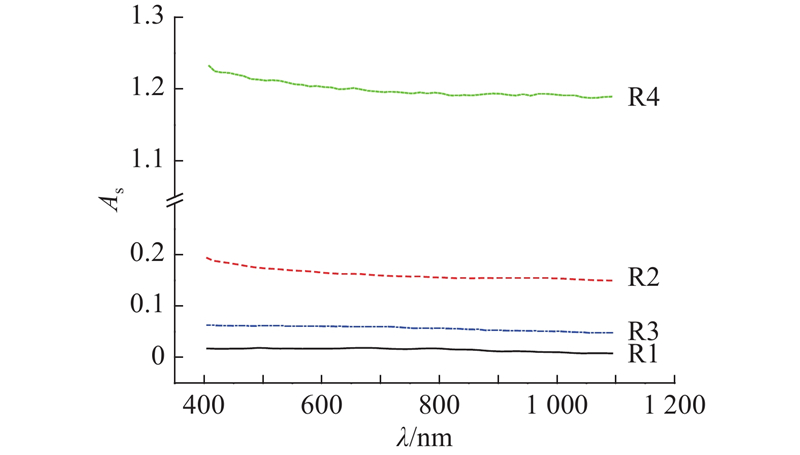
基于特殊构型法制备石墨烯感应元件的第一步是获得分散均匀且稳定的高浓度石墨烯分散液. 分散石墨烯常用的方法如下:使用分散剂改善石墨烯的表面状态,采用机械搅拌和超声作用将石墨烯均匀分散于溶剂中. 分散过程中的各个参数都对最终产物有较大影响. 通过石墨烯分散试验,分析不同分散剂和分散时间下石墨烯分散液的吸光度、石墨烯粒径和沉降时间的变化规律,研究其对分散液浓度、分散程度和稳定性的影响,筛选出合适的分散剂,制定最佳的分散流程.
表 1 RGO分散试验分组
Tab.1
| 编号 | 组分 |
| R1 | IPA+RGO |
| R2 | IPA+SCA+RGO |
| R3 | IPA+PVP+RGO |
| R4 | IPA+CNF+RGO |
制备RGO分散液的步骤如下.
2)将分散剂先加入IPA中磁力搅拌5 min后,再加入RGO搅拌5 min.
3)将混合溶液置于超声波细胞粉碎机中超声分散一定时间.
图 3
图 4
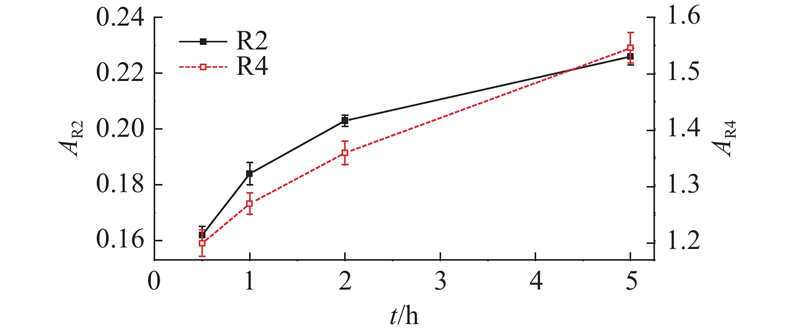
图 4 R2和R4组分散液吸光度随超声时间的变化
Fig.4 Absorbance variation of R2 and R4 dispersion solution with ultrasonic time
分散液中的RGO粒径可以反映RGO在IPA中分散的良好程度. 分散程度越好,RGO越少发生团聚. 采用马尔文粒径分析仪,分析R2、R4组分散液的RGO粒径. 2组分散液在不同超声时间t下的平均粒径如表2所示. 表中,dR2和dR4分别为R2和R4组的平均粒径.
表 2 R2和R4组分散液的平均粒径
Tab.2
| t/h | dR2 /nm | dR4 /nm |
| 0.5 | 604.1 | 1583.2 |
| 1 | 493.7 | 956.6 |
| 2 | 410.3 | 753.4 |
| 5 | 287.5 | 672.4 |
从表2可以看出,RGO平均粒径均随着超声时间的增长而减小. 在相同的超声时间下,dR4 > dR2. RGO在氧化还原过程中会保留一定量的羟基和羧基极性基团,CNF表面存在大量的羟基,可以通过氢键与RGO结合. CNF作为一维纳米材料,尺寸明显大于PVP和SCA分子;因此,R4组较大的平均粒径表明RGO与CNF之间良好的相互作用. 由于在制备CNF的过程中通常会引入带负电荷基团,基团间的排斥作用使得CNF能够在极性溶剂IPA中形成均匀、稳定的悬浮液,从而搭载RGO进行良好的分散.
分散液的稳定性可以通过观察其静置时的沉降现象来评价. 超声时间为2 h的R2和R4组分散液的表观状态随静置时间的变化如图5所示. 可以看出,随着时间的推移,R2组分散液由于RGO发生团聚,很快出现明显的沉淀;R4组分散液较稳定,呈现出均匀分散的状态. 实际上,R4组分散液在实验室放置超过了3个月,未出现沉淀现象,保持稳定的均匀分散状态.
图 5
图 5 R2和R4组分散液的表观状态随静置时间的变化
Fig.5 Apparent state variation of R2 and R4 dispersion solution with standing time
根据以上试验结果可以得出,SCA、PVP和CNF 3种分散剂均对RGO在IPA中的分散有一定程度的提升作用,其中CNF作用最显著,能够大幅地提升RGO分散液的浓度和稳定性. 超声作用有助于RGO的分散,随着超声作用时间的增加,分散液的RGO浓度增大,分散程度和稳定性增强,但是大量增加超声作用时间对RGO分散效果的提升不显著. 选择CNF作为RGO在IPA中的分散剂,将超声作用时间设置为2 h.
1.3.2. PDMS/RGO-CNF/PDMS感应元件的制备
采用特殊构型法制备PDMS/RGO-CNF/PDMS(PRCP)感应元件,制备过程如图6所示,包括以下步骤.
图 6
图 6 PDMS/RGO-CNF/PDMS感应元件的制备过程
Fig.6 Preparation process of PDMS/RGO-CNF/PDMS sensor
1)称取5 g PDMS与固化剂按质量比10∶1混合均匀,倒入模具中自然流平后,置于真空箱中脱气10 min,取出后置于恒温箱中在20 ℃下固化20 h.
2)称取40 mg RGO和40 mg CNF分别加入10 mL IPA中,以2 000 r/min的速度磁力搅拌1 min. 然后将两溶液混合后以2 000 r/min的速度磁力搅拌5 min,再将混合溶液置于超声波细胞粉碎机中在200 W下超声分散2 h,得到RGO-CNF/IPA分散液.
3)用移液器量取一定量的RGO-CNF/IPA分散液,涂敷于呈半固化状态的PDMS基底上,然后置于高频振动台上在20 Hz下振动1 min,使分散液均匀分布在基底上.
4)将涂敷有RGO分散液的PDMS基底置于恒温箱中在20 ℃下继续固化4 h,同时分散液中的IPA挥发. 半固化状态的PDMS已具备足够的支撑性和较好的黏性. 随着IPA的挥发,分散液中的部分RGO-CNF扩散于经IPA溶胀后的PDMS基底的表层,另一部分RGO-CNF黏附堆积于PDMS表面,形成一层多孔结构的RGO-CNF薄膜.
5)用导电银胶将铜箔电极粘贴于RGO-CNF薄膜上.
6)待导电银胶固结后,称取3 g PDMS和0.3 g固化剂混合均匀,涂敷于RGO-CNF薄膜上. 自然流平后,置于真空箱中除气30 min同时促使PDMS进入薄膜孔隙中,然后置于恒温箱中在20 ℃下固化48 h,按设计尺寸裁剪后即得具有层状结构的PRCP感应元件.
如图7(a)、(b)所示为步骤4)中IPA挥发后在PDMS上形成的RGO薄膜的扫描电子显微镜(scanning electron microscope, SEM)图. 可以看出,RGO薄膜呈三维多孔结构,有利于PDMS渗透填塞其中. 传感层包含2个部分:一部分为RGO扩散于经化学溶胀的PDMS中得到,另一部分为PDMS渗透填塞RGO网络得到. 这两部分基本同步形成,二者之间没有明确的界限,如图7(c)所示. 从图7(d)可以看出,RGO在PDMS中分散均匀,传感层与基底层和保护层相互渗透形成一个整体,相较于部分文献中直接在基底上堆积形成的单层石墨烯片层,避免了石墨烯与基底之间结合力不足而导致的变形不协调.
图 7
图 7 PRCP感应元件制备过程中各部分的SEM图
Fig.7 SEM images of various parts of PRCP sensor during preparation process
采用CNF对RGO表面进行修饰,改善了RGO的分散性以及与PDMS的相容性,有助于形成均匀稳定的导电网络结构,从而提高感应元件的性能. 通过控制RGO分散液的用量,可以得到不同结构参数的传感层,实现对感应元件灵敏系数K的设计. PDMS基底良好的柔韧性不仅可以适应不同表面形状的结构测量,而且能够承受较大的变形,使得感应元件具有较大的量程.
2. PRCP感应元件的力敏性能
使用万能材料试验机对感应元件进行力学性能测试,确定感应元件的弹性变形范围和工作量程. 使用Keithley DMM6500数字源表,采用2电极法对感应元件进行电学性能测试,选取合适的石墨烯掺量,测试过程如图8所示. 开展力敏性能测试,获取感应元件的应变电阻响应规律,确定感应元件的力敏性能参数. 设置万能材料试验机的拉伸程序参数(拉伸速率、拉伸长度、循环次数等)和数字源表电信号采集频率,感应元件拉伸时同步测量电阻. 根据同步记录的拉力、拉伸长度和电阻,计算感应元件的应力、应变和电阻变化率.
图 8
图 8 PRCP感应元件的应力-应变和电阻测试
Fig.8 Stress-strain and resistance test of PRCP sensor
2.1. 力学性能
由于PRCP感应元件的传感层厚度很小,不便于测量和计算石墨烯体积分数. 采用石墨烯分布密度DG表示感应元件中石墨烯的用量.
式中:
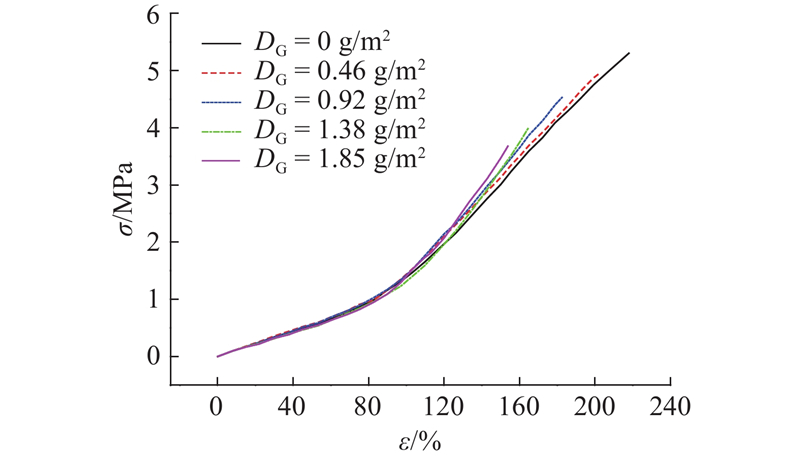
制备不同DG的PRCP感应元件进行静态拉伸试验,加载速率为4 mm/min. 每种DG制备3个感应元件进行测试. 感应元件的应力σ-应变ε曲线如图9所示.
图 9
图 9 不同石墨烯分布密度的PRCP感应元件的应力-应变曲线
Fig.9 Stress-strain curves of PRCP sensors with different graphene distribution density
2.2. 电学性能
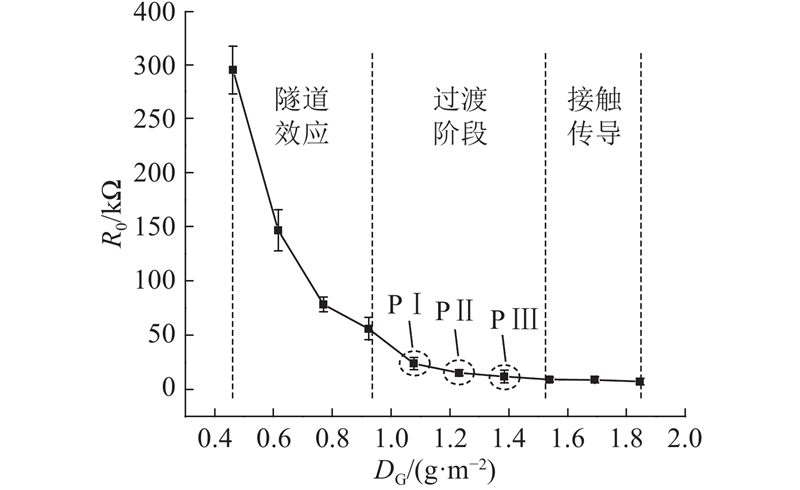
每种DG制备3个感应元件进行电阻测试,求取3个感应元件电阻的平均值. 感应元件初始电阻R0随DG的变化如图10所示. 可以看出,随着DG的增加,R0总体上呈先快速减小后逐渐平稳的趋势. 当DG从0.46 g/m2增加到0.92 g/m2时,R0变化较迅速;当DG从1.54 g/m2变化到1.85 g/m2时,R0变化平缓.
图 10
图 10 PRCP感应元件初始电阻随石墨烯分布密度变化曲线
Fig.10 Initial resistance versus graphene distribution density curve of PRCP sensors
PRCP感应元件的电阻取决于传感层,与内部相邻石墨烯的相对位置有很大关系. 当DG很小时,石墨烯间的距离较大,较难发生隧道效应,无法形成导电通路,此时,感应元件电阻率接近PDMS基体,电阻很大. 随着DG的增大,石墨烯间的距离变得足够小而较易发生隧道效应,且彼此之间相互连通形成较多的导电通路,电阻快速减小. 随着DG的继续增大,石墨烯间的距离继续减小,另外部分石墨烯间出现搭接,电阻继续降低. 当DG进一步增大时,更多的石墨烯搭接、重叠,形成密集且稳定的导电网络,电阻达到稳定状态. 随着DG的增大,感应元件的导电机制从隧道效应向接触传导转变.
感应元件电阻的这种非线性变化趋势是隧道效应和接触传导协同作用的结果,但两者之间没有明确的界限. 从图10可以看出,当DG为0.46~0.92 g/m2时,隧道效应占主导地位;当DG为0.92~1.54 g/m2时,导电机制处于隧道效应向接触传导过渡的阶段;当DG为1.54~1.85 g/m2时,接触传导占主导地位.
2.3. 力敏性能
2.3.1. 单调拉伸
当DG较小时,感应元件的电阻很大,不便于测量;当DG较大时,感应元件内石墨烯相互搭接,形成了较多的导电通路,密集的导电网路能够适应基体的变形,导致单位应变下的电阻变化很小,不仅不便于测量,而且影响感应元件的灵敏度和分辨率. 感应元件的初始电阻不宜过大或过小,根据图10选择编号为PⅠ、PⅡ和PⅢ 3种电阻处于过渡阶段的感应元件,在0~10%应变下以1 mm/min的速率进行单调拉伸测试.
图 11
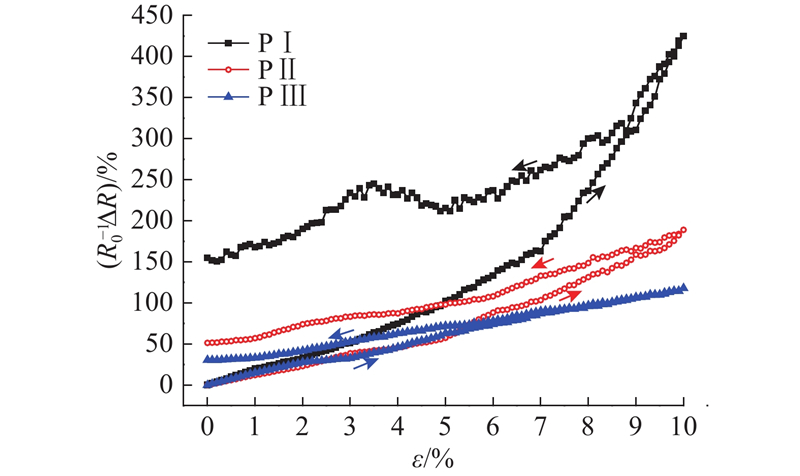
图 11 首次拉伸时PⅠ、PⅡ和PⅢ电阻变化率随应变的变化曲线
Fig.11 Resistance change rate versus strain curves of PⅠ, PⅡ and PⅢ under first tension
1)在拉伸过程中,随着应变的增加,感应元件的电阻逐渐变大,即“正应变电阻效应”. 这主要有以下2个原因. a)传感层内相邻石墨烯间的距离随着基体拉伸而增大,导致相邻电子跃迁的机率下降,造成感应元件的电阻变大. b)传感层内部的不完善导电通路在拉伸过程中发生破坏,如石墨烯发生断裂、卷曲和褶皱,造成石墨烯之间的接触状态发生变化,导致电阻变大.
2)在回复过程中,随着ε的减小,石墨烯间的距离减小,感应元件电阻随之降低. 回复过程中感应元件的电阻大于拉伸过程中相同ε时的电阻,即产生了残余电阻,表明传感层的导电网络不能随着应变回复而完全恢复至初始状态. 这主要是由于拉伸过程中,不完善导电通路被彻底破坏. 高分子聚合物基体材料的黏弹性形变的滞后效应会对导电网络的恢复有一定的影响,但PDMS交联度较好,在温度不变、应变率很小的情况下,影响几乎可以忽略不计.
3)随着DG的增大,感应元件的残余电阻逐渐减小. 这是由于当DG较大时,形成的导电通路越多,导电网路越趋于完善,拉伸过程中破坏的不完善导电通路占比越小. 另外,ΔR/R0与ε之间的线性相关程度随着DG的增大而增大.
2.3.2. 循环拉伸
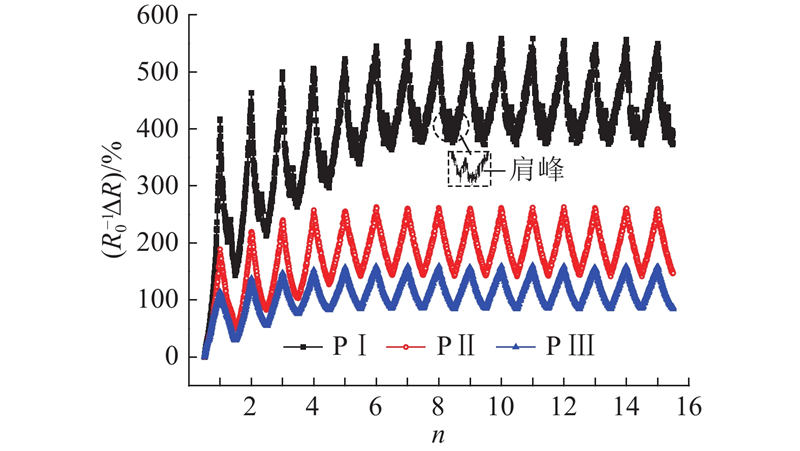
PⅠ、PⅡ和PⅢ在15次循环拉伸过程中电阻变化率ΔR/R0随应变ε的变化曲线如图12所示. 图中,n为循环拉伸次数. 每个拉伸循环的应变历程为0→10%→0,可得如下结论.
图 12
图 12 循环拉伸时PⅠ、PⅡ和PⅢ电阻变化率随应变的变化曲线
Fig.12 Resistance change rate versus strain curves of PⅠ, PⅡ and PⅢ under cyclic tension
1)随着循环次数的增加,感应元件在10%应变时的电阻先逐渐增大后趋于稳定,且每次循环内的残余电阻逐渐减小至趋于0. 在初始的几次拉伸过程中均有不完善导电通路发生完全破坏,但数量逐渐减少直至几乎消失,使得传感层导电网络的结构逐渐完善,表现出稳定的应变电阻响应行为.
2)在应变回复过程中,PⅠ的响应曲线中出现了“肩峰”,这与图11中PⅠ在应变回复时电阻的波动对应,而另外2种较高DG的PⅡ和PⅢ中未出现这种现象. 原因主要是DG较低时构建的导电网络不稳定,在拉伸过程中易被破坏而产生较大的电阻变化,在回复过程中同时出现了导电通路的“破坏”与“重构”,两者之间的竞争造成了电信号的波动.
每个循环内拉伸过程和回复过程中感应元件的ΔR/R0与ε近似呈线性变化,对ΔR/R0随ε的变化曲线分别进行线性拟合,拟合直线的斜率k(PⅠ由于肩峰的存在,采用割线斜率)随循环次数n的变化曲线如图13所示. 可以看出,随着循环次数的增加,拉伸过程和回复过程的斜率均先呈减小的趋势,在一定循环次数后两者趋于一致并几乎保持不变. 随着DG的增大,感应元件应变电阻响应稳定后的斜率变小,表明在相同ε时ΔR/R0降低,即应变电阻的响应强度减弱.
图 13
图 13 拟合直线斜率随循环次数的变化曲线
Fig.13 Slope of fitting straight line versus cycle number curves
以上结果均表明,初始的循环拉伸作用有助于传感层导电通路的重构,形成稳定的导电网络结构,从而使感应元件在后续的拉伸过程中表现出良好的可回复性、可重复性和线性相关性. 感应元件PⅠ、PⅡ和PⅢ分别在循环拉伸约7次、5次和5次后,应变电阻响应达到稳定. 除特别说明,感应元件的测试均在循环拉伸10次后进行.
2.3.3. 应变幅度
虽然混凝土开裂时的极限应变远小于10%,但是混凝土结构在服役过程中常伴随着较多裂缝的出现,裂缝可能会引起感应元件局部较大的变形,因此对裂缝的监测需要更大量程的应变传感器. 鉴于PDMS基底优异的弹性变形能力,研究感应元件在更大应变范围内的电阻响应行为.
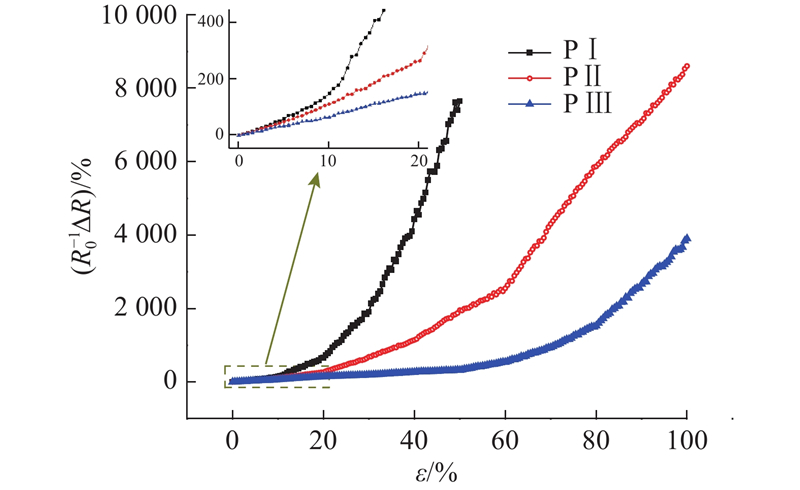
PⅠ、PⅡ和PⅢ在100%应变范围内的电阻响应曲线如图14所示. 可以看出,在整个拉伸过程中,感应元件表现出“正应变电阻效应”. PⅡ和PⅢ在0~20%应变下,电阻近似呈线性缓慢上升,在20%~100%应变下,电阻近似呈指数型快速变化. PⅠ的电阻线性变化范围较小,在应变超过10%后电阻呈指数变化,在约50%应变时,电阻过大超出量程,导电通路基本全部破坏. 这主要是由于DG较小,相邻石墨烯的初始间距较大,能够发生隧道效应的变形范围变小. 随着DG的增大,感应元件在相同应变时的电阻响应强度逐渐减小.
图 14
图 14 100%应变范围内PⅠ、PⅡ和PⅢ的应变电阻响应曲线
Fig.14 Strain resistance response curves of PⅠ, PⅡ and PⅢ within 100% strain range
2.3.4. 应变速率
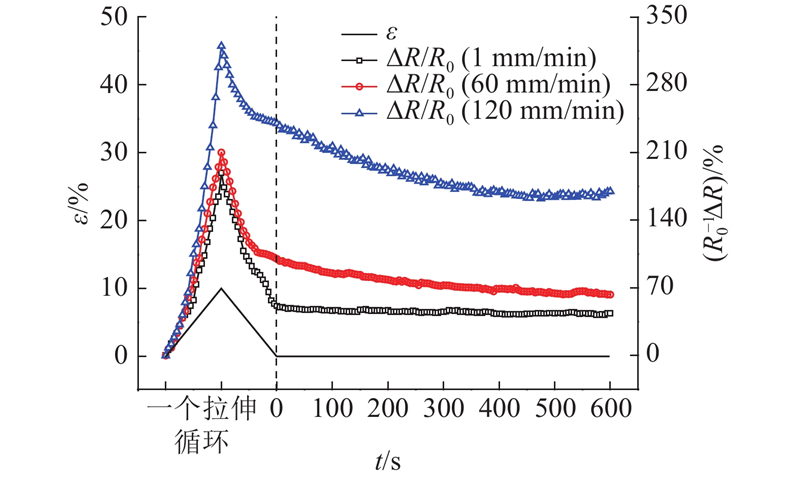
图 15
图 15 PⅡ以不同速率首次拉伸后电阻变化率随静置时间的变化曲线
Fig.15 Resistance change rate versus standing time curves of PⅡ after first tension at different speeds
从图15可以看出,PⅡ在一个拉伸循环应变回复至初始位置后,电阻继续减小,最后趋于稳定,但稳定后的电阻与初始电阻之间有较大的差值,即存在较大的残余电阻. 在应变回复至0后电阻继续减小,主要是由于聚合物基体的黏弹性引起的滞后效应导致的,但黏性变形引起的电阻变化占比均较小. 拉伸速率越大,电阻达到稳定时经历的时间越长,这是由于较大的拉伸速率产生的黏性变形较大,恢复需要的时间较长. 经一段时间稳定后仍有较大的残余电阻,表明拉伸过程中不完善导电通路的永久破坏是产生残余电阻的主要原因.
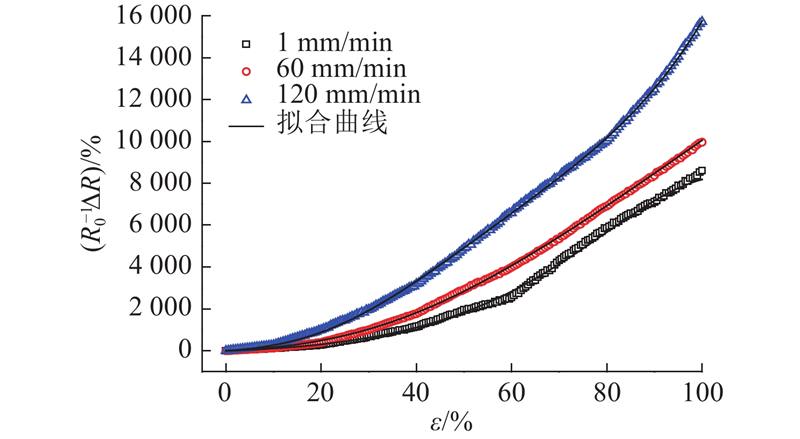
PⅡ经循环拉伸应变电阻响应稳定后,在不同拉伸速率下ΔR/R0随应变ε的变化曲线如图16所示. 从图15、16可以看出,在拉伸过程中,相同应变下的感应元件电阻变化率随着应变率的增加而变大,这主要是由于PDMS基体的力学行为存在明显的应变率相关性,弹性模量随着应变率的增大而明显提高,表现出应变率强化的特点[27-28]. 在相同的应变下,应变率高的感应元件承受较大的拉伸应力作用,相邻石墨烯更容易产生相对滑动,从而对导电网络造成更大的破坏,使得电阻变化率升高. 从图15的应变回复过程可知,高应变率对应的感应元件具有较高的残余电阻,这是因为在高应变率下,感应元件承受较高的拉伸应力,基体内部发生永久性破坏的导电通路增多. 聚合物大分子间的黏性阻力使得感应元件的变形产生滞后,在高应变率下,内部导电网络的调整回复时间较短.
图 16
图 16 PⅡ以不同速率拉伸时电阻变化率随应变的变化曲线
Fig.16 Resistance change rate versus strain curves of PⅡ tensioned at different speeds
2.4. 考虑应变率效应的应变电阻响应模型
从图14可以看出,PRCP感应元件在100%应变下的应变电阻响应行为与1.2节理论模型所描述的规律基本一致. PⅠ、PⅡ、PⅢ的石墨烯分布密度在逾渗阈值附近,内部石墨烯间距随着拉应变不断增大. 拉伸过程中隧道效应导电机制占主导地位,能够采用式(8)对试验结果进行拟合,得到感应元件的应变电阻响应模型参数. 式(8)没有考虑应变速率对电阻响应行为的影响,在推导式(8)的过程中引入应变率系数δ,将式(5)转变为
将式(13)代入式(7),可得
表 3 PⅡ以不同速率拉伸试验结果的拟合曲线的参数值
Tab.3
| v/(mm·min−1) | δ | A | B | C | D | γd0 |
| 1 | 0.19 | 4.68 | −6.46 | 5.54 | −2.77 | 17.12 |
| 60 | 0.26 | 6.50 | −10.51 | 5.67 | −1.29 | 15.46 |
| 120 | 0.30 | 10.11 | −19.95 | 13.02 | −2.90 | 15.08 |
3. 结 论
(1)CNF能够有效地协助RGO在IPA中均匀分散. 超声作用能够明显提升RGO的分散性,但大幅增加超声作用时间对分散效果的提升不显著,功率为200 W时的最佳超声分散时间为2 h.
(2)经化学溶胀和孔隙填充形成的PRCP感应元件传感层,与基底层、保护层相互渗透形成整体. 感应元件继承了PDMS基底优异的弹性变形能力,能够承受超过100%的拉伸应变.
(3)初始的循环拉伸有助于传感层形成稳定的导电网络. 当DG为0.92~1.54 g/m2时,感应元件经过约10次循环拉伸后,应变电阻响应基本达到稳定状态,表现出良好的可回复性和可重复性.
(4)在0~10%应变下,感应元件的电阻变化率随应变近似呈线性变化,灵敏系数可达15. 随着应变的继续增大,电阻变化率呈指数型增长,应变电阻的响应强度随应变率的增大而提高.
参考文献
建筑与基础设施全寿命周期智能化的研究现状及关键科学问题
[J].DOI:10.16262/j.cnki.1000-8217.2021.04.012 [本文引用: 1]
Key scientific issues and state-of-art in whole-lifecycle intelligentization of buildings and infrastructures
[J].DOI:10.16262/j.cnki.1000-8217.2021.04.012 [本文引用: 1]
本征自感知混凝土及其智能结构
[J].DOI:10.6052/j.issn.1000-4750.2021.06.ST02
Intrinsic self-sensing concrete for smart structures
[J].DOI:10.6052/j.issn.1000-4750.2021.06.ST02
人工智能时代的土木工程
[J].DOI:10.15951/j.tmgcxb.2019.05.001 [本文引用: 1]
Artificial intelligence for civil engineering
[J].DOI:10.15951/j.tmgcxb.2019.05.001 [本文引用: 1]
Effect of transverse sensitivity of strain gage on the accuracy of computed principle strain
[J].
Cracking assessment in concrete structures by distributed optical fiber
[J].DOI:10.1088/0964-1726/24/3/035005 [本文引用: 1]
Shear crack width assessment in concrete structures by 2D distributed optical fiber
[J].DOI:10.1016/j.engstruct.2019.05.079 [本文引用: 1]
Measurement of existing prestressing force in concrete structures through an embedded vibrating beam strain gauge
[J].DOI:10.1016/j.measurement.2016.01.031 [本文引用: 1]
A feasibility study on real-time evaluation of concrete surface crack repairing using embedded piezoceramic transducers
[J].DOI:10.1016/j.measurement.2017.09.015 [本文引用: 1]
Seismic health monitoring of a space reinforced concrete frame structure using piezoceramic-based sensors
[J].DOI:10.1061/(ASCE)AS.1943-5525.0000999 [本文引用: 1]
Concrete crack assessment using digital image processing and 3D scene reconstruction
[J].DOI:10.1061/(ASCE)CP.1943-5487.0000446 [本文引用: 1]
Crack and noncrack classification from concrete surface images using machine learning
[J].
基于残差注意力和金字塔上采样的图像语义分割
[J].
Image semantic segmentation based on residual attention and pyramid upsampling
[J].
Damage monitoring in fibre reinforced mortar by combined digital image correlation and acoustic emission
[J].DOI:10.1016/j.conbuildmat.2012.07.106 [本文引用: 1]
Wireless surface acoustic wave sensors for displacement and crack monitoring in concrete structures
[J].DOI:10.1088/0964-1726/25/3/035035 [本文引用: 1]
Lightweight conductive graphene/thermoplastic polyurethane foams with ultrahigh compressibility for piezoresistive sensing
[J].DOI:10.1039/C6TC03713E [本文引用: 1]
Strain sensing behaviors of GnPs/epoxy sensor and health monitoring for composite materials under monotonic tensile and cyclic deformation
[J].
Highly stretchable and sensitive strain sensors using fragmentized graphene foam
[J].DOI:10.1002/adfm.201501000 [本文引用: 1]
High-performance strain sensors with fish scale-like graphene sensing layers for full-range detection of human motions
[J].DOI:10.1021/acsnano.6b03813 [本文引用: 2]
Characterization of piezoresistive properties of graphene-supported polymer coating for strain sensor applications
[J].DOI:10.1016/j.sna.2016.11.002 [本文引用: 1]
石墨烯压阻复合材料及其在裂纹监测中的应用
[J].
Graphene-based piezoresistive composite and application in crack monitoring
[J].
Incorporation of electric-field penetration of the electrodes in the theory of electron tunnelling through a dielectric layer
[J].
Ordered gelation of chemically converted graphene for next-generation electroconductive hydrogel films
[J].DOI:10.1002/anie.201100723 [本文引用: 1]
A manufacturing perspective on graphene dispersions
[J].DOI:10.1016/j.cocis.2015.11.004 [本文引用: 2]
表面活性剂对高浓度石墨烯水分散液制备的影响
[J].DOI:10.11868/j.issn.1001-4381.2018.000566
Effect of surfactants on preparation of high concentration graphene aqueous dispersion
[J].DOI:10.11868/j.issn.1001-4381.2018.000566
Dispersion of graphene using surfactant mixtures: experimental and molecular dynamics simulation studies
[J].
Preparation of rubber/graphene oxide composites with in-situ interfacial design
[J].
硅橡胶拉伸行为的应变率相关性测试和表征
[J].DOI:10.11858/gywlxb.20180664 [本文引用: 2]
Experimental investigation and modeling of strain-rate dependence on tensile behavior of silicone rubbers
[J].DOI:10.11858/gywlxb.20180664 [本文引用: 2]
Piezoresistive response to changes in contributive tunneling film network of carbon nanotube/silicone rubber composite under multi-load/unload
[J].DOI:10.1016/j.sna.2012.09.030 [本文引用: 2]