车联网用户在使用基于位置的服务[1]应用时会生成大量的轨迹数据,直接发布会引起严重的隐私泄露问题[2-3]. k-匿名[4]、l-多样性[5]和t-近邻性[6]技术通过将数据匿名化实现隐私保护,但无法抵御组合攻击、同质攻击、背景知识攻击等窃取隐私的方法. Dwork[7]提出差分隐私(differential privacy,DP)技术,在数据中加入适量的噪声以实现隐私保护,可以抵御背景知识攻击. 若噪声添加过多,则会降低数据的可用性. Cheng等[8]提出个性化轨迹聚类和差分隐私保护机制,在数据效用方面有一定的提升,但未考虑轨迹属性中的时空特征. 本文引入时间图卷积网络(temporal graph convolutional network,T-GCN)模型,在涉及复杂空间的结构中,能够充分提取轨迹的时空特征,在隐私保护中能够实现隐私预算的合理分配.
针对大多数聚类质量损失数据的问题,Cai等[9]提出利用DBSCAN聚类的轨迹发布DPTD的机制,能够保护多数轨迹的隐私. Zhang等[10]提出LGAN-DP算法,利用深度学习方法合成轨迹,使用k-means聚类对轨迹结果集进行处理,提高了数据的私密性. k-means、DBSCAN聚类高度依赖用户指定的参数,性能不够稳定. Guan等[11]提出基于稳定隶属度的自动调优多峰值聚类SMMP算法,解决了参数调优问题,但只能应用在低维空间. 本文提出改进的稳定隶属度多峰值聚类(Improved stable-membership multi-peak clustering,ISMMPC)算法,可以自动调整聚类阈值,开展多原型聚类,解决多维度中应用的问题.
本文设计基于聚类和深度学习的轨迹隐私保护机制(trajectory privacy protection mechanism based on clustering and deep learning,PPCDL). 考虑轨迹空间的时空特征,分析通过时间戳划分轨迹区域带来的数据稀疏性对轨迹隐私保护的影响,设计ISMMPC算法和T-GCN模型,提高隐私保护的效果和轨迹数据的可用性.
1. 预备知识
1.1. 轨迹模型
定义1 网格图
定义2 特征矩阵
时空轨迹是在
式中:m为历史时间序列长度,
定义3 总数矩阵
定义4 密度矩阵
定义5 隐私预算矩阵
1.2. 差分隐私
定义6
则称算法
定义7 全局敏感度. 设函数
式中:
定义8 拉普拉斯机制. 对于给定数据集
1.3. 时间图卷积网络模型
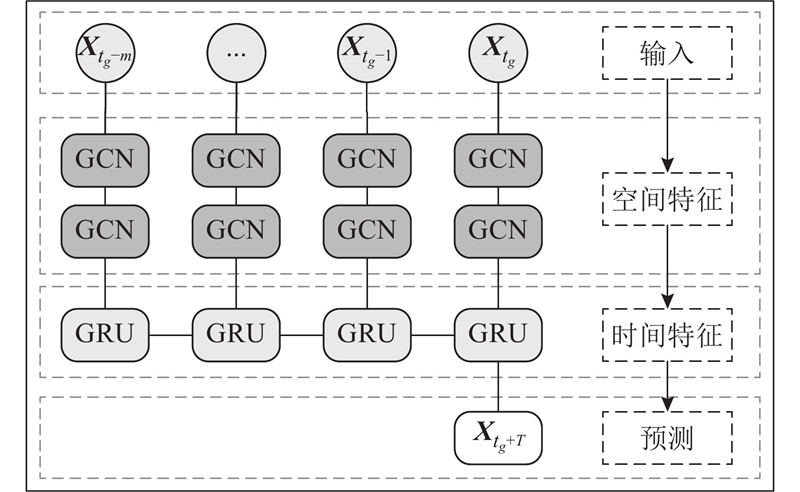
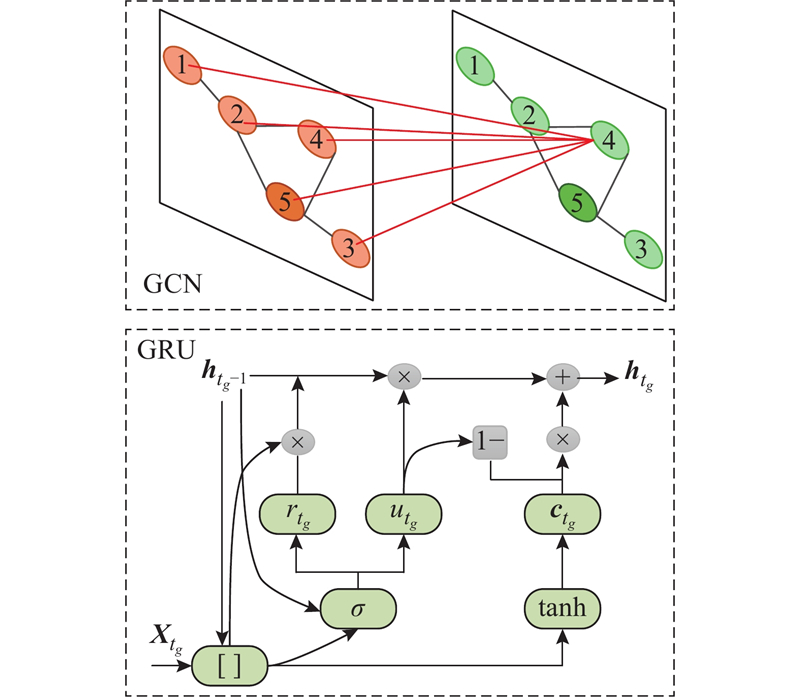
时间图卷积网络模型包括图卷积网络(GCN)和门控循环单元(GRU),如图1所示.
图 1
T-GCN使用m个时间序列数据作为输入,利用2层GCN模型进行图卷积操作,捕获路网区域位置复杂的拓扑结构,以学习空间特征. 将得到的具有空间特征的时间序列输入到GRU模型中,通过单元间的信息传递获得动态变化,捕获时间特征. T-GCN可以充分学习时空依赖性,实现轨迹预测. 具体可以表示为
式中:
2. PPCDL机制
2.1. 问题描述
车联网中许多保护轨迹数据的方法会忽略轨迹的时空特征. 地理空间的限制及时间序列上位置的相关性,使得攻击者有较大可能推断出用户的真实敏感位置和轨迹信息. 实际上,大多数的轨迹隐私保护机制只考虑单个位置点的隐私保护,忽略了连续位置点对轨迹隐私保护的影响. 这会使得攻击者很容易推断出2个位置点之间的地理位置关系,推断出用户经过或停留的位置点,导致用户的位置或轨迹隐私泄露. 轨迹中的位置是时间相关的,引入时间戳,用于获得不同时间的轨迹位置分布,探究位置之间的某种相关性及用户的行为模式. 时间戳的引入会使得轨迹数据变得稀疏,难以承受注入的噪声,降低了数据价值. 引入ISMMPC聚类,以减小时间戳导致的数据稀疏性. ISMMPC在对轨迹数据聚类的同时,保留了时间特征和空间特征. 根据聚类后的轨迹区域密度进行隐私预算预分配,形成隐私预算矩阵. 基于时间图卷积网络模型,对隐私预算矩阵进行预测. 在T-GCN模型的训练过程中,不断优化隐私预算的分配,在对数据减少注入噪声的同时,保护了轨迹数据的隐私安全.
2.2. PPCDL实现
2.2.1. 轨迹聚类
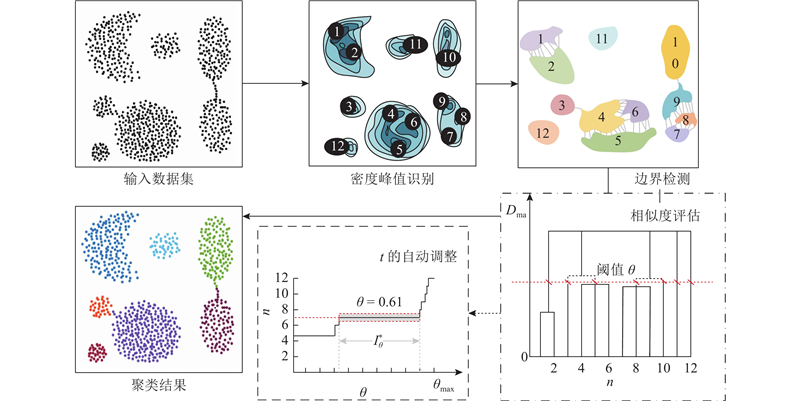
ISMMPC算法在时间戳划分后的区域实现聚类,捕获轨迹的位置分布. 根据轨迹的分布情况,形成任意形状和数量的子簇,无须预先确定聚类的子簇量. 图2给出ISMMPC聚类过程. 图中,n为子簇数量.
图 2
图 2 改进稳定隶属度多峰值聚类过程
Fig.2 Process of improved stable-membership multi-peak clustering clustering
算法中的隶属度是聚类函数
其中
ISMMPC算法利用密度峰值聚类技术[15]获取区域
式中:
用
对于2个相交的子簇,若所有边界链接样本的特定值几乎一样大,则它们是高相似的. 根据式(11)可知,相似矩阵中
算法1给出ISMMPC聚类的实现过程.
算法1 ISMMPC聚类算法的实现
输入:数据轨迹集
输出:聚类结果集C
1)获得
2)
3) for
4)计算每个区域的密度
5)end for
6) for
7)
8)end for
9) if
10)
11) end if
12) 具有相同
13) for 每对密度峰
14 ) 根据式(9)计算
15) 计算相似性
16) end for
17)
18) for
19) 统计聚类数量 count
20) end for
21)自动调整θ = mean (
22)自适应合并子簇
23) return 聚类结果
第1行是获取数据集. 第2~8行是开展每一点的k个周围点的选取,时间复杂度为O(
2.2.2. 时间图卷积隐私预算矩阵的预测
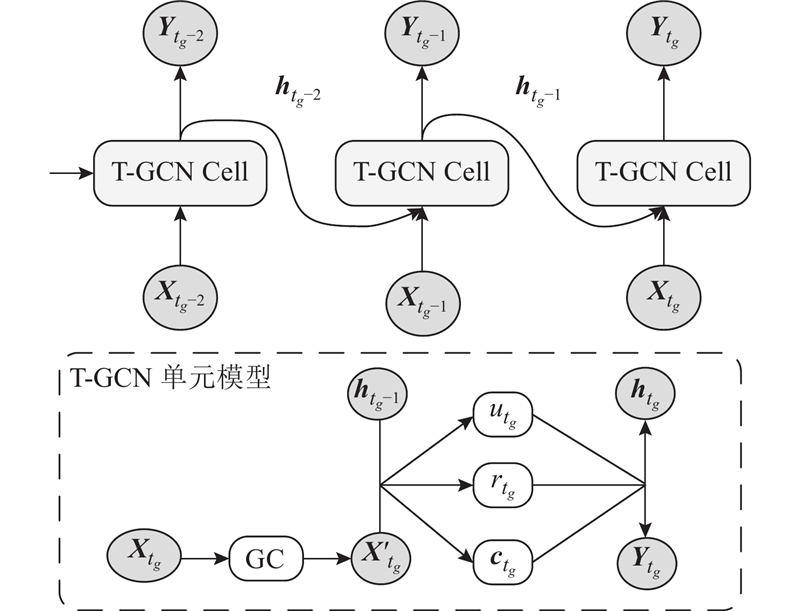
图3给出T-GCN组成结构,T-GCN模型可以从交通数据中学习空间特征. GRU以
图 3
图 3 时间图卷积网络模型的组成结构
Fig.3 Composition structure of temporal graph convolutional network model
将通过时间戳划分获得的每个区域的轨迹数据输入到T-GCN模型中. 在空间依赖关系和时序特征的作用下,由定义1、2得到区域轨迹的时空信息
根据差分隐私的定义,对于密集区域,
式中:
结合T-GCN模型提取数据的时间和空间特征,预测隐私预算矩阵
图 4
图 4 时间图卷积网络模型的时空预测过程
Fig.4 Spatiotemporal prediction process of temporal graph convolutional network model
3. 实验分析
采用真实数据集Divvy Bikes和T-drive进行仿真实验,验证PPCDL的数据有效性、时间开销,评估差分隐私的保护效果.
3.1. 实验数据集
T-GCN训练模型使用Adam优化器进行训练,激活函数为Elu. 对于输入层,将数据集的80%数据作为输入,其余数据作为测试过程的输入. 将PPCDL与DPTD[9]、LGAN-DP[10]、DPGeo[12]进行对比分析. Divvy Bikes数据集包含了芝加哥生活中的共享单车自2015年至2020年骑行使用的数据,其中有每次骑行的起始点和时间戳、起始时间、起始经纬度等. T-drive数据集包含北京市出租车的轨迹总距离约为900万km,位置点超过1 500万个,轨迹数据由每辆出租车的ID、时间戳、经度和纬度信息表示的GPS位置点序列组成. 在实验预处理中,数据集选用轨迹密度相对较大的区域.
3.2. 评价指标
隐私保护的目的是发布有用信息,同时隐藏敏感的信息. 当进行隐私保护时,既要保护用户的隐私安全,又要保证用户享受到较高的服务质量. 采用3种度量方法,量化原始数据和发布数据之间的差异.
使用均方根误差(root mean square error,RMSE),评估PPCDL的数据有效性. RMSE是衡量原始数据与发布数据间的差异,是评估发布数据准确性的常用方法. 设隐私预算矩阵的真实值为
使用查询误差(query error,QE),评估差分隐私的保护效果. 给定查询函数
使用JS(Jensen-Shannon divergence)散度,评估真实轨迹和加噪后轨迹间的相似性. 给定已发布的原始数据和加噪数据的概率分布函数
3.3. 实验结果分析
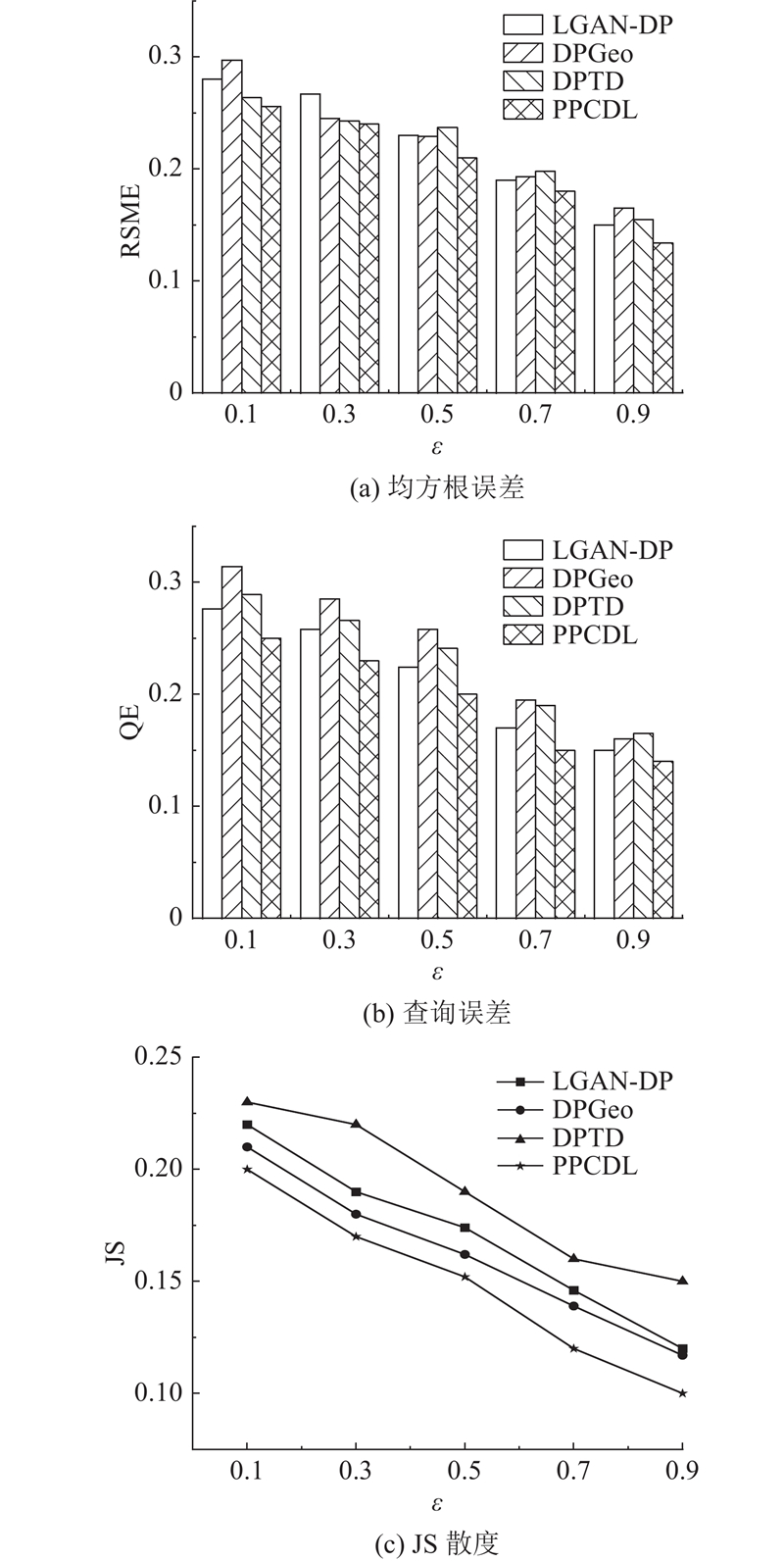
图 5
图 6
从图5(a) 可以看出,PPCDL的RMSE小于其他3个机制. 随着隐私预算的增加,RSME逐渐较小. 原因是
从图5(b)可以看出,
从图5(c)可以看出,2个数据集上的JS散度随着
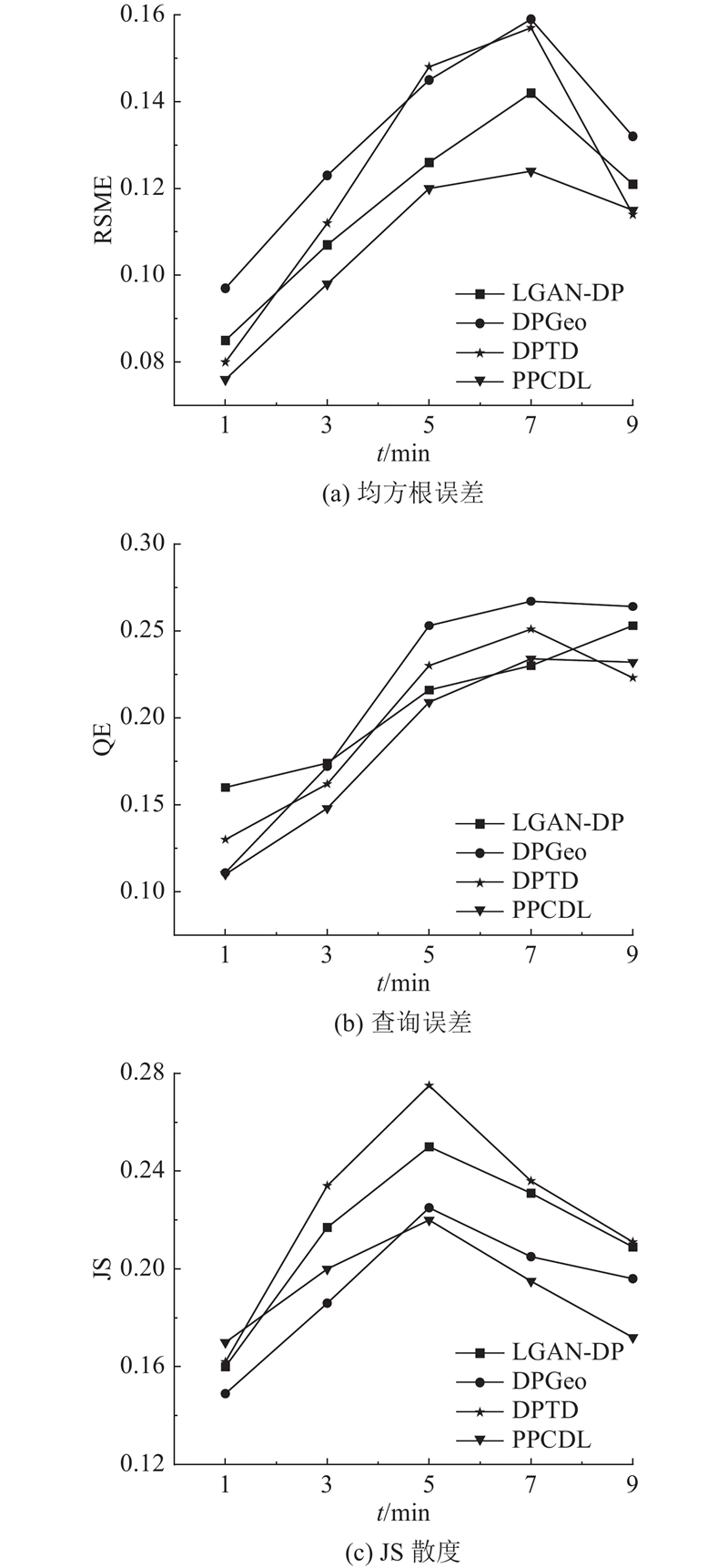
对T-drive数据集开展划分细粒度的实验. 在T-drive数据集上设置不同间隔的5个时间戳,设置相同的隐私预算,通过逐步加大时间戳的长度,查询当天的轨迹数据,得到指标的平均性能. 从图7可以看出,通过改变时间戳来验证划分对隐私保护的影响,PPCDL的RMSE误差、QE误差和JS散度都优于对比机制. 这是因为PPCDL合理地分配了隐私预算. 稠密区域的拉普拉斯噪声比稀疏区域大. 在每个位置合理添加噪声,实现了不同程度的隐私保护,提高了轨迹数据的可用性. 随着时间戳的不断增大,轨迹序列长度增大,RMSE误差呈现增大趋势,导致噪声不断增加,影响数据的可用性. 在时间戳延长到一定程度后,RSME减小,这是因为此时覆盖的轨迹序列长度比其他时间段大几倍,此时数据会受到非轨迹区域的噪声数据干扰,当计算平均指标时,RSME会减小. 对于QE误差来说,查询密集区域位置较容易实现,但加入的噪声量较大. 当计算QE误差时,QE随着噪声的增加而增大. 由于原始数据和发布数据的差异,JS散度随着噪声的增加而增大. 当JS散度较小时,表明该区域包含了大量不属于轨迹序列的位置.
图 7
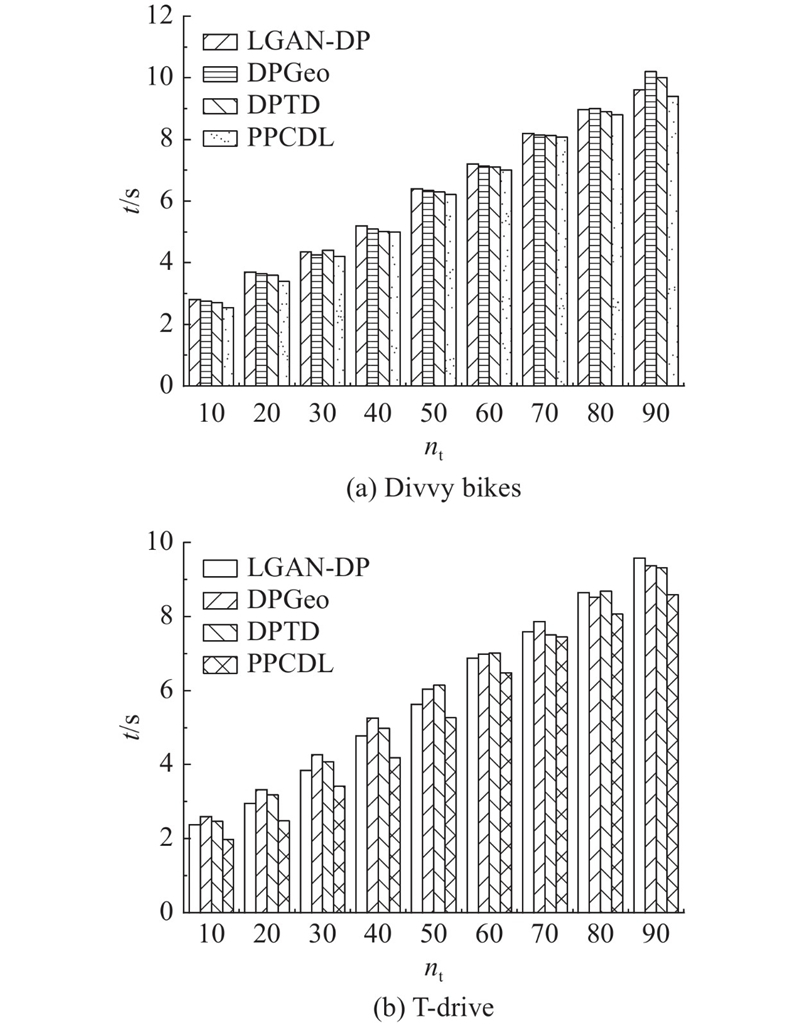
为了验证PPCDL的效率,在数据集中将轨迹划分成不同数量的分组,在
图 8
4. 结 论
(1)在相同的隐私预算下,PPCDL的隐私预算利用率和发布的轨迹数据集的有效性均优于对比机制. 预测的隐私预算可以防止攻击者利用数据发布的时间差来获取真实的轨迹.
(2)在未来的工作中,将关注如何更好地对隐私预算初始化,以提升深度学习的训练速度,更好地实现车联网轨迹隐私保护.
参考文献
P2SF-IoV: a privacy-preservation-based secured framework for Internet of vehicles
[J].DOI:10.1109/TITS.2021.3102581 [本文引用: 1]
Local differential privacy-based federated learning for Internet of things
[J].DOI:10.1109/JIOT.2020.3037194 [本文引用: 1]
Real-world K-anonymity applications: the KGen approach and its evaluation in fraudulent transactions
[J].
Distributed L-diversity using spark-based algorithm for large resource description frameworks data
[J].DOI:10.1007/s11227-020-03583-6 [本文引用: 1]
Enhanced clustering based OSN privacy preservation to ensure k-anonymity, t-closeness, l-diversity, and balanced privacy utility
[J].DOI:10.32604/cmc.2023.035559 [本文引用: 1]
OPTDP: towards optimal personalized trajectory differential privacy for trajectory data publishing
[J].DOI:10.1016/j.neucom.2021.04.137 [本文引用: 1]
A trajectory released scheme for the Internet of vehicles based on differential privacy
[J].DOI:10.1109/TITS.2021.3130978 [本文引用: 2]
LGAN-DP: a novel differential private publication mechanism of trajectory data
[J].DOI:10.1016/j.future.2022.12.011 [本文引用: 2]
SMMP: a stable-membership-based auto-tuning multi-peak clustering algorithm
[J].
Deep learning-based privacy-preserving framework for synthetic trajectory generation
[J].
基于深度学习的位置大数据统计发布与隐私保护方法
[J].DOI:10.11959/j.issn.1000-436x.2022006 [本文引用: 1]
Statistics release and privacy protection method of location big data based on deep learning
[J].DOI:10.11959/j.issn.1000-436x.2022006 [本文引用: 1]
基于本地化差分隐私的时序位置发布方案研究
[J].
Research on time-series location data publication based on local differential privacy
[J].
Density peaks clustering algorithm based on fuzzy and weighted shared neighbor for uneven density datasets
[J].