在无线EH协作网络资源分配领域,Han等[6]针对时变能量收集驱动的水下传感器网络,提出基于分层的深度强化学习框架,通过中继选择和功率分配的联合优化,提升上行链路的累积性能. Zhuang等[7]在环境反向散射通信中提出混合同步信息和能量传输(simultaneous wireless information and power transfer, SWIPT)辅助中继传输方案,利用拉格朗日对偶理论和次梯度推导得到基于功率分配和时间分配的联合优化迭代算法,最大化反向散射通信的吞吐量. Gu等[8]研究非线性EH下两跳多中继网络的吞吐量最大化问题,采用逻辑函数模型和常线性常数模型表征非线性,优化源-中继链路的传输功率和带宽的联合分配以及中继的功率分割(power splitting, PS)比. Liu等[9]研究基于SWIPT的全双工放大转发(amplify-and-forward, AF)多中继系统的资源分配问题,提出基于可证明收敛博弈论的分布式迭代注水算法;该算法在发射功率和能量收集约束下,最大限度提高了干扰信道的总速率. Euttamaraja等[10]针对采用解码转发策略的两跳SWIPT中继网络,提出基于椭球方法的迭代原对偶算法,推导源和中继功率分配以及PS的最优解析表达式,提高了端到端的可实现速率. Xu等[11]研究具有窃听者的EH协作中继网络的功率分配问题,提出基于凸函数差分规划的迭代算法;该算法在保证信息安全传输的同时达到了较高的可实现保密速率. Liu等[12]考虑基于时频块分配的EH中继网络的通信场景,以提高下行链路传输速率和降低功耗为目标,将时频块配对算法和块功率分配算法相结合. Chen等[13]研究混合能量收集的设备到设备(device to device, D2D)辅助边缘计算系统中的资源分配策略,采用量子粒子群优化算法得到次优解;该策略在计算延迟和能量收集的约束下最大限度地提高了系统能效. Salim等[14]针对中继辅助D2D的下行链路频谱共享的网络,提出低复杂度的EH辅助中继选择的资源和功率分配算法,该算法能够有效提高系统网络的频效和能效. Ojo等[15]研究射频(radio frequency, RF)供电的协作中继网络的最优功率分配问题,提出基于迭代节能算法的节能时间交换中继和节能功率分割中继协议,实现能量效率的最优化. Xu等[16]利用非线性EH研究不可信中继的节能安全通信,提出基于优化解耦、分数规划、拉格朗日对偶分解和凸函数差规划的双层算法,所提算法通过优化分段区域选择和功率分配提高能量利用率.
上述工作在开展时,很少考虑上行链路和下行链路的关联性. 在上下行链路共享频谱的情况中,信道特性存在差异,综合上下行链路的研究有助于掌握系统的全面性能. 同时,EH是解决无线通信设备能量短缺问题的有效技术[17-19],无线协作网络不但能扩大小区覆盖,而且能有效节约能量. 为了提高系统能效,将在无线EH协作网络中开展综合上下行链路的资源分配算法研究:1)通过联合优化带宽和功率分配,平衡上行和下行链路之间的能效,建立多中继节点的上下行链路频谱共享的系统模型,以最大化绿色能效和传统能效为目标;2)利用Dinkelbach方法对优化问题进行转化,通过KKT分析,求得节能资源分配的最优解,包括最优的发射功率、上下行链路最优的带宽分配、最优的功率分割以及最优的系统能效;3)归纳节能资源分配算法,对算法进行仿真对比,验证算法的有效性.
1. 系统模型
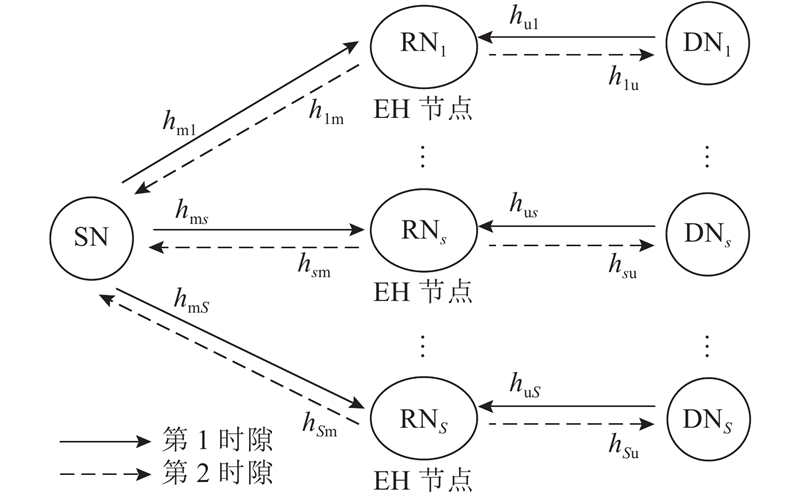
图 1
如图2所示,
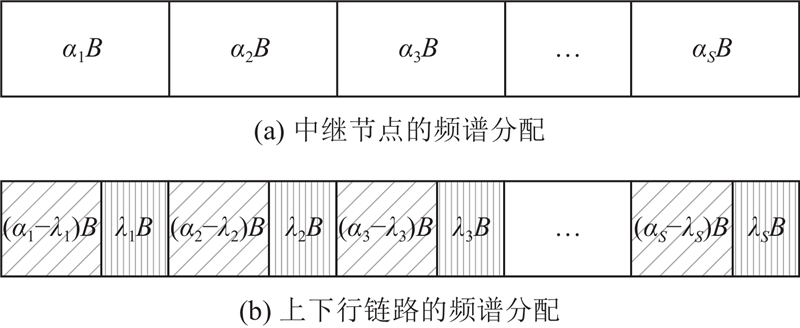
图 2
第1时隙,SN向第
式中:
式中:
第2时隙,RN利用上一时隙收集到的能量向DN发送信息,第s个RN到DN的下行链路传输速率为
式中:
式中:
式中:
上行传输中的可实现速率受DN到RN上行链路速率和RN到SN上行链路速率的限制,下行传输中的可实现速率受SN到RN下行链路速率和RN到DN下行链路速率的限制,因此引入变量
由于上下行链路的非对称特性,假设系统须保证下行可实现速率至少为上行可实现速率的
2. 优化问题
2.1. 绿色能效最大化的优化问题
如果重点关注系统收集能量的使用效率,则定义系统综合上下行传输的绿色能效为
为了便于衡量系统的能效性能,假设系统中源节点和目的节点的发射功率之和小于或等于
式中:
2.2. 系统能效最大化的优化问题
如系统模型所述,中继节点通过收集来自源节点和目的节点的信号能量供电,因此系统消耗的能量仅包括源节点和目的节点的能耗,为了方便推导且不影响结论,不考虑节点的电子器件功耗,只考虑空口的功耗,将系统功耗表示为
此时,定义系统综合上下行传输的能效为
在此基础上,形成最大化系统能效的优化问题P2:
P2的约束条件与P1的相同. 通过求解优化问题P2,可以获得节点(包括最优的源节点、中继节点和目的节点)的发射功率、最优的带宽分配以及最优的功率分割.
3. 优化问题求解
3.1. 优化问题P1的求解
P1是非线性分式规划问题,为此,定义系统最大绿色能效为
其中
定理1:系统的最大能效当且仅当
成立时得到[21]. 由于优化问题 P1的目标函数难以直接求解,受定理1启发,引入参数
令
P3是多变量耦合的优化问题,假设每单位载频的发射功率是恒定的[22],则SN到第s个RN的发射功率满足
P3的拉格朗日函数(Karush-Kuhn-Tucker, KKT)条件具有最优性,根据问题P3及原始可行性条件,引入拉格朗日乘子,将不等式约束条件转化为等式约束条件,即将离散的问题转化为连续的凸优化问题,构建多变量拉格朗日函数为
其中
对于互补松弛条件K11~K13,须考虑以下8种情况. 1)当
由
由
将
联合式(17)、(19)得到
将式(16)代入式(20),得到下行最优功率分割因子:
将
联合
将最优解
同理,DN到第s个RN的上行发射功率满足
将所求资源分配最优解代入式(12)得到最优能效值:
3.2. 优化问题P2的求解
令
P4是多变量耦合的优化问题,由优化问题P1的求解可知
继续使用求解优化问题P1的证明方法,结合约束条件C2″和K1~K4,构建拉格朗日函数,分别对
4. 综合上下行链路的资源分配算法
优化问题的数学推导,可以归纳得到基于绿色能效最大化的资源分配算法步骤如下.
1)通过以下过程获得最优的参数. 给定系统总功率值
2)第1个时隙,SN以带宽
3)第2个时隙,RN以带宽
4)一次协作传输完成.
基于能效最大化的资源分配算法与基于绿色能效最大化的资源分配算法具有相似的步骤,区别仅在于推导的参数表达式不同,因此只需要更换相应参数的计算公式即可.
5. 仿真分析
通过Matlab对本研究提出的绿色能效最大化资源分配算法HEEM-RAA和能效最大化资源分配算法EEM-RAA进行仿真验证,并与基于时频块分配的资源分配算法[12] TFB-RAA、双向中继资源分配算法[23] DDR-RAA进行对比,Han等[23]考虑双向AF中继辅助的通信场景,综合频谱共享、速率限制、双向功率控制等特征,提出双向资源分配方案. 在仿真过程中,仿真模型包括1个源节点、若干个中继节点和目的节点,SN与RN之间的信道以及RN与DN之间的信道均为瑞利平坦衰落信道,系统总带宽
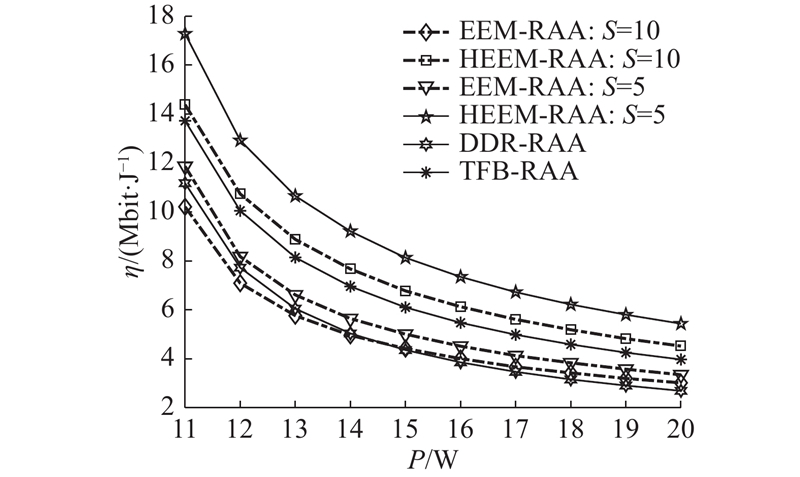
如图3所示为在不同的中继个数下,系统的绿色能效随总功率发射限制的变化情况. 可以看出,随着总功率的增加,绿色能效降低并趋于平稳. 随着总发射功率持续增加,尽管信道容量增加,但各节点的功耗越来越大,绿色能效降低. 在同等条件下,HEEM-RAA优化中继节点的绿色能效,有效降低系统消耗,因此绿色能效较优. 当总功率小于一定值时,EEM-RAA的总能效小于DDR-RAA. 原因是在总功率较小时,EEM-RAA分割给信息解码的能量较少,上下行链路的和速率较低,随着总功率增加,EEM-RAA收集的能量增加,功耗得到补偿,此时能效大于DDR-RAA的传统能效.
图 3
图 3 不同算法的系统能量效率和总功耗的关系
Fig.3 Relationship between system energy efficiency and total power of different algorithms
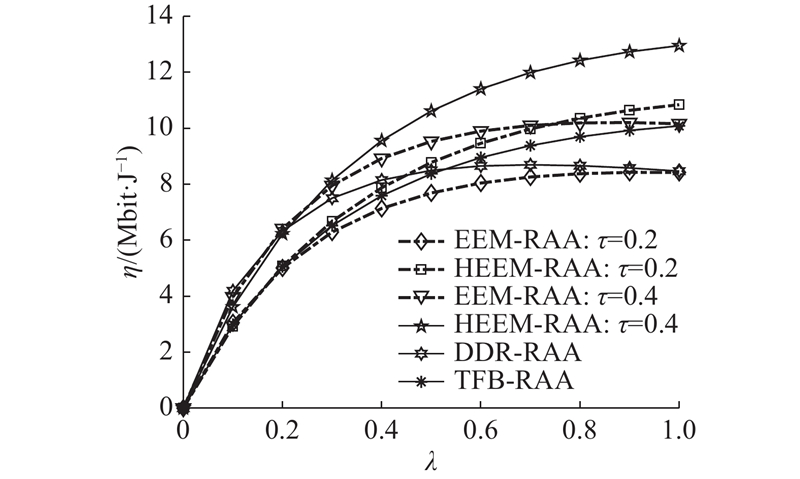
如图4所示为系统的绿色能效在不同功率分割因子
图 4
图 4 系统能量效率和带宽分配系数的关系
Fig.4 Relationship between system energy efficiency and bandwidth allocation coefficient
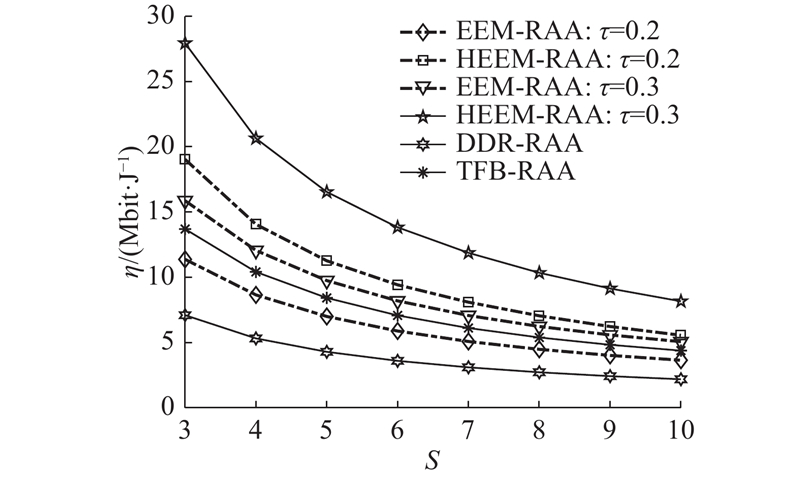
如图5所示为在不同的功率分割因子
图 5
图 5 不同算法的系统能量效率和中继数量的关系
Fig.5 Relationship between system energy efficiency and numbers of relay node of different algorithms
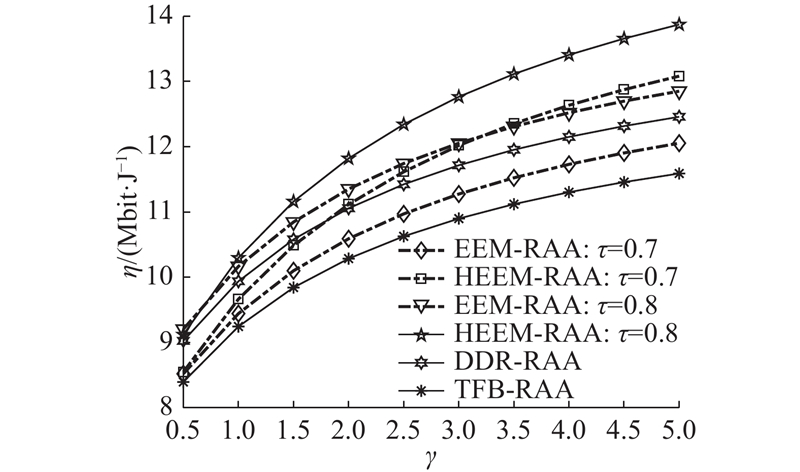
如图6所示为系统的绿色能效与上下行速率比值
图 6
图 6 不同算法的系统能量效率和上下行链路速率比值的关系
Fig.6 Relationship between system energy efficiency and rate ratio of downlink to uplink of different algorithms
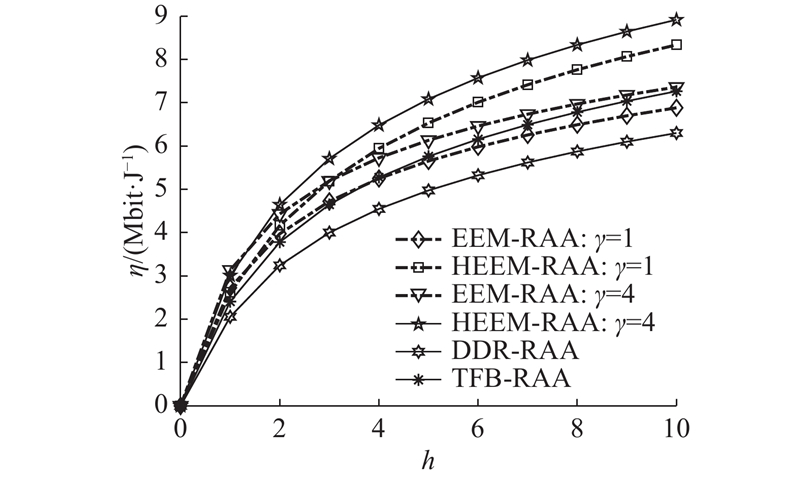
如图7所示为系统的绿色能效随平均信道增益的变化曲线. 仿真结果表明,随着平均信道增益增大,系统的绿色能效得到提高. 原因是信道增益影响上行与下行链路的最小可实现速率. 在同等条件下,HEEM-RAA的能耗得到优化,小于EEM-RAA的功耗,绿色能效优于EEM-RAA,DDR-RAA没有采用能量收集,因此绿色能效为0. 还可以发现,当信道增益固定时,随着
图 7
图 7 不同算法的系统能量效率和平均信道增益的关系
Fig.7 Relationship between system energy efficiency and average channel gain of different algorithms
6. 结 语
本研究针对无线EH协作网络考虑上下行链路频谱共享、中继节点频谱共享、上下行速率匹配等的联合优化问题,通过对优化问题的数学解析,得到功率、带宽、功率分割等的数学解析表达式. 提出可行的资源分配算法,并进行仿真验证. 仿真结果表明,从系统能效与带宽分配系数、中继数量、上下行传输速率比值、平均信道增益的变化关系来看,本研究算法均都取得良好的性能,对于研究无线EH协作网络的资源分配具有积极的意义. 未来计划考虑窃听场景下的保密协作通信系统,基于物理层安全的资源分配算法进一步研究优化系统的安全能效.
参考文献
Cooperative small cell HetNets with dynamic sleeping and energy harvesting
[J].DOI:10.1109/TGCN.2020.2985496 [本文引用: 1]
OFDM based bidirectional multi-relay SWIPT strategy for 6G IoT networks
[J].DOI:10.23919/JCC.2020.12.006 [本文引用: 1]
基于干扰效率多蜂窝异构无线网络最优基站选择及功率分配算法
[J].DOI:10.11999/JEIT190419 [本文引用: 1]
Interference efficiency-based station selection and power allocation algorithm for multi-cell heterogeneous wireless networks
[J].DOI:10.11999/JEIT190419 [本文引用: 1]
基于谱聚类的异构蜂窝超密集网络高能效资源分配算法
[J].
Spectral clustering-based energy-efficient resource allocation algorithm in heterogeneous cellular ultra-dense network
[J].
电力物联网中节能的免许可D2D接入算法设计
[J].
Energy saving and channel access algorithm of unlicensed D2D networks in power Internet of things
[J].
Joint relay selection and power allocation for time-varying energy harvesting-driven UASNs: a stratified reinforcement learning approach
[J].DOI:10.1109/JSEN.2022.3203028 [本文引用: 1]
Exploiting hybrid SWIPT in ambient backscatter communication-enabled relay networks: optimize power allocation and time scheduling
[J].DOI:10.1109/JIOT.2022.3193104 [本文引用: 1]
Optimal resource allocation in wireless powered relay networks with nonlinear energy harvesters
[J].DOI:10.1109/LWC.2019.2955696 [本文引用: 1]
Power allocation for SWIPT in full-duplex AF relay interference channels using game theory
[J].DOI:10.1109/LCOMM.2019.2963640 [本文引用: 1]
Energy-efficient joint power allocation and energy cooperation for hybrid-powered comp-enabled HetNet
[J].DOI:10.1109/ACCESS.2020.2972910 [本文引用: 1]
Simultaneous wireless information and power transfer based on time-frequency block allocation in OFDM cooperative communication system
[J].DOI:10.1109/JSYST.2021.3093572 [本文引用: 2]
Resource allocation strategy for D2D-assisted edge computing system with hybrid energy harvesting
[J].DOI:10.1109/ACCESS.2020.3032033 [本文引用: 1]
Optimal resource and power allocation with relay selection for RF/RE energy harvesting relay-aided D2D communication
[J].DOI:10.1109/ACCESS.2019.2924026 [本文引用: 1]
Optimal power allocation in cooperative networks with energy-saving protocols
[J].DOI:10.1109/TVT.2020.2978576 [本文引用: 1]
Secure energy efficiency maximization for untrusted wireless-powered full-duplex relay networks under nonlinear energy harvesting
[J].DOI:10.1109/JSYST.2021.3135515 [本文引用: 1]
Energy-efficient resource optimization for hybrid energy harvesting massive MIMO systems
[J].DOI:10.1109/JSYST.2021.3074542 [本文引用: 1]
Joint optimization of energy harvesting and information transmission for trapped user
[J].DOI:10.1007/s11276-022-03006-9
Optimal energy sharing for cooperative relaying in a random access network with energy harvesting nodes
[J].DOI:10.1109/TGCN.2020.3020524 [本文引用: 1]
Space-time signal optimization for SWIPT: linear versus nonlinear energy harvesting model
[J].
Energy-efficient resource allocation for secure OFDMA Systems
[J].DOI:10.1109/TVT.2012.2199145 [本文引用: 1]
Backhaul-aware user association and resource allocation for energy-constrained HetNets
[J].
Power control for two-way AF relay assisted D2D communications underlaying cellular networks
[J].DOI:10.1109/ACCESS.2020.3017799 [本文引用: 2]