输水盾构隧道复合结构是新型的输水管道结构,其外层为钢筋混凝土衬砌管片,内层为输水钢管,二者之间填充混凝土. 在承受荷载过程中,衬砌管片、填充混凝土和钢管将力分担,赋予隧道高承载能力. 衬砌管片和填充混凝土能够有效抵御外部环境因素侵蚀钢管,提升复合结构的耐久性. 由于施工期盾构掘进扰动、运营期邻近建构筑物施工、隧道下卧层土体特征差异以及隧道所处地层的水位变化等因素的作用,输水盾构隧道所在的地基不可避免地会发生不均匀沉降[1],导致隧道结构产生纵向弯曲. 特别是在地基不均匀沉降较大的情况下,隧道结构可能产生显著的弯曲变形,导致隧道出现管片接缝张开、管片破损,钢管腐蚀和屈曲等病害[2],严重威胁输水隧道的安全性和稳定性.
在盾构隧道纵向受弯性能研究中主要有2种理论模型: 1)纵向梁-弹簧模型[3];2)纵向等效连续模型[4]. 在模型1)中,衬砌段采用直梁模拟,接缝和螺栓采用轴向弹簧、剪切弹簧和旋转弹簧模拟。该模型存在的问题包括确定纵向梁-弹簧模型的环缝转动刚度非常困难,一些关键参数(如局部混凝土压缩刚度)需要通过试验确定,建模过程复杂. 模型2)针对环间接缝导致的隧道纵向刚度降低,将盾构隧道简化为纵向连续均质梁。该模型概念清晰、计算简单,在盾构隧道纵向力学性能分析中应用广泛. 随着盾构隧道纵向分析理论的不断发展,隧道纵向受弯分析模型越来越丰富,相关研究可以分为2个阶段:1)经典等效连续化计算模型[4]被提出,为盾构隧道纵向受弯性能的分析奠定了坚实的理论基础;2)经典等效连续化计算模型[4]的改进,例如考虑环缝的影响范围[5],考虑横向和纵向性能产生的耦合以及螺栓的弹塑性[6],考虑轴向力和弯矩的组合效应[7],考虑混凝土的弹塑性[8],考虑轴向力和弯矩的组合效应、横向与纵向性能的耦合效应[9]、研究类矩形管片的环缝影响范围和螺栓预紧力[10].
研究者虽然探索了单层衬砌结构盾构隧道纵向受弯分析计算模型,但三层复合结构的研究鲜见. 输水盾构隧道复合结构具有不同的结构特征,现有单层衬砌结构盾构隧道的纵向受弯分析模型不适用于三层复合结构的输水盾构隧道. 本研究基于隧道管片纵向等效连续化计算模型的基本原理,初步探索输水盾构隧道复合结构纵向受弯分析解析模型;依托杭州某输水隧道工程案例,研究隧道结构纵向受弯性能,并根据复合结构的临界状态求解对应的变形受力界限指标;对输水盾构隧道复合结构的结构设计进行优化.
1. 输水隧道复合结构解析模型建立
1.1. 力学模型
图 1
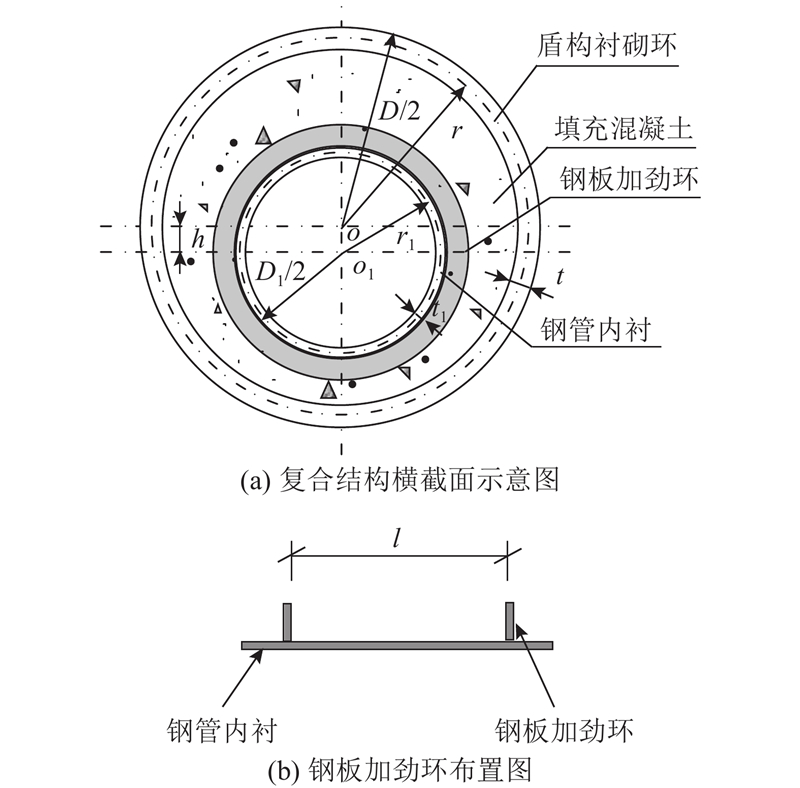
图 1 输水盾构隧道复合结构截面图
Fig.1 Cross-section diagram of composite structure in water-conveying shield tunnel
图 2
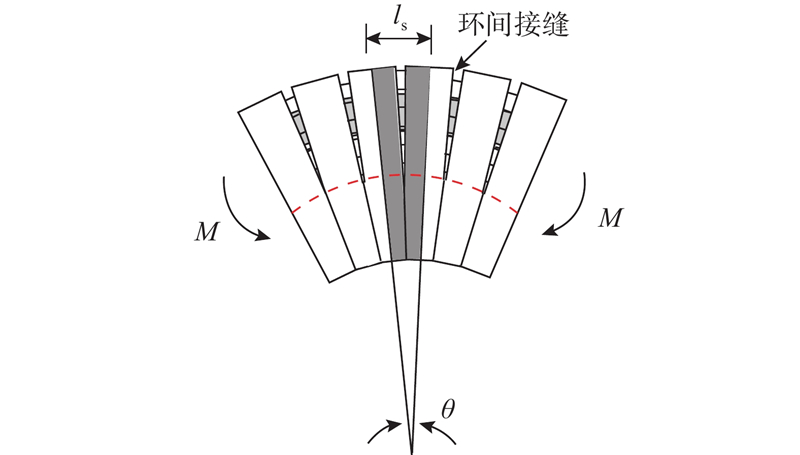
输水盾构隧道复合结构纵向受弯分析解析模型基本假定如下。1)文献[11]、[12]建议按照衬砌层间界面的抗剪强度对多层衬砌隧道复合结构计算模型进行分类. 如果抗剪强度足够大,按叠合结构进行结构计算; 否则按仅传递径向压力的复合结构进行结构计算[12]. 本研究假定忽略衬砌管片和填充混凝土之间的摩擦. 在对应的实际工程中,衬砌管片结构的螺栓孔、注浆孔、接缝等部位须进行填平处理,处理后的衬砌管片和填充混凝土结合面处具有足够的光滑度,无法传递剪力. 2)考虑到地基沉降引起隧道弯曲的曲率半径一般较大,隧道弯曲变形过程符合平截面假定[6]. 3)纵向螺栓采用沿隧道衬砌圆环连续均匀分布的弹簧模拟,受压时为完全刚性,受拉时为双线性材料[6]. 4)填充混凝土的抗压能力较强,但一般不铺设钢筋,其抗拉能力相对较弱. 为了方便推导方程和简化模型的使用,本研究重点考虑关键受力部位,假定受拉区的填充混凝土不参与受力.
图 3
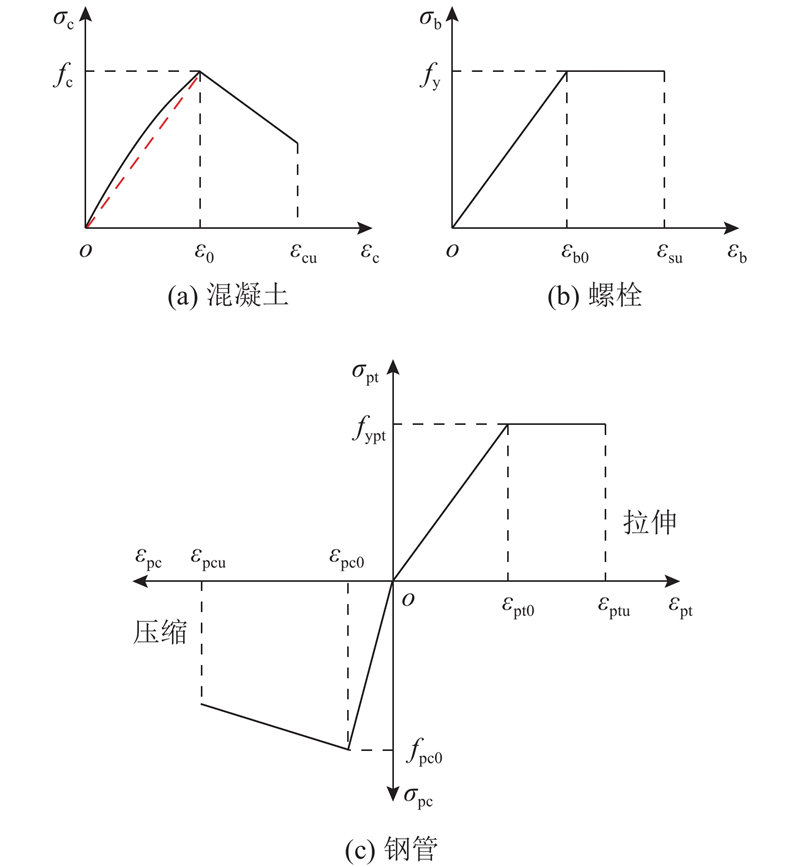
图 3 混凝土、螺栓和钢管的应力-应变曲线
Fig.3 Stress-strain curves of concrete, bolt and steel tube
式中:σb、εb分别为螺栓的应力和应变,fy为螺栓的屈服应力,εb0为与fy对应的应变,εsu为螺栓的极限应变. 3)加劲环增强了钢管与周围填充混凝土的整体性. 当钢管纵向受压时,作用在钢管上的压应力通过加劲环传递并分配到填充混凝土上;在计算时,可通过调整填充混凝土的抗压强度以等效考虑钢管的抗压能力. 为了方便建立控制方程,本研究将钢管受压侧屈服强度视为填充混凝土的抗压强度. 钢管受压时的应力应变关系曲线与混凝土受压时的应力应变关系曲线在趋势上是一致的[16],因此钢管受压时的应力应变关系曲线取为填充混凝土受压时的应力应变关系曲线. 钢管受拉时的应力应变关系曲线采用双线性理想弹塑性本构关系[16-17].
式中:fpc0为钢管的抗压强度,εpc0为与fpc0对应的应变,εpcu为钢管的受压极限应变.
1.2. 衬砌管片控制方程
基于假定1),复合结构受弯性能的分析计算可以分为2个部分:外部盾构隧道衬砌管片、内部填充混凝土-钢管,进行独立计算. 对于外部盾构隧道衬砌管片,考虑到由纵向等效连续化模型[4]计算得到的隧道纵向等效抗弯刚度值和试验及实测的差距较大,徐凌等[5-6]通过假定环缝长度影响系数
图 4
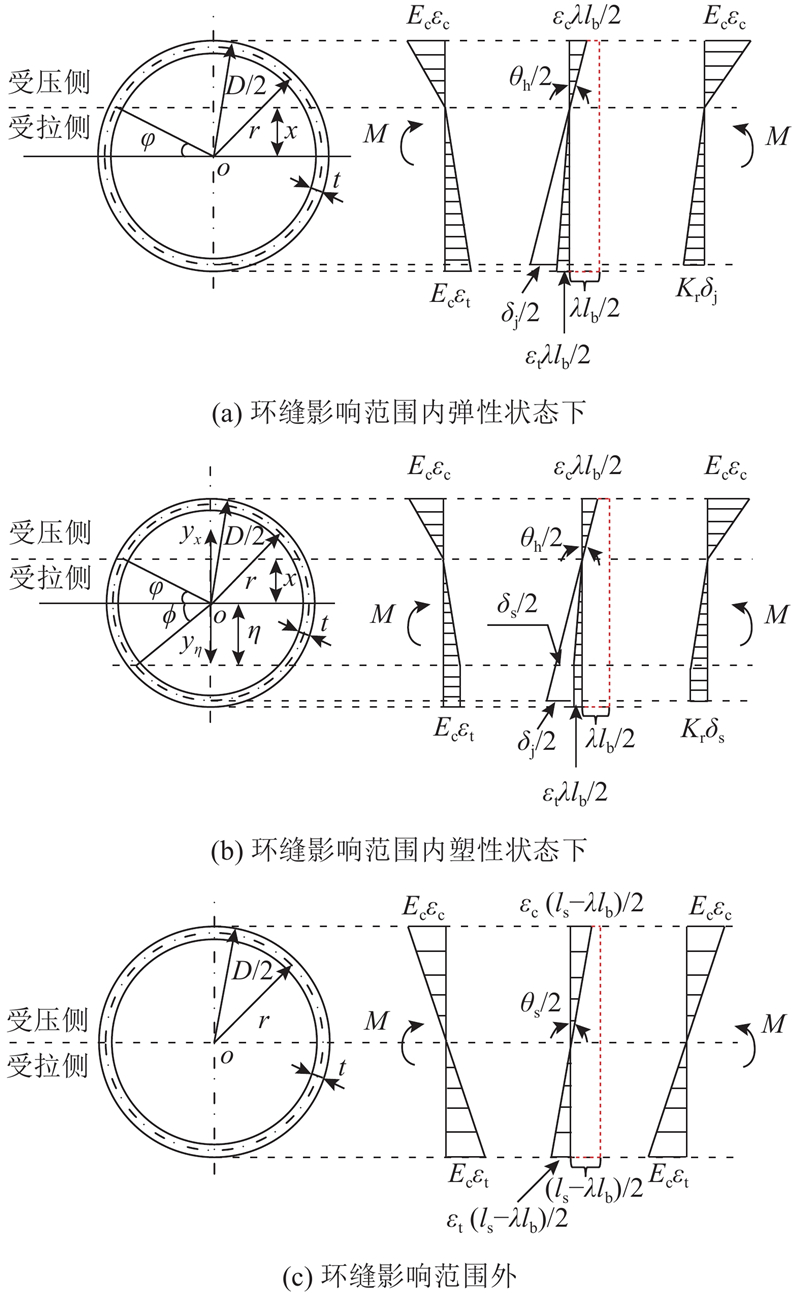
图 4 盾构隧道衬砌管片的应力和变形
Fig.4 Stress and deformation of shield tunnel lining segments
1.2.1. 环缝影响范围内
式中:
式中:Kr为螺栓平均线刚度,
2)螺栓进入塑性应力状态后,假设管段受拉侧最外缘的螺栓所受拉力大于螺栓的弹性极限拉力,螺栓进入塑性状态. 此时管段所受弯矩M大于其弹性极限弯矩My,随着M继续增大,各个螺栓将依次进入屈服状态. 由如图4(b)所示的变形协调条件可以得到
式中:
根据力矩平衡条件可以得到
1.2.2. 环缝影响范围外
取
式中:
衬砌管片在弯矩作用下的等效抗弯刚度为
1.3. 填充混凝土-钢管控制方程
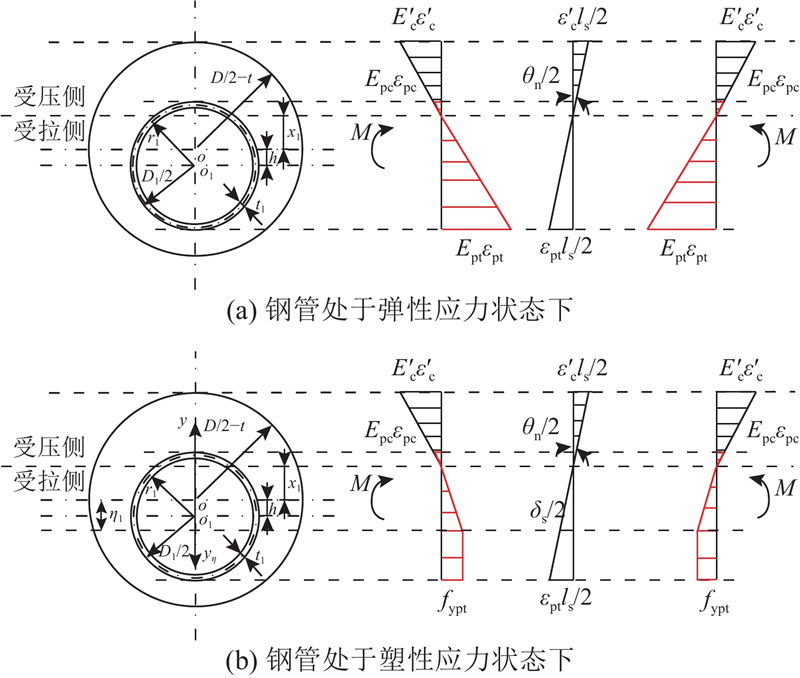
图 5
图 5 中性轴位于截面钢管外径内填充混凝土-钢管的应力和变形
Fig.5 Stress and deformation of filled concrete-steel tube when neutral axis is within outer diameter of steel tube
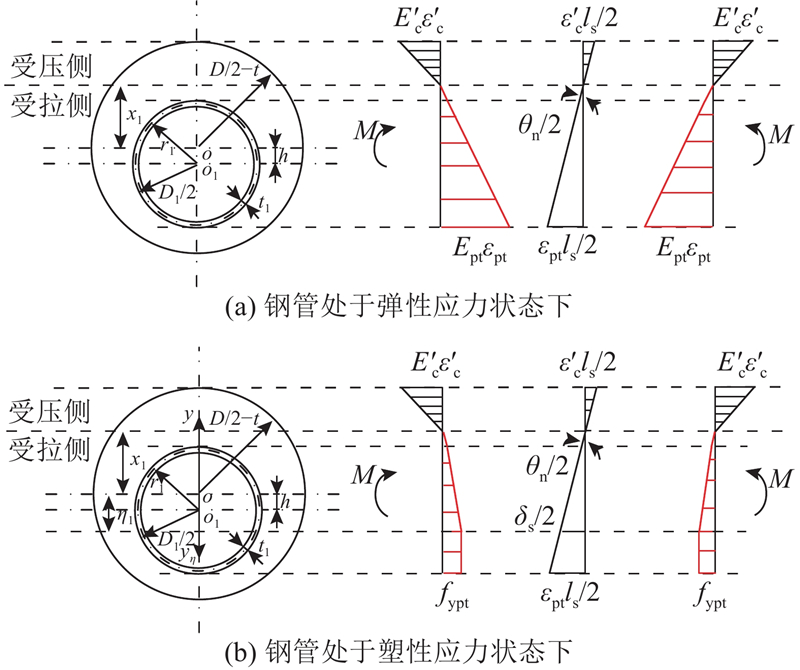
图 6
图 6 中性轴位于截面钢管外径外填充混凝土-钢管的应力和变形
Fig.6 Stress and deformation of filled concrete-steel tube when neutral axis is beyond outer diameter of steel tube
1.3.1. 中性轴位于截面钢管内径内
1)当钢管处于弹性应力状态时,假设受拉侧钢管最外缘所受的拉力小于钢管的弹性极限拉力,则此时单元处于完全弹性状态. 由图5(a)的变形协调条件可以得到
式中:
式中:
2)当钢管处于塑性应力状态时,假设受拉侧钢管最外缘所受拉力大于钢管的弹性极限拉力,钢管开始进入塑性状态. 此时管段所受弯矩M大于其弹性极限弯矩My,随着M继续增大,钢管逐渐进入屈服状态. 由图5(b)的变形协调条件可以得到
式中:
根据力矩平衡条件可以得到
1.3.2. 中性轴位于截面钢管厚度范围内
此时的变形协调条件不变,仅力的平衡条件和力矩平衡条件与中性轴位于截面钢管内径内时有所区别. 1)当钢管处于弹性应力状态时,由图5(a)的力的平衡条件可以得到
根据力矩平衡条件可以得到
2)当钢管处于塑性应力状态时,由图5(b)的力的平衡条件可以得到
根据力矩平衡条件可以得到
1.3.3. 中性轴位于截面钢管外径外
此时变形协调条件不变,仅力的平衡条件和力矩平衡条件与其他2种情况时的有所区别. 将力的平衡方程和力矩平衡方程中第2个积分项的积分上限x1改为D1/2−h即可. 1)当钢管处于弹性应力状态时,由图6(a)的力的平衡条件可以得到
根据力矩平衡条件可以得到
2)当钢管处于塑性应力状态时,由图6(b)的力的平衡条件可以得到
根据力矩平衡条件可以得到
填充混凝土-钢管在弯矩作用下的等效抗弯刚度为
1.4. 模型的求解
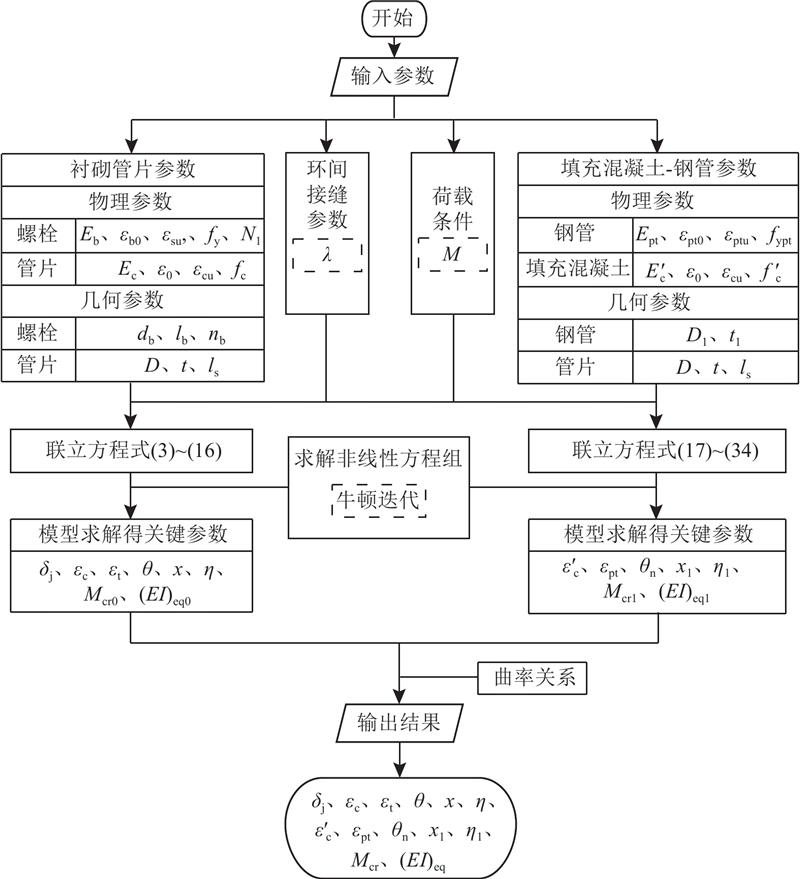
考虑到推导复合结构纵向等效抗弯刚度表达式比较复杂,本研究使用程序语言编写解析模型,并利用牛顿迭代计算复合结构的纵向等效抗弯刚度的具体数值. 如图7所示为解析模型计算流程. 1)联立衬砌管片的控制方程,当给出衬砌管片相关参数和弯矩时,就可以确定以下8个变量:环缝张开量δj、最大混凝土压应变εc、最大混凝土拉应变εt、纵向等效连续化模型在相同弯矩下的转角θ、中性轴到隧道横截面圆心所在水平线的距离x、螺栓弹性塑性应力状态临界位置到隧道横截面圆心所在水平线的距离η、衬砌管片的界限弯矩Mcr0及衬砌管片纵向等效抗弯刚度(EI)eq0. 2)联立填充混凝土-钢管的控制方程,当给出填充混凝土-钢管相关参数和弯矩时,就可以确定以下7个变量:填充混凝土的最大压应变
图 7
1.5. 模型的验证
鉴于尚无实验或现场测试结果可用于验证输水隧道复合结构解析模型,本研究在模型验证阶段对解析模型进行退化验证. 选取上海地铁一号线衬砌管片的纵向变形受力研究成果,对复合结构衬砌管片控制方程进行计算验证. 具体计算参数的取值如表1所示.
表 1 上海地铁一号线纵向接头主要参数[18]
Tab.1
| 结构 | 参数 | 数值 |
| 管片 | 隧道外径 D/m | 6.2 |
| 衬砌厚度 t/mm | 350 | |
| 环宽 ls/m | 1.0 | |
| 混凝土弹性模量 Ec/kPa | 3.45×107 | |
| 混凝土屈服应变 | 0.002 | |
| 螺栓 | 数量 nb | 17 |
| 直径 db/mm | 30 | |
| 长度 lb/mm | 400 | |
| 弹性模量 Eb/kPa | 2.06×108 | |
| 屈服应力 fy/kPa | 6.40×105 | |
| 极限应力 fu/kPa | 8.00×105 | |
| 预应力 N1/kPa | 7.00×104 |
鲁志鹏[19]考虑环缝影响长度,修正了等效纵向刚度模型[4],提出隧道结构的5类界限状态:1)纵向曲率半径ρ<15 000 m(管片应力、螺栓拉力和环缝张开量均处于较低的水平,隧道处在安全运行的工作状态)[6,19];2)管片最外侧受拉螺栓达到屈服应力[19];3)环缝张开量达到管片抵抗0.5 MPa水压的环缝容许张开量2 mm时[19];4)环缝张开量达到保证环缝密封垫不漏水的极限张开量6 mm时[19];5)管片最外侧受拉螺栓达到其破坏应力[19]. 从实用出发对上海地铁一号线隧道界限状态时的隧道曲率半径、环缝张开量进行计算分析,计算结果如表2所示. 由本研究模型计算结果可知,上海地铁一号线隧道达到界限状态时的顺序与文献[19]的结果相同. 在5类界限状态下,将衬砌管片对应的曲率半径和环缝张开量的界限指标计算结果与文献[19]模型的计算结果相比,在螺栓处于弹性阶段时,相对误差
表 2 管环衬砌变形受力对比验证
Tab.2
| 本研究模型 | 文献[19]模型 | | |||||
| ρ/m | δj/mm | M/(103 kN·m) | ρ/m | δj/mm | M/(103 kN·m) | ||
| 15 000 | 0.32 | 8.78 | 15 000 | 0.32 | 8.38 | 0 | |
| 8 780 | 0.55 | 14.99 | 8 694 | 0.55 | 14.00 | 0.99 | |
| 2 703 | 2.00 | 19.19 | 2 951 | 2.00 | 19.39 | 8.40 | |
| 943 | 6.00 | 19.78 | 971 | 6.00 | 21.21 | 2.88 | |
| 578 | 9.90 | 19.88 | — | — | — | — | |
| 369 | 15.60 | 19.93 | 369 | 15.60 | 24.00 | 0 | |
2. 输水隧道复合结构纵向结构受弯性能
表 3 输水隧道纵向接头主要参数
Tab.3
| 结构 | 参数 | 数值 |
| 管片 | 隧道外径D/m | 6.2 |
| 衬砌厚度t/mm | 350 | |
| 环宽ls/m | 1.0 | |
| 混凝土弹性模量Ec/kPa | 3.45×107 | |
| 混凝土屈服应变 | 0.002 | |
| 螺栓 | 数量nb | 17 |
| 直径db/mm | 30 | |
| 长度lb/mm | 400 | |
| 弹性模量Eb/kPa | 2.06×108 | |
| 屈服应力fy/kPa | 6.40×105 | |
| 极限应力fu/kPa | 8.00×105 | |
| 预应力N1/kPa | 7.00×104 | |
| 填充混凝土 | 弹性模量Ec/kPa | 2.80×107 |
| 屈服应变 | 0.002 | |
| 钢管 | 外径D1/m | 3.6 |
| 厚度t1/mm | 22 | |
| 弹性模量Ept/kPa | 2.09×108 | |
| 屈服应力fypt/kPa | 3.25×105 |
5)受拉钢管达到屈服应力,此后内部填充混凝土-钢管结构纵向抗弯刚度将快速下降,此时输水盾构隧道复合结构的整体应力水平仍然不高,钢管拉伸变形量低于设计值,复合结构仍能正常工作.
7)填充混凝土达到受压时的屈服应变,此后受压区填充混凝土的压应力将超过其抗压强度,混凝土可能被破坏.
2.1. 外部管环衬砌纵向结构受弯性能
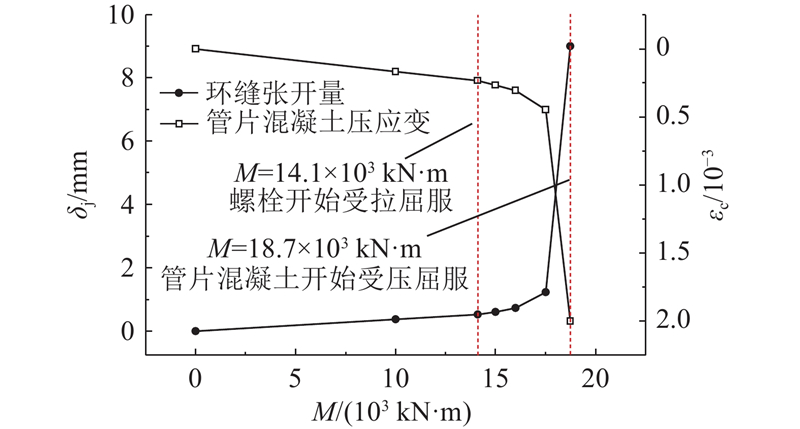
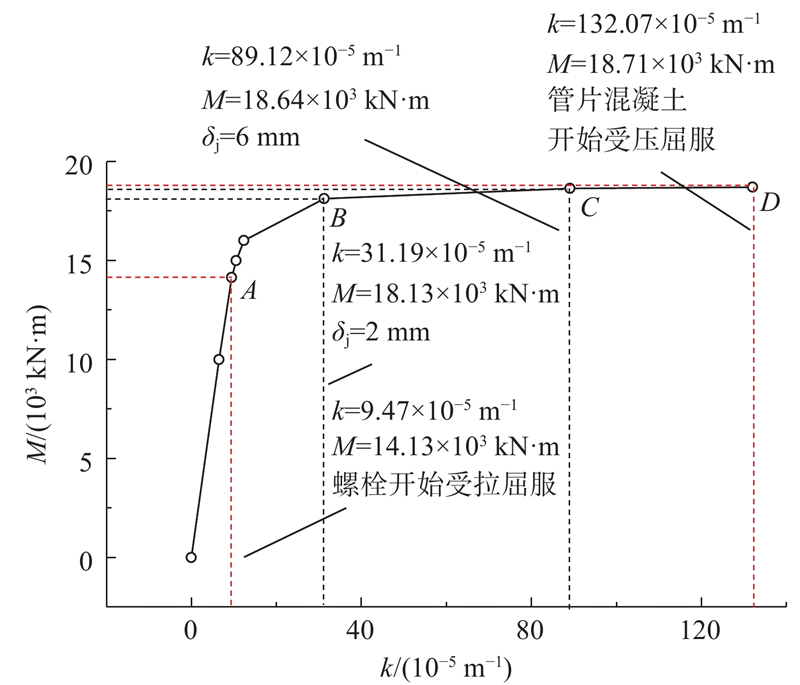
如图8所示,随着弯矩的增加,环缝张开量、最大管片混凝土压应变可以分为2个阶段. 1)弯矩相对较小,由于环缝的抗弯刚度保持不变,环缝张开量和最大管片混凝土压应变均线性增加,直到弯矩达到螺栓的屈服点. 由于螺栓和管片混凝土的应变都在弹性范围内,屈服点定义为螺栓开始受拉屈服,对应M=1.41×104 kN·m. 2)当弯矩增加到受拉螺栓的屈服点,随着纵向弯矩的增加,环缝张开量、最大管片混凝土压应变迅速增加,管片混凝土仍处于弹性状态. 当M=1.87×104 kN·m时,受压侧边缘的混凝土开始屈服,之后,环缝将随着弯矩的增加而损坏. 因此,混凝土受压屈服可以作为纯弯曲条件下环缝极限承载状态的标志. 管环衬砌抗弯刚度的非线性通过弯矩与曲率的关系来表现. 如图9所示,点A、B、C、D的横纵坐标分别对应隧道处于界限状态3)、1)、2)和6)时的曲率和弯矩.
图 8
图 8 环缝张开量和最大管片混凝土压应变
Fig.8 Opening of circumferential joints and maximum segment concrete compressive strain
图 9
图 9 管环衬砌弯矩与曲率的关系
Fig.9 Relationship of bending moment and curvature of pipe ring lining
2.2. 填充混凝土-钢管的纵向结构受弯性能
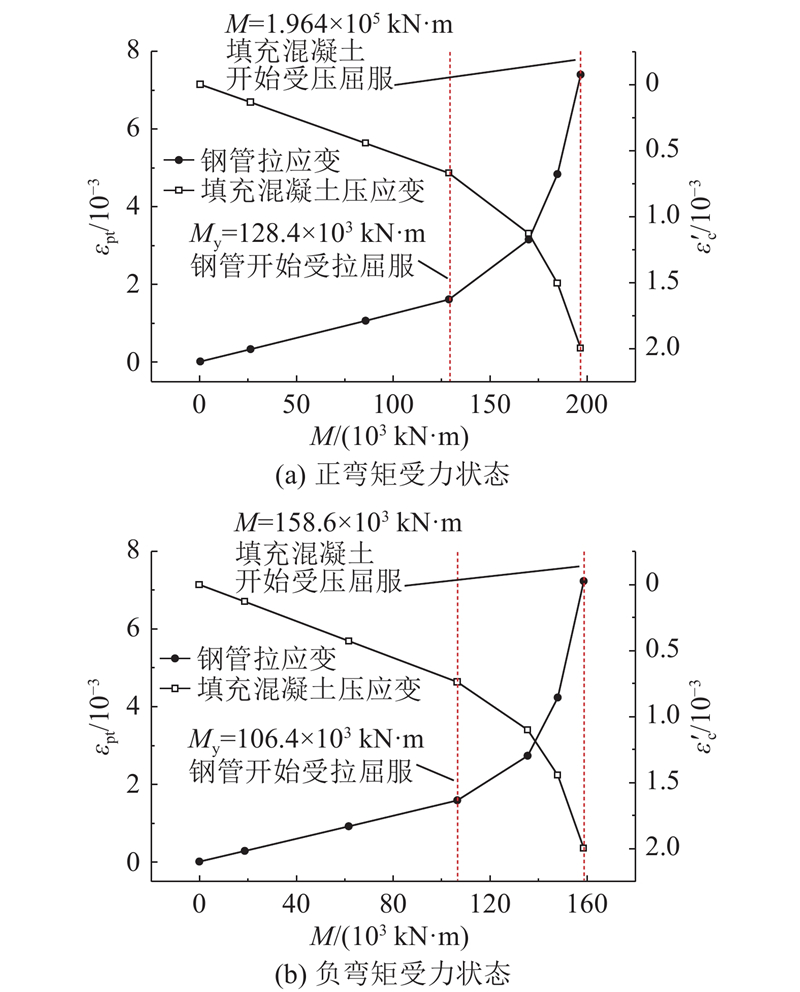
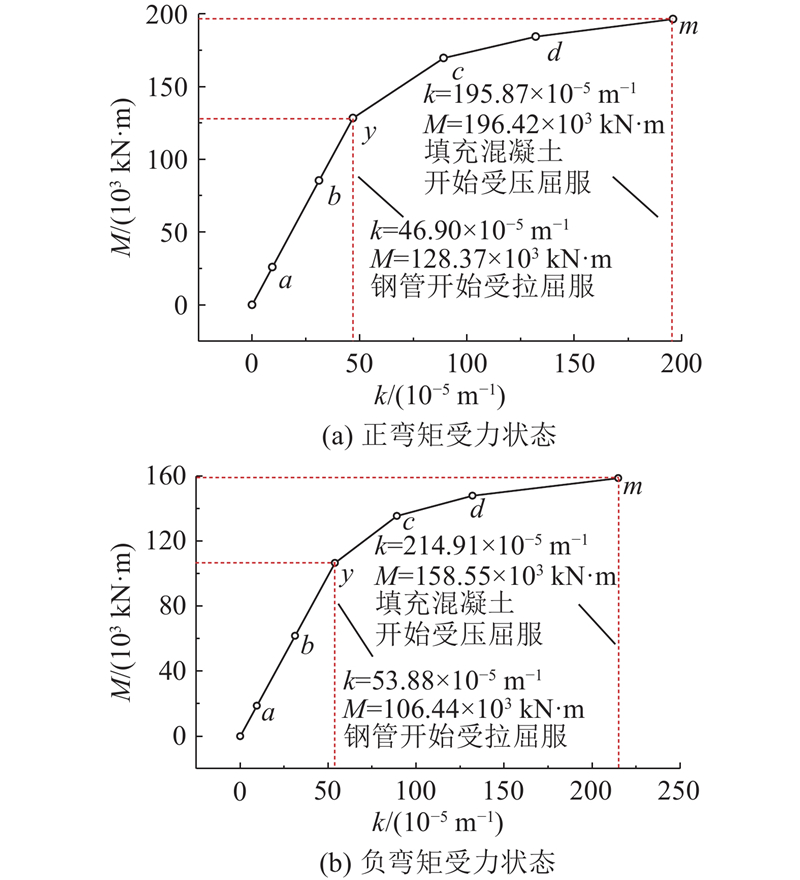
如图10所示,与外部管环衬砌类似,随着弯矩的增加,内部填充混凝土-钢管在正弯矩受力状态和负弯矩受力状态时均表现出类似的性状,即最大钢管拉应变、最大填充混凝土压应变可以分为2个阶段. 1)在纵向弯矩M<My的情况下,随着弯矩的增加,最大钢管拉应变、最大填充混凝土压应变成线性增加. 2)当弯矩超过My后,受拉钢管从最外侧开始陆续进入塑性状态,最大填充混凝土压应变、最大钢管拉应变随弯矩的增加迅速增大,当弯矩增大到填充混凝土开始受压屈服时,可视为纯弯曲条件下的极限承载状态. 填充混凝土-钢管抗弯刚度的非线性通过弯矩与曲率的关系来表现. 如图11所示,点a、b、y、c、d、m的横纵坐标分别对应隧道处于界限状态3)、1)、5)、2)、6)和7)时的曲率和弯矩.
图 10
图 10 最大钢管拉应变和最大填充混凝土压应变
Fig.10 Maximum steel tube tensile strain and maximum filled concrete compressive strain
图 11
图 11 填充混凝土-钢管弯矩与曲率的关系
Fig.11 Relationship of bending moment and curvature of filled concrete-steel tube
2.3. 复合结构纵向结构界限值确定
基于假定1),复合结构受弯性能分析计算可以分为2个部分:衬砌管片和填充混凝土-钢管进行独立计算,再根据曲率关系进行叠加. 如表4所示,当复合结构处于正弯矩或负弯矩受力状态下,隧道结构达到临界状态的顺序均为螺栓达到屈服应力、环缝张开2 mm(螺栓和管片混凝土被侵蚀)、钢管达到屈服应力、环缝张开6 mm(钢管和填充混凝土被侵蚀)、管片混凝土开始受压屈服、填充混凝土开始受压屈服、螺栓达到破坏应力. 与不考虑填充混凝土-钢管的存在相比,当隧道处于正弯矩受力状态时,螺栓开始屈服的弯矩从1.41×104 kN·m提高到4.01×104 kN·m,提高了1.84倍;管片混凝土开始受压屈服的弯矩从1.87×104 kN·m提高到2.03×105 kN·m,提高了9.86倍. 当隧道处于负弯矩受力状态时,螺栓开始屈服的弯矩从1.41×104 kN·m提高到3.28×104 kN·m,提高了1.33倍;管片混凝土开始受压屈服的弯矩从1.87×104 kN·m提高到1.67×105 kN·m,提高了7.93倍.
表 4 不同弯矩受力状态下复合结构临界状态对应的界限指标值
Tab.4
| 临界状态 | 正弯矩受力状态 | 负弯矩受力状态 | |||||
| ρ/m | δj/mm | M/(103 kN·m) | ρ/m | δj/mm | M/(103 kN·m) | ||
| 3) | 10 558 | 0.54 | 40.05 | 10 558 | 0.54 | 32.84 | |
| 1) | 3 206 | 2.00 | 103.49 | 3 206 | 2.00 | 79.75 | |
| 5) | 2 132 | 3.12 | 146.79 | 1 856 | 3.55 | 124.92 | |
| 2) | 1 122 | 6.00 | 188.24 | 1 122 | 6.00 | 153.99 | |
| 6) | 757 | 9.00 | 203.02 | 757 | 9.00 | 166.51 | |
| 7) | 510 | — | — | 465 | — | — | |
| 4) | 278 | 15.20 | — | 278 | 15.20 | — | |
3. 输水隧道复合结构的结构设计优化
与盾构隧道衬砌管片相比,填充混凝土-钢管对输水隧道复合结构抗弯刚度的贡献较大,本研究仅对填充混凝土-钢管进行结构设计优化分析.
3.1. 钢管偏心位置分析
为了探究钢管偏心位置h的影响,设定
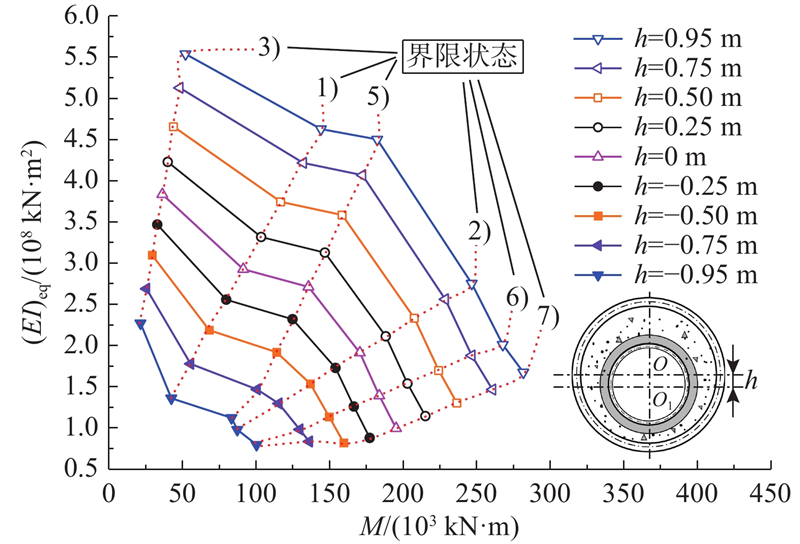
图 12
在实际工程中,输水隧道复合结构承受正弯矩或负弯矩时,当钢管与衬砌管片同心时为最有利工况,原因是此时钢管能够得到良好保护. 当钢管紧贴衬砌管壁时,则为最不利工况. 以隧道处于正弯矩受力状态为例,如图12所示,本研究的最不利工况定义如下. 最不利工况1):当钢管偏心位置 h=0.95 m时,虽然隧道纵向抗弯性能优于最有利工况,但钢管紧贴衬砌管壁下边缘,当衬砌管片环缝张开量达到保证环缝密封垫不漏水的极限张开量6 mm时,钢管将失去衬砌管片的保护,极易出现腐蚀现象. 最不利工况2):在钢管偏心位置 h=−0.95 m时,虽然钢管紧贴衬砌管壁上边缘,衬砌管片对钢管具有良好的保护作用,但此时隧道的纵向抗弯性能较差,填充混凝土和管片混凝土几乎同时达到受压屈服应变,导致隧道脆性破坏.
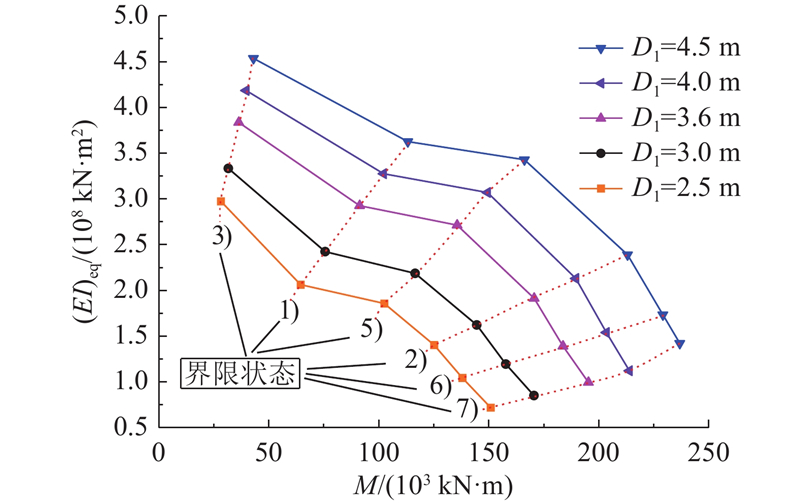
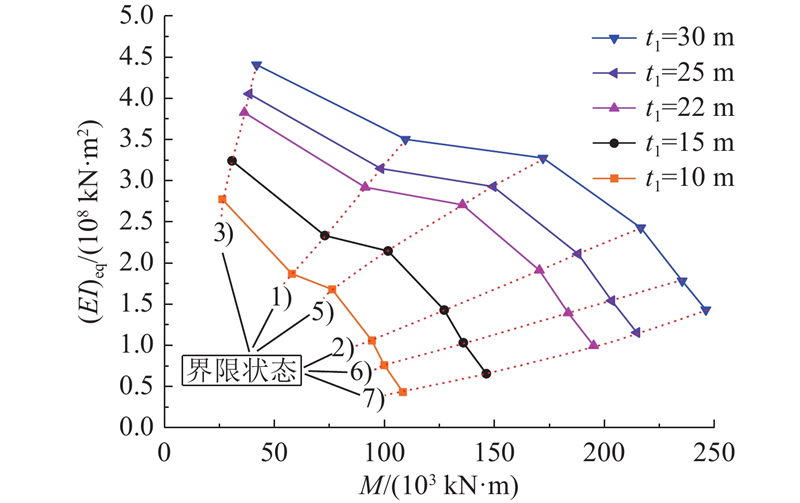
3.2. 钢管外径和厚度分析
以杭州市第二水源输水通道工程实际参数设计值为参考基础,以h=0 m为例,分析不同钢管外径D1和钢管厚度t1对隧道纵向等效抗弯刚度的影响. 如图13、14所示,随钢管外径D1及钢管厚度t1的增大,隧道的等效抗弯刚度和隧道达到临界状态3)、1)、5)、2)、6)和7)时的弯矩均逐渐增大. 具体而言,当D1从2.5 m增大到4.5 m,隧道弹性阶段的等效抗弯刚度增大了0.52倍,螺栓开始受拉屈服的弯矩增大了0.54倍,环缝张开2 mm的弯矩增大了0.77倍,钢管开始受拉屈服的弯矩增大了0.63倍,环缝张开6 mm的弯矩增大了0.70倍,管片混凝土开始受压屈服的弯矩增大了0.66倍,填充混凝土开始受压屈服的弯矩增大了0.58倍. 当t1从10 mm增大到30 mm,隧道弹性阶段的等效抗弯刚度增大了0.58倍,螺栓开始受拉屈服的弯矩增大了0.62倍,环缝张开2 mm的弯矩增大了0.90倍,钢管开始受拉屈服的弯矩增大了1.26倍,环缝张开6 mm的弯矩增大了1.31倍,管片混凝土开始受压屈服的弯矩增大了1.36倍,填充混凝土开始受压屈服的弯矩增大了1.28倍.
图 13
图 14
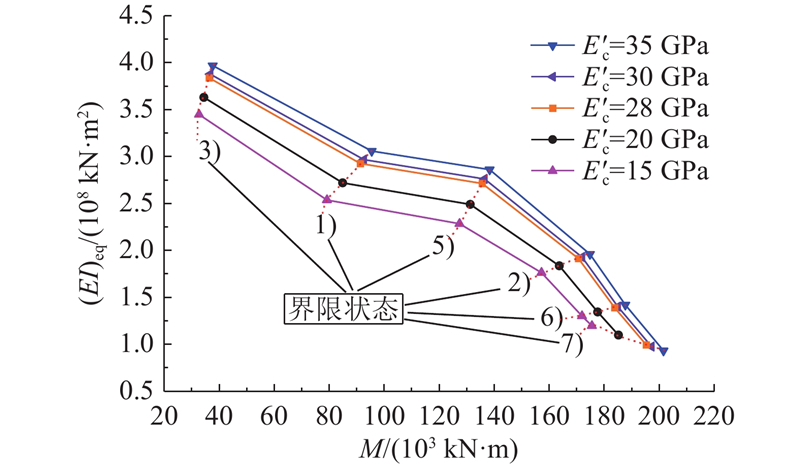
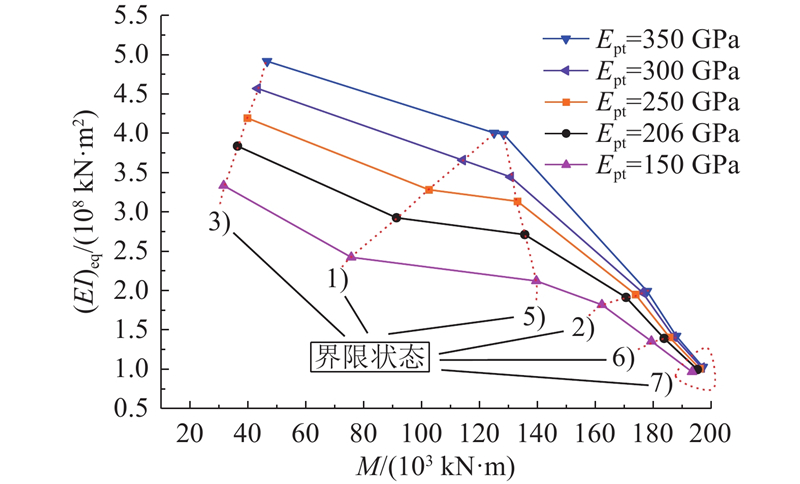
3.3. 填充混凝土和钢管弹性模量分析
以杭州市第二水源输水通道工程实际参数设计值为参考基础,以h=0 m为例,分析不同填充混凝土和钢管弹性模量对隧道纵向等效抗弯刚度的影响. 如图15、16所示,填充混凝土弹性模量对隧道纵向等效抗弯刚度及隧道达到临界状态3)、1)、5)、2)、6)和7)时的弯矩的影响较小;随着钢管弹性模量
图 15
图 15 填充混凝土弹性模量影响曲线
Fig.15 Influence curve of elastic modulus of filled concrete
图 16
4. 结 论
(1)考虑混凝土、螺栓和钢管的弹塑性变形特性,推导构建输水盾构隧道复合结构的受弯分析模型. 求解所建模型,得到隧道纵向接缝张开量、最大混凝土压应变及最大钢管拉应变等关键变形参数.
(2)输水盾构隧道达到临界状态的先后顺序:螺栓达到屈服应力、环缝张开2 mm(螺栓和管片混凝土被侵蚀)、钢管达到屈服应力、环缝张开6 mm(钢管和填充混凝土被侵蚀)、管片混凝土开始受压屈服、填充混凝土开始受压屈服、螺栓达到破坏应力.
(3)根据以杭州某输水隧道工程实际参数设计值为参考基础的分析结果表明,考虑填充混凝土-钢管的存在,输水盾构隧道复合结构的承载能力显著提升. 当隧道处于正弯矩受力状态时,螺栓开始屈服的弯矩提高了1.84倍,管片混凝土开始受压屈服的弯矩提高了9.86倍;当隧道处于负弯矩受力状态时,螺栓开始屈服的弯矩提高了1.33倍,管片混凝土开始受压屈服的弯矩提高了7.93倍.
(5)在输水盾构隧道复合结构的设计阶段,可以参考结构设计参数分析的结果对结构进行安全、经济的设计. 在输水盾构隧道复合结构的运营期,可以根据实测地基沉降结果对隧道的服役性能进行合理评估.
(6)本研究尚存在局限性:1)当输水盾构隧道复合结构衬砌管片和填充混凝土结合面处黏结较弱时可以采用本研究模型进行计算分析,当结合面处黏结较强时须更复杂的模型. 2)当地基沉降引起隧道弯曲的曲率半径较小时,隧道弯曲变形过程中不再符合平截面假定,隧道的变形可能会变得非线性,包括材料非线性、几何非线性、接触非线性等. 3)考虑到加劲环的作用不可忽略,本研究简化了钢管的应力应变关系曲线,但实际钢管的应力应变关系曲线须根据具体问题结合拉伸模型试验或者拉伸原型试验确定. 4)本研究构建的输水盾构隧道复合结构解析模型及其分析方法对类似工程具有较好的指导作用,且具有一定的通用性. 本研究基于特定工程案例分析得出的结论,并不一定具备普适性.
参考文献
Long−term settlement behaviour of metro tunnels in the soft deposits of shanghai
[J].
Observed long−term differential settlement of metro structures built on soft deposits in the Yangtze River Delta region of China
[J].DOI:10.1139/cgj-2018-0524 [本文引用: 1]
基于修正纵向等效连续化模型的隧道变形受力研究
[J].
Deformation and stress of tunnel structures based on modified longitudinal equivalent continuous model
[J].
Experimental and analytical study on longitudinal bending behavior of shield tunnel subjected to longitudinal axial forces
[J].DOI:10.1016/j.tust.2019.01.011 [本文引用: 1]
General solutions for the longitudinal deformation of shield tunnels with multiple discontinuities in strata
[J].DOI:10.1016/j.tust.2020.103652 [本文引用: 1]
An enhanced analytical model for predicting the nonlinear longitudinal equivalent bending stiffness of shield tunnels incorporating combined N−M actions
[J].DOI:10.1016/j.tust.2022.104567 [本文引用: 1]
类矩形盾构隧道纵向等效抗弯刚度解析解
[J].
Analytical solution of longitudinal equivalent flexural stiffness of quasi rectangular shield tunnel
[J].
Inelastic behavior in tests of eccentrically loaded short reinforced concrete columns
[J].
Behaviour of FRP−jacketed circular steel tubes and cylindrical shells under axial compression
[J].DOI:10.1016/j.conbuildmat.2006.06.016 [本文引用: 2]
钢管混凝土轴心受拉本构关系
[J].DOI:10.13204/j.gyjz1990.04.007 [本文引用: 1]
The axis tensile constitutive relationship of concrete filled steel tubes
[J].DOI:10.13204/j.gyjz1990.04.007 [本文引用: 1]
软土地铁隧道纵向不均匀沉降导致的管片接头环缝开裂研究
[J].
Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in soft soil
[J].
盾构隧道双层衬砌结构纵向等效弯曲刚度研究——以上海吴淞口长江隧道工程为例
[J].
Study of longitudinal equivalent bending stiffness of double−layered lining of shield tunnel: a case study of Wusongkou Yangtze River-crossing tunnel in Shanghai
[J].