学者们多采用室内试验和理论分析对裂隙岩体中的流固换热问题进行研究. 在渗流换热室内试验方面,近年来国内外学者多制备粗糙裂隙岩样,探索应力状态、岩体温度、裂隙开度等变量与裂隙岩样渗流换热特性的关系[6-8]. 赵坚[9]在进行花岗岩裂隙的水热特性试验时发现裂隙几何与表面粗糙度在岩石裂隙热传导中起着重要作用. Bai等[10]开展不同围压、温度、体积流量等条件下的换热试验,结果表明温度、流速、围压以及裂隙水力开度都会对换热效果造成影响. 李正伟等[11]制备光滑平直裂隙与粗糙裂隙岩样开展花岗岩试样换热特性试验,研究结果表明水-岩之间的换热强度与体积流量、岩石温度正相关,且粗糙裂隙对流强度较光滑平直裂隙的有所提高. 黄奕斌等[12]利用裂隙粗糙度(joint roughness coefficient,JRC)模板和3D打印技术,设置具有特定粗糙度的裂隙试样进行换热实验,发现裂隙面粗糙度会影响水-岩换热特性,在同等条件下顺水流方向粗糙度的增大会强化换热.
在渗流换热理论分析方面,学者们通过数值模拟进行渗流换热实验,探讨注入温度、体积流量、热物理参数等因素对于岩石换热特性的影响[13-14],研究成果与换热试验所得结论互为佐证. 换热系数作为表征岩石裂隙流体渗流换热特性的重要参数也是学者们研究的重点. 牛顿提出牛顿冷却定律,Chapman基于热边界层理论发展推导了换热系数的简单计算公式[15]. 后人多利用局部热非平衡法、二维导热方程对于边界条件进行不同程度的简化,采用裂隙内水温线性分布假设或者平行板内温度分布解析模型,推导出裂隙换热系数不同形式的解析解,这也导致了不同的公式存在一定的适用条件,当超出一定条件时理论值与真实情况会存在较大偏差[16-20]. Bai等[16]以进出口水温均值近似代替进出口裂隙面温度均值,提出简单的换热系数计算公式. 朱家玲等[17]采用局部热非平衡法和二维导热方程,推导出圆柱形试样裂隙换热系数的解,并对影响换热系数的因素进行敏感性分析,发现在同等条件下流速的影响大于裂隙开度的. Zhang等[18]利用二维热传导方程提出计算圆柱形试样裂隙换热系数的公式. Jiang[19]总结前人提出的几种计算换热系数公式,全面分析不同公式的适用性,对于公式中出现的数据异常,根据误差传播理论进行了解释. Zhao[20]基于光滑平行板内温度分布解析模型,分别利用局部热平衡和热非平衡对边界条件进行简化,推导换热系数的2种解析解,可进行三维长方体模型的换热系数计算. 就渗流换热机理方面,研究表明,低温流体与其所接触的高温岩体裂隙壁面之间存在着渗流换热耦合作用. 一方面,流体的渗流形态会影响其热对流和热传导;另一方面,流固换热会导致流体热物理性质发生改变,如运动黏度、比热容,进而影响渗流形态[21-22].
本研究研发可以解决上述问题的岩石裂隙水-岩渗流换热试验系统,制备裂隙花岗岩试样,开展粗糙裂隙花岗岩在不同温度和体积流量下的水-岩换热试验,对出口流体温度与裂隙试样温度及体积流量的关系、渗流规律进行分析,并开展花岗岩水-岩换热系数的影响因素研究及其敏感性分析. 本研究在裂隙试样温度为70~100 ℃时进行探索性试验,以期为深层地热资源开发提供一定参考.
1. 试验仪器与方法
1.1. 试验仪器
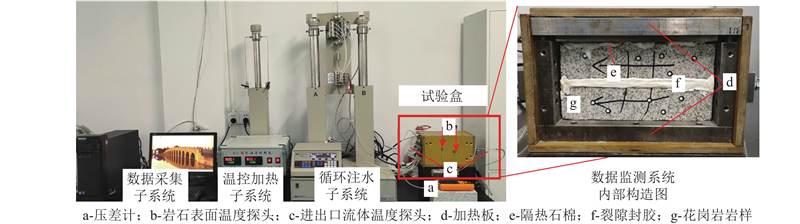
裂隙水-岩换热试验系统如图1所示,主要分为循环注水、温控加热、数据采集3个子系统.
图 1
图 1 裂隙水-岩换热试验系统实物图
Fig.1 Physical diagram of fracture water-rock heat transfer test system
循环注水子系统:Isco双泵系统,可以控制裂隙内通过流体的渗流体积流量. 协同工作可控体积流量为0~204 mL/min.
温控加热子系统:包括温控装置、上下表面2块加热板,通过温控装置控制施加特定温度对岩样进行加热,最高加热温度可达200 ℃;
数据采集子系统:主要由温度探头以及压差计组成. 在试样前后表面安装温度探头,可实时传回岩石表面温度,以便实现对于热边界条件的精准控制;在进出水口位置装有温度探头以及压差传感器,可以记录进出口流体温度以及压差.
该系统换热介质在进入岩样前后不会被加热,同时岩样表面布置多支温度传感器,皆提升了数据的准确性,同时采用长方体试样更有利于控制裂隙的位置、走向.
1.2. 试样制备
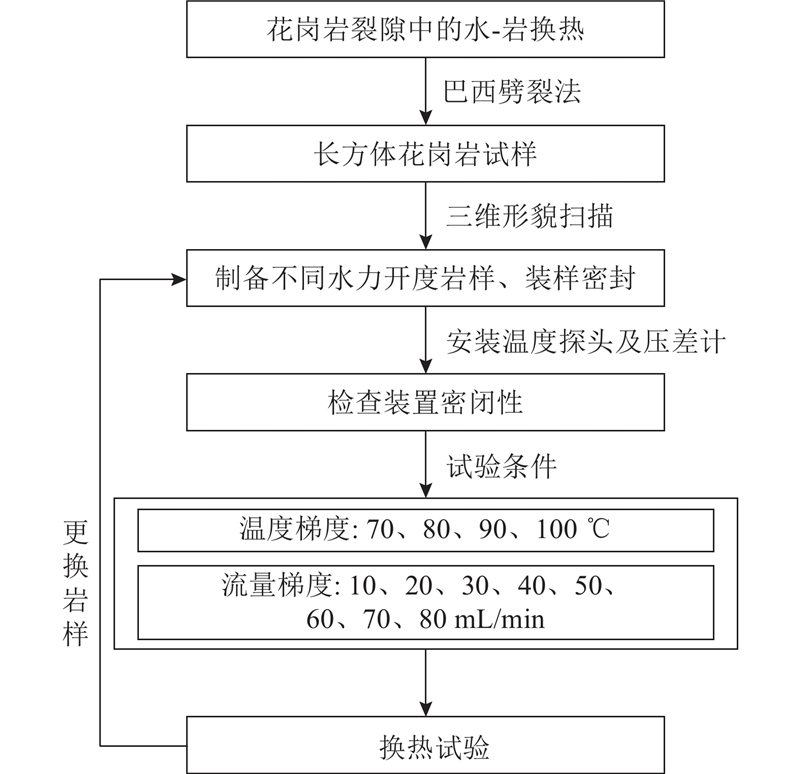
裂隙水-岩换热试验流程图如图2所示.
图 2
1)采用100 mm×100 mm×200 mm的长方体花岗岩试样,即裂隙面宽度为100 mm,长度为200 mm,利用岩石三轴伺服多场耦合试验系统,采用巴西劈裂法制备裂隙试样.
2)针对预先制备好的花岗岩裂隙试样,采用OKIO 3M三维形貌扫描系统对岩样裂隙面进行扫描,而后计算裂隙面坡度的一阶导数均方根Z2以及岩样的裂隙粗糙度JRC. 表达式如下:
式中:n为每一个剖面线上全部的采样点数量,zi为第i个采样点的粗糙高度,∆y为采样点之间的间隔.
裂隙试样H1~H4裂隙粗糙度分别为14.871、12.852、10.675、9.048.
1.3. 试验方法
1)处理好的岩样无错动贴合将导致无法过流,因此将其沿长边方向错动0.2~1.0 mm后固定以获取不同水力开度的裂隙岩样,采用耐高温的硅橡胶对花岗岩试样裂隙进行密封,并将其放置在试验盒中. 为了保证封水性以及隔热性,在进出口处布置密封垫和隔热板.
2)在裂隙试样进出水口、侧面布置共6支温度探头,实时记录岩样表面以及进出口温度,并通过温度控制箱与计算机相连接. 在进出口位置接入压差计,并通过压差计接入计算机,随时监测流体进出口压差数据.
3)将裂隙试样进水口与Isco泵相连,以体积流量为100 mL/min向裂隙内注入常温蒸馏水,如不存在明显渗漏现象,则说明裂隙密封良好.
4)通过温控装置调整加热板温度略高于70 ℃使岩样外壁加热温度升高,等到传感器温度维持在约70 ℃(30 min内变化不超过1 ℃),则认为裂隙试样温度已经达到恒温加热70 ℃的效果.
5)在恒温后启动Isco泵设置体积流量数值为10 mL/min,当流动和换热状态稳定之后,记录此时的进出口水温以及压差. 调整体积流量在10~80 mL/min逐步提高(8个体积流量等级),进行8次不同体积流量下的换热试验.
6)在各体积流量等级测量完成后,关闭Isco泵,调整岩样外壁加热温度至80、90 、100 ℃,重复上述步骤3)~5). 待一块岩样完成试验后,更换岩样重复所有,待所有岩样完成试验后整理仪器.
2. 基本裂隙渗流换热规律分析
2.1. 不同裂隙试样温度下出口水温与体积流量关系
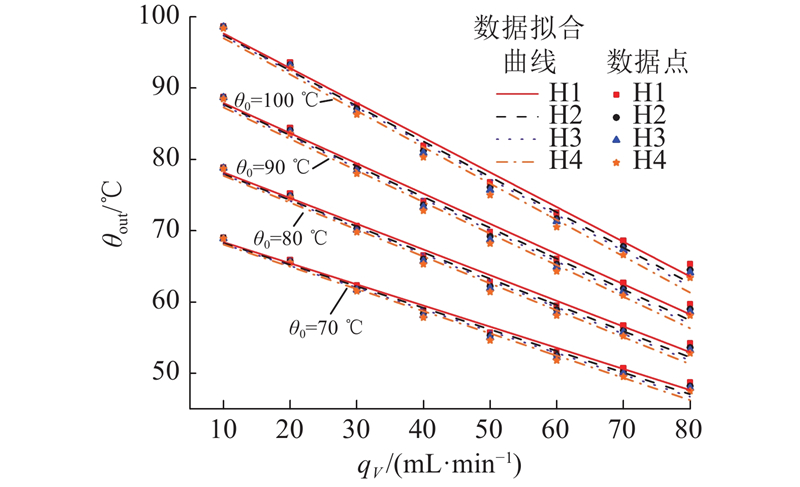
岩样在不同温度下的出口水流温度与体积流量之间的关系如图3所示. 图中, θ0为裂隙试样温度,qV为体积流量,Qout为裂隙出口水流温度. 以岩样H1为例,体积流量从10 mL/min增大至80 mL/min,当裂隙试样温度为70 ℃时,出口水流温度下降了29.4%,与裂隙试样温度为80 、90、100 ℃时相比,分别下降了31.3%、32.8%、33.8%. 在同一体积流量下,随着裂隙试样温度升高,出口流体温度也会越大. 不同温度下的出口水流温度与体积流量关系线性拟合如图3所示,可知拟合后R2皆为0.99,线性程度较高. 在相同的裂隙试样温度下,体积流量增大,出口水流温度随之减小. 这是因为体积流量越大,渗流水与岩石接触的时间越少,即热传递时间越少,出口水流温度越低. 在同一体积流量下随着裂隙试样温度的升高,换热量越高,相同时间内流体温度升高越明显.
图 3
图 3 裂隙出口水流温度随体积流量的变化
Fig.3 Variation of temperature of water flow at outlet of fissure with volume flow rate
其余岩样的出口水流温度与体积流量间关系基本与H1的表现一致,皆为拟合关系较好的线性关系. 不过不同岩样之间表现出一定差异性,随着试样裂隙粗糙度的降低,出口水流温度降低. 这是因为裂隙粗糙度降低,换热接触面积减少,换热量降低.
2.2. 裂隙渗流流态分析
式中:
图 4
图 4 裂隙压力梯度随体积流量的变化
Fig.4 Variation of fracture pressure gradient with volumet flow rate
3. 换热系数与影响因素分析
3.1. 换热系数计算
换热系数反映在流固接触单位温度差下,单位换热面积上在单位时间内所能传递的热量大小,是岩体裂隙换热评价的重要分析参数. Zhao[20]采用解析方法,根据局部热非平衡理论结合换热方程和相应边界条件,推导出岩体裂隙壁面温度的分布情况,然后基于岩体裂隙壁面温度进一步推出换热系数的表达式:
式中:R为裂隙面宽度的一半,R=50 mm;L为特征长度,通常取岩样流动方向的长度,取200 mm;
裂隙经典立方定律表达式 [29]如下:
式中:w为裂隙面宽度,为100 mm;μ为流体的动力黏滞系数.
3.2. 换热系数影响因素分析
3.2.1. 裂隙试样温度
在探究裂隙试样温度和渗流体积流量与换热系数之间关系的过程中,以试样H1为例得到不同的裂隙试样温度下换热系数h随渗流体积流量的变化,如表1所示.
表 1 不同裂隙试样温度下换热系数随体积流量的变化
Tab.1
| qV/ (mL·min−1) | h/(W·m−2·K−1) | |||
| θ0=70 ℃ | θ0=80 ℃ | θ0=90 ℃ | θ0=100 ℃ | |
| 10 | 140.90 | 176.37 | 213.94 | 256.79 |
| 20 | 334.97 | 370.93 | 455.73 | 515.61 |
| 30 | 472.10 | 555.96 | 633.69 | 705.97 |
| 40 | 599.58 | 708.38 | 702.37 | 911.37 |
| 50 | 723.75 | 780.62 | 875.88 | 1011.54 |
| 60 | 738.22 | 852.37 | 1031.18 | 1126.29 |
| 70 | 835.52 | 960.93 | 1072.72 | 1284.38 |
| 80 | 918.01 | 1178.87 | 1218.06 | 1313.51 |
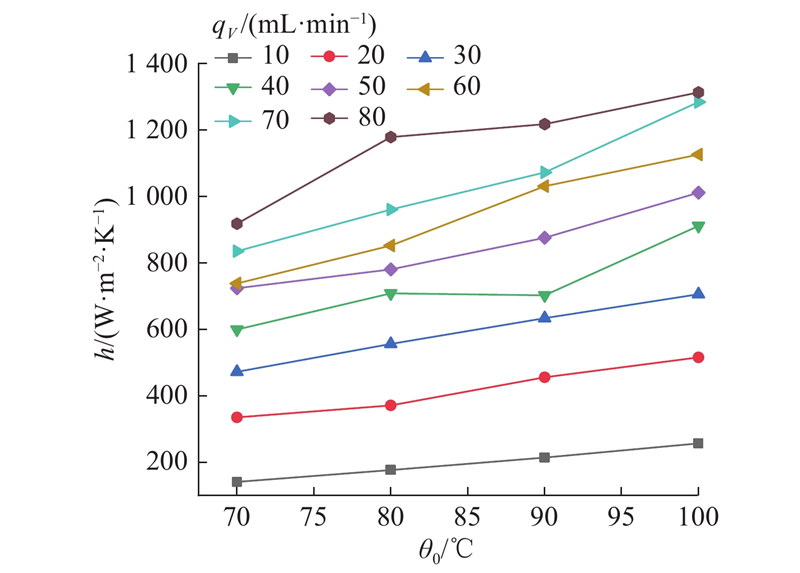
不同体积流量下换热系数随裂隙试样温度的变化如图5所示. 可以看出,当裂隙试样温度相同时,换热系数随着体积流量的增大而增大,70、80、90、100 ℃条件下体积流量从10 mL/min增大到80 mL/min,换热系数分别增加了551.5%、568.4%、469.3%和411.5%. 当渗流体积流量相同时,换热系数将随着温度升高而增加. 与70 ℃相比,80、90、100 ℃条件下体积流量为10 mL/min时增幅分别为25.2%、51.8%、82.2%. 根据热边界层理论,流体的运动黏滞系数减小以及流速的增大均会影响边界层厚度,使其减小,从而导致裂隙流体换热的阻力降低,换热强度提高,换热系数增大.
图 5
图 5 不同体积流量下换热系数随裂隙试样温度的变化
Fig.5 Variation of heat transfer coefficient with temperature of fissure specimen at different volume flow rates
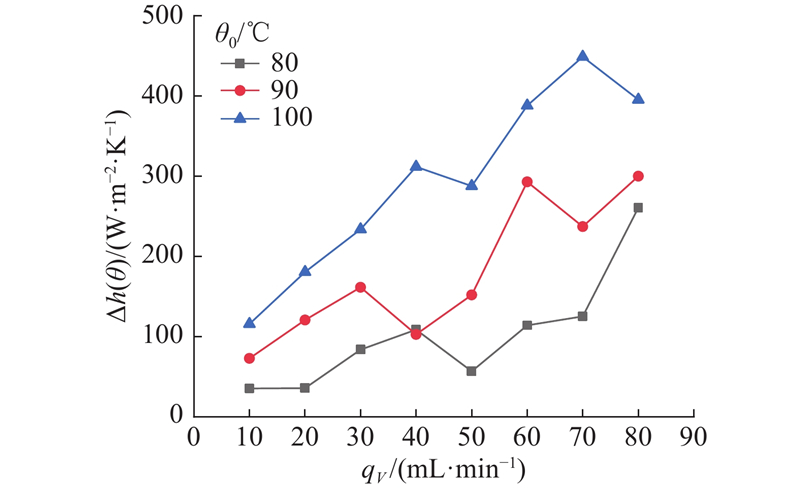
图 6
图 6 不同裂隙试样温度下换热系数差值随体积流量的变化
Fig.6 Variation of heat transfer coefficient difference with volume flow rate at different fracture specimen temperatures
试样H2~H4换热系数规律与试样H1的基本一致,因此不再讨论.
3.2.2. 渗流体积流量
归一化换热系数(h/h0)和归一化渗流流速(u/u0)间的关系可以表征换热系数与渗流流速之间的关系,研究表明其近似符合幂函数关系[17],表达式如下:
式中:
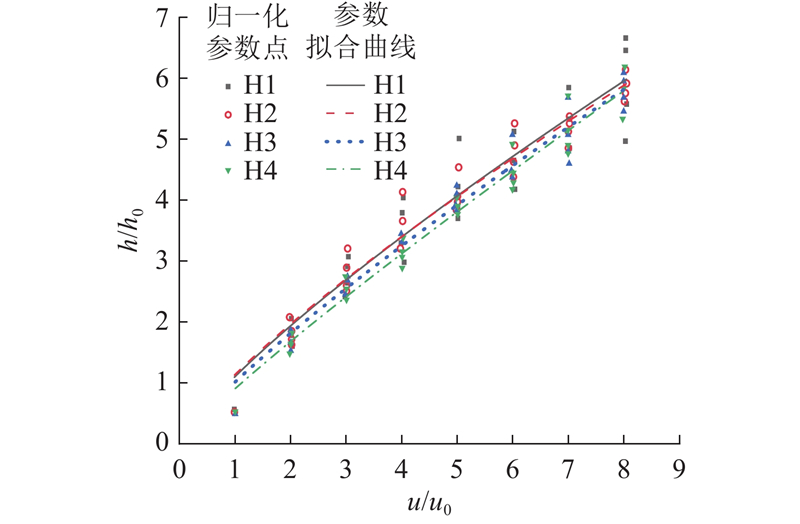
如图7所示为不同裂隙试样的归一化换热系数和归一化渗流流速之间的关系. 可以看出,拟合曲线较好地满足了如式(5)所示的幂函数关系,参数a的取值为0.90~1.14,参数b的取值为0.81~0.90,拟合曲线相关系数均大于0.90,拟合效果较好. 拟合曲线参数b的取值均小于1.0,说明换热系数与渗流流速之间并非简单的线性关系,而是随着流速的增大,换热系数一直增大,但增幅越来越小.
图 7
图 7 裂隙试样归一化换热系数和归一化流速的关系
Fig.7 Relationship between normalized heat transfer coefficient and normalized flow velocity for slit specimens
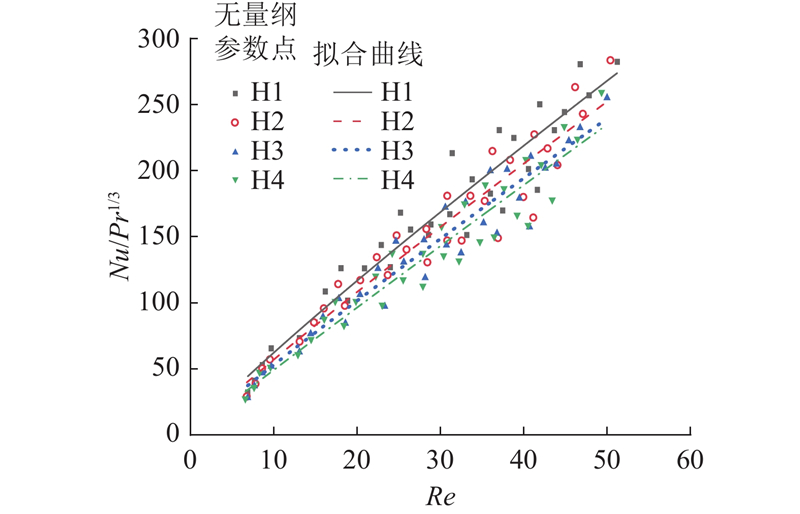
对换热问题中的重要无量纲特征数努塞尔数Nu、普朗特数Pr、雷诺数Re进行无量纲分析.
图 8
图 8 努塞尔数、普朗特数和雷诺数的无量纲分析
Fig.8 Nonscale analysis of Nusselt, Prandtl and Reynolds numbers
3.2.3. 水力开度
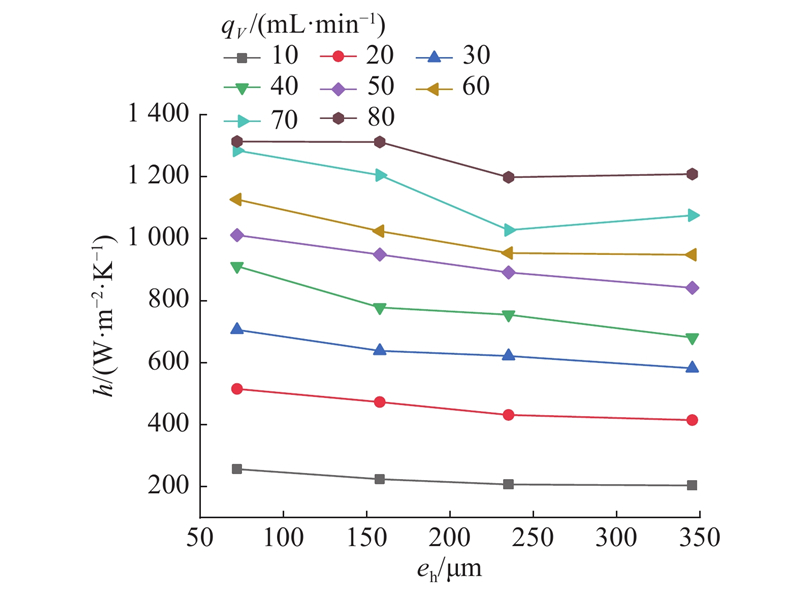
以裂隙试样温度为100 ℃时得到的数据为例,分析该裂隙试样温度下不同体积流量时对流换热系数随水力开度的变化规律,如图9所示. 可以看出,在相同裂隙试样温度和渗流体积流量下,随着裂隙水力开度的增大,总体上对流换热系数基本表现为线性减小,但是变化的幅度不大,水力开度由72.2 μm增至345.4 μm,减小幅度小于20%. 这是因为在相同渗流体积流量下,裂隙水力开度的增大导致裂隙过水断面面积增大,从而使渗流流速降低. 根据热边界层理论,流速降低使热边界层厚度增大,对流换热热阻增大,换热系数减小.
图 9
图 9 不同体积流量下换热系数随裂隙水力开度的变化
Fig.9 Variation of heat transfer coefficient with fracture hydraulic opening at different volume flow rates
3.2.4. 裂隙形貌
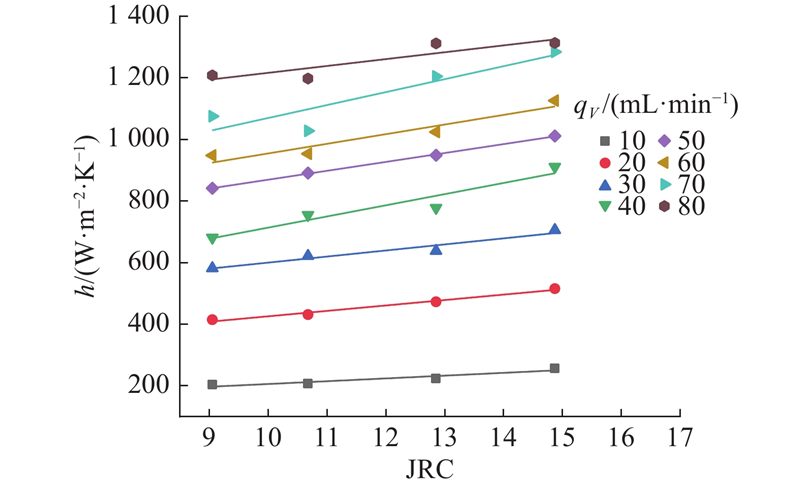
以裂隙试样温度为100 ℃时得到的数据为例,分析该裂隙试样温度下不同体积流量时对流换热系数随JRC的变化规律,如图10所示. 可以看出,随着裂隙粗糙度JRC的增大,换热系数基本表现为线性增大关系. 相关性系数R2皆大于0.80,拟合效果较好. 但是随着体积流量的增大,尤其是当体积流量大于60 mL/min后,线性拟合系数会低于0.90,换热系数与裂隙粗糙度JRC线性相关性降低,这是因为当体积流量大于一定数值时,换热介质的流态非线性程度较高,使得换热系数与岩石裂隙JRC数值之间不再是单纯的线性关系.
图 10
图 10 不同体积流量下换热系数随裂隙粗糙度的变化
Fig.10 Variation of heat transfer coefficient with fracture roughness at different volume flow rates
3.3. 换热系数敏感性分析
3.3.1. 基本原理
对换热系数进行敏感性分析的基本原理如下:对于一个系统的特性Z,其主要取决于n个影响因素
通过对不同因素下的特性进行拟合得到敏感性函数,而后将不同因素的基准状态代入到式(8)中即可得到不同因素的敏感性因子. 敏感性因子越大,表明该因素对特性的影响越显著.
3.3.2. 因素分析
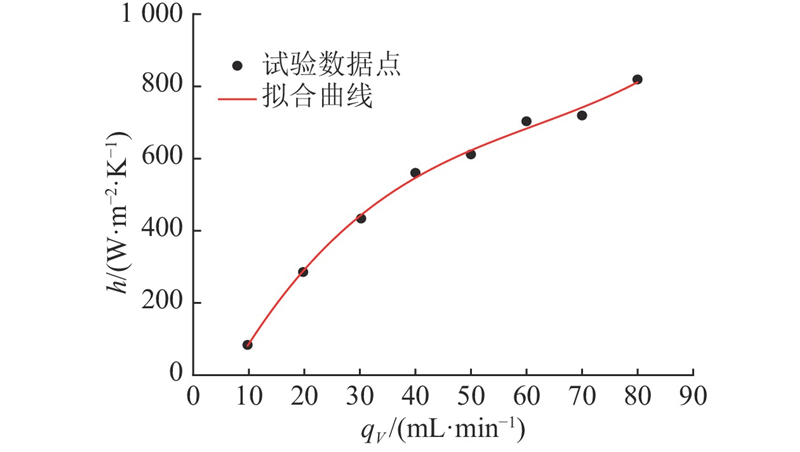
首先对渗流体积流量qV和裂隙水力开度
图 11
图 11 换热系数与体积流量的函数关系
Fig.11 Heat transfer coefficient as a function of volume flow rate
图 12
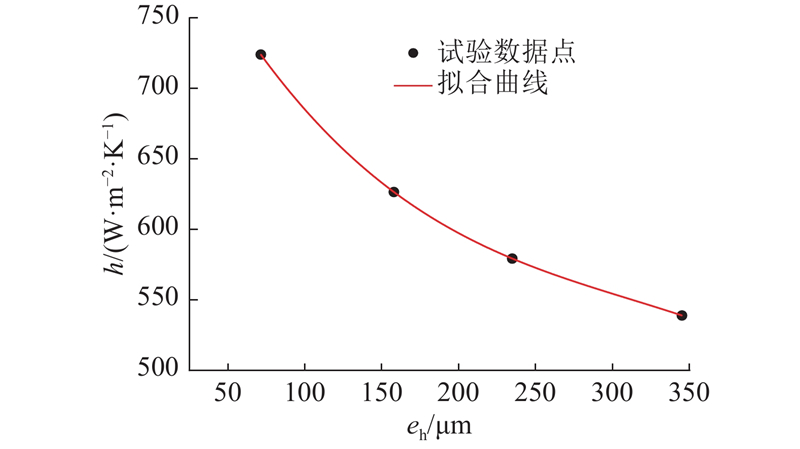
图 12 换热系数与裂隙水力开度的函数关系
Fig.12 Heat transfer coefficient as a function of hydraulic opening of fissure
拟合方程分别如下:
依据式(8)计算得到qV、eh分别对应的敏感性函数分别为
代入基准状态得到θ0=70 ℃条件下,S(
表 2 不同裂隙试样温度下换热系数关于体积流量和裂隙水力开度的敏感性因子
Tab.2
| θ0/℃ | S( | S( |
| 70 | 0.489 | 0.204 |
| 80 | 0.574 | 0.100 |
| 90 | 0.656 | 0.064 |
| 100 | 0.686 | 0.129 |
考虑温度的影响,继续对裂隙体积流量qV和裂隙试样温度θ0进行敏感性分析,选择基准状态为
表 3 不同岩样换热系数关于体积流量和裂隙试样温度的敏感性因子
Tab.3
| 岩样编号 | S( | S( |
| H1 | 0.628 | 0.967 |
| H2 | 0.686 | 1.173 |
| H3 | 0.709 | 1.190 |
| H4 | 0.711 | 1.239 |
综上,就qV、θ0、eh三个因素而言,换热系数h受裂隙试样温度θ0的影响最大,其次是裂隙体积流量qV,影响最小的是水力开度eh.
4. 结 论
(1)当体积流量与裂隙水力开度条件保持不变时,裂隙试样温度升高,出口水流温度线性升高;换热系数随温度升高而线性增大.
(2)在裂隙试样温度与裂隙水力开度保持不变的条件下,体积流量增大,出口水流温度随之线性减小;换热系数随体积流量的增大而增大,表现为指数小于1的幂函数关系.
(3)在相同裂隙试样温度和渗流体积流量下,随着裂隙水力开度的增大,换热系数随之线性减小,水力开度由72.2 μm增至345.4 μm,裂隙试样温度为100 ℃时减幅小于20%. 岩石裂隙JRC增大,换热系数线性增大.
(4)利用敏感性函数对换热系数进行影响因素的敏感性分析,换热系数受裂隙试样温度的影响最大,其次是裂隙渗流体积流量,影响最小的是水力开度.
(5)实际地热开发中深部岩石温度较高,本研究仅针对较低温条件展示试验,后续将对于实验仪器进一步改进,进而开展较高温下的裂隙渗流换热试验.
参考文献
Modelling flow and heat transfer in fractured rocks: conceptual model of a 3-D deterministic fracture network
[J].DOI:10.1016/0375-6505(95)00020-Q [本文引用: 1]
Compression-induced crack initiation and growth in flawed rocks: a review
[J].DOI:10.1111/ffe.13477 [本文引用: 1]
Experimental study on the growth, coalescence and wrapping behaviors of 3D cross-embedded flaws under uniaxial compression
[J].
Fracturing behavior study of three-flawed specimens by uniaxial compression and 3D digital image correlation: sensitivity to brittleness
[J].DOI:10.1007/s00603-018-1600-4 [本文引用: 1]
Experimental study on flow and heat transfer characteristics of water flowing through a rock fracture induced by hydraulic fracturing for an enhanced geothermal system
[J].DOI:10.1016/j.applthermaleng.2019.03.114 [本文引用: 1]
Transient heat transfer processes in a single rock fracture at high volume flow rates
[J].DOI:10.1016/j.geothermics.2020.101989
不同围压下粗糙裂隙渗流规律试验研究
[J].
Experimental study on seepage law of rough fractures under different confining pressures
[J].
岩石裂隙中的水流-岩石热传导
[J].
Experimental study of flow-rock heat transfer in rock fractures
[J].
Experimental and analytical study of the overall heat transfer coefficient of water flowing through a single fracture in a granite core
[J].
花岗岩单裂隙渗流传热特性试验
[J].
Experiment on convection heat transfer characteristics in a single granite fracture
[J].
考虑多级流速下的岩石粗糙单裂隙渗流传热特性试验研究
[J].
Experimental study of convection heat transfer characteristics in single rough rock fracture considering multi-level flow rates
[J].
Experimental investigation of seepage and heat transfer in rough fractures for enhanced geothermal systems
[J].
Numerical investigation of heat transfer performance of water flowing through a reservoir with two intersecting fractures
[J].DOI:10.1016/j.renene.2020.01.141 [本文引用: 1]
An analytical method for determining the convection heat transfer coefficient between flowing fluid and rock fracture walls
[J].DOI:10.1007/s00603-017-1202-6 [本文引用: 2]
裂隙通道内流固换热系数解析解及敏感性分析
[J].
Analytical solution and sensitivity analysis of fluid-solid heat transfer coefficient in fracture channel
[J].
Evaluative analysis of formulas of heat transfer coefficient of rock fracture
[J].DOI:10.1007/s10765-020-02679-8 [本文引用: 1]
On the heat transfer coefficient between rock fracture walls and flowing fluid
[J].DOI:10.1016/j.compgeo.2014.03.002 [本文引用: 3]
非线性渗流对裂隙岩体渗流传热过程的影响
[J].
Effect of nonlinear seepage on flow and heat transfer process of fractured rocks
[J].
Numerical investigation of heat transfer effect on flow behavior in a single fracture
[J].
碳酸盐岩酸蚀裂缝渗流-传热特性
[J].
Seepage and heat transfer characteristics of acid corroded fractures in carbonate rock
[J].
多级围压下砂岩单裂隙渗流传热试验研究
[J].
Experimental study on seepage and heat transfer of sandstone with single fracture under multi-level confining pressure
[J].
Disentangling the simultaneous effects of inertial losses and fracture dilation on permeability of pressurized fractured rocks
[J].DOI:10.1029/2019GL083355 [本文引用: 1]
The influence of fracture geometry variation on non-Darcy flow in fractures under confining stresses
[J].DOI:10.1016/j.ijrmms.2018.11.017
Forchheimer方程参数量化及达西—非达西转变临界点
[J].
Parameters quantification of Forchheimer equation and critical point of transition from Darcian to non-Darcian flow
[J].
A criterion for non-Darcy flow in porous media
[J].DOI:10.1007/s11242-005-2720-3 [本文引用: 1]
Experimental study on the effect of fracture geometric characteristics on the permeability in deformable rough-walled fractures
[J].DOI:10.1016/j.ijrmms.2017.07.003 [本文引用: 2]
Combined effect of tortuosity and surface roughness on estimation of volume flow rate through a single rough joint
[J].DOI:10.1088/1742-2132/10/4/045015
分形岩石裂隙中渗流扩散运动的试验研究
[J].
Experimental study on seepage diffusion movement in fractal rock fractures
[J].
The role of fracture surface roughness in macroscopic fluid flow and heat transfer in fractured rocks
[J].DOI:10.1016/j.ijrmms.2016.05.006 [本文引用: 1]
A study in forced convection of water in a single uneven planar rock fracture for geothermal application
[J].DOI:10.1016/0960-1481(94)90043-4 [本文引用: 1]
Fluid friction and heat transfer through a single rough fracture in granitic rock under confining pressure
[J].DOI:10.1016/j.icheatmasstransfer.2016.03.027 [本文引用: 1]