[1]
崔焕平, 崔燕平, 王宗敏 混凝土非线性有限元分析中的网格尺寸效应
[J]. 混凝土 , 2007 , (6 ): 27 - 29
[本文引用: 1]
CUI Huan-ping, CUI Yan-ping, WANG Zong-min Mesh size effect in nonlinear finite element analysis of concrete
[J]. Concrete , 2007 , (6 ): 27 - 29
[本文引用: 1]
[2]
邹德高, 刘锁, 陈楷, 等 基于四叉树网格和多边形比例边界有限元方法的岩土工程非线性静动力分析
[J]. 岩土力学 , 2017 , 38 (增2 ): 33 - 40
[本文引用: 1]
ZOU De-gao, LIU Suo, CHEN Kai, et al Nonlinear static and dynamic analysis for geotechnical engineer-ing based on quadtree mesh and polygon scaled bou-ndary finite element method
[J]. Rock and Soil Mechanics , 2017 , 38 (增2 ): 33 - 40
[本文引用: 1]
[3]
ZOU D, CHEN K, KONG X, et al An enhanced octree polyhedral scaled boundary finite element meth-od and its applications in structure analysis
[J]. Engineering Analysis with Boundary Elements , 2017 , 84 : 87 - 107
DOI:10.1016/j.enganabound.2017.07.007
[4]
ZOU D, TENG X, CHEN K, et al An extended polygon scaled boundary finite element method for the nonlinear dynamic analysis of saturated soil
[J]. Engineering Analysis with Boundary Elements , 2018 , 91 : 150 - 161
DOI:10.1016/j.enganabound.2018.03.019
[5]
邹德高, 陈楷, 刘锁, 等 非线性比例边界有限元在面板坝分析中的应用
[J]. 土木与环境工程学报(中英文) , 2019 , 41 (3 ): 11 - 18
ZOU De-gao, CHEN Kai, LIU Suo, et al Application of nonlinear scaled boundary polygon element method in analysis of concrete face rockfill dam
[J]. Journal of Civil and Environmental Engineering , 2019 , 41 (3 ): 11 - 18
[6]
ZOU D, SUI Y, CHEN K Plastic damage analysis of pile foundation of nuclear power plants under beyond-design basis earthquake excitation
[J]. Soil Dynamics and Earthquake Engineering , 2020 , 136 : 106179
DOI:10.1016/j.soildyn.2020.106179
[7]
GENES M C, KOCAK S Dynamic soilstructure interaction analysis of layered unbounded media via a coupled finite element/boundary element/scaled boun-dary finite element model
[J]. International Journal for Numerical Methods in Engineering , 2005 , 62 (6 ): 798 - 823
DOI:10.1002/nme.1212
[8]
BEHNKE R, KALISKE M Thermomechanical mod-eling of crack propagation in dynamically loaded ela-stomer specimens using a scaled boundary finite ele-ment approach
[J]. Pamm , 2015 , 15 (1 ): 121 - 122
DOI:10.1002/pamm.201510051
[9]
李上明 基于比例边界有限元法动态刚度矩阵的坝库耦合分析方法
[J]. 工程力学 , 2013 , 30 (2 ): 313 - 317
LI Shang-ming Transient analysis method for dam-r-eservoir interaction based on dynamic stiffness of S-BFEM
[J]. Engineering Mechanics , 2013 , 30 (2 ): 313 - 317
[10]
YU X, KONG X, ZOU D, et al Linear elastic and plastic-damage analyses of a concrete cut-off wall co-nstructed in deep overburden
[J]. Computers and Geotechnics , 2015 , 69 : 462 - 473
[本文引用: 1]
[11]
邹德高, 陈楷, 余翔, 等 基于跨尺度精细方法的面板坝面板损伤演化尺寸效应分析
[J]. 土木与环境工程学报(中英文) , 2019 , 41 (6 ): 36 - 42
[本文引用: 1]
ZOU De-gao, CHEN Kai, YU Xiang, et al Size effect analysis of face slab damage evolution for high concrete face dam under earthquakes based on cross- scale fine method
[J]. Journal of Civil and Environmental Engineering , 2019 , 41 (6 ): 36 - 42
[本文引用: 1]
[12]
邹德高, 陈楷, 张仁怡, 等 基于SBFEM的心墙坝基座跨尺度精细应力分析
[J]. 人民长江 , 2019 , 50 (9 ): 168 - 174
ZOU De-gao, CHEN Kai, ZHANG Ren-yi, et al Cross-scale refined stress analysis on base-support of core wall concrete dam based on scaled boundary finite element method
[J]. Yangtze River , 2019 , 50 (9 ): 168 - 174
[13]
ZOU D, CHEN K, KONG X, et al An approach integrating BIM, octree and FEM-SBFEM for highly efficient modeling and seismic damage analysis of building structures
[J]. Engineering Analysis with Boundary Elements , 2019 , 104 : 332 - 346
DOI:10.1016/j.enganabound.2019.03.038
[本文引用: 1]
[14]
殷德胜, 尹栓, 周宜红 裂缝分析的比例边界有限元与有限元耦合的虚拟结构面模型
[J]. 计算力学学报 , 2014 , 31 (6 ): 735 - 741
[本文引用: 1]
YIN De-sheng, YIN Shuan, ZHOU Yi-hong Coupled SBFEM and FEM for crack analysis based on virtual discontinuous surface method
[J]. Chinese Journal of Computational Mechanics , 2014 , 31 (6 ): 735 - 741
[本文引用: 1]
[15]
YANG Z J, DEEKS A J Fully-automatic modelling of cohesive crack growth using a finite element–scaled boundary finite element coupled method
[J]. Engineering Fracture Mechanics , 2007 , 74 (16 ): 2547 - 2573
DOI:10.1016/j.engfracmech.2006.12.001
[16]
CHEN K, ZOU D, KONG X, et al Elasto-plastic fine-scale damage failure analysis of metro structures based on coupled SBFEM-FEM
[J]. Computers and Geotechnics , 2019 , 108 : 280 - 294
DOI:10.1016/j.compgeo.2018.12.030
[17]
QU Y, ZOU D, KONG X, et al Seismic cracking evolution for antiseepage face slabs in concrete faced rockfill dams based on cohesive zone model in explicit SBFEM-FEM frame
[J]. Soil Dynamics and Earthquake Engineering , 2020 , 133 : 106106
DOI:10.1016/j.soildyn.2020.106106
[本文引用: 1]
[18]
YE W, LIU J, FANG H, et al High-performance an-alysis of the interaction between plate and multi-laye-red elastic foundation using SBFEM-FEM
[J]. Composite Structures , 2019 , 214 : 1 - 11
[本文引用: 1]
[19]
陈楷. 基于比例边界有限元的岩土工程精细化分析方法及应用[D]. 大连: 大连理工大学, 2019: 27-38.
[本文引用: 1]
CHEN Kai. Research on technique and application in refined analysis of complicated geotechnical engineering structures based on scaled boundary finite element method [D]. Dalian: Dalian University of technology, 2019: 27-38.
[本文引用: 1]
[20]
李华, 刘晓俭, 钟万勰 二维有限元网格图象的识别
[J]. 大连理工大学学报 , 1993 , (4 ): 373 - 379
[本文引用: 1]
LI Hua, LIU Xiao-jian, ZHONG Wan-xie Recognition for two-dimension finite element mesh drawings
[J]. Journal of Dalian University of Technology , 1993 , (4 ): 373 - 379
[本文引用: 1]
[21]
赵大洲, 王延红 一种人机结合式二维有限元网格生成法
[J]. 华北水利水电学院学报 , 1999 , 2 : 22 - 24
ZHAO Da-zhou, WANG Yan-hong An interactive method to generate 2D finite element mesh
[J]. Journalof North China Institute of Water Conservancy and Hydroelectric Power , 1999 , 2 : 22 - 24
[23]
田林, 孙志林 AutoCAD下非结构网格自动生成
[J]. 水动力学研究与进展(A辑) , 2002 , 1 : 124 - 128
[本文引用: 1]
TIAN Lin, SUN Zhi-lin Automatic generation of unstructured grid under AutoCAD
[J]. Chinese Journal of Hydrodynamics , 2002 , 1 : 124 - 128
[本文引用: 1]
[24]
杨星, 蔡开玺. 二维无结构三角形网格自适应生成技术[J]. 人民长江, 2008, 39(19): 101-104.
YANG Xing, CAI Kai-xi, Adaptive generation technology of two-dimensional unstructured triangular mesh[J]. Yangtze River, 2008, 39(19): 101-104.
[25]
冯占荣, 于建群, 王玉杰, 等 一种二维非结构网格改进算法的研究
[J]. 燕山大学学报 , 2010 , 34 (5 ): 405 - 410
FENG Zhan-rong, YU Jian-qun, WANG Yu-jie, et al An improved algorithm for generating two-dimension-al grid
[J]. Journal of Yanshan University , 2010 , 34 (5 ): 405 - 410
[26]
郭新强. 边界面法四边形网格生成研究与应用[D]. 长沙: 湖南大学, 2011: 10-27.
Guo Xin-qiang. Study on quadrilateral mesh generation for the boundary face method and their impleme-ntation [D]. Changsha: Hunan University, 2011: 10-27.
[27]
徐青, 奚鹏飞 四边形网格自动生成方法改进及工程应用
[J]. 中国农村水利水电 , 2018 , 9 : 182 - 186
[本文引用: 1]
XU Qing, XI Peng-fei The method improvement of quadrilateral mesh automatic generation and engineering application
[J]. China Rural Water ang Hydropower , 2018 , 9 : 182 - 186
[本文引用: 1]
[28]
籍冉冉, 郑晓朋, 雷娜, 等 用于保特征四边形网格生成的改进Morse算法
[J]. 大连理工大学学报 , 2020 , 60 (6 ): 647 - 653
[本文引用: 1]
JI Ran-ran, ZHENG Xiao-peng, LEI Na, et al Improved Morse algorithm for feature-preserving quadrilateral mesh generation
[J]. Journal of Dalian University of Technology , 2020 , 60 (6 ): 647 - 653
[本文引用: 1]
[29]
SONG C, WOLF J P The scaled boundary fniteelement methodalias consistent infinitesimal fnite-element cellmethod for elasto-dynamics
[J]. Computer Methods in Applied Mechanics and Engineering , 1997 , 147 (3-4 ): 329 - 355
DOI:10.1016/S0045-7825(97)00021-2
[本文引用: 1]
[30]
WOLF J P, SONG C Dynamic-stiffness matrix in time domain of unbounded medium by infinitesimal finite element cell method
[J]. Earthquake Engineering and Structural Dynamics , 1994 , 11 (23 ): 1073 - 1086
[本文引用: 1]
[31]
DUNCAN J M, CHANG C Nonlinear analysis of stress and strain in soils
[J]. Journal of the Soil Mechanics and Foundations Division , 1970 , 96 : 1629 - 1653
[本文引用: 1]
[32]
LI J, ZHANG J, WANG Y, et al Seismic response of earth dam with innovative polymer antiseepage wall
[J]. International Journal of Geomechanics , 2020 , 20 (7 ): 4020079
DOI:10.1061/(ASCE)GM.1943-5622.0001664
[本文引用: 1]
[33]
WAYNE C G, M. D J. Finite element analyses of retaining wall behavior [J]. Journal of the Soil Mechanics and Foundations Division, 1971, 97(12).
[本文引用: 1]
[34]
董景刚. 土与结构接触面力学特性研究[D]. 大连: 大连理工大学, 2011: 55-59.
[本文引用: 1]
DONG Jing-gang. Study on mechanical properties of interface between soil and structure[D]. Dalian: Dalian university of technology, 2011: 55-59.
[本文引用: 1]
[35]
傅华, 章为民. 坝基混凝土防渗墙与泥皮接触面试验研究 [C]// 第一届中国水利水电岩土力学与工程学术讨论会. 昆明: 中国水利学会, 2006: 498-500.
[本文引用: 1]
FU Hua, ZHANG Wei-min. Experimental study on c-ontact surface between concrete cutoff wall and mud cake in dam foundation [C]// 1th National Symposium on Geotechnical Engineering. Kunming: CHES, 2006: 458-500.
[本文引用: 1]
混凝土非线性有限元分析中的网格尺寸效应
1
2007
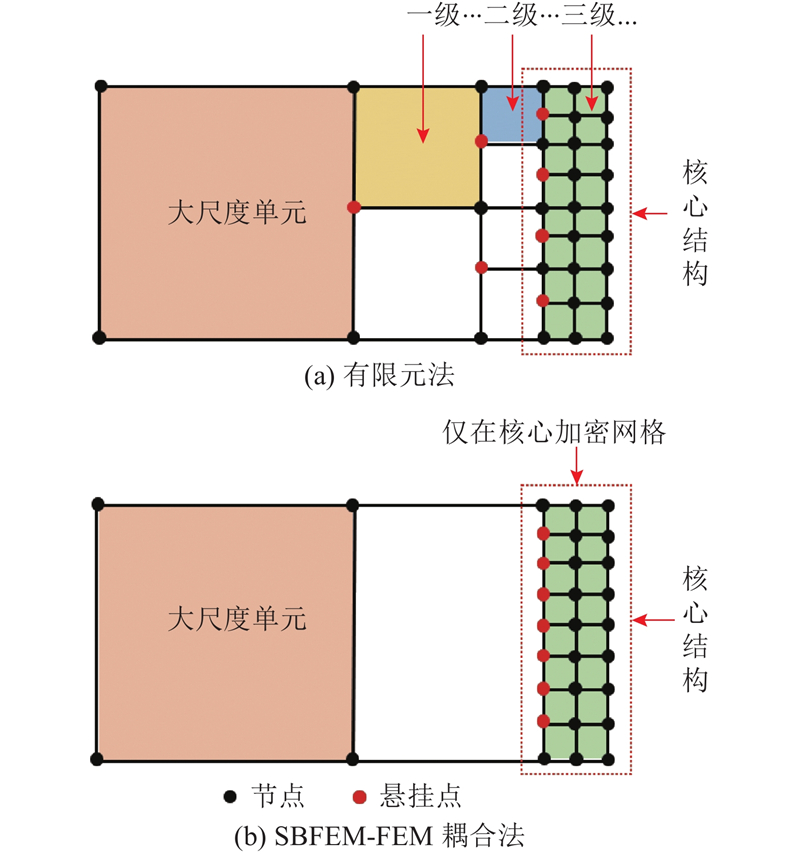
... 土石堤坝工程是我国重要的基础设施工程,为了保证设计的可靠性以及工程的安全性,常常会对工程结构的工作状态进行分析. 网格剖分是有限元数值模拟的基础,因此网格尺寸大小对数值计算结果的可靠性和精确性影响很大[1 ] . 防渗墙作为控制堤坝渗漏的关键结构,是堤坝安全的控制部位. 为了准确定位在不同运行条件下,防渗墙的薄弱部位会对防渗墙进行精细的网格剖分. 防渗墙与堤体尺度跨越巨大,若按照均匀尺度的原则对堤坝工程进行网格剖分,防渗墙的小尺度网格尺寸标准将会造成数值模型具有大量自由度,计算量难以承受. 相比于防渗墙,堤体的应力梯度一般较为平缓,常规尺度网格能够满足其精度要求. 数值模拟对防渗墙的核心结构进行精细网格剖分,其它部分采用常规尺度网格剖分,获得了跨尺度网格,并引入数值计算方法,数值分析的计算量和精度均能够得到可靠保证. 数值分析的计算量和精度同时得到保证是目前数值分析进一步推广应用的难题. ...
混凝土非线性有限元分析中的网格尺寸效应
1
2007
... 土石堤坝工程是我国重要的基础设施工程,为了保证设计的可靠性以及工程的安全性,常常会对工程结构的工作状态进行分析. 网格剖分是有限元数值模拟的基础,因此网格尺寸大小对数值计算结果的可靠性和精确性影响很大[1 ] . 防渗墙作为控制堤坝渗漏的关键结构,是堤坝安全的控制部位. 为了准确定位在不同运行条件下,防渗墙的薄弱部位会对防渗墙进行精细的网格剖分. 防渗墙与堤体尺度跨越巨大,若按照均匀尺度的原则对堤坝工程进行网格剖分,防渗墙的小尺度网格尺寸标准将会造成数值模型具有大量自由度,计算量难以承受. 相比于防渗墙,堤体的应力梯度一般较为平缓,常规尺度网格能够满足其精度要求. 数值模拟对防渗墙的核心结构进行精细网格剖分,其它部分采用常规尺度网格剖分,获得了跨尺度网格,并引入数值计算方法,数值分析的计算量和精度均能够得到可靠保证. 数值分析的计算量和精度同时得到保证是目前数值分析进一步推广应用的难题. ...
Nonlinear static and dynamic analysis for geotechnical engineer-ing based on quadtree mesh and polygon scaled bou-ndary finite element method
1
2017
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
Nonlinear static and dynamic analysis for geotechnical engineer-ing based on quadtree mesh and polygon scaled bou-ndary finite element method
1
2017
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
An enhanced octree polyhedral scaled boundary finite element meth-od and its applications in structure analysis
0
2017
An extended polygon scaled boundary finite element method for the nonlinear dynamic analysis of saturated soil
0
2018
非线性比例边界有限元在面板坝分析中的应用
0
2019
非线性比例边界有限元在面板坝分析中的应用
0
2019
Plastic damage analysis of pile foundation of nuclear power plants under beyond-design basis earthquake excitation
0
2020
Dynamic soilstructure interaction analysis of layered unbounded media via a coupled finite element/boundary element/scaled boun-dary finite element model
0
2005
Thermomechanical mod-eling of crack propagation in dynamically loaded ela-stomer specimens using a scaled boundary finite ele-ment approach
0
2015
基于比例边界有限元法动态刚度矩阵的坝库耦合分析方法
0
2013
基于比例边界有限元法动态刚度矩阵的坝库耦合分析方法
0
2013
Linear elastic and plastic-damage analyses of a concrete cut-off wall co-nstructed in deep overburden
1
2015
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
基于跨尺度精细方法的面板坝面板损伤演化尺寸效应分析
1
2019
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
基于跨尺度精细方法的面板坝面板损伤演化尺寸效应分析
1
2019
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
基于SBFEM的心墙坝基座跨尺度精细应力分析
0
2019
基于SBFEM的心墙坝基座跨尺度精细应力分析
0
2019
An approach integrating BIM, octree and FEM-SBFEM for highly efficient modeling and seismic damage analysis of building structures
1
2019
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
裂缝分析的比例边界有限元与有限元耦合的虚拟结构面模型
1
2014
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
裂缝分析的比例边界有限元与有限元耦合的虚拟结构面模型
1
2014
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
Fully-automatic modelling of cohesive crack growth using a finite element–scaled boundary finite element coupled method
0
2007
Elasto-plastic fine-scale damage failure analysis of metro structures based on coupled SBFEM-FEM
0
2019
Seismic cracking evolution for antiseepage face slabs in concrete faced rockfill dams based on cohesive zone model in explicit SBFEM-FEM frame
1
2020
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
High-performance an-alysis of the interaction between plate and multi-laye-red elastic foundation using SBFEM-FEM
1
2019
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
1
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
1
... 根据比例边界有限元法(scaled boundary finite element method, SBFEM)获得的网格单元对复杂几何边界适应能力强,具有实现跨尺度、精细化离散的特点. 邹德高等[2 -10 ] 对比例边界有限元法进行发展和改进,取得了一定的成果. 结合比例边界有限元法对构成单元节点没有限制的特点以及有限元法常规单元技术成熟易于求解的特点,SBFEM-FEM耦合求解分析逐渐发展起来. 邹德高等[11 -13 ] 将该耦合法应用于结构应力分析,验证了该耦合法的可行性. 殷德胜等[14 -17 ] 将耦合法应用于裂缝扩展和损伤破坏. Ye等[18 ] 将该耦合法应用于弹性板结构与多层无界弹性地基相互作用问题的求解. 目前SBFEM-FEM跨尺度分析所采用的数值网格通常由四分树法获得. 四分树法获得的网格单元形状固定、可控性差,无法适应土石堤坝中分层填筑和材料分区复杂的边界条件,难以根据实际情况相应做出合理的网格剖分方式,且可能造成需要精细模拟的部位会被忽略[19 ] . ...
二维有限元网格图象的识别
1
1993
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
二维有限元网格图象的识别
1
1993
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
判别二维有限元网格图的简便算法
1
2001
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
判别二维有限元网格图的简便算法
1
2001
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
AutoCAD下非结构网格自动生成
1
2002
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
AutoCAD下非结构网格自动生成
1
2002
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
四边形网格自动生成方法改进及工程应用
1
2018
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
四边形网格自动生成方法改进及工程应用
1
2018
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
用于保特征四边形网格生成的改进Morse算法
1
2020
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
用于保特征四边形网格生成的改进Morse算法
1
2020
... 为了增强网格剖分的可控性,在CAD软件中进行人为可控的网格划分,再识别并生成数值网格. 李华等[20 -22 ] 提出二维有限元网格的识别和生成方法. 田林等[23 -27 ] 在CAD环境下,对二维网格生成方法进行改善优化,提高了网格的质量和生成效率. 籍冉冉等[28 ] 对莫尔斯(Morse)算法进行优化,提高了所生成的四边形网格质量. 目前均是针对三角形和四边形单元的有限元数值网格,而有关非常规的多边形单元或SBFEM-FEM耦合数值网格识别与生成的研究十分少见. ...
The scaled boundary fniteelement methodalias consistent infinitesimal fnite-element cellmethod for elasto-dynamics
1
1997
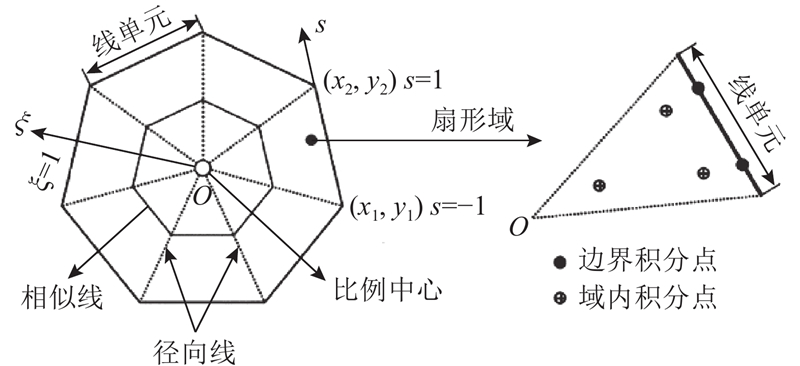
... 比例边界有限元法是由Wolf等[29 -30 ] 提出,该方法在边界处利用Galerkin方法进行数值离散,降低了一个空间的计算维度,可以在边界内部不需要基本了解的情况下利用解析的方法求解. 比例边界有限元法不仅具有较高的精度,而且对单元形状的容许度更高,不需要根据单元的结点数量开发相应单元类型,突破了常规有限元法的限制. 图1 为典型的多边形比例边界单元,图中ξ 为单元径向坐标,s 为环向坐标. ...
Dynamic-stiffness matrix in time domain of unbounded medium by infinitesimal finite element cell method
1
1994
... 比例边界有限元法是由Wolf等[29 -30 ] 提出,该方法在边界处利用Galerkin方法进行数值离散,降低了一个空间的计算维度,可以在边界内部不需要基本了解的情况下利用解析的方法求解. 比例边界有限元法不仅具有较高的精度,而且对单元形状的容许度更高,不需要根据单元的结点数量开发相应单元类型,突破了常规有限元法的限制. 图1 为典型的多边形比例边界单元,图中ξ 为单元径向坐标,s 为环向坐标. ...
Nonlinear analysis of stress and strain in soils
1
1970
... 堤坝体与堤坝基的静力分析了采用邓肯-张E-B非线性模型[31 ] ,坝体、坝基材料参数取自实际试验结果[32 ] . 参数如表3 所示. 其中 $ {\gamma _{\text{d}}} $ $ {\gamma _{\text{f}}} $ $ c $ $ \varphi $ $ \Delta \varphi $ $ k $ $ \;\beta $ $ {R_{\text{f}}} $ $ {k_{\text{b}}} $ q 分别为体积模量系数和指数参数; $ {k_{{\text{ur}}}} $ $ {n_{{\text{ur}}}} $
Seismic response of earth dam with innovative polymer antiseepage wall
1
2020
... 堤坝体与堤坝基的静力分析了采用邓肯-张E-B非线性模型[31 ] ,坝体、坝基材料参数取自实际试验结果[32 ] . 参数如表3 所示. 其中 $ {\gamma _{\text{d}}} $ $ {\gamma _{\text{f}}} $ $ c $ $ \varphi $ $ \Delta \varphi $ $ k $ $ \;\beta $ $ {R_{\text{f}}} $ $ {k_{\text{b}}} $ q 分别为体积模量系数和指数参数; $ {k_{{\text{ur}}}} $ $ {n_{{\text{ur}}}} $
1
... 采用Goodman接触单元模拟墙与土之间的接触面,用Clough-Duncan双曲线模型[33 ] 表达其应力-应变关系,该模型认为单元切向应力与切向相对位移之间的关系呈双曲线关系. 则切向刚度为 ...
1
... 董景刚[34 ] 对接触面单元的法向刚度应取值为相邻材料弹性模量的50~100倍,接触面模型的法向刚度与切向刚度的关系大致为 $ {k_{\text{n}}} = 2.5\;{k_{\text{s}}} $ . 法向刚度 $ {k_{\text{n}}} $ $ {\text{1}}{\text{.5}} \times {\text{1}}{{\text{0}}^{12}}{\text{ kN/}}{{\text{m}}} $ $ 6.0 \times {10^{11}}{\text{ kN/}}{{\text{m}}} $ [35 ] 参数如表5 所示. ...
1
... 董景刚[34 ] 对接触面单元的法向刚度应取值为相邻材料弹性模量的50~100倍,接触面模型的法向刚度与切向刚度的关系大致为 $ {k_{\text{n}}} = 2.5\;{k_{\text{s}}} $ . 法向刚度 $ {k_{\text{n}}} $ $ {\text{1}}{\text{.5}} \times {\text{1}}{{\text{0}}^{12}}{\text{ kN/}}{{\text{m}}} $ $ 6.0 \times {10^{11}}{\text{ kN/}}{{\text{m}}} $ [35 ] 参数如表5 所示. ...
1
... 董景刚[34 ] 对接触面单元的法向刚度应取值为相邻材料弹性模量的50~100倍,接触面模型的法向刚度与切向刚度的关系大致为 $ {k_{\text{n}}} = 2.5\;{k_{\text{s}}} $ . 法向刚度 $ {k_{\text{n}}} $ $ {\text{1}}{\text{.5}} \times {\text{1}}{{\text{0}}^{12}}{\text{ kN/}}{{\text{m}}} $ $ 6.0 \times {10^{11}}{\text{ kN/}}{{\text{m}}} $ [35 ] 参数如表5 所示. ...
1
... 董景刚[34 ] 对接触面单元的法向刚度应取值为相邻材料弹性模量的50~100倍,接触面模型的法向刚度与切向刚度的关系大致为 $ {k_{\text{n}}} = 2.5\;{k_{\text{s}}} $ . 法向刚度 $ {k_{\text{n}}} $ $ {\text{1}}{\text{.5}} \times {\text{1}}{{\text{0}}^{12}}{\text{ kN/}}{{\text{m}}} $ $ 6.0 \times {10^{11}}{\text{ kN/}}{{\text{m}}} $ [35 ] 参数如表5 所示. ...