[1]
李紫微, 林波荣, 陈洪钟 建筑方案能耗快速预测方法研究综述
[J]. 暖通空调 , 2018 , 48 (5 ): 8
[本文引用: 1]
LI Zi-wei, LIN Bo-rong, CHEN Hong-zhong Review of rapid prediction method of building energy consumption
[J]. Heating Ventilating and Air Conditioning , 2018 , 48 (5 ): 8
[本文引用: 1]
[3]
曹勇, 魏峥, 刘辉, 等 德国VDI3807标准对我国能耗定额的启示
[J]. 建设科技 , 2011 , (22 ): 78 - 81
DOI:10.3969/j.issn.1671-3915.2011.22.041
[本文引用: 1]
CAO Yong, WEI Zheng, LIU Hui, et al The enlightenment of German VDI3807 standard to Chinese energy consumption quota
[J]. Construction Science and Technology , 2011 , (22 ): 78 - 81
DOI:10.3969/j.issn.1671-3915.2011.22.041
[本文引用: 1]
[5]
朱明亚, 潘毅群, 吕岩, 等 能耗预测模型在建筑能效优化中的应用研究
[J]. 建筑科学 , 2020 , 36 (10 ): 35 - 46
DOI:10.13614/j.cnki.11-1962/tu.2020.10.05
[本文引用: 2]
ZHU Ming-ya, PAN Yi-qun, Lv Yan, et al Application review of energy consumption prediction models in building energy efficiency optimization
[J]. Building Science , 2020 , 36 (10 ): 35 - 46
DOI:10.13614/j.cnki.11-1962/tu.2020.10.05
[本文引用: 2]
[6]
U. S. department of energy’s ( DOE) building technologies office (BTO) energyplus [EB/OL]. [2022-03-25]. https://energyplus.net/.
[本文引用: 1]
[7]
TURHAN C, KAZANASMAZ T, UYGUN I E, et al Comparative study of a building energy performance software (KEP-IYTE-ESS) and ANN-based building heat load estimation
[J]. Energy and Buildings , 2014 , 85 : 115 - 125
DOI:10.1016/j.enbuild.2014.09.026
[本文引用: 1]
[8]
鲁艳蕊 基于Design Builder模拟的郑州高层办公建筑能耗研究
[J]. 山东农业大学学报: 自然科学版 , 2020 , 51 (2 ): 355 - 359
[本文引用: 1]
LU Yan-rui Study on energy consumption of high rise office buildings in Zhengzhou based on design builder simulation
[J]. Journal of Shandong Agricultural University: Natural Science Edition , 2020 , 51 (2 ): 355 - 359
[本文引用: 1]
[9]
LI K, HU C, LIU G, et al Building's electricity consumption prediction using optimized artificial neural networks and principal component analysis
[J]. Energy and Buildings , 2015 , 108 : 106 - 113
DOI:10.1016/j.enbuild.2015.09.002
[本文引用: 1]
[10]
WANG E, SHEN Z, GROSSKOPF K Benchmarking energy performance of building envelopes through a selective residual-clustering approach using high dimensional dataset
[J]. Energy and Buildings , 2014 , 75 : 10 - 22
DOI:10.1016/j.enbuild.2013.12.055
[本文引用: 1]
[12]
潘毅群. 实用建筑能耗模拟手册[M]. 北京: 中国建筑工业出版社, 2013: 45-48.
[本文引用: 1]
[13]
NETO A H, FIORELLI F A S Comparison between detailed model simulation and artificial neural network for forecasting building energy consumption
[J]. Energy and Buildings , 2008 , 40 (12 ): 2169 - 2176
DOI:10.1016/j.enbuild.2008.06.013
[本文引用: 1]
[14]
YANG Z, ROTH J, JAIN R K DUE-B: data-driven urban energy benchmarking of buildings using recursive partitioning and stochastic frontier analysis
[J]. Energy and Buildings , 2018 , 163 : 58 - 69
DOI:10.1016/j.enbuild.2017.12.040
[本文引用: 1]
[15]
LIU J, CHEN H, LIU J, et al An energy performance evaluation methodology for individual office building with dynamic energy benchmarks using limited information
[J]. Applied Energy , 2017 , 206 : 193 - 205
DOI:10.1016/j.apenergy.2017.08.153
[本文引用: 1]
[16]
YALCINTAS M An energy benchmarking model based on artificial neural network method with a case example for tropical climates
[J]. International Journal of Energy Research , 2010 , 30 (14 ): 1158 - 1174
[本文引用: 1]
[17]
LI Y, O'NEILL Z, ZHANG L, et al Grey box modeling and application for building energy simulations a critical review
[J]. Renewable and Sustainable Energy Reviews , 2021 , 146 : 111174
DOI:10.1016/j.rser.2021.111174
[本文引用: 1]
[19]
石欣, 张琦, 赵莹, 等 RC热网络建筑能耗预测模型综述
[J]. 仪器仪表学报 , 2014 , 35 (S2 ): 59 - 65
DOI:10.19650/j.cnki.cjsi.2014.s2.009
[本文引用: 1]
SHI Xin, ZHANG Qi, ZHAO Ying, et al Review of RC thermal network building energy consumption forecasting model
[J]. Chinese Journal of Scientific Instrument , 2014 , 35 (S2 ): 59 - 65
DOI:10.19650/j.cnki.cjsi.2014.s2.009
[本文引用: 1]
[20]
XIAO H, WEI Q, JIANG Y The reality and statistical distribution of energy consumption in office buildings in China
[J]. Energy and Buildings , 2012 , 50 : 259 - 265
DOI:10.1016/j.enbuild.2012.03.048
[本文引用: 1]
[21]
HUO T, REN H, ZHANG X, et al China's energy consumption in the building sector: a statistical year book energy balance sheet based splitting method
[J]. Journal of Cleaner Production , 2018 , 185 : 665 - 679
DOI:10.1016/j.jclepro.2018.02.283
[22]
ZHANG M, GE X, ZHAO Y, et al Creating statistics for China’s building energy consumption using an adapted energy balance sheet
[J]. Energies , 2019 , 12 (22 ): 4293
DOI:10.3390/en12224293
[本文引用: 1]
[23]
Characteristic values of energy consumption in buildings − Heating and electricity: VDI 3807 Sheet 2[S]. Verband Deutscher Ingenieure/Association of German Engineers. 1998: 87-97.
[本文引用: 1]
[24]
YAN D, O’BRIEN W, HONG T, et al Occupant behavior modeling for building performance simulation: current state and future challenges
[J]. Energy and Buildings , 2015 , 107 : 264 - 278
DOI:10.1016/j.enbuild.2015.08.032
[本文引用: 1]
[26]
YANG Z, BECERIKGERBER B A model calibration framework for simultaneous multi-level building energy simulation
[J]. Applied Energy , 2015 , 149 : 415 - 431
DOI:10.1016/j.apenergy.2015.03.048
[本文引用: 1]
[27]
DENG H, FANNON D, ECKELMAN M Predictive modeling for US commercial building energy use: a comparison of existing statistical and machine learning algorithms using CBECS microdata
[J]. Energy and Buildings , 2017 , 163 : 34 - 43
[28]
DAHLIN J. Accelerating monte Carlo methods for Bayesian inference in dynamical models [M]. Sweden: LUEP, 2016: 59-67.
[本文引用: 4]
[29]
DRONKELAAR C V, DOWSON M, SPATARU C, et al A review of the regulatory energy performance gap and its underlying causes in nondomestic buildings
[J]. Frontiers in Mechanical Engineering , 2016 , 1 : 1 - 14
[30]
WEI Y, ZHANG X, SHI Y, et al A review of data driven approaches for prediction and classification of building energy consumption
[J]. Renewable and Sustainable Energy Reviews , 2018 , 82 : 1027 - 1047
DOI:10.1016/j.rser.2017.09.108
[本文引用: 1]
[32]
BOLKER B M, BROOKS M E, CLARK C J, et al Generalized linear mixed models: a practical guide for ecology and evolution
[J]. Trends in Ecology and Evolution , 2009 , 24 (3 ): 127 - 135
DOI:10.1016/j.tree.2008.10.008
[33]
HARRISON X A, DONALDSON L, CORREA CANO M E, et al A brief introduction to mixed effects modelling and multi-model inference in ecology
[J]. Peer J , 2018 , 6 : 4794
DOI:10.7717/peerj.4794
[34]
KELLY R, HEALY K, ANAND M, et al Climatic and evolutionary contexts are required to infer plant life history strategies from functional traits at a global scale
[J]. Ecology Letters , 2021 , 24 (5 ): 970 - 983
DOI:10.1111/ele.13704
[35]
NAKAGAWA S, SCHIELZETH H A general and simple method for obtaining R2 from generalized linear mixed effects models
[J]. Methods in Ecology and Evolution , 2013 , 4 (2 ): 133 - 142
DOI:10.1111/j.2041-210x.2012.00261.x
[本文引用: 1]
[37]
SANKARARAMAN S, MCLEMORE K, MAHADEVAN S. Bayesian methods for uncertainty quantification in multi-level systems [C]// Topics in Model Validation and Uncertainty Quantification, Volume 4: Proceedings of the 30th IMAC, A Conference on Structural Dynamics . New York: Springer, 2012: 67-74.
[本文引用: 3]
[38]
WANG C K, TINDEMANS S, MILLER C, et al Bayesian calibration at the urban scale: a case study on a large residential heating demand application in Amsterdam
[J]. Journal of Building Performance Simulation , 2020 , 13 (3 ): 347 - 361
DOI:10.1080/19401493.2020.1729862
[本文引用: 1]
[39]
LAMBERT P C, SUTTON A J, BURTON P R, et al How vague is vague, a simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS
[J]. Stat Med , 2005 , 24 (15 ): 2401 - 2428
DOI:10.1002/sim.2112
[本文引用: 1]
[40]
WANG X, HE C Z, SUN D Bayesian population estimation for small sample capture-recapture data using noninformative priors
[J]. Journal of Statistical Planning and Inference , 2007 , 137 (4 ): 1099 - 1118
DOI:10.1016/j.jspi.2006.03.004
[本文引用: 1]
[41]
尹爱军, 赵磊, 吴宏钢 相关法动平衡校正中的3σ准则误差处理方法
[J]. 重庆大学学报 , 2013 , 36 (10 ): 22 - 26
[本文引用: 1]
YIN Ai-jun, ZHAO Lei, WU Hong-gang Error process based on 3σ rule used in balancing by correlation theory
[J]. Journal of Chongqing University , 2013 , 36 (10 ): 22 - 26
[本文引用: 1]
[43]
GELMAN A, HWANG J, VEHTARI A Understanding predictive information criteria for Bayesian models
[J]. Statistics and Computing , 2014 , 24 (6 ): 997 - 1016
DOI:10.1007/s11222-013-9416-2
[本文引用: 1]
[44]
BROOKS S P, GELMAN A General methods for monitoring convergence of iterative simulations
[J]. Journal of Computational and Graphical Statistics , 1998 , 7 (4 ): 434 - 455
[本文引用: 1]
[45]
GELMAN A, CARLIN J B, STERN H S, et al. Bayesian data analysis, third edition [M]. Boca Raton: CRCP, 2013: 281-286.
[本文引用: 1]
[46]
ASHRAE. ASHRAE Guideline 14–2014: Measurement of energy, demand, and water savings[S]. Atlanta: ASHRAE, 2014: 21-25.
[本文引用: 1]
[47]
住房和城乡建设部. 民用建筑能耗标准: GB/T 51161[S]. 北京: 中国建筑工业出版社, 2016: 8-10.
[本文引用: 1]
建筑方案能耗快速预测方法研究综述
1
2018
... 我国民用建筑终端能耗和碳排放分别占全国总量的21.2%和21.6%,其中北方城镇建筑供热能耗占建筑终端能耗已近1/4,是建筑领域实现“双碳”规划目标的重点领域. 德、英、美、丹麦等国已经应用整体能效法对建筑能耗进行管控,而我国目前仍处于向能耗限额法和整体能效法的过渡阶段[1 ] . 建筑能耗限额、整体能效分析是建筑能耗基准分析的基础环节. 不同时空尺度建筑实际能耗与能耗基准之间的对比,可以作为建筑设计、建造及运行阶段用能情况的评估方法[2 ] . 建筑能耗基准分析已成为现阶段建筑全过程节能优化领域的研究热点. ...
建筑方案能耗快速预测方法研究综述
1
2018
... 我国民用建筑终端能耗和碳排放分别占全国总量的21.2%和21.6%,其中北方城镇建筑供热能耗占建筑终端能耗已近1/4,是建筑领域实现“双碳”规划目标的重点领域. 德、英、美、丹麦等国已经应用整体能效法对建筑能耗进行管控,而我国目前仍处于向能耗限额法和整体能效法的过渡阶段[1 ] . 建筑能耗限额、整体能效分析是建筑能耗基准分析的基础环节. 不同时空尺度建筑实际能耗与能耗基准之间的对比,可以作为建筑设计、建造及运行阶段用能情况的评估方法[2 ] . 建筑能耗基准分析已成为现阶段建筑全过程节能优化领域的研究热点. ...
建筑能耗基准研究综述
2
2021
... 我国民用建筑终端能耗和碳排放分别占全国总量的21.2%和21.6%,其中北方城镇建筑供热能耗占建筑终端能耗已近1/4,是建筑领域实现“双碳”规划目标的重点领域. 德、英、美、丹麦等国已经应用整体能效法对建筑能耗进行管控,而我国目前仍处于向能耗限额法和整体能效法的过渡阶段[1 ] . 建筑能耗限额、整体能效分析是建筑能耗基准分析的基础环节. 不同时空尺度建筑实际能耗与能耗基准之间的对比,可以作为建筑设计、建造及运行阶段用能情况的评估方法[2 ] . 建筑能耗基准分析已成为现阶段建筑全过程节能优化领域的研究热点. ...
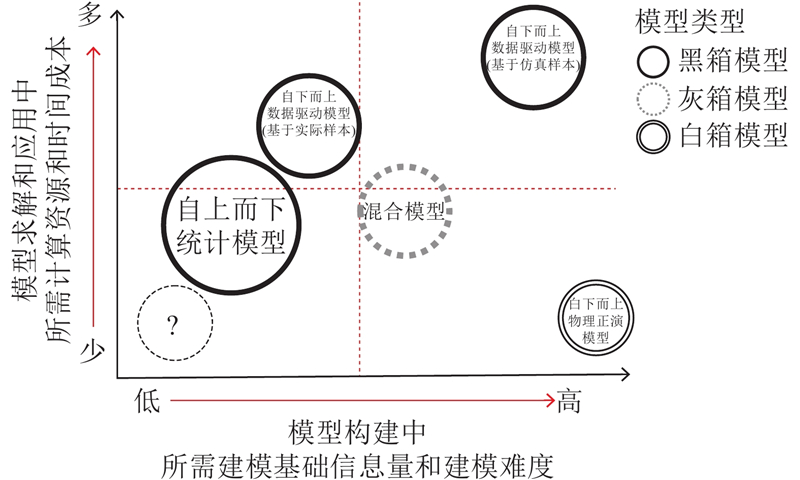
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
建筑能耗基准研究综述
2
2021
... 我国民用建筑终端能耗和碳排放分别占全国总量的21.2%和21.6%,其中北方城镇建筑供热能耗占建筑终端能耗已近1/4,是建筑领域实现“双碳”规划目标的重点领域. 德、英、美、丹麦等国已经应用整体能效法对建筑能耗进行管控,而我国目前仍处于向能耗限额法和整体能效法的过渡阶段[1 ] . 建筑能耗限额、整体能效分析是建筑能耗基准分析的基础环节. 不同时空尺度建筑实际能耗与能耗基准之间的对比,可以作为建筑设计、建造及运行阶段用能情况的评估方法[2 ] . 建筑能耗基准分析已成为现阶段建筑全过程节能优化领域的研究热点. ...
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
德国VDI3807标准对我国能耗定额的启示
1
2011
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
德国VDI3807标准对我国能耗定额的启示
1
2011
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
英国公共建筑能耗基准评价方法对我国建筑能耗定额方法的启示
1
2011
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
英国公共建筑能耗基准评价方法对我国建筑能耗定额方法的启示
1
2011
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
能耗预测模型在建筑能效优化中的应用研究
2
2020
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
... [5 ],采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
能耗预测模型在建筑能效优化中的应用研究
2
2020
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
... [5 ],采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
1
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Comparative study of a building energy performance software (KEP-IYTE-ESS) and ANN-based building heat load estimation
1
2014
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
基于Design Builder模拟的郑州高层办公建筑能耗研究
1
2020
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
基于Design Builder模拟的郑州高层办公建筑能耗研究
1
2020
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Building's electricity consumption prediction using optimized artificial neural networks and principal component analysis
1
2015
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Benchmarking energy performance of building envelopes through a selective residual-clustering approach using high dimensional dataset
1
2014
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Benchmarking building energy efficiency using quantile regression
1
2018
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
1
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Comparison between detailed model simulation and artificial neural network for forecasting building energy consumption
1
2008
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
DUE-B: data-driven urban energy benchmarking of buildings using recursive partitioning and stochastic frontier analysis
1
2018
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
An energy performance evaluation methodology for individual office building with dynamic energy benchmarks using limited information
1
2017
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
An energy benchmarking model based on artificial neural network method with a case example for tropical climates
1
2010
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Grey box modeling and application for building energy simulations a critical review
1
2021
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
An inverse gray-box model for transient building load prediction
1
2002
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
RC热网络建筑能耗预测模型综述
1
2014
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
RC热网络建筑能耗预测模型综述
1
2014
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
The reality and statistical distribution of energy consumption in office buildings in China
1
2012
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
China's energy consumption in the building sector: a statistical year book energy balance sheet based splitting method
0
2018
Creating statistics for China’s building energy consumption using an adapted energy balance sheet
1
2019
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
1
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Occupant behavior modeling for building performance simulation: current state and future challenges
1
2015
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
Urban building energy modeling a review of a nascent field
1
2016
... 建筑能耗预测分析方法对能耗基准指定的支撑显得尤为重要. 大量学者开展对建筑能耗预测模型、方法和模式的研究及应用实践. 在国家、省级区域尺度上,德国通过VDI 3807标准统计全国调查样本的分类建筑实际能耗概率,概率分布中前四分位数、中位数作为能耗标准值和指导值[3 ] . 英国、澳大利亚等国实施的EEBPP项目、step to benchmark energy use项目采用样本数据调查和统计分析结合方法确定建筑基准能耗[2 ,4 ] . 在单体建筑、街区等尺度上,部分学者提出利用物理正演模拟、正向模型仿真来描述建筑能耗与建筑特征参数之间的“目标-特征”关系[5 ] ,采用物理仿真模型和计算流体力学技术结合的能耗模拟引擎和工具,如DOE2[6 ] 、Energy Plus[7 ] 、Design Builder[8 ] 等;另一部分学者提出数据驱动的黑箱或反向模型描述上述数学联系,建立神经网络[9 ] 、广义线性回归[10 -11 ] 、人工智能[12 ] 等黑箱模型,通过带有建筑特征和能耗响应数据的建筑仿真样本或建筑实际样本对模型进行训练及校验,如支持向量机(support vector machines,SVM)[13 ] 、决策树和随机森林等基于树的模型[14 -15 ] 、人工神经网络(artificial neutral network,ANN)[16 ] 等. 部分学者结合物理正演和数据驱动算法[17 ] 提出白、黑箱模型结合的混合模型,如阻容(RC)热网络模型等[18 -19 ] . 上述建筑能耗预测方法用于城市尺度建筑能耗基准分析,仍存在一些不足之处:一方面我国研究中仍缺乏自上而下的统计模型来计算能耗基准所需的数据基础, 统计数据存在时空分辨率较低的问题,在统计口径、范围、完整性和准确性方面仍存在诸多争议[20 -22 ] ;另一方面通过自下而上的模型发现,若采用物理正演模型,模型构建中所需建筑形态等建模基础信息量较大且通常难以获得,建模难度高[23 ] . 若采用数据驱动模型或者混合模型,在训练模型采用仿真样本时,数值仿真建模和求解所需计算资源和时间成本通常过高[5 ] ,采集样本和建模所需的基础信息量、建模难度、计算资源和时间成本有所下降[24 -25 ] . 因此,如何在城市尺度建筑样本数量和维度有限的情况下,降低校准模型有限输入和不确定性对预测性能的影响,仍是目前待解决的问题. ...
A model calibration framework for simultaneous multi-level building energy simulation
1
2015
... 在建筑使用过程中,供热能耗影响因素众多且庞杂,因素作用效应各异,受采集样本缺乏、反映建筑或热力站能耗特征的数据维度不足的训练数据限制,难以充分观察全部能耗因素及其数据水平. 将供热能耗影响因素尽然纳入建模过程,且需考虑建模中难以观测的遗漏变量、采集范围抽样偏差、采集数据偏误等数据不确定性对模型准确性的影响. 根据已有数据库的数据量和数据维度情况,参考能耗预测[26 -30 ] 和循证医学领域[31 -35 ] 类似多因素、少样本、因素异质性、不确定性和因素效应耦合下建模的探索. 本研究构建了基于贝叶斯框架建筑能耗预测的混合效应概率模型,模型框架为一种采用随机待估超参数的分层、变截距、变斜率、广义线性固定效应的数据驱动模型, 目标函数为 ...
Predictive modeling for US commercial building energy use: a comparison of existing statistical and machine learning algorithms using CBECS microdata
0
2017
4
... 根据贝叶斯原理,模型利用观测数据,并将似然分布和先验分布结合,推断、构建模型的后验分布函数. 将模型调整超参数视为随机参数[28 ,36 -37 ] ,观测数据和建筑特征相关参数视为模型输出和输入的随机变量,基于贝叶斯原理的后验分布函数为 ...
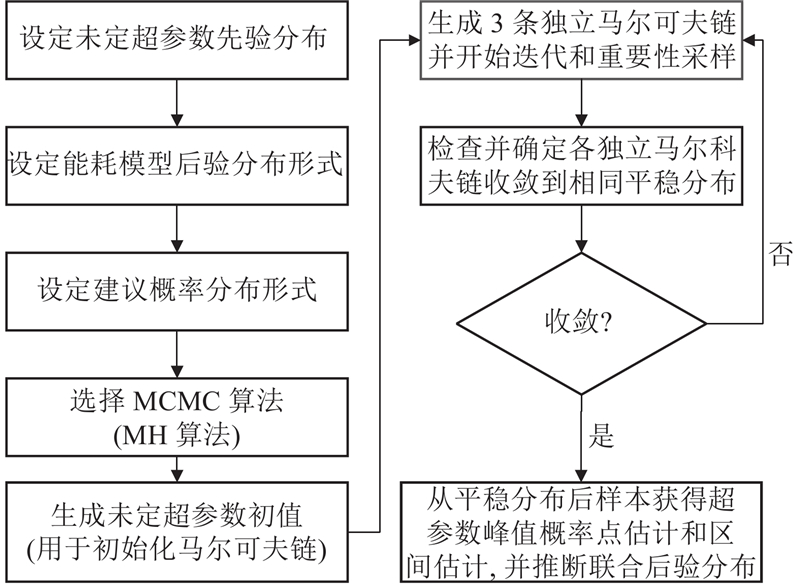
... 模型超参数的联合后验分布 ${}{P}{(}{{\boldsymbol{\theta }}}\left|{y}\right.{)}$ ${}{P}{(}{{\boldsymbol{\theta}} }\left|{y}\right.{)}$ [28 ,36 ] ,MCMC方法流程如图2 所示. ...
... 重要性采样中采用梅特罗波利斯−黑斯廷斯(Metropolis Hastings,MH)算法生成3条马尔可夫链[28 ,36 ] . 在MH算法中采用细致平衡条件 ${{J}}_{{t}} {(}{\boldsymbol{\theta}}^{{*}}{\left|{\boldsymbol{\theta}}\right.}^{{(t-1)}}{)} = {{J}}_{{t}}{(}{\boldsymbol{\theta}}^{{(t-1)}}{\left|{\boldsymbol{\theta}}\right.}^{{*}}{)}$
... 该算法通过完成指定迭代次数并判断马尔科夫链达到收敛后结束[28 ,36 ] ,从而使遍历马尔可夫链的极限分布收敛于平稳分布. ...
A review of the regulatory energy performance gap and its underlying causes in nondomestic buildings
0
2016
A review of data driven approaches for prediction and classification of building energy consumption
1
2018
... 在建筑使用过程中,供热能耗影响因素众多且庞杂,因素作用效应各异,受采集样本缺乏、反映建筑或热力站能耗特征的数据维度不足的训练数据限制,难以充分观察全部能耗因素及其数据水平. 将供热能耗影响因素尽然纳入建模过程,且需考虑建模中难以观测的遗漏变量、采集范围抽样偏差、采集数据偏误等数据不确定性对模型准确性的影响. 根据已有数据库的数据量和数据维度情况,参考能耗预测[26 -30 ] 和循证医学领域[31 -35 ] 类似多因素、少样本、因素异质性、不确定性和因素效应耦合下建模的探索. 本研究构建了基于贝叶斯框架建筑能耗预测的混合效应概率模型,模型框架为一种采用随机待估超参数的分层、变截距、变斜率、广义线性固定效应的数据驱动模型, 目标函数为 ...
Mixed models offer no freedom from degrees of freedom
1
2020
... 在建筑使用过程中,供热能耗影响因素众多且庞杂,因素作用效应各异,受采集样本缺乏、反映建筑或热力站能耗特征的数据维度不足的训练数据限制,难以充分观察全部能耗因素及其数据水平. 将供热能耗影响因素尽然纳入建模过程,且需考虑建模中难以观测的遗漏变量、采集范围抽样偏差、采集数据偏误等数据不确定性对模型准确性的影响. 根据已有数据库的数据量和数据维度情况,参考能耗预测[26 -30 ] 和循证医学领域[31 -35 ] 类似多因素、少样本、因素异质性、不确定性和因素效应耦合下建模的探索. 本研究构建了基于贝叶斯框架建筑能耗预测的混合效应概率模型,模型框架为一种采用随机待估超参数的分层、变截距、变斜率、广义线性固定效应的数据驱动模型, 目标函数为 ...
Generalized linear mixed models: a practical guide for ecology and evolution
0
2009
A brief introduction to mixed effects modelling and multi-model inference in ecology
0
2018
Climatic and evolutionary contexts are required to infer plant life history strategies from functional traits at a global scale
0
2021
A general and simple method for obtaining R2 from generalized linear mixed effects models
1
2013
... 在建筑使用过程中,供热能耗影响因素众多且庞杂,因素作用效应各异,受采集样本缺乏、反映建筑或热力站能耗特征的数据维度不足的训练数据限制,难以充分观察全部能耗因素及其数据水平. 将供热能耗影响因素尽然纳入建模过程,且需考虑建模中难以观测的遗漏变量、采集范围抽样偏差、采集数据偏误等数据不确定性对模型准确性的影响. 根据已有数据库的数据量和数据维度情况,参考能耗预测[26 -30 ] 和循证医学领域[31 -35 ] 类似多因素、少样本、因素异质性、不确定性和因素效应耦合下建模的探索. 本研究构建了基于贝叶斯框架建筑能耗预测的混合效应概率模型,模型框架为一种采用随机待估超参数的分层、变截距、变斜率、广义线性固定效应的数据驱动模型, 目标函数为 ...
An efficient Bayesian experimental calibration of dynamic thermal models
7
2018
... 根据贝叶斯原理,模型利用观测数据,并将似然分布和先验分布结合,推断、构建模型的后验分布函数. 将模型调整超参数视为随机参数[28 ,36 -37 ] ,观测数据和建筑特征相关参数视为模型输出和输入的随机变量,基于贝叶斯原理的后验分布函数为 ...
... 城市尺度建筑能耗模型的预测和校准过程往往会有数据不足的问题[38 ] . MLE估计的渐近特性将导致当观测数据不足时不能很好地利用有限的数据,从而容易导致过拟合和一类误差问题[36 -37 ] . 因此,提出在贝叶斯框架下与MAP估计相结合的建模方式是提高有限样本信息利用以及提高预测效果的关键改进. ...
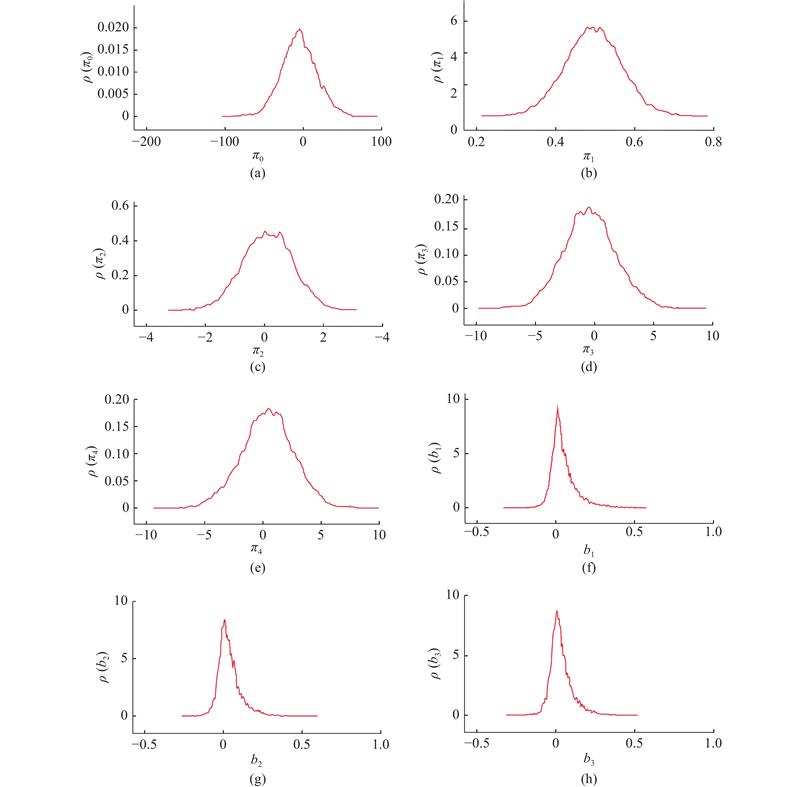
... 先验分布 $ {P}{(}{\theta }{)} $ [39 -40 ] . 在模型超参数的先验分布设定中采用无信息先验. 无信息先验等模糊先验与信息先验相比,未对后验分布推断进行约束,使得超参数的推断处于可以接受的范围内[36 -37 ] . 通过模糊先验归一化,可以适应观测数据存在信息缺失、信息弱或稀疏的情况. 模型中超参数 $ {{\pi}}_{{1}}{、}{{\pi}}_{{2}}{、}{{\pi}}_{{3}}{、}{{\pi}}_{{4}} $ $ {{\pi}}_{{0}} $ $ {G}{(0,}{}{1\times 1}{{0}}^{{-6}}{)} $ b 的先验分布设定为伽马分布 $ {{\rm{Ga}}\;(}{{\alpha}}_{{{\rm{f}}}}{,}\;{{\beta}}_{{{\rm{f}}}}{)} $ $ {{\alpha}}_{{b}} $ $ \;{{\beta}}_{{b}} $ $ {1\times }{{10}}^{{-3}} $ ${{ \varepsilon }}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\rm{Ga}}\;(1\times }{{10}}^{{-3}}{,1\times }{{10}}^{{-3}}{)}$
... 模型超参数的联合后验分布 ${}{P}{(}{{\boldsymbol{\theta }}}\left|{y}\right.{)}$ ${}{P}{(}{{\boldsymbol{\theta}} }\left|{y}\right.{)}$ [28 ,36 ] ,MCMC方法流程如图2 所示. ...
... 重要性采样中采用梅特罗波利斯−黑斯廷斯(Metropolis Hastings,MH)算法生成3条马尔可夫链[28 ,36 ] . 在MH算法中采用细致平衡条件 ${{J}}_{{t}} {(}{\boldsymbol{\theta}}^{{*}}{\left|{\boldsymbol{\theta}}\right.}^{{(t-1)}}{)} = {{J}}_{{t}}{(}{\boldsymbol{\theta}}^{{(t-1)}}{\left|{\boldsymbol{\theta}}\right.}^{{*}}{)}$
... 该算法通过完成指定迭代次数并判断马尔科夫链达到收敛后结束[28 ,36 ] ,从而使遍历马尔可夫链的极限分布收敛于平稳分布. ...
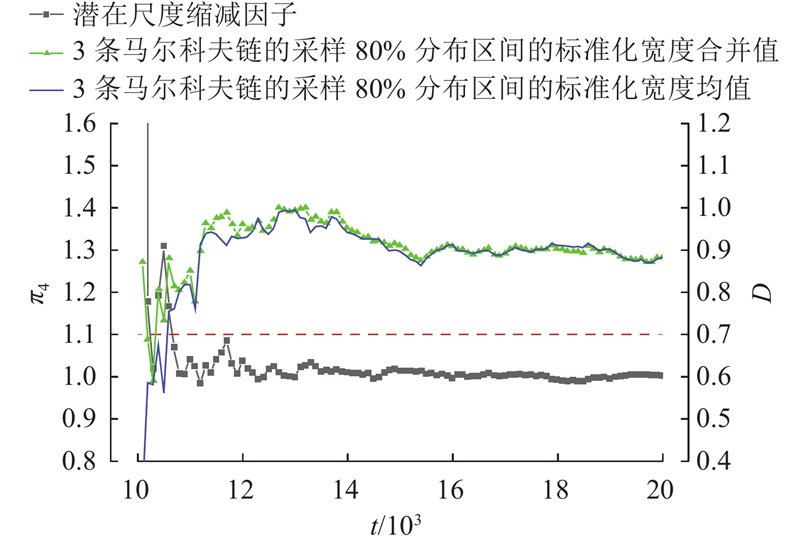
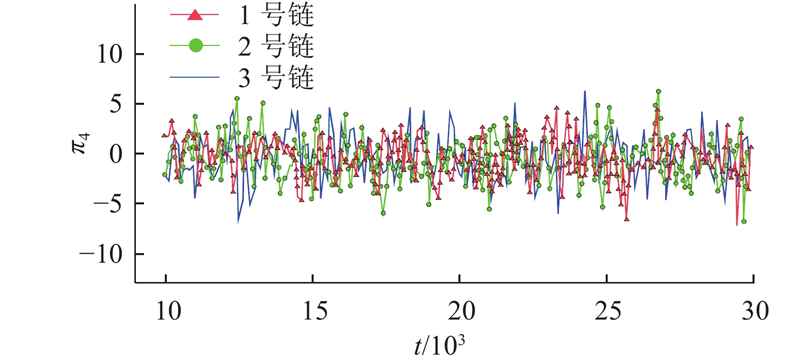
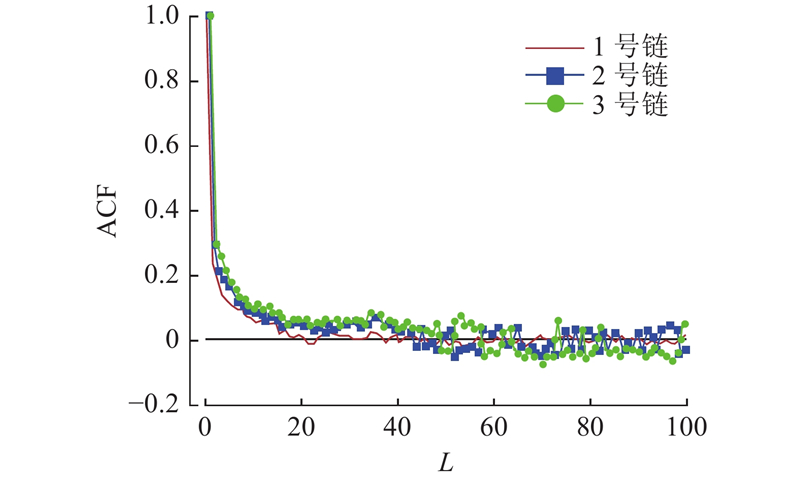
... 通过马尔科夫链蒙特卡洛(MCMC)方法模拟重要性采样,获得的样本可用前提是马尔科夫链达到收敛,收敛性可以通过计算并检查潜在尺度缩减因子 $ \hat{{R}} $ [43 -44 ] . 当模拟开始时,M 条马尔科夫链在N 个样本中,进行连续并随机采样,利用每条链的轨迹图来检查和设定退火时间 $ {{N}}_{\text{burn}\text{-}\text{in}} $ M +M 链中均有 $ \left({N}{-}{{N}}_{\text{burn-in}}\right)/\text{2}\mathrm{的} $ M +M 链在2阶段中,迭代结果差异已经达到设定精度要求,则说明该链趋于平稳,迭代N 次已经足够,否则迭代应继续进行. 所需迭代次数根据因子 $ \hat{{R}} $ $ \hat{{R}} $ M +M )[36 ,45 ] . ...
3
... 根据贝叶斯原理,模型利用观测数据,并将似然分布和先验分布结合,推断、构建模型的后验分布函数. 将模型调整超参数视为随机参数[28 ,36 -37 ] ,观测数据和建筑特征相关参数视为模型输出和输入的随机变量,基于贝叶斯原理的后验分布函数为 ...
... 城市尺度建筑能耗模型的预测和校准过程往往会有数据不足的问题[38 ] . MLE估计的渐近特性将导致当观测数据不足时不能很好地利用有限的数据,从而容易导致过拟合和一类误差问题[36 -37 ] . 因此,提出在贝叶斯框架下与MAP估计相结合的建模方式是提高有限样本信息利用以及提高预测效果的关键改进. ...
... 先验分布 $ {P}{(}{\theta }{)} $ [39 -40 ] . 在模型超参数的先验分布设定中采用无信息先验. 无信息先验等模糊先验与信息先验相比,未对后验分布推断进行约束,使得超参数的推断处于可以接受的范围内[36 -37 ] . 通过模糊先验归一化,可以适应观测数据存在信息缺失、信息弱或稀疏的情况. 模型中超参数 $ {{\pi}}_{{1}}{、}{{\pi}}_{{2}}{、}{{\pi}}_{{3}}{、}{{\pi}}_{{4}} $ $ {{\pi}}_{{0}} $ $ {G}{(0,}{}{1\times 1}{{0}}^{{-6}}{)} $ b 的先验分布设定为伽马分布 $ {{\rm{Ga}}\;(}{{\alpha}}_{{{\rm{f}}}}{,}\;{{\beta}}_{{{\rm{f}}}}{)} $ $ {{\alpha}}_{{b}} $ $ \;{{\beta}}_{{b}} $ $ {1\times }{{10}}^{{-3}} $ ${{ \varepsilon }}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\rm{Ga}}\;(1\times }{{10}}^{{-3}}{,1\times }{{10}}^{{-3}}{)}$
Bayesian calibration at the urban scale: a case study on a large residential heating demand application in Amsterdam
1
2020
... 城市尺度建筑能耗模型的预测和校准过程往往会有数据不足的问题[38 ] . MLE估计的渐近特性将导致当观测数据不足时不能很好地利用有限的数据,从而容易导致过拟合和一类误差问题[36 -37 ] . 因此,提出在贝叶斯框架下与MAP估计相结合的建模方式是提高有限样本信息利用以及提高预测效果的关键改进. ...
How vague is vague, a simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS
1
2005
... 先验分布 $ {P}{(}{\theta }{)} $ [39 -40 ] . 在模型超参数的先验分布设定中采用无信息先验. 无信息先验等模糊先验与信息先验相比,未对后验分布推断进行约束,使得超参数的推断处于可以接受的范围内[36 -37 ] . 通过模糊先验归一化,可以适应观测数据存在信息缺失、信息弱或稀疏的情况. 模型中超参数 $ {{\pi}}_{{1}}{、}{{\pi}}_{{2}}{、}{{\pi}}_{{3}}{、}{{\pi}}_{{4}} $ $ {{\pi}}_{{0}} $ $ {G}{(0,}{}{1\times 1}{{0}}^{{-6}}{)} $ b 的先验分布设定为伽马分布 $ {{\rm{Ga}}\;(}{{\alpha}}_{{{\rm{f}}}}{,}\;{{\beta}}_{{{\rm{f}}}}{)} $ $ {{\alpha}}_{{b}} $ $ \;{{\beta}}_{{b}} $ $ {1\times }{{10}}^{{-3}} $ ${{ \varepsilon }}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\rm{Ga}}\;(1\times }{{10}}^{{-3}}{,1\times }{{10}}^{{-3}}{)}$
Bayesian population estimation for small sample capture-recapture data using noninformative priors
1
2007
... 先验分布 $ {P}{(}{\theta }{)} $ [39 -40 ] . 在模型超参数的先验分布设定中采用无信息先验. 无信息先验等模糊先验与信息先验相比,未对后验分布推断进行约束,使得超参数的推断处于可以接受的范围内[36 -37 ] . 通过模糊先验归一化,可以适应观测数据存在信息缺失、信息弱或稀疏的情况. 模型中超参数 $ {{\pi}}_{{1}}{、}{{\pi}}_{{2}}{、}{{\pi}}_{{3}}{、}{{\pi}}_{{4}} $ $ {{\pi}}_{{0}} $ $ {G}{(0,}{}{1\times 1}{{0}}^{{-6}}{)} $ b 的先验分布设定为伽马分布 $ {{\rm{Ga}}\;(}{{\alpha}}_{{{\rm{f}}}}{,}\;{{\beta}}_{{{\rm{f}}}}{)} $ $ {{\alpha}}_{{b}} $ $ \;{{\beta}}_{{b}} $ $ {1\times }{{10}}^{{-3}} $ ${{ \varepsilon }}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\sigma}}_{{{\rm{f}}}}$ ${{\rm{Ga}}\;(1\times }{{10}}^{{-3}}{,1\times }{{10}}^{{-3}}{)}$
相关法动平衡校正中的3σ准则误差处理方法
1
2013
... 本研究通过热力站能耗监测系统自动抄表数据库中汇总的逐时能耗数据,将年供热能耗强度的数据进行整理,包括2017、2018、2019年共3年供暖季,同时采集接入相应热力站的建筑相关特征数据. 考虑到数据采集设备可能存在运行异常等情况,造成所采集的数据存在异常值和缺失值,为了保证样本数据质量,采用 $ \text{3}\sigma $ [41 ] 对数据异常值进行剔除,采用拉格朗日插值法[42 ] 对数据缺失值进行插补. ...
相关法动平衡校正中的3σ准则误差处理方法
1
2013
... 本研究通过热力站能耗监测系统自动抄表数据库中汇总的逐时能耗数据,将年供热能耗强度的数据进行整理,包括2017、2018、2019年共3年供暖季,同时采集接入相应热力站的建筑相关特征数据. 考虑到数据采集设备可能存在运行异常等情况,造成所采集的数据存在异常值和缺失值,为了保证样本数据质量,采用 $ \text{3}\sigma $ [41 ] 对数据异常值进行剔除,采用拉格朗日插值法[42 ] 对数据缺失值进行插补. ...
权重归一化拉格朗日插值及其空间降尺度应用
1
2019
... 本研究通过热力站能耗监测系统自动抄表数据库中汇总的逐时能耗数据,将年供热能耗强度的数据进行整理,包括2017、2018、2019年共3年供暖季,同时采集接入相应热力站的建筑相关特征数据. 考虑到数据采集设备可能存在运行异常等情况,造成所采集的数据存在异常值和缺失值,为了保证样本数据质量,采用 $ \text{3}\sigma $ [41 ] 对数据异常值进行剔除,采用拉格朗日插值法[42 ] 对数据缺失值进行插补. ...
权重归一化拉格朗日插值及其空间降尺度应用
1
2019
... 本研究通过热力站能耗监测系统自动抄表数据库中汇总的逐时能耗数据,将年供热能耗强度的数据进行整理,包括2017、2018、2019年共3年供暖季,同时采集接入相应热力站的建筑相关特征数据. 考虑到数据采集设备可能存在运行异常等情况,造成所采集的数据存在异常值和缺失值,为了保证样本数据质量,采用 $ \text{3}\sigma $ [41 ] 对数据异常值进行剔除,采用拉格朗日插值法[42 ] 对数据缺失值进行插补. ...
Understanding predictive information criteria for Bayesian models
1
2014
... 通过马尔科夫链蒙特卡洛(MCMC)方法模拟重要性采样,获得的样本可用前提是马尔科夫链达到收敛,收敛性可以通过计算并检查潜在尺度缩减因子 $ \hat{{R}} $ [43 -44 ] . 当模拟开始时,M 条马尔科夫链在N 个样本中,进行连续并随机采样,利用每条链的轨迹图来检查和设定退火时间 $ {{N}}_{\text{burn}\text{-}\text{in}} $ M +M 链中均有 $ \left({N}{-}{{N}}_{\text{burn-in}}\right)/\text{2}\mathrm{的} $ M +M 链在2阶段中,迭代结果差异已经达到设定精度要求,则说明该链趋于平稳,迭代N 次已经足够,否则迭代应继续进行. 所需迭代次数根据因子 $ \hat{{R}} $ $ \hat{{R}} $ M +M )[36 ,45 ] . ...
General methods for monitoring convergence of iterative simulations
1
1998
... 通过马尔科夫链蒙特卡洛(MCMC)方法模拟重要性采样,获得的样本可用前提是马尔科夫链达到收敛,收敛性可以通过计算并检查潜在尺度缩减因子 $ \hat{{R}} $ [43 -44 ] . 当模拟开始时,M 条马尔科夫链在N 个样本中,进行连续并随机采样,利用每条链的轨迹图来检查和设定退火时间 $ {{N}}_{\text{burn}\text{-}\text{in}} $ M +M 链中均有 $ \left({N}{-}{{N}}_{\text{burn-in}}\right)/\text{2}\mathrm{的} $ M +M 链在2阶段中,迭代结果差异已经达到设定精度要求,则说明该链趋于平稳,迭代N 次已经足够,否则迭代应继续进行. 所需迭代次数根据因子 $ \hat{{R}} $ $ \hat{{R}} $ M +M )[36 ,45 ] . ...
1
... 通过马尔科夫链蒙特卡洛(MCMC)方法模拟重要性采样,获得的样本可用前提是马尔科夫链达到收敛,收敛性可以通过计算并检查潜在尺度缩减因子 $ \hat{{R}} $ [43 -44 ] . 当模拟开始时,M 条马尔科夫链在N 个样本中,进行连续并随机采样,利用每条链的轨迹图来检查和设定退火时间 $ {{N}}_{\text{burn}\text{-}\text{in}} $ M +M 链中均有 $ \left({N}{-}{{N}}_{\text{burn-in}}\right)/\text{2}\mathrm{的} $ M +M 链在2阶段中,迭代结果差异已经达到设定精度要求,则说明该链趋于平稳,迭代N 次已经足够,否则迭代应继续进行. 所需迭代次数根据因子 $ \hat{{R}} $ $ \hat{{R}} $ M +M )[36 ,45 ] . ...
1
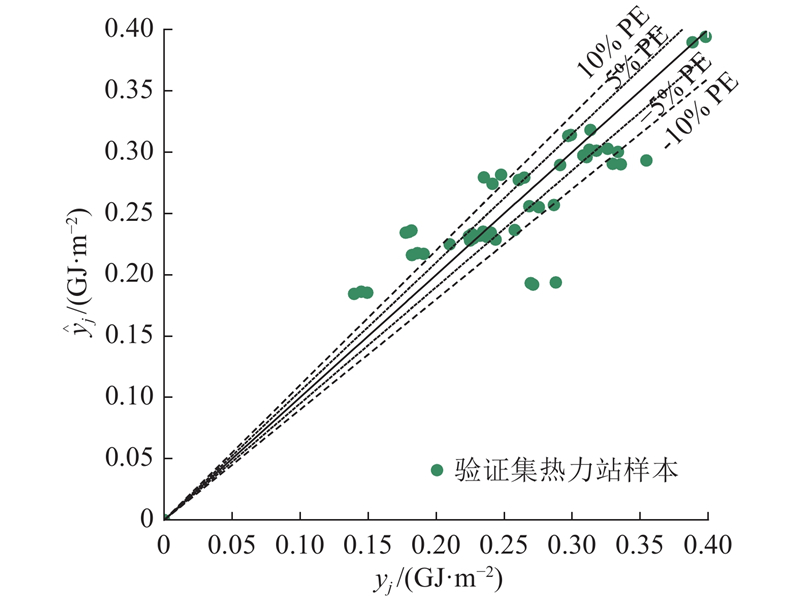
... 参考关于广泛用于评估能耗校准模型和预测模型的ASHRAE指南14-2004标准[46 ] ,采用绝对百分比误差(percentage error, PE)、归一化平均偏差(normalized mean bias error, NMBE)、均方根误差(root mean sqnare error, RMSE)和均方根误差变异系数(cofficient of variation root mean squaren error, CVRMSE)等预测精度统计评估指标进行误差分析,即 ...
1
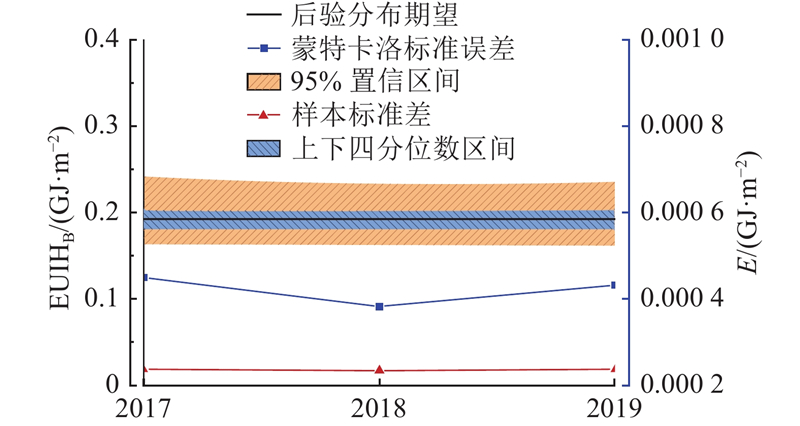
... 图8 为北京市居住建筑EUIH的联合后验分布计算结果,左轴为EUIH基准值EUIHB (GJ/m2 ),右轴为蒙特卡洛标准误差E (GJ/m2 ),下轴为年份. 联合后验分布具有峰值概率的EUIH期望值,可以设定作为北京市居住建筑EUIH的基准值,2017、2018、2019年EUIH基准值分别为0.194、0.192、0.193 $ \text{}\text{GJ/}{\text{m}}^{\text{2}} $ . 若根据城市管理不同实际需要,将不同可信区间上下限EUIH数值设定作为能耗准入值或限定值、先进值或引导值[47 ] ,如95%可信区间上下限、上下四分位数等. 以2018年为例,95%可信区间上下限、上下四分位数由高至低分别为0.163、0.180、0.201、0.233 $ \text{GJ/}{\text{m}}^{\text{2}} $ $ \text{GJ/}{\text{m}}^{\text{2}} $ $ \text{GJ/}{\text{m}}^{\text{2}} $ $ \text{GJ/}{\text{m}}^{\text{2}} $