浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(9): 1804-1813 doi: 10.3785/j.issn.1008-973X.2023.09.012

机械工程、能源工程

考虑工人疲劳的双资源柔性作业车间调度优化

郭鹏,, 郝东辉, 郑鹏, 王祺欣

1. 西南交通大学 机械工程学院，四川 成都 610031

2. 轨道交通运维技术与装备四川省重点实验室，四川 成都 610031

Scheduling optimization of dual resource-constrained flexible job shop considering worker fatigue

GUO Peng,, HAO Dong-hui, ZHENG Peng, WANG Qi-xin

1. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China

2. Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province, Chengdu 610031, China

收稿日期: 2022-09-19  

基金资助: 国家重点研发计划资助项目(2020YFB1712202)；四川省自然科学基金资助项目(2022NSFSC0459)

Received: 2022-09-19  

Fund supported: 国家重点研发计划资助项目(2020YFB1712202)；四川省自然科学基金资助项目(2022NSFSC0459)

作者简介 About authors

郭鹏（1988—），男，副教授，从事智能优化调度研究.orcid.org/0000-0001-5520-7701.E-mail：pengguo318@swjtu.edu.cn , E-mail：pengguo318@swjtu.edu.cn

摘要

针对生产制造过程中的工人疲劳问题，在人机双资源约束柔性作业车间调度问题的基础上，以最小化完工时间为目标，构建混合整数规划模型，保证工人疲劳不超过限定水平. 提出改进的自适应大规模邻域搜索算法，以解决工件排序、机器分配、工人指派和工人疲劳等高度复杂的子问题. 所提算法使用8种启发式规则生成初始解，引入6类破坏算子和6类修复算子实现对解空间的高效搜索. 通过不同规模的算例对比，验证所提算法的有效性. 相较于Gurobi求解器、遗传算法、Jaya算法和标准ALNS算法，所提算法具有良好的寻优性能，能够有效解决作业车间调度过程中的工人疲劳问题.

关键词： 双资源约束 ; 柔性作业车间 ; 工人疲劳 ; 混合整数规划 ; 自适应大邻域搜索

Abstract

The flexible job shop scheduling problem with human-machine dual resource limitations was studied. A mixed integer programming model was developed to minimize the completion time ensuring the worker fatigue was below the limited level in the manufacturing process. An improved adaptive large neighborhood search algorithm was proposed to resolve highly complex sub-problems such as job sequencing, machine assignment, worker assignment and worker fatigue. Eight heuristic rules were used to build the initial solutions, and six types of destruction operators and six types of repair operators were introduced to achieve an efficient search of the solution space in the proposed algorithm. The effectiveness of the proposed algorithm was demonstrated by comparing the numerical examples of various scales. Compared with the Gurobi optimizer, genetic algorithm, Jaya algorithm and standard ALNS algorithm, the proposed algorithm has good optimization performance and can successfully address the issue of worker fatigue in the job shop scheduling.

Keywords： dual resource constraints ; flexible job shop ; worker fatigue ; mixed integer programming ; adaptive large neighborhood search

PDF (833KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

郭鹏, 郝东辉, 郑鹏, 王祺欣. 考虑工人疲劳的双资源柔性作业车间调度优化. 浙江大学学报(工学版)[J], 2023, 57(9): 1804-1813 doi:10.3785/j.issn.1008-973X.2023.09.012

GUO Peng, HAO Dong-hui, ZHENG Peng, WANG Qi-xin. Scheduling optimization of dual resource-constrained flexible job shop considering worker fatigue. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(9): 1804-1813 doi:10.3785/j.issn.1008-973X.2023.09.012

随着工业4.0的稳步推进，在装备制造、轨道交通、航空等高端制造行业中，人的价值越来越高，人机协同的工作模式备受关注. 在此模式下的工人疲劳无法避免，长期积累的疲劳损伤会对个人健康安全及作业效率造成不利的影响[1-3]，甚至引起严重的安全事故和巨大的经济损失[4]. 合理安排工人的休息时间和作业内容，可以在保障工人安全生产的同时有效缩短生产周期，提高资源利用率[5].

人机协同的工作模式属于双资源约束柔性作业车间调度问题(dual resource constrained flexible job-shop scheduling problem, DRCFJSP)，具有多重复杂性，难以使用精确式算法在有限时间求得最优解. 为了求解DRCFJSP，研究者大多采用智能优化算法，如遗传算法(genetic algorithm, GA)[6-8]、粒子群算法(particle swarm optimization, PSO)[9]、人工神经网络(artificial neural network, ANN)[10-11]等. Jamshidi[12]强调人在调度系统中的维护作用，提出基于疲劳恢复的数学模型.针对工作疲劳导致操作员工作效率下降的现象，Ferjani等[13]使用适应性强的动态任务启发式方法解决动态多技能工人分配问题. Meng等[14]考虑工人的灵活性，基于空闲时间和空闲能量思想建立混合整数规划模型，并使用可变邻域搜索算法求解能源约束的DRCFJSP. Mokhtari等[15]以最小化总加权迟到时间和最大完成时间为优化目标，研究双资源约束作业车间调度问题，针对NP难问题提出混合人工蜂群算法来解决大规模问题实例. Zhang等[16]针对操作人员在加工前后的时间差异问题，提出基于量子遗传算法的DRCFJSP优化模型. 该模型使用的量子突变策略和捏合技术，有效提高了算法的收敛性. Tan等[17]开发增强的NSGA-II算法来解决具有疲劳意识的DRCFJSP，旨在通过机器和工人的联合调度，使工人在缓解疲劳的同时提高生产率. Defersha等[18]提出基于工人资源约束的柔性作业车间调度问题数学模型，并扩展使用模拟退火算法求解双资源约束调度问题. Farjallah等[19]提出基于多启动禁忌智能体的算法，用于解决需要机器和人力资源的车间调度问题，并通过实验表明该算法的有效性.

由于疲劳累计率、操作熟练度的个体差异，工人在同一机器上加工同一工件的效率不同[20]，而工人的生产效率影响整个生产过程. 现有研究大多没有考虑工人疲劳或未注意工人的个体差异，考虑工人疲劳的调度方案仍然缺乏有效性. 自适应大邻域搜索(adaptive large neighborhood search, ALNS)[21]算法具有搜索效率高、收敛速度快的特点，被较多地应用于处理车辆路径问题(vehicle routing problem, VRP)[22-24]，在柔性作业车间调度问题或DRCFJSP领域[25]的应用鲜见. 本研究针对考虑工人疲劳的DRCFJSP特点，以最小化完工时间为优化目标，提出改进的ALNS算法. 所提算法采用三级编码方式表示可行解，通过设计多组破坏算子和修复算子，自适应选择机制，在迭代中不断寻找和更新最优解. 为了防止陷入局部最优，在当前解多次迭代未找到更优解时，所提算法随机接受劣解，以保证算法的寻优性能. 通过对比分析不同规模的算例、不同算法进行所提算法的可行性验证和寻优性能评定.

1. 问题描述与模型建立

1.1. 问题描述与假设

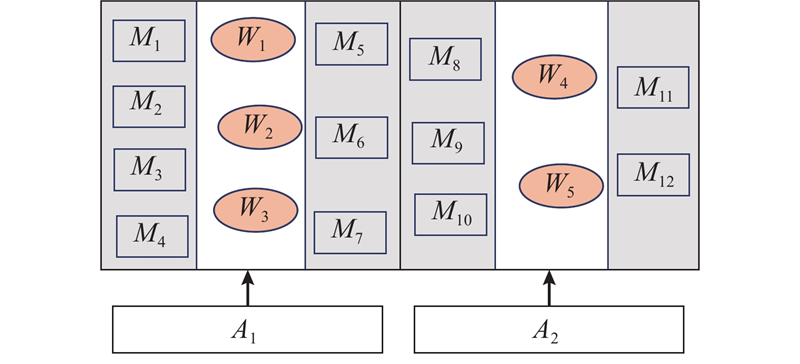
假设车间有一定数量的加工机器M={M1, M2, ···, Mc}和工人W={W1, W2, ···, Wd}, 调研发现，车间被走廊分成不同生产单元(cell)，每个生产单元上有不同数量的机器和工人，相同类型的机器放在同一生产单元，由于职责和分工不同，工人只能操作所属单元上的机器类别. 如图1所示为某加工车间示例，在生产单元A1上有机器集合{M1, M2, ···, M7}和工人集合{W1, W2, W3}，表示工人W1~W3可操作的机器为M1~M7，其余机器不可操作；其他生产单元依此类推.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   作业车间示意图

Fig.1   Diagram of job shop


计划加工工件J={J1, J2, ···, Jn}，受加工环境(加工机器、工人效率)的影响，工件在不同类型机器上的加工时间不同，但在同一类型机器上的加工时间相同，其他假设条件如下. 1) 每个工件仅一道加工工序，工序分为工人处理部分和机器加工部分：先由工人在加工机器上辅助安装加工模具和上料，再由机器自动加工；2) 每个工件仅加工一次；3) 1个加工机器在同一时刻只允许加工1个工件；4) 1个工人同一时刻只能在1个加工机器上负责处理1个加工任务；5) 每个工人或加工机器在开始某项工作后不能中断，直至当前工作完成；6) 忽略工人和工件在不同加工机器上的转移时间；7)工人过度疲劳将导致工件损坏，造成物料、时间、人工等成本增加. 在生产过程中，工人的疲劳值不允许超过指定值. 调度的目标：将工件合理地分配给各个机器和工人，确定加工顺序以及每个工件加工的开始时间和结束时间，最小化任务的最大完工时间.

1.2. 工人疲劳模型

工人的疲劳值过高会影响生产效率和生产质量，疲劳值持续过高也会对工人自身的安全和健康产生负面作用. 在生产调度的过程中考虑工人的疲劳因素，有利于提高生产效率和保障工人健康.指数型疲劳模型[26]能够较好描述工人在工作以及休息过程中的疲劳值变化，表达式为

$ {f_{t+1}} = {x_t} \times (1 - (1 - {f_t}) \times {{\rm{e}}^{ - \lambda }})+(1 - {x_t}) \times {f_t} \times {{\rm{e}}^{ - \mu }}. $

式中：ft为工人在t时刻末的疲劳值，取值范围为[0,1.0]； λ、μ分别为与工人个人身体素质相关的疲劳累计率和疲劳恢复率；xt∈{0,1}为决策变量，表示工人在t时刻的工作状态，工作时为1，休息时为0. 假设工人在0时刻末的疲劳值为f0，当工人处于工作状态，且持续工作时长为T时，xt始终为1，式(1)等价为

$ {f_{t+1}} = 1 - (1 - {f_t}) \times {{\rm{e}}^{ - \lambda }}. $

在0时刻末至1时刻末有

$ {f_1} = 1 - (1 - {f_0}) \times {{\rm{e}}^{ - \lambda }}. $

在1时刻末至2时刻末有

$ \begin{split} {f_2} =& 1 - (1 - {f_1}) \times {{\rm{e}}^{ - \lambda }} = \\ & 1 - (1 - (1 - (1 - {f_0}) \times {{\rm{e}}^{ - \lambda }})) \times {{\rm{e}}^{ - \lambda }} = \\ & 1 - (1 - {f_0}) \times {{\rm{e}}^{ - 2\lambda }}. \\ \end{split} $

推导式(3)、(4)得到T时刻末工人的疲劳值为

$ {f_T} = 1 - (1 - {f_0}) \times {{\rm{e}}^{ - T\lambda }}. $

同理，休息状态时工人的疲劳计算式为

$ {f_T} = {f_0} \times {{\rm{e}}^{ - T\mu }}. $

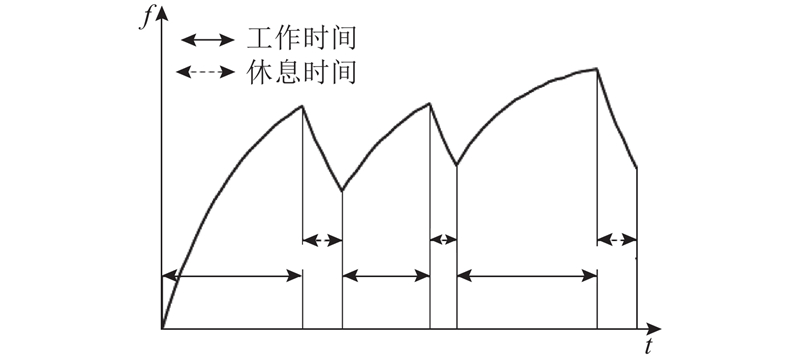
如图2所示为工人在工作与休息交替进行时的疲劳变化曲线.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   工人工作和休息时的疲劳曲线

Fig.2   Fatigue curve of worker during work and rest


1.3. 混合整数规划模型

基于问题描述与假设，构建混合整数规划模型. 目标函数为

$ \min {C_{\max }}. $

约束为

$ \sum\limits_{j \in J} {\sum\limits_{w \in W} {\sum\limits_{m \in M} {{x_{sjwm}}} } } = 1;\;\forall s \in S. $

$ \sum\limits_{s \in S} {\sum\limits_{w \in W} {\sum\limits_{m \in M} {{x_{sjwm}}} } } = 1;\;\forall j \in J. $

$ \sum\limits_{j \in J} {\sum\limits_{w \in W} {\sum\limits_{m \in M} {{b_{wm}} \times {x_{sjwm}}} } } = 1;\;\forall s \in S. $

$ {d_{swm}} \geqslant {h_{s'm}};\;\forall s \in S,\;s' \in S',\;w \in W,\;m \in M. $

$ {d_{swm}} \geqslant {g_{s'w}};\forall s \in S,\;s' \in S',\;w \in W,\;m \in M. $

$ {g_{sw}} = \sum\limits_{j \in J} {\sum\limits_{m \in M} {({d_{swm}}+{t_{jm1}}) \times {x_{sjwm}}} } ;\; \forall s \in S,\; w \in W. $

$ \begin{split} {h_{sm}} =& \sum\limits_{j \in J} {\sum\limits_{w \in W} {({d_{swm}}+{t_{jm1}}+{t_{jm2}}) \times {x_{sjwm}}} } ; \\ & \forall s \in S,\; m \in M. \\ \end{split} $

$ {p_{sw}} = \sum\limits_{j \in J} {\sum\limits_{m \in M} {{t_{jm1}} \times {x_{sjwm}}} } ;\; \forall s \in S,\; w \in W. $

$ \begin{split} {q_{sw}} =& \sum\limits_{j \in J} {\sum\limits_{m \in M} {({d_{swm}} - {g_{(s - 1)w}}) \times {x_{sjwm}}} } ; \\ & \forall s \in S,w \in W. \\ \end{split} $

$ {u_{sw}} = 1 - (1 - {v_{sw}}) \times {{\rm{e}}^{ - {\lambda _w} \times {p_{sw}}}};\; \forall s \in S,w \in W. $

$ {v}_{sw}={u}_{(s-1)w}\times {{\rm{e}}}^{-{\mu }_{w}\times {q}_{sw}};\; \forall s\in S,\; w\in W. $

$ {u_{sw}} \leqslant {f_e};\;\forall s \in S,\; w \in W. $

$ {C_{\max }} = \mathop {\max }\limits_{s \in S,\; m \in M} ({h_{sm}}). $

式中：S、J、M、W分别为加工顺序集合、工件集合、机器集合、工人集合，bwm表示工人w是否可以操作机器m（是为1，否为0），tjm1、tjm2分别为工件j在机器m上加工时需要工人处理的时间和需要机器加工的时间，λw、μw、fe分别为工人w的疲劳累计率、疲劳恢复率以及疲劳上限，dswm分别为在顺序s上由工人w和机器m加工时的开始时间，gsw、hsm分别为在顺序s上工人w的结束时间和机器m的结束时间，psw、qsw分别为在顺序s上工人w的工作时间和休息时间，usw、vsw分别为在顺序s上工人w工作后的疲劳值和休息后的疲劳值，xsjwm表示在顺序s上是否由工人w和机器m加工工件j (是为1，否为0)，Cmax为最大完工时间. 式(7)表示最小化完工时间；式(8)确保每台机器在同一时刻只能分配1个工人和1个工件，式(9)确保每个工件仅可被加工1次，式(10)确保工人只能在所属单元的机器上工作，式(8)~(10)共同作用，保证解的可行性；式(11)、(12)要求工件的开始加工时间不能早于机器和工人的可开始时间；式(13)、(14)分别定义工人和机器的结束时间；式(15)、(16)定义工人的工作时间和休息时间；式(17)、(18)分别基于式(5)、(6)计算工人在工作后和休息后的疲劳值；式(19)限定工人的疲劳值不能超过规定上限；式(20)为目标函数最大完工时间的计算式.

2. 改进的自适应大邻域搜索算法

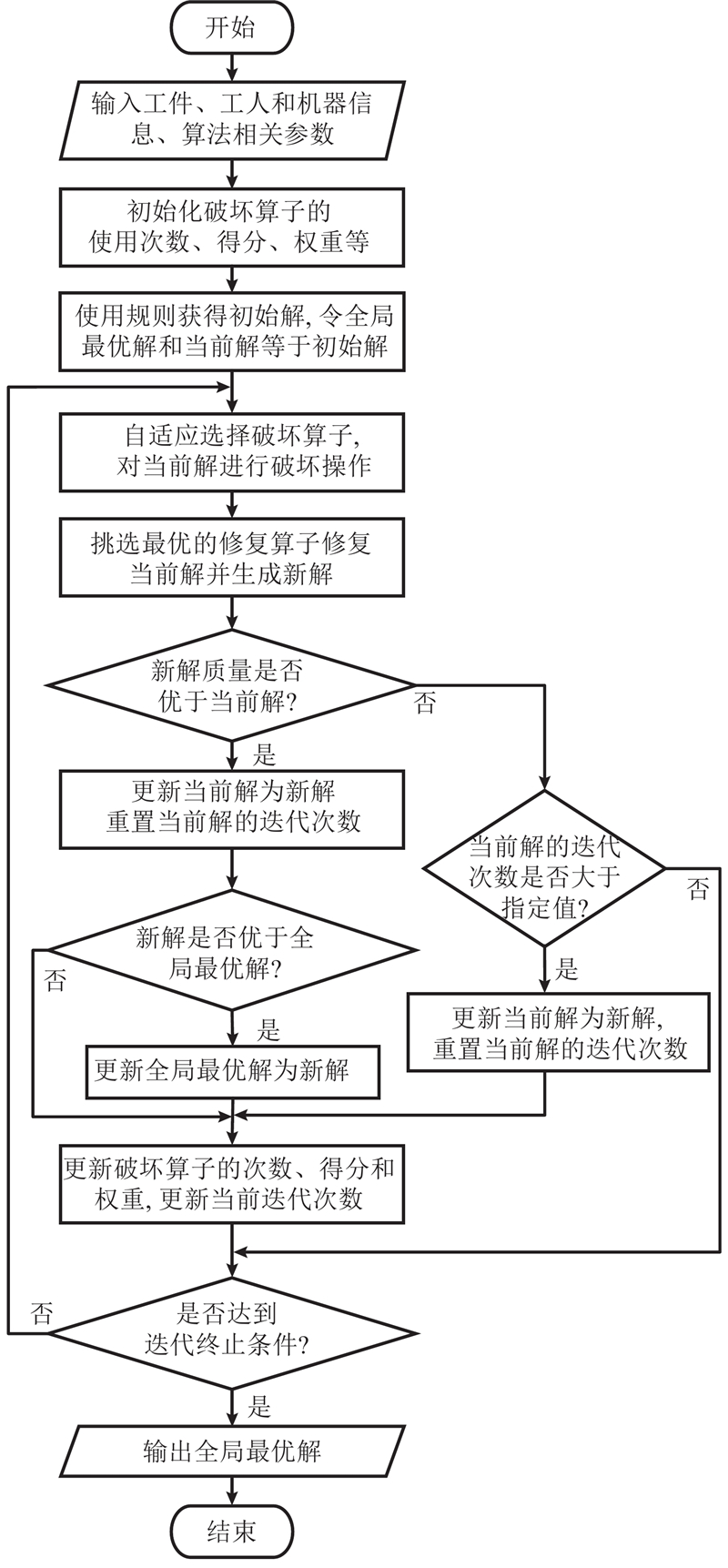
ALNS算法[21]能够在下一次迭代时，自适应选择历史表现选择好的操作算子，使算子的搜索性能得到充分发挥. 当标准ALNS算法用来求解DRCFJSP时，操作算子的权重和得分只有在获得更优解后才得到更新，同时由于随机因素的存在，每次迭代并不能准确地选择到当前最优的修复算子，导致算法在搜索的前期不能取得较好的效果，且容易在获得当前邻域的局部最优解之前进入下一邻域，即早熟问题. 本研究所提改进的ALNS算法使用多组破坏算子和修复算子，每次迭代根据历史表现只对破坏算子进行自适应选择，再挑选最优的修复算子，经破坏和修复后获得新解. 为了避免陷入局部最优，当多次迭代仍未找到更优解时，所提算法随机选择劣解更新当前解.

2.1. 编码与解码

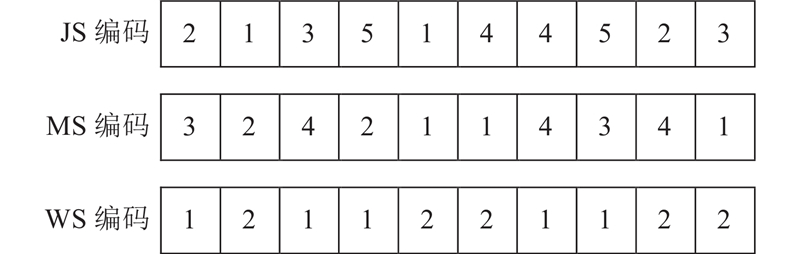
DRCFJSP的可行解可以用一定规则的编码来表达. 双资源约束的调度问题可被细分为工件排序、设备分配、工人指派3个子问题；相对应地，采用三级编码的方式，一级为工件排序(job sequence, JS)编码、二级为设备分配(machine sequence, MS)编码、三级为工人指派(worker sequence, WS)编码；二级和三级的编码长度与一级编码长度相同，即一一对应. JS编码的数字为工件序号；MS编码的数字表示为对应位置工件所选择的设备序号数；WS编码的数字为工人序号，其位置对应关系和MS编码相同. 如图3所示为2个工人操作4台设备加工5个工件(每个工件有2道工序)时的编码示例，其中JS编码左起第2、第5位置中的“1”分别表示工件1的第1、第2道工序，负责加工这2道工序的分别为机器2和工人2、机器1和工人2.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   可行解的编码示意图

Fig.3   Coding diagram of feasible solution


解码是将编码转化为目标函数的过程，不同的解码方式会影响目标函数的大小. 1）根据 JS编码中的顺序，依次为当前工件分配对应的机器和工人；2）由机器和工人的最早可开始时间确定当前工件的开始加工时间(机器的可开始时间是指机器加工上一个工件的结束时间，工人的可开始时间取决于工人加工上一个工件的结束时间和工人当前的疲劳值)，直至最后一个工件；3）获得最大完工时间，即目标函数的大小.

2.2. 初始解生成

初始解的生成基于一定的规则，且在一定程度上决定算法后续的优化效率. 合适的生成规则可以生成较好的初始解，有利于找到最优解. 本研究根据所要解决问题的特点，对工人、机器和工件的分配设计如下8种规则.

1)选择最早可用机器，再从可操作此机器的空闲工人中挑选最小疲劳值的工人，最后分配工件. 工件的优先级排序：工人操作时间升序、机器处理时间升序.

2) 与1)规则类似，工件的排序：工人操作时间升序、机器处理时间降序.

3) 与1)规则类似，工件的排序：工人操作时间降序、机器处理时间升序.

4) 与1)规则类似，工件的排序：工人操作时间降序、机器处理时间降序.

5)选择最早可用机器，再从可操作此机器的空闲工人中挑选最小疲劳值的工人，最后分配工件. 分配工件时，先计算所选工人的可继续加工时长，候选小于等于此时长的所有工件，再以工人操作时间降序、机器处理时间升序的方法排序.

6) 与5)规则类似，工件的排序：工人操作时间降序、机器处理时间降序.

7)选择最早完工工人，再从工人可操作的机器中挑选最早可用机器，最后分配工件. 分配工件时，先计算所选工人的可继续加工时长，将小于等于此时长的所有工件作为候选集，再以工人操作时间降序、机器处理时间升序的方法排序.

8) 与7)规则类似，工件的排序：工人操作时间升序、机器处理时间降序.

上述8种规则在运行前，须标记每个工件的加工用时最少的处理单元，即最优处理单元. 分配工件时，优先选择属于最优处理单元中的工件.

2.3. 操作算子

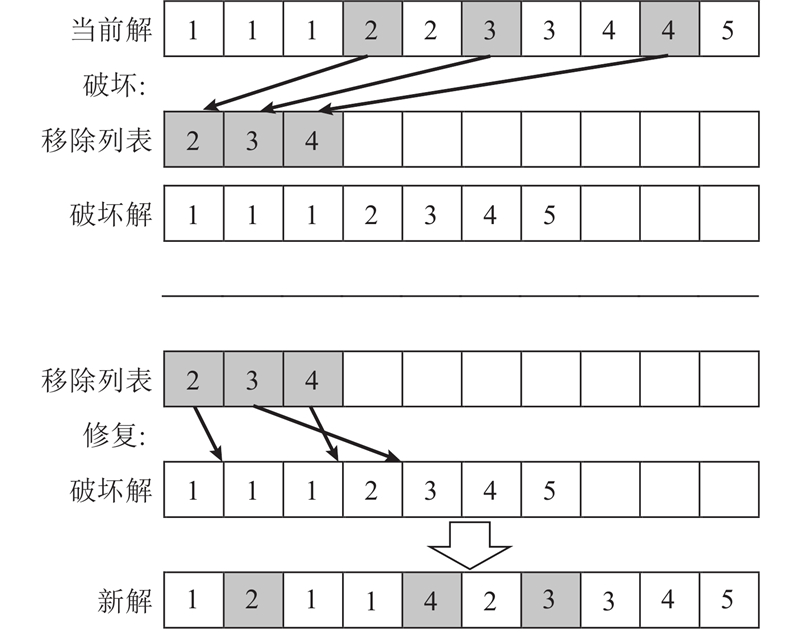
在生成初始解后，算法通过破坏算子对当前解中的若干个工件进行移除操作，再将移除的工件通过修复算子按照一定规则再插入，最终得到新的可行解，如图4所示. 针对破坏操作和修复操作，改进的ALNS算法设计6组不同的破坏算子和修复算子.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   操作算子的破坏和修复过程

Fig.4   Destruction and repair process of operator


2.3.1. 破坏算子

1) 随机破坏算子：随机选择原序列中的k个工件进行移除. 2) 贪婪破坏算子1：依次计算当前工件移除后对原序列成本的影响，取对成本影响最大的前k个工件作为最终要移除的工件. 3) 贪婪破坏算子2：依次计算当前工件移除后对原序列成本的影响，取对成本影响最大的工件作为当前要移除的工件，更新当前序列并重复此步骤k次. 4) 相似破坏算子：随机移除1个工件，计算移除工件对剩余工件的相似度，再移除相似度较高的k−1个工件，共计k个. 5) 贪心破坏算子1：与贪婪破坏算子1相似，但移除的是对成本影响最小的工件. 6) 贪心破坏算子2：与贪婪破坏算子2相似，但移除的是对成本影响最小的工件.

2.3.2. 修复算子

1) 随机修复算子：随机选择k个位置，将移除的工件依次插入. 2) 最优修复算子：从移除列表的第一个工件开始，每次选择成本最小的位置进行插入，直至所有工件插入完毕. 3) 随机最优修复算子：与最优修复算子相似，但移除工件列表要先随机打乱顺序. 4) 次优修复算子：与最优修复算子类似，但插入的位置是成本第2小的位置. 5) 后悔修复算子：计算每个移除工件的最优插入和次优插入的成本，后悔值即两者的成本差，根据后悔值由大到小对移除工件列表排序，按照最优修复算子进行相同的操作. 6) 逆序最优修复算子：与最优修复算子相似，但移除工件列表要进行逆序操作.

2.4. 自适应过程

ALNS算法的自适应是指在算法的执行过程中，动态调整算子权重并使用轮盘赌策略选择操作算子. 算子权重的更新公式[21]为

$ \omega = \omega \times (1 - \rho )+\rho \times {\alpha }/{\beta }. $

式中：ω为算子权重，α为算子分数，β为算子的使用次数，ρ为权重更新系数.

2.5. 改进的ALNS算法流程

所提算法使用得分机制自适应选择破坏算子，挑选最有利于当前解的修复算子，使得算法在每次迭代中都能找到较好的破坏-修复的组合方式. 若当前解在当前邻域经多次迭代仍未找到更优解，则认为其到达局部最优，此时随机选择劣解继续寻优. 算法的整体流程如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   改进自适应大邻域搜索算法流程图

Fig.5   Flow chart of improved adaptive large neighborhood search algorithm


3. 计算测试与分析

算法编程基于Python3.9实现，运行环境为英特尔i7-12700H CPU的Windows 11操作系统.

3.1. 算例生成

采用文献[26]中的方法生成算例，随机生成工件加工时间、工人疲劳率、工人疲劳上限等信息，以求解考虑工人疲劳的DRCFJSP. 小规模、中规模、大规模和超大规模的16个拓展算例命名为D1~D16，其中包括生产线总数A、工件总数n、待加工的工件编号、工人总数W、每条生产线工人数w、机器总数M、每条生产线机器的个数m，具体内容如表1所示.

表 1   算例的规模、工人及机器定义表

Tab.1  Table of scale, workers and machine definitions for examples

规模 算例 A n 工件编号 W w M m
小规模 D1 2 10 J1~J10 3 [2,1] 6 [4,2]
D2 2 10 J21~J30 3 [2,1] 6 [4,2]
D3 2 15 J1~J15 3 [2,1] 6 [4,2]
D4 2 15 J31~J45 3 [2,1] 6 [4,2]
中规模 D5 3 25 J1~J25 5 [2,2,1] 10 [4,4,2]
D6 3 25 J51~J75 5 [2,2,1] 10 [4,4,2]
D7 3 30 J1~J30 5 [2,2,1] 10 [4,4,2]
D8 3 30 J61~J90 5 [2,2,1] 10 [4,4,2]
大规模 D9 4 40 J1~J40 8 [3,2,2,1] 14 [5,4,3,2]
D10 4 40 J81~J120 8 [3,2,2,1] 14 [5,4,3,2]
D11 4 50 J1~J50 8 [3,2,2,1] 14 [5,4,3,2]
D12 4 50 J101~J150 8 [3,2,2,1] 14 [5,4,3,2]
超大规模 D13 5 70 J1~J70 11 [3,3,2,2,1] 20 [6,5,4,3,2]
D14 5 70 J101~J170 11 [3,3,2,2,1] 20 [6,5,4,3,2]
D15 5 90 J1~J90 11 [3,3,2,2,1] 20 [6,5,4,3,2]
D16 5 90 J81~J170 11 [3,3,2,2,1] 20 [6,5,4,3,2]

新窗口打开| 下载CSV


3.2. 休息方案

在考虑工人疲劳的DRCFJSP中，工人的休息方式是重要的影响因素. 休息时间过短，工人得不到有效休息；休息时间过长，生产的完工时间将受到影响. 为了避免工人的疲劳值超过规定上限，使用动态的休息方案：工人是否休息以及休息时长由工人当前疲劳值和下一个分配工件的加工时间动态确定. 根据工人当前疲劳值计算工人可继续加工时长，若工人下一个要加工的工件时长大于工人可继续加工时长，则工人需要休息(工人可继续加工时长会随休息时间而变化)，直至工人可继续加工时长大于等于工件时长.

假设工人疲劳的休息标准为fe，工人当前疲劳值为f0 (f0＜fe)，工人加工的下一个工件的加工时长为tw. 工人可继续加工时长的计算式为

$ {t_{\text{c}}} = \frac{1}{\lambda } \times \ln \frac{{1 - {f_0}}}{{1 - {f_{\text{e}}}}}. $

若tc≥tw，工人可继续工作；否则，工人需要休息，休息时长为τ，

$ \begin{split} {f_{\text{e}}} =& 1 - (1 - {f_1}) \times {{\rm{e}}^{ - \mu \times {t_{\text{w}}}}},\; {f_1} = {f_0} \times {{\rm{e}}^{ - \mu \times \tau }}, \\ &\tau = \frac{{\ln {f_0} - \ln {f_1}}}{\mu }. \\ \end{split} $

3.3. 规则对比

规则生成初始解时具有较快的速度，为了比较各个规则之间的差异，分别计算8个生成规则对应16个算例的性能，结果如表2所示，其中C1~C8分别表示算例在规则1)~8)的完工时间. 由表可知，每个算例的最优规则不尽相同，规则1)~8)取得最好结果的算例个数分别为6、3、0、0、2、2、4、5，其中规则1)最多，规则8)其次，规则7)第三.

表 2   规则和算例的比较实验结果

Tab.2  Comparative experimental results of rules and examples min

算例 C1 C2 C3 C4 C5 C6 C7 C8
D1 213 213 195 195 188 200 198 198
D2 249 249 221 221 217 217 219 219
D3 304 304 341 341 293 305 263 263
D4 305 302 282 282 280 293 279 279
D5 283 286 281 302 288 285 266 246
D6 280 285 336 382 319 340 286 286
D7 333 324 360 345 338 349 308 321
D8 302 312 323 330 315 294 317 300
D9 314 278 295 276 303 306 286 272
D10 283 283 353 301 307 297 297 297
D11 329 329 396 394 336 335 341 340
D12 361 394 398 399 397 375 374 369
D13 335 335 438 465 413 355 345 346
D14 398 429 421 402 369 390 355 359
D15 411 422 557 535 433 484 412 401
D16 414 435 500 507 445 432 430 420

新窗口打开| 下载CSV


由于算例的生成是随机的，为了避免实验偶然性带来的误差，使用相对百分比偏差指标来衡量算法的综合性能. 相对偏差越小，规则所得结果质量越高，计算每个规则在所有算例的偏差总和，取值最小的方案即为综合性能最好的首选规则. 相对百分比偏差计算式为

$ {P_{\text{D}}} = \frac{{{C_{\max }} - {C_{{\text{best}}}}}}{{{C_{{\text{best}}}}}} \times 100 \text{%} . $

式中：Cbest为当前算例所有规则Cmax的最小值. 由式（24）计算得到8个规则的偏差总和分别1.09、1.24、2.70、2.66、1.34、1.42、0.51、0.31，可以看出，规则8)偏差总和最小，具有最好的综合性能. 从理论上分析，规则8)为工人分配工件时会优先选择此工人可继续工作时长内的最大时长工件，有利于工人和工件资源的充分利用，因此选择规则8)作为算法初始解的生成规则.

3.4. 参数调试

算法参数的设置会影响算法的收敛速度和求解质量，改进ALNS算法主要涉及2个关键参数：迭代次数和破坏数量k. 从小、中、大、超大4个规模中各随机选择1个算例，测算最大迭代次数为300时，k=1~5的表现. 结果表明，无论k取何值，迭代次数超过100的完工时间已趋于稳定，考虑到过多的迭代次数会有较高的时间成本，因此选择迭代次数为100. 程序运行时间随着k的增大呈线性增长；本研究的优化目标是最小化完工时间，数据显示，随着k的增大目标函数值的提升空间逐渐缩小，为了避免过多的时间消耗，选择k=3，此时有较好的寻优效果和适中的运行时间. 本次实例计算分析设置算法参数如下：迭代次数为100，破坏数量k=3.

3.5. 实验结果与分析

改进ALNS算法存在随机因素，为了减少随机误差的影响，每个算例重复独立运行10次，并使用平均值AVE、最优值OPT、标准差STD、变异系数CV、平均运行时间ART 指标来衡量算法的性能，其中变异系数是标准差与平均值的比值，用来衡量样本的离散程度. 实验结果如表3所示. 可以看出，程序运行结果的标准差和变异系数都控制在较小范围内，表明所提算法在不同规模的算例上都能够保证一定的稳定性.

表 3   改进自适应大邻域搜索算法重复实验的结果

Tab.3  Results of repeated experiments on improved adaptive large neighborhood search algorithm

算例 OPT/min AVE/min STD CV ART/s
D1 171 171.8 0.40 0.002 1.9
D2 178 179.1 0.83 0.005 1.9
D3 237 238.5 1.02 0.004 4.7
D4 231 232.3 0.90 0.004 4.7
D5 235 237.4 1.80 0.008 13.8
D6 230 233.1 1.92 0.008 13.6
D7 284 285.2 1.17 0.004 20.3
D8 274 275.4 1.02 0.004 20.1
D9 259 261.2 1.83 0.007 35.8
D10 253 258.5 2.69 0.010 35.8
D11 308 312.1 2.39 0.008 57.0
D12 319 319.2 0.40 0.001 57.3
D13 304 307.9 2.66 0.009 115.5
D14 322 326.2 2.14 0.007 116.1
D15 376 380.8 1.99 0.005 194.9
D16 390 395.3 3.10 0.008 195.2

新窗口打开| 下载CSV


为了验证所提算法中自适应策略和初始解策略的有效性，设置随机选择操作算子和随机生成初始解的ALNS算法作为所提算法的对照实验，结果如表4所示，其中CS1、CS2、CS3分别表示算例在随机选择操作算子的ALNS算法、随机生成初始解的ALNS算法、所提算法的完工时间.结果显示，所提算法在全部算例中都取得了最好的结果，相较于随机选择操作算子和随机生成初始解的策略，自适应策略和规则生成初始解策略可以有效提高算法的寻优性能.

表 4   不同策略下自适应大邻域搜索算法对比实验结果

Tab.4  Comparative experimental results of adaptive large neighborhood search algorithm under different strategies

算例 CS1/min CS2/min CS3/min
D1 176 173 171
D2 180 178 178
D3 248 242 237
D4 232 231 231
D5 242 241 235
D6 247 243 230
D7 284 289 284
D8 283 281 274
D9 265 265 259
D10 265 261 253
D11 320 322 308
D12 327 323 319
D13 319 329 304
D14 329 333 322
D15 401 388 376
D16 409 398 390

新窗口打开| 下载CSV


使用Gurobi求解器[27]求解数学规划模型；生成规则具有计算量低、速度快、求解质量往往不高的特点，通常用于生成初始解；遗传算法是应用较为广泛的经典启发式算法；Jaya算法求解柔性作业车间调度问题的性能较好[28]；标准ALNS算法用于比较改进算法改进部分的优势. 对比上述5种算法，以进一步验证改进ALNS 算法的性能和效率. 其中设置Gurobi的最大求解时间为3 h，“—”表示Gurobi未在指定时间内获得可行解. 最终得到的实验结果如表5所示，其中C表示求解结果，RT表示算法耗时. 所提算法寻找的是最优的修复算子，因此耗时与标准ALNS算法的相比略有增加，但在求解质量上有了一定提升；所提算法相较于Jaya算法具有较好的寻优速度，相较于生成规则、遗传算法和标准ALNS算法具有较好的求解质量. 由于数学规划模型中加入了非线性的疲劳约束，在线性化处理的过程中须引入多个中间变量，使得Gurobi算法的求解难度增大，在有限的时间内的求解结果不如其他算法，如表中算例D1~D6.

表 5   6种优化算法的求解结果与耗时

Tab.5  Solution results and runtime of six optimization algorithms

算例 Gurobi求解器 生成规则 遗传算法 Jaya算法 标准ALNS算法 本研究算法
C/min RT/s C/min RT/s C/min RT/s C/min RT/s C/min RT/s C/min RT/s
D1 174 10800 188 <1 174 4.1 172 15.0 176 0.5 171 1.9
D2 183 10800 217 <1 180 4.3 187 15.1 180 0.5 178 1.9
D3 271 10800 263 <1 238 6.3 242 33.1 243 1.1 237 4.7
D4 338 10800 279 <1 236 6.1 243 34.3 238 1.2 231 4.7
D5 356 10800 246 <1 251 10.4 246 91.1 246 3.5 235 13.8
D6 368 10800 280 <1 249 10.2 253 89.3 239 3.1 230 13.6
D7 — 10800 308 <1 297 12.5 291 126.4 290 5.0 284 20.3
D8 — 10800 294 <1 294 12.4 280 122.7 288 5.0 274 20.1
D9 — 10800 272 <1 270 16.5 269 220.7 265 8.7 259 35.8
D10 — 10800 283 <1 270 16.4 267 221.5 264 8.4 253 35.8
D11 — 10800 329 <1 329 20.4 321 321.3 319 12.7 308 57.0
D12 — 10800 361 <1 337 20.7 329 377.0 332 14.6 319 57.3
D13 — 10800 335 <1 336 29.5 336 769.6 335 27.3 304 115.5
D14 — 10800 355 <1 344 30.1 342 769.2 332 29.4 322 116.1
D15 — 10800 401 <1 426 38.8 425 1159.0 401 46.1 376 194.9
D16 — 10800 414 <1 438 39.9 416 1105.3 420 51.1 390 195.2

新窗口打开| 下载CSV


为了减小求解难度，使用更小规模的算例X1、X2验证数学规划模型的正确性. 其中X1和X2的单元总数为1、工件总数为6、工人总数为2、机器总数为4，X1、X2要加工的工件分别为J1~J6、J21~J26. 超小规模算例在6中算法的求解结果和耗时结果如表6所示. 由表可知，在超小规模算例中，Gurobi、遗传算法、Jaya算法、标准ALNS算法、改进ALNS算法都取得了最优解，验证了本研究混合整数规划模型的正确性.

表 6   超小规模算例的求解结果与耗时

Tab.6  Solution results and runtime of ultra-small scale example

算例 Gurobi 遗传算法 Jaya算法 标准ALNS算法 本研究算法
C/min RT/s C/min RT/s C/min RT/s C/min RT/s C/min RT/s
X1 141 1800 141 1.1 141 3.2 141 0.4 141 0.8
X2 138 1800 138 1.1 138 3.2 138 0.4 138 0.8

新窗口打开| 下载CSV


综上所述，本研究所提改进ALNS算法具有如下特点：1) 寻优性能强，可获得比标准ALNS算法更高质量的解；2) 具有一定的稳定性；3) 能够应用于多规模问题的求解.

4. 结　语

本研究基于DRCFJSP，考虑工人的疲劳因素，建立相应的混合整数规划模型. 在超小规模场景下，Gurobi、遗传算法、Jaya算法、标准ALNS算法相同的求解结果验证了本研究数学规划模型的正确性. 所提改进ALNS算法，设置6组破坏算子、6组修复算子求解不超过工人疲劳上限的最早完工时间. 通过不同规模大小的算例验证了所提算法的稳定性，与遗传算法、Jaya算法、标准ALNS算法的求解质量和求解效率对比验证了所提算法的良好求解性能. 所提算法可以有效解决作业车间调度过程中的工人疲劳问题，保障工人的身心健康和安全，提高联合调度过程中的资源利用率和生产率. 未来计划在更复杂约束下考虑工人疲劳的DRCFJSP（如考虑工件有多个加工工序、工件和工人在不同机器上的转移时间、工件的临时变动与插单、机器的不确定性故障等）；此外，还将进一步优化算法的性能，提出更好的搜索方法来提升算法的搜索效率.

参考文献

LERMAN S E, ESKIN E, FLOWER D J, et al

Fatigue risk management in the workplace

[J]. Journal of Occupational and Environmental Medicine, 2012, 54 (2): 231- 258

DOI:10.1097/JOM.0b013e318247a3b0      [本文引用: 17]

CAVUOTO L, MEGAHED F. Understanding fatigue and the implications for worker safety [C]// ASSE Professional Development Conference and Exposition. Atlanta: [s.n.], 2016: 1457-1465.

[本文引用: 44]

SAWATZKY S

Worker fatigue: understanding the risks in the workplace

[J]. Professional Safety, 2017, 62 (11): 45- 51

[本文引用: 21]

BALAS J. How you could pay the price for exhausted employees [EB/OL]. (2018-06-18)[2022-08-30]. https://www.constructionbusinessowner.com/safety/how-you-could-pay-price-exhausted-employees.

[本文引用: 21]

EL MOUAYNI I, ETIENNE A, LUX A, et al

A simulation-based approach for time allowances assessment during production system design with consideration of worker's fatigue, learning and reliability

[J]. Computers and Industrial Engineering, 2020, 139: 105650

DOI:10.1016/j.cie.2019.01.024      [本文引用: 9]

SUN W, PAN Y, LU X, et al

Research on flexible job-shop scheduling problem based on a modified genetic algorithm

[J]. Journal of Mechanical Science and Technology, 2010, 24 (10): 2119- 2125

DOI:10.1007/s12206-010-0526-x      [本文引用: 5]

赵诗奎, 方水良, 顾新建

柔性车间调度的新型初始机制遗传算法

[J]. 浙江大学学报: 工学版, 2013, 47 (6): 1022- 1030

ZHAO Shi-kui, FANG Shui-liang, GU Xin-jian

Genetic algorithm with new initialization mechanism for flexible job shop scheduling

[J]. Journal of Zhejiang University: Engineering Science, 2013, 47 (6): 1022- 1030

王雷, 蔡劲草, 唐敦兵, 等

基于改进遗传算法的柔性作业车间调度

[J]. 南京航空航天大学学报, 2017, 49 (6): 779- 785

[本文引用: 1]

WANG Lei, CAI Jin-cao, TANG Dun-bing, et al

Flexible job shop scheduling problem based on improved genetic algorithm

[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2017, 49 (6): 779- 785

[本文引用: 1]

NOUIRI M, BEKRAR A, JEMAI A, et al

An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem

[J]. Journal of Intelligent Manufacturing, 2018, 29 (3): 603- 615

DOI:10.1007/s10845-015-1039-3      [本文引用: 1]

ZHANG G, LU X, LIU X, et al

An effective two-stage algorithm based on convolutional neural network for the bi-objective flexible job shop scheduling problem with machine breakdown

[J]. Expert Systems with Applications, 2022, 203: 117460

DOI:10.1016/j.eswa.2022.117460      [本文引用: 1]

TEYMOURIFAR A, OZTURK G

A neural network-based hybrid method to generate feasible neighbors for flexible job shop scheduling problem

[J]. Universal Journal of Applied Mathematics, 2018, 6 (1): 1- 16

DOI:10.13189/ujam.2018.060101      [本文引用: 1]

JAMSHIDI R

Maintenance and work-rest scheduling in human-machine system according to fatigue and reliability

[J]. International Journal of Engineering, 2017, 30 (1): 85- 92

[本文引用: 1]

FERJANI A, AMMAR A, PIERREVAL H, et al

A simulation-optimization based heuristic for the online assignment of multi-skilled workers subjected to fatigue in manufacturing systems

[J]. Computers and Industrial Engineering, 2017, 112: 663- 674

DOI:10.1016/j.cie.2017.02.008      [本文引用: 1]

MENG L, ZHANG C, ZHANG B, et al

Mathematical modeling and optimization of energy-conscious flexible job shop scheduling problem with worker flexibility

[J]. IEEE Access, 2019, 7: 68043- 68059

DOI:10.1109/ACCESS.2019.2916468      [本文引用: 1]

MOKHTARI G, ABOLFATHI M

Dual resource constrained flexible job-shop scheduling with lexicograph objectives

[J]. Journal of Industrial Engineering Research in Production Systems, 2021, 8 (17): 295- 309

[本文引用: 1]

ZHANG S, DU H, BORUCKI S, et al

Dual resource constrained flexible job shop scheduling based on improved quantum genetic algorithm

[J]. Machines, 2021, 9 (6): 108- 123

DOI:10.3390/machines9060108      [本文引用: 1]

TAN W, YUAN X, WANG J, et al

A fatigue-conscious dual resource constrained flexible job shop scheduling problem by enhanced NSGA-II: an application from casting workshop

[J]. Computers and Industrial Engineering, 2021, 160: 107557

DOI:10.1016/j.cie.2021.107557      [本文引用: 1]

DEFERSHA F M, OBIMUYIWA D, YIMER A D

Mathematical model and simulated annealing algorithm for setup operator constrained flexible job shop scheduling problem

[J]. Computers and Industrial Engineering, 2022, 171: 108487

DOI:10.1016/j.cie.2022.108487      [本文引用: 1]

FARJALLAH F, NOURI H E, BELKAHLA DRISS O. Multi-start Tabu agents-based model for the dual-resource constrained flexible job shop scheduling problem [C]// International Conference on Computational Collective Intelligence. [S.l.]: Springer, 2022: 674-686.

[本文引用: 1]

孙宝凤, 任欣欣, 郑再思, 等

考虑工人负荷的多目标流水车间优化调度

[J]. 吉林大学学报: 工学版, 2021, 51 (3): 900- 909

[本文引用: 1]

SUN Bao-feng, REN Xin-xin, ZHENG Zai-si, et al

Multi-objective flow shop optimal scheduling considering worker’s load

[J]. Journal of Jilin University: Engineering and Technology Edition, 2021, 51 (3): 900- 909

[本文引用: 1]

ROPKE S, PISINGER D

An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows

[J]. Transportation Science, 2006, 40 (4): 455- 472

DOI:10.1287/trsc.1050.0135      [本文引用: 3]

伍国华, 毛妮, 徐彬杰, 等

基于自适应大规模邻域搜索算法的多车辆与多无人机协同配送方法

[J]. 控制与决策, 2023, 38 (1): 201- 210

[本文引用: 1]

WU Guo-hua, MAO Ni, XU Bin-jie, et al

The cooperative delivery of multiple vehicles and multiple drones based on adaptive large neighborhood search

[J]. Control and Decision, 2023, 38 (1): 201- 210

[本文引用: 1]

徐倩, 熊俊, 杨珍花, 等

基于自适应大邻域搜索算法的外卖配送车辆路径优化

[J]. 工业工程与管理, 2021, 26 (3): 115- 122

XU Qian, XIONG Jun, YANG Zhen-hua, et al

Route optimization of takeout delivery vehicles based on adaptive large neighborhood search algorithm

[J]. Industrial Engineering and Management, 2021, 26 (3): 115- 122

MARA S T W, NORCAHYO R, JODIAWAN P, et al

A survey of adaptive large neighborhood search algorithms and applications

[J]. Computers and Operations Research, 2022, 146: 105903

DOI:10.1016/j.cor.2022.105903      [本文引用: 1]

RIFAI A P, NGUYEN H T, DAWAL S

Multi-objective adaptive large neighborhood search for distributed reentrant permutation flow shop scheduling

[J]. Applied Soft Computing, 2016, 40: 42- 57

DOI:10.1016/j.asoc.2015.11.034      [本文引用: 1]

DU H, QIAO F, WANG J, et al. A hybrid metaheuristic algorithm with novel decoding methods for flexible flow shop scheduling considering human fatigue [C]// 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Melbourne: IEEE, 2021: 2328-2333.

[本文引用: 2]

Gurobi Optimization. Gurobi optimizer quick start guide, [EB/OL]. [2022-08-30]. https://www.gurobi.com/documentation/quickstart.html.

[本文引用: 1]

郭鹏, 赵文超, 雷坤

基于改进Jaya算法的双资源约束柔性作业车间优化调度

[J]. 吉林大学学报: 工学版, 2023, 53 (2): 480- 487

[本文引用: 1]

GUO Peng, ZHAO Wen-chao, LEI Kun

Dual-resource constrained flexible job shop optimal scheduling based on an improved Jaya algorithm

[J]. Journal of Jilin University: Engineering and Technology Edition, 2023, 53 (2): 480- 487

[本文引用: 1]

/

〈 〉