随着社会经济发展和城市化进程加快，资源环境问题日益突出^[1]. 电动汽车（electric vehicle, EV）作为交通运输领域清洁能源技术的代表，具有能量密度高、环境污染小的优点，EV保有量持续增加，使得充电服务需求迅速扩大^[2-3]. 充电基础设施规划不尽合理；充电市场面临充电站投建不精准、布局不合理，投建后利用率低、管理不到位、投资回报率不高等实际问题. 例如，集中于主城区的日益增长的充电需求与城市郊区充电桩的高闲置率，构成城市充电设施供需不平衡的主要矛盾. 可见，充电设施布局和定价策略的研究不仅关乎充电站经济效益和充电设施资源配置，也与经济社会可持续发展息息相关. 本研究建立EV用户效用最大化模型，结合多项Logit（multinominal Logit model, MNL）模型分析平台利润最大化以及社会福利最大化，推导最优定价以及充电设施数量满足的卡罗需−库恩−塔克（Karush-Kuhn-Tucker, KKT）条件，分析相关参数敏感性. 研究旨在在满足用户服务需求和充电站实际约束的前提下，为推动形成适度超前、布局均衡、智能高效的充电基础设施体系提供参考.

在充电设施定价方面，EV用户充电行为是定价的重要依据，涉及平台、用户、电网的多方博弈分析. 孙丙香等^[4]采用Logit模型并结合消费者、运营商以及政府的博弈理论进行分析，为政府决策提供参考. 洪奕等^[5]基于差异化理论构建混合型需求响应策略，研究新能源消费者的不同响应. 赵星宇等^[6]将定价作为主要策略，研究利润最大化下的充电行为，并应用深度强化学习进行求解. Gong等^[7]的研究表明，充电负荷分布会影响充电定价.

在充电负荷特性方面，已有研究考虑移动特性的停车生成率模型，包括车型差异和电池特性分析. Aujla等^[8]针对充电桩用户和充电桩运营商构建斯塔克伯格博弈模型，分析如充电时长、用电量、电池特性和电动汽车类型等一系列充电负荷特性参数的敏感性，从不同角度制定了共享定价方案.

在充电设施或加油站的数量优化和站点规划方面，已有研究集中于站点的选址布局优化. 高建树等^[9]运用遗传算法对充电桩的选址进行优化，基于电动汽车运行规律，将行车距离和充电时长最小化. 魏秀岭等^[10]基于Voronoi生成方法和粒子加权算法，将站点服务范围与站点参数相关联，对充电站布局和充电桩类型进行探究. Capar等^[11]在截流选址模型基础上，分别设计给定加油站数量的流续航选址模型和考虑车辆行程和路线的广义流续航选址模型. Chen等^[12]研究高速公路场景下的快速充电优化方法，利用多输出充电策略提高充电桩利用率. 宋建^[13]研究电网和电动汽车的博弈体系，提出基于博弈论的电动汽车优化充电策略. 一方面，上述研究主要从用户侧出发，探讨如何更好地满足补能需求，如最小化出行成本、降低充电或加油的等待时间，关注运营商效益等优化目标，但对充电站本身属性（如充电站规模、充电设施数量、充电站电价等）的研究较少，未调控区域间的充电需求.

针对充电平台供给和用户需求的时空供需协调问题，本研究建立EV用户充电效用及行为决策模型，分别考虑多区域间利润最大化和社会福利最大化目标函数，分析主要参数的敏感性，在优化模型基础上，提出具有区域差异化的充电站布局规划，形成充电桩投放数量和时空差异化定价的协同优化策略.

假设存在营利性充电设施平台，为 $ M $个区域提供电动汽车充电服务，充电时段分为高峰期和低谷期，充电市场中除该平台外还存在私人充电桩. 区域 $ i $有 $ {N}_{i} $个充电桩，每天充电需求量为 $ {D}_{i} $， $ i\in I\equiv \{\mathrm{1,2},\cdots ,M\} $. 用户可选择前往不同区域充电，考虑因素包括不同区域的充电价格、临近区域是否为高峰期、寻找闲置充电桩的时间成本和绕路行驶成本等. 用户驾驶EV从区域 $ j $前往区域 $ i $充电，定义 $ t $时段从区域 $ j $前往区域 $ i $充电的用户效用为

(1) $ {u}_{ij}^{t}=-{p}_{i}^{t}B-2{L}_{ij}+\gamma \left(1-{\alpha {L}_{ij}}/{B}\right)-{C}_{{\rm{s}}}\left({N}_{it}^{{\rm{v}}}\right) . $

式中： $ {p}_{i}^{t}\mathrm{为}\mathrm{单}\mathrm{位}\mathrm{充}\mathrm{电}\mathrm{价}\mathrm{格} $，影响用户充电意愿， $ {p}_{i}^{t} $越小，用户前往该区域充电的意愿越高； $ B\mathrm{为}\mathrm{用}\mathrm{户} \mathrm{心}\mathrm{理}\mathrm{预}\mathrm{期}\mathrm{的}\mathrm{待}\mathrm{充}\mathrm{电}\mathrm{量} $； $ {L}_{ij} $为开往其他区域比停留本区域多出的EV耗电量，包括耗电成本、时间成本、不方便性成本等，满足 $ {L}_{ii}=0,i\in I $. 假设综合绕路成本转化为耗电量的量纲转换系数为 $ \alpha $，用户从区域 $ j $充满电后回到区域 $ i $的耗电量为 $ \alpha {L}_{ij} $，回到区域 $ i $的剩余电量比例为 $ 1-\alpha {L}_{ij}/B $； $ \gamma \mathrm{为}\mathrm{用}\mathrm{户}\mathrm{充} \mathrm{满}\mathrm{电}\mathrm{获}\mathrm{得}\mathrm{的}\mathrm{感}\mathrm{知}\mathrm{效}\mathrm{用} $，充完电后返回原区域的感知效用为 $ \gamma \left(1-\alpha {L}_{ij}/B\right) $. $ \alpha $越大， $ {u}_{ij}^{t} $越小，即充电距离越远，用户越不愿意前往充电； $ \gamma $越大， $ {u}_{ij}^{t} $越大. $ {N}_{it}^{{\rm{v}}}\mathrm{为}\mathrm{用}\mathrm{户}\mathrm{效}\mathrm{用}\mathrm{增}\mathrm{加} \mathrm{区}\mathrm{域}i\mathrm{的}\mathrm{空}\mathrm{余} \mathrm{充}\mathrm{电}\mathrm{站}\mathrm{数}\mathrm{量} $，模拟充电桩是否充足对用户心理的影响. $ {C}_{{\rm{s}}}\left({N}_{it}^{{\rm{v}}}\right)$为成本函数， 代表区域 $ i $内用户的寻桩成本. 因此， $ {N}_{it}^{v} $越大， $ {u}_{ij}^{t} $越大，平台运营成本 $ C $就越大.

为了贴合实际情况，考虑充电排队情形，在此基础上，引入MNL模型刻画用户前往不同区域的充电选择行为，

(2) $ {D}_{ij}^{t}={D}_{j}^{t}\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\theta }_{i}^{t}{u}_{ij}^{t}\right)}{\mathrm{exp}\left({\theta }_{i}^{t}{\overline{u}}_{i}^{t}\right)+{\displaystyle\sum }_{{j}^{\text{'}}\in I}\mathrm{e}\mathrm{x}\mathrm{p}\left({\theta }_{i}^{t}{u}_{i{j}^{\text{'}}}^{t}\right)} . $

式中： $ {D}_{j}^{t}\mathrm{为}\mathrm{模}\mathrm{型}\mathrm{调}\mathrm{控}\mathrm{前}t\mathrm{时}\mathrm{段}j\mathrm{区}\mathrm{域}\mathrm{的}\mathrm{需}\mathrm{求}\mathrm{量}，{D}_{ij}^{t} $为模型调控后 $ t\mathrm{时}\mathrm{段}\mathrm{区}\mathrm{域}j $前往区域 $ i $的新需求量，所构成的充电需求矩阵为 $ {{\boldsymbol{D}}}^{t} $； $ {\theta }_{i}^{t} $为敏感度； ${\overline{u}}_{i}^{t}$为在 $ t $时段区域 $ i $的外部选择效用，比如暂且不充电或选择私人充电桩充电的效用，引入外部选择完善模型中的用户选项. 加入空余充电桩数量用于模型描述寻桩排队对用户的影响，为了减少出现用户排队充电现象，引入空余充电桩数量：

(3) $ {N}_{it}^{{\rm{v}}}={N}_{i}-{\sum }_{j\in I}\beta B{D}_{ij}^{t} . $

式中： $ \;\beta $为充电敏感度因子，表示单位电池容量的充电时长； $ {N}_{i} $ 为区域 $ i $ 内建设的充电桩总数； $ {\displaystyle\sum }_{j\in I}\beta B{D}_{ij}^{t} \mathrm{为}\mathrm{被}\mathrm{占}\mathrm{用} \mathrm{的}\mathrm{充}\mathrm{电}\mathrm{桩}\mathrm{数}\mathrm{量} $.

将平台充电桩数量和充电价格进行协同优化以实现利润最大化，在不同时段设定不同充电桩的充电价格和充电桩数量以降低总成本. 模型中的平台综合运营成本 $ C $包含建桩成本和电费2个部分. 在建桩成本中，外生参数 $ {r}_{i} $为在区域 $ i $建设并维持1个充电桩的成本均摊（考虑地租价格）；在电费成本参数中， $ {k}^{t} $为 $ t $时段的电价，根据实际场景中分时定价的设定，高峰时期电价上涨，平台成本随之增加. 定义T为不同时段的集合，平台综合运营成本函数表达式为

(4) $ C={\sum }_{i\in I}\left({r}_{i}{N}_{i}+{\sum }_{t\in T}{\sum }_{j\in I}B{k}^{t}{D}_{ij}^{t}\right) . $

充电平台成本主要包括充电桩建设成本及电力成本，平台运营的主要利润来自于EV充电用户，充电价格和充电意愿决定充电需求量. 平台综合运营收入 $ E $可以表示为各区域、各时间段的充电费用收入之和。平台利润 ${\varPi }$等于运营收入 $ E $减去运营成本 $ C $. 综上，平台利润最大化模型可以表示为

(5) $ \begin{split} \underset{{p}_{i}^{t},{N}_{i}}{\mathrm{max}}\;{\varPi }=&E-C .\\ & \mathrm{s}.\mathrm{t}.\;\mathrm{式}(1)\sim (4),\;{N}_{it}^{{\rm{v}}} \geqslant 0 . \end{split} $

(6) $ E={\sum }_{t\in T}{\sum }_{i\in I}{\sum }_{j\in I}{p}_{i}^{t}B{D}_{ij}^{t} . $

调节平台在不同时段的充电价格、服务价格以及在该区域内设置合理的充电桩数量，让用户获得较高的充电意愿，兼顾用户满意度和平台合理收益，在双方互利共赢基础上，实现社会福利 $ \mathrm{S}\mathrm{W} $最大化：

(7) $ \begin{split} \underset{{p}_{i}^{t},{N}_{i}}{\mathrm{max}}\;\mathrm{S}\mathrm{W}=&{\eta_{\rm{p}}}\varPi +{\eta }_{{\rm{u}}}{\sum }_{i,j\in I}{\sum }_{t\in T}{u}_{ij}^{t}{D}_{ij}^{t}.\\ &\mathrm{s}.\mathrm{t}.\;\mathrm{式}(1)\sim (4),\;{N}_{\mathit{it}}^{{\rm{v}}}\geqslant 0 . \end{split} $

式中： $ {\displaystyle\sum }_{i,j\in I}{\displaystyle\sum }_{t\in T}{u}_{ij}^{t}{D}_{ij}^{t} $为所有区域及所有时段的用户总效用， $ {\eta }_{{\rm{p}}} $、 $ {\eta }_{{\rm{u}}} $分别为对应于平台利润和用户总效用的权重系数. 政府税收与社会福利是相辅相成、密不可分的整体，对于起步阶段的新兴产业，在社会福利计算中给予企业盈利较高的权重，有利于企业获得长足发展，兼顾用户积极性，综合考虑企业利润以及个人效用，提高用户幸福满意度. 本研究参考企业所得税与个人所得税的税收比，确定平台利润和用户总效用的权重系数.

以杭州市的3个行政区为例（ $ M=3 $），设置1为上城区（中心区域），2为西湖区（较近区域），3为余杭区（较远区域），考虑高峰期和低谷期2个典型时段 $ T=\left\{\mathrm{0,1}\right\} $. 定义 $ B=44 $ kW·h，根据杭州市区域内工业用电文件规定，假设高峰期电价为0.7元/kW·h，低谷期电价为0.4元/kW·h. 从市中心到市郊的充电桩场地租金成本 $ r=[100,\mathrm{ }72,\mathrm{ }53] $ 元，由于市区到市郊的建设标准递减，租金成本亦为递减. $ \alpha =0.2 $、 $\; \beta =1/300 $、 $ \gamma =180 $. 社会福利模型权重 $ {\eta }_{\rm{p}} $、 $ {\eta }_{\rm{u}} $与政府税收密不可分. 2017—2021年全国公共税收C_T情况 ^[14]如表1所示. 企业所得税与个人所得税比重为3∶1, 本研究设置社会福利模型权重为 $ {\eta }_{\rm{p}}=0.75 $、 $ {\eta }_{\rm{u}}=0.25 $. 根据平台业务数据统计，得到高峰期、低谷期所研究的3个行政区的日均EV充电需求量 $\mathop D\nolimits_{\dot J}^0 、\mathop D\nolimits_{\dot J}^1 $如表2所示. 平台业务数据统计得到3个区域的充电桩及充电日均需求量分布如图1所示。可以看出，充电桩在居民区和景区的分布较为密集. 高峰期时段3个区域之间的通行成本 $ {L}_{ij} $如表3所示. 需要注意的是， $ {L}_{ij} $仅代表区域间通行成本，若不需要跨区域出行，区域内的绕路和寻桩成本已包含在成本项 $ {C}_{\rm{s}} $当中.

如图2所示，根据多区域协同调价数据模型，分析价格P、充电桩数量N_i和利润的趋势关系。当P=0~4元、N_i=0~1 000时，多区域协同调价决策变量的利润在高峰期、低谷期都呈现凸性，可以求得最优解，本研究通过KKT条件求解利润最大化目标下的最优价格和充电桩数量.

如图3所示，根据多区域协同调价数据模型分析价格、充电桩数量和社会福利的趋势关系。当P=0~4元、N_i=100~1 000时，多区域协同调价决策变量的社会福利在高峰期、低谷期都呈现凸性，可以求得最优解，本研究通过KKT条件求解社会福利最大化目标下的最优价格和充电桩数量.

选择合适区间，对3个区域协同优化结果进行分析，如表4、5所示. 在利润最大化目标下，高峰期、低谷期的充电价格均表现为越接近中心区域价格越高，越接近郊区价格越低，且高峰期价格递减幅度大于低谷期. 充电桩最优数量同样从中心到郊区递减，但空余充电桩数量存在中间区域偏多的情况，这是由于为满足高峰需求量设置较多空桩但实际需求在其他时段远低于中心区域. 由表4可以看出，用户在本区域的充电需求量远大于跨区域充电，通过合理定价和优化配置充电桩数量可以在一定程度上调控充电需求量，提升平台利润.

根据设定的参数及协同优化模型求解社会福利最大化模型的最优解，如表6、7所示. 在利润最大化情况下，上城区、西湖区、余杭区的高峰期最优价格分别为1.67、1.62、1.57元，低谷期最优价格分别为1.35、1.32、1.28元，多区域最大化利润为235 618.45元；在社会福利最大化情况下，高峰期最优价格分别为1.62、1.56、1.51元，低谷期最优价格分别为1.28、1.23、1.20元；多区域最大化社会福利为287 292.40元. 可以看出，3个区域均表现出社会福利最大化价格略低于利润最大化价格，原因在于平台设置较低定价以增加用户满意度，平台为实现社会福利最大化舍弃了一部分利润，用于增加用户满意度，具有现实含义. 无论是利润最大化条件还是社会福利最大化条件，3个区域均表现出低谷期价格差异比高峰期更为明显，原因是当处在充电高峰期时，位于中心区域的用户在本区域本难以找到充电桩，增加了向附近区域充电的动机；在低谷期时间段时，用户在本区域内找到合适充电桩的概率更大，只有在邻区价格较低时才能吸引用户. 3个不同区域不同时段的价格差异类似，可见在2个目标函数下时段对不同区域的影响是相似的.

对比社会福利最大化情形与利润最大化情形的充电桩数量设置，上城区、西湖区、余杭区高峰期的最优充电桩数量分别为288、278、183个，在社会福利最大化条件下同期价格为309、300、195个. 3个区域均表现出社会福利最大化情形的数量略高于利润最大化情形，原因在于平台设置更多的充电桩数量以减少排队时间. 无论高峰期还是低谷期，上城区、西湖区2个区间的最优充电桩数量差值为10个左右，西湖、余杭2个区间的最有充电桩数量相差接近100个，可见充电站位置与中心区域距离的影响因素对充电桩数量的影响呈现放大趋势，原因是当充电距离增加到达一定数值时，用户选择远区域的意愿会大大降低，需求量也会随之下降，再低廉的价格也无法吸引用户跨越远距离充电，因此只需设置较少充电桩就能满足郊区需求.

以上优化结果表明，在平台利润最大化以及社会福利最大化目标下，充电价格和充电桩数量均呈现从市区到郊区呈递减趋势，价格递减幅度平稳，充电桩数量递减幅度随距离增加而增加. 原因是充电平台需要在较远区域适当降价来吸引用户，以减轻市中心负担，更充分利用较远区域的充电设施资源，符合实际应用中的充电供需关系.

用户效用结果显示，就区域内而言，郊区的用户效用比市区高，说明郊区用户满意度更高；就区域间而言，前往郊区的充电意愿相对较低，距离越远用户意愿越低，在实际应用中极少出现用户远距离充电的情况. 空余充电桩数量的结果显示，中间区域的空余充电桩数量相对较多. 原因在于市中心和郊区建桩量已经过优化，得到了更有效利用，但中间区域在满足高峰需求的情况下更易出现低谷期充电桩剩余，无法兼顾需求和成本，在后续研究中可以深入探究如何优化低谷期空桩量，不造成资源浪费.

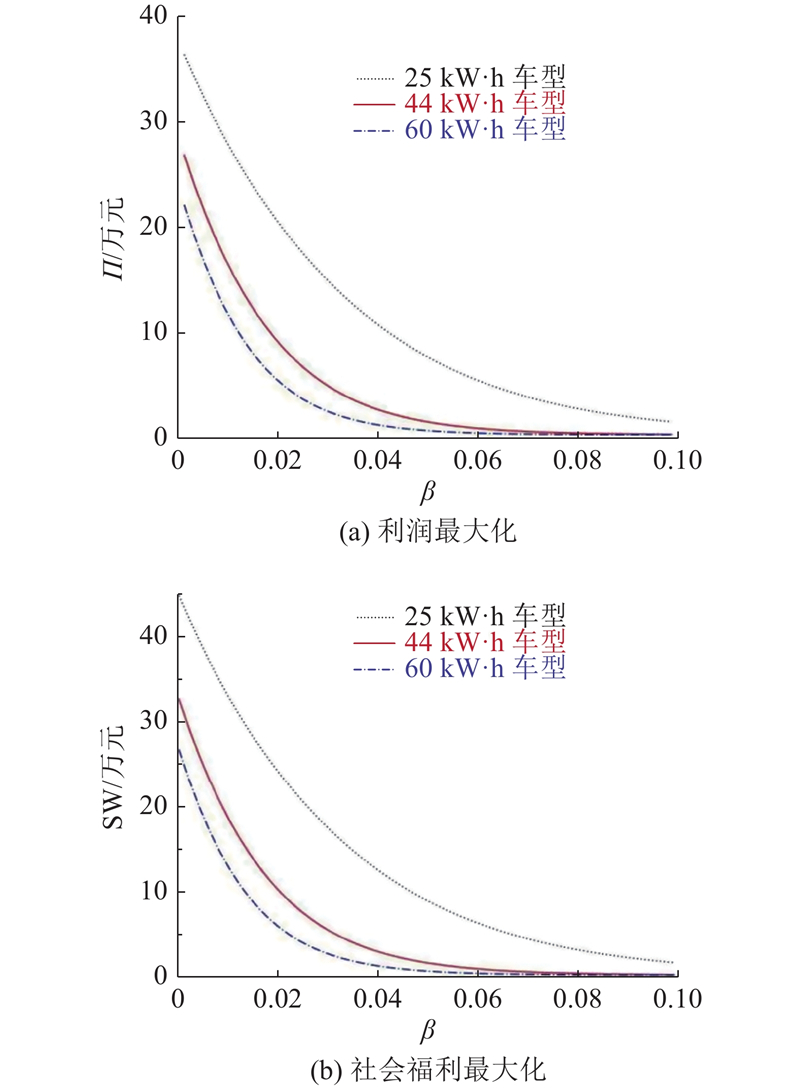
如图4所示，分析多区域价格优化条件的EV电池容量和充电敏感度因子的敏感性，揭示对平台利润和社会福利的影响效应. 当电池容量增大时，利润和社会福利均下降，可见单纯增大电池容量参数，与平台收益和社会福利无明显正相关. 当 $ \;\beta $∈[0.001, 0.100]时，平台利润和社会福利的曲线均呈下降趋势，其中当 $ \;\beta $∈(0.001, 0.020)时，社会福利的曲线比平台利润的更显著；当 $ \;\beta $﹤0.01时，中小型电池车辆的利润和社会福利降幅尤为明显. 3种车型的平台利润和社会福利变化随着 $ \;\beta $的变大而变小，说明充电速度越快平台利润越大，社会福利越大，用户满意度就越强. 从中小型电池车辆在2种情况中目标数值降幅都尤为明显可知，用户对充电快慢敏感度高，可以针对这一特性，在实际应用中建设更多快充电桩来平衡用户需求，更快更好地获得社会指标成效.

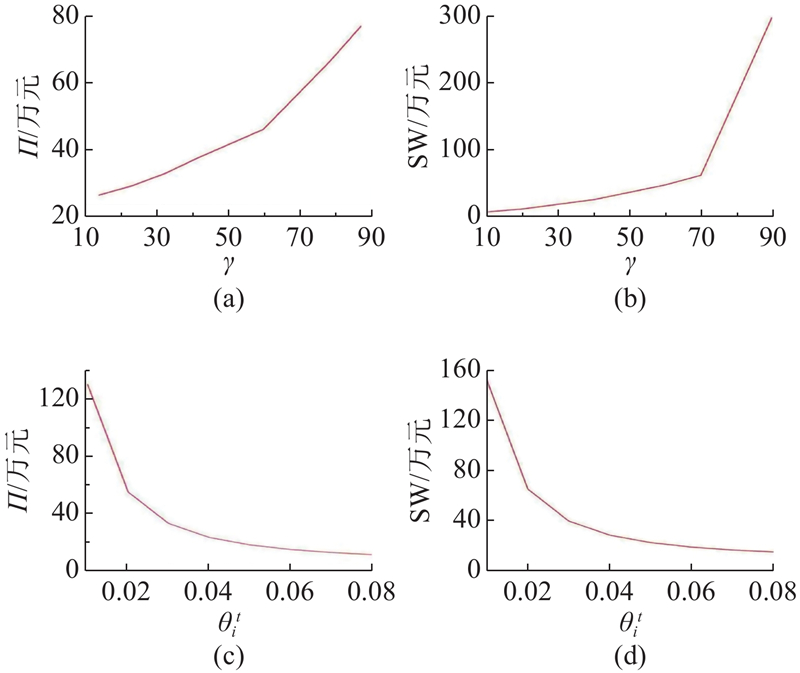
如图5所示，通过对MNL模型敏感度 $ {\theta }_{i}^{t} $、用户充满电所获得的感知效用 $ \gamma $与平台利润、社会福利敏感性分析可知，平台利润和社会福利都随着感知效用的增大而增大，原因是当充满电的回程电量因素与低价相比更为重要时，平台更容易掌握用户对剩余电量“里程焦虑”心理，通过提高价格获得更多利润，社会福利同理. 平台利润和社会福利都随着敏感度 $ {\theta }_{i}^{t} $的增大而减小，且减小的幅度逐渐减缓. 原因是当用户对效用更敏感时，平台必须在定价和充电桩数量上提供更多保障，这类举措会影响平台收入，增加平台成本，降低利润和社会福利，且前期对平台收入的影响更为显著.

本研究基于充电平台经营策略，建立充电效用及行为决策模型，对比利润、社会福利最大化2种目标下的最优结果，进行参数敏感性分析. 协同优化结果表明，当价格区间为0~4元，建桩数量为0~1 000时，平台利润及社会福利均存在唯一极大值点. 在空间上，郊区的充电价格低于中心市区价格，以实现对市区用户的引流、减轻中心市区充电桩的服务压力；充电桩数量从市区到郊区都呈现递减趋势，以适应需求在空间上的不均匀分布. 在时间上，高峰期定价高于低谷期；相较于利润最大化，社会福利最大化状态下的高峰期与低谷期价格差异更为显著. 社会福利最优价格普遍低于利润最大化情形，后者的充电桩数量多于前者，各区域、各时段实现的需求量均更高. 敏感性参数分析结果表明，充电敏感性因子、电池容量、MNL模型中的敏感度与目标结果呈现负相关，用户充满电所获得的感知效用与目标结果呈正相关. 本研究模型通过趋势分析和求得数值最优解，结合参数敏感性分析，为电动汽车充电平台定价及布设方案提供参考. 本研究提出的电动汽车充电途径只适用于无储能场景的充电平台，未来研究可以考虑更为复杂的充放电场景，提出更具前瞻性的电动汽车平台优化策略.