在混合体系梁式桥中,混凝土部分一般采用悬臂浇筑法施工,为了加快施工进度并保证结构的整体性,钢箱梁部分一般采用整体吊装法[4-5]施工. 因此如何保证合龙时钢箱梁端与混凝土梁端平顺对接,是施工的关键和重点,特别是当结构体系不对称[6-7]时,中间的T构将反复承受较大的不平衡荷载,导致主梁的最大悬臂处产生较大的反复变形(包括水平变形、竖向变形和转角)。钢箱梁在无应力制造时必须考虑这些变形,并以这些变形作为无应力制造尺寸计算的依据. 若加工时未能准确控制无应力制造尺寸,可能会造成现场合龙困难,强行合龙后桥梁也会由于受力不合理而降低使用寿命. 在整体吊装法的施工实践中,已经发展、完善了多种施工控制技术[8-9],特别是无应力状态法[10-13]概念的提出及应用,在一定程度上方便了施工控制工作,但介绍钢箱梁制造尺寸计算[14-15]方法的文献较少. 准确计算钢箱梁制造尺寸,以满足其在安装定位、连接时的要求,是确保主桥成桥后线形满足设计要求、桥梁安全、顺利修建的关键.
1. 工程背景
1.1. 发展现状
表 1 国内已建成混合体系梁式桥统计
Tab.1
| 桥名 | 桥型 | l/m | h/m | D/m | m/t |
| 石板坡长江大桥 | 连续刚构 | 330 | 4.5 | 108 | 1400 |
| 福州马尾大桥 | 连续梁 | 240 | 3.8~4.2 | 96 | 1184 |
| 宁杭高铁下穿桥 | 连续梁 | 180 | 4.1 | 88 | 900 |
| 小榄水道桥 | 连续刚构 | 220 | 3.6 | 87 | 800 |
| 瓯江大桥 | 连续刚构 | 200 | 3.5 | 80 | 660 |
| 无锡京杭运河桥 | 连续梁 | 100 | 2.5 | 47 | 220 |
1.2. 总体布置
如图1所示,依托工程(龙翔大桥主航道桥)是四跨预应力混凝土连续-刚构混合体系桥梁,其跨径布置为118 m+2×202 m+93 m,桥梁全长615 m,其中3#墩为墩梁固结布置,其余桥墩墩顶布置摩擦摆式支座. 2个主跨的跨中各布置1个长度为75 m的钢箱梁,整体吊装施工;2#、3#墩混凝土梁段长度均为118.4 m,采用悬臂浇筑法施工[21];2#墩边跨布置长度为53.8 m的钢箱梁,支架上拼接;4#墩混凝土梁段长152.2 m,采用悬臂浇筑和支架现浇施工. 桥宽2×16.5 m,分左右两幅,桥面铺装采用10 cm钢纤维混凝土+8 cm沥青混凝土铺装. 主墩墩顶处梁高10.4 m;跨中钢箱梁部分梁高4.2 m,等截面布置;全桥合龙后再张拉体外索.
图 1
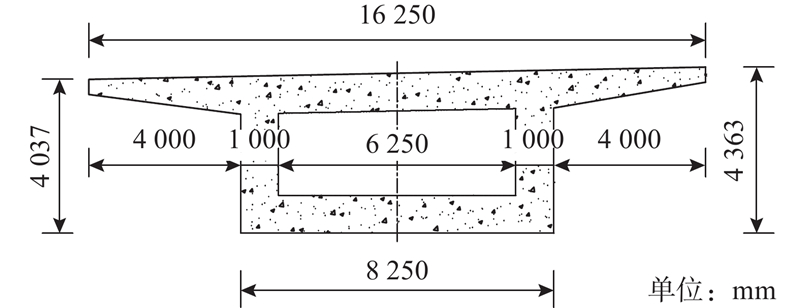
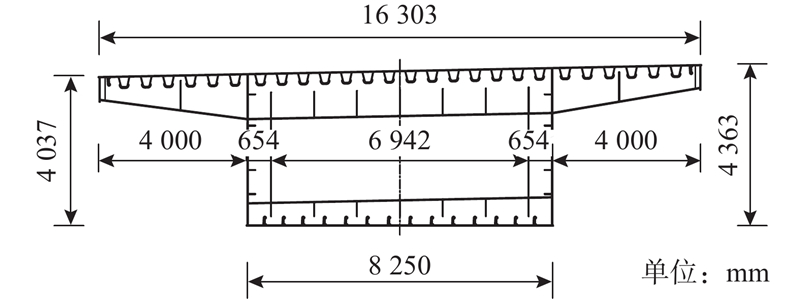
1.3. 截面布置
图 2
图 3
1.4. 施工工序
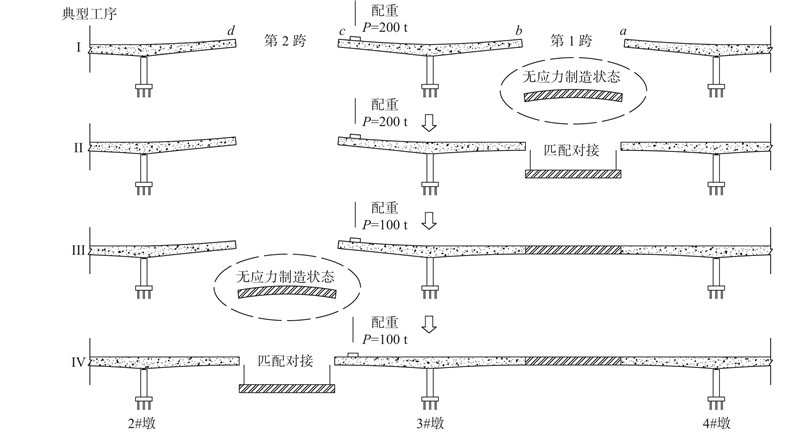
从结构总体布置可知,依托工程为非对称布置结构体系,在施工方法上,受航道通航要求的影响,在混凝土箱梁采用悬臂浇筑施工到最大悬臂状态且2个边跨均合龙之后,2个中跨的大节段钢箱梁采用分开依次进行吊装合龙的办法,即先完成3#墩到4#墩的钢箱梁吊装和合龙,再完成2#墩到3#墩的钢箱梁吊装和合龙,如图4所示。图中,a、b、c、d分别代表4#墩大里程侧、3#墩大里程侧、3#墩小里程侧、2#墩大里程侧主梁与钢箱梁的匹配对接断面,P为配重.
图 4
本结构体系属于四跨非对称布置,施工方法也属于非对称施工,且钢箱梁的质量非常大,导致本桥在钢箱梁吊装过程中受力和变形特别复杂. 为了保证3#墩受力安全,其主梁一侧须配重,桥墩发生朝配重侧的变形,当钢箱梁吊装时,又发生朝吊装处的变形。钢箱梁质量大,无论是在第一个还是第二个主跨在吊装钢箱梁中,每个T构、特别是3#墩须承受较大的不平衡荷载并出现偏离墩中心的变形。变形不仅仅包括主梁自身的变形,而且还包括3#墩墩身转动带来的附加变形,水平、竖向、转角3个方向均有较大变形,因此必须都考虑. 由于主梁的最大悬臂处在各个阶段都会产生很大的反复变形(包括竖向、水平和转角),复杂性远大于三跨对称结构体系,选取主梁与钢箱梁的4个匹配对接断面a、b、c、d,在典型工序下的形心轴变形结果如表2所示。表中,Δu为匹配对接断面处主梁形心轴的水平变形增量,Δv为匹配对接断面处主梁形心轴的竖向变形增量,β为匹配对接断面处主梁形心轴的转角变形增量,下标a、b、c、d分别对应各匹配对接断面;+表示向大桩号侧或向上变形以及顺时针转动,−反之.
表 2 吊装时主梁形心轴变形增量
Tab.2
| 典型工序 | Δua/mm | Δub/mm | Δuc/mm | Δud/mm | Δva/mm | Δvb/mm | Δvc/mm | Δvd/mm | βa/(°) | βb/(°) | βc/(°) | βd/(°) |
| Ⅰ | 0.0 | −16.2 | −16.1 | 0.0 | 0.0 | +42.9 | −61.4 | 0.0 | — | −0.064 | −0.072 | — |
| Ⅱ | −22.4 | +35.9 | +32.1 | 0.0 | −98.8 | −130.9 | +86.3 | 0.0 | −0.129 | +0.138 | +0.074 | — |
| Ⅲ | +6.1 | +5.9 | +6.8 | 0.0 | −5.9 | −14.1 | +27.1 | 0.0 | — | — | +0.042 | — |
| Ⅳ | −22.8 | −24.2 | −25.1 | +13.1 | +22.2 | +49.3 | −102.8 | −79.7 | — | — | −0.112 | +0.108 |
在主梁最大悬臂端预应力张拉完成后,开始准备钢箱梁合龙,将这个阶段视为钢箱梁合龙施工的初始阶段,并假定此时主梁各个截面坐标值为0. 工序Ⅰ在3#墩小里程侧施加配重,跨中T构受到不平衡荷载,引起截面b、c坐标变化;截面a、d受力状态未发生变化,其坐标值仍为0。工序Ⅱ进行3#墩到4#墩间钢箱梁合龙施工,钢箱梁荷载传递到跨中T构和4#墩T构,a、b、c截面坐标变化。工序Ⅲ将3#墩小里程配重由200 t卸载至100 t,由于此时跨中T构和4#墩T构已经形成整体结构,受力状态随着配重的变化而变化,引起截面a、b、c坐标发生变化。工序Ⅳ进行2#墩到3#墩钢箱梁合龙施工,钢箱梁荷载传递到整个主桥结构,a、b、c、d截面坐标发生变化. 由表2可知,吊装过程中最大竖向变形增量达到130.9 mm,最大水平变形增量达到35.9 mm,最大转角变形达到0.138°,这给钢箱梁制造尺寸的设计增加了难度,若不考虑这些变形,将会造成合龙时钢箱梁长度过长或过短、合龙标高与控制标高差距过大以及匹配断面转角不适配的情况,甚至有可能导致钢箱梁无法顺利合龙.
1.5. 配重设置原则
在进行3#墩到4#墩的钢箱梁吊装时,配重的大小根据不平衡弯矩控制原则来确定,即T构两端的配重荷载和钢箱梁荷载在墩顶处引起的不平衡弯矩尽可能小,以保证T构的稳定性. 在实际施工过程中,配重荷载不会与钢箱梁荷载同步施加,而是在钢箱梁吊装前全部布置好,2种荷载的施加存在时间差,因此令配重引起墩顶负弯矩为钢箱梁引起墩顶负弯矩的一半,这样能使T构在吊装过程中最大不平衡弯矩达到最小. 配重P的计算式为
式中:
1.6. 钢箱梁的吊装及合龙温度考虑
钢箱梁段采用整体吊装法,提升设备采用4台350 t的千斤顶,采用计算机控制系统监测每个千斤顶的荷载和行程,并进行自动调节,确保各千斤顶的同步性,具体步骤如下. 1)驳船将跨中钢箱梁运抵桥位处,并进行绞锚定位,安装钢箱梁提升吊点和4台液压连续千斤顶. 2)检查各项准备工作无误后,进行跨中钢箱梁提升,确保提升过程4点同步,提升总高度约25 m,共7.5 h完成1片钢箱梁提升. 3)钢箱梁提升至设计高程位置后,用临时锁定装置进行锁定,校对调整对接位置,满足要求后在顶、底、腹板上的加劲肋上采用高强螺栓连接. 4)待钢箱梁准确定位后,选择合适的合龙温度,将所有高强螺栓拧紧,再进行端断面接口的顶、底、腹板及嵌补段焊接. 如图5所示为依托工程钢箱梁现场吊装情况.
图 5
钢箱梁在确定最终的制造尺寸前,应严格关注合龙时的气温变化情况. 温度变化引起的结构变形考虑±10 ℃的影响,在升温10 ℃时,由混凝土伸长引起合龙口的缩短量为12.2 mm,钢箱梁梁端的伸长量为7.2 mm,合龙口的相对变形为19.4 mm,降温时数值相反. 如果合龙实际温度跟设计合龙温度相差过大,可能会导致焊缝过宽或过窄,甚至会造成合龙困难,因此,在钢箱梁合拢前一个月,实测系统温度对合拢口宽度的影响。在施工现场夜间温度相对稳定的条件下,连续测量合龙口的宽度及大气温度,确定合龙时间,同时在钢梁预制厂内测量钢箱梁自身由于温度变化引起的伸缩量,校正匹配量,以确保钢箱梁的精确合龙.
1.7. 钢箱梁整体吊装合龙施工要求
图 6
式中:
2. 钢箱梁制造尺寸的计算
2.1. 几何控制法概述
几何控制法是基于无应力状态法的理论基础衍生而来的,可以概况为几何体系(包括结构体系的形式、构件的无应力尺寸和形状等)一定的弹性结构在某一时刻的内力和变形状态唯一地取决于此刻结构所受的作用体系(包括荷载、温度),与此前构件的安装历程、作用的施加和变迁历程无关. 通过制造和现场吊装阶段对钢箱梁无应力线形的控制来实现最终成桥线形满足理想成桥状态. 本研究将钢箱梁的施工控制划分为4个阶段:准备阶段、制造阶段、安装阶段以及成桥阶段,综合考虑施工阶段变形以及钢箱梁在自重作用下的转角,并以合龙时匹配断面相互平行、相对缝宽不超过规定限值为依据,确定钢箱梁的制造尺寸,基于几何控制法的施工控制流程框架如图7所示.
图 7
图 7 基于几何控制法的施工控制流程框架
Fig.7 Construction control flow frame based on geometric control method
2.2. 梁端制造倾角的计算方法
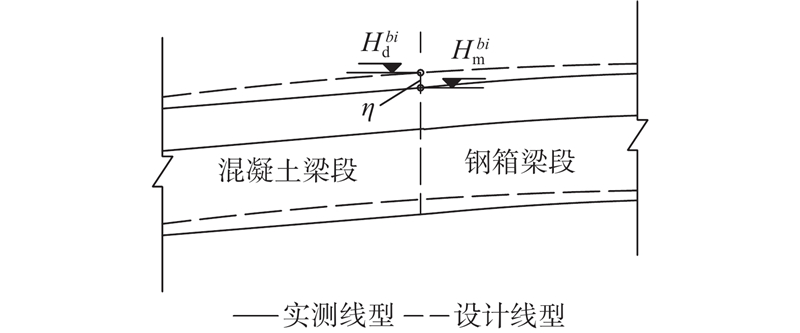
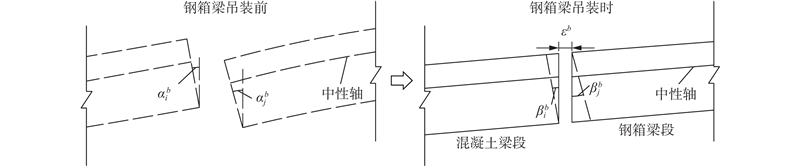
在合龙口匹配对接的工况下,如何保证钢箱梁与混凝土梁断面的平行匹配,是整体吊装法施工的关键,也是施工监控实现目标成桥状态的关键点. 如图8所示,定义钢箱梁与混凝土匹配断面
图 8
式中:
具体计算时,
式中:q为钢箱梁自重荷载集度,L为钢箱梁长度,EI为钢箱梁抗弯刚度,
若实际过程中的钢箱梁制造尺寸忽略制造倾角
由于钢箱梁制造尺寸不当而带来的相对缝宽误差,在不利的情况下可能会减小实际施工控制中依靠缝宽来调整其他匹配断面的余地,更为不利的情况是这一误差造成的实际缝宽超过施工要求限值,造成合龙困难的局面.
2.3. 顶、底板配切长度的计算方法
在大节段整体吊装时,钢箱梁自重作用传递到混凝土梁段上,使得混凝土梁端断面产生较大的纵向位移
图 9
钢箱梁顶、底板制造尺寸的计算式为
式中:D为钢箱梁吊挂前混凝土端断面b和a之间的实测距离,
3. 理论与实测结果分析
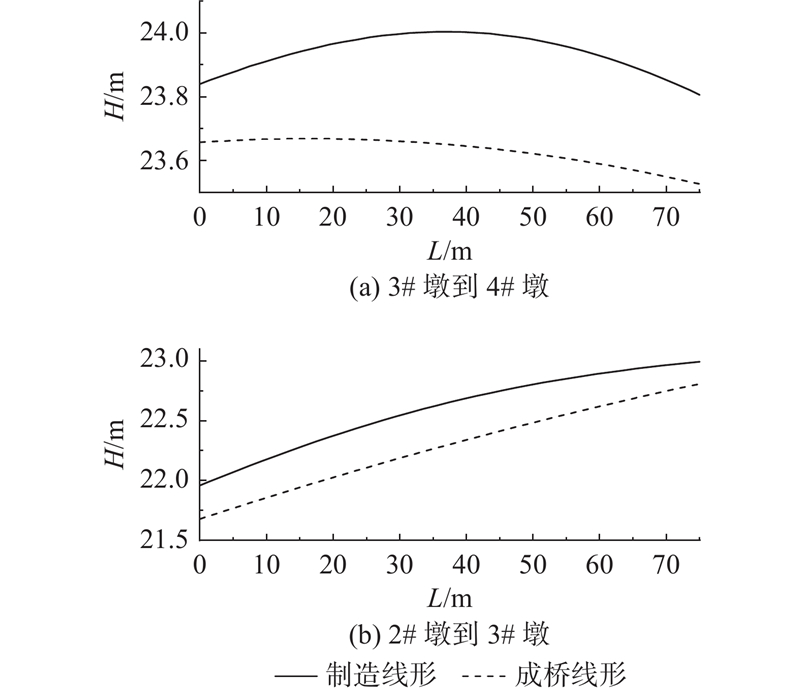
3.1. 制造尺寸计算结果
从正装仿真模型中提取相应的参数,结合部分实测参数,对钢箱梁端制造倾角及其所对应的顶、底板配切长度进行计算,求得钢箱梁制造尺寸. 计算影响制造尺寸的各个修正参数,确定如表3所示的修正值. 表中,
表 3 尺寸修正参数计算结果
Tab.3
| 匹配断面 | | | | | | | | | |
| a | +0.108 | −0.129 | −0.154 | +0.140 | 1603 | 2597 | −26.0 | −16.5 | +15.0 |
| b | −0.152 | +0.138 | +0.154 | −0.172 | 1603 | 2597 | +38.7 | +29.6 | +30.0 |
| c | +0.120 | −0.112 | −0.154 | +0.162 | 1603 | 2597 | −28.2 | −20.0 | +15.0 |
| d | −0.112 | +0.108 | +0.154 | −0.158 | 1603 | 2597 | +16.1 | +8.2 | +30.0 |
表 4 制造尺寸计算结果
Tab.4
| mm | ||||||
| 钢箱梁 | | | | | | |
| 3#-4# | 75086 | 75079 | −79 | −105 | 75007 | 74974 |
| 2#-3# | 75084 | 75075 | −81 | −89 | 75003 | 74986 |
图 10
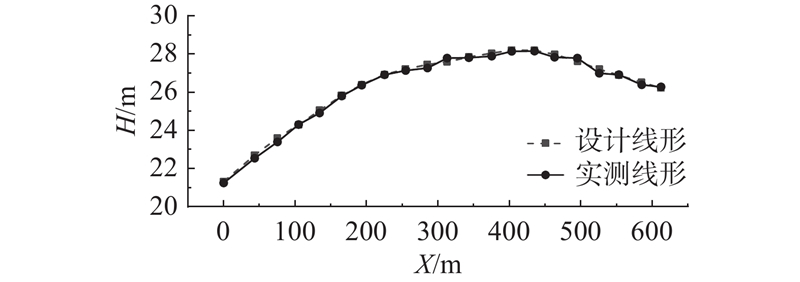
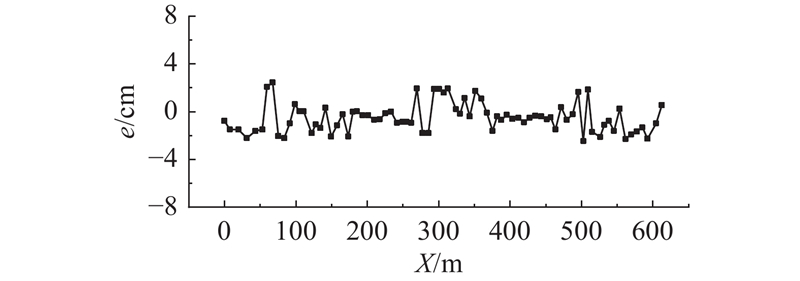
3.2. 现场匹配情况
制造尺寸明确后的两跨钢箱梁先后合龙,钢梁入槽情况如图11所示。吊装实践结果表明:该桥各梁段均顺利匹配、一次吊装成功,各匹配断面缝宽都在理想范围内、现场无需重新配切梁段或拼接板高强螺栓孔扩孔,合龙工作顺利. 两跨大节段各匹配断面的入槽缝宽实测结果汇总如表5所示,其中
图 11
表 5 入槽缝宽实测结果
Tab.5
| mm | |||
| 匹配断面 | | | |
| a | 12 | 20 | 8 |
| b | 30 | 35 | 5 |
| c | 18 | 20 | 2 |
| d | 35 | 40 | 5 |
图 12
图 13
4. 结 语
本研究1)根据几何控制法,从钢箱梁悬吊时匹配断面应保持相互平行的关系着手,基于施工阶段分析结果和部分现场实测参数,提出简单高效的非对称结构体系两跨钢箱梁制造尺寸计算方法. 2)计算方法综合考虑了混凝土梁端水平变形、自重引起的混凝土及钢箱梁梁端倾角,最终钢箱梁各匹配断面的入槽相对缝宽均小于规定限值,基本实现匹配断面的平行对接,无需再采取强制调整措施,现场监测结果及桥梁的顺利合龙,验证了本研究所提方法的精确性. 3)本研究所提方法和相关结果可以为整体吊装法非对称混合体系梁式桥的施工实践提供有益的参考,并实现对成桥线形的有效控制. 本研究对横向荷载因素考虑较少,实际合龙时其影响不可忽视,下一步工作可以针对横向温度梯度荷载、横向风荷载这些影响合龙精度的因素开展进一步研究.
参考文献
钢−混混合梁连续刚构桥设计关键技术
[J].
Key technology for designing of steel-concrete hybrid girder continuous rigid frame bridge
[J].
福州马尾大桥主桥设计关键技术
[J].
Key technology for design of main bridge of Mawei bridge in Fuzhou
[J].
中山小榄水道混合梁刚构桥关键技术
[J].
Key technology of hybrid beam rigid frame of Xiaolanshuidao bridge
[J].
温州瓯江大桥钢箱梁整体提升安装施工技术
[J].
Construction techniques for integral lifting and installation of steel box girder of Wenzhou Oujiang River bridge
[J].
Geometric state transfer method for construction control of a large-segment steel box girder with hoisting installation
[J].DOI:10.1631/jzus.A1900213 [本文引用: 1]
Refined analysis and construction parameter calculation for full-span erection of the continuous steel box girder bridge with long cantilevers
[J].DOI:10.1631/jzus.A1900322 [本文引用: 1]
基于平面梁单元的几何非线性线形控制方程建立与应用
[J].DOI:10.3969/j.issn.1003-4722.2022.04.007 [本文引用: 1]
Establish-ment and application of geometric shape governing equations for geometric nonlinearity based on plane beam elements
[J].DOI:10.3969/j.issn.1003-4722.2022.04.007 [本文引用: 1]
Correction to: stress-free-state based structural analysis and construction control theory for staged construction bridges
[J].DOI:10.1186/s43251-021-00047-6
Control of self-adaptive unstressed configuration for incrementally launched girder bridges
[J].
基于逐段安装线形的钢箱梁制造尺寸计算研究
[J].
Research on calculation of manufacturing dimensions of steel box girder based on piecewise installation line
[J].
分阶段施工中钢箱梁制造参数的通用计算方法
[J].
General calculation method for manufacturing para-meters of steel box girder in staged construction
[J].
桥梁悬臂拼装施工中钢箱梁制造尺寸的确定
[J].
Determination of fabrication dimensions of steel box girders in cantilever erection construction of bridge
[J].
短线节段预制拼装桥梁几何线形三维控制方法
[J].
Three-dimensional geometric alignment control method for short-line matching segmental precast girder assembling bridge
[J].
悬拼施工中钢箱梁制造尺寸的确定
[J].DOI:10.3969/j.issn.0258-2724.2014.05.002
Determina-tion of fabrication dimensions of steel box girders in cantilever construction
[J].DOI:10.3969/j.issn.0258-2724.2014.05.002
短线法节段梁预制拼装过程控制技术研究
[J].
Reasearch on control technology of precasting and assembling process of segment beam with short-line method
[J].
大曲率短线匹配连续刚构桥空间几何线形控制
[J].
Spacial geometric alignment control for short-line matching continuous rigid frame bridge with large curvature
[J].
重庆石板坡长江大桥复线桥总体设计
[J].
Overall design of double-line bridge of Shibanpo Changjiang River bridge in Chongqing
[J].
盘龙河3号大桥悬臂浇筑施工关键技术控制
[J].
Control of key construction technologies for the cantilever pouring of the NO. 3 Panglong River bridge
[J].
Discussion on manufacturing tech-nology of steel box girder of cross-line bridge engineering in Xiamen Hele road
[J].