快速路在城市道路中承担了大量机动车的交通需求,在交织区存在大量的车辆汇合与分离,导致该区间内分道直行与换道车流相互影响. 在大流量、多换道交通量工况时,交织区分流、合流段会产生严重拥堵,影响城市道路系统的正常运行[1]. 作为城市快速路的关键节点,交织区交织段的通行能力与交通流量控制了整个快速路网的运行效率.
1. 随机交通流理论与动力学方程
1.1. 随机交通流理论发展
以元胞自动机[11-12]为代表的在时域上推进的时间发展仿真类交通模型是由判别规则(跟驰[13-14]与换道[15])确定下一时步每一车辆动作的选择[16-19],使得仿真过程具备了随机的特性,仿真结果也会与经典模型有所不同. 三相交通流理论建立在大量的观测数据基础上,与经典路段交通流方程明显区别的是,它指出了基本图在最大流量处存在亚稳态区以及在拥挤区存在同步流区域,这都表明在较大交通流密度工况下车流量和车流速会产生随机分裂[20]. Baër等[21]建立的路段交通流模型能够表达随机车流基本图的各种形状,从而适应车流参量的随机变化. Wang等[22]提出了一种测量交通震荡幅度的新方法,揭示了随机线性跟驰模型的震荡特性. 目前,交通流随机性研究主要集中在离散选择[23]、跟驰模型[24-26]、行程时间可靠性[27-29]、网络交通流分配[30-31]、车辆换道等多个方面. 虽然随机交通流逐步成为交通研究的热点问题,但利用随机微分方程研究交通流随机性的成果尚不多见.
1.2. 考虑换道的交通流方程
车辆换道是常见的交通行为,在低速高密度工况下车辆换道、交织行为常常诱发交通流速度的明显变化. Laval等[32]基于运动波理论分析,将LWR方程右端的产生/离去率改为净车道变换率,提出了车辆换道竞争与平衡模型. 模型的核心是通过换道折减系数表示影响单位时间、单位长度的侧向换道率,通过驶入车道最大可用容量对强制换道流率进行限制. 这种限制反映了驶入车道密度增加,换道难度随之增加的交通现象,但Laval模型不表达换道时间与车速的随机性,只表达了平衡状态,方程的具体表达式如下.
式中:
文献[33]在交通流速度梯度模型基础上,引入了换道过程影响项和换道完成后的滞后变化项描述换道过程和换道流量对交通流状态的影响,继承了Laval模型换道难度随驶入车道密度变化的思想,提出了考虑换道难度和过程影响的交通流动力学方程. 表达式如下.
式中:
动力学方程(式(2)~(4))可以描述包括换道行为的交通流的非稳定流态,刻画交通过程中交通流在时间和空间上的确定变化,虽然方程不描述随机性,但它为构建考虑换道时间随机性的偏微分方程提供了基础.
2. 换道时间随机的交通流动力学方程
2.1. 换道时间的随机性
车辆换道是一个复杂的过程,包括加速、减速、转向、避让、停车等候和竞争等多个过程,换道车辆会与周边的其他车辆发生相互作用,完成换道耗费的时间无法确定. 随着驶入和驶出车道车流密度的增加,车辆之间相互作用的概率也相应提高. 即使在相同的交通流参数下,不同车辆完成换道所耗费的时间也不尽相同. 车辆换道时间的随机性对驶入和驶出车道车流稳定性产生直接影响,同时也改变相关车道局部的车流密度和车流速,影响换道后车流的随机演化的过程.
以往研究表明,同一路段上道路交通车辆行程(走行)时间符合对数正态分布[35],将车辆换道时间看成完成一个车道宽度行程的侧向行程的时间,车道宽度被视为“同一路段”,换道时间
一般情况下有换道时间tc的期望与方差如下:
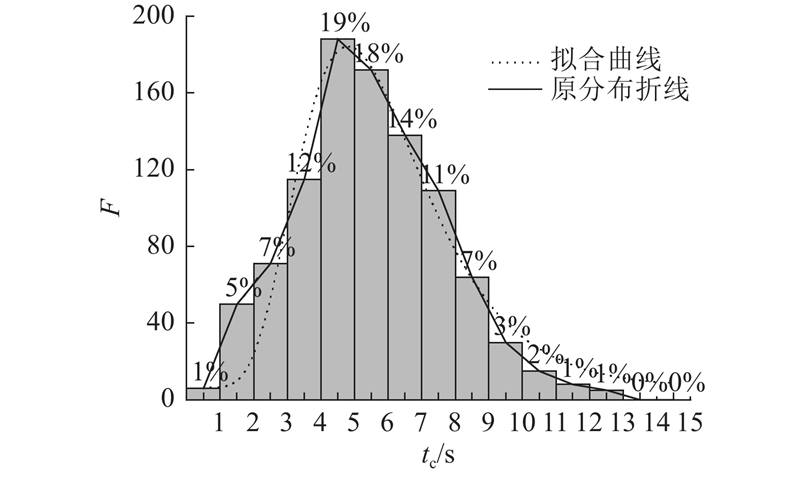
采集一周南京市鼓楼区江东快速路草场门隧道至定淮门隧道入口交织段在8:00—8:30的车辆早高峰期换道时间数据. 由于拥堵和来车随机,车流车辆换道时间方差较大,换道时间在1~14 s变动. 具体分布图及对其进行对数正态分布拟合后的曲线如图1所示. 图中,黑色点线表示拟合后对数正态分布曲线,F为换道频次. 拟合后分布表达式如下:
图 1
图 1 高峰时段换道时间分布频次直方图及其拟合曲线
Fig.1 Frequency histogram of lane change time distribution in rush hours and its fitting curve
拟合优度为0.932,符合对数正态分布的长尾性特征. 因此,对数正态分布可以作为换道时间的概率密度分布函数以简化相关计算.
2.2. 随机动力学方程
将随机换道时间引入交通流方程(式(2)~(4)),构建随机交通流偏微分动力学方程. 方程中换道难度影响项
式中:
随机换道时间的交通流随机微分方程组由式(2)、(3)、(9)、(10)组成,其中式(10)中
3. 随机交通流模型的计算
3.1. 网格剖分与方程离散
大部分随机偏微分方程难以求出解析解,交通流的随机微分方程也必须通过剖分计算区域、离散时间和空间参量,求得数值解. 与普通偏微分方程不同的是,已知输入的连续随机量必须在概率密度上进行分割,通过各分割概率密度区间对应的离散参量求解方程组. 各离散参量的对应解拼接成完整的随机偏微分方程的解,获得所求随机变量不同发生概率的数值解和分布的概率密度函数. 交通流随机偏微分方程的求解必须转换为时空剖分的离散方程的求解.
图 2
图中,某快速路A型交织区主车道由2车道组成,根据车道进行网格剖分. 上行匝道与车道1网格0相接,下行匝道与车道1网格9相接. 其中,车道1、2的网格0设置为输入边界,车道1与2的网格9设置为输出边界,其余网格为计算区域内网格. 车道1输入边界单元(即0号网格)在给定主干道输入车流量的基础上还要考虑加入上行匝道的输入量;车道1网格9输出边界同样也包括下行匝道的输出量.
随机微分方程(式(2)、(3)、(10))的稳定离散求解形式如下:
式中:
基本图与三参数关系的离散如下:
式中:
3.2. 计算步骤
高峰期车流的交织运行工况按照如表1所示的OD矩阵进行计算,计算依据OD矩阵展开(O表示入口,即上行匝道以及车道1、2上游路段驶入车辆;D表示出口,即下行匝道和车道1、2下游路段驶出车辆). 表中,数据表示交织区单位时间的流量流向.
表 1 高峰期交织区小时OD矩阵
Tab.1
| O | D | |
| 主线出口 | 下行匝道 | |
| 入口车道1 | 1200 | 50 |
| 入口车道2 | 1000 | 150 |
| 上行匝道 | 180 | 10 |
计算过程如图1所示. 将换道时间密度函数分布分为14个区间,每个分区对应一个定常的
计算t = 0 s时刻,须对所有计算网格进行交通流初始状态(u,k)的赋值,包括边界网格和内网格. 状态数据来自于现场实测或初始设定,所赋交通流参数必须满足模型(式(12)、(13)).
时间步长为
车辆换道分为强制换道和自由换道,强制换道为依据表1的OD矩阵所必须的换道. 自由换道则是由于两车道车流速度差而产生,车辆由低速车道向高速车道变换. 由于研究重点分析高密度工况,在计算中暂不考虑自由换道.
各方向换道车辆数或单位时间换道率必须与OD矩阵一致. 换道位置在网格1~8处,换道地点由实测或按先验分布计算确定,一般可以按泊松分布进行预算,以表达空间位置的随机分布. 计算结果为随机微分方程提供换道网格地点依据.
3.3. 结果分析
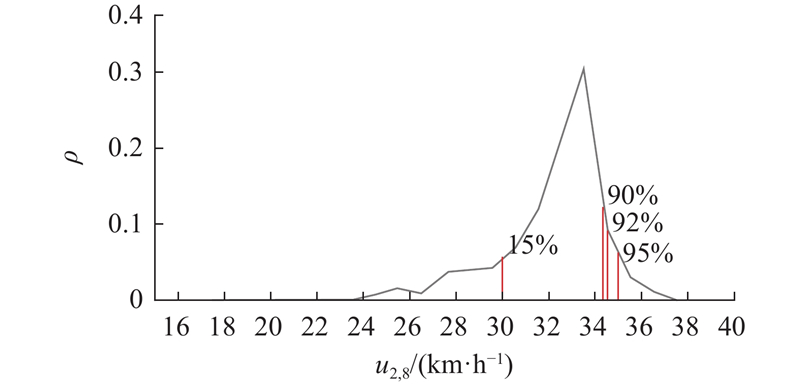
在高密度工况
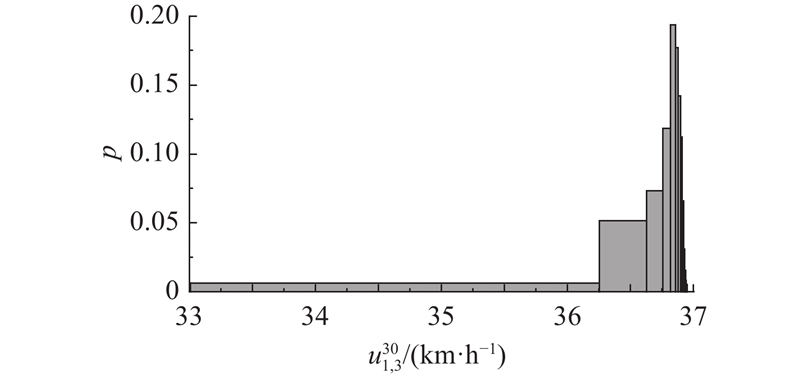
以如图1所示的概率分布直方图作为输入,依据数值解法,得到所有计算域单元的历时速度概率分布直方图,如图3所示. 图中,p为概率,
图 3
图 3 车道1网格单元3第30 s分段速度概率分布
Fig.3 Velocity probability distribution in 30 s segment of grid cell 3 in lane 1
图 4
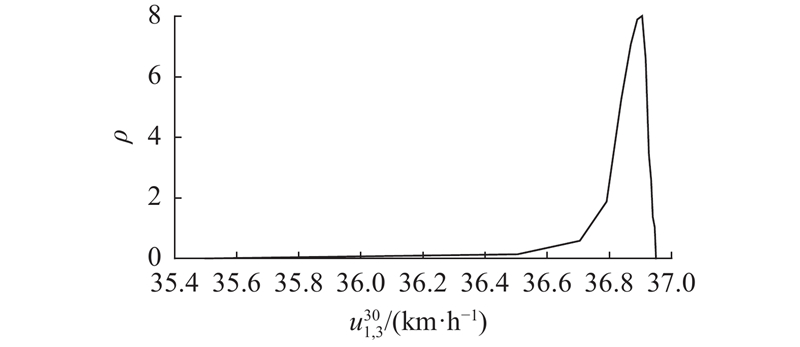
图 4 车道1网格单元3第30 s速度概率密度
Fig.4 Speed probability density in 30 s segment of grid cell 3 in lane 1
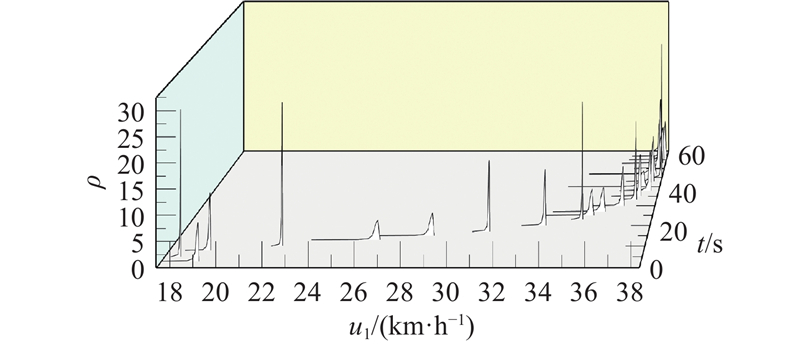
交通流随机动力学方程是时间发展型偏微分方程,其求解结果的特征是在时间历程和空间计算域上给出变化的网格单元速度概率分布. 如图5所示为车道1网格3单元的0~60 s历时30个离散时刻点上的速度密度的变化. 图中,
图 5
图 5 车道1网格单元3在0~60 s历时下每2 s时间点的速度概率密度
Fig.5 Speed probability density at every 2 s time point in 0~60 s duration of grid cell 3 in lane 1
图 6
图 6 交织区车道2网格单元8时均车流速度概率密度
Fig.6 Probability density of average vehicle velocity in grid cell 8 of lane 2 at weaving area
4. 结 论
(1)由换道过程时间随机性构建的交通流随机微分方程可以描述复杂交通流相关参量演变的随机变化特征.
(2)所提的随机偏微分方程数值解法可以求解描述包括换道行为在内的交通流随机动力学方程.
(3)在低速高密度工况下,交织与换道对局部车流速的概率密度分布影响较大,也降低了车流的稳定性. 随机交通流方程提供了交通设施、管理与控制和交通可靠性研究的新方法. 对复杂交通环境下的设施设计以及通行能力估算有积极意义.
(4)所提随机微分方程主要表达了换道耗费时间上的随机,对于换道空间上的随机性,除了采用先验预算外,也可以在给定约束条件下采用蒙特卡罗的方法多次利用随机微分方程迭代求解.
(5)随机动力学微分方程在交通流研究上的应用尚处于起步阶段,在换道影响项的细化和准确表述上须进一步完善,对于时空联合随机性的表达和求解还须深入探索.
参考文献
Impact of traffic oscillations on freeway crash occurrences
[J].DOI:10.1016/j.aap.2009.10.009 [本文引用: 1]
Efficient evaluation of stochastic traffic flow models using Gaussian process approximation
[J].DOI:10.1016/j.trb.2022.08.003 [本文引用: 1]
Stochastic factors and string stability of traffic flow: analytical investigation and numerical study based on car-following models
[J].DOI:10.1016/j.trb.2022.09.007 [本文引用: 1]
A Bayesian inference to estimate change point for traffic intensity in M/M/1 Queueing Model
[J].
On kinematic waves. II. a theory of traffic flow on long crowded roads.
[J].
Shock waves on the highway
[J].DOI:10.1287/opre.4.1.42 [本文引用: 1]
速度梯度模型的高速公路交通流状态估计方法
[J].
Freeway traffic state estimation by using speed gradient model
[J].
Why are highway speed limits really justified? An equilibrium speed choice analysis
[J].
非均匀路段交通流的元胞自动机模拟
[J].
Simulation of traffic flow on non-uniform road sections with cellular automaton model
[J].
基于元胞自动机的高速铁路列车运行仿真研究
[J].
Simulation study of high-speed railroad train operation based on cellular automata
[J].
Efficiency performance and safety evaluation of the responsibility-sensitive safety in freeway car-following scenarios using automated longitudinal controls
[J].DOI:10.1016/j.aap.2022.106799 [本文引用: 1]
基于分位数回归的随机优化速度跟驰模型
[J].
Stochastic optimal velocity car-following model based on quantile regression
[J].
Distributed cooperative trajectory and lane changing optimization of connected automated vehicles: freeway segments with lane drop
[J].DOI:10.1016/j.trc.2022.103761 [本文引用: 1]
元胞自动机交通流模型的随机规则
[J].DOI:10.3969/j.issn.1672-4747.2007.03.018 [本文引用: 1]
Randomization rules of 1D cellular automaton traffic flow model
[J].DOI:10.3969/j.issn.1672-4747.2007.03.018 [本文引用: 1]
基于元胞自动机模型的交织区通行能力特性分析
[J].
Analysis of capacity of weaving section based on cellular automata model
[J].
Traffic behavior around the weaving section in cellular automata model
[J].DOI:10.1142/S012918311001518X [本文引用: 1]
Three-phase traffic theory and two-phase models with a fundamental diagram in the light of empirical stylized facts
[J].
Threshold queueing to describe the fundamental diagram of uninterrupted traffic
[J].DOI:10.1287/trsc.2018.0850 [本文引用: 1]
Stability analysis of stochastic linear car-following models
[J].DOI:10.1287/trsc.2019.0932 [本文引用: 1]
基于离散多项Logit模型的多时段控制过渡方案选择
[J].
Multinomial logit model based time-of-day control transition scheme selection
[J].
Memoirs on highway traffic flow theory in the 1950s
[J].DOI:10.1287/opre.50.1.173.17802 [本文引用: 1]
The origins of traffic theory
[J].DOI:10.1287/opre.50.1.69.17776
智能网联环境下异质交通流基本图和稳定性分析
[J].DOI:10.3963/j.jssn.1674-4861.2021.05.010 [本文引用: 1]
Fundamental diagram and stability analysis of heterogeneous traffic flow in a connected and autonomous environment
[J].DOI:10.3963/j.jssn.1674-4861.2021.05.010 [本文引用: 1]
Decomposition of travel time reliability into various sources: incidents, weather, work zones, special events, and base capacity
[J].
基于四阶矩的路网总行程时间可靠性评价
[J].
Evaluation of road network total travel time reliability based on fourth-moment
[J].
考虑决策惯性的随机网络路径选择与交通流分配模型
[J].
Route choice model in stochastic network and its application in traffic assignment with consideration to travelers' decision inertia
[J].
基于有效路径集逐步生成的网络交通流分配方法
[J].
Network traffic assignment method based on gradually extending the set of effective paths
[J].
Lane-changing in traffic streams
[J].DOI:10.1016/j.trb.2005.04.003 [本文引用: 1]
考虑换道过程影响的城市交通流动力学方程
[J].
Dynamic equation of urban traffic flow considering the influence of lane-changing process enhanced publishing
[J].
A new dynamics model for traffic flow
[J].DOI:10.1007/BF03187201 [本文引用: 1]
The α-reliable mean-excess traffic equilibrium model with stochastic travel times
[J].DOI:10.1016/j.trb.2009.11.003 [本文引用: 1]