颗粒材料在自然界、工程建设和工业生产中广泛存在,是一种由大量离散固体组成的多尺度耗散体系,其力学特性较复杂,根据颗粒的运动状态,可以表现出气体、流体和固体的力学行为[1]. 当颗粒材料以类似于固体的形式存在时,离散的颗粒在微观上相互接触、相互作用,以承受施加在它们身上的外部荷载. 在岩土工程领域,砂土地基和土工构筑物的变形和稳定问题都与颗粒物质力学密切相关[2]. 滑坡、泥石流、管涌等典型的地质灾害现象也与颗粒物质力学密切相关,其本质为碎散物质组成的地质体的固-液转变[3]. 因此,颗粒材料的宏细观多尺度力学特性一直是水利、岩土、交通、地质等领域的热门课题之一[4]. 从微观尺度研究砂土受剪切作用并逐渐失稳的动力学过程对理解颗粒材料具有重要意义[5].
颗粒体系内大量的离散颗粒在微小扰动下即可产生非线性相互作用,例如颗粒间的相对滑动与接触演化. 这使得颗粒材料在剪切作用下容易发生塑性变形,如发生局部化失稳[20]或分散性失稳[21]. 颗粒体系内部发生局部塑性变形意味着内部局域结构的演化,这与颗粒材料的物理力学性能密切相关. 因此,识别和量化颗粒体系的关键局部结构特征有助于预测局部塑性变形的演化,从而将其与宏观性质联系,形成对颗粒体系塑性行为跨尺度的理解. 当前,虽然诸多学者探索了颗粒材料局部塑性变形的空间和时序相关性[22],但细观尺度塑性变形行为的产生和演化及其与宏观性质的直接联系仍有待进一步研究. 并且,目前研究偏向于单分散颗粒体系和简单球颗粒形状,对复杂颗粒形状的研究较少[23].
本研究使用X射线断层扫描技术进行渥太华砂的原位三轴剪切试验,使用图像处理算法完成渥太华砂的多尺度形态表征,并基于颗粒形貌指标序列实现大规模颗粒的准确匹配与跟踪,研究剪切颗粒体系微观动力学与宏观力学响应之间的联系,为颗粒材料的力学特性研究提供了新的思路.
1. 实验研究
1.1. X-ray CT系统及三轴试验装置
本试验所采用的X-ray CT扫描设备为天津三英精密仪器公司生产的nano Voxel-4000开管反射式高穿透CT系统. 该CT系统搭配高电压的微焦点射线源,能够获得比医学CT更高的扫描精度,适合高分辨率检测. 此外,该CT系统具备较大的内部空间及足够承载能力的样品台,满足三轴试验需求. 射线源电压为200 kV,电流为300 A,空间分辨率为16.5 µm.
本次试验使用的三轴试验装置具备体积小、重量轻的特点,满足在CT机内进行原位三轴剪切试验的需求. 如图1(a)所示为试验仪器布置图,三轴仪被固定于CT系统内部的转台上,射线源发射X射线穿透试样,探测器接收后根据射线衰减程度生成一系列二维切片图像. 如图1(b)所示为三轴试验装置的结构示意图,该装置由轴压控制系统、围压控制装置、压力室及数据采集与控制系统构成. 轴向加载装置位于机身顶部,由步进电机、力位移传感器、加载杆等部件组成. 围压由标准体积压力控制器提供,使用的液体介质为纯净水. 压力室位于机身的底部,外壳采用便于X射线穿透的聚醚酮材料,该材料具备良好的韧性和刚性,最大可承受10 MPa的围压,满足各类试验需求. 数据采集与控制系统通过数据线与三轴试验装置连接,与标准体积压力控制器一同置于CT机外.
图 1
1.2. 试样制备
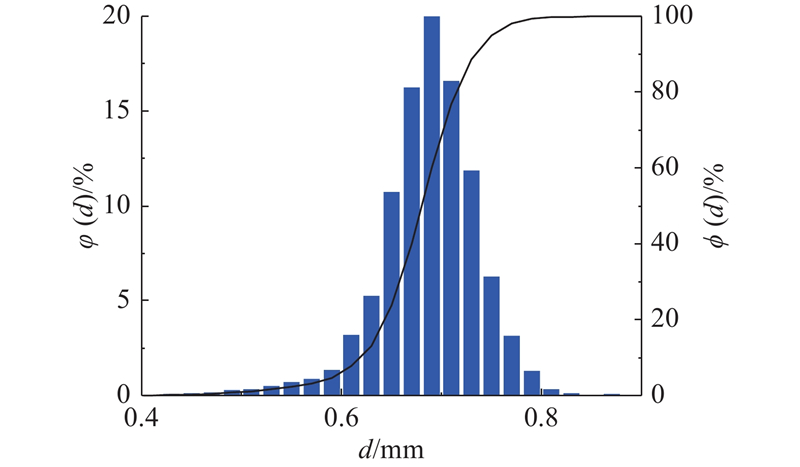
图 2
图 2 渥太华砂及其扫描电镜图像
Fig.2 Ottawa sand and its images obtained by scanning electron microscope
图 3
图 4
1.3. 试验过程
在试验开始前,将三轴仪固定于转台上,将围压加载至300 kPa. 在开始加载前进行第1次扫描,之后步进电机以25 µm/min的恒定速率进行加载,每隔1%或2%轴向应变进行一次扫描,共计15次,在扫描过程中围压保持恒定. 由于扫描时间相对加载时间较短,围压对试样产生的固结影响微弱.
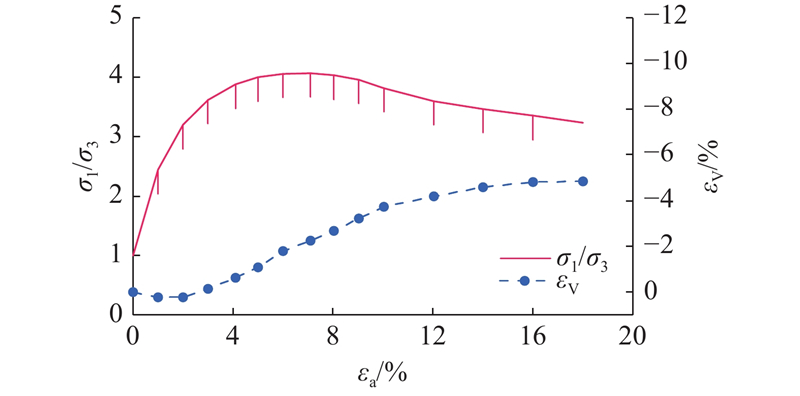
如图5所示为试验的宏观力学响应曲线. 图中,σ1/σ3为应力比,εV为体积应变,εa为轴向应变. 在扫描时颗粒体系会出现应力松弛现象,应力水平明显下降,这是扫描时暂停加载引起的. 在恢复加载后,应力水平会恢复至下降前的值. 本次试验的偏应力峰值出现在轴向应变6.62%下,最大应力比为4.09,且在峰值后出现了明显的应力软化现象. 在体积响应方面,试样首先体积缩小,在3%的轴向应变后试样体积开始膨胀,加载结束时体积应变为−4.83%.
图 5
图 5 渥太华砂三轴剪切试验宏观力学响应曲线
Fig.5 Macroscopic mechanical response curve of Ottawa sand triaxial shear test
2. X-ray CT图像处理
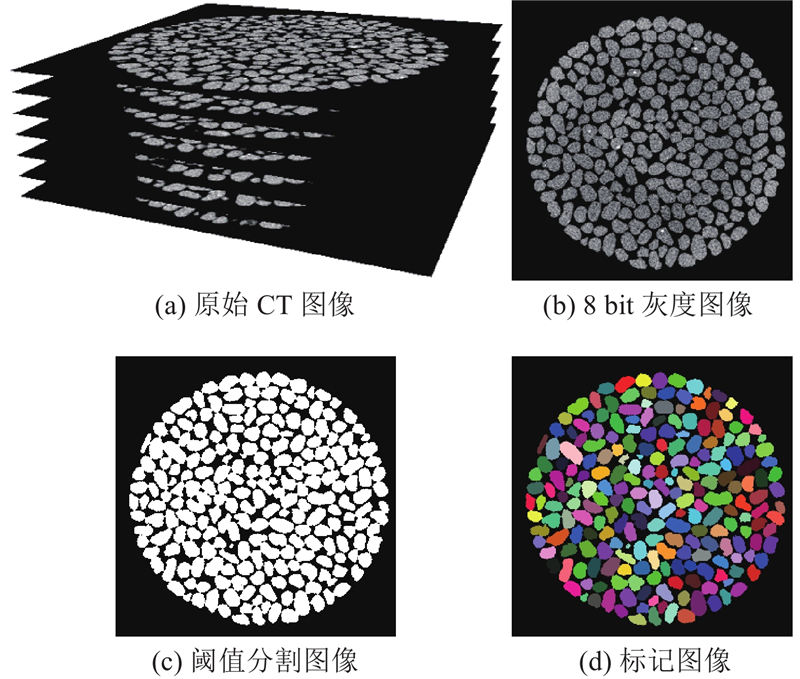
在CT扫描完成后将获得15组水平方向的试样二维切片(见图6 (a)). 初始状态包含1491张切片,在加载终止时18%的轴向应变状态下包含1241张切片.
图 6
2.1. 颗粒分割
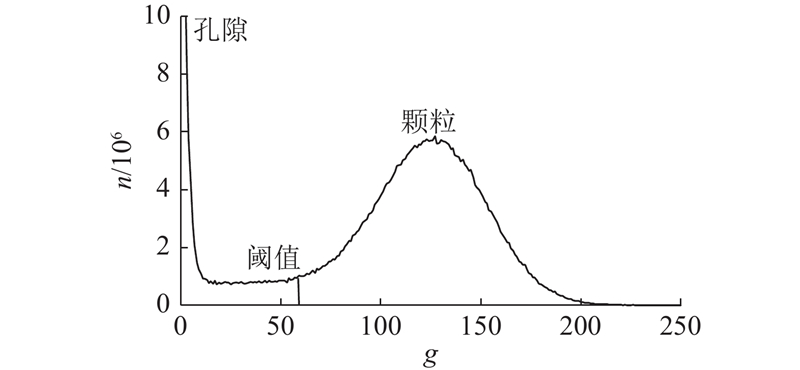
首先,15组切片须裁成相同大小,且每组切片的坐标原点须一致,以确保后续颗粒匹配的准确性. 随后,将原始的32 bit图像转化为8 bit (见图6 (b)),以缩减图片大小,提高计算效率. 之后对图像进行阈值分割,选取合适的灰度阈值对颗粒和孔隙像素进行区分(见图6 (c)). 由于CT扫描的局部体积效应,颗粒与孔隙的交界处会出现图像模糊的现象,因此在选取灰度阈值时应综合考虑多张切片图像. 如图7所示为所有切片图像的灰度值分布结果. 图中,g为灰度值,n为像素数量,在波谷范围内微调阈值,通过测算分割得到的颗粒总体积,并对比根据颗粒密度计算测得的真实颗粒体积,来确定最终的分割阈值,以保证颗粒间接触检测的准确性. 该方法是CT图像处理的常用方法,已得到多位学者的验证[19].
图 7
2.2. 颗粒形态特征统计
式中:r为颗粒顶点的极半径,
图 8
在完成颗粒的表面重构后,计算每个颗粒的几何特性,如质心、体积、表面积、主轴方向等. 本研究采用主成分分析法确定颗粒的长轴、中轴和短轴方向. 由于构成每个颗粒像素单元的权重相等,颗粒绕空间中任意一点旋转的惯性可以用惯性张量进行描述,每个颗粒的主惯性轴方向可以用3个正交的单位向量表示.
由颗粒的质心坐标
式中:N为颗粒边界顶点的个数.
其协方差矩阵的特征值对应的3个特征向量
采用球度
式中:
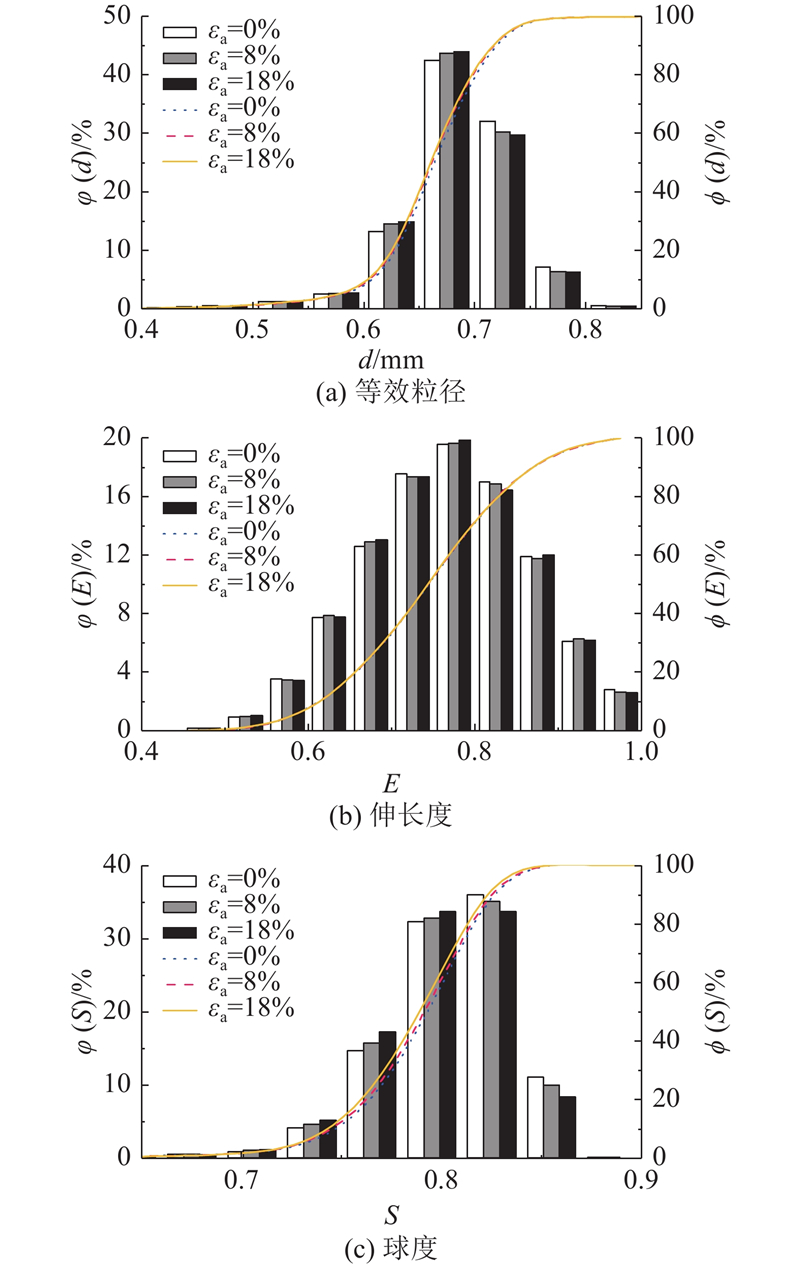
如图9所示,展示了初始状态(
图 9
图 9 渥太华砂形状参数的频率分布演化
Fig.9 Evolution of frequency distribution of Ottawa sand grain shape parameters
2.3. 颗粒匹配与追踪
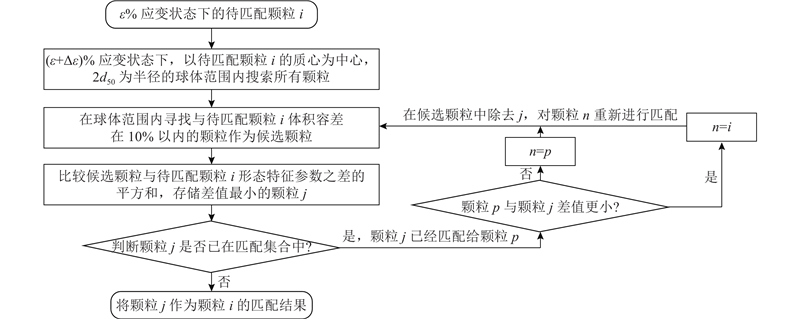
由于同一颗粒在不同应变状态下的编号独立,须对颗粒进行匹配与追踪[17]. 如图10所示为颗粒匹配的基本流程. 对于
图 10
式中:k为轴向应变状态;q为选取的形态特征指标编号;Q为形态特征指标的数量,本研究共选取了5个指标,故Q=5. 将平方和最小的颗粒作为匹配颗粒. 若该颗粒此前已与其他颗粒匹配成功,则检查2次匹配的平方和,较小值对应的配对关系不变,另一组重新匹配.
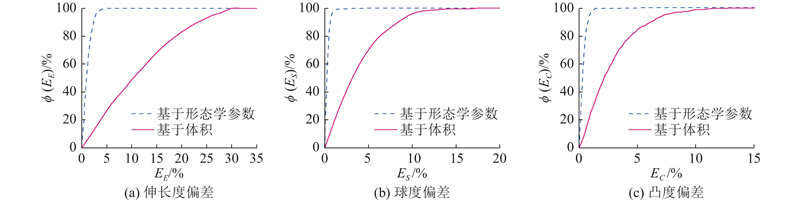
为了验证颗粒匹配结果的准确性,同时采取传统基于体积的颗粒匹配方法对相邻应变状态下的颗粒进行匹配,共得到1222个匹配结果不同的颗粒,计算这些颗粒与2种算法得到的匹配颗粒的形态学参数差值,即可对比2种方法匹配结果的准确性. 如图11所示为2种匹配方法的结果对比. 图中,EE、ES、EC分别为伸长度、球度、凸度偏差. 可以看出,基于形态学参数的颗粒匹配效果明显优于基于体积的匹配算法的,且匹配得到颗粒的各类形态参数误差较小,验证了匹配结果的准确性. 基于以上过程可以实现所有轴向应变状态下颗粒的精确匹配,并追踪每个颗粒在整个加载过程中的运动过程,继而进行颗粒动力学分析.
图 11
图 11 2种匹配算法的颗粒形态参数偏差
Fig.11 Deviation of particle shape parameters of two matching algorithms
3. 颗粒动力学分析
3.1. 颗粒动力学参数计算
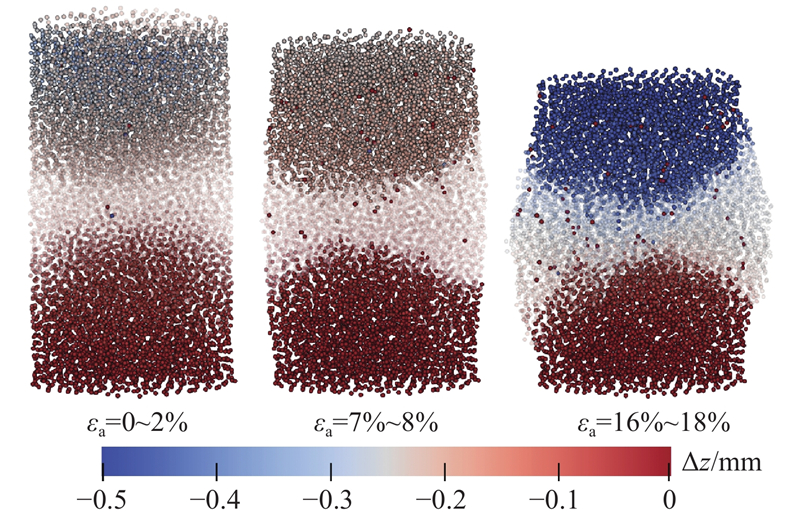
颗粒在整个加载过程中的运动,包括平动与转动2类. 如图12所示为不同加载阶段颗粒的竖向位移增量Δz的计算结果. 图中,将处于中值范围内的颗粒做透明化处理. 可以看出,颗粒的竖向位移随加载的进行不断增大,且在峰值后在颗粒体系的顶部和底部发育了2个锥形区域,并且颗粒逐渐向侧向运动使得颗粒体系发生膨胀. 如图13所示为颗粒转动角度θ的计算结果,通过主成分分析获取颗粒在各个状态下的主惯性轴方向,计算相邻2个应变状态下颗粒的主惯性轴角度差值,得到颗粒在该应变区间内的转动角度. 由颗粒转动角度θ的计算结果可知,在达到应力峰值状态后,颗粒体系中部颗粒转动值开始增大,剪切带逐渐开始形成. 在应力峰值过后,试样中部开始出现明显的X型剪切带,剪切带的中部较厚,且越靠近剪切带中心的颗粒转动值越大,表明剪切带内部颗粒产生较多的塑性变形,是颗粒体系破坏的主要诱因.
图 12
图 13
式中:
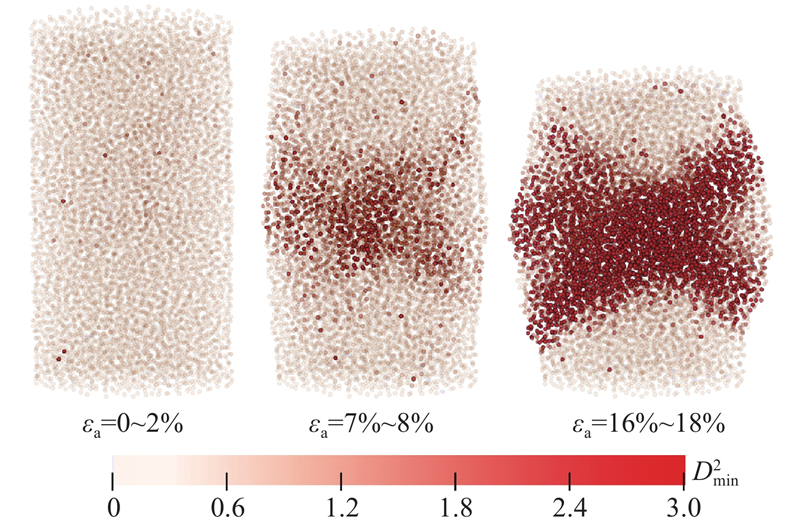
如图14所示为
图 14
图 14 3个轴向应变状态下的颗粒非仿射运动空间分布
Fig.14 Spatial distribution of nonaffine motion of particles under three axial strain states
3.2. 颗粒结构学参数计算
为了研究颗粒的结构特性与其动力学响应的内在联系,对颗粒系统的部分结构特征量进行统计. 根据以往学者的研究[33],颗粒的配位数CN与局部体积分数
将未分割的二值化图像减去分水岭分割后的图像数据,可以识别出相邻2个颗粒之间的接触信息[34]. 颗粒接触对的识别须检索每个接触像素的邻接像素,像素单元之间的邻接情况有3种:以面的形式连接、以边的形式连接和以角的形式连接. 一个像素共包含6个面、12条边和8个顶点,总共包含26种连接方式,只要满足一种连接即认为2个像素单位为邻接像素.
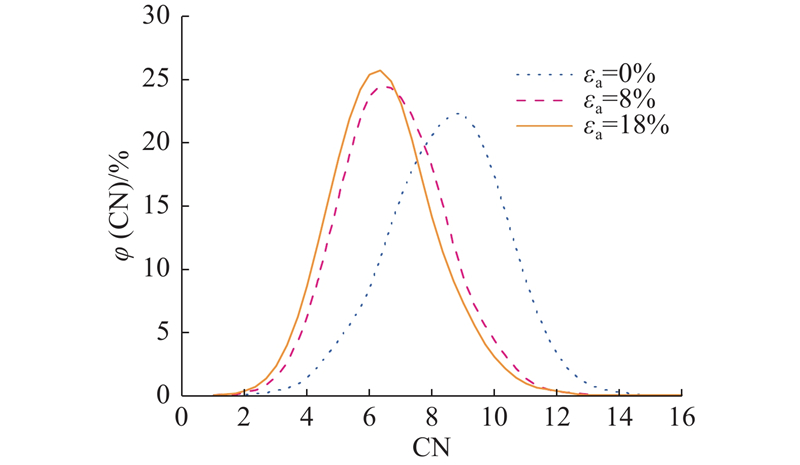
通过计算可以得到初始状态下颗粒体系的平均配位数为8.48,18%轴向应变状态下的平均配位数为6.46,颗粒体系平均配位数不断减小. 如图15所示为颗粒在剪切过程中配位数的演化过程. 可以看出,随着剪切的进行,颗粒间配位数的频率分布向配位数小的方向移动.
图 15
图 15 剪切过程中配位数频率的分布演化
Fig.15 Evolution of frequency distribution of coordination number during shearing
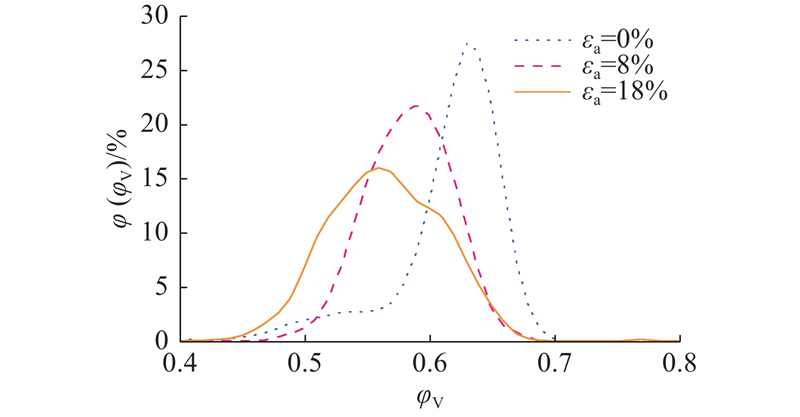
如图16所示为不同轴向应变状态下的颗粒体系局部空隙率分布演化. 可以看出,随着加载的进行,颗粒的平均局部体积分数不断减小,也验证了颗粒体系发生剪胀的现象.
图 16
图 16 剪切过程中局部体积分数频率的分布演化
Fig.16 Evolution of frequency distribution of local volume fraction during shearing
3.3. 颗粒结构学参数与动力学参数相关性分析
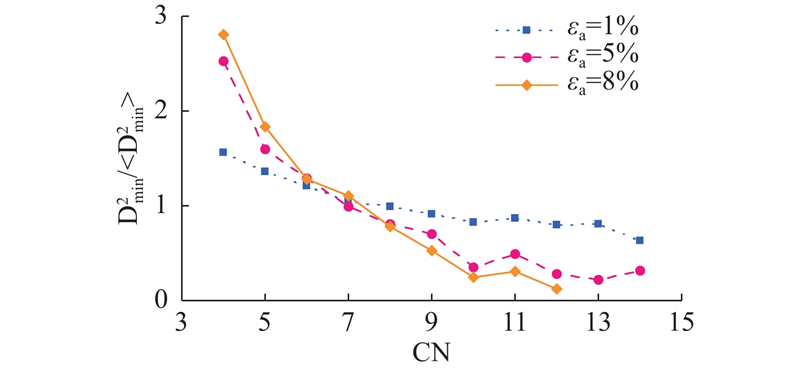
本研究重点关注应力峰值前颗粒的结构特性与动力学响应的相关性. 使用
图 17
图 17 配位数对于颗粒非仿射运动的影响
Fig.17 Effect of coordination number on nonaffine motion of particles
图 18
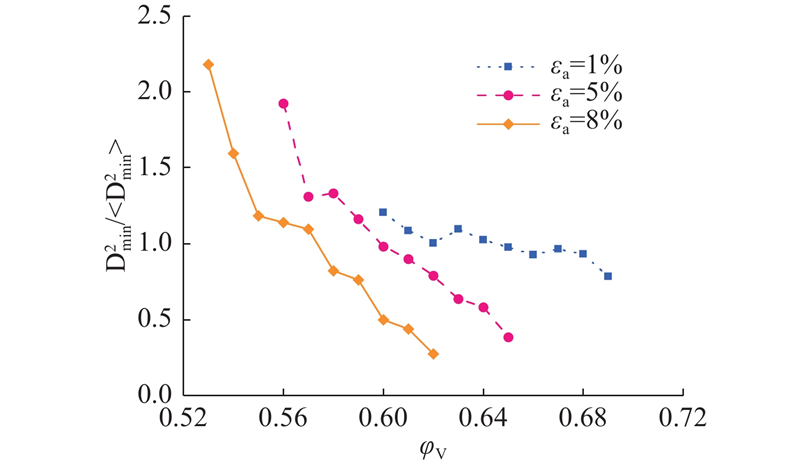
图 18 局部体积分数对于颗粒非仿射运动的影响
Fig.18 Effect of local volume fraction on nonaffine motion of particles
4. 结 论
(1)基于图像处理技术和分水岭分割算法,获取了各个加载阶段颗粒的多尺度形态信息. 统计了颗粒整体形态和局部圆度的信息,并提出了基于颗粒多尺度形态特征的匹配算法,实现了相邻应变间隔下颗粒的精准匹配与追踪,为颗粒动力学分析奠定了基础.
(2)通过非放射变形
(3)在当前状态下颗粒配位数和局部体积分数与后续颗粒的局部塑性活动之间有着较强的相关性,表明颗粒微观动力学与其微观结构之间存在显著因果关系. 具体而言,有较低配位数和局部体积分数的部位更易发生局部塑性变形.
(4)本研究证明了颗粒材料的局部结构对局部塑性行为存在显著影响,此结果可为探究颗粒材料局域结构对宏观力学性能的影响提供依据,但本研究未能实现对颗粒塑性变形的预测,后续可引入机器学习的方法建立颗粒局部结构与局部塑性变形的定量联系,以进一步了解颗粒材料的变形特性.
参考文献
颗粒物质的多尺度结构及其研究框架
[J].DOI:10.3321/j.issn:0379-4148.2009.04.002 [本文引用: 1]
The multiscale structure of granular matter and its mechanics
[J].DOI:10.3321/j.issn:0379-4148.2009.04.002 [本文引用: 1]
颗粒物质及其多尺度结构统计规律
[J].
Granular matter and the scaling laws
[J].
颗粒物质力学及其在工程地质领域中的应用初探
[J].DOI:10.13544/j.cnki.jeg.2021-0017 [本文引用: 1]
Mechanics of granular material and the application in engineering geology
[J].DOI:10.13544/j.cnki.jeg.2021-0017 [本文引用: 1]
高堆石坝筑坝材料宏细观变形分析研究进展
[J].DOI:10.1360/N092018-00279 [本文引用: 1]
Review of macro-and mesoscopic analysis on rockfill materials in high dams
[J].DOI:10.1360/N092018-00279 [本文引用: 1]
An enhanced tool for probing the microscopic behavior of granular materials based on X-ray micro-CT and FDEM
[J].DOI:10.1016/j.compgeo.2020.103974 [本文引用: 1]
A comparative study on optical techniques for the estimation of granular flow velocities
[J].DOI:10.1016/j.ces.2015.03.045 [本文引用: 1]
Speckle-visibility spectroscopy: a tool to study time-varying dynamics
[J].DOI:10.1063/1.2037987 [本文引用: 1]
Granular materials flow like complex fluids
[J].DOI:10.1038/nature24062 [本文引用: 1]
垂直载荷下颗粒物质的声波探测和非线性响应
[J].
Acoustic detection and nonlinear response of granular materials under vertical vibrations
[J].
用于颗粒土微观力学行为试验的微型三轴试验仪
[J].DOI:10.16285/j.rsm.2016.0577 [本文引用: 1]
A mini-triaxial apparatus for testing of micro-scale mechanical behavior of granular soils
[J].DOI:10.16285/j.rsm.2016.0577 [本文引用: 1]
3D characterization of general-shape sand particles using microfocus X-ray computed tomography and spherical harmonic functions, and particle regeneration using multivariate random vector
[J].DOI:10.1016/j.powtec.2017.09.030 [本文引用: 1]
3D quantitative shape analysis on form, roundness, and compactness with μCT
[J].DOI:10.1016/j.powtec.2015.12.029
A self-adaptive gradient-based particle swarm optimization algorithm with dynamic population topology
[J].DOI:10.1016/j.asoc.2022.109660 [本文引用: 1]
Porosity variation within a porous bed composed of multisized grains
[J].DOI:10.1016/j.powtec.2018.07.039 [本文引用: 1]
3D characterization and analysis of pore structure of packed ore particle beds based on computed tomography images
[J].DOI:10.1016/S1003-6326(14)63131-9 [本文引用: 1]
Measuring the evolution of contact fabric in shear bands with X-ray tomography
[J].DOI:10.1007/s11440-019-00869-9 [本文引用: 1]
A particle-tracking method for experimental investigation of kinematics of sand particles under triaxial compression
[J].
Multiscale characterization and modeling of granular materials through a computational mechanics avatar: a case study with experiment
[J].DOI:10.1007/s11440-015-0405-9 [本文引用: 1]
Grain-scale experimental investigation of localised deformation in sand: a discrete particle tracking approach
[J].DOI:10.1007/s11440-011-0151-6 [本文引用: 2]
土石混合料-基岩接触面剪切力学特性及剪切带变形特征研究
[J].
Study on shear mechanical properties and deformation characteristics of shear zone of soil-rock mixture-bedrock interface
[J].
基于复杂网络的岩土颗粒材料分散性失稳先兆研究
[J].
Study on precursors of diffuse instability of granular materials based on complex network theory
[J].
Spatial correlation and temporal evolution of plastic heterogeneity in sheared granular materials
[J].DOI:10.1016/j.powtec.2020.09.053 [本文引用: 2]
Modeling the fragmentation of rock grains using computed tomography and combined FDEM
[J].DOI:10.1016/j.powtec.2016.11.046 [本文引用: 1]
A miniature triaxial apparatus for investigating the micromechanics of granular soils with in situ X-ray micro-tomography scanning
[J].DOI:10.1007/s11709-019-0599-2 [本文引用: 1]
An investigation of single sand particle fracture using X-ray micro-tomography
[J].
Modeling three-dimensional morphological structures using spherical harmonics
[J].DOI:10.1111/j.1558-5646.2008.00557.x [本文引用: 1]
A novel particle tracking method for granular sands based on spherical harmonic rotational invariants
[J].
Micromorphology characterization and reconstruction of sand particles using micro X-ray tomography and spherical harmonics
[J].DOI:10.1016/j.enggeo.2014.11.009 [本文引用: 1]
Three-dimensional sphericity, roundness and fractal dimension of sand particles
[J].
砂土颗粒三维形态的定量表征方法
[J].DOI:10.16285/j.rsm.2017.1825 [本文引用: 1]
A quantitative characterization method of 3D morphology of sand particles
[J].DOI:10.16285/j.rsm.2017.1825 [本文引用: 1]
Microscopic origin of shape-dependent shear strength of granular materials: a granular dynamics perspective
[J].DOI:10.1007/s11440-021-01403-6 [本文引用: 1]
The structure-property relationship of granular materials with different friction coefficients: insight from machine learning
[J].DOI:10.1016/j.eml.2022.101759 [本文引用: 2]
Experimental investigation of inter-particle contact evolution of sheared granular materials using X-ray micro-tomography
[J].DOI:10.1016/j.sandf.2018.08.008 [本文引用: 1]
Set Voronoi diagrams of 3D assemblies of aspherical particles
[J].DOI:10.1080/14786435.2013.834389 [本文引用: 1]
椭球颗粒体系剪切过程中自由体积的分布与演化
[J].DOI:10.6052/0459-1879-21-255 [本文引用: 1]
Distribution and evolution of free volume of ellipsoidal particle systems during shearing
[J].DOI:10.6052/0459-1879-21-255 [本文引用: 1]
Local origin of global contact numbers in frictional ellipsoid packings
[J].DOI:10.1103/PhysRevLett.114.158001 [本文引用: 1]
Finding defects in disorder: strain-dependent structural fingerprint of plasticity in granular materials
[J].DOI:10.1063/5.0068508 [本文引用: 1]
Spatiotemporal analysis of strain localization in dense granular materials
[J].DOI:10.1007/s11440-018-0685-y [本文引用: 1]