建筑结构在长期服役过程中,受环境侵蚀、材料老化、荷载、疲劳效应和突发灾害等因素作用,难以避免地会产生性能退化和结构损伤. 建筑结构的破坏,特别是大型公共建筑及设施的破坏会造成重大的人员伤亡和经济损失. 因此,有必要对既有结构进行全寿命周期的监控与安全性评估[1]. 相比于传统的确定性评价方法(如专家打分法),基于结构可靠度理论的概率评价方法从概率的角度度量了结构在规定的时间和条件下完成预定功能的能力,能够以更加客观统一的标准对结构安全性进行度量[2]. 结构健康监测系统则为结构安全性的评估提供了宝贵的荷载输入和结构响应数据,为结构荷载效应水平估计及不确定性度量提供了可靠依据[3]. 因此,基于健康监测数据的结构可靠度评估在结构工程领域已经有了较为广泛的研究和应用[2-5]. 应力应变传感器一般布置于结构构件上,对构件实际应力状态进行监测,直接反映了构件荷载效应的大小. 因此,大部分基于监测数据的可靠度研究首先根据应变数据对结构构件可靠度进行评估[6-7],进而将结构体系视作串并联系统,得到结构整体可靠度[8]. 然而,对于一些复杂结构,例如具有三维传力特征的空间结构,其构件与体系间的关系很难用串并联系统来清楚表达. 因此须发展能够描述结构构件破坏与体系破坏间关系的方法,来实现复杂结构的安全状态评价.
贝叶斯网络(Bayesian network, BN)是概率统计与图论相结合的一种概率图模型,最早由Pearl提出[9]. 贝叶斯网络能够直观地表达随机变量间的相关性,被广泛应用于机电系统、机械系统、交通设施系统等各类系统可靠度的分析中[10-13]. 建筑结构可以视作由各个构件作为“元件”构成的复杂系统. 一定数量和位置的构件失效会导致结构整体的失效. 根据结构失效模式建立的贝叶斯网络为结构安全状态定量评价提供了新的思路. 目前基于贝叶斯网络的结构可靠度评估方法已经被成功用于简单框架结构及桥梁结构[14-17],其中构件可靠度根据结构设计阶段的各种随机变量的不确定性计算. 一些学者还进一步将结构健康监测或定期检测信息与贝叶斯网络相结合,基于某些可观测的结构性能退化指标(如构件疲劳裂缝发展程度[18-19]、构件腐蚀发展程度[20]、结构动态特性[21]等)建立BN模型,从而实现结构体系可靠度的更新. 然而,针对既有结构,考虑荷载效应的时变性,结合应力应变这一最常见监测指标的基于贝叶斯网络的体系安全状态实时评价还须进一步研究.
本研究基于应力应变监测数据和贝叶斯网络,对结构体系失效概率的计算方法进行研究. 首先根据结构健康监测数据和贝叶斯动态模型估计结构构件的荷载效应概率分布,得到构件可靠度,然后采用贝叶斯网络描述构件失效与结构体系失效间的依赖关系,进而得到结构体系的失效概率,以此来评价结构整体的安全状态.
1. 方法概述
1.1. 贝叶斯网络
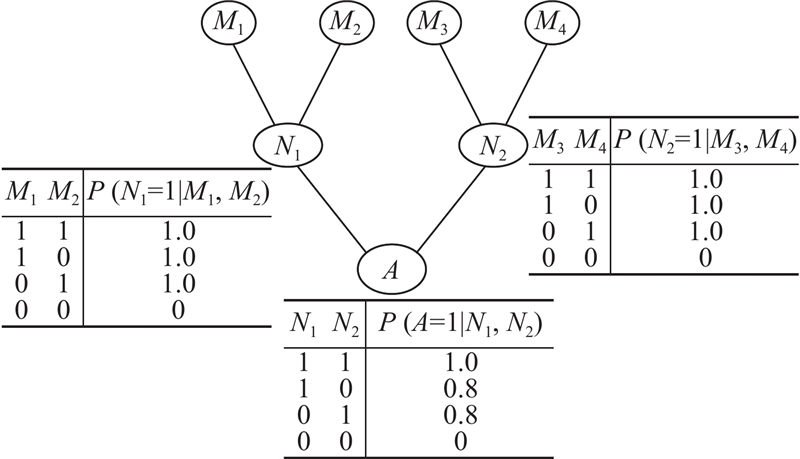
贝叶斯网络是概率统计与图论相结合的模型,是有向非循环的图形模型,其中节点代表问题相关的随机变量,节点间的有向弧代表变量之间的直接依赖关系. 每个节点均附有一个条件概率分布表,用以表述该节点与相关节点间的依赖关系. 如图1所示为简单系统的可靠度计算的贝叶斯网络示例. 图中,M1~M4为系统基本元件对应的根节点;N1、N2为中间子系统对应的中间节点;(M1,M2)、(M3,M4)分别为N1和N2的父节点,N1和N2分别为(M1,M2)和(M3,M4)的子节点;A表示系统节点,其父节点为N1、N2. 若变量取1表示元件或系统失效,取0表示元件或系统未失效,则P(Mi=1)表示基本元件i的失效概率,P(Mi=0)表示相应元件的可靠度. 除了根节点以外,其他节点附有的条件概率分布表列出了此节点相对于其父节点所有可能的条件概率. 例如,系统节点A对应的条件概率表列出的
图 1
图 1 简单系统的可靠度计算的贝叶斯网络
Fig.1 Bayesian network of reliability calculation for simple system
1.2. 贝叶斯网络的概率推理
在贝叶斯网络中,当一个节点的父节点、子节点以及共享子节点的配偶节点给定后,该节点与其他所有节点都是独立的. 利用这一特性,一个包含n个节点的贝叶斯网络所有节点的联合概率密度表达式如下:
式中:
根据式(2),贝叶斯网络中任一节点的概率可以由根节点的概率分布出发,逐步经过概率推理得到. 不过,贝叶斯网络的精确推理过程仅适用于父节点数目有限的单连通的贝叶斯网路的推理. 节点概率分布计算的复杂程度随父节点的数目的增多而显著增加,因此若要采用这种精确推理,须在贝叶斯网络的建立中尽量减少父节点的数目.
1.3. 根节点概率估计
1.3.1. 构件失效概率及可靠指标
在结构体系失效概率计算的贝叶斯网络中,根节点的概率代表结构构件的状态. 因此,根节点的概率评估,即构件的失效概率评估是结构状态评价的基础. 应力应变传感器一般直接布置于结构构件上,对构件实际应力状态进行监测. 因此,本研究采用应力应变监测数据对结构构件的失效概率进行评估. 根据结构可靠度理论,假定t时刻结构的抗力随机变量为Rt,荷载效应随机变量为St,其相应的概率密度函数为
为了简化计算,一般采用可靠指标来表达结构失效概率. 若暂时不考虑抗力随时间的退化,结构抗力R的概率分布可以根据材料特性试验统计得到[23],假设其服从正态分布
可靠指标
式中:
1.3.2. 结构荷载效应概率分布估计
式中:
通过式(6)~(8),即可采用贝叶斯递推(或称卡尔曼滤波),根据新的监测数据
式中:
式(10)可以写为
2. 数值模拟算例
2.1. 简单三杆桁架结构破坏过程模拟
图 2
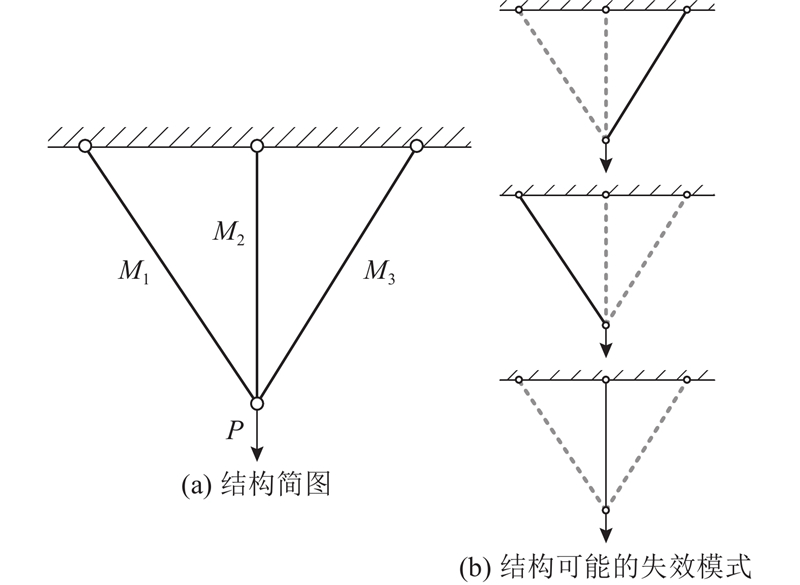
图 2 三杆桁架结构简图及可能的失效模式
Fig.2 Structural diagram of three-bar truss and its possible failure modes
图 3
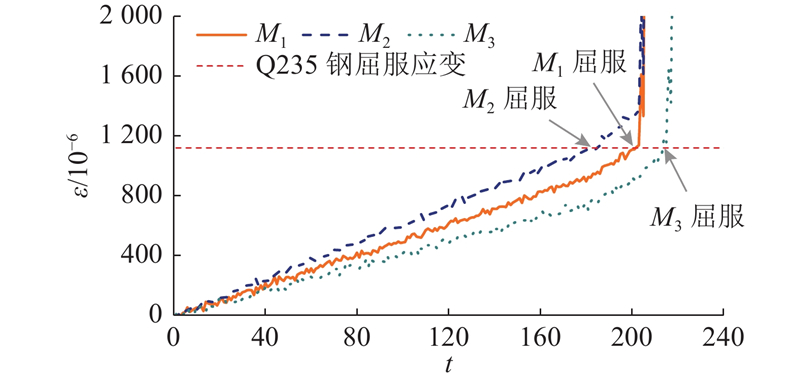
图 3 三杆桁架结构加载过程中的模拟应变数据
Fig.3 Simulated strain data of three-bar truss structure during loading process
2.2. 贝叶斯网络建立
图 4
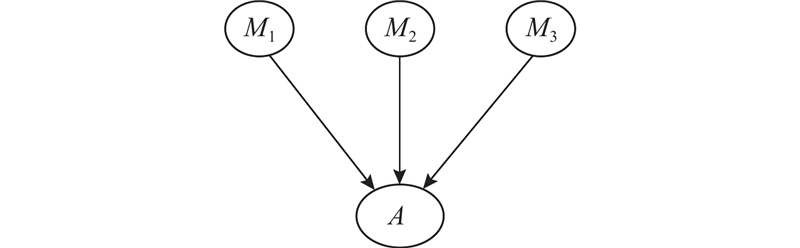
图 4 三杆桁架结构可靠度评估的贝叶斯网络
Fig.4 Bayesian network for reliability assessment of three-bar truss structure
表 1 三杆桁架结构贝叶斯网络的系统节点条件概率表
Tab.1
| | | | |
| 1 | 1 | 1 | 1.0 |
| 0 | 1 | 1 | 1.0 |
| 1 | 0 | 1 | 1.0 |
| 1 | 1 | 0 | 1.0 |
| 其他 | 0 | ||
根据贝叶斯网络递推的原则,系统节点A的概率分布为
则系统节点A的失效概率为
式中:
2.3. 构件可靠指标
为了得到结构体系失效概率,首先根据构件应变数据计算网络根节点的失效概率. 为了方便计算,采用可靠指标代替失效概率评估构件状态. 其中,Q235钢的轴向抗拉屈服应变(即抗力)的均值和方差可以按规范对结构用钢材的材料性质要求进行取值,即
图 5
图 5 三杆桁架结构应变的BDLM预测分布结果
Fig.5 Prediction distribution results of BDLM for strains of three-bar truss structure
图 6
图 6 三杆桁架结构的构件可靠指标
Fig.6 Component reliability index of three-bar truss structure
2.4. 结构体系可靠指标及失效概率
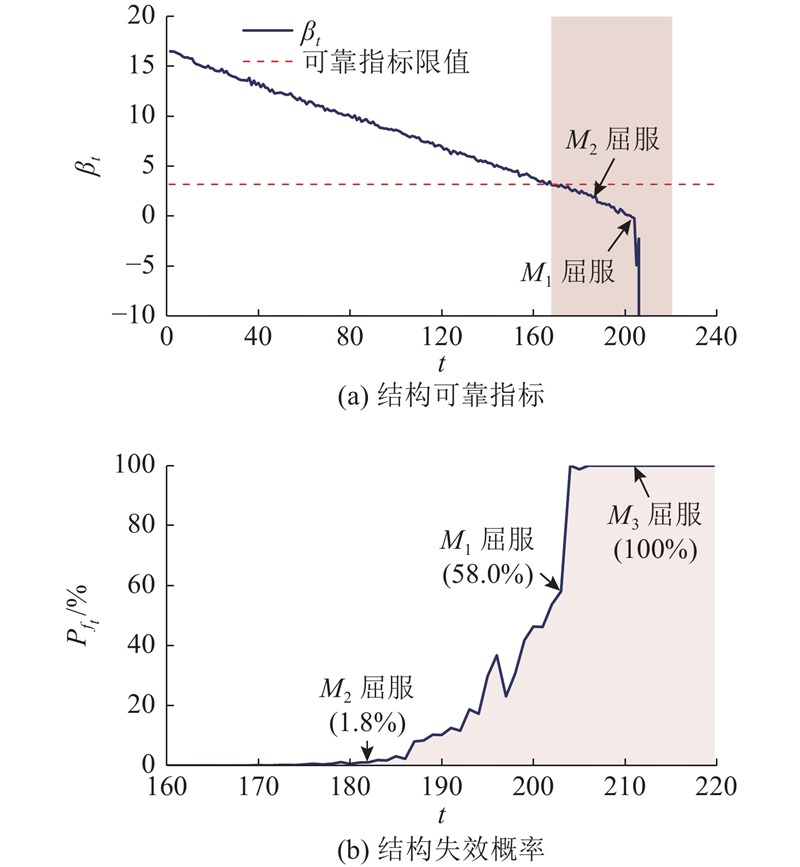
将构件可靠指标代入式(5),即可得到构件的失效概率,进而可以根据前文所述的贝叶斯网络的递推计算求得结构体系的失效概率和相应的时变可靠指标,如图7所示. 其中结构失效概率仅给出了可靠指标小于限值到结构失效这段时间范围的曲线,可靠指标大于限值阶段的结构失效概率是一个非常接近0的值. 由图7可以看出,结构体系可靠指标在第166个时间步开始小于可靠度限值,说明此时结构体系已不再具备足够的安全储备,应当发出预警. 在杆件
图 7
图 7 三杆桁架结构的体系可靠指标及失效概率
Fig.7 System reliability index and failure probability of three-bar truss structure
3. 某单层网壳缩尺模型失效概率评估
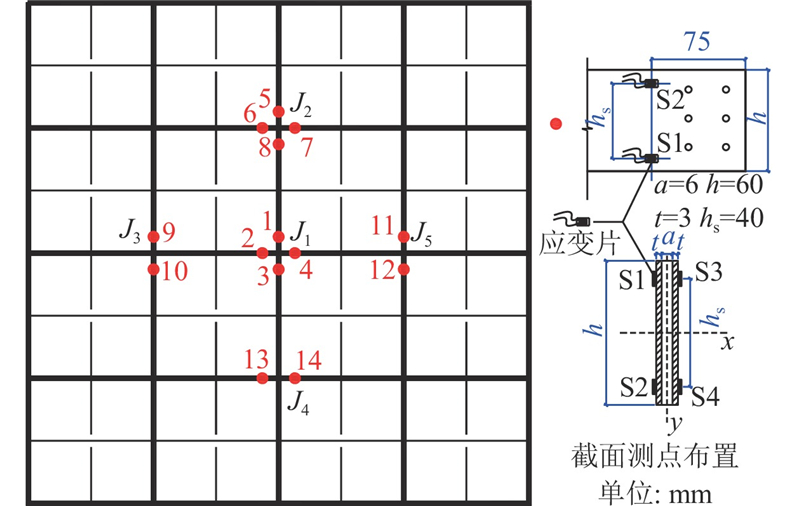
3.1. 缩尺模型介绍和测点布置
图 8
图 8 单层网壳静力破坏试验模型简图及现场照片
Fig.8 Diagram and photo of static failure test model for single layer reticulated shell
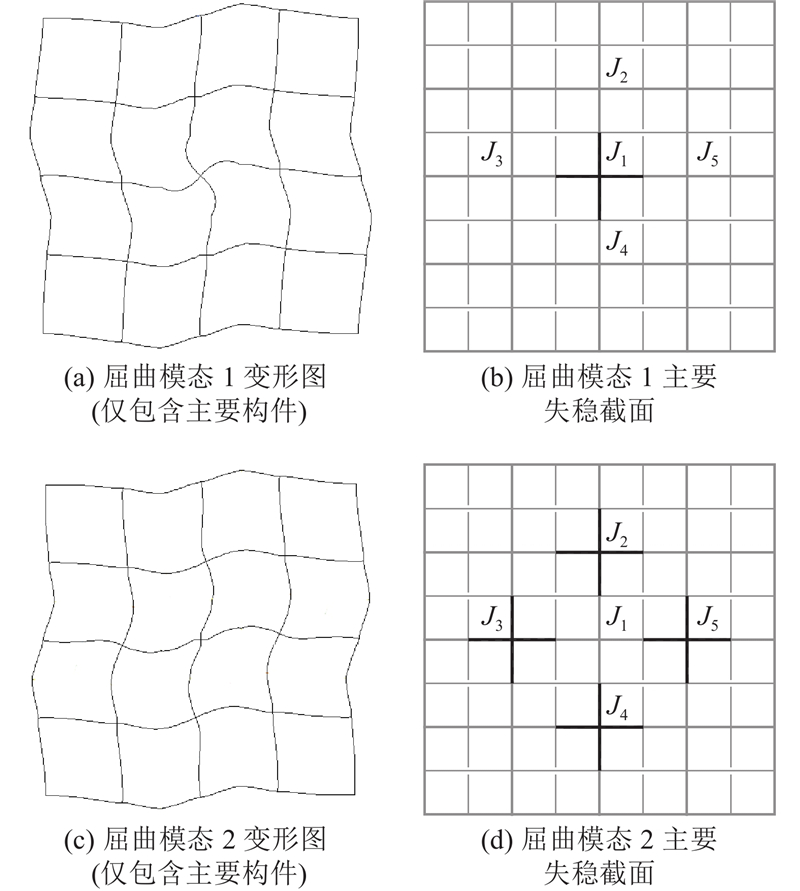
根据有限元模型分析可知,在竖向荷载作用下,结构的前2个主要屈曲模态如图9(a)、(c)所示,对应的主要构件失效截面位置如图9(b)、(d)所示. 其中第1个屈曲破坏模态主要是与节点
图 9
图 9 结构主要屈曲模态及对应的主要失稳截面
Fig.9 Main buckling modes of structure and corresponding main buckling sections
图 10
图 11
3.2. 贝叶斯网络建立
图 12
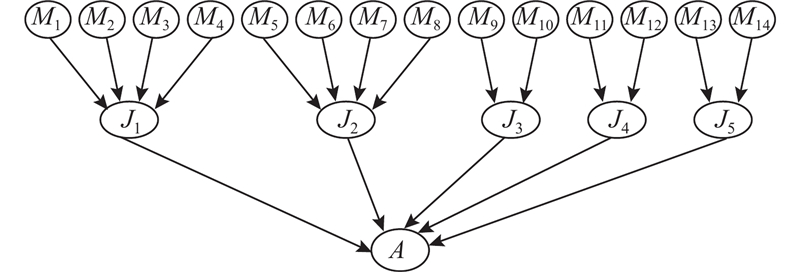
图 12 单层网壳结构可靠度评估的贝叶斯网络
Fig.12 Bayesian network for reliability assessment of single-layer reticulated shell structure
表 2 单层网壳结构整体节点A的条件概率表
Tab.2
| | | | | | |
| 1 | 0, 1 | 0, 1 | 0, 1 | 0, 1 | 1.0 |
| 0 | 1 | 1 | 1 | 1 | 1.0 |
| 其他 | 0 | ||||
对中间节点
如表3所示为以
表 3
节点
Tab.3
| 网络类型 | | | | | |
| 网络1 | 1 | 1 | 1 | 1 | 1.0 |
| 其他 | 0 | ||||
| 网络2 | 1 | 1 | 1 | 1 | 1.0 |
| 1 | 1 | 1 | 0 | 1.0 | |
| 1 | 0 | 1 | 1 | 1.0 | |
| 0 | 1 | 1 | 1 | 1.0 | |
| 其他 | 0 | ||||
| 网络3 | 1 | 1 | 1 | 1 | 1.0 |
| 1 | 1 | 1 | 0 | 1.0 | |
| 1 | 0 | 1 | 1 | 1.0 | |
| 0 | 1 | 1 | 1 | 1.0 | |
| 1 | 1 | 0 | 0 | 1.0 | |
| 1 | 0 | 1 | 0 | 1.0 | |
| 1 | 0 | 0 | 1 | 1.0 | |
| 0 | 1 | 1 | 0 | 1.0 | |
| 0 | 1 | 0 | 1 | 1.0 | |
| 0 | 0 | 1 | 1 | 1.0 | |
| 其他 | 0 | ||||
3.3. 构件可靠指标
本算例中的构件可以视为双肢格构式构件,应变测点所在位置的纤维对应的应力大小不能直接代表整个截面的受力情况,截面整体的受力应当满足《钢结构设计规范》(GB—50017)[31]的要求. 对于本研究算例中的单层网壳结构,各杆件为压弯破坏,首先会发生失稳破坏,因此根据规范中关于稳定性的要求计算构件可靠指标. 理想结构中的构件为单向压弯构件,但由于板片制作和安装误差以及各节点加载不同步的原因,构件实际上为双向压弯构件. 规范规定,弯矩作用在2个主平面内的双肢格构式压弯构件应分别按整体和分肢计算其稳定性要求. 在平截面假定的基础上,根据材料力学可以由4个测点处应变计算得到构件整体弯矩和轴力:
式中:
同理,可以求得构成该格构式构件的各分肢的轴力和弯矩:
式中:
由整体轴力和弯矩,根据规范[31]可以求得构件整体稳定性的等效应力
抗力R的统计参数根据实际Q235材料力学性能相关文献[23],取
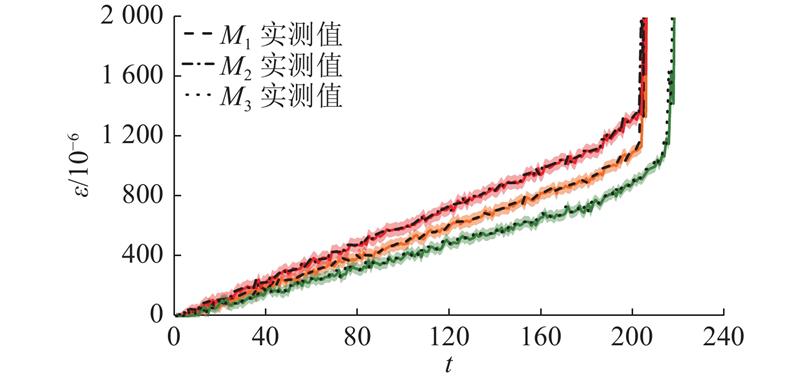
图 13
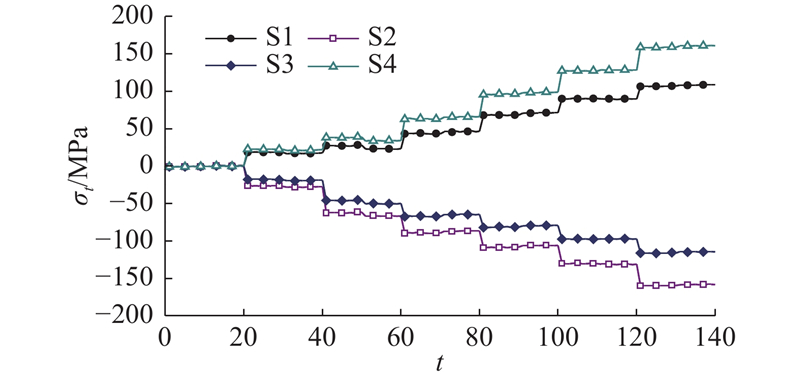
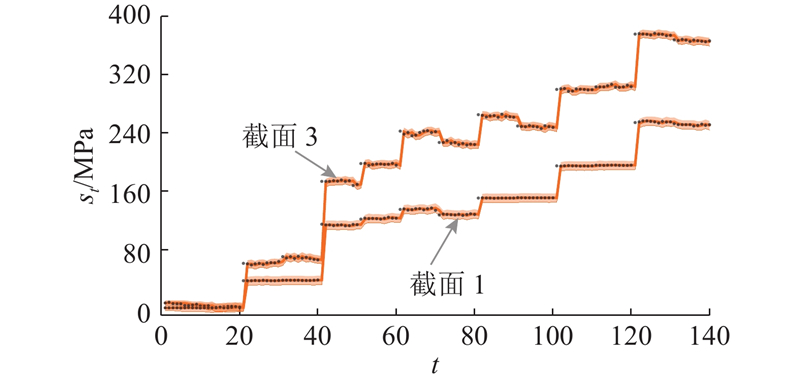
图 13 截面1和3等效应力的BDLM预测分布结果
Fig.13 Prediction distribution results of BDLM for equivalent stresses of section 1 and 3
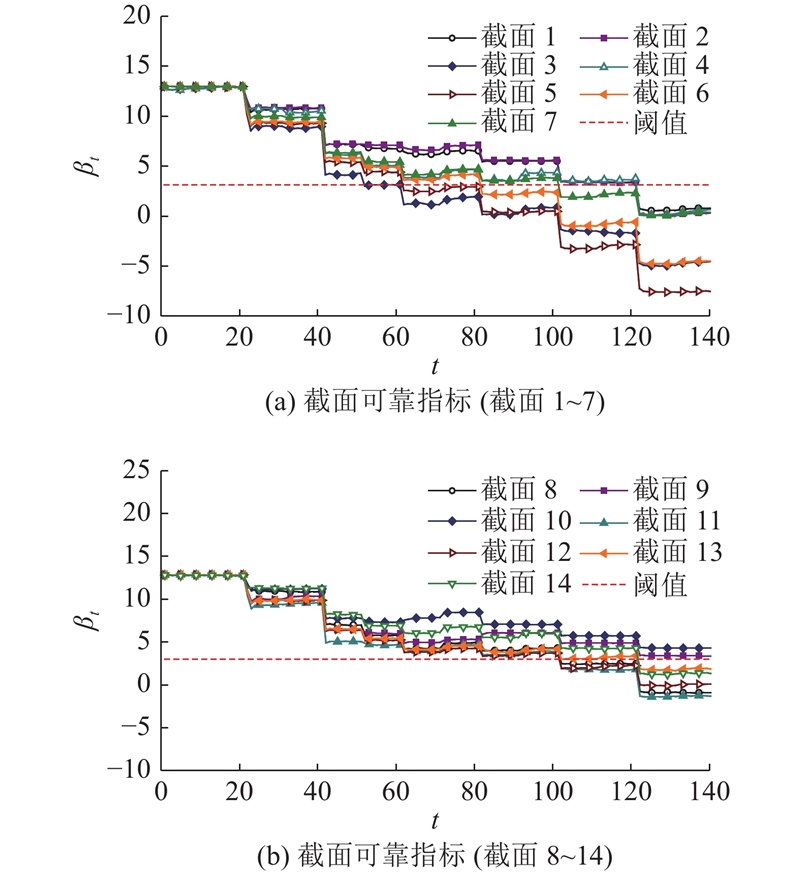
将抗力和各截面BDLM估计得到的荷载效应概率分布估计结果代入式(4)即可得到构件基于稳定性要求的各截面可靠指标,如图14所示.可以看出,大部分构件在第6个荷载步的可靠指标就开始小于阈值,部分截面的可靠指标在第6个荷载步之前就已经小于阈值,说明这些截面所在的构件存在较大的发生失稳破坏的可能性,不再满足结构对安全性的要求. 部分截面(截面3、5、6、7、8、11、12)的可靠指标甚至减小到了负值,发生失稳破坏的失效概率超过了50%,极有可能已经发生了局部的失稳破坏. 实际结构在第7个荷载步发生破坏,这些可靠指标小于0的截面对应构件的变形也非常明显.
图 14
图 14 单层网壳结构的构件可靠指标
Fig.14 Component reliability index of single-layer reticulated shell structure
3.4. 结构体系可靠指标及失效概率
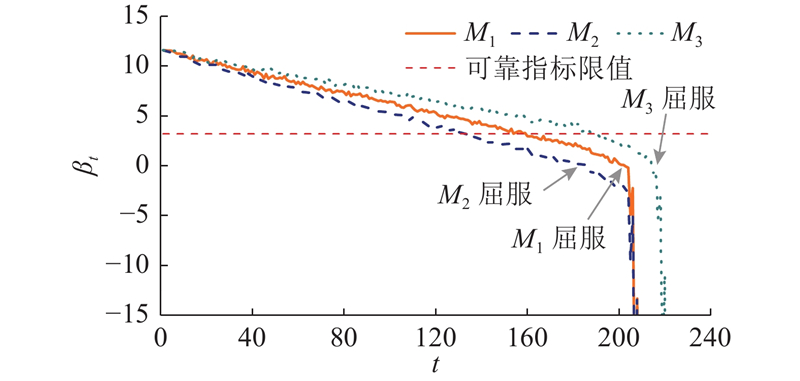
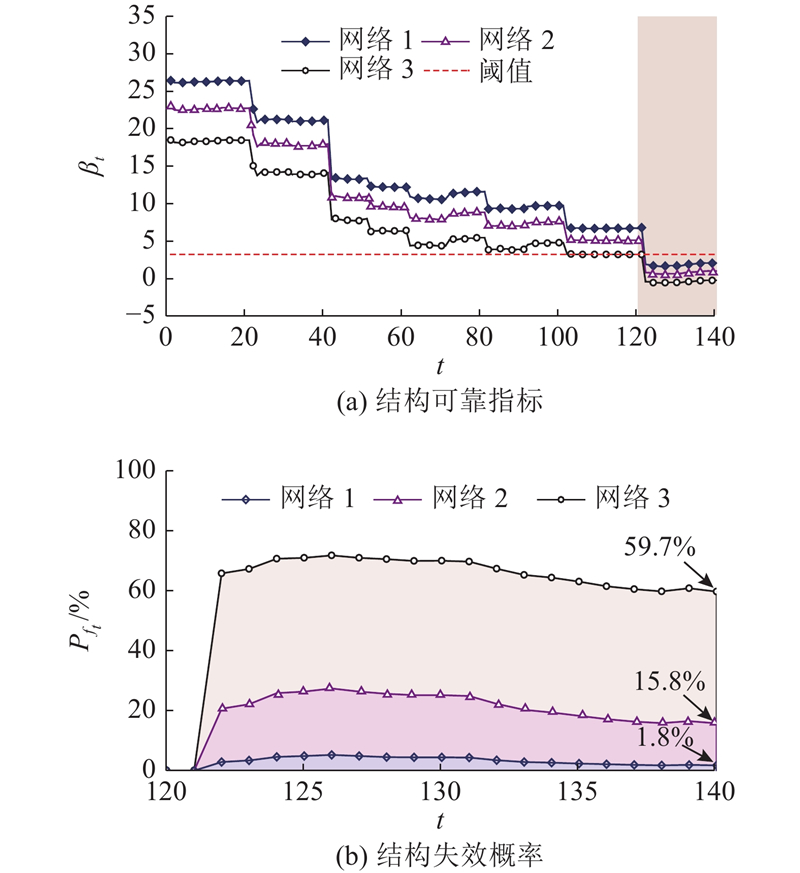
如图15所示为根据贝叶斯网络推理得到的结构可靠指标及相应的结构失效概率. 3种贝叶斯网络对应的结构可靠指标在第6个荷载步均小于了阈值3.2,说明结构有可能发生失效. 其中网络3的可靠指标减小为负值,对应的结构失效概率也较大. 在最后一个加载步,3种网络得到的失效概率分别为1.8%、15.8%和59.7%. 在实际试验中虽然此时结构还未发生整体失效,但在下一个荷载步加载的过程中即发生了整体失稳破坏. 3种贝叶斯网络得到的结构可靠度结果都成功预警了结构的破坏,其中网络3的预警最为有效.
图 15
图 15 单层网壳结构的体系可靠指标及失效概率
Fig.15 System reliability index and failure probability of single-layer reticulated shell structure
实际结构的破坏情况如图16所示,结构破坏后结构各节点均发生一定的扭转和大变形. 结构失稳破坏发展的过程更接近失效模式1,即由中间节点
图 16
图 16 单层网壳结构实际破坏情况
Fig.16 Actual failure situation of single-layer reticulated shell structure
综上所述,本研究所提出的基于贝叶斯网络的结构整体可靠度能够较好地反映结构状态,并对结构可能出现的破坏做出提前预警.
4. 结 论
(1) 基于结构健康监测数据和贝叶斯动态模型的构件可靠度评估考虑了健康监测中的不确定性,从概率的角度给出构件发生某种破坏的可能性,较好地反映了构件的工作状态,并成功预警了构件的破坏.
(2) 贝叶斯网络能够通过拓扑结构和条件概率表描述结构构件失效与整体失效间的因果关系,从而将结构整体可靠度计算转化为概率推理过程,实现了体系可靠度的实时评估. 基于贝叶斯网络和构件可靠度计算得到的结构整体可靠度从概率的角度给出了结构发生整体破坏的可能性,较好地反映了结构整体的工作状态.
(3) 上述数值模拟算例和缩尺模型试验中所建立的贝叶斯网络主要基于某种荷载作用形式下的已知失效模式建立. 未来针对更复杂的结构系统,还须进一步引入其他先进的潜在失效模式识别方法,对结构失效概率评估的贝叶斯网络作进一步深化研究.
参考文献
Novel outlier-resistant extended Kalman filter for robust online structural identification
[J].DOI:10.1061/(ASCE)EM.1943-7889.0000810 [本文引用: 1]
Stable robust extended Kalman filter
[J].DOI:10.1061/(ASCE)AS.1943-5525.0000665 [本文引用: 1]
Anomaly detection of structural health monitoring data using the maximum likelihood estimation-based Bayesian dynamic linear model
[J].DOI:10.1177/1475921720977020 [本文引用: 1]
Experimental and numerical study on stability behavior of reticulated shell composed of plate members
[J].DOI:10.1016/j.jcsr.2020.106102 [本文引用: 1]
考虑杆件失稳的单层球面网壳稳定性分析与试验研究
[J].DOI:10.14006/j.jzjgxb.2017.07.004 [本文引用: 1]
空间结构健康监测研究现状与展望
[J].
Research status and future prospects of space structure health monitoring
[J].
Principal component analysis and polynomial chaos expansion for time-variant reliability problems
[J].DOI:10.1016/j.ress.2017.06.024 [本文引用: 2]
Structural health monitoring and reliability estimation: long span truss bridge application with environmental monitoring data
[J].DOI:10.1016/j.engstruct.2008.01.013 [本文引用: 1]
基于贝叶斯更新和逆高斯过程的在役钢筋混凝土桥梁构件可靠度动态预测方法
[J].
Dynamic prediction of reliability of in-service RC bridges using the Bayesian updating and inverse gaussian process
[J].
al. Stability analysis and test research of single-layer latticed dome considering bar buckling
[J].DOI:10.14006/j.jzjgxb.2017.07.004 [本文引用: 1]
车载下大跨度桥梁动力可靠度评估
[J].
Dynamic reliability assessment for long-span bridges under vehicle load
[J].
Strain monitoring based bridge reliability assessment using parametric Bayesian mixture model
[J].DOI:10.1016/j.engstruct.2020.111406 [本文引用: 1]
Incorporation of structural health monitoring data on load effects in the reliability and redundancy assessment of ship cross-sections using Bayesian updating
[J].DOI:10.1177/1475921713495082 [本文引用: 1]
基于贝叶斯网络的MEMS安全系统可靠性分析
[J].DOI:10.15918/j.tbit1001-0645.2020.065 [本文引用: 1]
Reliability analysis on MEMS S&A device based on Bayesian network
[J].DOI:10.15918/j.tbit1001-0645.2020.065 [本文引用: 1]
基于动态贝叶斯网络的TBM卡机风险预测
[J].
Risk prediction of TBM jamming based on dynamic Bayesian network
[J].
Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas
[J].DOI:10.1016/j.engappai.2010.06.002
Reliability assessment of critical infrastructure using Bayesian networks
[J].DOI:10.1061/(ASCE)IS.1943-555X.0000384 [本文引用: 1]
Development of Bayesian networks for the multi-hazard fragility assessment of bridge systems
[J].DOI:10.1016/j.strusafe.2016.01.006 [本文引用: 1]
Bayesian network enhanced with structural reliability methods: application
[J].DOI:10.1061/(ASCE)EM.1943-7889.0000170
Bayesian network enhanced with structural reliability methods: methodology
[J].DOI:10.1061/(ASCE)EM.1943-7889.0000173
Bayesian networks for disaggregation of structural reliability
[J].DOI:10.1016/j.strusafe.2019.101892 [本文引用: 2]
Reliability analysis and updating of deteriorating systems with dynamic Bayesian networks
[J].DOI:10.1016/j.strusafe.2016.03.004 [本文引用: 1]
A dynamic discretization method for reliability inference in dynamic Bayesian networks
[J].DOI:10.1016/j.ress.2015.01.017 [本文引用: 1]
Integrated pipeline corrosion growth modeling and reliability analysis using dynamic Bayesian network and parameter learning technique
[J].DOI:10.1080/15732479.2019.1692363 [本文引用: 1]
Reliability assessment of deflection limit state of a simply supported bridge using vibration data and dynamic Bayesian network inference
[J].DOI:10.3390/s19040837 [本文引用: 1]
工程结构体系可靠度分析的最新研究进展
[J].
Recent research progress on structural system reliability analysis
[J].
用可靠度理论确定屈曲约束支撑钢框架的设计原则
[J].DOI:10.16226/j.issn.1002-8412.2010.02.017 [本文引用: 2]
Determination of design principle of steel frames with buckling restrained braces using Reliability Theory
[J].DOI:10.16226/j.issn.1002-8412.2010.02.017 [本文引用: 2]
Bayesian forecasting approach for structure response prediction and load effect separation of a revolving auditorium
[J].
Selection of noise parameters for Kalman filter
[J].DOI:10.1007/s11803-007-0659-9 [本文引用: 1]