随着电子商务的快速发展，物流配送需求激增. 传统的自营配送模式面临着配送员短缺问题. 为了解决该问题，一种利用社会潜在运力的众包（crowdsourcing）配送模式被提出. 该模式通过互联网集结社会空闲运力，不仅可以扩展物流运力，而且能提高物流效率^[1]，值得大力推广.

在实践中，众包配送模式主要存在2种形式. 第1种为全众包配送模式，即众包员承担所有配送任务，如盒马配送模式. 研究者对该模式下的配送路径规划、客户分配以及服务定价方法展开了广泛的研究. 刘春玲等^[2]考虑时间窗与客户满意度，提供了基于全众包模式的冷链物流配送路径优化方法. Wang等^[3]基于最小费用最大流提供了一种在线众包客户分配方法. 杜子超等^[4]针对以派单为主、抢单为辅的订单分配模式，构建任务分配模型，并结合蚁群算法和粒子群算法获得任务分配方案. 王文杰等^[5]基于动态优化理论提供了一种最大化平台收益的动态众包服务定价方法. 随后，考虑众包平台的竞争，对上述研究进行了拓展^[6].

第2种形式为选择性众包配送模式，即将一部分配送任务交由众包员完成，另一部分由专职配送员完成. 为了提高选择性众包配送模式的效率，研究者对该模式下的配送方案优化方法展开了研究，如Huang等^[7]假设众包员数量已知，提出了客户分配与配送路径联合优化方法；Kafle等^[8]根据众包员对客户的选择结果，通过构建混合整数规划模型，基于禁忌搜索设计启发式求解算法，制定出选择性众包配送方案. 然而，现有方法基本都假设众包员数量已知，未考虑众包服务价格对众包员参与度的影响，所得方案常常会因缺少众包员的参与而无法执行.

本研究考虑众包服务价格与供给量关系，开展选择性众包配送优化研究，解决现有方法不实用的问题，为众包配送模式的发展提供保障. 首先，以众包服务价格、客户分配与配送路径为决策变量，以最小化配送成本为目标，构建考虑服务定价的选择性众包配送优化模型. 其次，为了求解问题的大规模案例，基于自适应大邻域搜索算法框架，结合节约算法、禁忌搜索算法和模拟退火算法设计一种启发式求解算法. 最后，开展参数敏感度分析，为选择性众包配送模式提供管理建议.

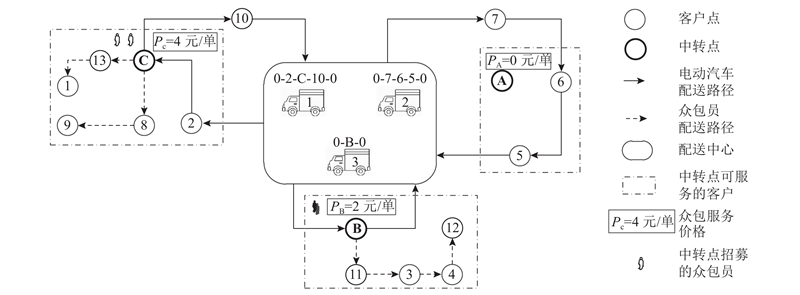
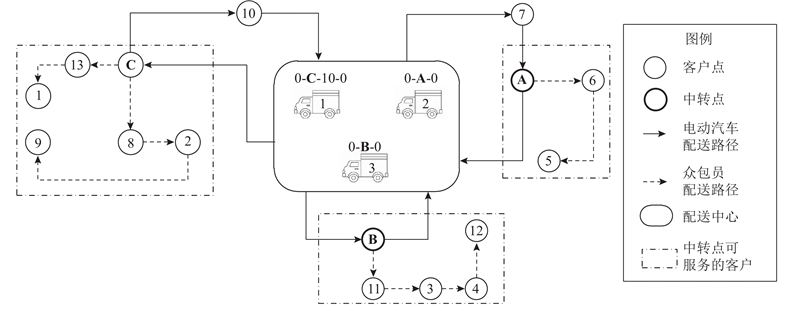
考虑服务定价的选择性众包配送优化问题如图1所示. 一个物流企业的配送中心 $o$为若干客户 $i (i \in {\mathit{I}})$提供配送服务. 配送中心的配送任务可以由专职人员利用电动汽车完成，也可以招募众包员完成. 众包员在中转点 $m (m \in {\mathit{M}})$集结. 配送中心、中转点与客户的位置是确定的，它们之间的欧氏距离为 ${d_{i,j}}(i,j \in \left\{ o \right\} \cup {\mathit{M}} \cup {\mathit{I}})$. 配送中心的营业时间为 $\left[ {{S_o},{L_o}} \right]$. 客户 $i$的货物重量为 ${q_i}$，服务时间(从到达客户点到派送完货物离开客户点的时间)为 ${s_i}$，接受配送服务的时间窗为 $\left[ {{S_i},{L_i}} \right]$. 客户的货物不可交换.

配送中心拥有无限辆同质电动汽车. 电动汽车的额定载重为 ${Q_{\text{e}}}$，行驶速度为 ${V_{\text{e}}}$，单位时间行驶成本为 ${C_{\text{f}}}$，固定使用成本为 ${C_{\text{e}}}$. 每辆电动汽车从配送中心出发为客户配送货物，并且在配送完货物之后，返回配送中心. 众包员则从中转点接收所要配送货物. 众包员所要配送的货物由电动汽车从配送中心配送至中转点. 众包员在配送完货物后，自行离去，无须再次返回中转点. 中转点m可招募到的众包员数量 $ N_m^{} $与该中转点的众包服务价格 $ {p_m} $呈正相关关系，具体关系为 $ N_m^{} = {E_m}{p_m} $( $ {E_m} $为众包供给价格敏感度)^[9]. 由于配送距离限制，中转点 $m$的众包员仅为部分客户 ${I_m}$提供服务. 这些客户也可以由电动汽车服务. 它们的最终服务者是电动汽车还是众包员，由配送成本决定. 众包员一次可配送货量为 ${Q_{\text{c}}}$，行驶速度为 ${V_{\text{c}}}$.

为了最小化配送成本，配送中心应如何制定众包服务价格，分配客户并规划配送路径?

本研究通过建模，设计优化算法，解决上述问题. 首先，对问题进行数学建模. 上述问题包含3个相互关联的子问题：1）客户分配，即将客户交由电动汽车服务，还是众包员服务？2）确定电动汽车配送路径，一个闭环车辆路径问题；3）确定各中转点众包服务价格，即确定各中转点所需众包员数量，由众包配送路径决定. 众包配送路径为一个开环车辆路径问题. 据此，本研究基于车辆路径( vehicle routing problem,VRP)模型进行建模.

本研究设定的目标函数表达式如下：

(1) $ \min\,\left[ \sum\limits_{j \in {{\mathit{I}}_{\text{B}}}}^{} {{{{C}}_{\text{e}}}{x_{o,j}}} {\text+}\sum\limits_{i \in {{\mathit{I}}_{\rm{A}}}}^{} {\sum\limits_{j \in {{\mathit{I}}_{\text{A}}}}^{} {\left( {{{{C}}_{\text{f}}}d_{i,j}^{}{x_{i,j}}} \right)/{{{V}}_{\text{e}}}} } +\sum\limits_{m \in M}^{} {\sum\limits_{i \in I}^{} {{p_m}{z_{m,i}}} } \right].$

式中：第1、2、3项分别为电动汽车固定成本、电动汽车行驶成本以及众包员服务成本，众包员服务成本等于众包服务价格与众包员服务的客户数量乘积； ${{\mathit{I}}_{\text{B}}}$为客户和中转点构成的集合， $ {I_{\text{B}}} = {\mathit{{ I}}} \cup {\mathit{M}} $； $ {I_{\text{A}}} $为配送中心、中转点和客户构成的集合， ${I_{\text{A}}} = I\cup M \cup \left\{ o \right\}$； ${x_{i,j}}$和 ${z_{m,i}}$均为决策变量.

(2) $\left.\begin{array}{l} {x}_{i,j}\text{=}\left\{ \begin{array}{l}\begin{array}{l}\text{1,}\; 电动汽车从节点\text{ }i\text{ }到节点\text{ }j,i,j\in {I}_{\text{A}},i\ne j; \\ \text{0,}\; 其他,i,j\in {I}_{\text{A}},i\ne j. \end{array} \end{array} \right.\\ {z}_{m,i}\text{=}\left\{ \begin{array}{l}1,\; 中转点\text{ }m\text{ }服务节点\text{ }i,m\in M,i\in {I}_{\text{B}}; \\ 0,\; 其他,m\in M,i\in {I}_{\text{B}.} \end{array}\right. \\\displaystyle\sum\limits_{i \in {{\mathit{I}}_{\rm{A}}}}^{} {{x_{i,j}}} +\displaystyle\sum\limits_{m \in {{{ M}}}}^{} {{z_{m,j}}} = 1;\;\forall j \in I. \end{array} \right\}$

式(2)表明每个客户均须被电动汽车或者众包员服务，且仅服务一次.

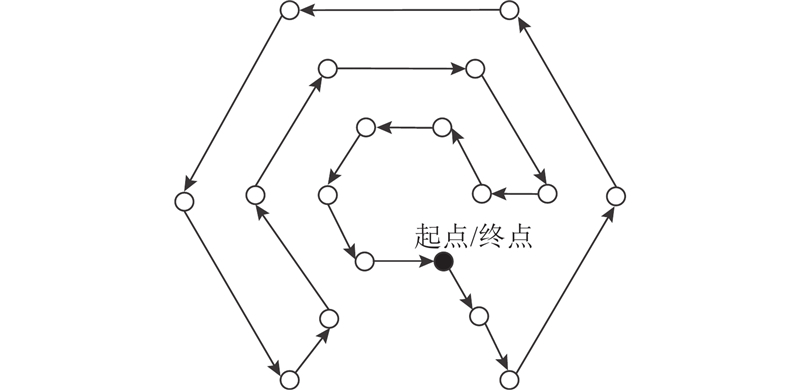
如图2所示，限制电动汽车路径为哈密尔顿回路，表达式如下.

(3) $ \sum\limits_{j \in {{\mathit{I}}_{\rm{B}}}}^{} {{x_{o,j}}} {\text{ = }}\sum\limits_{j \in {{\mathit{I}}_{\rm{B}}}}^{} {{x_{j,o}}} . $

(4) $ \sum\limits_{i \in {I_{\text{A}}}}^{} {{x_{i,j}}} - \sum\limits_{i \in {I_{\text{A}}}}^{} {{x_{j,i}}} = 0; \forall j \in {I_{\text{B}}}.$

客户服务时间限定表达式如下.

(5) ${a_j} \geqslant {a_i}+{s_i}+d_{i,j}^{}/{V_{\text{e}}}+U({x_{i,j}} - 1);\;\forall i \in {I_{\text{A}}},j \in {I_{\text{B}}},i \ne j. $

(6) $ {a_j} \geqslant {a_i}+{s_i}+d_{i,j}^{}/{V_{\text{c}}}+U({O_{i,j}} - 1);\;\forall i \in {I_{\text{B}}},j \in I,i \ne j.$

(7) $ S_i^{} \leqslant {a_i} \leqslant L_i^{};\;\forall i \in {{I}} \cup \left\{ o \right\}. $

式中： ${a_i}$为一个决策变量，表示车辆开始服务节点 $i$的时刻， $i \in {I_{\text{A}}}$； $U$为一个足够大的数； $O_{i,j}^{}$为决策变量.

$ {O}_{i,j}\text{=}\left\{\begin{array}{l}1,\;众包员从节点\text{ }i\text{ }到节点\text{ }j,\;i\in {I}_{\text{B}},j\in I,i\ne j; \\ 0,\; 其他,\;i\in {I}_{\text{B}},j\in I,i\ne j. \end{array}\right.$

电动汽车须在配送中心关闭之前返回，限定表达式如下：

(8) $ {a_i}+{s_i}+d_{i,o}^{}/V_{\text{e}}^{}+U({x_{i,o}} - 1) \leqslant {L_o};\;\forall i \in {I_{\text{B}}} . $

电动汽车载重约束表达式如下.

(9) $ {g_j} \geqslant {g_i}+{q_i}+U({x_{i,j}} - 1); \forall i \in I,j \in {I_{\text{A}}},\;i \ne j. $

(10) $ {g_j} \geqslant {g_m}+\sum\limits_{i \in {{\mathit{I}}_{\mathit{m}}}} {{z_{m,i}}{q_i}} +U({x_{m,j}} - 1);\;\forall m \in M,j \in {I_{\text{A}}}, i \ne j. $

(11) $ {g_i} \leqslant {Q_{\text{e}}};\;\forall i \in {I_{\text{A}}}. $

式中： ${g_i}$为决策变量，表示到达节点 $i$时电动汽车的载重量， $i \in {I_{\text{A}}}$.

众包员供给量约束表达式如下：

(12) $ \sum\limits_{j \in {{\mathit{I}}_{{m}}}}^{} {{O_{m,j}}} \leqslant {E_m}{p_m};\;\forall m \in M. $

众包员配送起点与电动汽车停留点的关联关系表达式如下：

(13) $ \sum\limits_{j \in {{\mathit{I}}_{{m}}}}^{} {{O_{m,j}}} \leqslant U\sum\limits_{i \in {I_{\text{A}}}}^{} {{x_{i,m}}} ;\;\forall m \in M. $

众包员路径限制表达式如下.

(14) $ \sum\limits_{i \in {{\mathit{I}}_{\rm{B}}}}^{} {{O_{i,j}}} - \sum\limits_{i \in {{\mathit{I}}_{\rm{B}}}}^{} {{O_{j,i}}} {\text{ = 0}};\;\forall j \in I. $

(15) $ \sum\limits_{i \in {{\mathit{I}}_{\rm{B}}}}^{} {{O_{i,j}}} \leqslant 1;\;\forall j \in I. $

众包员载重约束表达式如下.

(16) $ {w_j} \leqslant {w_i} - {q_i}+U(1 - {O_{i,j}});\;\forall i \in {I_{\text{B}}},j \in I,i \ne j. $

(17) $ {w_i} \leqslant {Q_{\text{c}}};\;\forall i \in {I_{\text{B}}}. $

式中： ${w_i}$为决策变量，表示到达节点 $i$时众包员的载重量， $i \in {I_{\text{B}}}$.

对于每个中转点，众包员服务的客户数量表达式如下.

(18) $ {z}_{m,i}\text=0;\;\forall m\in M,\;i\in I/{I}_{{m}}.$

(19) $ {z_{m,m}} = 1;\;m \in M. $

(20) $ \begin{split} U\left( {{O_{i,j}} - 1} \right) \leqslant & \sum\limits_m^{} {{R_m}{z_{m,i}} - } \sum\limits_m^{} {{R_m}{z_{m,j}}} \leqslant \\ & U\left( {1 - {O_{i,j}}} \right);\;\forall i \in {I_{\text{B}}},j \in {I_{\text{B}}},i \ne j. \end{split} $

(21) $ \sum\limits_{i \in {\mathit{I}}}^{} {{z_{m,i}} \leqslant } U\sum\limits_{j \in {{\mathit{I}}_{{m}}}}^{} {{O_{m,j}}} ;\;\forall m \in M.$

(22) $ \sum\limits_{j \in {{\mathit{I}}_{{m}}}}^{} {{O_{m,j}}} \leqslant \sum\limits_{i \in I}^{} {{Z_{m,i}}} ;\;\forall m \in {\mathit{M}}. $

(23) $ \sum\limits_{i \in {{\mathit{I}}_{\rm{B}}}} {\sum\limits_{j \in {\mathit{I}}}^{} {{O_{i,j}}} } - \sum\limits_{m \in {\mathit{M}}}^{} {\sum\limits_{j \in I}^{} {{Z_{m,j}}} } = 0. $

式中：R_m为中转点编号.

决策变量取值约束表达式如下：

(24) $ \left. \begin{array}{l} {x_{i,j}} \in \left\{ {0,1} \right\},{O_{i,j}} \in \left\{ {0,1} \right\},{z_{m,i}} \in \left\{ {0,1} \right\}, \\ {p_m} \geqslant 0,{a_i} \geqslant 0,{g_i} \geqslant 0,{w_i} \geqslant 0. \end{array}\right\} $

目标函数中存在2个决策变量的乘积项 ${p_m}{z_{m,i}}$，因此所建模型为非线性规划模型. 非线性规划模型的局部最优点众多，全局最优解难以获得. 线性规划模型的局部最优点即全局最优解，求解相对容易. 因此，在求解前，本研究利用大M法^[10]将上述非线性规划模型等价转化为线性规划模型. 令 ${G_{m,i}} = {p_m}{z_{m,i}}$，转化后的线性规划模型如下.

(25) $\left.\begin{aligned} &{\rm{min}} \;\sum\limits_{j \in {I_{\text{B}}}}^{} {{C_{\text{e}}}{x_{o,j}}} {\text+}\sum\limits_{i \in {{\mathit{{ I}}}_{\text{{\rm A}}}}}^{} {\sum\limits_{j \in {{\mathit{I}}_{\text{A}}}}^{} {\left( {{{{C}}_{\text{f}}}d_{i,j}^{}{x_{i,j}}} \right)/{{{V}}_{\text{e}}}} } +\sum\limits_{m \in M}^{} {\sum\limits_{i \in {\mathit{I}}}^{} {{G_{m,i}}} }.\\ &{\rm{s.t.}}\qquad U{z_{m,i}}+{p_m} - {G_{m,i}} \leqslant U;\;\forall m \in {\mathit{M}},i \in I.\\ &\qquad {G_{m,i}}+U{z_{m,i}} - {p_m} \leqslant U;\;\forall m \in {\mathit{M}},i \in I.\\ &\qquad {{{G}}_{m,i}} \geqslant 0;\;\forall m \in {\mathit{M}},i \in I. \end{aligned}\right\}$

其他约束与式(2)~(24)相同.

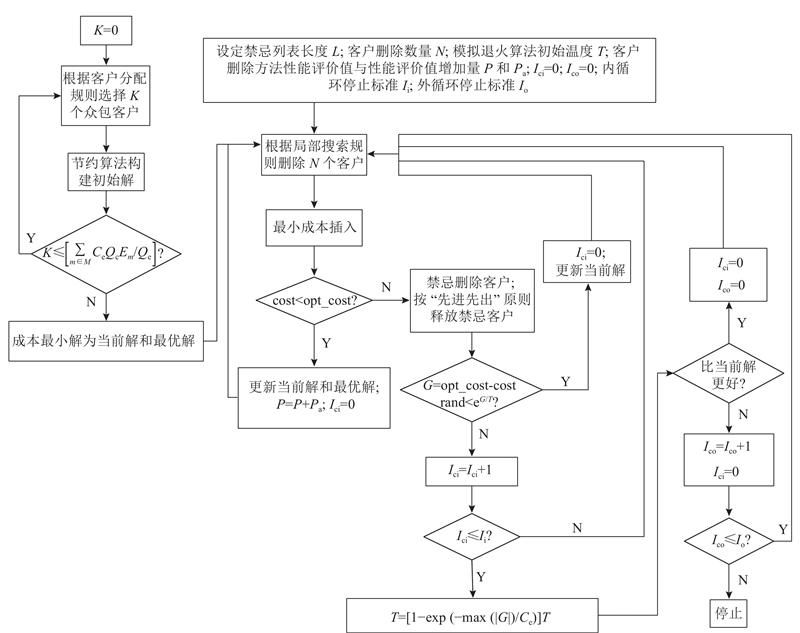
转化后的线性规划模型是一个混合整数线性规划模型. 混合整数线性规划模型不存在多项式精确算法，即大规模案例的精确解难以在可接受时间内获得. 为此，本研究基于自适应大邻域搜索算法框架^[11]，结合节约算法^[12]、禁忌搜索算法^[13]和模拟退火算法^[11]，设计了一种用于求解问题大规模案例的启发式算法，具体流程如图3所示. 算法利用客户分配规则与节约算法生成高质量的初始解，即初始电动汽车配送路径、初始众包员配送路径和各个中转点的众包服务价格；利用基于问题领域知识设计的4个局部搜索规则探索解空间；设计禁忌规则减少重复性搜索，提高解空间的探索效率；基于模拟退火算法思想接受次优解，避免算法陷入局部最优解. 将该启发式算法称为自适应大邻域搜索算法(adaptive large neighborhood search, ALNS).

ALNS由2个阶段组成：初始解构造阶段和改善阶段. 第1阶段为初始解构造阶段. 首先，将众包距离最大的前 $K$个客户分配给众包员. 众包距离表达式如下：

(26) $ {\text{C}}{{\text{S}}_i} = \sum\limits_{j = 1}^J {{d_{i,{f_i}\left( j \right)}}} /J+{d_{o,i}}. $

式中： ${f_i}\left( j \right)$为离客户 $i$最近的第 $j$个客户， $J$为众包距离考虑的最近客户点数量.

该众包距离旨在将电动汽车配送费用较高的客户委托给众包员，即将距离配送中心较远，距离其他客户也较远的客户委托给众包员. 在客户分配后，基于节约算法构造电动汽车和众包员配送路径. 分别试算 $K\in \left[ {0,\left\lfloor {\displaystyle \sum\nolimits_{m \in M} {{C_{\text{e}}}{Q_{\text{c}}}{E_m}/{Q_{\text{e}}}} } \right\rfloor } \right]$时的配送成本，将配送成本最小的解设为当前解和最优解. $\displaystyle \sum\nolimits_{m \in M} {{C_{\text{e}}}{Q_{\text{c}}}{E_m}/{Q_{\text{e}}}}$的设计原理在于：众包员单位载重配送成本 $\left({p}_{m}{N}_{{\rm{cu}}}\right)/\left({P}_{m}{E}_{m}{Q}_{\text{c}}\right)\text{=}{N}_{{\rm{cu}}}/\left({E}_{m}{Q}_{\text{c}}\right)$（ $ {N}_{{\rm{cu}}} $为众包员服务的客户数量）小于等于电动汽车单位载重配送成本 ${C_{\text{e}}}/{Q_{\text{e}}}$时，使用众包配送才可以节约成本，因此，每个中转点众包员至多服务 ${C_{\text{e}}}{Q_{\text{c}}}{E_m}/{Q_{\text{e}}}$个客户.

第2阶段为改善阶段. 该阶段利用根据问题领域知识设计的4种局部搜索规则探索解空间，寻找满意解. 4种局部搜索规则如下.

1）随机删除路径中的客户.

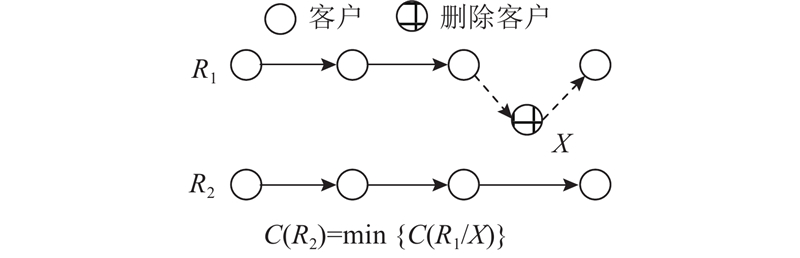
2）删除引起配送成本增加最多的客户. 如图4所示，路径1删除1个客户 $X$后变为路径2. 图中，C表示配送路径成本. 如果路径2是路径1删除1个客户后的最小配送成本路径，则从路径1中删除客户 $X$.

3）随机选择1个路径，将该路径中连续的3个客户删除，如图5所示.

4）删除时间窗最接近的客户. 时间窗最接近的判断规则为： $\mathop {\min }\limits_{i,j}\; \left( {\left| {{S_i} - {S_j}} \right|+\left| {{L_i} - {L_j}} \right|} \right),i,j \in {\mathit{I}},i \ne j$.

改善阶段的具体操作步骤如下.

1）根据4种局部搜索规则的性能值，以轮盘赌方式选择一种方法，删除 ${{N}}$个客户. 各局部搜索规则被选择的概率如下：

(27) $ {\text{P}}{{\text{M}}_i} = {P_i}\Bigg/\sum\limits_{i = 1}^4 {{P_i}} . $

式中： $ {\text{P}}{{\text{M}}_i} $为局部搜索规则 $i$的被选概率， $ {P_i} $为局部搜索规则 $i$的性能评价值.

2）将删除的客户重新以最小成本方式插入到配送路径，得到新解. 这里的配送路径包括电动汽车配送路径、众包员配送路径和新建路径.

3）如果新解的质量优于最优解，则将新解作为当前解和最优解，并提高所用局部搜索规则的性能评价值（每种局部搜索规则的初始性能评价值为1），返回步骤1）；否则，以概率 ${{\text{e}}^{G/T}}$( $G$为新解与最优解的配送成本差，是一个负值)接受新解为当前解，将删除的客户加入禁忌列表，返回步骤1）；否则，连续 ${I_{\text{i}}}$次，未改善当前解，则降温，令 $T = \left[ {1 - \exp \,\left( { - \max\, (\left| G \right|)/{C_{\text{e}}}} \right)} \right]T$，返回步骤1）；否则，连续降温 ${I_{\text{o}}}$次，未改善最优解，则停止计算.

参考文献[7]，基于VRP标准案例(Solomon案例)^[14]，对模型和算法的有效性进行验证. 本研究问题的已知条件比Solomon案例多中转点位置和数量. 为此，首先给Solomon增加8个中转点. 这8个中转点在配送区域随机设置. 其次，选择Solomon案例的前10个客户，构造小案例集；取Solomon案例的所有客户，构造大案例集. 所有新构造的案例编号仅在Solomon案例编号的基础上，增加案例规模，如c101_10（小案例）和c101_100（大案例）. 其余案例参数如下： ${C_{\text{e}}} = 90$ 元/辆， ${C_{\text{f}}} = $1 元/小时， ${Q_{\text{e}}} = 200$ kg， ${Q_{\text{c}}} = 25$ kg， $ {E}_{m}=0.5 \;人/ \left(元/单\right) $， $\forall m \in M$， ${V_{\text{e}}} = 1$ km/h和 ${V_{\text{c}}} = 1$ km/h.

每个案例都采用GUROBI 9.1求解器和ALNS求解. ALNS采用MATLAB编程实现. GUROBI求解器和ALNS都在配置为Inter I5 with 8 GB RAM的电脑上运行. ALNS的参数如下： $N = 25$， $T = 25$， ${I_{\text{i}}} = 15$， ${I_{\text{o}}} = 15$.

为了验证所建模型的正确性，利用GUROBI求解器对c101_10案例进行求解. 求解结果如表1所示. 表中，R为电动汽车访问的节点编号. 可以看出，众包服务价格 ${p_m}$为0 元/单，电动汽车配送路径经过了所有的客户点，未使用众包员，满足众包服务价格与众包供给量关系式. 同时，客户服务开始时刻都在客户要求的时间窗内，且电动汽车载重量一直小于其额定载重量，满足客户时间窗和车辆载重约束. 以上结果表明，文中所建数学规划模型有效.

对选择性众包配送模式、全众包配送模式和无众包配送模式的配送成本进行对比分析，探究选择性众包配送模式的性能. 选择性众包配送模式以最小成本为导向，对众包客户进行选择；全众包配送模式将在众包员服务范围内的客户，全部交由众包员服务，如图6所示；在无众包配送模式下，所有客户都由专职人员利用电动汽车直接服务. 3种配送模式下的小规模案例求解结果，如表2所示. 表中， ${\text{TC}}$为配送成本，等于车辆配送成本与众包配送成本之和； ${\text{VC}}$为车辆配送成本； ${\text{CC}}$为众包配送成本，等于平均众包服务价格与众包模式服务的客户数量的乘积；AP为平均众包服务价格；CN为众包模式服务的客户数量.

对比全众包配送模式与无众包配送模式的配送成本可知，除了案例r105_10和rc105_10以外，其他8个案例的全众包配送模式的配送成本都大于无众包配送模式的. 原因如下：1）在全众包配送模式下，为了将货物交于众包员，电动汽车须多走一些路程，如案例c101_10，在全众包配送模式下，电动汽车配送成本大于无众包配送模式的车辆配送成本；2）在全众包配送模式下，物流企业除支付车辆配送费用外，还须额外支付众包员服务成本. 当众包员的服务成本大于车辆配送成本节约量时，使用众包配送模式会增加配送成本，如案例r101_10，利用众包配送模式后，车辆配送成本节约1.97元，而众包员使用成本为2.00元，最终导致配送成本增加0.02元. 选择性众包模式根据车辆配送成本节约量与众包服务成本选择合适的配送服务模式，因此它的配送成本总是最小. 因此，为了降低配送成本，末端配送服务应采用选择性众包配送模式，根据配送成本合理地选择配送服务提供者.

与此同时，根据案例rc105_10选择性众包模式的计算结果可知，物流企业须将众包服务价格设定为 $ {p}_{m}=2.0\text{ }元/单 $，以至招募到1个众包员完成1个配送订单. 如果不考虑众包服务价格与众包供给数量的关系，物流企业盲目地将众包服务价格设定为 $ {p}_{m}=1.0\text{ }元/单 $. 这时，物流企业只能招募到0.5个众包员，也就是说，其制订的选择性众包配送服务方案是无效的. 如果物流企业将众包供给价格设定为 $ {p}_{m}=4.0\text{ }元/单 $，物流企业可以招募到足够的众包员，但却多支付了众包服务费用. 因此，物流企业在制定选择性众包配送方案时，应考虑众包服务价格对众包供给数量的影响.

从求解质量和求解时间两方面，验证ALNS的性能. 如表3所示为4个方法求解所有小规模和大规模案例获得的最好解和求解时间. 表中，GUROBI列呈现了GUROBI求解器在2 h求解时间限制下获得的最好解与求解时间；E-R-T-R列呈现了基于最早配送规则（earliest ready time rule, ERTR）获得的最好满意解与求解时间；S-A列为节约算法（saving algorithm, SA）获得的最好满意解与求解时间；ALNS列为本研究设计的启发式算法获得的最好满意解与求解时间. 其中，CT为求解时间，GAP为算法求解质量差异比，等于某一算法求得的配送成本与GUROBI求得的配送成本之差占GUROBI求得的配送成本的百分比.

ALNS是一种改善算法，通过不断优化初始解获得满意解. 算法性能严重依赖于初始解质量. 对比E-R-T-R列和S-A列可知，S-A构建的解质量显著优于E-R-T-R构建的解，尤其当案例规模较大时. 因此，本研究利用S-A构建ALNS的初始解.

对于小规模案例，ALNS获得的解质量与GUROBI求解器得到的解质量基本相同：11个案例，解的质量相同；2个案例，解的质量差异小于1%. 仅1个案例，ALNS的求解时间大于GUROBI求解器的. 对于大规模案例，GUROBI求解器无法在2 h内获得所有案例的最优解. 这是因为问题的解空间随客户规模指数级增加. 虽然ALNS的求解时间也会随客户规模的增加而有所增加，但其增幅较小，最大求解时间不超过1 min，远小于GUROBI求解器所用时间. 就解质量来看，73%的案例，ALNS获得的解不劣于GUROBI求解器的，差异最高超过18.0%，平均为5.5%. 剩余27%的案例，虽然ALNS获得的解质量不如GUROBI求解器，但解质量差异较小，最高不超过4.0%，平均为1.6%. 综上可知，ALNS性能优于GUROBI求解器、最早配送规则和节约算法.

为了获取选择性众包配送模式管理建议，对众包供给价格敏感度、中转点数量以及时间窗宽度对选择性众包配送方案的影响展开分析. 在分析每个因素的影响时，其他参数值保持不变.

如表4所示为不同众包供给价格敏感度下，案例c101_10和c101_100的配送方案情况. 表中，CM为可由众包员服务的客户数量. 当众包供给价格敏感度大于特定值时，如案例c101_10， $ {E}_{m}\text{=}1.5\text{ }人/\left(元/单\right) $时，众包模式才会被使用. 随着众包供给价格敏感度提高，众包模式服务的客户数逐渐增多，配送成本降低. 众包供给价格敏感度对众包模式的使用与配送成本的节约有正向作用.

基于不同中转点数量获得的配送方案如表5所示. 随着中转点数量增加，案例c101_10_2和c101_100的配送成本会轻微下降，众包模式服务的客户数量会增加. 这是中转点增加众包供给量与众包模式需求量所致. 案例c101_10_1的配送成本与众包模式服务的客户数量无变化表明，中转点位置选择需谨慎，否则，可能由于位置偏远或者与已有中转点太过重合而无效. 一种可行的中转点选择方法是将所有客户点以及潜在中转点都设置为备选中转点，然后根据本研究方法获得的结果，将服务客户的备选中转点设置成中转点.

如表6所示为不同时间窗宽度下的配送方案. 表中，PR为时间窗宽度改变比例，VN为车辆数. 可以看出，配送成本会随时间窗宽度的增加而降低. 这是因为客户时间窗越宽，位置接近的客户更有可能被同一辆车服务，因而会减少车辆行驶里程和所需的车辆数. 如案例r105_10，在时间窗宽度增大到1.0倍时，需要3辆电动汽车服务客户，而在时间宽度增大到1.2倍时，仅需要2辆电动汽车. 因此，为了节约配送成本，配送中心可以通过奖励之类的措施激励客户松弛配送时间窗. 由表6还可以看出，客户时间窗越紧，众包模式的使用率就越高，如时间窗宽度缩小至0.7倍时，众包模式服务的客户数比时间窗宽度增大到1.3倍时的多. 这可以解释为时间窗越紧，服务相同数量客户所需的车辆或众包员就越多，而众包员的服务成本远低于车辆的固定使用成本，因而会优先被使用.

基于Solomon案例，证实本研究提出的众包服务价格与配送方案联合优化方法是有效的. 通过敏感度分析证实：在降低配送成本方面，选择性众包配送服务模式优于全众包配送服务模式和无众包配送服务模式；众包配送服务模式适用于众包供给价格敏感度高、客户服务时间窗紧的场景；在合适的位置增加中转点或拓宽客户时间窗宽度都可以降低配送成本.

未来在算法方面，可以进一步探讨强化学习的应用效果；在问题方面，可以考虑客户配送需求的动态性以及电动汽车的多次使用情况对研究问题进行扩展.