有些学者通过优化扰动步长,改善稳态和动态性能. Liu等[10]提出变步长的增量电导法,扰动步长正比于功率关于电压导数(dP/dV)的绝对值. 在MPP附近,dP/dV趋近于零,则步长也能趋于零. Fathabadi[11]同时考虑功率关于电压的导数(dP/dV)和功率关于电流的导数(dP/di),根据两者的值设置5个阈值来选取合适的步长. Zhou等[12]利用电流和功率关于电压的导数(dP/dV)来设置步长变化系数,以期获得平滑的步长变化曲线. Tafti等[13]提出柔性的自适应扰动观测方法跟踪指定功率,根据dP/dV设计稳态期间的迭代电压步骤,以实现稳定的恒功率输出. 上述的步长优化方法都利用了以下光伏特性:越接近MPP,dP/dV的绝对值越小. 虽然动态跟踪速度有所提高,但是由于零分母约束和时域dP/dV或dP/di计算的噪声敏感性,稳态振荡仍然存在. 有些方法尝试引入状态识别模块,通过模式切换暂停扰动,以消除振荡. 李向丽等[14]利用MPP点附近压差符号变化的特性来识别稳态. Bhattacharyya等[15]在变步长的P&O和InC方法基础上,增加了稳态识别模块. 当光伏电压连续3次符合稳态电压振荡模式时,暂停扰动,以消除稳态振荡. 为了在环境变化下重启扰动观测模块,需要增加动态识别模块,这会增大控制复杂度,为了防止误判而增加的阈值又会影响输出性能.
本文提出基于空间域dP/dV计算的控制方法,旨在为上文提出的问题提供可行的解决方案. 本文采用二维数组来构建空间域,利用基于电压索引的历史运行数据维护空间域. 每一次dP/dV计算都使用当前的运行数据和在空间域中相邻的历史数据,可以避免零分母问题,以实现不同dP/dV参考值下的零误差跟踪和零稳态振荡. 该方法在最大功率跟踪(maximum power point tracking, MPPT)(dP/dV = 0)和功率热备运行模式(dP/dV < 0)下都取得了较好的输出性能.
1. 光伏特性
基于均匀光照下的光伏数学模型揭示光伏
1.1. P-V特性
理想的光伏阵列数学模型为
由此,光伏阵列的输出功率可以表示为
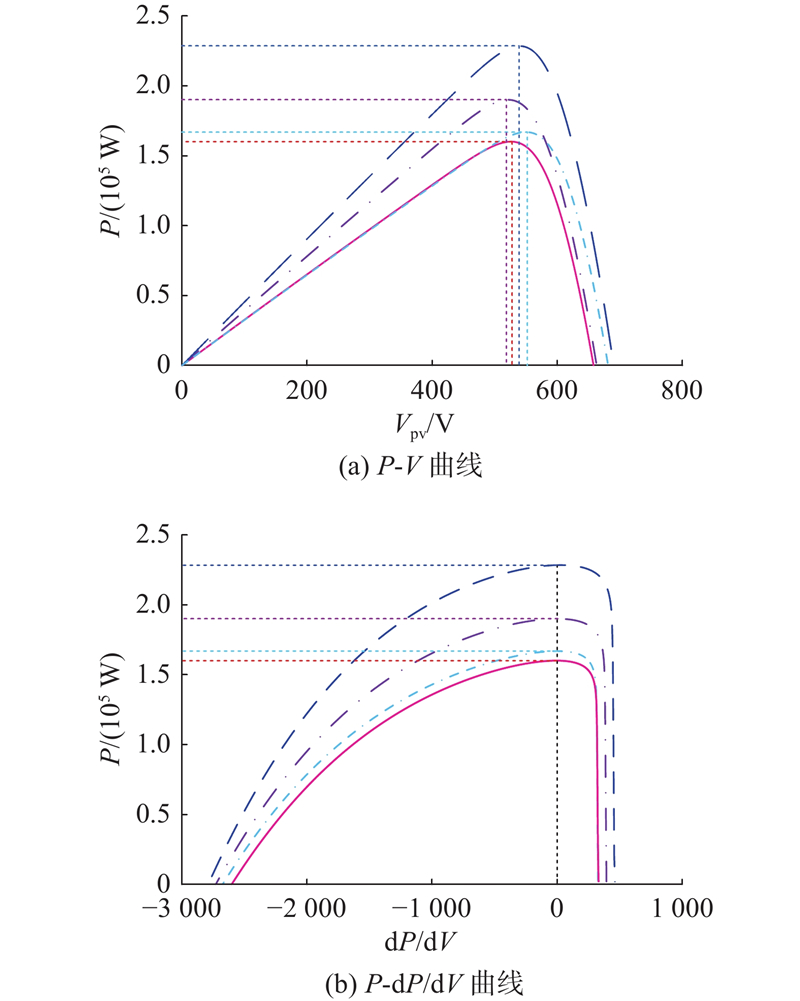
从式(2)可知,光伏输出功率和电压之间是非线性相关的,且受环境辐照度和温度的影响. 这意味着在不确定的环境条件下,光伏的输出具有随机性和间断性. 如图1 (a)所示,为了直观地理解这一特性,绘制了KC200GT光伏阵列在不同辐照度和温度下的P-V曲线. 图中,每条曲线都有1个最大点和2段被最大点分割的线段,最大点表示光伏阵列在特定环境条件下能产生的最大电量. 在最大点左侧,输出功率随着电压的增加而增加;在最大点右侧,输出功率随着电压的增加而下降. 在不断变化的环境条件下,可用功率(最大功率)随之波动.
图 1
图 1 KC200GT阵列在不同的温度和辐照度下的特性曲线
Fig.1 Curves of KC200GT modules under different temperature and solar irradiance
1.2. P-dP/dV特性
功率对电压的导数可以表示为
功率对电压的二阶导数为
显然,式(4)恒小于零,即dP/dV是单调递减的. dP/dV的极值点为
由式(2)~(5)可得以下结论. 1)在区间
如图1 (b)所示为同一个KC200GT光伏面板的P-dP/dV曲线. 各P-dP/dV曲线特性均符合上述结论:光伏输出功率可以通过dP/dV调节;当dP/dV = 0时,无论环境条件如何变化,光伏面板始终工作在最大功率点;当dP/dV为负值时,光伏面板削减一部分功率而工作在功率热备模式,且dP/dV越小,削减的功率比例越大.
2. 基于空间域dP/dV计算的控制算法
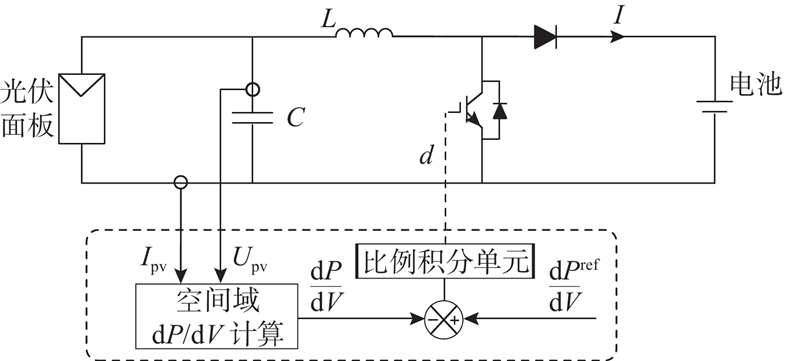
如图2所示为基于空间域dP/dV计算的控制结构. 所提方法移除了P&O模块,把dP/dV作为控制变量直接进行控制. dP/dV参考值由上层控制给定, dP/dV实际值基于当前工作点电压和电流计算得到,两者之间的差值经过比例积分模块生成占空比d. 实现该控制方法的关键在于dP/dV的计算,也是本文的创新之处,即空间域dP/dV的计算方法.
图 2
图 2 基于空间域dP/dV计算的光伏系统控制结构
Fig.2 Spatial-domian dP/dV calculation based PV control scheme
2.1. 空间域dP/dV计算原理
通过和时间域dP/dV计算原理的对比,揭示空间域dP/dV计算原理. 在时间域dP/dV计算中,一般用2个连续时刻的运行点数据计算dP/dV,表达式为
式中:
式(6)的计算方法存在缺陷:当输出趋于稳态的时候会发生零分母问题,即
提出空间域dP/dV计算方法,避免稳态下的零分母问题. 通过2个空间上相邻的运行点来计算dP/dV,运算表达式为
式中:
对比式(6)、(7)可知,空间域和时间域之间的区别在于
2.2. 空间域dP/dV计算的实现方法
为了建立空间域,定义如图3所示的二维数组
图 3
式中:M为数组长度,
下面通过举例说明空间域的存储过程. 设在
在另一时刻
若
每一次dP/dV的计算都取空间域中的2列数据,一个是当前运行点数据,另一个是空间上相邻的数据. 如图4所示为空间域dP/dV计算的流程图. 在数组初始化后,控制器循环执行以下操作:
图 4
采样当前光伏运行点的电压
式中:
向后找到距离m列最近的非空列n,即
式中:
计算dP/dV,即
式中:
2.3. 参数设定
1)数组长度M. 数组是用来存储运行中采样的数据,必须能够存放运行中最大电压下的数据,即
式中:
2)空间间隔
图 5
光伏P-V曲线可以近似地拟合成抛物线[20]:
式中:
设B点和C点的坐标为
式中:
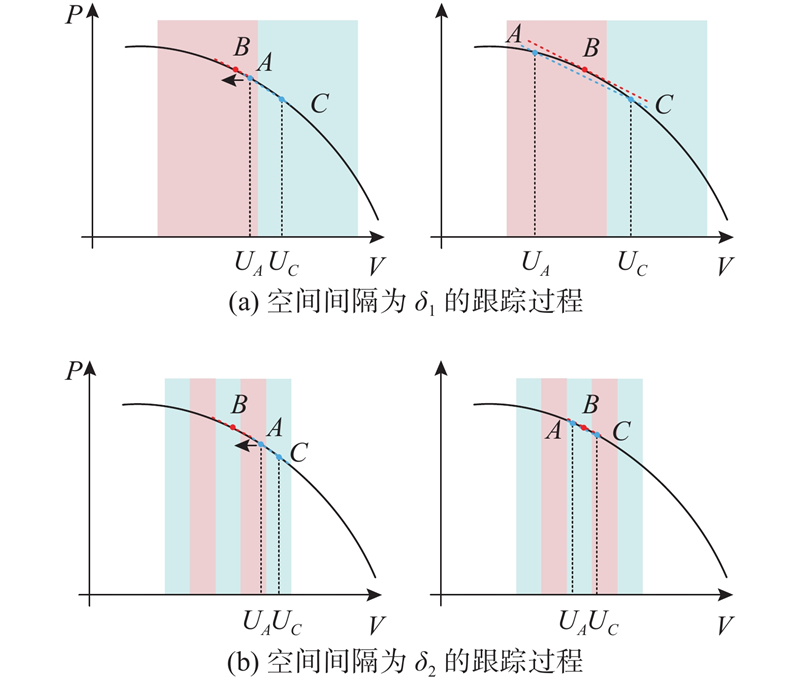
如图5所示,在稳态时AC直线的斜率等于B点的斜率,满足下式:
式中:
结合式(16)、(18),可得
即稳态点和理想点的电压偏差为
图 6
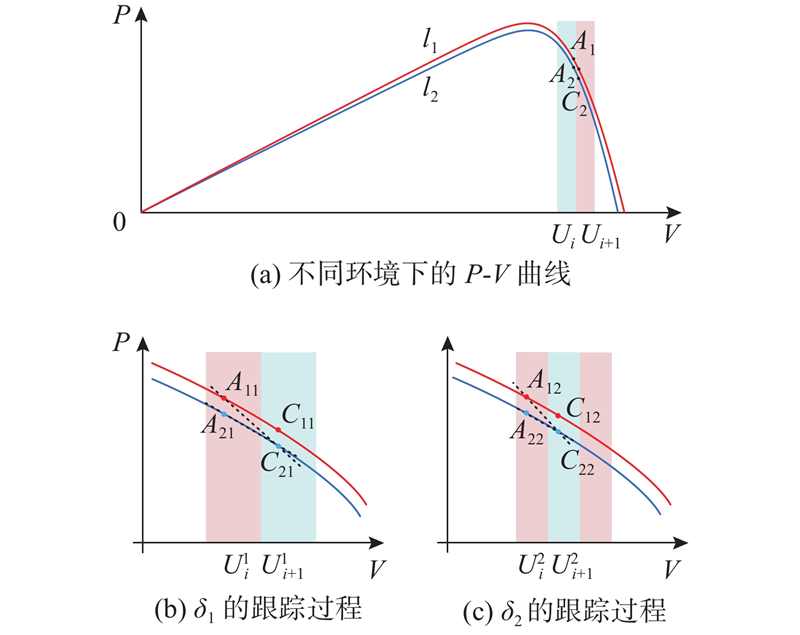
为了从数学角度阐明
由此,可以确定
则直线
环境变化导致空间域计算下dP/dV的改变量为
其中
空间间隔越小,则跟踪精度越高,且对环境变化的响应速度越快,所以理想情况下
式中:N为数字采样分辨率.
3. 仿真结果
表 1 光伏系统参数
Tab.1
| 参数 | 参数值 |
| 电容C/μF | 1 000 |
| 电感L/mH | 3 |
| 开关频率 fs/kHz | 20 |
| 电池电压 Vb/V | 110 |
| MPP处功率 Pmpp/W | 1 601 |
| MPP处电压 Vmpp/V | 52.6 |
| MPP 处电流 Impp/A | 30.44 |
| 开路电压 Uoc/V | 65.9 |
| 短路电流 Isc/A | 32.8 |
测试分为以下2个场景. 1)最大功率跟踪性能. 评估所提控制算法在辐照度恒定、斜坡变化和阶跃变化下的最大功率点跟踪性能,和其他2种算法进行对比. 2)功率热备性能. 在辐照度恒定的环境条件下,评估所提控制算法在不同dP/dV参考值下的输出性能,并和基于时域dP/dV计算的算法进行对比.
3.1. MPPT性能对比
所提算法中的dP/dV参考值设置为0,以实现MPPT功能. 在相同的环境条件下,对提出的方法、最流行的经典P&O-MPPT算法和最新的SOFT-MPPT算法[15]进行比较. 温度恒定为25 ℃,辐照度变化如下. 1) 辐照度的初始值为600
如图7 (a)所示为经典P&O MPPT算法的仿真结果. 图中,Ve为电压误差,Pe为功率误差. 经典P&O方法以固定步长搜寻MPP. 利用该算法,实现了3种不同太阳辐照度下的最大功率点跟踪. 固定步长扰动会在MPP附近带来稳态振荡. 可用功率越高,功率损耗越大. 减小稳态振荡的一种自然方法是减小步长. 较小的步长会导致较慢的动态响应,反之亦然.
图 7
SOFT-MPPT方法采用基于dP/dV的变步长扰动观测和稳态识别机制,以实现快速的动态响应和零稳态振荡. 如图7 (b)所示,当辐照度在4 s时以阶跃方式变化时,dP/dV的计算偏差导致电压发生较大偏移,这种偏移需要较多的扰动步骤才能达到稳态. 由于时域dP/dV计算的零分母问题,在稳态时存在振荡,SOFT-MPPT算法利用稳态检测模块来识别稳态振荡的电压模式. 一旦检测到电压模式,则算法会停止扰动观测模块,并工作在恒电压模式. 为了在环境变化后重启扰动观测模块以跟踪新的最大功率点,算法增加了动态检测模块. 为了防止误判,动态检测模块需要满足一定的裕量,这导致了动态响应的滞后. 如图7(b)所示,虽然辐照度从第7 s时开始变化,但是算法在0.5 s后才重启扰动观测模块. 因为稳态检测模块存在裕量以防止误判,当辐照度从斜坡变化变为恒定时,辐照度变化积累的误差仍在裕量内,导致过早的收敛而存在电压偏差,即11 s后,扰动观测模块没能重启以跟踪新的最大功率点.
如图7 (c)所示,利用本文方法实现了更快的动态跟踪和无稳态振荡. 虽然在第4 s辐照度发生突变时,光伏电压发生了较大的振荡,但是在极短的时间内达到了稳态. 这一快速动态响应得益于以dP/dV作为控制变量,跟踪误差可以通过反馈控制实时响应输出. 在所提的空间域dP/dV计算模块中,dP/dV的计算不会出现零分母问题. dP/dV可以稳定在参考值,利用光伏系统可以实现无误差跟踪并消除稳态振荡. 虽然在辐照度斜坡变化下,与SOFT-MPPT算法相比,所提算法表现不突出,但是所提算法对辐照度变化的响应更快,且在辐照度稳定后能够更精确地跟踪新的最大功率点. 在第7 s辐照度开始变化时,所提算法在极短时间内响应了该变化. 在第11 s辐照度停止变化后,快速跟踪到了最新的最大功率点.
3.2. 功率热备运行性能对比
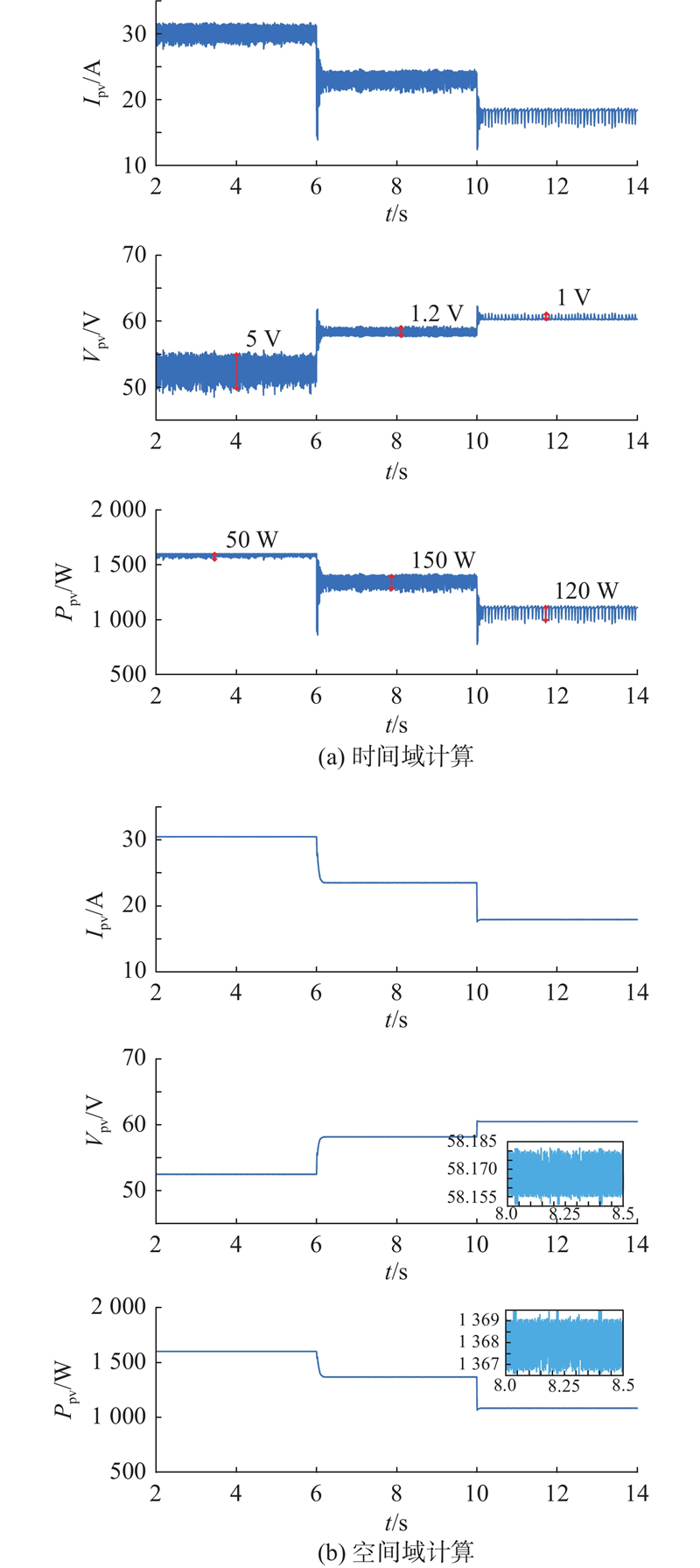
基于dP/dV调节光伏输出是便捷的方法. Cai等[16]用dP/dV控制作为内环来满足外环的控制需求,但是用到了时间域dP/dV的计算方法. 为了表明本文所提空间域dP/dV计算方法的优势,在相同的条件下进行对比. 环境参数保持在标准条件(1000
图 8
图 8 不同dP/dV计算方法下的功率热备输出
Fig.8 Power reserved mode with different dP/dV calculation methods
图 9
4. 实验分析
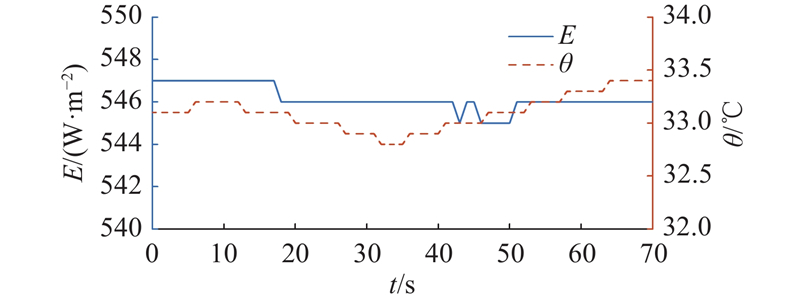
由于实际环境条件复杂且具有不确定性,为了获得相对公平的结果,在70 s内依次对比了各算法的表现,各算法的环境条件视为一致. 温度θ和辐照度E的变化曲线如图10所示,温度最高为33.4 ℃,最低为32.9 ℃,辐照度最高为547
图 10
图 11
图 11 基于所提空间域dP/dv计算方法的光伏输出
Fig.11 PV behaviors with proposed spatial-domain dP/dv calculation method
图 12
图 12 传统P&O MPPT算法下的光伏输出
Fig.12 PV behaviors with conventional P&O MPPT algorithm
图 13
图 14
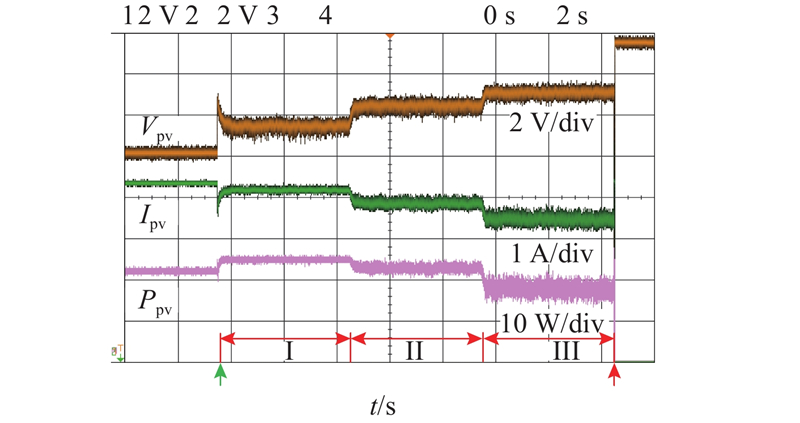
图 14 基于时域dP/dV计算的方法在不同dP/dV参考值下的光伏输出
Fig.14 PV output of time-domain dP/dV calculation based control method under different dP/dV references
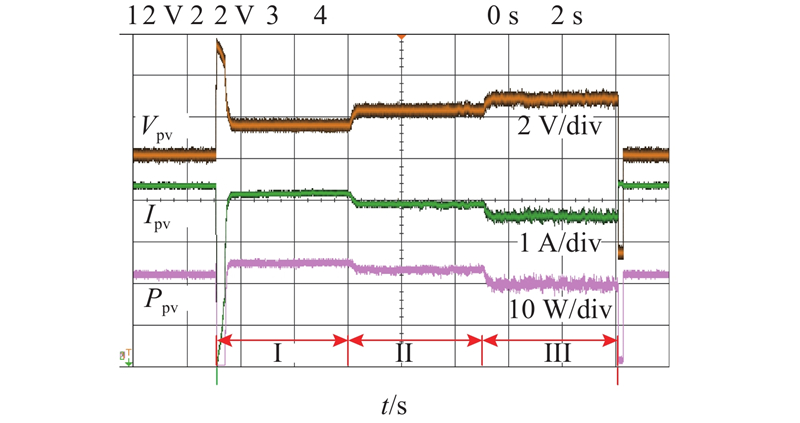
图 15
图 15 基于空间域dP/dV计算的方法在不同的dP/dV参考值下的光伏输出
Fig.15 PV output of spatial-domain dP/dV calculation based control method under different dP/dV references
4.1. MPPT性能对比
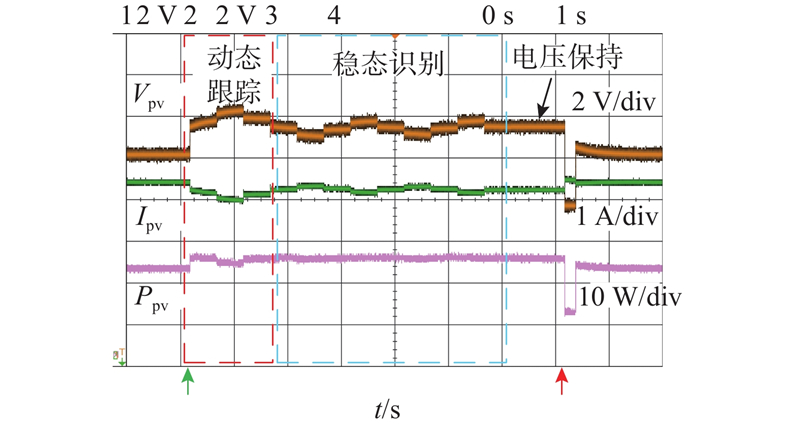
这3种方法的稳态性能与仿真结果一致. 采用所提算法实现了无稳态振荡,传统的扰动观测方法围绕MPP振荡,SOFT-MPPT方法在检测到振荡的电压模式时暂停扰动观测模块,以消除振荡. 与仿真结果不同,SOFT-MPPT方法会花费更多的步骤来识别稳态,因为稳态识别的判断受到噪声和测量误差的影响.
4.2. 功率热备运行对比
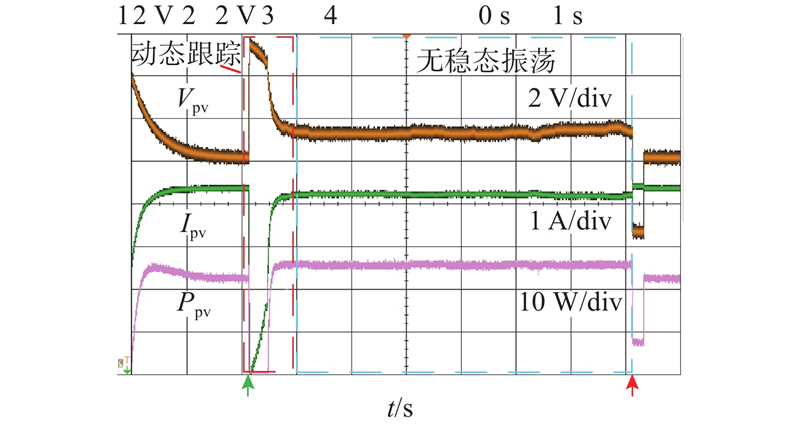
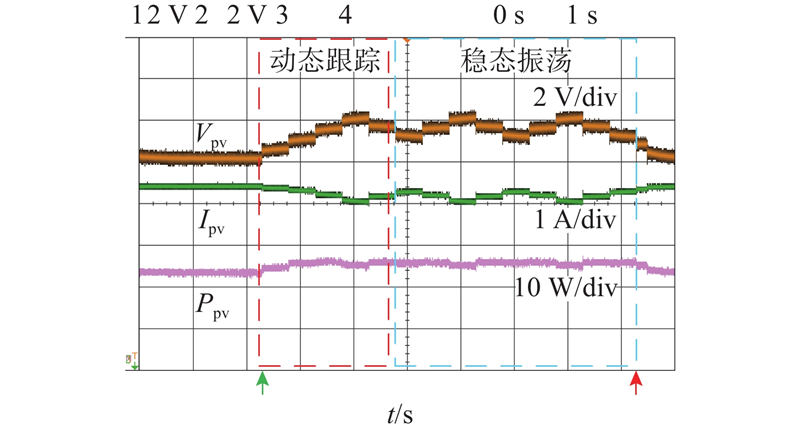
如图14、15所示为基于时间域dP/dV计算的算法[16]和基于所提空间域dP/dV计算的算法的实验结果. 2种算法采用相同的控制参数,以对比2种dP/dV计算模块的性能. 各算法的测试都持续15 s,可以分为3个阶段,每个阶段的dP/dV参考值不同. 阶段I的dP/dV参考值为0,阶段II的dP/dV参考值变为−5,阶段III的dP/dV参考值为−10. 2种算法都在阶段I实现了最大功率跟踪,并在阶段II、III实现了功率热备运行,且dP/dV参考值越小,预留的热备功率越多,与1节分析的P-dP/dV特性相符. 受开关器件和噪声的影响,实际输出波形不如仿真结果理想,但控制效果可以在波动幅度上进行比较. 结果表明,由于时域dP/dV计算的零分母问题增加了稳态振荡,时域方法的电压波动几乎是空间域方法的2倍.
5. 结 论
(1)本文阐述了所提控制方法的运行机制和空间域dP/dV计算的工作原理,说明了该控制方法相对于时间域dP/dV计算的优越性.
(2)提供了空间域dP/dV计算的实施流程图和参数设置方法.
(3)通过仿真和实验测试,验证了基于空间域dP/dV计算的控制方法的有效性. 与传统的P&O方法和最新的SOFT-MPPT方法进行比较,证明了所提方法在最大功率跟踪方面的优越性;与基于时间域dP/dV计算的控制方法进行比较,证明了在功率热备运行控制上的优势.
参考文献
碳中和目标下的光伏发电技术
[J].DOI:10.16085/j.issn.1000-6613.2021-2500 [本文引用: 1]
Photovoltaic technology under carbon neutrality
[J].DOI:10.16085/j.issn.1000-6613.2021-2500 [本文引用: 1]
Extended functionalities of photovoltaic systems with flexible power point tracking: recent advances
[J].DOI:10.1109/TPEL.2020.2970447 [本文引用: 1]
Critical review on PV MPPT techniques: classical, intelligent and optimisation
[J].
高比例新能源电力系统的惯量控制技术与惯量需求评估综述
[J].DOI:10.16081/j.epae.202107030 [本文引用: 1]
Review of inertia control technology and requirement evaluation in renewable-dominant power system
[J].DOI:10.16081/j.epae.202107030 [本文引用: 1]
风光混合发电系统的功率协调控制
[J].DOI:10.3969/j.issn.1007-449X.2013.06.013 [本文引用: 1]
Coordinated control of power for hybrid wind-PV generation system
[J].DOI:10.3969/j.issn.1007-449X.2013.06.013 [本文引用: 1]
基于扰动式MPPT控制的光伏并网系统间谐波分析模型
[J].DOI:10.13334/j.0258-8013.pcsee.180020
Interharmonic analysis model of photovoltaic grid-connected system based on perturbed MPPT control
[J].DOI:10.13334/j.0258-8013.pcsee.180020
Generation-storage coordination for islanded DC microgrids dominated by PV generators
[J].DOI:10.1109/TEC.2018.2860247 [本文引用: 1]
Small-signal modelling and design validation of PV-controllers with INC-MPPT using CHIL
[J].DOI:10.1109/TEC.2018.2874563 [本文引用: 1]
一种基于增量电导法的变步长MPPT算法
[J].
A variable step-size MPPT algorithm based on incremental conductance method
[J].
A variable step size INC MPPT method for PV systems
[J].DOI:10.1109/TIE.2008.920550 [本文引用: 1]
Novel fast dynamic MPPT (maximum power point tracking) technique with the capability of very high accurate power tracking
[J].DOI:10.1016/j.energy.2015.10.133 [本文引用: 1]
Maximum power point tracking strategy based on modified variable step-size incremental conductance algorithm
[J].
An adaptive control scheme for flexible power point tracking in photovoltaic systems
[J].DOI:10.1109/TPEL.2018.2869172 [本文引用: 1]
光伏系统稳态无振荡扰动观察MPPT研究
[J].
Research of steady state without oscillation in perturband observe maximum power point tracking of PV system
[J].
Steady output and fast tracking MPPT (SOFT-MPPT) for P&O and INC algorithms
[J].DOI:10.1109/TSTE.2020.2991768 [本文引用: 2]
V-dP/dv droop control for PV sources in DC microgrids
[J].DOI:10.1109/TPEL.2017.2771803 [本文引用: 5]
Comprehensive approach to modeling and simulation of photovoltaic arrays
[J].DOI:10.1109/TPEL.2009.2013862 [本文引用: 1]
Accuracy improvement of the ideal PV model
[J].DOI:10.1109/TSTE.2015.2412694 [本文引用: 1]
A MATLAB-simulink-based PV module model and its application under conditions of nonuniform irradiance
[J].DOI:10.1109/TEC.2012.2216529 [本文引用: 1]
A new frequency regulation strategy for photovoltaic systems without energy storage
[J].DOI:10.1109/TSTE.2013.2261567 [本文引用: 1]