乘波体构型钝化方法的研究起步较早,相关理论较为丰富. 该方法以移除材料法和增加材料法为主[8-11],其中增加材料法对升力特性和流场结构影响更小;该方法的钝化尺度分为一致边缘钝化和非一致边缘钝化. 钝化曲线类型以圆弧和Bézier曲线为主[8]. 刘济民等[12-13]利用改进的移除材料法、改进的增加材料法研究了飞行器气动力热特性变化规律. 陈小庆等[14-15]通过一致边缘钝化研究钝化对气动性能的影响,认为钝化能有效降低最大热流密度,在进行升力体外形设计时应综合考虑气动力热的设计指标再选择钝化半径. 刘建霞等[16-17]提出非一致边缘钝化方法,根据飞行器表面受热非均匀的特征对边缘不同位置采用不同尺度钝化,降低钝化后的气动力损失. 相比一致边缘钝化方法,非一致边缘钝化方法的优越性显著[18],得到广泛应用[11,19]. Rodi等[20-21]先后提出基于Bézier曲线和有理Bézier曲线构造前缘钝化曲线. 陈雪冬等[22]添加圆弧过渡钝化边缘,使飞行器下表面不变,平移上表面,保证原有前缘位置不变,降低了钝化对升力的影响.
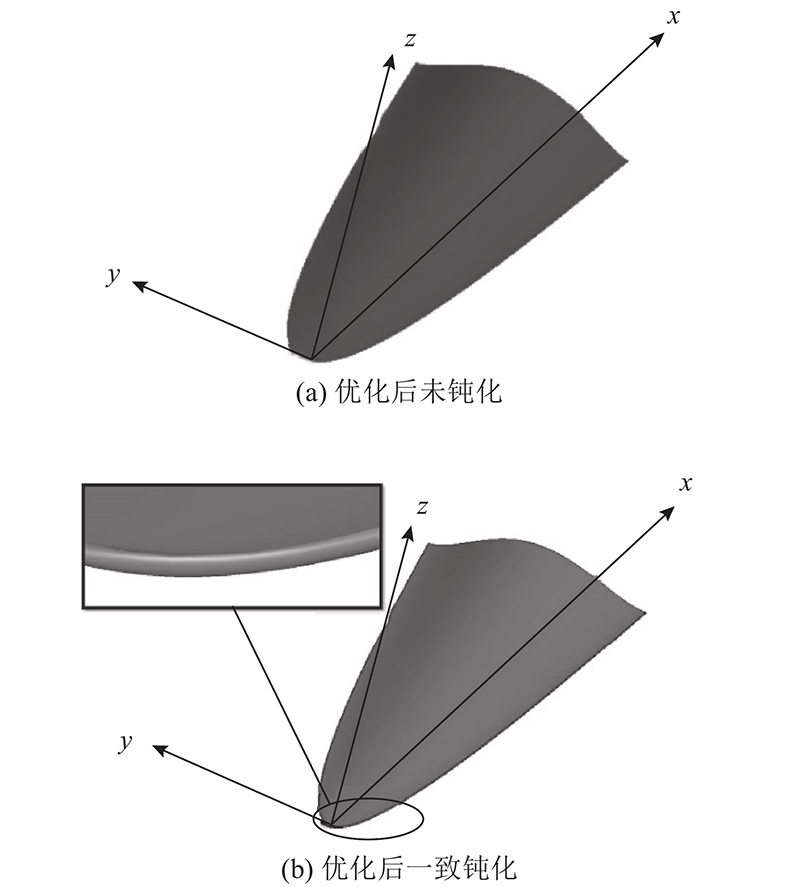
参考乘波体钝化方法,本研究提出外切圆延伸法. 该方法通过平移升力体下表面添加圆弧钝化,基于CST函数实现升力体和钝化边缘的参数化. 对钝化前后外形开展灵敏度分析,研究各设计参数对气动性能的影响规律,进行未钝化外形的多目标优化. 对优化后外形分别采用一致钝化法、非一致钝化法钝化尖锐边缘,分析钝化对气动力热特性产生的影响,并对比2种钝化方法生成外形的气动性能差异.
1. 升力体生成和钝化方法
1.1. 基础外形
CST函数生成的升力体构型表达式为
式中:x为型线所在位置处的轴向坐标,y为上、下表面型线上点的周向坐标,
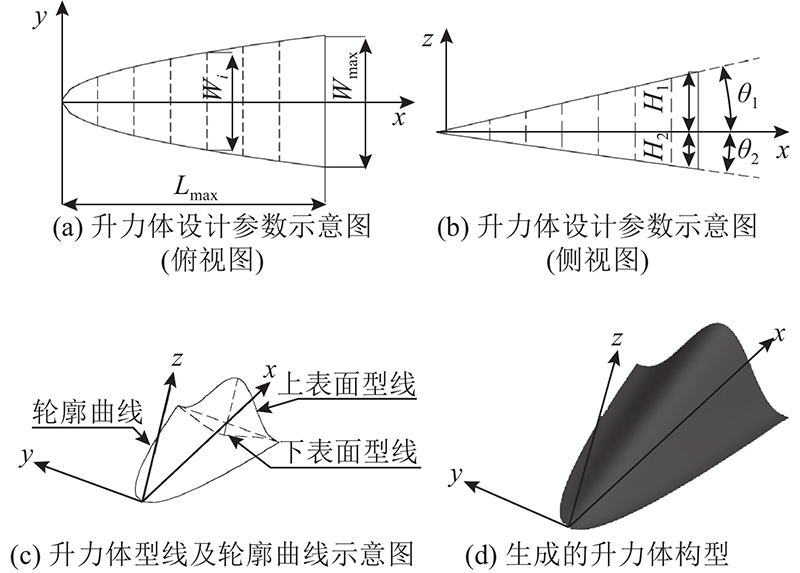
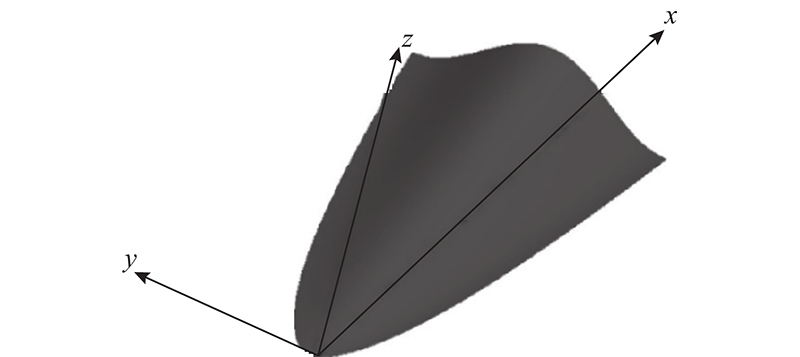
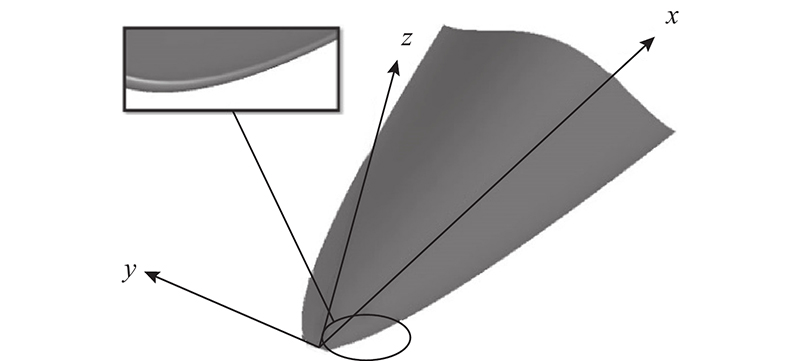
图 1
图 1 基于CST函数生成的升力体构型
Fig.1 Lifting body configuration generated based on CST function
1.2. 外切圆延伸钝化方法
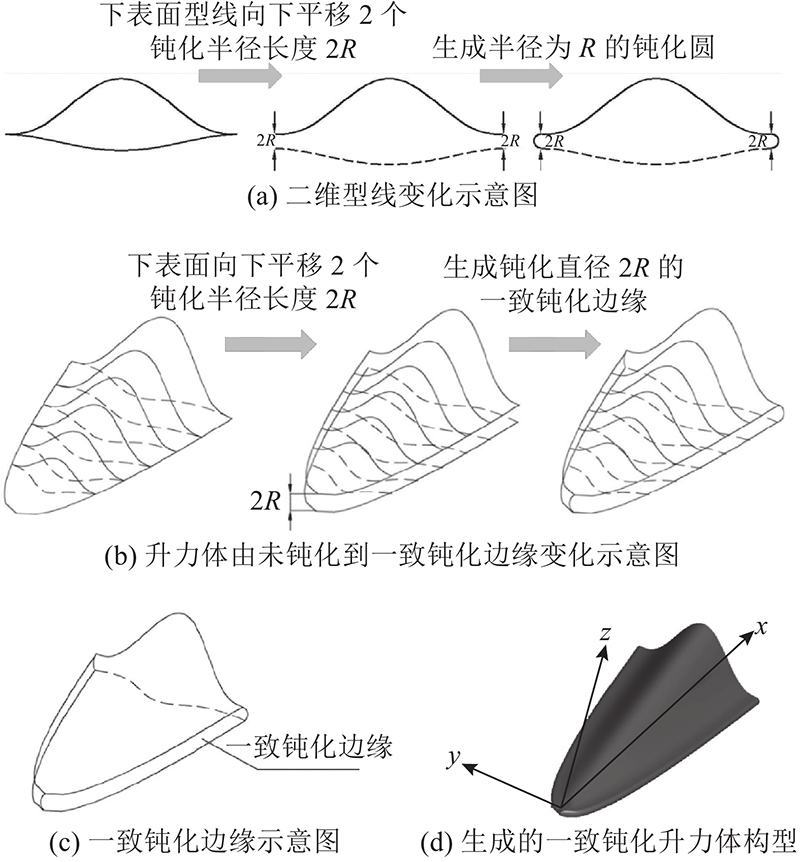
外切圆延伸方法实现一致边缘钝化的原理如图2所示. 保持升力体上、下表面形状及面积不变,将下表面所有坐标点沿z方向平移2个钝化半径长度2R,添加半圆弧过渡实现边缘一致钝化.
图 2
图 2 外切圆延伸方法实现一致边缘钝化的原理
Fig.2 Principle of uniform blunt by tangential extension method
式中:
根据边缘处y=±0.5W,得到上、下表面型线相接处斜率为0,即添加的半圆弧钝化曲线使上、下表面之间曲率连续,实现光滑过渡,保持了机身的连续性.
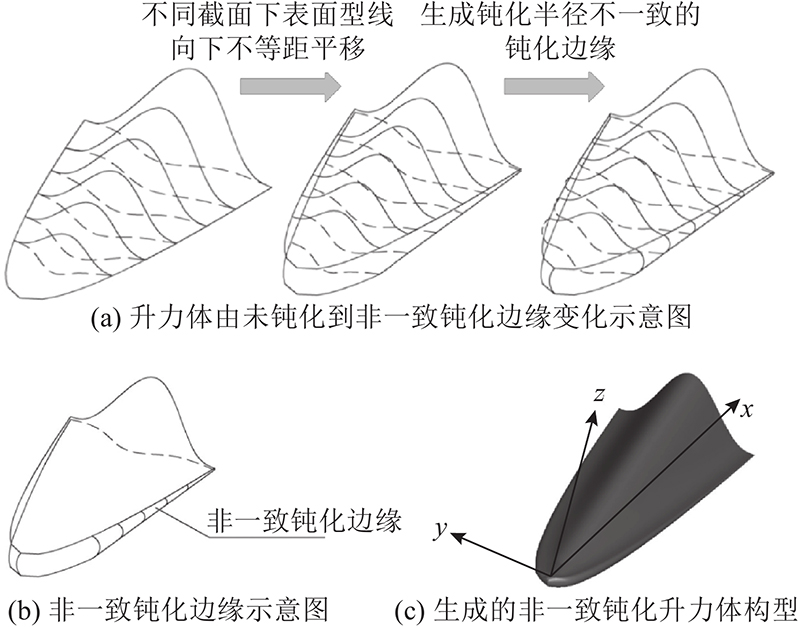
外切圆延伸方法实现非一致边缘钝化的原理如图3所示. 基于CST函数生成的升力体是由多条沿轴向的上、下表面型线组成的截面拉伸形成,通过使不同截面上、下表面型线间的钝化参数取值不同,可以实现非一致边缘钝化直径从驻点到飞行器底面的过渡. 因此,外切圆延伸钝化方法不仅可以实现升力体的一致边缘钝化,也可以实现升力体的非一致边缘钝化.
图 3
图 3 外切圆延伸方法实现非一致边缘钝化的原理
Fig.3 Principle of non-uniform blunt by tangential extension method
2. 数值模拟方法
2.1. 计算格式
采用CFD数值模拟方法进行钝化前后升力体的气动特性评估. 将三维可压缩的N-S方程作为控制方程,通过有限体积法离散控制方程. 在方程求解过程中,对流项通过AUSMPW+格式进行离散,黏性通量采用中心型差分格式离散,时间离散采用LU-SGS隐式格式. 入口边界条件采用来流条件,出口边界条件通过质心外推获得,飞行器表面采用无滑移的等温壁面条件,壁温设置为300 K.
由式(5)得到飞行条件的当地雷诺数小于转捩雷诺数,因此计算时选取层流模型. 因为升力体模型对称且本研究只针对气动力和气动热特性,所以仅进行半模外流场的数值模拟.
2.2. 计算格式验证
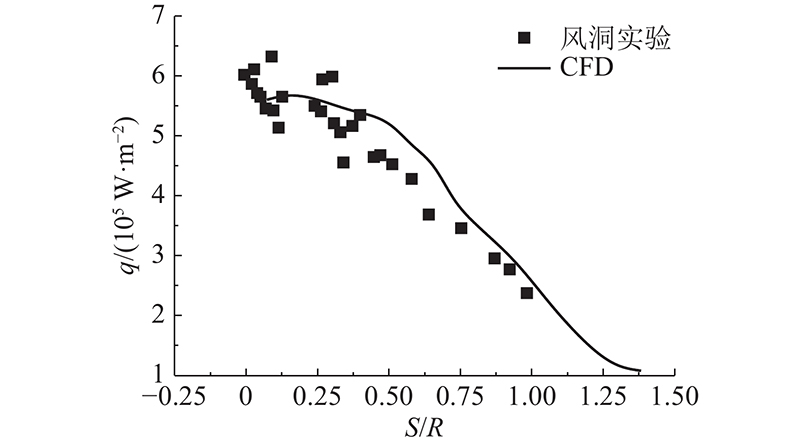
为了验证计算格式的可靠性,采用2.1小节所述的计算格式对高超声速圆柱绕流开展CFD计算,并与风洞实验数据[24]进行对比. 风洞实验来流马赫数
图 4
图 5
图 5 数值模拟与实验数据的壁面热流密度对比
Fig.5 Comparison of wall heat flux density between numerical simulation and experiment
2.3. 网格无关性分析
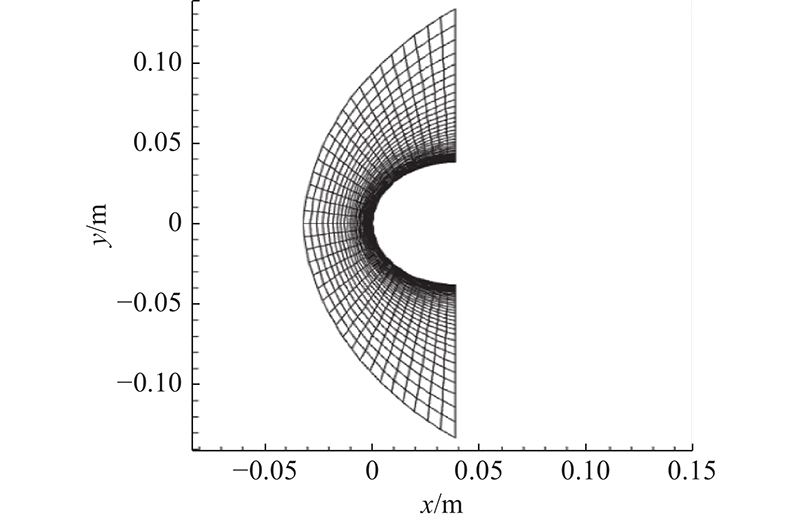
为了保证边界层的计算精度,在壁面附近进行加密处理,壁面法向第1层网格高度为1.0×10−5 m. 增加网格数量将使流场模拟更为细致,但会增加计算成本. 为此,在开展钝化研究前进行网格无关性分析,分析过程中的计算外形如图6所示. 生成数量Nm=0.98×106、1.87×106、4.68×106、9.89×106的4套网格. 在Ma=10、α=5°、H=50 km的条件下,分别计算气动力系数和壁面最大热流密度,结果如表1所示. 表中CL为升力系数,CD阻力系数,K为升阻比,qmax为壁面最大热流密度. 括号内为相应数量网格与9.89×106网格气动系数的相对偏差. 网格数量达到1.87×106后再继续加密网格相对偏差已经小于1%. 权衡计算精度与计算效率,本研究选取的网格数量为1.87×106.
图 6
图 6 网格无关性分析过程中选用的模型
Fig.6 Model selected in process of grid independence analysis
表 1 不同网格下的气动系数及壁面最大热流密度对比
Tab.1
| Nm/106 | CL | CD | K | qmax/(106 W·m−2) |
| 9.89 | 0.17198 | 0.04176 | 4.12 | 2.221 |
| 0.98 | 0.16964 | 0.04247 | 4.00 | 2.206 |
| 1.87 | 0.17109 | 0.04180 | 4.09 | 2.213 |
| 4.68 | 0.17119 | 0.04202 | 4.07 | 2.218 |
3. 计算结果分析
对升力体构型设计参数进行灵敏度分析,研究升阻比K、容积V、容积率η随设计参数的变化规律.
式中:A为飞行器的投影面积[18]. 基于灵敏度分析开展未钝化升力体构型优化设计,对优化后的升力体构型的尖锐边缘进行一致边缘钝化、非一致边缘钝化,分析钝化对升力体构型气动力和气动热性能的影响.
3.1. 采样设计与代理模型
表 2 升力体构型的设计参数及其取值范围
Tab.2
表 3 代理模型的精度
Tab.3
| 性能参数 | RM2 | |
| 未钝化 | 一致钝化 | |
| K | 0.99698 | 0.99426 |
| V | 0.99692 | 0.99626 |
| η | 0.99778 | 0.99822 |
3.2. 灵敏度分析与优化设计
图 7
图 7 升力体构型未钝化时设计参数对性能参数的贡献率
Fig.7 Contribution of design parameters to performance parameters in absence of lift body blunting
图 8
图 8 升力体构型一致钝化时设计参数对性能参数的贡献率
Fig.8 Contribution of design parameters to performance parameters in lift body uniform blunting
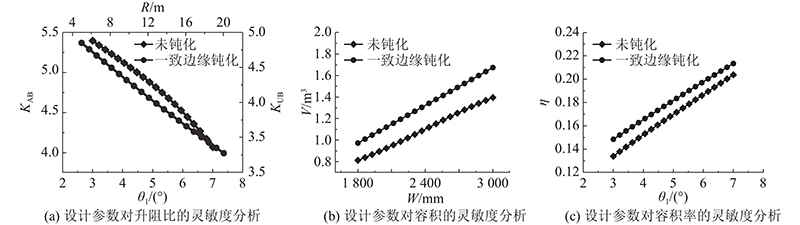
对钝化前后各性能参数贡献率最大的设计参数开展灵敏度分析,得到设计参数的敏感性规律,如图9所示. 图中,KAB、KUB分别为升力体构型未钝化、一致钝化的升阻比. 可以看出,钝化不会使参数对性能指标的作用规律发生改变,但同一参数会对升阻比和容积率产生相反的影响趋势. 因此须通过优化设计实现高升阻比和高容积率的目标.
图 9
图 9 钝化前后对各性能指标具有最大贡献程度参数的灵敏度分析
Fig.9 Sensitivity analysis of parameters that have greatest contribution to each performance index before and after blunt
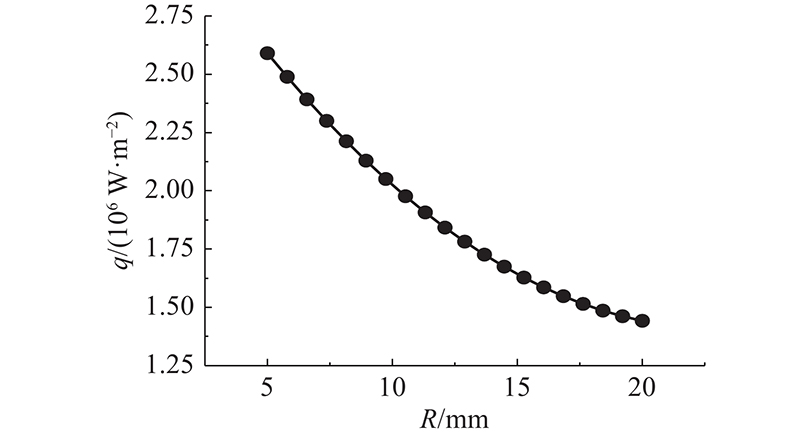
如图10所示为采用一致边缘钝化的升力体构型钝化半径对壁面热流密度的灵敏度分析. 钝化半径越大,壁面最大热流密度越低,但随着半径增大对热流的缓解能力逐渐减弱. 为此,折中选取R=10 mm作为一致边缘钝化的钝化半径. 基于代理模型对未钝化的升力体构型开展以升阻比、容积、容积率各自最大化为目标的优化设计,对多个子目标同时实施最优化. 优化的约束条件为飞行器机身长为5 m. 采用存档微遗传算法(archive-based micro genetic algorithm, AMGA)寻优.多目标优化函数表达式为
图 10
图 10 钝化半径对壁面最大热流密度的灵敏度分析
Fig.10 Sensitivity analysis of blunted radius to maximum wall heat flow
式中:
图 11
3.3. 钝化对气动性能的影响
对钝化前后外形开展数值模拟,结果对比如表4所示. 优化后的未钝化外形具有4.32的高升阻比和0.219的高容积率,但壁面最大热流密度较高,说明气动热环境较为恶劣. 一致边缘钝化后升阻比相比钝化前下降了9.49%, 容积相比钝化前增大了6.86%,容积率升高6.86%,壁面最大热流密度减小77%,热环境得到改善.
表 4 优化外形钝化前后性能参数对比
Tab.4
| 钝化类型 | K | V/m³ | η | qmax/(106 W·m−2) |
| 未钝化 | 4.32 | 2.77 | 0.219 | 8.418 |
| 一致边缘钝化 | 3.91 | 2.96 | 0.227 | 1.916 |
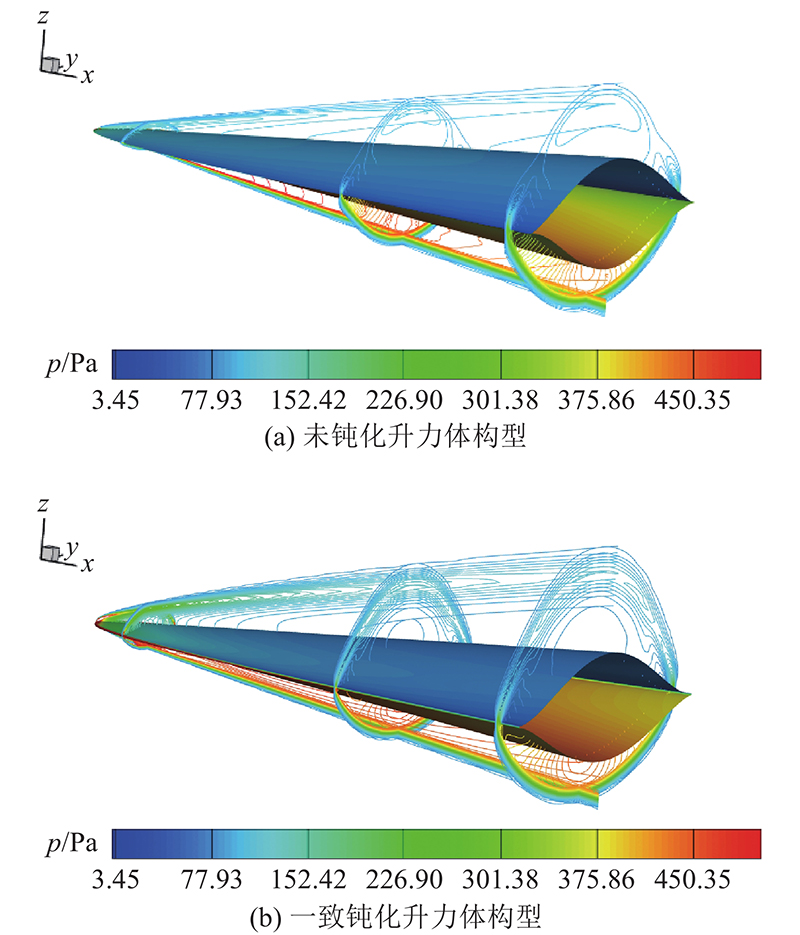
钝化前后升力体构型表面流场及压力p分布如图12所示. 升力体构型下表面为高压区,上表面为低压区,下表面激波后气流压缩,上表面激波后气流膨胀. 钝化后升力体构型上表面气流膨胀趋势更为显著,头部出现弓形激波区域,激波脱体距离由于钝化增大,上、下表面气流流通增强,导致下表面高压气体更多地泄漏至上表面. 因此,相比钝化前,钝化后的边缘流场压力增大、钝化后的升力下降.
图 12
图 12 升力体构型钝化前后的压力云图
Fig.12 Pressure distribution of lift body before and after blunt
钝化前后升力体构型的阻力系数如表5所示. 表中,CD,S为激波阻力系数,CD,F为摩擦阻力系数. 钝化后上表面的波阻、摩阻降低,下表面摩阻升高. 钝化边缘产生摩阻,脱体激波存在,因此钝化边缘还会产生波阻. 各部分阻力综合作用导致总阻力升高. 钝化导致流场结构发生变化,飞行器升力下降、总阻力升高,因而升阻比相比未钝化时减小.
表 5 钝化前后升力体构型的阻力系数
Tab.5
| 构型状态 | CD,S | CD,F | CD | |||||
| 上表面 | 下表面 | 钝化边缘 | 上表面 | 下表面 | 钝化边缘 | |||
| 未钝化 | 1.28×10−4 | 4.31×10−2 | — | 6.09×10−3 | 1.22×10−2 | — | 6.15×10−2 | |
| 一致钝化 | 1.46×10−5 | 4.78×10−2 | 6.85×10−3 | 4.74×10−3 | 4.78×10−2 | 2.89×10−3 | 7.24×10−2 | |
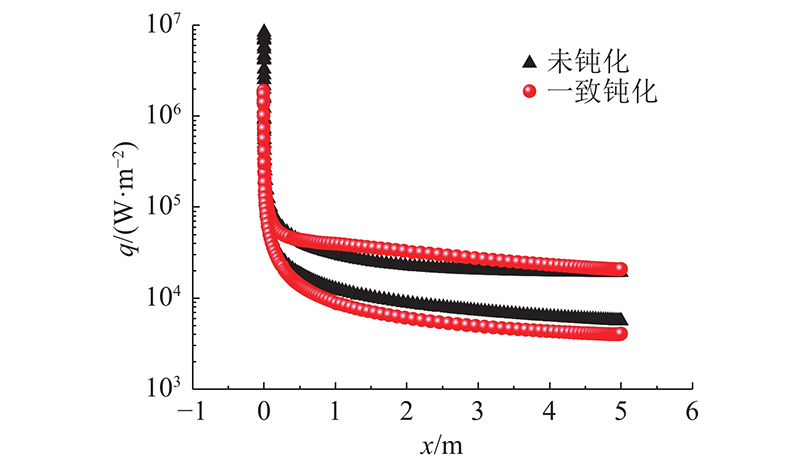
图 13
图 14
图 14 钝化前后热流密度云图沿子午线分布
Fig.14 Heat flow distribution along meridian before and after blunt
3.4. 一致钝化与非一致钝化的差异
图 15
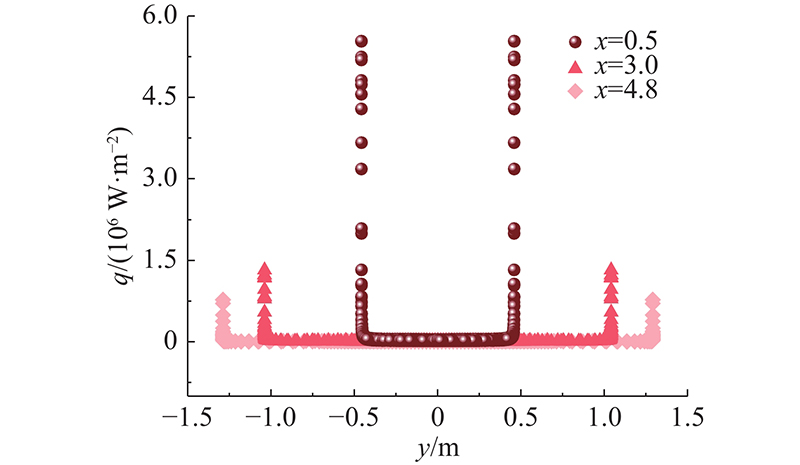
图 15 不同截面位置处沿展向分布的热流密度
Fig.15 Heat flow distribution along spanwise at different section positions
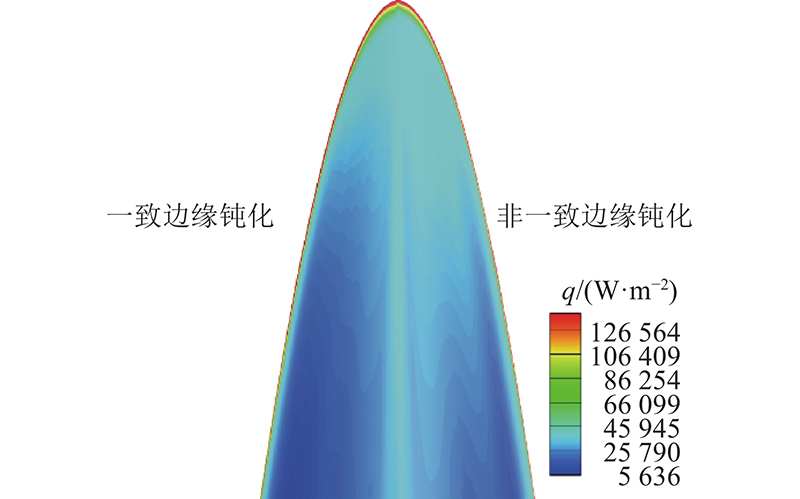
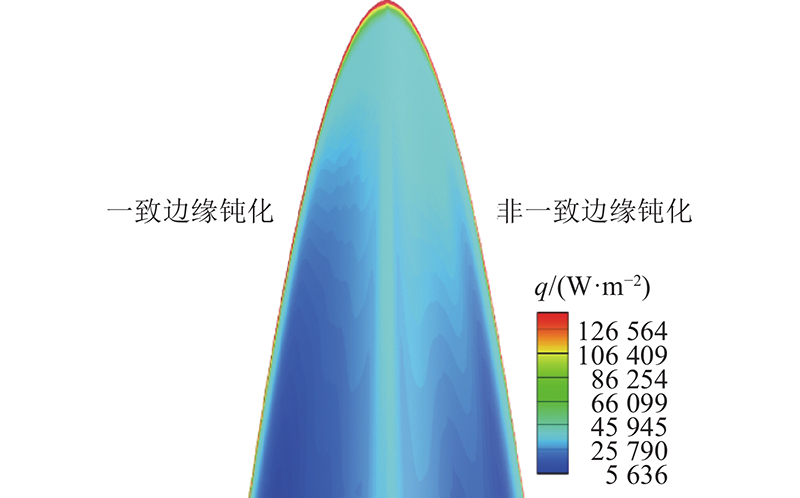
根据式(8)计算钝化半径得到非一致边缘钝化后的外形如图16所示,对该外形开展数值模拟. 2种钝化方法升力体构型性能参数对比如表6所示. 非一致钝化后升阻比相比一致钝化时升高了4.09%;容积减小了5.40%,容积率降低了2.64%,但仍大于未钝化时的容积和容积率;壁面最大热流密度升高了0.10%,仍远小于未钝化时的最大热流密度. 如图17所示为升力体构型2种方法钝化后的压力云图,如图18所示为x=0.5 m截面处的压力展向分布. 从云图中可以看出,升力体构型非一致钝化时上表面低压气体等压线相比一致钝化时的更密集,上表面气流压力更低. 从截面处压力的展向分布可以看出,升力体构型非一致钝化时边缘气流压力更高,相比一致钝化时上表面气流压力更低、下表面气流压力更高. 表明非一致钝化减小了升力体构型上、下表面间的气流流通,下表面高压气体泄漏减少,上、下表面压差相比一致钝化时的增大,升力因而升高. 如图19所示为升力体构型采用2种方法钝化后迎风面的热流密度分布. 可以看出,采用2种钝化方法对边缘处热流密度变化的影响不大,但在轴向相同位置,一致钝化后机身热流密度明显低于非一致钝化的,低热流区域出现在机身更靠前的位置,对热环境改善更大.
图 16
表 6 2种钝化方法的性能参数对比
Tab.6
| 钝化类型 | K | V/m³ | η | qmax/(106 W·m−2) |
| 一致边缘钝化 | 3.91 | 2.96 | 0.227 | 1.916 |
| 非一致边缘钝化 | 4.07 | 2.80 | 0.221 | 1.918 |
图 17
图 17 升力体采用2种方法钝化后的压力云图
Fig.17 Pressure distribution of lift body after blunt by two methods
图 18
图 18 2种方法钝化后外形截面的压力展向分布(x=0.5 m)
Fig.18 Pressure spanwise distribution of profile after blunt by two methods (x=0.5 m)
图 19
图 19 升力体采用2种方法钝化后的热流密度云图
Fig.19 Wall heat flow distribution of lift body after blunt by two methods
4. 结 论
(1)钝化不会改变升力体构型设计参数对气动性能的影响规律. 同一设计参数对升阻比和容积率的影响趋势相反. 钝化半径越大壁面最大热流密度越低,钝化半径越大对热流的缓解能力越弱.
(2)升力体构型钝化后相比未钝化时的容积增大,容积率升高;上、下表面气流流通增强,边缘流场压力增大;升阻比相比未钝化时的下降,壁面最大热流密度降低,边缘热环境得到改善.
(3)相比一致钝化,升力体非一致钝化后升阻比略有升高,下表面高压气体泄漏减少,壁面最大热流密度略有升高,但远小于未钝化时的最大热流密度,对热环境有明显的改善作用.
(4)在未来的研究中,计划对采用非一致钝化的升力体构型开展灵敏度分析,在优化过程中将非一致钝化半径、非一致分区位置作为优化变量考虑,优化得到更接近工程应用需求的升力体构型.
参考文献
高超声速滑翔式升力体外形设计与优化
[J].
Configuration optimization design of hypersonic gliding lifting body
[J].
基于遗传算法的升力体外形优化设计
[J].
Configuration design of lifting body based on genetic
[J].
升力体外形布局参数对横侧向耦合稳定性的影响分析
[J].
Lateral-direction stability analysis on aerodynamic shape parameters for a lifting-body configuration
[J].
基于数据挖掘的飞行器气动布局设计知识提取
[J].
Knowledge discovery for vehicle aerodynamic configuration design using data mining
[J].
一种半径可控的参数化三维前缘钝化设计方法研究
[J].
Study on a parametric design method for blunting 3D leading edge with specified radius
[J].
Navier-Stokes computation of a viscous optimized waverider
[J].DOI:10.2514/3.26450
乘波构型钝化方法分析及性能研究
[J].
Blunt methods for the leading edge of waverider
[J].
前缘钝化对乘波体非设计点性能影响分析
[J].
Performance analysis of waverider with blunt leading edge in off-design regimes
[J].
乘波构型的钝化方法及其对性能影响研究
[J].
Blunted method for waverider and its effect on performance
[J].
边缘钝化对乘波构型性能影响分析
[J].
The blunt leading edge’s influence to the performance of waverider
[J].
Bluntness impact on performance of waverider
[J].DOI:10.1016/j.compfluid.2011.03.011 [本文引用: 1]
一种乘波构型边缘钝化方法的仿真与试验研究
[J].
Numerical and experimental study of one blunt method for waverider configuration
[J].
类乘波构型机身的设计及钝化对其性能的影响
[J].
Design of quasi-waverider fuselage and the effect of bluntness on its performance
[J].
Aerodynamic performance investigation on waverider with variable blunt radius in hypersonic flows
[J].DOI:10.1016/j.actaastro.2017.05.001 [本文引用: 1]
钝化前缘乘波布局及其一体化构型气动特性
[J].
Aerodynamic characteristics of waverider and its integrated configuration with blunt leading edge
[J].
高超声速滑翔飞行器气动性能的数值模拟研究
[J].
Numerical simulation on the aerodynamic performance of hypersonic glide vehicle
[J].