土坝渗透稳定可靠性分析方法及应用
1
2008
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
土坝渗透稳定可靠性分析方法及应用
1
2008
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
Porous metals and metallic foams: current status and recent developments
1
2008
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
部分润湿多孔介质渗流规律实验研究
1
2021
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
部分润湿多孔介质渗流规律实验研究
1
2021
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
颗粒级配对管涌发展的影响试验研究
1
2016
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
颗粒级配对管涌发展的影响试验研究
1
2016
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
Wasserbewegung durch Boden
1
1901
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
Permeability of saturatedsands, soils and clays
2
1939
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
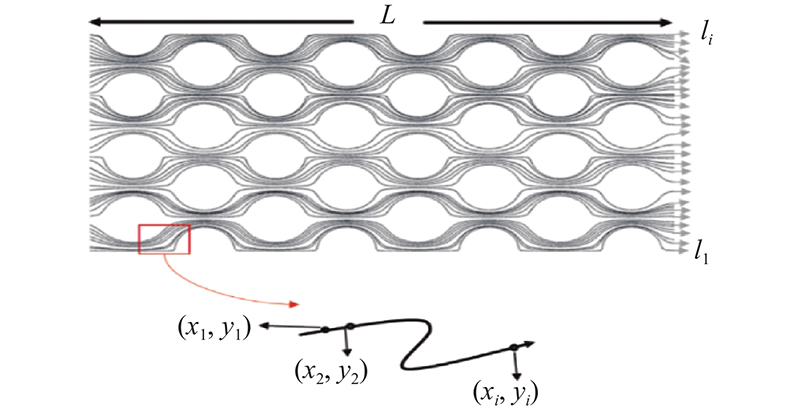
... 迂曲度是影响多孔介质渗透率的重要参数,也是定量描述颗粒排列方式对多孔介质渗透性影响的最重要指标. 迂曲度越大,表明流体在孔隙中的流动路径越曲折,进而造成更大的流阻. Carman[6]将迂曲度定义为有效流线长度与模型长度的比值. 基于上述理论,采取数值模拟方法求解流线长度,取 $ h=0.025\;{\rm{mm}} $处的剖面作为特征平面,得到每个芯片模型的平均迂曲度值,对多孔介质的渗透性影响进行量化: ...
Determination of the effective diffusion coefficient in porous media including Knudsen effects
1
2008
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
Instability in Poiseuille flow in a porous medium with slip boundary conditions
1
2013
... 多孔介质渗流现象广泛存在于自然界及工程应用中,如土壤中的地下水渗流、土石坝工程的稳定性、石油天然气的开采等[1-2]. 长期以来,许多学者对多孔介质的渗流特性开展大量的研究,传统的多孔介质渗流实验往往基于宏观尺度的土柱实验和箱型模型试验等[3-4]. 最早描述渗流规律的公式是由法国工程师Darcy于1856年通过实验总结得到的Darcy模型,后期不断有学者对Darcy模型进行修正,得到其他一些半经验模型,如Darcy-Forchheimer修正模型[5]等. 在理论方面,对于多孔介质渗流特性的研究将多孔介质的微细观结构参数与渗流行为关联起来,得到相应的解析解,目前在实际工程中应用较为广泛的是Kozeny-Carman方程[6]. 现有的研究表明,影响多孔介质渗流特性的主要因素有输送流体的物性、孔隙率、孔隙连通性、颗粒形状、比表面积等[7-8]. 由于多孔介质结构的复杂性及微米尺度孔隙间的动态渗流过程难以捕捉,精确描述多孔介质内部渗流机理仍是一个富有挑战的课题. ...
Influence of wetting conditions on drainage in porous media: a microfluidic study
1
2011
... 基于激光刻蚀技术制备而成的微观孔隙模型,可以在准二维尺度上复刻多孔介质的微细观孔隙结构,且采用显微镜和照相机直接观测微米尺度下的渗流状态,能够采集到比三维透明土土柱实验更高分辨率的流体运动图像[9]. 因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究热点,尤其是应用于地下油气驱替开采[10]、二氧化碳封存[11]等方向. Akarbi等[12]使用微模型研究了流体流进矩形通道后的压力变化,并与任意截面通道压降理论解相比较,发现两者能较好地符合. Joseph等[13]对原位的储层岩心进行取样扫描,提取岩心的孔隙结构构建二维裂隙通道模型,发现岩心的渗透率随多孔介质的孔隙和喉道数量增加而明显上升.Tamayol 等[14]构建1D、2D和3D特征单元的纤维多孔结构,并利用Navier-Stokes方程,求解较大雷诺数( $ 0.01 < {R}{e} < 200 $)下模型的渗透率,结果表明模型渗透率是孔隙率和纤维排列的函数关系. 现有的文献结果表明,微流控模型的实验压降数据与Darcy模型和Hagen-Poiseuille方程预测结果具有良好的一致性. ...
Characterization of nanometer-scale porosity in reservoir carbonate rock by focused ion beam-scanning electron microscopy
1
2012
... 基于激光刻蚀技术制备而成的微观孔隙模型,可以在准二维尺度上复刻多孔介质的微细观孔隙结构,且采用显微镜和照相机直接观测微米尺度下的渗流状态,能够采集到比三维透明土土柱实验更高分辨率的流体运动图像[9]. 因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究热点,尤其是应用于地下油气驱替开采[10]、二氧化碳封存[11]等方向. Akarbi等[12]使用微模型研究了流体流进矩形通道后的压力变化,并与任意截面通道压降理论解相比较,发现两者能较好地符合. Joseph等[13]对原位的储层岩心进行取样扫描,提取岩心的孔隙结构构建二维裂隙通道模型,发现岩心的渗透率随多孔介质的孔隙和喉道数量增加而明显上升.Tamayol 等[14]构建1D、2D和3D特征单元的纤维多孔结构,并利用Navier-Stokes方程,求解较大雷诺数( $ 0.01 < {R}{e} < 200 $)下模型的渗透率,结果表明模型渗透率是孔隙率和纤维排列的函数关系. 现有的文献结果表明,微流控模型的实验压降数据与Darcy模型和Hagen-Poiseuille方程预测结果具有良好的一致性. ...
超临界 $ {\mathrm{C}\mathrm{O}}_{2} $-水两相流与 $ {\mathrm{C}\mathrm{O}}_{2} $毛细捕捉: 微观孔隙模型实验与数值模拟研究
1
2017
... 基于激光刻蚀技术制备而成的微观孔隙模型,可以在准二维尺度上复刻多孔介质的微细观孔隙结构,且采用显微镜和照相机直接观测微米尺度下的渗流状态,能够采集到比三维透明土土柱实验更高分辨率的流体运动图像[9]. 因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究热点,尤其是应用于地下油气驱替开采[10]、二氧化碳封存[11]等方向. Akarbi等[12]使用微模型研究了流体流进矩形通道后的压力变化,并与任意截面通道压降理论解相比较,发现两者能较好地符合. Joseph等[13]对原位的储层岩心进行取样扫描,提取岩心的孔隙结构构建二维裂隙通道模型,发现岩心的渗透率随多孔介质的孔隙和喉道数量增加而明显上升.Tamayol 等[14]构建1D、2D和3D特征单元的纤维多孔结构,并利用Navier-Stokes方程,求解较大雷诺数( $ 0.01 < {R}{e} < 200 $)下模型的渗透率,结果表明模型渗透率是孔隙率和纤维排列的函数关系. 现有的文献结果表明,微流控模型的实验压降数据与Darcy模型和Hagen-Poiseuille方程预测结果具有良好的一致性. ...
超临界 $ {\mathrm{C}\mathrm{O}}_{2} $-水两相流与 $ {\mathrm{C}\mathrm{O}}_{2} $毛细捕捉: 微观孔隙模型实验与数值模拟研究
1
2017
... 基于激光刻蚀技术制备而成的微观孔隙模型,可以在准二维尺度上复刻多孔介质的微细观孔隙结构,且采用显微镜和照相机直接观测微米尺度下的渗流状态,能够采集到比三维透明土土柱实验更高分辨率的流体运动图像[9]. 因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究热点,尤其是应用于地下油气驱替开采[10]、二氧化碳封存[11]等方向. Akarbi等[12]使用微模型研究了流体流进矩形通道后的压力变化,并与任意截面通道压降理论解相比较,发现两者能较好地符合. Joseph等[13]对原位的储层岩心进行取样扫描,提取岩心的孔隙结构构建二维裂隙通道模型,发现岩心的渗透率随多孔介质的孔隙和喉道数量增加而明显上升.Tamayol 等[14]构建1D、2D和3D特征单元的纤维多孔结构,并利用Navier-Stokes方程,求解较大雷诺数( $ 0.01 < {R}{e} < 200 $)下模型的渗透率,结果表明模型渗透率是孔隙率和纤维排列的函数关系. 现有的文献结果表明,微流控模型的实验压降数据与Darcy模型和Hagen-Poiseuille方程预测结果具有良好的一致性. ...
Pressure drop in rectangular micro channels as compared with theory based on arbitrary cross section
5
2009
... 基于激光刻蚀技术制备而成的微观孔隙模型,可以在准二维尺度上复刻多孔介质的微细观孔隙结构,且采用显微镜和照相机直接观测微米尺度下的渗流状态,能够采集到比三维透明土土柱实验更高分辨率的流体运动图像[9]. 因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究热点,尤其是应用于地下油气驱替开采[10]、二氧化碳封存[11]等方向. Akarbi等[12]使用微模型研究了流体流进矩形通道后的压力变化,并与任意截面通道压降理论解相比较,发现两者能较好地符合. Joseph等[13]对原位的储层岩心进行取样扫描,提取岩心的孔隙结构构建二维裂隙通道模型,发现岩心的渗透率随多孔介质的孔隙和喉道数量增加而明显上升.Tamayol 等[14]构建1D、2D和3D特征单元的纤维多孔结构,并利用Navier-Stokes方程,求解较大雷诺数( $ 0.01 < {R}{e} < 200 $)下模型的渗透率,结果表明模型渗透率是孔隙率和纤维排列的函数关系. 现有的文献结果表明,微流控模型的实验压降数据与Darcy模型和Hagen-Poiseuille方程预测结果具有良好的一致性. ...
... 由于压力传感器测量的压力值为芯片模型入口和出口处的压力差值,并非芯片模型内部两端,需要对所测压力值进行修正[12]: ...
... 对于直角转弯处和管道中截面变化产生的压降 $ \Delta {P}_{\mathrm{b}} $、 $ \Delta {P}_{\mathrm{i}\mathrm{n}} $和 $ \Delta {P}_{\mathrm{e}\mathrm{x}} $,文献[12]中给相应的计算公式: ...
... 式中: $ \mathrm{Q} $为流量; $ {A}_{\mathrm{t}} $为圆形管道截面积; $ {K}_{c}\mathrm{、}{K}_{e} \mathrm{和}{K}_{b} $均为损失系数,均取1.2. Akbari 等[12]经过计算,发现在低雷诺数下,直角转弯处和管道中截面变化产生的压降之和占模型测量压降值的百分比小于1%;在较高雷诺数下( ${R}{e}\ge 100$),直角转弯处和管道中截面变化产生的压降之和占比小于5%. 实验的研究范围主要集中在低雷诺数流速区间,为了简化计算,忽略该值的影响. ...
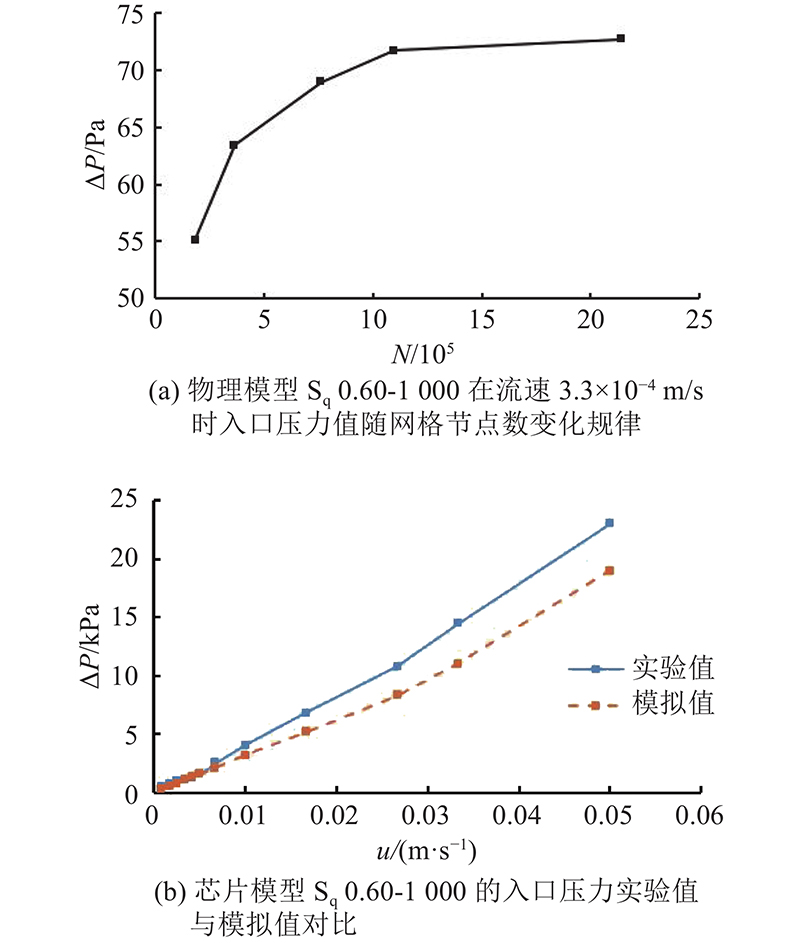
... 对于 $ \Delta {P}_{\mathrm{e}\mathrm{v}} $和 $\Delta {P}_{\mathrm{d}}$,由于芯片为玻璃制作,变更且内部流态为层流,在不同流速和不同孔隙率模型下,与测量压降值的占比小于0.3%[12],因此可以忽略不计. 结合芯片模型尺寸及式(9)~(13)求解式(8),得到芯片模型内部主体的压降修正值 $ \Delta P $. 图4给出在孔隙率均为0.60时,微柱直径分别为500 、1 000 和2 000 µm的3种芯片模型在微柱方形排列方式下的实验单位压降随流速的变化规律. 在整个实验流速阶段( $0.001 \; \mathrm{ }67\mathrm{ }\sim 0.067\;\mathrm{ }00\;\mathrm{ }\mathrm{m}/\mathrm{s}$), 3种芯片模型的单位压降与流速的线性拟合度分别为0.999 4、0.998 2和0.996 9,均具有良好的线性关系. 由Darcy渗透公式可知,在该流速范围内,芯片模型中的流态为层流. 在相同排列方式下,微柱直径小的芯片模型在相同流量下表现出更大的压降. ...
On-chip porous media: porosity and permeability measurements
1
2013
... 基于激光刻蚀技术制备而成的微观孔隙模型,可以在准二维尺度上复刻多孔介质的微细观孔隙结构,且采用显微镜和照相机直接观测微米尺度下的渗流状态,能够采集到比三维透明土土柱实验更高分辨率的流体运动图像[9]. 因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究热点,尤其是应用于地下油气驱替开采[10]、二氧化碳封存[11]等方向. Akarbi等[12]使用微模型研究了流体流进矩形通道后的压力变化,并与任意截面通道压降理论解相比较,发现两者能较好地符合. Joseph等[13]对原位的储层岩心进行取样扫描,提取岩心的孔隙结构构建二维裂隙通道模型,发现岩心的渗透率随多孔介质的孔隙和喉道数量增加而明显上升.Tamayol 等[14]构建1D、2D和3D特征单元的纤维多孔结构,并利用Navier-Stokes方程,求解较大雷诺数( $ 0.01 < {R}{e} < 200 $)下模型的渗透率,结果表明模型渗透率是孔隙率和纤维排列的函数关系. 现有的文献结果表明,微流控模型的实验压降数据与Darcy模型和Hagen-Poiseuille方程预测结果具有良好的一致性. ...
Effects of micro structure on flow properties of fibrous porous media at moderate Reynolds number
1
2012
... 基于激光刻蚀技术制备而成的微观孔隙模型,可以在准二维尺度上复刻多孔介质的微细观孔隙结构,且采用显微镜和照相机直接观测微米尺度下的渗流状态,能够采集到比三维透明土土柱实验更高分辨率的流体运动图像[9]. 因此,利用简化的二维模型研究多孔介质的渗透特性也是很多学者的研究热点,尤其是应用于地下油气驱替开采[10]、二氧化碳封存[11]等方向. Akarbi等[12]使用微模型研究了流体流进矩形通道后的压力变化,并与任意截面通道压降理论解相比较,发现两者能较好地符合. Joseph等[13]对原位的储层岩心进行取样扫描,提取岩心的孔隙结构构建二维裂隙通道模型,发现岩心的渗透率随多孔介质的孔隙和喉道数量增加而明显上升.Tamayol 等[14]构建1D、2D和3D特征单元的纤维多孔结构,并利用Navier-Stokes方程,求解较大雷诺数( $ 0.01 < {R}{e} < 200 $)下模型的渗透率,结果表明模型渗透率是孔隙率和纤维排列的函数关系. 现有的文献结果表明,微流控模型的实验压降数据与Darcy模型和Hagen-Poiseuille方程预测结果具有良好的一致性. ...
Creeping flow through ordered arrays of micro-cylinders embedded in a rectangular mini channel
2
2012
... 数值模拟在微米尺度下的多孔介质渗流机理研究方面发挥重要作用. 常用的数值模拟方法有计算流体力学方法(CFD)[15-16]、格子玻尔兹曼方法(lattice Boltzmann method, LBM)[17]、孔隙网络模型方法(pore network model, PNM)[18]等. Tamayol 等[15]利用计算流体方法对矩形微通道的渗流特性进行模拟,并将模拟结果与实验数据进行对比,结果吻合良好. Yazdchi等[19]通过联合数学解析和有限单元模拟,探究孔隙微结构对规则颗粒排列的微模型渗透性的影响. 黄永平等[16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
... [15]利用计算流体方法对矩形微通道的渗流特性进行模拟,并将模拟结果与实验数据进行对比,结果吻合良好. Yazdchi等[19]通过联合数学解析和有限单元模拟,探究孔隙微结构对规则颗粒排列的微模型渗透性的影响. 黄永平等[16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
2
... 数值模拟在微米尺度下的多孔介质渗流机理研究方面发挥重要作用. 常用的数值模拟方法有计算流体力学方法(CFD)[15-16]、格子玻尔兹曼方法(lattice Boltzmann method, LBM)[17]、孔隙网络模型方法(pore network model, PNM)[18]等. Tamayol 等[15]利用计算流体方法对矩形微通道的渗流特性进行模拟,并将模拟结果与实验数据进行对比,结果吻合良好. Yazdchi等[19]通过联合数学解析和有限单元模拟,探究孔隙微结构对规则颗粒排列的微模型渗透性的影响. 黄永平等[16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
... [16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
2
... 数值模拟在微米尺度下的多孔介质渗流机理研究方面发挥重要作用. 常用的数值模拟方法有计算流体力学方法(CFD)[15-16]、格子玻尔兹曼方法(lattice Boltzmann method, LBM)[17]、孔隙网络模型方法(pore network model, PNM)[18]等. Tamayol 等[15]利用计算流体方法对矩形微通道的渗流特性进行模拟,并将模拟结果与实验数据进行对比,结果吻合良好. Yazdchi等[19]通过联合数学解析和有限单元模拟,探究孔隙微结构对规则颗粒排列的微模型渗透性的影响. 黄永平等[16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
... [16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
A general model for the permeability of fibrous porous media based on fluid flow simulations using the lattice Boltzmann method
1
2009
... 数值模拟在微米尺度下的多孔介质渗流机理研究方面发挥重要作用. 常用的数值模拟方法有计算流体力学方法(CFD)[15-16]、格子玻尔兹曼方法(lattice Boltzmann method, LBM)[17]、孔隙网络模型方法(pore network model, PNM)[18]等. Tamayol 等[15]利用计算流体方法对矩形微通道的渗流特性进行模拟,并将模拟结果与实验数据进行对比,结果吻合良好. Yazdchi等[19]通过联合数学解析和有限单元模拟,探究孔隙微结构对规则颗粒排列的微模型渗透性的影响. 黄永平等[16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
The effects of wettability and trapping on relationships between interfacial area, capillary pressure and saturation in porous media: a pore-scale network modeling approach
1
2009
... 数值模拟在微米尺度下的多孔介质渗流机理研究方面发挥重要作用. 常用的数值模拟方法有计算流体力学方法(CFD)[15-16]、格子玻尔兹曼方法(lattice Boltzmann method, LBM)[17]、孔隙网络模型方法(pore network model, PNM)[18]等. Tamayol 等[15]利用计算流体方法对矩形微通道的渗流特性进行模拟,并将模拟结果与实验数据进行对比,结果吻合良好. Yazdchi等[19]通过联合数学解析和有限单元模拟,探究孔隙微结构对规则颗粒排列的微模型渗透性的影响. 黄永平等[16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
Micro structural effects on the permeability of periodic fibrous porous media
1
2011
... 数值模拟在微米尺度下的多孔介质渗流机理研究方面发挥重要作用. 常用的数值模拟方法有计算流体力学方法(CFD)[15-16]、格子玻尔兹曼方法(lattice Boltzmann method, LBM)[17]、孔隙网络模型方法(pore network model, PNM)[18]等. Tamayol 等[15]利用计算流体方法对矩形微通道的渗流特性进行模拟,并将模拟结果与实验数据进行对比,结果吻合良好. Yazdchi等[19]通过联合数学解析和有限单元模拟,探究孔隙微结构对规则颗粒排列的微模型渗透性的影响. 黄永平等[16]利用计算流体力学模型建立层流条件下多孔介质内部渗流的理论模型,并进行数值模拟,分析流体在多孔介质内部的流动特性. 研究结果表明,多孔介质内部的孔隙结构对渗流特性有着重要的影响. 相比于其他的数值模拟方法,计算流体力学方法的优点在于模型参数较少,无须标定,但是对计算资源的要求较高. ...
1
... 由于受到微流控模型尺寸、形状与边壁摩擦等因素影响,已有的研究表明传统的宏观渗流模型不能准确预测微流控模型的渗流特征. 比如,Kosar等[20]采用低长宽比的微模型探究层流条件下的压降和摩擦因数,发现宏观条件下试验模型不能预测微细观尺度下的试验结果. Yeom等[21]考虑多孔介质的内部结构对渗透率的影响,但是忽略了边界效应. Gunda等[22]测量低雷诺数下带有集成微柱的微通道两端的压降和流阻,通过Darcy方程计算出模型的渗透率,但是实验结果和理论值存在一定偏差. ...
Low Reynolds number flow across an array of cylindrical microposts in a micro channel and figure-of-merit analysis of micro post-filled micro reactors
1
2009
... 由于受到微流控模型尺寸、形状与边壁摩擦等因素影响,已有的研究表明传统的宏观渗流模型不能准确预测微流控模型的渗流特征. 比如,Kosar等[20]采用低长宽比的微模型探究层流条件下的压降和摩擦因数,发现宏观条件下试验模型不能预测微细观尺度下的试验结果. Yeom等[21]考虑多孔介质的内部结构对渗透率的影响,但是忽略了边界效应. Gunda等[22]测量低雷诺数下带有集成微柱的微通道两端的压降和流阻,通过Darcy方程计算出模型的渗透率,但是实验结果和理论值存在一定偏差. ...
Measurement of pressure drop and flow resistance in micro channels with integrated micro pillars
2
2013
... 由于受到微流控模型尺寸、形状与边壁摩擦等因素影响,已有的研究表明传统的宏观渗流模型不能准确预测微流控模型的渗流特征. 比如,Kosar等[20]采用低长宽比的微模型探究层流条件下的压降和摩擦因数,发现宏观条件下试验模型不能预测微细观尺度下的试验结果. Yeom等[21]考虑多孔介质的内部结构对渗透率的影响,但是忽略了边界效应. Gunda等[22]测量低雷诺数下带有集成微柱的微通道两端的压降和流阻,通过Darcy方程计算出模型的渗透率,但是实验结果和理论值存在一定偏差. ...
... 根据研究对象的不同,主要有基于孔隙尺寸、颗粒直径和渗透率的3种雷诺数表达式[24]. 在准二维微流控芯片模型中,参考文献[22], $ d $ 取微柱直径D. 本次实验条件下的雷诺数为0.1~210.0. ...
基于二维微流控模型的多孔介质渗透特性
1
2021
... 2) 微观模型观测子系统由微观模型安装平台、倒置的光学显微镜 (Ti2,Nikon Corp,Japan)和内置高速相机(Zyla 4.0,Andor Technology,Belfast,UK)组成. 微观模型长 $ L=20\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}\mathrm{m} $,宽 $ W=10\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}\mathrm{m} $,深度 $ h=50 $ µm,内部设计有不同直径D和排列方式的微柱. 本次实验所用芯片尺寸如表1所示. 芯片模型前后出口均为环形树枝分叉状,分叉通道的宽为800 μm,其余尺寸如图1(c)所示. 由于二维聚二甲基硅氧烷(PDMS)弹性模量较小,在孔隙压力较大时将发生较大弹性变形,对实验压力的测量分析带来较大干扰[23], 因此本实验采用玻璃制作微流控芯片模型. ...
基于二维微流控模型的多孔介质渗透特性
1
2021
... 2) 微观模型观测子系统由微观模型安装平台、倒置的光学显微镜 (Ti2,Nikon Corp,Japan)和内置高速相机(Zyla 4.0,Andor Technology,Belfast,UK)组成. 微观模型长 $ L=20\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}\mathrm{m} $,宽 $ W=10\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}\mathrm{m} $,深度 $ h=50 $ µm,内部设计有不同直径D和排列方式的微柱. 本次实验所用芯片尺寸如表1所示. 芯片模型前后出口均为环形树枝分叉状,分叉通道的宽为800 μm,其余尺寸如图1(c)所示. 由于二维聚二甲基硅氧烷(PDMS)弹性模量较小,在孔隙压力较大时将发生较大弹性变形,对实验压力的测量分析带来较大干扰[23], 因此本实验采用玻璃制作微流控芯片模型. ...
Experimental and numerical investigation of fluid flow hydrodynamics in porous media: characterization of pre-Darcy, Darcy and non-Darcy flow regimes
2
2016
... 根据研究对象的不同,主要有基于孔隙尺寸、颗粒直径和渗透率的3种雷诺数表达式[24]. 在准二维微流控芯片模型中,参考文献[22], $ d $ 取微柱直径D. 本次实验条件下的雷诺数为0.1~210.0. ...
... 图5所示在孔隙率 $ \varepsilon =0.60 $,不同微柱直径和排列方式下流阻随流速变化规律. 当流速大于 $ 0.005\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}/\mathrm{s} $时,流阻S随着流速u的增加基本保持不变;在相同流速和微柱排列方式条件下,微柱直径越小,芯片模型的流阻更大;在相同流量和微柱直径条件下,错开排列芯片模型比方形排列芯片模型具有更大的流阻. 然而在流速较小时( $ u < 0.005\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}/\mathrm{s} $),4种芯片模型的结果均表现为先减小后增大,并且初始最大值大于后期稳定值. Kundu等[24]对颗粒直径分别为 $2.5\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{}\mathrm{}\mathrm{、} 3.5\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{}\mathrm{}\mathrm{和} 5\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}\mathrm{m}$的土柱进行渗流实验,发现在流速处于 $2.88\times {10}^{-5} \sim 1.90\times {10}^{-4}\;\mathrm{m}/\mathrm{s}$时,流阻随着流速的增大而减小. 当流速持续增大时,流阻随着流速的增加保持不变,即由前达西流流态进入达西流流态. 在本实验中,当流速 $ u < 0.003\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }5\;\mathrm{ }\mathrm{m}/\mathrm{s} $时,前达西流流态比较明显. 在低流速时,孔隙通道中由电渗力和毛细力产生的流动势能在与流体方向相反的壁面上产生小的逆流[27]. 当流速处于 $ 0.003\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }5\sim 0.005\;\mathrm{ }0\mathrm{ }\mathrm{m}/\mathrm{s} $时,注射泵动力系统的脉冲效应比较明显,这对实验结果造成一定的影响. ...
1
... 对于 $ \Delta {P}_{\mathrm{c}} $,Bahrami等[25]基于矩形断面的Poiseuille流,结合达西公式提出相应的解析解: ...
1
... 式中: $ {f}_{f} $为扩散摩擦因子;L为通道长度; $ {D}_{\mathrm{h}} $为矩形截面的特征长度; $ \xi $为通道矩形截面的纵横比,并且 $\xi < 1.0$; ${{{Re}}}A^ {{1/2}}$为雷诺数. Yovanovich[26]通过研究发现,对于非圆形截面通道, $ {A^{1/2}} $作为特征长度用于计算雷诺数更为合适,A为矩形通道截面面积,在本实验中, $D_{\rm{h}}= {A^{1/2}} $. ...
Flow regimes in packed beds of spheres from predarcy to turbulent
1
2014
... 图5所示在孔隙率 $ \varepsilon =0.60 $,不同微柱直径和排列方式下流阻随流速变化规律. 当流速大于 $ 0.005\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}/\mathrm{s} $时,流阻S随着流速u的增加基本保持不变;在相同流速和微柱排列方式条件下,微柱直径越小,芯片模型的流阻更大;在相同流量和微柱直径条件下,错开排列芯片模型比方形排列芯片模型具有更大的流阻. 然而在流速较小时( $ u < 0.005\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}/\mathrm{s} $),4种芯片模型的结果均表现为先减小后增大,并且初始最大值大于后期稳定值. Kundu等[24]对颗粒直径分别为 $2.5\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{}\mathrm{}\mathrm{、} 3.5\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{}\mathrm{}\mathrm{和} 5\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{m}\mathrm{m}$的土柱进行渗流实验,发现在流速处于 $2.88\times {10}^{-5} \sim 1.90\times {10}^{-4}\;\mathrm{m}/\mathrm{s}$时,流阻随着流速的增大而减小. 当流速持续增大时,流阻随着流速的增加保持不变,即由前达西流流态进入达西流流态. 在本实验中,当流速 $ u < 0.003\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }5\;\mathrm{ }\mathrm{m}/\mathrm{s} $时,前达西流流态比较明显. 在低流速时,孔隙通道中由电渗力和毛细力产生的流动势能在与流体方向相反的壁面上产生小的逆流[27]. 当流速处于 $ 0.003\;\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }5\sim 0.005\;\mathrm{ }0\mathrm{ }\mathrm{m}/\mathrm{s} $时,注射泵动力系统的脉冲效应比较明显,这对实验结果造成一定的影响. ...
About a correlating equation for predicting pressure drops through packed beds of spheres in a large range of Reynolds numbers
1
2007
... 式中: $ k=c{\tau }^{2} $为KC常数,影响大小的因素主要有孔隙率、孔隙形状和大小、迂曲度等[28-29]. ...
Pore-scale derivation of the Ergun equation to enhance its adaptability and generalization
1
2008
... 式中: $ k=c{\tau }^{2} $为KC常数,影响大小的因素主要有孔隙率、孔隙形状和大小、迂曲度等[28-29]. ...
Principles of heat transfer in porous media
1
1996
... 在大量实验基础上,Kaviany[30]提出当迂曲度 $ \tau $为 $\sqrt 2$时,球形颗粒组成的多孔介质中的Kozeny常数 $ c $值大致为2.5,因此KC常数为5.0. 对于泥炭层介质,Mathava等[31]发现KC常数为3.4. ...
Coalescence filtration of an oil-in-water emulsion in a peat bed
1
1992
... 在大量实验基础上,Kaviany[30]提出当迂曲度 $ \tau $为 $\sqrt 2$时,球形颗粒组成的多孔介质中的Kozeny常数 $ c $值大致为2.5,因此KC常数为5.0. 对于泥炭层介质,Mathava等[31]发现KC常数为3.4. ...
Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry
1
2008
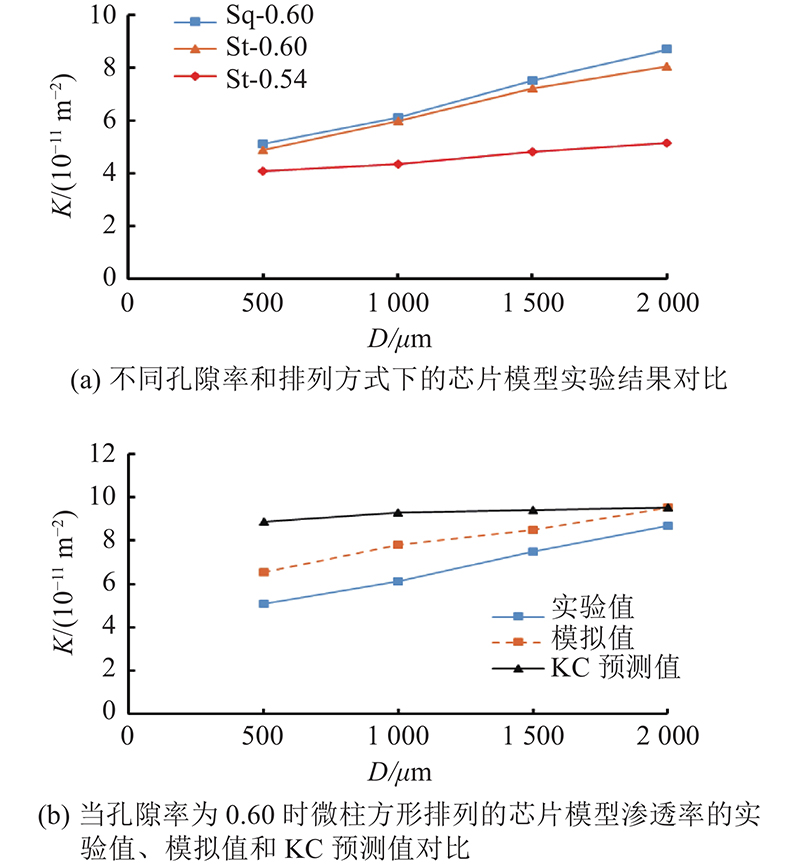
... 为了探究KC公式对微流控芯片模型渗透率预测的适用性,图6(b)给出在孔隙率为0.60时,不同芯片模型渗透率的实验值、模拟值和KC预测值的对比. 对于KC预测值,由于微流控芯片模型在尺寸比例上更接近煤炭层介质结构,故取KC常数为3.4. 图中数据表明,模拟值和KC预测值均大于实验值. 模拟值比实验值的误差范围为9.78%~28.43%,KC预测值比实验值的误差范围为9.67%~73.97%,并且误差随着微柱直径的增大而减小. 造成模拟值与实验值误差的原因主要有:1)在芯片模型主体压降值的计算过程中,采取部分简化处理;2)在数值模拟运算过程中,做部分假设;3)加工工艺无法保证芯片模型内壁面完全光滑;4)流量泵的脉冲影响. KC公式是在三维实验的基础上提出的半经验公式,KC常数也是一个受孔隙率和孔隙结构影响的系数,并且随孔隙率的增大而增大[32],并非固定不变,因此对于准二维微流控芯片模型的渗透率预测,KC公式存在较大误差. ...
1
... 芯片模型孔隙率越大,内部流体流态越接近平板流. 平板流的渗透率表达式为[33] ...
A fractal scaling law between tortuosity and porosity in porous media
1
2020
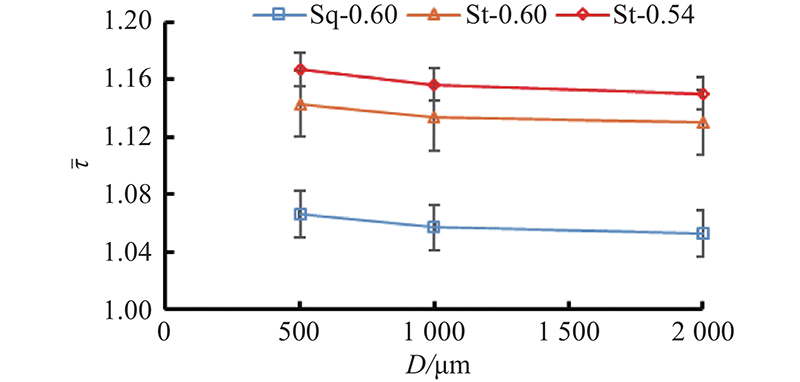
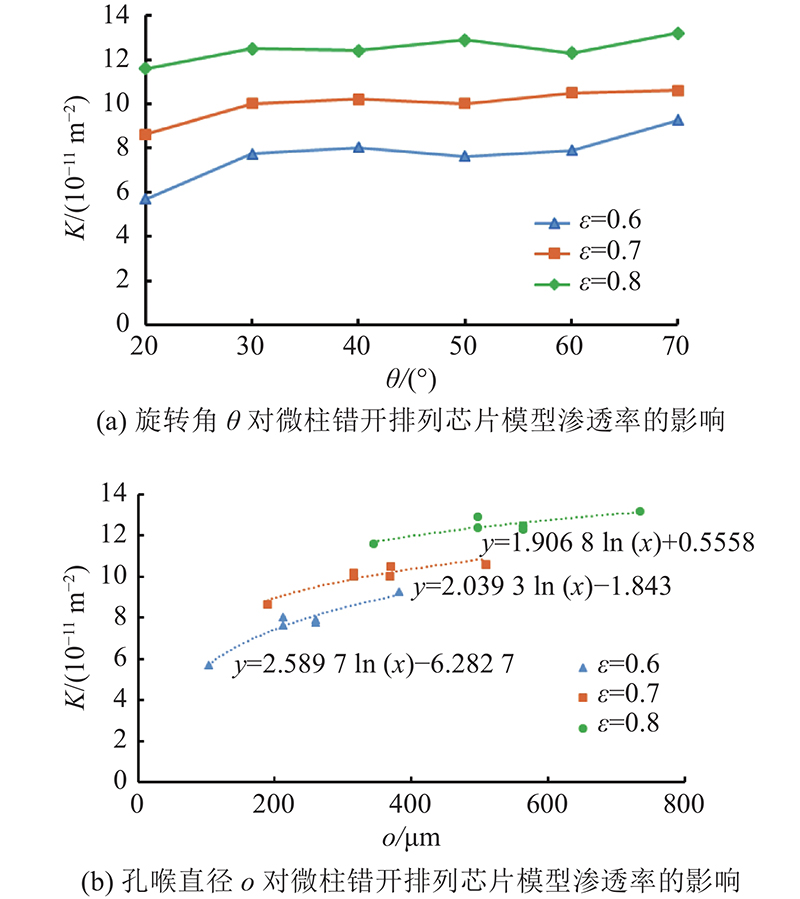
... 根据上述迂曲度的定义,在流速为0.016 7 m/s时,利用数值模拟方法求得的芯片模型平均迂曲度值如图9所示. 不同流速下流线形态发生变化,平均迂曲度值将发生细微变化,但波动幅值在5%以内. 由图中曲线可知,当孔隙率固定时,平均迂曲度的值随微柱直径增大而减小,且下降趋势减弱. 例如,当孔隙率为0.60时,方形排列的芯片模型在微柱直径分别是 $ 500$、 $ 1\;000 $和 $ 2\;000$ µm时,平均迂曲度值分别为1.1670、1.156 5和1.150 1. 在微柱排列方式相同下,方形排列的芯片模型的平均迂曲度值为1.05左右,明显小于错开排列的芯片模型平均迂曲度值1.13. 在相同排列方式下,孔隙率越小,平均迂曲度越大. 相比于排列方式,孔隙率对平均迂曲度的影响更大. 这从微观视角解释了图6(a)的实验结果. 上述模拟结果表明,迂曲度并非常数21/2,而是一个和孔隙率、颗粒排列方式、颗粒直径等因素相关的参数. 上述结果也显示,在相同孔隙率条件下,颗粒直径的影响小于2%. 因此在实际工程应用中,颗粒直径对迂曲度的影响可以忽略,影响迂曲度的因素主要为孔隙率、颗粒排列、孔隙大小和分布[34]. ...
Fine clay particle migration and deposition behavior in two-dimensional microfluidic models
1
2022
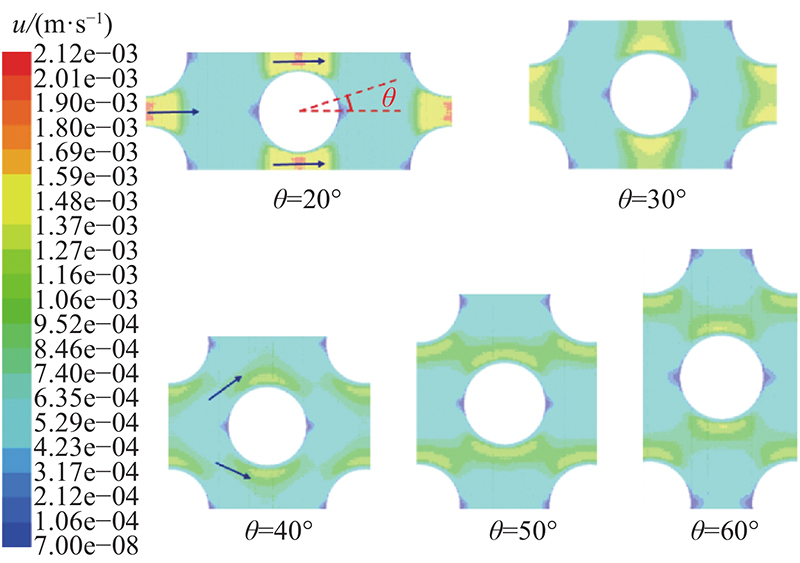
... 在相同孔隙率下,芯片模型微柱排列方式的各向异性将对芯片模型渗透率产生影响. 如图10所示,在孔隙率为0.60时,旋转角 $ \theta $分别是20°、30°、40°、50°和60°这5种微柱错开排列模式下的芯片模型数值模拟流速场云图. 随着旋转角的增大,微柱孔喉间的最大流速逐渐较小;在流动方向上,微柱颗粒的前后两端出现三角形状的“低速区”;在垂直流动方向上出现“高速区”、“低速区”面积远小于“高速区”面积; “高速区”随着旋转角的增大而减小,形状也由三角形变成“香蕉形”. 当孔隙中发生细颗粒迁移时,“低速区”极易形成颗粒堆积[35]. ...
A new model for determining mean structure parameters of fixed beds from pressure drop measurements: application to beds packed with parallelepipedal particles
1
1989
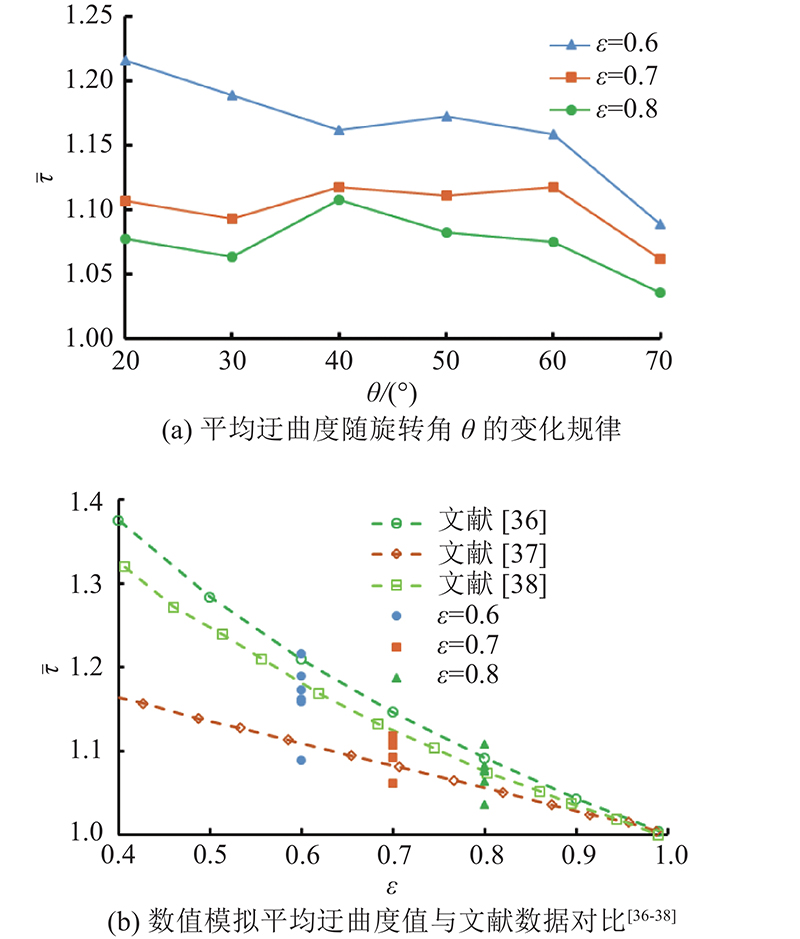
... 为了进一步探究流体在芯片模型中的流动特性,图12(a)展示芯片模型平均迂曲度随旋转角 $ \theta $的变化规律. 曲线表明迂曲度在 $ \theta =20{\text{°}} $时最大,在 $ \theta =70{\text{°}} $时最小. 在旋转角度相同情况下,孔隙率越小,迂曲度越大. 图12(b)所示为芯片模型平均迂曲度值与相关文献中的数据对比分析. Comiti等[36]提出的模型与旋转角较小时芯片模型的平均迂曲度值吻合较好.当旋转角较大时,芯片模型平均迂曲度值落在最下方,表明3种模型都不能单独预测该排列情况下的平均迂曲度值;当旋转角在 $ 30{\text{°}}\sim 60{\text{°}} $时,芯片模型平均迂曲度值均落在文献[37-38]中,具有较强的一致性. 每个模型的假设条件不同,参考文献中提出的迂曲度模型的适用对象并不具有普适性. 后期的研究方向可以聚焦于无序排列和三维颗粒堆积方面的实验和模拟. ...
Analytical tortuosity–porosity correlations for Sierpinski carpet fractal geometries
1
2015
... 为了进一步探究流体在芯片模型中的流动特性,图12(a)展示芯片模型平均迂曲度随旋转角 $ \theta $的变化规律. 曲线表明迂曲度在 $ \theta =20{\text{°}} $时最大,在 $ \theta =70{\text{°}} $时最小. 在旋转角度相同情况下,孔隙率越小,迂曲度越大. 图12(b)所示为芯片模型平均迂曲度值与相关文献中的数据对比分析. Comiti等[36]提出的模型与旋转角较小时芯片模型的平均迂曲度值吻合较好.当旋转角较大时,芯片模型平均迂曲度值落在最下方,表明3种模型都不能单独预测该排列情况下的平均迂曲度值;当旋转角在 $ 30{\text{°}}\sim 60{\text{°}} $时,芯片模型平均迂曲度值均落在文献[37-38]中,具有较强的一致性. 每个模型的假设条件不同,参考文献中提出的迂曲度模型的适用对象并不具有普适性. 后期的研究方向可以聚焦于无序排列和三维颗粒堆积方面的实验和模拟. ...
Boundary effects on the tortuosity and permeability of idealized porous media
1
2021
... 为了进一步探究流体在芯片模型中的流动特性,图12(a)展示芯片模型平均迂曲度随旋转角 $ \theta $的变化规律. 曲线表明迂曲度在 $ \theta =20{\text{°}} $时最大,在 $ \theta =70{\text{°}} $时最小. 在旋转角度相同情况下,孔隙率越小,迂曲度越大. 图12(b)所示为芯片模型平均迂曲度值与相关文献中的数据对比分析. Comiti等[36]提出的模型与旋转角较小时芯片模型的平均迂曲度值吻合较好.当旋转角较大时,芯片模型平均迂曲度值落在最下方,表明3种模型都不能单独预测该排列情况下的平均迂曲度值;当旋转角在 $ 30{\text{°}}\sim 60{\text{°}} $时,芯片模型平均迂曲度值均落在文献[37-38]中,具有较强的一致性. 每个模型的假设条件不同,参考文献中提出的迂曲度模型的适用对象并不具有普适性. 后期的研究方向可以聚焦于无序排列和三维颗粒堆积方面的实验和模拟. ...